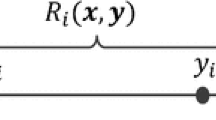A Novel Data Representation Based on Dissimilarity Increments

Abstract

Many pattern recognition techniques have been proposed, typically relying on feature spaces. However, recent studies have shown that different data representations, such as the dissimilarity space, can help in the knowledge discovering process, by generating more informative spaces. Still, different measures can be applied, leading to different data representations. This paper proposes the application of a second-order dissimilarity measure, which uses triplets of nearest neighbors, to generate a new dissimilarity space. In comparison with the traditional Euclidean distance, this new representation is best suited for the identification of natural data sparsity. It leads to a space that better describes the data, by reducing the overlap of the classes and by increasing the discriminative power of features. As a result, the application of clustering algorithms over the proposed dissimilarity space results in reduced error rates, when compared with either the original feature space or the Euclidean dissimilarity space. These conclusions are supported on experimental validation on benchmark datasets.

1 Introduction

The learning process encompasses developing computer methods to model categories/classes of objects or to assign objects to one of the different classes. In that sense, a representation of the objects is required, which can be a vector, string of symbols or even a graph. Afterwards, a decision rule may be constructed based on that representation of objects, and the objective is to discriminate between different classes achieving high accuracy values [1, 3, 8].

Typically, objects are represented by a set of features, which should characterize the objects and be relevant to discriminate among the classes; the Euclidean vector spaces are the most popular representation of objects [3]. A problem with the feature-based representation of objects is the difficulty to obtain a complete description of objects, forcing to an overlap of the classes, leading to an inefficient learning process. That difficulty in describing objects through a set of features is due to high-dimensional data or sometimes it is necessary to describe objects using continuous and categorical variables.

To overcome the limitations of feature-based representations, another representations of data can be used. One possibility is the dissimilarity representation, which is based on comparisons between pairs of objects [10]. This representation solves the problem of class overlap that exists in feature representations, since only identical objects have a dissimilarity of zero.

Also, a suitable dissimilarity measure can be used to compare pairs of objects, and dissimilarity vectors for each object are constructed to obtain the dissimilarity space. Measures that compare the entire objects may be considered or measures can be derived from raw measurements, strings or graphs. Defining features that can have a high discriminant power may be a difficult task for some applications (e.g. shape recognition) than define a dissimilarity measure.

Dissimilarities have been used in pattern recognition, either explicitly or implicitly, in many procedures, like in cluster analysis, which uses dissimilarities instead of feature spaces [14]. In the last years, based on the work of Pekalska and Duin [11], some classification methods for dissimilarity data have been proposed [2, 4, 13]. This type of classifiers are useful to tackle problems in computer vision, bioinformatics, information retrieval, natural language processing, among other fields [5, 9].

Moreover, the dissimilarity space can be constructed using a feature representation and some appropriate dissimilarity measure [4, 12]. This measure may be asymmetric and does not require to fulfill mathematical properties for metrics. Over the dissimilarity space, any classifier or clustering procedure that works in vector spaces can be applied.

The purpose of this paper is to present a novel dissimilarity representation of data, the dissimilarity increments space, based on a second-order dissimilarity measure, consisting on triplets of nearest neighbors [6]. This dissimilarity space is built by the increment in dissimilarity between an object and a set of representative objects, which are defined as an edge between a prototype and its nearest neighbor. To fairly compare the proposed dissimilarity space, an Euclidean space is built by relying on the Euclidean distance to measure the set of representative objects. Both dissimilarity spaces are used as feature-based dissimilarity spaces, which consist in representing each object as a vector of dissimilarities, and typical clustering algorithms are applied to those spaces.

To compare the spaces, we use two different approaches. We start by presenting an insightful characterization of the spaces by relying on a set of geometrical measures. Then we apply a set of unsupervised learning methods in order to analyze the spaces behavior under clustering problems. Experimental results with an extensive set of datasets show that the proposed second-order dissimilarity space leads to a substantial improvement in accuracy when compared to the original feature space and to the feature-based Euclidean space.

This paper is organized as follows: Sect. 2 explains how to build dissimilarity spaces, and proposes a new dissimilarity space based on a second-order dissimilarity measure – the dissimilarity increments space. Section 3 presents some measures to characterize each dissimilarity space and understand if a learning problem becomes easier in these spaces. The proposed dissimilarity increments space is evaluated in the context of unsupervised learning, in comparison with other dissimilarity spaces, in Sect. 4. Conclusions and final remarks are drawn in Sect. 5. The datasets used in the experimental evaluation of methods are described in appendix.

2 Dissimilarity Representation

A dissimilarity representation consists of a matrix with the dissimilarities between an object and a set of representative objects. Thus, the resulting dissimilarity matrix is considered as a set of row vectors, where each vector represents a direction from the dissimilarity space, whose dimension corresponds to the cardinality of the set of representative objects.

Let $X = \{\mathbf {x}_1,\ldots ,\mathbf {x}_n\}$ represent a set of objects. In general, $\mathbf {x}_i$ may not be a vector, but an image or signal. However, in this paper and given the datasets used in the experimental validation (see appendix), we assume that $\mathbf {x}_i$ is a feature vector in $\mathbb {R}^p$, $\mathbf {x}_i = [x_{i1} \ldots x_{ip}]$. Also, let $R = \{\mathbf {e}_1,\ldots ,\mathbf {e}_r\}$ be the set of representative or prototype objects, such that $R \subseteq X$.

In [11], a dissimilarity space is defined as a data-dependent mapping

$$\begin{aligned} D(\cdot ,R) : X \rightarrow \mathbb {R}^r, \end{aligned}$$

(1)

given a dissimilarity function. Therefore, each object $\mathbf {x}_i$ from the set X is described by a r-dimensional dissimilarity vector

$$\begin{aligned} D(\mathbf {x}_i,R) = [d(\mathbf {x}_i,\mathbf {e}_1) \ldots d(\mathbf {x}_i,\mathbf {e}_r)], \end{aligned}$$

(2)

where $d(\cdot ,\cdot )$ is a dissimilarity measure. So, $D(\mathbf {x}_i,R)$ is a row of the $n\times r$ dissimilarity matrix D, obtaining the dissimilarity space. Now, we define the dissimilarity space as a vector space Y by $Y = D$, where the i-th object is represented by the dissimilarity vector of the $D_{ij}$ values.

For simplicity, we assume that R is the entire set X, meaning that all objects of X are used as representatives. Therefore, in this paper, the dissimilarity space is represented as a $n \times n$ dissimilarity matrix.

In this paper, we consider two dissimilarity spaces: the Euclidean space and the Dinc space, detailed below.

Euclidean space. This space is obtained assuming that $d(\cdot ,\cdot )$ in (2) is the Euclidean distance,

$$\begin{aligned} d(\mathbf {x}_i,\mathbf {e}_j) = \left( \sum _{k=1}^p (x_{ik} - e_{jk})^2 \right) ^{1/2}. \end{aligned}$$

(3)

Thus, each element, $D_{ij}$, of the dissimilarity matrix D, is the Euclidean distance between i-th and j-th objects.

Dinc space. This space is obtained using a second-order dissimilarity measure between triplets of neighboring objects, and its explained in detail in Sect. 2.1.

2.1 Dissimilarity Increments Space

Firstly, we need to define the concept of dissimilarity increments. Given $\mathbf {x}_i$, $(\mathbf {x}_i,\mathbf {x}_j,\mathbf {x}_k)$ is a triplet of nearest neighbors, obtained as follows:

$$\begin{aligned} (\mathbf {x}_i,\mathbf {x}_j,\mathbf {x}_k)&- \text { nearest neighbor triplet} \\ \mathbf {x}_j&: j = \arg \min _l \{ d(\mathbf {x}_l,\mathbf {x}_i), l \ne i \} \\ \mathbf {x}_k&: k = \arg \min _l \{ d(\mathbf {x}_l,\mathbf {x}_j), l \ne i, l \ne j \}. \end{aligned}$$

The dissimilarity increments [6] between neighboring objects is defined as

$$\begin{aligned} d_\text {inc}(\mathbf {x}_i,\mathbf {x}_j,\mathbf {x}_k) = \left| d(\mathbf {x}_i,\mathbf {x}_j) - d(\mathbf {x}_j,\mathbf {x}_k) \right| , \end{aligned}$$

(4)

where $d(\cdot ,\cdot )$ is any dissimilarity measure between pairs of objects; in this paper, we assume that $d(\cdot ,\cdot )$ is the Euclidean distance.

This measure gives information about the structure of a dataset compared to pairwise distances, i.e. the dissimilarity increments between neighboring objects should not occur with abrupt changes, and between well separated classes will have higher values. Moreover, this measure can identify easily objects in a sparse class, while most of the distance measures used in the literature discard objects that are far apart in a sparse class.

We propose to define the set of representative objects as edges between two specific objects, i.e., a representative object $\mathbf {e}_j$ is an edge between a prototype $\mathbf{m}_j$ (a sample of the dataset) and its nearest neighbor $\mathbf {x}_{\mathbf{m}_j}$. So, $d(\mathbf {e}_j)$ is the weight of that edge, i.e. $d(\mathbf {e}_j) = d(\mathbf{m}_j,\mathbf {x}_{\mathbf{m}_j})$. Moreover, the distance between any object $\mathbf {x}_i$ and the representative object $\mathbf {e}_j$ is defined as

$$\begin{aligned} d(\mathbf {x}_i,\mathbf {e}_j) = \min \{ d(\mathbf {x}_i,\mathbf{m}_j), d(\mathbf {x}_i,\mathbf {x}_{\mathbf{m}_j}) \}. \end{aligned}$$

(5)

Furthermore, we propose a new representation of data based on the dissimilarity increments measure, called dissimilarity increments space and we will refer to that space as Dinc space. Similar to the Euclidean space, each object is described by a n-dimensional dissimilarity vector (2). However, $d(\cdot ,\cdot )$ is no longer the Euclidean distance, but a dissimilarity increment between each object $\mathbf {x}_i$ and a representative object $\mathbf {e}_j$ (see Fig. 1 for an example how to compute the elements in Dinc space). Thus, the (i, j)-th element of our dissimilarity space is defined as

$$\begin{aligned} D(\mathbf {x}_i,\mathbf {e}_j) = | d(\mathbf {x}_i,\mathbf {e}_j) - d(\mathbf {e}_j) |. \end{aligned}$$

(6)

Fig. 1.

Set of patterns to illustrate how to compute elements from the Dinc space D and to demonstrate its asymmetry. If a is a prototype, $e_a$ is the representative object constructed as an edge between a and its nearest neighbor b. Then, $D(c,e_a)$ is the dissimilarity increment between c and the representative object, $e_a$, computed from (6). $D(c,e_a) \ne D(a,e_c)$ since different triplets of patterns are used to compute D.

From (6), it is easy to see that the dissimilarity matrix D is non-negative. Moreover, D is asymmetric, and to see that consider a set of patterns distributed as shown in Fig. 1. If a is a prototype, $e_a$ is an edge between a and its nearest neighbor b, and will be the representative object. Now, the dissimilarity increment between c and the representative object, $e_a$, is $D(c,e_a)$. On other hand, when c is a prototype, the representative object, $e_c$, is the edge between c and its nearest neighbor d, and, thus, $D(a,e_c)$ is the dissimilarity increment between a and the representative object. Therefore, $D(c,e_a) \ne D(a,e_c)$ (see Fig. 1).

3 Characterization of the Dissimilarity Spaces

So far, we constructed feature-based dissimilarity spaces to represent a set of objects. Both dissimilarity spaces, Euclidean and Dinc spaces, are constructed on top of feature spaces. In the following we will characterize these spaces based on some measures to characterize the geometrical complexity of classification problems proposed by Ho et al. [7]. Those measures are based on the analysis of different classifiers to understand the separability of classes or even the geometry, topology and density of manifolds. Thus, we used some of those measures to understand if a learning problem in the dissimilarity space becomes easier than in the feature space. According to [7], those measures can be divided into three categories:

• 1. Measures of overlaps in feature values from different classes focus on how good the features are in separating the classes. These type of measures examine the range and spread of values in the dataset within each class, and check for overlaps among different classes. Here, we only consider two measures: the maximum Fisher’s discriminant ratio (F1) and the collective feature efficiency (F4). F1 computes the maximum discriminant power of each feature, and high values of this measure indicates that, at least, one of the features turns the problem of separating the samples of different classes easier. On the other hand, F4 computes the discriminative power of all the features.

• 2. Measures of separability of classes evaluate, based on the existence and shape of class boundary, to what extent two classes are separable. Here, we consider three measures: the training error of a linear classifier (L2), the ratio average intra/inter class nearest neighbor distance (N2) and the leave-one-out error rate of the one-nearest neighbor classifier (N3). L2 shows if the classes of the training data are linearly separable. N2 compares the within class distances with distances to the nearest neighbors of other classes, and higher values indicate that samples of the same class are disperse. N3 verifies how close the objects of different classes are, and lower values means that there is a high gap in the class boundary.

• 3. Measures of geometry, topology, and density of manifolds characterize classes, assuming that each class is composed by a single or multiple manifolds, and their shape and position determines how well two classes are separated. Here, we considered two measures: the nonlinearity of a linear classifier (L3) and the nonlinearity of the one-nearest neighbor classifier (N4). L3 measures, for linearly separable problems, the alignment of the decision surface of linear classifiers with the class boundary, and N4 measures the alignment of the nearest neighbor boundary with the shape of the gap or overlap between the convex hulls of the classes.

Some of the measures are designed for two-class problems, namely L2 and L3. In this paper, we consider the average value between one versus all classes problems for datasets with more than two classes. Table 1 presents the results of the measures presented above, over the datasets described in the appendix, in the Feature space and in both dissimilarity spaces.

Table 1. Measures to characterize the geometrical complexity of classification problems in the original feature space, and in both dissimilarity spaces considered in this paper, Euclidean space and Dinc space. High values for F1 and F4 is better (thus the $\uparrow$ sign), while lower values for the remaining measures is better ($\downarrow$ sign). The values presented correspond to median (Med), minimum (Min), maximum (Max), first and third quartiles (Q1 and Q3, respectively), over all datasets. The best space (on median) according to each geometrical measure are boldfaced.

From Table 1 we notice that both dissimilarity spaces have high discriminant power of features in separating the classes, corresponding to higher values of F1 and F4 than the Feature space. Moreover, F4 in the Feature space has a minimum of zero and that value increased in both dissimilarity spaces, which means that the collective feature efficiency increased. Thus, the datasets are better described in the dissimilarity spaces, even with the increase of dimensionality on those spaces, compared to the Feature space.

In both dissimilarity spaces, there is a decrease in L2 and N2 values, indicating that there exists less overlap between the classes, which may facilitate the learner to separate the samples of different classes. However, in both dissimilarity spaces, the measure for geometry and topology of the manifold N4 has higher values, indicating that, even if the classes are more separable they are nonlinearly separable by the one-nearest neighbor classifier.

4 Unsupervised Learning in Dissimilarity Spaces

Typically, dissimilarity measures have been used in cluster analysis or in classification, as a tool to decide which objects are closer to each other. They also can be used to describe objects, and, consequently, build dissimilarity spaces. In this paper we proposed a new dissimilarity space based on a second-order dissimilarity measure. We further investigate if clustering results can be improved by transforming a feature space into a dissimilarity space, namely the Euclidean space and the Dinc space.

We applied, to the datasets described in appendix, four hierarchical clustering algorithms: single-link (SL), average-link (AL), centroid-link (CeL) and median-link (MeL). Moreover, we set the number of clusters in each clustering algorithm as being equal to the true number of classes (see Table 4). The results presented in this section are error rates, i.e. the percentage of misclassified samples, and number of datasets with better error rates (see Table 2). Also, a statistical significance difference between each space, in each clustering algorithm considered, is achieved by applying the Wilcoxon signed rank test over all datasets [15]. A statistical significance difference is achieved for p-value $<$ 0.05.

Table 2. Number of datasets with better error rate, for single-link (SL), average-link (AL), centroid-link (CeL), and median-link (MeL), when comparing pairs of spaces. “=” means equal error rate in both spaces. Mean difference indicates that, when one space wins, it is better on average x% than the other space. Last column presents the p-value for the Wilcoxon signed rank test between two spaces, in each clustering algorithm. A statistical significance difference is achieved when p-value $<$ 0.05.

Figure 2 shows the error rates, for each clustering algorithm, comparing the Feature space with the Euclidean space. Notice that if the points (which represents a dataset) in the plots are lying on the line $y=x$, this means that the error rate are equal in both spaces. This situation happens for SL: almost all points (datasets) have equal error in both spaces. Furthermore, all the remaining clustering algorithms are better in the Euclidean space compared to the Feature space, being the CeL the one with better error rates for the Euclidean space.

Fig. 2.

Error rates with different clustering algorithms when comparing the Feature space with the Euclidean space. Dots represent datasets and the solid line, $y=x$, indicate equal error rate between the two spaces. The dash line represents a linear regression line forced to be parallel to $y=x$, to indicate which space is better (on average) and how much is the improvement.

Table 2 presents the number of datasets that have lower error rates for each clustering algorithm. We notice that the Euclidean space is always better than the Feature space, and that difference is statistically significant (p-value $<$ 0.01), except when we apply SL (p-value = 0.355). For all the remaining clustering algorithms, the Euclidean space is better in more than 20 datasets compared to the Feature space. The most significant difference on average error rates occurs for CeL, because when the Feature space is better than the Euclidean space, its improvement is on average 2.9 %, and it is better on average 16.1 %, when the Euclidean space is better than the Feature space.

Figure 3 shows the error rates of the comparison between the Feature space and the Dinc space. Again, SL seems to have similar performance in both spaces, except for three datasets. However, all the remaining clustering algorithms perform better in the Dinc space, with the highest improvement for the CeL. From Table 2, the Dinc space wins the Feature space in more than 20 datasets out of 36 when we apply any clustering algorithm, except SL, which it wins, by 12 out of 36 datasets against 9 datasets. When the Dinc space wins, it is better over 11 % on average than the Feature space for any clustering algorithm, and around 3 % when the Feature space wins, except for SL. The differences between Dinc and Feature spaces are statistically significant for all clustering algorithms, except for SL, since p-value $<$ 0.01.

Fig. 3.

Error rates with different clustering algorithms when comparing the Feature space with the Dinc space. Dots represent datasets and the solid line, $y=x$, indicate equal error rate between the two spaces. The dash line represents a linear regression line forced to be parallel to $y=x$, to indicate which space is better (on average) and how much is the improvement.

So far we compared both dissimilarity spaces with the Feature space. Now, we present in Fig. 4 the comparison between both dissimilarity spaces. All clustering algorithms have similar error rates in both dissimilarity spaces. However, MeL has a tendency to have lower error rates in the Dinc space. MeL wins in 18 out of 36 datasets, for the Dinc space, against 8 out of 36 datasets for the Euclidean space, corresponding to an improvement of 7.1 % on average, when the Dinc space is better and 4.0 % on average when the Euclidean space is better (see Table 2). There are statistically significant differences between Euclidean and Dinc spaces (p-value $<$ 0.05) for CeL and MeL. For AL and SL, the differences are not statistically significant, as can be seen from the higher number of datasets with equal error rate between the two spaces.

Fig. 4.

Error rates with different clustering algorithms when comparing the Euclidean space with the Dinc space. Dots represent datasets and the solid line, $y=x$, indicate equal error rate between the two spaces. The dash line represents a linear regression line forced to be parallel to $y=x$, to indicate which space is better (on average) and how much is the improvement.

Table 3 presents the correlations between the measures of geometrical complexity mentioned in Sect. 3 and the error rates of each clustering algorithm. We notice that there exists a negative correlation between F1 and the error rate of each clustering algorithm, and that correlation is higher in the dissimilarity spaces, indicating that whenever F1 increases, the error rate decreases. In fact, from Table 1, F1 is higher in both dissimilarity spaces than in the Feature space, and looking at the plots of the error rates between the Feature space and one of the dissimilarity spaces (Figs. 2 and 3), the dissimilarity spaces have lower error rates, except for SL.

Table 3. Correlations between measures of geometrical complexity and error rates of each clustering algorithm (single-link (SL), average-link (AL), centroid-link (CeL), and median-link (MeL) for each space).

Figures 3 and 4 shows that, for CeL and MeL, the Dinc space is better than the Feature space and the Euclidean space. The correlations between L3 and the error rates may explain these results. The Feature and Euclidean spaces have lower correlations, than the Dinc space and those correlations are positive correlations. This means that if L3 decreases, then the error rate decreases, and L3 has a lower value in the Dinc space compared to the other two spaces (see Table 1). Moreover, N2 have higher and positive correlation in both dissimilarity spaces compared to the Feature space, indicating that whenever N2 decreases, the error rate also decreases. Analysing Figs. 2 and 3, we notice that AL, CeL and MeL have better performances than the Feature space. Accordingly, CeL and MeL have a better performance in both dissimilarity spaces, however the Dinc space shows a slightly improvement compared to the Euclidean space.

Table 4. Datasets used in the analysis of dissimilarity spaces. N is the number of samples, p the dimension of the feature space and Nc the number of classes.

Overall, if we do not consider SL, F1, N2, N3, N4 and L3 have a higher correlation in the dissimilarity spaces than in the Feature space, and the Dinc space has higher correlation values than the Euclidean space. This suggests that, the dissimilarity spaces, especially the Dinc space, have better discriminant features and the classes are easier to separate using clustering techniques. Although we increased the dimensionality of the dissimilarity spaces, the assigning of samples to each class by a clustering algorithm seems much effective.

5 Conclusions

In this paper we proposed a novel dissimilarity representation for data based on a second-order dissimilarity measure. That measure is computed over triplets of nearest neighbors and has some advantages over pairwise dissimilarities, namely it can identify sparse classes. Each element of the Dinc space is a dissimilarity increment between an object and a set of representative objects, which are defined as an edge between an object and its nearest neighbor.

In this paper we considered that the set of representative objects corresponds to the entire dataset, which increased the dimensionality of the each dissimilarity space. Although, the dimensionality of the Dinc space was higher than the Feature space, we have shown that features in the Dinc space are more discriminative and the overlap of the classes has decreased, which facilitate the learning task to separate the objects from different classes. In future work, we will study different techniques for prototype selection, in order to obtain a smaller set of representative objects, leading to lower dimensionality of dissimilarity spaces.

Unsupervised learning techniques were also applied, namely hierarchical clustering algorithms, to the Dinc space, the original Feature space and to a dissimilarity space, built using the Euclidean distance. Overall, the Dinc space had lower error rates compared to the other two spaces, especially for centroid-link and median-link.

Appendix: Datasets

A total of 36 benchmark datasets from two repositories are used for the experimental evaluation of methods. The majority of the datasets are from the UCI Machine Learning Repository¹, and only a few datasets are from the 20-Newsgroups database². A summary of the datasets in terms of number of samples, dimension of the feature space and number of classes is presented in Table 4.