Acceptance Sampling with R

Abstract

Undoubtedly, an effective but expensive way of providing conforming items to a customer is making a complete inspection of all items before shipping. In an ideal situation, a process designed to assure zero defects would not need inspection at all. In practice, a compromise between these two extremes is attained, and acceptance sampling is the quality control technique that allows reducing the level of inspection according to the process performance. This chapter shows how to apply acceptance sampling using R and the related ISO standards.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The basic problem associated with acceptance sampling is as follows: whenever a company receives a shipment of products (typically raw material) from a supplier a decision has to be made about the acceptance or rejection of the product. In order to make such a decision, the company selects a sample out of the lot, measures a specified quality characteristic and, based on the results of the inspection decides among:

• Accepting the lot (and send it to the production line);

• Rejecting the lot (and send it back to the supplier);

• Take another sample before deciding (if results are not conclusive).

Sampling plans can be classified in attribute and variables. The attribute case corresponds to the situation where the inspection simply determines if the item is “good” or “bad,” this means it complies or not with a certain specification . This kind of inspection is cheaper, but larger sample sizes are required. The variable case, on the other hand, corresponds to the situation where the quality characteristic is measured, thus allowing the inspector to decide based on the value obtained. This kind of inspection is more expensive, but smaller sample sizes are required.

In practice, the procedure to be followed is very simple; whenever the company receives a shipment of N units, a random sample of n units is taken from the lot and if d or less units happen to be considered as defective then the lot is accepted. The procedure described corresponds to the case of attribute inspection; the variable case is somewhat more sophisticated but conceptually equivalent. For details on sampling methods, see Chapter 6

As any other hypothesis test, acceptance sampling is not a perfect tool but just a useful one. There always exists the possibility of accepting a lot containing too many defective items, as well as rejecting another one with very few defectives. Fortunately, an upper bound for these two probabilities can be set up in all cases by adequately selecting the parameters n and d.

This chapter provides the necessary background to understand the fundamental ideas of acceptance sampling plans. Section 7.1 describes the philosophy of the acceptance sampling problem. Sections 7.2 and 7.3, respectively, develop the basic computational methods for attribute and variable acceptance sampling as well as the way to implement them with R. Finally, Sect.7.4 provides a selection of the ISO standards available to help users in the practice of acceptance sampling.

2 Sampling Plans for Attributes

As it was stated in Sect. 7.1 a sample plan for attributes is defined by means of the following three parameters:

N :

lot size;

n :

sample size (taken at random from the lot);

d :

maximum number of defective units in the sample for acceptance.

The result of the inspection of the sample is:

x :

number of defectives found in the sample

The decision rule is:

• 1. Accept the lot if x ≤ d;

• 2. Reject the lot if x > d.

This kind of sampling plans, the simplest ones, are called single sampling plans because the lot’s fate is decided based on the results of a unique sample. There exist other kinds of sampling plans where two values of d are established; the lot is accepted if $x \leq d_{\mathrm{lower}}$; rejected if x ≥ d _upper; and a second sample taken if $d_{\mathrm{lower}} < x < d_{\mathrm{upper}}$. This kind of sampling plans are called double sampling plans.

The performance of a determined sampling plan is described by its operating characteristic (OC) curve. This curve is a graphical representation of the probability of accepting the lot as a function of the lot’s defective fraction. This probability can be computed by means of the binomial probability distribution (see Chapter 5), as long as the lot size be much larger than the sample size (n∕N < 0. 1):

$$\displaystyle{ P_{a} =\sum _{ x=0}^{d} \frac{n!} {x!(n - x)!}p^{x}(1 - p)^{n-x}, }$$

(7.1)

where P _a stands for the probability of accepting the lot and p stands for the lot’s fraction defective.

Example 7.1.

single sampling plan.

If we assume that n = 100 and d = 5, the resulting OC curve should look like Figure 7.1, which has been produced with the following R code:

Fig. 7.1

OC curve for a simple sampling plan. The parameters of this OC curve are n = 100, d = 5

 □ 

There is a specific OC curve for every different sample plan; this means that if

we change either n or d, the curve will also change. But the general behavior of all the curves will be similar; they start at P _a  = 1 for p = 0, decrease more or less rapidly as p increases, and finish at P _a  = 0 for p = 1.

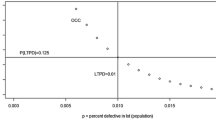
Two points in the OC curve are of special interest. The point of view of the producer is that he requires a sampling plan having a high probability of acceptance for a lot with a low (agreed) defective fraction. This low defective fraction is called “acceptable quality level” (AQL), and the probability of such a good quality lot being rejected is called “producer’s risk” (α). On the other hand, the point of view of the customer is that he requires a sampling plan having a high probability of rejection for a lot with a high (agreed) defective fraction. This high defective fraction is called “lot tolerance percent defective” (LTPD), and the probability of such a low quality lot being accepted is called “consumer’s risk” (β). Figure 7.2 illustrates these two probabilities for a typical OC curve.

Fig. 7.2

OC curve risks illustration. The fraction defective values AQL and LTPD are agreed. A sampling plan yields then a producer’s risk α and a consumer’s risk β

The problem with acceptance sampling plans is then to choose n and d in such a way that reasonable values for α and β are achieved for AQL and LTPD. In mathematical terms, the problem is equivalent to solving the following system of equations, where the unknowns are n and d:

$$\displaystyle\begin{array}{rcl} 1-\alpha & =& \sum _{x=0}^{d} \frac{n!} {x!(n - x)!}p_{\mathrm{AQL}}^{x}(1 - p_{\mathrm{ AQL}})^{n-x}, {}\\ \beta & =& \sum _{x=0}^{d} \frac{n!} {x!(n - x)!}p_{\mathrm{LTPD}}^{x}(1 - p_{\mathrm{ LTPD}})^{n-x}. {}\\ \end{array}$$

The solution to this system is not easy and even not feasible all the times, so that in general an acceptable solution will be as far as we could go. For “acceptable” solution we understand a sampling plan that leads to actual α and β values close enough to target values. Traditionally, nomographs (also called nomograms) have been used to get approximate values of n and d given α and β with paper and pencil, see, for example, [15]. Computational methods can be used, though. R and a simple iterative method will greatly help in finding such an acceptable solution. The iterative method we suggest is as follows:

Step 1):

Choose your target α and β values.

Step 2):

Start with a sampling plan like n = 10 and d = 1. Calculate α and β values with R. Normally, such an initial plan will give α _actual close to α _target and $\beta _{\mathrm{actual}} >>\beta _{\mathrm{target}}$.

Step 3):

There are two possibilities: If $\alpha _{\mathrm{actual}} >>\alpha _{\mathrm{target}}$, then change d to d + 1. Calculate α and β values with R and repeat Step 3.

Or

If $\beta _{\mathrm{actual}} >>\beta _{\mathrm{target}}$, then change n to n +δ _n . Calculate α and β values with R and repeat Step 3.

Normally, δ _n should range between 10 to 50 depending on how large be the difference between α _actual and α _target. Larger δ _n correspond to larger differences.

Step 4):

If the solution happens to be feasible, final values obtained for α _actual and β _actual will be close to their target values. If not, judgement will have to be used in order to decide the best values for n and d.

Example 7.2.

Iterative method to select a sampling plan.

An example will illustrate this method. Let us suppose we need a sampling plan that will provide us with α _target = 0. 05 for AQL = 5 % and β _target = 0. 10 for LTPD = 16 %. The following R code runs the method above getting the result in Table 7.1.

Table 7.1 Iterative sampling plan selection method

Note that we fix 10 iterations and make a decision depending on which risk is farther away from the target. A customized function can be programmed taking into account the specific problem at hand. In the eighth iteration we get a plan that yields producer’s and customer’s risks very close to the targets.

 □ 

In addition to the iterative method described above, we can use the AcceptanceSampling R package [14] . Function OC2c plots OC curves for attribute acceptance sampling plans, and function find.plan finds a simple sampling plan with smallest sample size.

Example 7.3.

OC curve and acceptance sampling plan with the AcceptanceSampling R package.

The following code gets the OC curve for the sampling plan in Example 7.1, i.e., with n = 100 and d = 5. The result is in Fig. 7.3.

Fig. 7.3

OC curve with the AcceptanceSampling package. Graphical parameters can be added to customize the plot

Now let us compute the sampling plan proposed by the find.plan function for the requirements in Example 7.2, i.e., α = 0. 05 for AQL = 5 % and β = 0. 10 for LTPD = 16 %. The arguments of the find.plan function are the producer risk point (PRP) and consumer risk point (CRP). Each argument should be a vector of two numbers, the first number being AQL or LTPD, and the second one being the corresponding probability of acceptance, i.e., 1 −α and β, respectively.

Thus, the proposed plan is drawing samples of size 64 and reject the lot if there are seven or more defectives. We can create an object of class OC2c for this plan in order to plot the OC curve (see Fig. 7.4) and assess its performance. The assess function returns the plan and its probabilities of acceptance, and compares them with the required ones.

Fig. 7.4

OC curve for the found plan. The found plan can be plotted and assessed

Note that the result is slightly different to the one obtained in Example 7.2. Both are close to risk targets and probably acceptable approximations for both parts.

 □ 

Throughout this section, the assumption was made that the binomial probability distribution could be used for the purpose of calculating the probabilities associated with the sampling process. As it was stated before, this assumption holds as long as the sample size be small in comparison with the lot size (n < < N). This will therefore guarantee that the probability of finding a defect in one sampled item will remain approximately constant. But in the general case this assumption is not true, and the more accurate hypergeometric distribution, which was described in Chapter 5 should be employed instead. Nevertheless, the methods are the same, just changing probability functions to the appropriate distribution. As for the AcceptanceSampling package, functions OC2c and find.plan accept a type argument whose possible values are binomial, hypergeom, poisson, and normal (the latter for sampling plans for variables in the next section).

3 Sampling Plans for Variables

A variable sampling plan corresponds to the situation where a certain quality characteristic is measured in a continuous scale for every item selected from the lot. The distinction between a “good” and a “bad” individual value results from its comparison with the specified limit. Technical specifications may incorporate a lower (LSL) or an upper (USL) specification limit. In some cases two simultaneous limits may exist. But in variable sampling we are not specially interested in individual values. What is done is to compute the mean of the measured values and calculate the statistic

$$\displaystyle{ Z_{\mathrm{USL}} = \frac{\mathrm{USL} -\overline{x}} {\sigma }, }$$

(7.2)

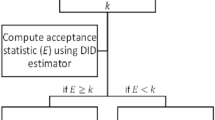
where USL is the Upper Specification Limit, $\overline{x}$ is the sample mean, and σ is the process standard deviation. This case corresponds to the situation where only the USL exists, and the standard deviation of the distribution of the individual values is assumed to be known. If the so calculated Z _USL value is larger than k (a value known as “acceptability constant”), then the lot may be accepted. Fig. 7.5 illustrates this concept.

Fig. 7.5

Variables acceptance sampling illustration. Maximum allowable defective fraction and acceptability constant

In a way equivalent to what is done for attribute sampling, OC curves are generated for variable sampling. The two elements that constitute a variable sampling plan, namely: n, the sample size, and k, the acceptability constant, are calculated to assure that:

• a) For a lot with a low (agreed) fraction defective (AQL), the probability of rejection (producer’s risk) is equal to α;

• b) For a lot with a high (agreed) fraction defective (LTPD), the probability of acceptance (consumer’s risk) is equal to β.

Conceptually, the situation is illustrated in Figures 7.6 and 7.7. Figure 7.6 corresponds to the situation where the population has a defective fraction p ₁ equal to AQL, whereas Figure 7.7 corresponds to the situation where the population has a defective fraction p ₂ equal to LTPD.

Fig. 7.6

Probability of acceptance when p=AQL. Probability of acceptance for a population with defective fraction equal to AQL

Fig. 7.7

Probability of acceptance when p=LPTD. Probability of acceptance for a population with defective fraction equal to LPTD

Sample size and the acceptability constant are chosen in such a way that the probability of acceptance approximately corresponds to (1 −α) for Figure 7.6 and (β) for Figure 7.7. Note that sample size has a clear effect on sample mean distribution variance, as long as

$$\displaystyle{ \sigma _{\mathrm{mean}} = \frac{\sigma _{\mathrm{individual}}} {\sqrt{n}}. }$$

The resulting formulae corresponding to the case when there is a single specification limit and the standard deviation is known are:

$$\displaystyle{ n = \left ( \frac{Z_{\alpha } + Z_{\beta }} {Z_{1} - Z_{2}}\right )^{2}\quad \text{and}\quad k = \frac{K_{1} + K_{2}} {2}, }$$

where:

$$\displaystyle{K_{1} = Z_{1} - \frac{Z_{\alpha }} {\sqrt{n}},\quad K_{2} = Z_{2} + \frac{Z_{\beta }} {\sqrt{n}},}$$

and:

Z ₁ :

is the (1 − p ₁) × 100 percentile of the standard normal distribution;

p ₁ :

is the AQL;

Z ₂ :

is the (1 − p ₂) × 100 percentile of the standard normal distribution;

p ₂ :

is the LTPD;

Z _α :

is the (1 −α) × 100 percentile of the standard normal distribution;

Z _β :

is the (1 −β) × 100 percentile of the standard normal distribution.

Example 7.4.

Variable acceptance sampling. Known standard deviation.

A simple example will illustrate how these formulae are implemented in R. Let us suppose we wish to develop a variable sample plan where:

AQL:

p ₁ = 1 %

LTPD:

p ₂ = 5 %

producer’s risk:

α = 5 %

consumer’s risk:

β = 10 %

σ :

assumed known

To find the sampling plan for these requirements, we use again the find.plan function. In this case, we need to add a new argument to the function call, namely type, in order to get the sampling plan for continuous variables.

Thus, the sampling plan is n = 19, k = 1. 949. □ 

In general, for a quality characteristic with only an upper specification limit (USL), we would proceed with the implementation of an acceptance plan as follows:

• 1. Take random samples of n items from each lot;

• 2. Compute the sample mean $\overline{x}$;

• 3. Compute the Z _USL value in Eq. (7.2);

• 4. Compare Z _USL with k;

• 5. Decide whether to accept (Z _USL > k) or reject (Z _USL ≤ k) the lot.

Example 7.5.

Variable acceptance sampling. Implementation for the metal plates thickness example.

A numerical example will illustrate the procedure. Let us simulate the process described in Example 5.1 of Chapter 5. The quality characteristic was the thickness of a certain steel plate produced in a manufacturing plant. Nominal thickness of this product was 0.75 in. Let us assume that the standard deviation is known and equal to 0.05, and the USL is 1 in. A simulated sample of this process can be obtained with the following code:

Now we compute the sample mean and the Z _USL value as follows:

As Z _USL > k, this lot must be accepted. We suggest the reader to run this simulation for different values of the mean and standard deviation and see how lots are rejected as mean shifts or increase in variation occur. The following convenient function helps automate this decision process¹:

Thus, if a new sample whose mean is 0.92 is drawn, then the lot should be rejected.

 □ 

In the example above, we assumed that the standard deviation of the population was known. If this is not the case, the sampling plan must be more conservative as we have less knowledge about the process. The resulting formulae corresponding to the case when there is a single specification limit and the standard deviation is unknown are:

$$\displaystyle{ n = \left (1 + \frac{k^{2}} {2} \right )\left ( \frac{Z_{\alpha } + Z_{\beta }} {Z_{1} - Z_{2}}\right )^{2}\quad \text{and}\quad k = \frac{Z_{\alpha }Z_{2} + Z_{\beta }Z_{1}} {Z_{\alpha } + Z_{\beta }}. }$$

Example 7.6.

Variable acceptance sampling (cont). Unknown standard deviation.

If the standard deviation in Example 7.4 is unknown, then the sampling plan corresponding with the conditions:

AQL:

p ₁ = 1 %

LTPD:

p ₂ = 5 %

producer’s risk:

α = 5 %

consumer’s risk:

β = 10 %

σ :

assumed unknown

is obtained with the following code:

Notice that we only have to change the s.type argument in the find.plan function (by default "known"). Now we need much more items to be sampled in order to achieve the objectives. We can simulate a new sample from our production process, but now we need to estimate σ in Eq. (7.2) through the sample standard deviation s.

 □ 

In this chapter we have assumed a smaller-the-better quality characteristic. In the case when the quality characteristic is a larger-the-better one, we have only a lower specification limit (LSL), and the procedure is the same we have explained so far just using $Z_{\mathrm{LSL}} = \frac{\overline{x}-\mathrm{LSL}} {\sigma }$ instead of Eq. (7.2). When both limits exist (nominal-is-best characteristic), both Z _USL and Z _LSL must be larger than k in order to accept the lot. The computation of k for different situations may vary depending on the software used and the specific model that applies. Some of these models can be found in the corresponding ISO standards (see the following section) and all of them can be implemented with R similarly to what we have done in this chapter. In addition to numerical computations, ISO standards provide a set of tabulated sampling plans given the most common values for producer and customer risks, AQL, and LTPD. Moreover, different rules to change from normal to reduced and rigorous sampling can also be applied in sequential plans.

We have focused on simple sampling plans for both attributes and variables. There exist more complex sampling plans which are out of the scope of this book, such as double, multiple, or sequential plans. Double and multiple sampling plans for attributes can be created and assessed with the AcceptanceSampling R package just providing sample sizes n _i and maximum number of defects d _i for each i stage as vectors to the OC2c function.

4 ISO Standards for Acceptance Sampling and R

The complete list of Standards related to the topic addressed in this chapter can be found from Subcommittee SC5, ISO/TC 69/SC 5—acceptance sampling. The most relevant of them are in the following.

• ISO 2859-1:1999 Sampling procedures for inspection by attributes – Part 1: Sampling schemes indexed by acceptance quality limit (AQL) for lot-by-lot inspection [8] . This International Standard specifies an acceptance sampling system for inspection by attributes. It is indexed in terms of the AQL. Its purpose is to induce a supplier through the economic and psychological pressure of lot non-acceptance to maintain a process average at least as good as the specified AQL, while at the same time providing an upper limit for the risk to the consumer of accepting the occasional poor lot.

• ISO 2859-3:2005 Sampling procedures for inspection by attributes – Part 3: Skip-lot sampling procedures [9] .

  This International Standard specifies generic skip-lot sampling procedures for acceptance inspection by attributes. The purpose of these procedures is to provide a way of reducing the inspection effort on products of high quality submitted by a supplier who has a satisfactory quality assurance system and effective quality controls. The reduction in inspection effort is achieved by determining at random, with a specified probability, whether a lot presented for inspection will be accepted without inspection.

• ISO 2859-5:2005 Sampling procedures for inspection by attributes – Part 5: System of sequential sampling plans indexed by AQL for lot-by-lot inspection [10] .

  This International Standard contains sequential sampling schemes that supplement the ISO 2859-1 acceptance sampling system for inspection by attributes, whereby a supplier, through the economic and psychological pressure of lot non-acceptance, can maintain a process average at least as good as the specified AQL, while at the same time provide an upper limit for the risk to the consumer of accepting the occasional poor lot.

• ISO 3951-1:2013 Sampling procedures for inspection by variables – Part 1: Specification for single sampling plans indexed by AQL for lot-by-lot inspection for a single quality characteristic and a single AQL [6] .

  This International Standard specifies an acceptance sampling system of single sampling plans for inspection by variables. It is indexed in terms of the AQL and is designed for users who have simple requirements.

• ISO 3951-2:2013 Sampling procedures for inspection by variables – Part 2: General specification for single sampling plans indexed by AQL for lot-by-lot inspection of independent quality characteristics [7] .

  This International Standard specifies an acceptance sampling system of single sampling plans for inspection by variables. It is indexed in terms of the AQL and is of a technical nature, aimed at users who are already familiar with sampling by variables or who have complicated requirements.

• ISO 3951-3:2007 Sampling procedures for inspection by variables – Part 3: Double sampling schemes indexed by AQL for lot-by-lot inspection [5] .

  This International Standard specifies an acceptance sampling system of double sampling schemes for inspection by variables for percent nonconforming. It is indexed in terms of the AQL.

• ISO 3951-5:2006 Sampling procedures for inspection by variables – Part 5: Sequential sampling plans indexed by AQL for inspection by variables (known standard deviation) [11] .

  This International Standard specifies a system of sequential sampling plans (schemes) for lot-by-lot inspection by variables. The schemes are indexed in terms of a preferred series of AQL values, ranging from 0.01 to 10, which are defined in terms of percent nonconforming items. The schemes are designed to be applied to a continuing series of lots.

Other standards useful for acceptance sampling are ISO 24153 [12] (Random sampling and randomization procedures), ISO 3534-4 [4] (vocabulary and symbols about sampling) and parts 1 and 2 of ISO 3534 (Vocabulary and symbols about Statistics, Probability, and Applied Statistics) [2, 3] .

Acceptance Sampling can be usually found in any SPC book, see, for example, the ones by Juran [13], Ishikawa [1], or Montgomery [15]. A more complete book, devoted entirely to Acceptance Sampling, is the one by Schilling [16] where you can find more details about acceptance sampling techniques.