Towards a Formal Model for Dynamic Networks Through Refinement and Evolving Graphs

Abstract

Due to the highly dynamic behavior and the time complexity in Mobile Ad-hoc NEtworks (MANETs), modeling distributed algorithms and looking at their assumptions represent a challenging research task. Also, proving the correctness of these algorithms for dynamic networks is a topic of intensive research. In fact, the solutions which have been proposed to express and prove the correctness of distributed algorithms are usually done manually. In addition, all these solutions lack a consensus about their development and their proof. The main contribution of this paper is to propose a general and formal model for dynamic networks based on evolving graphs and Event-B formal method. In fact, evolving graphs is a powerful tool to express fine-grained properties. This model allows to handle topological events and to characterize the concept of time with some particularities. We implement it with Event-B, based on refinement technique. To illustrate the proposed model, we investigate an example of a distributed algorithm encoded by local computations models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

1.1 Overview

In recent years, wireless communication networks have witnessed rapid advances in the computing industry and are widely available in our everyday life. A MANET [13] is a form of wireless networks. It is composed of mobile computing devices, called nodes, such as laptops, smartphones, etc. These nodes are dynamically connected in an arbitrary manner, without the support of any fixed infrastructure or centralized administration. MANETs cover a large range of applications like military operations, emergency relief, wireless sensor networks, etc.

Due to node mobility, disconnections and failures that can be produced, MANETs are extremely dynamic and the connections between nodes vary in time. One well-known challenge in these networks is modeling such dynamics and creating a reference model on which results could be compared and reproduced. In this context, a MANET can be naturally represented as a dynamic graph whose nodes are mobile devices and the edges are instantaneous wireless links between the nodes. The evolving graph formalism has been proposed by A. Ferreira [8] as a combinatorial model for dynamic networks. In this model, a dynamic graph can be decomposed as a discrete sequence of static graphs. Each static graph is a snapshot of the dynamic network at a given time.

In a dynamic graph, the communication between nodes can be ensured by a distributed algorithm [14]. The latter is designed to run on interconnected autonomous computing entities for achieving a common task. In order to encode distributed algorithms, we use local computations model and particularly graph relabelling systems [12]. In this context, a node can realize a computation step if there is a specific rule that describes the corresponding label modifications. The rule can be applied if it is consistent with the states of the node and its neighbours.

To specify the abstraction provided by local computation, we use a formal method. In fact, formal methods provide a real help for expressing correctness with respect to safety properties in the design of distributed algorithms. Particularly, the correct-by-construction approach [11] provides a way to prove algorithms. It can be supported by a progressive and incremental process controlled by the refinement [3] of models for distributed algorithms. This process allows to simplify the proofs and to validate the integration of requirements. The Event-B modeling language [1] can support this methodological proposal suggesting proof-based guidelines. It is supported by a tool called “RODIN” [2] which provides an environment for developing correct-by-construction models for software-based systems.

1.2 Contribution

In this paper, we propose a reusable model for dynamic networks by combining the evolving graphs formalism and the refinement approach of the Event-B method. More precisely, we develop a general and formal solution which defines the different topological events in a dynamic network and the resulting changes in the evolving graph. In addition, we focus in this model on the concept of time to present the situations which need a time evolution. Moreover, the proposed model gives primitives to analyze an evolving graph. Our model takes into consideration only the variation of edges in the network. It can be extended in the future to address the movements of nodes.

Formally, we propose a refinement strategy that allows to enrich a model in a step by step fashion. The refinement is the foundation of the correct-by-construction which is a well suited approach to prove algorithms. The main objective of our model is to enable reuse during the development. In fact, different components of the model can be refined and reused to specify distributed algorithms in dynamic networks. Hence, we can save effort on proving correct algorithms.

To illustrate our model, we present an example of a counting algorithm encoded by local computations models. The main goal of this example is to demonstrate how we can use and refine the proposed model.

1.3 Related Work

Evolving graphs are an effective and powerful formalism which helps to capture the dynamic behavior of MANETs. That’s why, it has drawn the attention of the research community in the last few years. Several research works have been based on this formalism to deal with network dynamics.

In [6], A. Casteigts proposed an analysis framework for distributed algorithms on dynamic networks. The proposed framework provides general formalisms and methods for studying the main properties of the distributed algorithms in dynamic networks. It allows to characterize the necessary and/or sufficient connectivity conditions required for the success of a distributed algorithm in a dynamic network. It is based on the combination of the evolving graphs and graph relabellings [12]. This framework is illustrated by the analysis of three simple algorithms (propagation algorithm, centralized counting and decentralized counting) whose necessary and sufficient conditions were derived into a sketch of classification of dynamic networks.

Furthermore, P. Floriano et al. [9] presented a study of necessary and sufficient conditions, in dynamic networks, for two distributed problems which are mutual exclusion and K-mutual exclusion. To do this, they exploit the framework proposed by A. Casteigts [6].

The author [10] provided a sufficient condition for the decentralized counting algorithm suggested by A. Casteigts [6]. In fact, he shows that a complete underlying graph was sufficient for the decentralized counting algorithm to succeed. Moreover, he introduces the concept of tight conditions, to strengthen the guarantees offered by necessary and sufficient conditions. Then, he demonstrates the tightness of the sufficient condition provided for the decentralized counting algorithm.

In addition, M. Barjon et al. [4] proposed an algorithm which maintains a forest of spanning trees in dynamic networks. The proposed algorithm aims to maintain exactly one token (root) per tree. It is based on three operations on tokens: circulation, merging and regeneration. To do this, a computation step takes as input the state of a pair of nodes and modifies these states according to some rules.

Throughout the related works outlined above, we note a lack of consensus about the development and proof of distributed algorithms in dynamic networks. Moreover, the proofs which have been presented are done manually. In addition, most of the distributed algorithms which have been investigated, in dynamic networks, are simple.

1.4 Organization of the Paper

The remainder of this paper is organized as follows: In Sect. 2, we present basic concepts of the evolving graph and the Event-B formal method. Section 3 introduces our proposed model for dynamic networks based on the evolving graphs formalism. In Sect. 4, we present the formal development of the proposed model. Section 5 applies our model to develop an example of a distributed algorithm. Finally, the last section concludes and outlines areas for our future research.

2 Preliminaries

2.1 Evolving Graphs

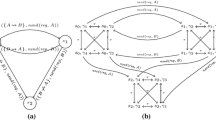
The formalism of evolving graphs has been proposed as a combinatorial model for dynamic networks. In this model, the evolution of the network topology is simply recorded as a sequence of static graphs. As an example, we consider the four snapshots taken at different time intervals of a MANET, as shown in Fig. 1. Each static graph is a snapshot of the dynamic network at a given time. This view is precisely adopted by A. Ferreira [8].

Fig. 1

Sucessive snapshots of a MANET evolution over time

Formally, an evolving graph g is a triplet (G, $S_{G}$, $S_\mathbb {T}$), where:

• $S_\mathbb {T}=t_{0},t_{1}, \ldots ,t_{n}$ is an ordered sequence of dates used to capture the static graphs. These dates correspond to every time step in a discrete-time system $(\mathbb {T} \subseteq \mathbb {N})$. Except for $t_{0}$ and $t_{n}$, each $t_{i}$ corresponds to one or more topological events that modifies the network. Each edge is labeled with the dates of its presence.

• $S_{G}=G_{0},G_{1}, \ldots ,G_{n-1}$ is the sequence of undirected static graphs. Each $G_{i}$ represents the network topology during the period $[t_{i} , t_{i+1}[$ in the evolving graph g.

• G represents the union of all $G_{i}$ in $S_{G}$, called the underlying graph of g (see Fig. 2). The edges are labeled with the date of their presence. For example, the presence of the edge “ae” in Fig. 1 at the dates “2” and “3” is represented in Fig. 2 by an edge “ae” labeled “2, 3”.

We will use the simple notations “V” and “E” to denote respectively the sets of nodes and edges of the underlying graph “G”.

Fig. 2

The evolving graph corresponding to the MANET in Fig. 1

2.2 Event-B Overview

The Event-B modeling language [1] defines mathematical structures into contexts and the formal model of the system into machines. The modeling process starts by identifying the domain of the problem expressed by means of context. This latter is characterized by a list of sets, list of constants, list of axioms and theorems that can be derived from the axioms of the context. An Event-B machine describes a reactive system by a set of invariants properties and a finite list of events modifying state variables. A machine “M” may see a context “C”, this means that all carrier sets and constants defined in “C” can be used in “M”.

The key tool behind the Event-B method is the refinement [3]. The refinement of a specification allows to enrich it in a step-by-step fashion. It is the foundation of the correct-by-construction approach. It provides a way to strengthen invariants and add details to a model. It is also used to transform an abstract model into a more concrete version by modifying the state definition. This is done by extending the list of state variables, by refining each abstract event into a corresponding concrete version and by adding new events.

An Event-B specification is considered as correct only if each machine, as well as the process of refinement, are proved by adequate theorems named Proof Obligations (PO). The management of proof obligations is a technical task supported by RODIN tool [2], which provides an environment for developing correct-by-construction models for software based systems.

3 The Proposed Model

Based on evolving graphs, we propose in this section a formal and general model for dynamic networks. The proposed model defines the different topological changes in a dynamic network allowing to specify a distributed algorithm, the manner of time evolution and the primitives to analyze the evolving graph. The main objective of this model is to be reused or instantiated to specify distributed algorithms in dynamic network.

As mentioned earlier, the formalism of evolving graphs allows to represent the changing connectivity of a dynamic network as a sequence of static graphs.

Let $g = (G, S_{G}, S_{T})$ be an evolving graph. Every static graph, $G_{i}\in S_{G}$, corresponds to the network topology during the interval of time $[t_{i}, t_{i+1}[$ where “$t_{i}$” represents the date when one or several topological events occur in the system. In our work, the time evolution from a date “$t_{i}$” to a date “$t_{i+1}$” is performed after one or many topological events. We can distinguish two situations of these events:

• Adding edge:

  Pre-condition: appearance of a new edge in the network at the current date “t”.

  Post-condition: addition of the new edge labeled “t”.

• Removing edge:

  Pre-condition: presence of an edge in the network at the date “t-1” and its disappearance at the current date “t”. Post-condition: no change takes place in the evolving graph.

There is another event that requires changing the evolving graph without affecting the time evolution. We call this event “Maintaining edge”. We talk about this situation if an edge is present at the date “t-1” and it undergoes no change at the date “t”. In this case, we add the date “t” to the label of the concerned edge.

In our proposed model, we take into account some hypotheses. On the one hand, we will consider only the variation of edges in the network. In contrast, we don’t consider the appearance or disappearance of nodes. On the other hand, a distributed algorithm in the local computation model is simply given by a set of relabelling rules. So, we suppose that such distributed algorithm can apply its rewriting rule(s) to every edge before the final date “$t_{n}$”. In order to analyze distributed algorithms on dynamic networks, we combine the evolving graphs and the formalism of graph relabellings [12]. As illustrated in Fig. 3, each static graph $G_{i}$ in $S_{G}$ covers the time interval $[t_{i}, t_{i+1}[$. We denote by “$Event_{t_{i}}$” the one or more topological events occurring at the time “$t_{i}$”. Between two consecutive topological events, any number of relabellings may take place. For a given algorithm A and two consecutive dates $t_{i}, t_{i+1} \in S_\mathbb {T}$, we denote by:

• $G_{i[}$ the labeled graph representing the network state just before “$Event_{t_{i}}$”;

• $G_{i}$ the labeled graph representing the state of the network just after the topological events of the date “$t_{i}$”;

• $R_{A_{[t_{i} ,t_{i+1}[}}$ one of the possible relabelling sequence induced by the algorithm A on the graph $G_{i}$ during the period $[t_{i}, t_{i+1}[$.

Then, we have $Event_{t_{i}}(G_{i[})=G_{i}$ and $R_{A_{[t_{i} ,t_{i+1}[}}(G_{i})=G_{i+1[}$.

Fig. 3

Combination of graph relabellings and evolving graphs

4 Formal Development

We remember that the specification of our proposed model is performed with Event-B method and done with RODIN platform. In our work, the development strategy of our model is composed of one context “c” and two machines “M0” and “M1”. We begin by presenting the context which describes static properties of the network. After that, we detail the specification of the two machines. In fact, we start with a very abstract model and then we add details, to obtain a correct and concrete model.

4.1 Formal Development of the Context “c”

The context “c” describes the static properties of the network. Formally, a graph namely “g” is modeled by a set of nodes called “V”. However, we have supposed in our work that the dynamic graph is composed of stable nodes and variable edges. For this reason, we define “V” in the context as an abstract set. Moreover, we add “tn” as a constant which represents the final system date. By means of the “axm1”, we state that “tn” is an integer different to the start date of the system. Furthermore, we add “axm2” to indicate that the number of nodes in the network is finite. The axioms specification of the context “c” is done as follows:

4.2 Formal Development of the First Level: Machine M0

In this level, a network can be formally modeled as a connected, undirected and simple graph “g” where nodes denote processors and edges denote direct communication links (see inv1). A graph is undirected if there is no distinction between two nodes associated with each edge (see inv2). A simple graph means that it does not have more than one edge between any two nodes and no edge starts and ends at the same node (see inv3). The invariants specification of M0 is done as follows:

In the first level, we can notice the appearance of new edges and the maintain of the existing ones from a graph $G_{i}$ to the following graph $G_{i+1}$. In fact, the basic idea of the evolving graph is the superposition of graphs one another. As a consequence, we do not consider the concept of time and the removing of edges. Nevertheless, it is necessary to have another level which refines the first. In Fig. 4, we present an example of evolving-graphs sequence which we can see in the first level. This sequence corresponds to the network topology taken in Fig. 1. Formally, we introduce two events “Adding_Edge” and “Maintaining_Edge”.

Fig. 4

Example of evolving-graphs sequence in M0

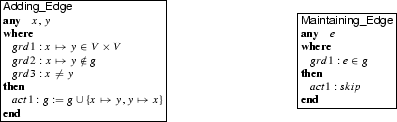
• Adding_Edge: In this event, if an edge does not belong to the graph “g” (grd1, grd2 and grd3), then we can add it to “g” (act1). To respect the invariant “inv2”, we add both “$x\mapsto y$” and “$y\mapsto x$”. We provide below the specification of this event.

• Maintaining_Edge: Based on the evolving graphs, if an edge exists in a graph $G_{i}$ then it still exists in the following graph $G_{i+1}$. Formally, in the guard component, we define “grd1” to verify the existence of an edge “e” in the graph “g”. This event with no action is considered to have the action skip.

  

4.3 Formal Development of the Second Level: Machine M1

The second machine, called M1, refines the previous one. In fact, we keep the variables, invariants and events of the machine M0 and we add details to transform an abstract model into a more concrete version. If an invariant refers to both the abstract and concrete model, we call it a “gluing invariant” (inv3, inv4). The gluing invariants are used to relate the states between the concrete and abstract machines. In this level, we introduce the concept of time to distinguish the situations of appearance, disappearance and maintain of an edge in the network. Indeed, each edge has a label that indicates the dates when it is present in the network.

• The appearance of a new edge in the network at the date “t” requires the addition of this edge labeled “t”;

• The disappearance of an edge does not change anything in the evolving graph;

• The presence of an existing edge at the current date “t” requires adding the date “t” to the label of the concerned edge.

To illustrate these details, we present an example of evolving-graphs sequence in Fig. 5 which refines the first level.

Fig. 5

Example of evolving-graphs sequence in M1

In order to specify these events, we refine the “Adding_Edge” event of M0 by another event “Adding_Edge” which add more details. Also, we refine the “Maintaining_Edge” event to obtain two events “Maintaining_Edge” and “Removing_Edge”. Moreover, we introduce a new event called “Incrementing_Time”, to ensure the incrementation of time when one or many topological changes occur in the network.

Formally, we specify the machine M1 by adding two variables “t” and “LE”. The variable “t” represents the current time and “LE” is a function that assigns a label to each edge. The specification of this function takes the following form: $LE \in g \rightarrow \mathbb {P}(N)$. The addition of these two variables involves the addition of new properties in the invariant component (inv1, inv2, inv3 and inv4).

Initially, the system time is initialized to zero (t = 0). Then, the edges which are present at the time “t = 0” have the label “0” (LE=$\{0\}$).

If we say that an edge “e” exists in “g” (e $\in$ g), then its label contains at least one date “t1” knowing that t1 $\le$ t (see inv3).

As we said above, the incrementation of time, from a date “t” to a date “t+1”, is done after one or several topological events (adding edge, removing edge). To do so, we introduce a new variable of type integer called “change” (see inv4). This variable is initialized to zero (change=0) and if an event takes place, then “change=1”.

In order to express the different topological changes over time, based on the evolving graphs, we explain and we specify the different events as follows:

• Adding_Edge: By introducing the concept of time, the appearance of a new edge in the network requires the addition of the edge and a label containing the current date “t”. Thus, the “Adding_Edge” event presented in M0 is refined by modifying the action component. In fact, we add the new edge and then we add a label containing the current date. Also, the variable “change” receives the value “1” (act2) to indicate that a topological change has been produced. We provide below the specification of the “Adding_Edge” event.

• Maintaining_Edge: If an edge has appeared at a date “t1”, with “t1” strictly lower than the current date “t”, and it still exists at the date “t”, then we call this event “Maintaining_Edge”. Formally, in the guard component, we define “grd1” to verify the existence of an edge “e” in the graph “g” before the date “t”. Also, we add “grd2” to guarantee that the date “t” does not belong to the label of the edge “e”. In the action component, we update the label of the edge “e” by adding the date “t” to the existing label (act1). The variable “change” does not change since the network has not undergone any modification. The “Maintaining_Edge” event is specified as follows:

  

• Removing_Edge: An edge has been removed at the actual date “t” if it exists at the date “t-1” (see grd1 and grd2), but it does not exist at the date “t” (see grd3). In this situation, nothing will change in the evolving graph. So, in the action component, we modify only the variable “change” (act1). We provide the specification of the “Removing_Edge” event below.

• Incrementing_Time: We have introduced a new event, called “Incrementing_ Time”, which ensure the incrementation of time. In the guard component, we verify that t $\ge$0 and t $<$ tn (grd1). This event is activated when one or several topological events (Adding_Edge, Removing_Edge) occur in the network, which means that “change” is equal to 1 (grd2). In the action component, we increment the time to “t +1” and we reset the variable “change” (act2). Then, we have no topological change at the time “t +1”. The “Incrementing_Time” specification is done as follows:

  

Using the proposed model, it is possible to find the historical data of a dynamic network. So, it is a way to analyze an evolving graph. In fact, through the function “LE”, we can obtain the presence dates of each edge in the network. Then, we can verify the connectivity over time [7] of the network. Also, we can find the set of all possible paths over time from one node to another, called journeys. Thus, it is possible to compute optimal journeys in dynamic networks like the minimum delay of path (fastest journey), the earliest arrival date (foremost journey) and the minimum number of hops (shortest journey) [5].

5 Example

In this section, we present an illustration of our model by specifying a distributed algorithm encoded by local computations model. For this purpose, we choose a simple example of algorithm, called centralized counting algorithm. It is a distributed algorithm which computes all the nodes in a network. In fact, each entity executes asynchronously the same code and interacts locally with its immediate neighbours. The proposed model can be applied to other distributed algorithms. The main objective of this section is to demonstrate how our model can be used and incorporated during development. Through this example, we list and we discuss the instantiation of the different model components, by refinement technique, to generate a correct specification. We begin in this section by presenting the chosen algorithm. After that, we illustrate how we obtain an instance of the proposed model.

5.1 Algorithm Presentation

Fig. 6

Execution example of the centralized counting algorithm over evolving graph

The centralized counting algorithm, depicted in Algorithm 1, assumes a distinguished node at initial time. This node, called the counter, is in charge of counting all the nodes it meets during the execution. Therefore, the counter node has two labels (C, i), meaning that it is the counter (C), and that it has already counted i nodes (initially 1, i.e., itself). The other nodes are labeled either “F” or “N”, depending on whether they have already been counted or not. The counting rule is given by the relabelling rule “R” in Algorithm 1. An execution example of this algorithm over the evolving graph is given in Fig. 6.

5.2 Formal Specification

To explain the specification of the centralized counting algorithm, we present in Fig. 7 how the proposed model is used to construct a correct distributed algorithm. In fact, we begin by specifying the application field of the algorithm. Then, we introduce a new context called “c1”, as an extension of the context “c”, which describes the specific algorithmic properties. Generally, the development of a distributed algorithm starts with a very abstract algorithm and then by successive refinement we obtain a concrete one that expresses the local behavior of the processor in the network.

According to this development strategy and with respect to the given algorithm, three basic levels are necessary to build a correct distributed algorithm.

In the first level, we define a machine M0’ which refines M0. Then, it includes the events “Adding_Edge” and “Maintaining_Edge”. M0’ can access to all components of the context “c1” (via the clause SEES). It expresses only the goal of the distributed algorithm through a new event “oneshot” which does not describe how the solution is computed. In the second level, M1 is incorporated into M1’ (via the clause INCORPORATES). Thus, M1’ includes the events “Adding_Edge”, “Maintaining_Edge”, “Removing_Edge” and “Incrementing_Time” as defined in M1. In addition, we refine the events “Adding_Edge” and “Maintaining_Edge” of M0’ in the same manner as the refinement done in the proposed model. Also, we refine the event “oneshot”. In the third level, we introduce a machine, called M2, which refines M1’. In this level, we specify the local label modification and encode the relabelling rule described above.

The details of the context and machines development will be explained afterwards.

Fig. 7

Using the model in Event-B development (Example: centralized counting algorithm)

• The context “c1” In this context, we define the node “c0” as a constant which is in charge of counting all the nodes it meets during the execution. We denote node labels by a set called “LN”: The node “c0” is labeled “C”. The other nodes are labeled “F” if they have already been counted and “N” if they have not (see axm 2). All these specific algorithmic properties are specified as follows:

  

• The first level: Machine M0’ In this level, the “Adding_Edge” and the “Maintaining_Edge” events remain unchanged and we add an event called “oneshot”. This event avows the result of the distributed algorithm when its execution is completed. Then, it returns the number of nodes in the network without describing how the solution is computed. In order to specify the “oneshot” event, we introduce two variables “nodes” and “nb_nodes” which will contain respectively the sets of nodes that have been counted and the resulting number of nodes. These new variables are specified by the following invariants:

  

  Initially, “nodes” contains the center “c0”. Thus, “nb_nodes” is equal to 1. The following initialization establishes the invariants:

  

  We provide the specification of the “oneshot” event below. In the guard component, all nodes, except “c0”, must be connected to the center “c0”. In the action component, the variable “nodes” contains all the network nodes and “nb_nodes” is the number of nodes in the network. We prove by means of the theorem “Th1” that the graph “g” is connected.

  

• The second level: Machine M1’ The refinement of M0’, named M1’, remains in a high level abstraction. It encodes the algorithm and computes its result without considering the relabelling rules. The specification presented in the second level of the model still exists. However, we have to refine the “oneshot” event defined in M0’, due to the presence of the time aspect in this level. In fact, the “grd1” presented in M0’ is reinforced by a new condition called “grd2”. It ensures that each node “x” in the graph, except “c0”, will be linked to the node “c0” at one or several dates. Then, the label of each edge “$c0\mapsto x$” in the graph contains one or several dates. The guard “grd2” of the “oneshot” event specification is given as follows:

  

• The third level: Machine M2 The third machine, called M2, refines the previous one. It introduces labels of nodes and edges. The “oneshot” event still exists but it is more concrete. However, the other events (Adding_Edge, Maintaining_Edge, Removing_Edge), presented in M1’, remain unchanged. Let “lab” be the variable which describes the states of nodes: “$lab \in V \rightarrow LN$” (inv1) where “LN” is defined in the context “c1” as the set of possible labels for the nodes. At every time, each node is in a particular state and this state will be encoded by a node label. According to its own state and to the states of its neighbours, each node may decide to perform a computation step by applying the relabelling rule. Initially, the node “c0” is labeled “C” and the other nodes are labeled “N”, since they have not been counted. The initialization of the variable “lab” is defined as follows:

  

  Formally, the relabelling rule “R” is specified by the event “Rule” as follows:

  

  We also define a gluing invariant called “gluing_inv”. Generally, the gluing invariants are used to relate the states between the concrete and abstract machines. In our context, if a node “x” belongs to “nodes”, which represents the sets of nodes that have been counted, then it is connected to the center “c0” and labeled “F”. Furthermore, the edge joining the node “x” and “c0” should be present in one or several times. The gluing invariant specification of M2 is done as follows:

  

  In this level, we refine the “oneshot” event by adding new guards and reinforcing the action “act1” of the abstract event. In fact, we reinforce the guard component by adding “grd3”, “grd4” and “grd5” which ensure that the node “c0” is labeled “C” (grd3), all the other nodes are labeled “F” (grd4) and no node is labeled “N” (grd5). The added guards in the “oneshot” event specification is given as follows:

  

  Also, we reinforce the action “act1” to indicate that, at the end of the execution of the algorithm, the nodes are labeled “C” or “F”.

  

  We prove by means of the theorem 2 (Th2) that our algorithm can apply its rewriting rules to every edge before “tn”.

  

6 Conclusion and Future Work

In this paper, we have presented a formal and general model for dynamic networks based on the evolving graph formalism. It aims to define the different topological changes and the situations of time evolution. It is also a way to analyze the evolving graph. The proposed model is based on the refinement technique by using the Event-B formal method and the RODIN platform. The main characteristic of this model is that it enables reuse in the development and minimizes efforts on proving distributed algorithms. We have illustrated it by investigating an example of the centralized counting algorithm.

We are currently working on dealing with other examples of distributed algorithms which are more complex. We plan to extend our model by introducing some properties related to evolving graphs such as connectivity over time, journeys, etc. Moreover, it is interesting to choose a case study supporting the dynamic behavior of the network in order to apply the proposed model in realistic scenarios.