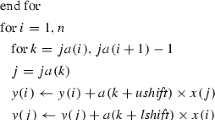αAMG Based on Weighted Matching for Systems of Elliptic PDEs Arising from Displacement and Mixed Methods

Abstract

Adaptive Algebraic Multigrid (or Multilevel) Methods (αAMG) are introduced to improve robustness and efficiency of classical algebraic multigrid methods in dealing with problems where no a priori knowledge or assumptions on the near-null kernel of the underlined matrix are available. Recently we proposed an adaptive (bootstrap) AMG method, αAMG, aimed to obtain a composite solver with a desired convergence rate. Each new multigrid component relies on a current (general) smooth vector and exploits pairwise aggregation based on weighted matching in a matrix graph to define a new automatic, general-purpose coarsening process, which we refer to as “the compatible weighted matching”. In this work, we present results that broaden the applicability of our method to different finite element discretizations of elliptic PDEs. In particular, we consider systems arising from displacement methods in linear elasticity problems and saddle-point systems that appear in the application of the mixed method to Darcy problems.

1 Introduction

Algebraic Multigrid Methods (AMG) were introduced in the mid-1980s as plug-in solvers for large and sparse linear systems of equations A x = b, with the final aim to define automatic coarsening process only depending on the coefficient matrix [4, 15]. These methods are particularly efficient for systems arising from scalar second-order elliptic partial differential equations (PDEs), where a characterization of the algebraically smooth error, which is the error component not reduced by a simple relaxation scheme (such as Gauss-Seidel relaxation), is available [9]. This error, corresponding to the eigenvectors of A with small associated eigenvalues (near-null kernel of A), must be nearly exactly represented in the coarse-space in order to be eliminated by the coarse-grid correction process. Therefore, a main focus in the current state-of-the-art AMG methods is to define strategies for building coarse variables and intergrid operators which are able to adapt themselves to the properties of the near-null kernel of the problem at hand in order to preserve efficiency and robustness for dealing with more general classes of problems than the traditional scalar elliptic PDEs, including systems of elliptic PDEs, convection-diffusion equations and also more general non-PDE problems. In this direction, Adaptive Algebraic Multigrids (αAMG) have been proposed [6, 8], where main idea is to use appropriate adaptive steps aimed to “identify” smooth error components which the current solver is not able to efficiently handle so that they can be used to improve the solver by modifying the coarsening scheme without using any specific a priori knowledge about these error components. In [11] we proposed a new αAMG method which relies on a bootstrap strategy aimed to compute a composite solver with a desired convergence rate. We demonstrated its effectiveness when applied to symmetric positive definite (s.p.d.) systems arising from finite element discretization of highly anisotropic scalar elliptic PDEs on structured and unstructured meshes. Here, we extend the application of the method to systems of elliptic PDEs coming from linear elasticity and Darcy flow in porous media in mixed setting. In Sect. 2 we outline the αAMG based on the compatible weighted matching; in Sect. 3 we describe the model problems and introduce the Bramble-Pasciak transformation used for extending our method in dealing with symmetric indefinite systems stemming from the mixed finite element discretization of Darcy problems; finally, in Sect. 4 we present results obtained by a prototype Matlab version of our αAMG solver.

2 Main Features of αAMG Based on Compatible Weighted Matching

In [11], we proposed a bootstrap process aimed to build a composite solver of the following form:

$$\displaystyle{ \mathbf{x}_{k} =\prod _{ r=0}^{2m+1}(I - B_{ r}^{-1}A)\mathbf{x}_{ k-1},\quad \quad k = 1,2,\ldots, }$$

(1)

with B _m+r = B _m+1−r ,  r = 1,  …,  m + 1. Each B _r is an AMG-cycle built with its own aggregation procedure of unknowns driven by a weighted matching for the original matrix graph with weights depending on the most recently computed algebraically smooth vector x _k with respect to the current composite solver. In more details, starting from a general (random) given vector, we build an initial AMG-cycle represented by the operator B ₀ and apply it to the homogeneous system A x = 0, starting with a nonzero random initial iterate x ₀, and successively computing x _k : = (I − B ₀ ⁻¹ A)x _k−1 for a fixed number of iterations. The iterative process provides an approximation to the eigenvector of B ₀ ⁻¹ A corresponding to the minimal eigenvalue of B ₀ ⁻¹ A, i.e., of the algebraically smooth vector corresponding to the current solver. This last vector is then used to build a new AMG-cycle represented by the operator B ₁ to be composed as in (1) and tested on the homogeneous system. The bootstrap process is stopped when the process represented by (1) reaches a desired convergence rate.

Each new AMG operator B _r is built by using pairwise aggregation of unknowns driven by weighted matching algorithms for the matrix graph. Such matching algorithms are widely exploited in sparse matrix computations to enhance matrix diagonal dominance [12]. More aggressive coarsening (than pairwise aggregation) can be obtained by combining multiple steps of the pairwise aggregation. Our main idea was to exploit the concept of compatible relaxation introduced in [5] for selecting the coarse-vector space. Since for the coarse space, we choose piecewise constant interpolant (that interpolates exactly the current smooth vector), we choose a complementary space such that on each aggregate (of pair of vertices) it is spanned by a vector orthogonal to the restriction of the smooth vector to that (pairwise) aggregate. To actually choose the aggregates, we use weights based on these orthogonal vectors so that the resulting A _f matrix corresponding to the space complementary to the coarse space have maximal product of its diagonal entries. For the actual details on the respective algorithms and results on scalar PDEs, we refer to [11]. Here, we investigate the use of more accurate interpolation operators obtained by weighted-Jacobi smoothing of the piecewise constant interpolation operators coupled with aggressive coarsening. This leads to smoothed aggregation type adaptive AMG method [7], which exhibits improved convergence and scalability properties with general reduction of setup costs.

Our coarsening process, which we referred to as compatible weighted matching, has the advantage to be independent of user-defined parameters; furthermore, it overcomes the limitations of the characterization of strength of connectivity between pairs of unknowns, well motivated only for algebraic systems with M-matrices. The latter concept is generally used in both the coarse space selection and in the interpolation scheme for classical AMG schemes. We stress that computing optimal matching has a super-linear computational complexity, whereas we are interested in (optimal) AMG with linear complexity, that is why we apply an approximate algorithm to find sub-optimal weighted matchings in a graph [13]; this approach was demonstrated to be effective in computing suitable compatible weighted matchings in the difficult case of highly non-grid aligned anisotropic scalar elliptic PDEs.

3 Case Studies: Linear Elasticity and Darcy Problems

We focus on two types of elliptic PDEs particularly relevant for many engineering applications, such as Lamé equations for linear elasticity and Darcy equations for flow in porous media in mixed system setting. Of main interest is to demonstrate the feasibility of our method on general s.p.d linear systems, where the coefficient matrix is not an M-matrix, as well as, on some symmetric but indefinite systems of saddle-point form.

The most widely used mathematical model for studying deformation of materials due to the application of external forces are the following Lamé equations, which are equilibrium equations written in terms of the displacement field u:

$$\displaystyle{ \mu \varDelta \mathbf{u} + (\lambda +\mu )\mathop{\mathrm{grad}}\nolimits (\mathop{\mathrm{div}}\nolimits \mathbf{u}) = \mathbf{f}\quad \quad \mathbf{x} \in \varOmega }$$

(2)

where u = u(x) is the displacement vector, Ω is the 3D spatial domain, and λ and μ are the Lamé constants. A mix of Dirichlet boundary conditions and so-called traction conditions are usually applied to have a unique solution. Discretization of (2) by finite element method, if each scalar component of the displacement vector u = (u, v, w) is considered separately (unknown-based [14] discretization), leads to s.p.d. systems of equations whose coefficient matrix can be written in the following block form:

$$\displaystyle{A = \left [\begin{array}{ccc} A_{uu} & A_{uv} & A_{uw} \\ A_{vu} & A_{vv} & A_{vw} \\ A_{wu}&A_{wv}&A_{ww} \end{array} \right ]}$$

We note that if μ > > λ, the above matrix is spectrally equivalent to its block diagonal, corresponding to the matrix coming from discretization of Laplace equation per each unknown component. In this case, block-wise version of the classical AMG are efficient solver. In general, A is not strongly block-diagonally dominant and problem-dependent multigrid operators have to be considered to improve convergence of AMG [1]. In the present work we demonstrate that our αAMG is able to obtain a solver with a desired convergence rate for general elasticity problems, without any a priori information on the problem neither on the discretization scheme.

The second type of systems of PDEs we considered in this work comes from the Darcy problem of flows in porous media. It is a boundary value problem associated to the following second order elliptic equation:

$$\displaystyle{ -\mathop{\mathrm{div}}\nolimits k(\mathbf{x})\mathop{\mathrm{grad}}\nolimits p = f(\mathbf{x})\quad \quad \mathbf{x} \in \varOmega, }$$

(3)

where p = p(x) is the flow pressure, Ω is the spatial domain, and k(x) is the permeability coefficient. In a mixed finite-element formulation, the flow velocity field u = −k∇p is introduced and Eq. (3) becomes $\mathop{\mathrm{div}}\nolimits \mathbf{u} = f$. The resulting problem is a system of two first order vector equations which can be discretized by using a pair of finite element spaces leading to the following indefinite system of saddle-point form:

$$\displaystyle{\left [\begin{array}{cc} A&B^{T} \\ B & 0 \end{array} \right ]\left [\begin{array}{c} \mathbf{u}\\ p \end{array} \right ] = \left [\begin{array}{c} \mathbf{f}\\ f \end{array} \right ],}$$

where A is an s.p.d. matrix. Such linear systems, especially for highly variable or discontinuous permeability coefficient, are very challenging for general iterative solvers, and more specifically for algebraic multigrid (see [2, 16]). Here we propose to use an approach based on the Bramble-Pasciak preconditioner [3] which transforms the saddle-point matrix into a s.p.d. matrix. They utilize a preconditioner matrix M for the A block, such that A − M is s.p.d., and transform the saddle-point matrix into the following s.p.d. one:

$$\displaystyle{ \widehat{\mathcal{A}} = \left [\begin{array}{cc} AM^{-1} - I & 0 \\ BM^{-1} & - I \end{array} \right ]\left [\begin{array}{cc} A&B^{T} \\ B & 0 \end{array} \right ] = \left [\begin{array}{cc} AM^{-1}A - A &(AM^{-1} - I)B^{T} \\ B(M^{-1}A - I)& BM^{-1}B^{T} \end{array} \right ]. }$$

(4)

A good choice in practice is a diagonal matrix M assembled from the local element-based diagonal matrices diag(M _fem ), where M _fem = 1∕2λ _min D _fem and D _fem = diag(A _fem ). Here, A _fem is the local element mass matrix for each finite element and λ _min is the minimal eigenvalue of the generalized local eigenvalue problem A _fem q = λD _fem q. In this case the transformed matrix (4) can be explicitly computed at a cost of a moderate increase in the total number of nonzero elements. In the following Section we report some numerical results related to the application of our adaptive AMG on Darcy problems discretized by the mixed finite-element method, in the above transformed s.p.d. form.

4 Numerical Results

In this Section we report some preliminary results which illustrate the ability of our method to solve the systems of equations introduced in Sect. 3 both in 2D and in 3D domains. We investigate the convergence behavior and the setup cost for increasing mesh size of the discretization. The setup cost is measured in terms of AMG components nstages built by the bootstrap process to reach a desired convergence rate set to 0. 7. The obtained convergence rate ρ was estimated by applying the solver in (1) for 15 iterations at each new built. We also report, per each test case and per each mesh with n nodes, the average number of levels nlev of all solver components and the average of their operator complexity cmpx, which gives information on the cost of the application of one cycle; cmpx is defined as the ratio between the sum of nonzero entries of the matrices of all levels and the number of nonzero entries of the fine-grid matrix. Each AMG component, built on the base of the compatible weighted matching coarsening method, is a general ν-fold cycle [16], where one-sweep is alternated with three sweeps in the next level; In this way, we ensure linear cost per cycle since our coarsening is based on pairwise aggregation. Symmetric Gauss-Seidel relaxation (one iteration) is employed as pre/post smoothing while direct solver (based on LU factorization) is used at the coarsest level. In order to achieve aggressive coarsening we combine four steps of pairwise aggregation based on compatible matching, which allows us to define coarse matrices with a coarsening ratio of at most 16 at each level; the process is stopped when the size of the coarsest matrix is at most 100.

As test case for linear elasticity, we consider Eq. (2) on a beam characterized by μ = 0. 42 and λ = 1. 7; one side of the beam is considered fixed and the opposite end is pushed downward. The problem is discretized using linear finite elements on triangular (2D) and tetrahedral meshes (3D) on different mesh sizes, obtained by uniform refinement, with the software package MFEM (http://mfem.googlecode.com). In Table 1, we summarize our results obtained both in the case of constant piecewise interpolation, i.e., unsmoothed aggregation, (on the left) and with smoothed aggregation (on the right).

Table 1 Linear elasticity problems: setup cost when unsmoothed (on the left) and smoothed aggregation (on the right) are used

We observe that our method is able to achieve convergence factors less than the desired one for all the cases, although no a priori information on the spectral properties of the matrices neither on the particular features of the system of PDEs and of its discretization were used. We notice that the number of the necessary bootstrap steps generally increases with increasing the mesh size, especially for 3D problems; the largest size mesh requires five more bootstrap steps with respect to the medium size mesh. The total number of bootstrap steps, as expected, is reduced if the smoothed aggregation is applied; furthermore, smoothed aggregation coupled with our aggressive coarsening based on a combination of more steps of pairwise aggregation produces a moderate increase in the operator complexity, leading to a general reduction both in the setup and the application cost of the method. For the Darcy problems, we consider saddle-point systems stemming from a realistic problem with highly variable permeability coefficients, describing a 3D petroleum reservoir obtained from the 10th Society of Petroleum Engineers (SPE) Comparative Solution Project [10]. We present results for Dirichlet problems (i.e. pressure given on the boundary) discretized by using MFEM with structured hexahedral meshes. For discretization, we used first-order Raviart-Thomas spaces [16] for velocity and piecewise-constant functions for pressure. We apply the Bramble-Pasciak transformation described in Sect. 3 to obtain the corresponding s.p.d. matrix (4). We observe that for the considered test case and the employed mesh sizes, the number of nonzeros in the transformed matrix has an increase of about 80 % with respect to the original saddle-point matrix. In Table 2 we report results for different mesh sizes (note that here n is the size of the saddle-point matrix) for both unsmoothed and smoothed aggregation, when the algorithmic choices were the same as in the elasticity problems. We observe that the adaptive solver is able to obtain the required convergence rate with a moderate number of setup steps, demonstrating the potential of the coupling between Bramble-Pasciak transformation and the adaptive solver to handle well indefinite systems of saddle-point type coming from realistic flow problems. The increase in the number of bootstrap steps needed to obtain the desired convergence rate for increasing mesh size is moderate, showing good scalability properties also in the case of unsmoothed aggregation. We also observe that in this case the impact of smoothed aggregation based on a weighted Jacobi smoother on the convergence behaviour and scalability is not as significant.

Table 2 Darcy problems: setup cost when unsmoothed (on the left) and smoothed aggregation (on the right) are used