Neutron Scattering: Introduction

Abstract

Neutron scattering is an important method for characterization of materials. The chapter starts with a presentation of the properties of neutrons and how they are produced. The interaction with matter is the main part of this chapter. The notion of scattering length and cross section are explained as well as the differences between coherent and incoherent scattering. The chapter ends with a short overview of elastic, inelastic and quasi-elastic neutron scattering. The goal of this chapter is to provide to a beginner the essential background for the comprehension of the other neutron related chapters of this book.

2.1 Introduction

In order to determine where atoms are and what they do in materials we need a probe with a size of the same order of magnitude as the typical distance between atoms, i.e. around 10⁻¹⁰ m or 0.1 nm. Historically, the Ångström has been used as a unit with 1 Å = 0.1 nm. The German physicist Wilhelm Röntgen discovered X-rays in 1895 and in the beginning of the twentieth century X-ray diffraction developed rapidly based on X-rays with wavelengths in the range between 0.1 and 0.2 nm. X-ray diffraction turned out to be a great success and was accompanied by electron diffraction in the early 1930s. Electron diffraction utilizes the fact that electrons behave like waves, and can therefore interfere with each other and produce a diffraction pattern. The wavelength of the electron was determined by Louis de Broglie, already in 1924:

$$ \lambda =\frac{h}{p} $$

(2.1)

where λ is the wavelength, h the Planck constant, and p the momentum carried by the electron. Today this equation is referred to as the de Broglie relation. It is very powerful because it applies to all non-relativistic particles with a mass similar to the mass of atoms. A quite fortunate coincidence is that the mass of the neutron is just right to give it a de Broglie wavelength similar to X-rays used for most scattering studies, i.e. 0.1–0.2 nm. Neutrons were first discovered by James Chadwick in 1932. The first nuclear reactor went critical at Oak Ridge National Laboratory in the USA in late 1943, and the first neutron diffraction experiments were carried out already in 1944. Within a few years it was clear that neutron scattering would be an important tool for characterization of materials, including diffraction, spectroscopy, and imaging. Based on the pioneering work in those days, Clifford Shull and Bertram N. Brockhouse received the Nobel Prize in Physics in 1994. Each of the three scattering techniques, based on neutrons, X-rays, and electrons, respectively, has evolved into an array of different techniques, each specially designed to study particular aspects of crystal structures and dynamics of materials.

X-ray and electron scattering share the same severe shortcoming: they are not very effective to determine atomic positions of light elements, such as hydrogen, carbon, and oxygen in compounds with both light and heavier elements. Furthermore, these probes cannot distinguish between neighboring elements in the periodic table because of almost equal scattering power. Using neutrons the scattering from light and heavier elements are typically comparable (see Fig. 2.1), and thus neutron scattering can give detailed information about both at the same time. Furthermore, neighboring elements in the periodic table can have rather different interactions with neutrons, and in such cases neutron scattering is a unique method. The different scattering by isotopes can also be significant, for example, by hydrogen (protium) and deuterium, and thus isotope labelling can give specific information on the compounds.

Fig. 2.1

Coherent scattering lengths as a function of atomic weights [3, 4]

The key to understanding neutron scattering is the way neutrons interact with matter. In contrast to X-rays and electrons, which interact with the electrons around a nucleus, the neutron interacts with the nucleus itself. Since the neutrons are neutral they are only deflected when they hit a nucleus. Neutrons are therefore scattered equally well by light elements as the heavier ones. Thus the position of hydrogen atoms in crystalline materials can only be accurately determined with neutron scattering.

This brings us over to the second advantage of neutrons: As mentioned earlier neutron scattering has in several cases the ability to distinguish between scattering from neighboring elements in the periodic table. The reason for this is that neutrons are scattered by nuclei, and different types of nuclei have different scattering power. Sometimes they are very different, such as for scandium and titanium (see Fig. 2.1). This effect also applies to isotopes of the same element. ¹H (protium) and ²H (deuterium) for example, or ⁵⁸Ni and ⁶²Ni differ greatly in scattering power (Fig. 2.1).

The fact that neutrons are uncharged means that they can penetrate deeply into matter, in several cases many centimeters and up to meters, before being deflected or absorbed. X-rays from laboratory source setups are nearly not affected by hydrogen atoms, but only a few micrometers of lead is enough to stop them completely, although high-energy X-rays used at synchrotron facilities penetrate more deeply into matter. Neutrons with wavelengths in the range of 0.1–0.2 nm can on the other hand travel through more than 2 m of lead and almost 1 m of aluminium before the intensity is reduced to 50 %. This makes it possible to study samples being kept inside more complicated sample environments than what can easily be used with X-rays. It is therefore possible to measure the bulk properties, for example, in car engines or pipelines. The absence of charge also means that neutrons do not ionize the sample, like X-ray or electron beams, and thus opens up the possibility for studies of fragile specimens such as organic crystals or invaluable archeological artifacts. It should be added that some elements and isotopes, for example, boron, gadolinium, and cadmium, absorb neutrons strongly, but isotope labelling can reduce the absorption enormously. For example ¹⁰B (which accounts for 20 % of natural boron) is a strong neutron absorber while ¹¹B has a very weak absorption, and natural boron is therefore difficult to use in neutron scattering experiments.

The neutron is uncharged because it is composed of one up quark, with a charge of 2/3e, and two down quarks, each with charge −1/3e. Even though the total charge is zero this arrangement leads to a tiny charge distribution that gives rise to a magnetic moment, which in turn makes neutrons interact with the unpaired electrons in magnetic atoms. The possibility to determine magnetic structures on an atomic scale is a unique property of neutron scattering and yet another powerful advantage compared to X-rays.

A final advantage is the similar magnitude of atomic excitations and the kinetic energy of thermal neutrons. By measuring the change in kinetic energy of a neutron when it is scattered inelastically by an atom, information about energy transitions and interatomic forces can be extracted.

It might sound like neutron scattering would render other techniques obsolete, but due to several disadvantages this is not the case. Firstly, the relative ease of penetrating into matter (when there are no neutron-absorbing elements) is a two-edged sword. Not only does it mean that neutrons are weakly scattered, but it makes detection of them tricky. Secondly, the flux of neutrons emanating from a nuclear reactor is low compared to X-ray sources. The ILL (Institut Laue-Langevin) high flux reactor in Grenoble, France, is the most powerful research reactor in the world and has a neutron flux, ϕ, near its core of around 10¹⁵ n cm⁻² s⁻¹. For thermal neutrons with velocity v = 2200 m/s, this corresponds to a neutron density of N = ϕ/ v = 4.5×10¹⁵ n m⁻³. Assuming the same density of gas molecules in air it would produce a pressure of 10⁻⁷ mbar, which is a quite decent vacuum. To put the 58 MW ILL reactor’s flux further into perspective, to obtain a similar flux with photons we would then only need a 1 W light bulb.

Based on the low neutron flux compared to photons, it is paramount that neutrons should be used as efficiently as possible. One obvious way of increasing the neutron flux is to use a neutron beam with a large cross section, and 50–100 cm² can easily be achieved. At the same time, however, the sample has to be large in order to make use of all the incoming neutrons. In many cases it is impossible to synthesize huge samples. Therefore, in the last two decades, many different concepts have been developed to increase the neutron flux on the sample, e.g., focusing monochromators and focusing neutron guides, or making better use of the incoming and/or scattered neutrons, e.g., by using a wide wavelength band and using large 2-dimensional detectors. There are about 40 neutron research centers worldwide [1], most of which use a reactor as the neutron source. As the flux is a significant limitation for reactors new powerful spallation sources have recently been constructed in the USA (Spallation Neutron Source, SNS, Oak Ridge National Laboratory) and Japan (J-PARC). Furthermore, a new target station was added to the ISIS facility in the UK. The most ambitious project, the European Spallation Source (ESS), is supposed to deliver a neutron beam with a brightness that is 30 times higher than at existing facilities [2]. In many cases, as will be evident in the following chapters, neutrons are complementary to X-rays, and both techniques are needed to solve many problems. Table 2.1 lists some basic properties of the neutron together with some useful conversions.

Table 2.1 Basic properties of the neutron and some useful conversions

2.2 Production and Detection of Neutrons

2.2.1 Production of Neutrons

Neutrons can be generated by different nuclear reactions. However for scattering experiments the neutrons have to be produced with such a high rate (~10¹⁶–10¹⁸ neutrons per second), and thus the only possibility is either with nuclear reactors or spallation of heavy elements using high-energy particles. Research reactors usually use uranium as the fuel and produce on average around one extra neutron per fission reaction. Spallation sources operate completely differently. Here protons are accelerated to very high energies (in the range of GeV) and directed at a heavy-metal target, such as tungsten, tantalum, or liquid mercury. The collisions generate around 20–30 neutrons per incoming proton. The produced neutrons are directed to the different instruments with neutron guides.

A common feature to reactors and spallation sources is the production of neutrons with energies in the range of several or even hundreds of MeV. These energies are far too high for use in scattering experiments. Typically the energy needs to be lowered a billion times, to a few tens of meV, in order to get a desired wavelength around the atomic spacing in materials of around 0.1 nm. Neutrons having these low energies are called thermal neutrons. Fortunately, lowering the neutron energy is fairly easy to accomplish by passing the neutrons through a moderating medium. The neutrons lose their high energy due to the interaction with the nuclei of the moderator material and finally reach thermal equilibrium with the moderator. Normal (“light”) and heavy water are excellent moderators, and at room temperature will slow neutrons down to around 2200 m/s corresponding to a wavelength of 0.18 nm.

It is important to note that the neutrons emerging from the moderator have a spread in energy, which can be described fairly well with the Maxwell–Boltzmann distribution. The peak of the spectrum is at an energy equal to k _B T, where k _B is the Boltzmann constant and T the absolute temperature. A simulation of the neutron flux around a single uranium oxide fuel rod immersed in heavy water at different distances from the fuel rod at 327 K is shown in Fig. 2.2.

Fig. 2.2

Simulated flux of neutrons (symbols) as a function of energy around a uranium oxide fuel rod immersed in heavy water. The flux is calculated for a position close to a fuel rod and at 25 and 55 cm away from the rod, respectively. A Maxwell–Boltzmann distribution at 327 K is superimposed over the data as a solid line

The Maxwell–Boltzmann distribution superimposed as a solid line on the data can only be used to model the flux at low energies because the function does not contain terms that can model the tail observed in the simulated data. The disappearance of the hump at MeV-energies at the end of the tail, when moving from the surface of the fuel rod to 25 cm away, illustrates well how the spectrum is shifted to lower energies when the neutrons are being moderated along their path outwards from the fuel rod. This leads to an increase in the flux of thermal neutrons along the same path since more and more fast neutrons are being moderated, which is illustrated in Fig. 2.3. The shift of the spectrum towards lower energies can also be seen in this figure.

Fig. 2.3

A zoomed in view of Fig. 2.2 showing the neutron flux at thermal energies increases with the distance from the fuel rod. Additional points from a calculation at 5 cm separation from the fuel rod are shown as triangles. A Maxwell–Boltzmann distribution at 327 K is superimposed over the data as a solid line

The spectrum can be shifted further to longer or shorter wavelengths by using either a cold or a hot moderator, respectively. A typical cold moderator consists of a container filled with liquid H₂ or D₂ at about 20 K, while a hot moderator is usually a graphite block kept at 2000 K. Table 2.2 lists some typical values for the energy and wavelength of moderated neutrons.

Table 2.2 Typical values for neutrons passing through different moderators

At reactor sources the neutrons emerge from the moderator as a continuous stream with different energies. This spread in energy is not suited in many scattering experiments where a monochromatic beam of neutrons, i.e. neutrons with a narrow energy band, is required. Such a condition is obtained by placing a single crystal, or several pieces of single crystal material of a highly reflective material, such as pyrolytic graphite, germanium, copper, or silicon, between the neutron source and the sample. This is the so-called monochromator, and it will only transmit neutrons with wavelengths satisfying the Bragg law (see Sect. 2.5.1) in the direction of the sample. The wavelength is determined both by the scattering angle (monochromator take-off angle) and the corresponding set of scattering planes. A velocity selector with a set of choppers can also be used to create a monochromatic beam. Only neutrons with a certain velocity can pass both the first and last chopper blade placed along the direction of the beam. Unfortunately a severe downside to monochromating the beam is that a majority of the neutrons (up to 99 %) are wasted.

The energy spectrum from the source is handled differently at spallation sources. The neutrons are produced in pulses several times per second, thus there is no continuous beam, and a monochromator is not used. Instead, a technique called Time Of Flight (TOF) is employed. Here neutrons in a wide energy range are utilized by measuring the time it takes for each neutron in the polychromatic beam to travel from the moderator, via the sample, to the detector. As the distance from source to detector is well known, it is possible to determine the neutron velocity, and thus the neutron’s energy and wavelength. The fastest neutrons with the shortest wavelength arrive first, while the slowest neutrons are hitting the detector just before the fast neutrons of the next pulse arrive. Instead of measuring a diffraction pattern as a function of scattering angle (as for monochromatic neutrons), the TOF-instrument measures it as a function of time (or wavelength) with a fixed scattering angle. TOF-instruments are not limited to spallation sources. They are frequently being used at reactor sources as well.

A brief introduction to the theory of neutron scattering will be covered later in this chapter, while diffraction techniques in general are covered in Chap. 3.

2.2.2 Detection of Neutrons

Common to all neutron scattering and imaging instruments is the need to detect the neutrons. This is not a trivial task, because the neutron is a particle with low kinetic energy and no charge, and the interaction with matter occurs through very weak nuclear and magnetic forces. The only practical method of detecting a neutron is therefore to produce charged particles in a nuclear reaction involving the neutron and to detect the charged particles instead.

One of the main detection principles is the proportional counter. This is a gas filled tube with a wire, kept at a high positive voltage, placed in the center of the tube. The two traditional gases used to react with neutrons are either ³He or ¹⁰B-enriched BF₃ gas, while a mix of several other filler gases such as CH₄, Ar, and CO₂ serve as the ionization medium. The nuclear reactions following absorption of a neutron are:

$$ \mathrm{n} + {}^3\mathrm{H}\mathrm{e}\ \to {}^3\mathrm{H}+\mathrm{p}+765\ \mathrm{keV} $$

(2.2)

for the ³He-capture and

$$ \mathrm{n} + {}^{10}\mathrm{B}\ \to {}^4\mathrm{H}{\mathrm{e}}^{+}+{}^7\mathrm{L}\mathrm{i}+2310\ \mathrm{keV} $$

(2.3)

for the ¹⁰B-capture.

Both reactions create charged and highly energetic particles that ionize the gas. This results in a cascade of electrons giving an electric pulse which is detected by the positive wire. The neutron detectors are operated in an energy range where the electric pulse is proportional to the energy of the ionizing particles, meaning that these kinds of detectors allow an efficient discrimination of the smaller pulses obtained from γ-rays, which are almost always present in the background. By using fast electronics it is possible to determine the position of the discharge along the wire either with the so-called charge or time division methods. These kinds of detectors are so-called position sensitive detectors (PSD) and have a typical spatial resolution of about 1.5 mm. The extreme toxicity of BF₃ makes it challenging to use, and the availability of ³He has significantly been reduced since around 2010, followed by an enormous increase in the price. Thus it has become urgent to develop new efficient neutron detector technologies.

The neutron scintillator is one of the possible replacements for the ³He-detector and has successfully been put in use at several instruments at ISIS and J-PARC. In a scintillator the neutrons are absorbed by ⁶Li embedded in a conversion material, either a plastic or a glass plate, leading to the following nuclear reaction:

$$ \mathrm{n} + {}^6\mathrm{L}\mathrm{i}\ \to {}^4\mathrm{H}\mathrm{e}+{}^3\mathrm{H}+4790\ \mathrm{keV}. $$

(2.4)

The charged reaction products have high energy, and excite ZnS that is embedded together with ⁶Li inside the conversion material. ZnS returns to its ground state with the emission of 470 nm light, which is guided via fiber optics to a photomultiplier where it is transformed into an electric signal. Each absorbed neutron produces around 160,000 photons, making the event easy to detect with modern electronics. Discrimination against γ-rays, which also excite ZnS, is done electronically by analyzing the shape of the electric pulse. Numerous designs of neutron scintillators have been developed. These comprise 2D PSD, semiconductor detectors with ⁶Li-containing thin films, and ⁶Li-containing single crystals with the typical compositions Cs₂LiYCl₆ or LiCaAlF₆. Neutron imaging, analogous to X-ray imaging, detects neutrons using a two-dimensional CCD-sensor with a ⁶Li-ZnS scintillator screen mounted on the surface. A light-spot with a diameter of around 50–80 μm appears on the scintillator screen where the neutrons hit. The light from this spot is subsequently detected by the CCD-sensor and fed through a computer. This allows for high resolution imaging of, for example, water transport in the channels of an operating fuel cell, or hydrogen content in the walls of pipelines.

The main drawbacks of the neutron scintillator are limited detection efficiency due to the opaqueness of its own light which limits the thickness of the conversion material, and the limited neutron counting rate as a result of the relatively long afterglow after a neutron capture.

The most recent approach to a replacement technology is the boron-lined converter, which on the other hand displays a high neutron counting rate. The principle is similar to the BF₃-counter, but instead of having ¹⁰B supplied in gaseous form, it is provided by a solid micrometer-sized film (e.g., B₄C) covering the inside of the walls of the gas filled cylinder. When a neutron hits the film, and is captured by ¹⁰B, the charged reaction products from Eq. 2.3 ionize the filler gas creating the electric pulse. The drawbacks of this design are increased cost and complexity, and lower detection efficiency than with ³He-detectors. However, still the boron-lined converter is proposed to be implemented in the first large-area detectors at the coming spallation source ESS when it comes online in 2022–2023.

2.3 Interaction of Neutrons with Matter

2.3.1 Introduction

From the perspective of a neutron solid matter is quite spacious. This is because the size of the scattering center, the nucleus, is around 100,000 times smaller than the distance between these centers. The interaction with matter is produced by short-range nuclear forces (~10⁻¹⁵ m). As a consequence, the non-charged neutron can travel far inside solid matter before being scattered or absorbed by a nucleus. Neutrons interact with matter mainly in three ways: elastic scattering, inelastic scattering, and in absorption processes. The first two are interactions between the neutron and either a nucleus or the magnetic field produced by unpaired electrons. The absorption processes, on the other hand, lead to emission of secondary charged or neutral particles, emission of electromagnetic radiation or fission. Here we will not go into details about absorption interactions, but will mainly focus on the scattering, which is the foundation of most of the neutron characterization techniques. We will describe the different concepts of neutron scattering, followed by a simplistic mathematical derivation of expressions describing neutron scattering. Finally a brief overview of some neutron scattering techniques, relevant to hydrogen containing materials, will be presented.

2.3.2 Scattering Length

Since the nucleus is much smaller than the wavelength of the neutron, the nucleus acts like a point scatterer, i.e. the scattered neutron wave is spread out as a spherical wave (Fig. 2.4). For an incident plane wave e ^ik∙x, consisting of neutrons travelling along x with an initial speed v = | v | and an incoming wave vector k, the scattered wave can be expressed as (−b/r)e ^ik∙r, where the outgoing wave vector k is oriented parallel to r. k and v are related by:

$$ \frac{h\mathbf{k}}{2\pi }=m\mathbf{v} $$

(2.5)

where m and m v are the mass and momentum of the neutron, respectively. The amplitude of the scattered wave is proportional to the so-called scattering length, b:

$$ b={b}_c+{b}_i $$

(2.6)

b is a measure of the strength of the neutron–nucleus interaction, measured in fm (10⁻¹⁵ m) and varies in an erratic manner throughout the periodic table (Fig. 2.1). It consists of two parts: the coherent scattering length, b _c , which is plotted in Fig. 2.1 as a function of atomic weight, and the incoherent scattering length, b _i , which is discussed later in this chapter. A large absolute value of b means that the neutron is scattered strongly by the nucleus (i.e., on average more of the incoming neutrons are scattered). The neutron scattering length is analogous to the atomic form factor used in X-ray and electron scattering. A positive b means a minus sign in the wave function implying a repulsive interaction between the neutron and the nucleus. Most elements and isotopes have a positive b, but some are negative. A negative b leads to the opposite sign of the scattering amplitude compared to a positive b, equivalent to a 180° phase difference for the outgoing scattered wave. The protium (¹H) isotope of hydrogen for example, has a negative scattering length while deuterium (²H) has a positive one. Combinations of positive and negative b-values can also tune the average scattering length of a compound. This is utilized in contrast matching experiments where light and heavy water are mixed in a certain ratio resulting in an averaged scattering length equal to certain parts of a specimen immersed in water. For certain experiments (e.g., small angle neutron scattering or neutron reflectometry) that rely on a scattering length density (SLD) contrast these parts will scatter identically to the surrounding water and be masked away. Contrast matching is explained further in Chaps. 5 and 6.

Fig. 2.4

2D representation of a neutron wave with wave function e ^ik∙x scattered as spherical wave, (−b/r)e ^ik∙r, from a fixed nucleus

As shown in Fig. 2.1 some isotopes and neighboring elements display significantly different scattering lengths. For example scandium exists only as one isotope with non-zero spin and has a large positive b _c of 12.1 fm, while titanium consists of several different isotopes with both positive and negative values of b _c , which results in a final combined b _c of −3.37 fm. In several cases the large variations in scattering length between neighboring elements give rise to a significant scattering contrast, while for X-rays and electrons the difference will be too small to be observable.

The strong variations in b arise from the strong dependence on the spin of the nucleus. Isotopes with an even number of both protons and nucleons have nuclear spin I equal to zero and therefore only one scattering length. However those with I different from zero have two different scattering lengths, b ₊ or b ₋ , respectively (not to be confused with positive and negative values of b), since the spin of the compound nucleus (neutron + nucleus) is either J = I + ½ or J = I − ½. ¹H, for example, has spin ½ and consequently it has two different scattering lengths: b ₊ = 10.81 fm and b ₋ = −47.42 fm, respectively. ¹²C, on the other hand, has spin zero and therefore only one scattering length of b = 6.65 fm.

The scattering lengths have to be determined experimentally because we do not have an adequate theory of nuclear forces to predict these values from the properties of the nucleus. In practice we are only able to measure one b-value, and thus the separate values of b ₊ and b ₋ must be calculated based on this value. The scattering length of an element will be a mix of the scattering lengths of its different isotopes, just as the scattering length of an isotope is a mix based on the isotope’s different nuclear spins.

The sum of scattering lengths in a certain volume of a sample is defined as the SLD, and it is usually denoted by ρ:

$$ \rho =\frac{1}{\mathrm{volume}}{\displaystyle \sum_j{b}_j}=N\cdot b $$

(2.7)

where b _j is the scattering length of atom j and N is the atomic number density (1/m³).

2.3.3 Scattering and Absorption Cross Section

The scattering length gives information about the strength of the interaction between the neutron and the nucleus of the studied compound. The likelihood of such interactions is determined by the effective area of the nucleus as “seen” by a passing neutron. This is called the total cross section, σ _tot, and it is simply the sum of the scattering cross section, σ _s , and the absorption cross section, σ _a , for a given nucleus:

$$ {\sigma}_{\mathrm{tot}}={\sigma}_s+{\sigma}_a $$

(2.8)

The physical cross section of a heavy nucleus is around 10⁻²⁸ m², and the unit one barn is equal to a cross section of 10⁻²⁸ m². Because of the direct relationship between the scattering cross section and the scattering length (Eqs. 2.10 and 2.11), the scattering cross section also varies erratically with atomic numbers.

The probability of absorption of a neutron by a nucleus is expressed as the absorption cross section, σ _a , also measured in barn. The speed, or rather the energy, of the incoming neutron is important for the determination of σ _a . The values for the scattering lengths, and the scattering and absorption cross sections, measured for neutrons moving freely at T = 293 K, having a kinetic energy of E = k _B T = 25.3 meV (corresponding to a speed of v = 2200 m/s or a wavelength of λ = 0.1798 nm), can be found at NIST’s webpage [3] or in reference [4].

As a general rule σ _a decreases with increasing neutron velocity as 1/v. In addition, the isotopic composition has a substantial influence. Natural boron for instance has σ _a  = 768 barn, which is very large compared to most other elements. However, boron’s two isotopes, ¹⁰B and ¹¹B, have spectacularly different absorption cross sections of 3835 barn and a miniscule 0.0055 barn, respectively. Even though natural boron only consists of 20 % ¹⁰B the final absorption cross section becomes huge. Gadolinium is another spectacular example. σ _a equals a very large 49,700 barn for naturally occurring Gd, composed of a lesser, yet still significant, 85.1 barn for ¹⁵⁴Gd, and an astoundingly large 259,000 barn for ¹⁵⁷Gd. By using ¹¹B-enrichment neutron scattering experiments on boron compounds are feasible. While neutron scattering on gadolinium compounds seems impossible, it is not as challenging as one might think. Ryan and Cranswick [5], for instance, describe a rather straightforward experimental setup used for neutron diffraction on Gd-containing samples. The reason for these apparently abnormal absorption cross sections for some isotopes is strong resonances between the neutron and the nucleus at certain neutron energies. At these energies other events may be more likely to occur, such as for instance the (n,γ)-reaction, where a neutron is absorbed by the nucleus and a gamma ray plus a secondary neutron is emitted.

2.3.4 Reflection and Refraction

Analogous to reflection of light, neutrons obey Snell’s law, and at very small scattering angles they are reflected from surfaces or can be refracted at interfaces between two different media, such as between air and a thin film of some material, or between two different thin films. The critical angle of total reflection is proportional to the square root of the coherent SLD (see Chap. 5, Eq. 5.4). By performing neutron reflectometry experiments (see Chap. 5 for details), it is possible to determine the average SLD profile perpendicular to the surface and estimate the local composition. Layered structures lead to typical interference patterns in the reflectivity curve. By using this effect we can measure the thickness of layers, while the amount of diffuse reflection can give information about the roughness of the surface. Neutron reflectometry is limited to thin films and layers (<300 nm) or the regions very close to the surface of a sample. The differences in scattering lengths between neighboring elements of the periodic table and between isotopes, and strong scattering from light elements, such as hydrogen, are important advantages compared to the related X-ray reflectometry method. Chapter 5 presents neutron reflectometry in detail and in particular how it can be utilized to study hydrogen storage materials.

2.4 Coherent and Incoherent Scattering

2.4.1 Coherent and Incoherent Scattering Cross Sections

The coherent and incoherent contributions to the scattering length, b, were introduced earlier. In a similar manner the total scattering cross section, σ _s , is divided into a coherent part, σ _c , and an incoherent part, σ _i :

$$ {\sigma}_s={\sigma}_c+{\sigma}_i, $$

(2.9)

In a neutron scattering experiment we are measuring the combined intensity from all waves scattered by all atoms in the sample being exposed to the neutron beam. Consequently, the measured intensities will be determined by the interplay of the different waves with each other, leading to interference effects. Coherent scattering describes interference between waves produced by the scattering of a single neutron with waves coming from all nuclei in the sample. This type of scattering varies strongly with the scattering angle. Examples of coherent processes are so-called Bragg scattering and inelastic scattering by phonons or magnons. The coherent scattering cross section σ _c is given by the square of the average value of b:

$$ {\sigma}_c=4\pi {\left({\displaystyle \sum_j{f}_j{b}_j}\right)}^2=4\pi {\left(\overline{b}\right)}^2 $$

(2.10)

where f _j is the relative percentage of a nucleus with a specific scattering length b _j inside the sample.

Incoherent scattering, on the other hand, can be considered as the remaining part of the total scattering when the coherent scattering has been subtracted. The incoherent scattering cross section σ _i is given by:

$$ {\sigma}_i=4\pi \left({\displaystyle \sum_j{f}_{\kern-.15em j}{b}_j^2}-{\left({\displaystyle \sum_j{f}_{\kern-.15em j}{b}_j}\right)}^2\right)=4\pi \left(\overline{b^2}-{\left(\overline{b}\right)}^2\right) $$

(2.11)

In the case of incoherent scattering waves from different nuclei do not interfere with each other, meaning that no structural information can be extracted from this type of scattering. Particle dynamics, however, such as diffusion, is possible to extract because the incoherent scattering gives information about correlations between the positions of the same nucleus at different times. Equation 2.11 is basically telling us that the cause of incoherent scattering is random deviations from the mean scattering length of an element. These variations are resulting from the random distribution of spins (I ± ½) and/or isotopes throughout a sample.

Both the coherent and incoherent cross sections (Eqs. 2.10 and 2.11) depend on the scattering length b, which in turn is dependent on the spin state I of the nucleus. With b equal for all nuclei in a sample, which is the case for nuclei with zero spin, the incoherent scattering cross section in Eq. 2.11 becomes zero and the scattering is purely coherent. Naturally occurring helium, carbon, and oxygen are very close to mono-isotopic. Because the most abundant isotope of each of these elements has zero spin, the scattering from these naturally occurring elements will therefore almost only scatter coherently.

2.4.2 The Double-Differential Scattering Cross Section

We measure the total scattered intensity, I(Q,E), in a neutron scattering experiment. This is a function of both the scattering vector Q (Eq. 2.15) and the energy of the scattered neutrons, E. A detector measures I(Q,E) by counting the number of neutrons scattered into an element of solid angle dΩ in the direction 2θ,φ (see Fig. 2.5), having an energy between E and E + ΔE, per the incoming particle flux, Φ. We refer from now on to I(Q,E) as the double-differential cross section:

Fig. 2.5

Scattering geometry for a sample mounted at the point O

$$ \begin{array}{l}I\left(\mathbf{Q},E\right)=\frac{d^2\sigma }{d\varOmega d E}=\\ {}\frac{\begin{array}{l}\mathrm{Number}\ \mathrm{of}\ \mathrm{neutrons}\ \mathrm{scattered}\ \mathrm{per}\ \mathrm{second}\ \mathrm{in}\mathrm{to}\ \\ {}d\varOmega\ \mathrm{in}\ \mathrm{the}\ \mathrm{direction}\ 2\theta, \varphi, \mathrm{with}\ \mathrm{final}\ \mathrm{energy}\ \\ {}\mathrm{between}\ \mathrm{E}\ \mathrm{and}\ \mathrm{E}+\varDelta \mathrm{E}\end{array}}{\varPhi d\varOmega d E}\end{array} $$

(2.12)

In most cases the detectors measure the whole range of energies, thereby integrating over the energy. Then the measured quantity, called the differential cross section is:

$$ \frac{d\sigma }{d\varOmega }={\displaystyle {\int}_0^{\infty}\frac{d^2\sigma }{d\varOmega dE}dE}. $$

(2.13)

The total scattering cross section, σ _s , is defined as:

$$ {\sigma}_s={\displaystyle {\int}_{\mathrm{All}\ \mathrm{directions}}\left(\frac{d\sigma }{d\varOmega}\right)}d \varOmega. $$

(2.14)

The scattering vector Q is further defined by:

$$ \mathbf{Q}={\mathbf{k}}_{\mathbf{f}}-{\mathbf{k}}_{\mathbf{i}} $$

(2.15)

where k _i is the incoming wave vector and k _f is the scattered wave vector (see Fig. 2.5). When $\left|{\mathbf{k}}_{\mathbf{i}}\right|=\left|{\mathbf{k}}_{\mathbf{f}}\right|$, the scattering is said to be elastic. If we consider scattering at an angle 2θ, i.e. axial symmetry, it can be shown by applying a little trigonometry to the scattering triangle in Fig. 2.6 (and using Eqs. 2.1 and 2.5), that Q = (4π/λ) sin θ. θ is half the scattering angle and λ the wavelength of the incoming neutrons.

Fig. 2.6

Scattering triangle where $\mathbf{Q}={\mathbf{k}}_{\mathbf{f}}-{\mathbf{k}}_{\mathbf{i}}$ is the difference between the wave vectors of the scattered and incoming neutrons and 2θ the scattering angle

A general expression for the scattered intensity, I(Q,E) in Eq. 2.12, was derived by Van Hove in 1954 [6] and is presented in Eq. 2.16. The actual derivation of this quantum mechanical equation is outside the scope of this book, but is explained in detail in several text books, for example, by Bacon [7], Squires [8], or in Los Alamos Science [9]. Van Hove showed that:

$$ I\left(\mathbf{Q},E\right)=\frac{1}{2\pi \hslash}\frac{k_f}{k_i}{\displaystyle \sum_{j,k}{b}_j{b}_k{\displaystyle {\int}_{-\infty}^{\infty}\left\langle {e}^{i\mathbf{Q}\cdot {\mathbf{r}}_k(0)}{e}^{-i\mathbf{Q}\cdot {\mathbf{r}}_j\left(\mathrm{t}\right)}\right\rangle {e}^{-i\omega t}dt}} $$

(2.16)

where the double sum is over pairs of atoms labelled j and k, with scattering lengths b _j and b _k , respectively, $\hslash =h/2\pi$ is the reduced Planck constant, and ω is defined by ħω = E − E ₀ (i.e., the difference in energy between the initial and final quantum states of the scattering system). The nucleus k is at position r _k at time zero and the nucleus j is located at position r _j at time t. The angular brackets denote that we need to perform an average over all thermodynamic states.

Equation 2.16 may seem simple, but since the position vectors r _j and r _k are quantum mechanical operators, its evaluation is not straightforward. For instructive purposes we ignore it here and treat the system in a classical manner. Then the double sum on the right side in Eq. 2.16 can be written as:

$$ \begin{array}{l}{\displaystyle \sum_{j,k}{b}_j{b}_k\left\langle {e}^{i\mathbf{Q}\cdot {\mathbf{r}}_k(0)}{e}^{-i\mathbf{Q}\cdot {\mathbf{r}}_j\left(\mathrm{t}\right)}\right\rangle }={\displaystyle \sum_{j,k}{b}_j{b}_k\left\langle {e}^{i\mathbf{Q}\cdot \left({\mathbf{r}}_k(0)-{\mathbf{r}}_j\left(\mathrm{t}\right)\right)}\right\rangle}\\ {}\kern10.6em ={\displaystyle \sum_{j,k}{b}_j{b}_k{\displaystyle {\int}_{-\infty}^{\infty}\left\langle \delta \left(\mathbf{r}-\left[{\mathbf{r}}_k(0)-{\mathbf{r}}_j(t)\right]\right)\right\rangle {e}^{i\mathbf{Q}\cdot \mathbf{r}}{d}^3\mathbf{r}}}\end{array} $$

(2.17)

where δ(r) is the Dirac delta function which is zero for all position vectors not equal to r. If we now assume an ideal one-isotope sample, all scattering lengths are equal to each other (b _j  = b _k  = b). The scattering lengths can now be moved outside of the summation, and Eq. 2.16 becomes:

$$ I\left(\mathbf{Q},E\right)=\frac{n{b}^2}{2\pi \hslash}\frac{k_f}{k_i}{\displaystyle {\int}_{-\infty}^{\infty }{\displaystyle {\int}_{-\infty}^{\infty }G\left(\mathbf{r},t\right){e}^{i\mathbf{Q}\cdot \mathbf{r}}{e}^{-i\omega t}{d}^3\mathbf{r}dt}} $$

(2.18)

n is the number of nuclei in the sample and G(r, t) is the time-dependent pair distribution function, which in this classical derivation can be defined as:

$$ G\left(\mathbf{r},t\right)=\frac{1}{n}{\displaystyle \sum_{j,k}\left\langle \delta \left(\mathbf{r}-\left[{\mathbf{r}}_k(0)-{\mathbf{r}}_j(t)\right]\right)\right\rangle }. $$

(2.19)

G(r, t) gives the probability to find a nucleus at the origin of a coordinate system at time zero as well as a nucleus at position r at time t. From Eq. 2.18 we see that the scattered intensity is proportional to the space and time Fourier transforms of G(r, t). This is a powerful result showing that in theory the crystal structure and its corresponding changes as a function of time is obtained by inverse Fourier transformation of the measured intensity. In reality this is not possible due to the so-called phase problem in crystallography, i.e. the phase information is lost when only the intensity (the scattering amplitude squared) is measured. However during the years several efficient methods to determine crystal structures from scattering data have been developed (see Chap. 3).

Earlier we assumed the sample to be mono-isotopic with just one value of b. In a sample containing more than one isotope, all scattering lengths appearing in Eq. 2.16 are not equal any longer, thus resulting in some important modifications to this equation. If A _j,k is an abbreviation for the integral in Eq. 2.16 and we omit the constants, we now get:

$$ I\left(\mathbf{Q},E\right)=\frac{\sigma_c}{4\pi }{\displaystyle \sum_{j,k}{A}_{j,k}}+\frac{\sigma_i}{4\pi }{\displaystyle \sum_j{A}_{j,j}} $$

(2.20)

${\sigma}_c=4\pi {\left(\overline{b}\right)}^2$ and ${\sigma}_i=4\pi \left(\overline{b^2}-{\left(\overline{b}\right)}^2\right)$ are the coherent and incoherent cross sections from Sect. 2.4, respectively. The first term in Eq. 2.20 represents the coherent scattering leading to interference effects. From Eqs. 2.16 and 2.20 we see that it depends on the correlation between the positions of different nuclei at different times. On the other hand, the incoherent scattering, represented by the second term in Eq. 2.20, is only dependent on the correlations between the positions of the same nucleus at different times. The incoherent contribution is generally independent of the scattering angle, resulting in a featureless addition to the background that is mostly ignored when performing neutron diffraction experiments. Yet incoherent scattering is very important for studies of diffusion processes using quasielastic neutron scattering.

A classic example of the peculiar nature of incoherent scattering is the big difference between protium and deuterium. Protium is a strong spin-incoherent scatterer because the triplet (total spin moment neutron + nucleus, J = 1) and the singlet states (J = 0) have very different scattering lengths (b ₊  = 10.81 fm, b ₋  = −47.42 fm), resulting in σ _i  = 80.3 and σ _c  = 1.76 barn, respectively. Deuterium has only one spin state in its ground state of I = 1, and b ₊  = 9.53 fm and b ₋  = 0.97 fm, and the corresponding values for deuterium are σ _i  = 2.05 and σ _c  = 5.59 barn, respectively. Therefore, naturally occurring hydrogen scatters mostly incoherently leading to a strong and featureless background in the neutron diffraction patterns of hydrogen containing samples. This means if possible deuterided samples should be used for diffraction experiments in order to reduce the incoherent scattering. When performing inelastic or quasielastic neutron scattering, on the other hand, the incoherent scattering is being used for studying diffusion, hence hydrogen is preferred over deuterium due to the much larger incoherent contribution.

By synthesizing compounds where there are specific units or groups of atoms including hydrogen and others with deuterium, the significant difference in scattering is used to mask and enhance specific parts of the compounds. See Chap. 6.

2.4.3 Magnetic Scattering

Due to the magnetic moment of neutrons, they interact with unpaired electrons in magnetic materials. This makes neutron scattering a unique method to determine magnetic properties in materials. The magnetic interaction experienced by the neutron is of similar strength as the nuclear interaction, and thus magnetic scattering is of similar intensity as nuclear scattering. In ferromagnetic materials all the magnetic moments are oriented along the same direction. The magnetic unit cell is in this case equal to the crystallographic one, and therefore the magnetic scattering gives additional contribution to the crystalline Bragg peaks only. However, for other kinds of magnetic ordering, for example, antiferromagnetic materials (commensurate or incommensurate with the crystal structure) or magnetic helices, magnetic scattering gives additional peaks in the diffraction patterns. In addition to determination of the type of magnetic ordering, it is also possible from the data treatment to determine both the direction and sizes of the magnetic moments. Neutrons interact with the unpaired electrons and therefore the scattering is determined by the magnetic form factor which is a function of the scattering angle. Thus the strongest magnetic scattering appears at low angles in the diffraction patterns.

2.5 Elastic, Inelastic, and Quasielastic Neutron Scattering

2.5.1 Elastic Scattering: Bragg Diffraction

Neutron scattering is a multifaceted discipline that has evolved into a vast array of different techniques. The most basic is elastic neutron diffraction, often called Bragg scattering or Bragg diffraction (similar for neutrons and X-rays). These experiments do not require the determination of the energy of the scattered neutrons and from the coherent term in Eq. 2.20 the intensity of the scattered beam as a function of the scattering vector Q is given by:

$$ I\left(\mathbf{Q}\right)={\displaystyle \sum_{j,k}{b}_j{b}_k{e}^{i\mathbf{Q}\cdot \left({\mathbf{r}}_j-{\mathbf{r}}_k\right)}}={\left|F\left(\mathbf{Q}\right)\right|}^2 $$

(2.21)

with coherent scattering lengths b _j and b _k , and the structure factor F(Q) is defined as:

$$ F\left(\mathbf{Q}\right)={\displaystyle \sum_j{b}_j{e}^{i\mathbf{Q}\cdot {\mathbf{r}}_j}}. $$

(2.22)

Crystalline materials are built up of identical entities, called unit cells. The unit cell is a parallelepiped spanned by three translation vectors a, b, and c (see Fig. 2.7). The unit cell itself is positioned by a lattice vector r _uvw  = u a + v b + w c, where u, v, w, are integers. The atomic position for each atom within the unit cell is given by r _j (see Eq. 2.22), and the overall position of the atom can be expressed as r _j  = r _uvw  + r _j ^unitcell (see Fig. 2.7).

Fig. 2.7

Unit cell of a face-centered orthorhombic lattice with lattice constants a, b, c. r _j ^unitcell is the equilibrium position of atom j in the unit cell

From this expression of r _j the structure factor in Eq. 2.22 can be expressed as:

$$ \begin{array}{l}{F}_{hkl}\left(\mathbf{Q}\right)={\displaystyle \sum_j^{n_{\mathrm{unitcell}}}{\displaystyle \sum_{u,v,w=-\infty}^{\infty }{b}_j{e}^{i\mathbf{Q}\cdot \left({\mathbf{r}}_{uvw}+{\mathbf{r}}_j^{\mathrm{unitcell}}\right)}}}\\ {}\kern3em ={\displaystyle \sum_{u,v,w=-\infty}^{\infty }{e}^{i\mathbf{Q}\cdot {\mathbf{r}}_{uvw}}}{\displaystyle \sum_j^{n_{\mathrm{unitcell}}}{b}_j{e}^{i\mathbf{Q}\cdot {\mathbf{r}}_j^{\mathrm{unitcell}}}}\end{array} $$

(2.23)

The first sum is over all unit cells in the crystal, typically assumed to be infinite, and the second sum is over all the n _unitcell atoms in the unit cell. The infinite triple sum can be expressed as a sum of δ-functions that describes a lattice, which leads us to the final expression for the structure factor (often named Laue’s interference function):

$$ {F}_{hkl}\left(\mathbf{Q}\right)=\frac{1}{V}{\displaystyle \sum_j^{n_{\mathrm{unitcell}}}{b}_j{e}^{i\mathbf{Q}\cdot {\mathbf{r}}_j^{\mathrm{unitcell}}}}{\displaystyle \sum_{h,k,l=-\infty}^{\infty}\delta \left(\mathbf{Q}-{\mathbf{Q}}_{hkl}\right)} $$

(2.24)

where Q _hkl  = 2π(h a* + k b* + l c*), a*, b*, and c* are the reciprocal vectors of a, b, and c defined by a · a* ≡ b · b* ≡ c · c* ≡ 1 and a · b* ≡ a · c* ≡ b · a* ≡ … ≡ 0. h, k, l are integers, while V is the volume of the unit cell. This implies that a crystal with perfect translational symmetry only scatters in certain directions, namely where Q = Q _hkl . The scattering in these directions corresponds to the Bragg scattering. F _hkl (Q) is zero everywhere else due to the sum of δ-functions which is zero except for Q = Q _hkl .

The condition for Bragg scattering is visualized in Fig. 2.8 and is usually expressed as the Bragg’s law:

$$ \lambda =2{d}_{hkl} \sin \left({\theta}_{hkl}\right) $$

(2.25)

Fig. 2.8

Illustration of Bragg’s law. Scattering of neutrons, with wavelength λ, regarded as specular reflection from a set of crystallographic planes shown as horizontal lines

where λ is the wavelength of the incoming and outgoing neutrons, d _hkl is the distance between the family of planes that cut the unit cell vectors a, b, and c, h, k, and l times, respectively, and θ _hkl is half the scattering angle between k _i and k _f as seen in Fig. 2.6. The Bragg scattering is often regarded as specular reflections from these planes (Fig. 2.8), hence the scattering in a direction 2θ _hkl is called a Bragg reflection where hkl are the so-called Miller indices for this reflection.

The expression in Eq. 2.24 is only valid for purely stationary atoms. In a real sample thermal energy makes the atoms oscillate about their equilibrium positions and the expression becomes:

$$ {F}_{hkl}\left(\mathbf{Q}\right)=\frac{1}{V}{\displaystyle \sum_j^{n_{\mathrm{unitcell}}}{b}_j{e}^{i\mathbf{Q}\cdot {\mathbf{r}}_j^{\mathrm{unitcell}}}{e}^{-{Q}^2\left\langle {u}_j^2\right\rangle /2}}{\displaystyle \sum_{h,k,l=-\infty}^{\infty}\delta \left(\mathbf{Q}-{\mathbf{Q}}_{hkl}\right)} $$

(2.26)

where ${e}^{-{Q}^2\left\langle {u}_j^2\right\rangle /2}$is the Debye–Waller factor that is taking into account the thermal vibrations of the atoms, and 〈u ² _j 〉 is the average of the squared displacement of atom j. The displacements can also come from static disorder and thus this parameter is designated as an atomic displacement parameter. Since an atom only contributes to the Bragg scattering when it is located at the center of its vibration ellipsoid, the intensity of the Bragg reflection becomes weaker due to the thermal vibrations, and the effect increases for increasing scattering angles. Chapter 3 covers powder neutron diffraction which is one of the major techniques used in studying, for example, hydrogen storage materials.

2.5.2 Inelastic Neutron Scattering: Phonons, Magnons

One of the advantages of using neutrons as a probe when studying condensed matter is that they can be used to measure atomic and molecular vibrations with inelastic coherent scattering, and thereby measuring energy transitions and energy levels in atoms. The term inelastic means that the magnitude of the neutron’s wave vector changes as well as the direction during the scattering process, hence the kinetic energy of the scattered neutron is modified. Vibrations of atoms in solid materials are correlated with each other into lattice waves, which are superpositions of waves of different frequencies and wavelengths. These waves are called phonons, and have quantized energies of E = hv, where v is the frequency of the collective motion of all atoms linked to a given phonon.

Analogous to a phonon, a magnon is a quantized energy packet resulting from collective oscillations of the magnetic moments in solid materials. These oscillations are called spin waves. The magnon carries an energy of E = hν where ν is the frequency of the spin wave. An excitation of a magnon corresponds to the reversal of one spin ½.

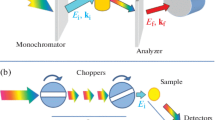
An incoming neutron can interact with a phonon or a magnon, and will either give or take up the quantized energy before being scattered. This process is called inelastic because it involves a change of the kinetic energy of the neutron. Since the energy of a typical phonon or magnon is on the same order as the kinetic energy of the incoming neutrons, the change in energy of the scattered neutron is significant and possible to measure quite accurately. From the change of the neutron energy the phonon and magnon frequencies can be determined. A typical setup (Fig. 2.9) uses either a monochromatic incoming beam, and measures the scattered neutrons with the time of flight method to find the energy transfer (direct geometry), or it measures the scattered neutrons using an analyzer crystal after the sample (indirect geometry). The latter type is commonly referred to as a triple-axis spectrometer. More on this technique can be found in Chap. 9.

Fig. 2.9

Geometries of inelastic neutron scattering setups

2.5.3 Quasielastic Neutron Scattering

As mentioned earlier the incoherent contribution to the scattering in a typical diffraction experiment is handled like a featureless background, which may imply that there is no information obtainable from this. On the contrary, a fair deal of knowledge can be extracted from this signal. In quasielastic neutron scattering (QENS) we can make use of the incoherent contribution to the inelastic scattering to measure diffusion processes. Since diffusion in its simplest form is one particle jumping between lattice sites, it makes sense to analyze the incoherent scattering, because it provides the dynamics of individual particles. On the other hand, inelastic coherent scattering is due to correlated motions of atoms, e.g., phonons. The big incoherent scattering cross section of hydrogen enables excellent contrast when studying hydrogen diffusion.

Similarly to inelastic scattering, QENS measures energy transitions using similar setups found in Fig. 2.9. The name quasielastic comes from the fact that the measurements are probing events having energy transfers much lower than the incoming energy, with deviations very close to the elastic scattering. Consequently, the energy has to be measured with high resolution. The energy transitions are generally not quantized, leading to a continuous Lorentzian broadening of the elastic peak (where the energy transfer is zero). More on incoherent neutron scattering and QENS can be found in Chaps. 8 and 9, respectively.

2.6 Summary

Technique	Physical principle	Information provided
Diffraction (Chaps. 3 and 4)	Elastic scattering	Crystal structure on atomic scale: positions of atoms including hydrogen, lattice constants, phase fractions, pair distribution functions
Reflectometry (Chap. 5)	Refraction	Layer thickness and scattering length density profile (e.g., hydrogen profile) with nm resolution and absorption/desorption studies in real time
Small angle neutron scattering (Chap. 6)	Elastic scattering	Structure on a mesoscopic scale (~1–100 nm): macromolecules, porous and biological systems, aggregates of particles in a matrix or scaffolds
Radiography/Neutron imaging (Chap. 7)	Absorption	Structure on a macroscopic level (typical resolution in the order of 50 microns), absorption and desorption studies in real time
Incoherent neutron scattering (Chap. 8)	Incoherent scattering	H2/D2 content and absorption/desorption studies in real time
Inelastic scattering (Chap. 9)	Coherent and incoherent inelastic scattering	Dynamic processes: vibrational/rotational states, binding energies
Quasielastic scattering (Chap. 9)	Incoherent inelastic scattering	Dynamic processes: H2/D2 diffusion, molecular vibrations and rotations, activation energy