Towards Fast and Accurate Solutions to Vehicle Routing in a Large-Scale and Dynamic Environment

Abstract

The delivery and courier services are entering a period of rapid change due to the recent technological advancements, E-commerce competition and crowdsourcing business models. These revolutions impose new challenges to the well studied vehicle routing problem by demanding (a) more ad-hoc and near real time computation - as opposed to nightly batch jobs - of delivery routes for large number of delivery locations, and (b) the ability to deal with the dynamism due to the changing traffic conditions on road networks. In this paper, we study the Time-Dependent Vehicle Routing Problem (TDVRP) that enables both efficient and accurate solutions for large number of delivery locations on real world road network. Previous Operation Research (OR) approaches are not suitable to address the aforementioned new challenges in delivery business because they all rely on a time-consuming a priori data-preparation phase (i.e., the computation of a cost matrix between every pair of delivery locations at each time interval). Instead, we propose a spatial-search-based framework that utilizes an on-the-fly shortest path computation eliminating the OR data-preparation phase. To further improve the efficiency, we adaptively choose the more promising delivery locations and operators to reduce unnecessary search of the solution space. Our experiments with real road networks and real traffic data and delivery locations show that our algorithm can solve a TDVRP instance with 1000 delivery locations within 20 min, which is 8 times faster than the state-of-the-art approach, while achieving similar accuracy.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The vehicle routing problem (VRP) aims to find a set of routes at a minimal cost (e.g., total distance or travel time) for a set of geographically dispersed delivery locations which are assigned to a fleet of delivery vehicles. Each location is visited only once, by only one vehicle, and each vehicle has a limited capacity. VRP is an NP-hard combinatorial optimization problem. Exact algorithms based on branch-and-bound or dynamic programming are slow and only capable of solving relatively small instances (e.g., less than 30 delivery locations), thus heuristics are mainly used in practice.

While VRP and its variations (e.g., VRP with time windows and VRP with multiple depots) have been extensively studied in the literature [1], in recent years we are witnessing a renewed interest to this problem due to two very important transformations. First, the traffic data at a very high resolution have become available that can significantly enhance the accuracy of the routes assigned to delivery vehicles and can consequently result in considerable benefit. For example, according to UPS [2] the company can save $50 million a year if the average daily travel distance of its drivers can be reduced by one mile, which is typically less than 1 % of the daily travel distance of a delivery vehicle. Second, due to the increasing popularity of on-line shopping (i.e., E-commerce), there is a growing need for fast delivery to very large number of customers; to the point that some E-commerce companies (e.g., Google Express [3]) are developing their own proprietary delivery solutions to stay ahead of the competition. This is because the existing solutions provided by the major delivery companies (e.g., FedEx and UPS) assume that the delivery orders (and their locations) are known (at least a day) in advance. It is also not hard to envision an Uber-type application for deliveries in near-future, democratizing the delivery business.

These two transformations have challenged the traditional approaches to VRP. The basis of all the traditional approaches are to utilize some sort of Operation Research (OR) technique (e.g., integer programming) to solve VRP. Consequently, as an input to all these approaches, a pairwise distance matrix is required, which contains the distances between every two delivery locations. Without the dynamism resulting from traffic data and in the world where delivery plans were prepared the night before for a small number of delivery locations, creating such a matrix a priori was acceptable. However, considering travel-time as the “distance”, different time intervals in the day require different distance matrices (due to traffic congestions), which increases the complexity of preparing the input for the OR approaches. The increase in the complexity along with more delivery locations and less time to prepare the delivery plans render the OR data-preparation phase impractical.

Therefore, in this paper, we take a completely different approach to solve VRP by utilizing the lessons learned from the field of spatial-databases. First, considering the vehicle routing problem in time-dependent road networks, we compute network distance (i.e., travel-time) on-the-fly utilizing a time-dependent shortest path technique from the spatial-database literature [4]. Note that although some OR-based approaches are developed for the Time-Dependent version of VRP [5, 6] (called TDVRP hereafter), they still rely on the time-consuming data preparation phase. In fact, the complexity of that phase becomes even worse because now it requires the computation of the pairwise distance matrix for each and every time interval in a day. We, however, completely eliminate the data preparation phase by on-demand calculation of shortest path between two delivery locations and at the same time caching the partial results from the expansion of shortest path computation for future use. As a byproduct, our proposed approach could start finding the solutions as soon as the delivery requests are received.

Second, we improve another phase in the OR approach known as local search, by exploiting the spatial information of the locations in the search. In particular, the local search starts from an initial solution and iteratively moves to new solution by selecting from a neighborhood of the current solution through “the move operators”. The main bottleneck of the local search is that it needs large number of iterations to find neighborhood solutions and this number grows exponentially with the number of delivery locations. We observe that local search relies on blind evaluation of delivery locations and move operators towards finding neighborhood solutions in which they treat each delivery locations and operators equally. However, we argue that not all delivery locations are equally important: some delivery locations are more promising to generate the effective neighborhood solutions and hence we assign weights to each delivery location. The delivery locations with higher weights are more likely to be chosen and their weights are adjusted adaptively based on their previous performance. A similar idea applies to the operators: operators with higher weights are more likely to be applied. Consequently, our algorithm leverages a spatially guided search by selecting promising delivery locations and operators first, which significantly reduces the running time while generating high-quality solution.

We conducted extensive experiments on real world road network of Los Angeles with real traffic data. Experimental results show that (1) by leveraging the real time-dependent traffic pattern, we can reduce the travel cost of routes by 7 % on average with respect to its static counterparts, and (2) our algorithm can solve TDVRP with 1000 delivery locations within 20 min, which is 8 times faster than the state-of-the-art approach, while achieving similar accuracy.

The remainder of this paper is organized as follows. In Sect. 2, we formally define our Vehicle Routing Problem in Time-dependent road network. In Sect. 3, we present our spatial-search-based framework to solve this problem. Experiment results are reported in Sect. 4. In Sect. 5, we review the related work and Sect. 6 concludes the paper.

2 Problem Definition

In this section, we formally define the vehicle routing problem in time-dependent road networks. We model the road network as a time-dependent weighted graph where the non-negative weights are time-dependent travel times (i.e., positive piece-wise linear functions of time) between the nodes.

Definition 1

(Time-dependent Graph). A Time-dependent Graph ($G_T$) is defined as $G_T = (V, E)$, where V and E represent set of nodes and edges, respectively. For every edge $e(v_i, v_j)$, there is a cost function $c(v_i ,v_j, t)$ which specifies the travel cost from $v_i$ to $v_j$ at time t.

Definition 2

(Time-dependent Travel Cost). Let $\{s = v_1, v_2 , \cdots , v_k = d\}$ represents a path which contains a sequence of nodes where $e(v_i , v_{i+1}) \in E$ and $i = 1, \cdots , k-1$. Given a $G_T$, a path (s, d) from source s to destination d, and a departure-time at the source $t_s$, the time-dependent travel cost $TT(s \rightsquigarrow d, t_s)$ is the time it takes to travel along the path. Since the travel time of an edge varies depends on the arrival time to that edge (i.e., arrival dependency), the travel time is computed as follows:

$$\begin{aligned} TT(s\rightsquigarrow d, t_s) = \sum _{i = 1}^{k - 1}{c(v_i, v_{i + 1}, t_i)} \end{aligned}$$

$\text {where } t_1 = t_s,\, t_{i+1} = t_i + c(v_i, v_{i+1}, t_i), i = 1, \cdots k.$

Definition 3

(Time-dependent Shortest Path). Given a $G_T, s, d$ and $t_s$, the time-dependent shortest path TDSP$(s, d, t_s)$ is a path with the minimum travel-time among all paths from s to d starting at time $t_s$.

Definition 4

(Vehicle Routing Problem in Time-dependent Road Network). Given a time-dependent graph $G_T$, a depot $v_d \in V$, a start time $t_s$, k delivery vehicles with capacity C, and a set of delivery locations $V_c \subset V$, each delivery location $v_i \in V_c$ has a demand of $d_i$, TDVRP aims to find k routes with the minimum total time-dependent travel cost subject to the following constraints:

• all routes start and end at the depot;

• each delivery location in $V_c$ is visited exactly once by exactly one vehicle;

• the total demands of delivery locations in a route must not exceed C;

Note that the input TD road network $G_t$ could have more than 100 thousand nodes and edges, the delivery locations are a small subset of nodes in the given road network and the travel time between each delivery location is not known in advance. This is different with the typical input of VRP, which requires a pairwise cost matrix between each pair of delivery locations per instance.

3 Proposed Algorithm

In this section, we first investigate one state-of-the-art local search based algorithm termed RTR [7]. RTR has shown [8] to be able to generate high quality solutions for large-scale delivery locations for static network. However, we discover that RTR has two major drawbacks. First, like other Operation Research (OR) approaches, RTR relies on the time consuming data-preparation step. In addition, we further identify that the blind evaluation of neighborhood solution dominates the search process of RTR.

To address the above two issues, we propose a Spatial-Search-Based Local Search (SSBLS) framework (Sect. 3.3) which incorporates on-the-fly shortest path computation (Sect. 3.5) into the local search framework. To avoid the unnecessary search of the solution space, we adaptively choose more promising delivery locations and move operators (Sect. 3.4). Note that our proposed improvements can be easily adopted into other local search based algorithms which iteratively generates and improves the neighborhood solutions.

3.1 Local Search Based Approach

Local search is a popular framework which is proven to provide a high-quality solution for VRP. Local search starts from an initial solution and iteratively moves to one of the neighborhood solutions based on heuristics. Typically, a local search algorithm is developed by the following general framework:

• Step 1: choose an initial solution. (Initial solution)

• Step 2: generate one or more neighborhood solutions by applying operators to the current solution. (Neighborhood generation)

• Step 3: select one solution to continue using heuristic, e.g., the first, the best or arbitrary one. (Acceptance criteria)

• Step 4: if the stop condition is not satisfied, e.g., the solution is not considered as optimal, then goto Step2, else stop. (Stop condition)

In general, the initial solution is generated based on some heuristic methods (e.g., Clarke-wright heuristic [9]), consequently a local move procedure is used to generate neighborhood solution. The definition of local move is as follows:

Definition 5

(Local Move). Local move is the process of generating a new solution by removing k edges in the current solution and replacing them with other k edges.

Local move is performed by applying one operator at a time to the existing solution. In this paper, we use three basic operators studied in [7], i.e., One-Point (OP), Two-Point (TP) and Two-Opt (TO), because the combination of these operators is enough to generate high-quality solution for large scale delivery locations. Specifically, each operator uses three parameters to complete the local move. Given a current solution S, a selected location $v_x$, and one of its neighboring location $v_y$, $OP(S, v_x, v_y)$ moves $v_x$ to the new position after $v_y$(i.e., $v_x$ is visited after $v_y$), $TP(S, v_x, v_y)$ swaps the positions of $v_x, v_y$ in S; and finally $TO(S, v_x, v_y)$ removes the two edges $e(v_x, v_x'), e(v_y, v_y')$ in S by replacing them with $e(v_x, v_y)$ and $e(v_x', v_y')$.

Fig. 1.

Neighborhood solution generation through One-Point Move

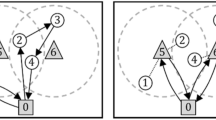
Figure 1 shows the process of applying One-Point operator to a solution S which contains two routes $r_1$ and $r_2$. After applying $OP(S, v_j, v_a)$, point $v_j$ in $r_2$ is relocated to the position after $v_a$ in $r_1$, thus generating a new neighborhood solution which contains $r_1'$ and $r_2'$. In this way, the three edges $e(v_i, v_j), e(v_j, v_k)$ and $e(v_a, v_b)$ in S are replaced by $e(v_i, v_k), e(v_a, v_j)$ and $e(v_j, v_b)$. Once the neighborhood solution is generated, the algorithm checks its feasibility by evaluating its cost and decides whether to choose this solution to continue.

3.2 Baseline Approach: RTR

RTR follows local search framework: (1) An initial feasible solution S is generated using the classic Clarke-Wright heuristic [9], (2) The neighborhood generation and improvement over S is shown in Algorithm 1. The algorithm interleaves with two search procedures: record-to-record and downhill search. The major difference between the two search procedures is that: for record-to-record search, when we apply one operator op to one location $v_i$, a non-improving solution with a small range of deviation to the current best solution is allowed to jump out of the local optimal (lines 13–14); on the other hand, only the improved solution is accepted for the downhill search. In terms of acceptance criteria, RTR uses the first-accept standard, i.e., whenever a better solution is found, the local search for the current location $v_i$ is stopped and we move to the next location (lines 9–11). (3) RTR stops when no better solution can be found after K continuous executions of Algorithm 1.

Although RTR is one of the best choices for large-scale VRP, it is inefficient for Time-dependent road networks where each edge has different (time-varying) costs for each time instance throughout the day. In the following, we analyze the bottleneck in this search process. As shown in Algorithm 1, during each search procedure (record-to-record and downhill), each operator is applied to each delivery location of each route, which means that the algorithm needs to generate and evaluate all these newly generated solutions to determine whether to accept it or not. In addition, with RTR, all other delivery locations are treated as the neighbors of one delivery location (line 4). Clearly such exhaustive search dominates the running time of RTR algorithm because the number of generate-and-evaluate process grows exponentially with the size. Moreover, compared to static road networks, the evaluation of neighborhood solution with TD road network is more time consuming (line 6). This is because changing the edges in a route due to operators could lead to different arrival times of the corresponding delivery locations, which in turn changes the weight of the following edges.

To illustrate, consider Fig. 1, in static case, the total travel cost of the new solution $S'$ can be calculated using the following equation:

$$\begin{aligned}&c(S') = c(r_1') + c(r_2') = c(r_1) + \varDelta c(r_1) + c(r_2) + \varDelta c(r_2) \end{aligned}$$

$\varDelta c(r_1)$ and $\varDelta c(r_2)$ are calculated via the following equation:

$$\begin{aligned} \varDelta c(r_1)&= -c(v_a, v_b) + c(v_a, v_j) + c(v_j, v_b),\varDelta c(r_2)&= c(v_i, v_k) - c(v_i, v_j) - c(v_j, v_k) \end{aligned}$$

where $c(v_i, v_j)$ represents the static travel cost between delivery locations $v_i$ and $v_j$, and c(r) represent the static cost of route r.

In the static case, the evaluation involves five delivery locations (i.e., $v_a$, $v_b$, $v_i$, $v_j$, $v_k$) and can be calculated in constant time when the cost matrix is given. However, in TD case, because the arrival times of delivery location $v_j$ and $v_k$ are changing, the arrival times for the following delivery locations (e.g., $v_c$ and $v_l$) are also changing which result in re-calculating the cost of the whole path.

Fig. 2.

Methods to improve efficiency

3.3 Spatial-Search-Based Local Search Framework

By analyzing RTR, we find that two processes dominant its total running time and make RTR less practical for the new delivery application: (1) the neighborhood generation and evaluation process. (2) the data-preparation process which computes the travel cost between each pair of nodes at each time interval.

The above observations lead us to the road map of how to improve the efficiency of RTR while maintain the high accuracy. As shown in Fig. 2, we aim to eliminate the data preparation process as well as reduce the evaluation time¹. Towards this end, we propose a Spatial-Search-Based Local Search (SSBLS) framework, which is shown in Algorithm 2.

SSBLS starts with an initial solution which is generated using the Clarke-Wright algorithm (line 2). During each search procedure (record-to-record and downhill search), in order to generate the neighborhood solution, it adaptively selects an operator op and a delivery location $v_i$ (lines 5–6) based on their weights (See Sect. 3.4). Subsequently, the algorithm applies the selected operator to the delivery location $v_i$ and iterates through the neighborhood solution (lines 7–16). The newly generated solution $S'$ is evaluated via our on-demand shortest path calculation procedure (See Sect. 3.5), and thus the algorithm determines whether to accept $S'$. If a solution is accepted, the current best record r and the solution S are updated accordingly (lines 14–15). The weights of delivery locations and operators are updated based on whether they yield a better neighborhood solution in every I iterations (lines 9–10). Consequently, the algorithms repeats this process until the stop condition is satisfied. In this paper, we use the same stop condition as RTR, i.e., the maximum number failure to find a better solution. To save space, we omit the specific steps for record-to-record search in Algorithm 2, which is the same as those listed in Algorithm 1.

3.4 Adaptive Point and Operator Selection

A straightforward method to improve the efficiency is to restrict the number of candidate neighbors of a delivery location. This is because when applying operators to one specific location (line 4 in Algorithm 1), RTR treats all other delivery locations as the neighbor of that location. Therefore, to reduce the number of evaluations, we can only apply operators to a fixed number of its nearest neighbors (rather than all other delivery locations) for a delivery location [7].

Besides restricting the neighborhood size, we further propose a novel approach to reduce the number of evaluations. The intuition of our algorithm is that not all delivery locations and operators are equally important in order to generate the new neighborhood solutions. Towards this end, we first define“Effective Local Move” and explain some observations based on the empirical study on real-world dataset with 100 delivery locations on Los Angeles road network. Similar observations exists for larger datasets (see more details in Sect. 4).

Definition 6

(Effective Local Move). Effective local move is defined as the local move whose corresponding solution is accepted by the algorithm based on variable criterion, e.g., down-hill, simulate-annealing.

Observation 1

Only very small portion of local moves will become effective local move, most of the new solutions generated by local moves are not effective and hence not be accepted.

In the process of local search, we record the number of evaluated local moves and the number of resulted effective moves. Table 1 shows the statistic of three types of local moves. We observe that only $0.21\,\%$ of the local moves become effective, i.e., the corresponding solutions are accepted by the algorithm. Because a large portion of the evaluation is useless, our idea to reduce the number of evaluations is via selectively evaluating the promising moves. Intuitively, some operators (e.g., One-Point) are more suited for one type of instance while others are best suited for another type of instance. In addition, instead of using the same sequence to iterate operators and customers in Algorithm 1, we believe that alternating between different customers (operators) makes the heuristic more robust. In the following, we discuss how to decide on the promising delivery locations and operators.

Table 1. Local move statistics

Promising Delivery Locations and Weights Assignment. Figure 3 shows the distribution of the effectiveness of each delivery location. The effectiveness is measured by the percentage of local move that leads to the effective local move via applying operators to one specific delivery location. From Fig. 3, we observe that some delivery locations are much more effective than the remaining locations (e.g., the effectiveness of the top 1 delivery location is at least 20 times higher than the least effective point), which leads us to the following observation and define the promising delivery locations.

Fig. 3.

Distribution of the effectiveness of delivery locations (x-axis is ordered by the effectiveness)

Observation 2

Delivery locations are not equally effective in generating better result. In other words, applying operators on some delivery locations are more likely to generate a solution with lower travel cost than others.

To capture the effectiveness of the delivery locations, we assign weight $w_i$ to each delivery location $v_i$ (initially they have the same weights), and a delivery location is selected with probability that is proportional to its weight. Moreover, we adjust the weight of a delivery location in the search process based on its performance in the previous iterations, i.e., the better it performs, the more likely its weight will be increased.

Specifically, we divide the whole local search process into separate parts, each part contains I iterations. Suppose we are in the kth part of the search process, the weight of one delivery location in the $(k+1)$th part is updated once we completed the I iteration in the kth part by the following equation (line 10 in Algorithm 2):

$$\begin{aligned} w_i^{k+1} = (1-\eta ) w_i^{k} + \eta \frac{\lambda _i^{k}}{\varLambda _i^{k}} \end{aligned}$$

(1)

where $\varLambda _i^{k}$ is the total number of local moves that involves delivery location $v_i$ during the kth part, $\lambda _i^{k}$ is the corresponding total number of effective local moves that involves $v_i$ during the kth part, and $\eta$ is learning rate which captures the trade-off about how much we should rely on the performance of the kth part or the previous $(k-1)$ parts. If $\eta = 0$, the weight only relies on the previous $(k-1)$ parts of the search process, otherwise if $\eta = 1$, the weight only relies on the performance on the kth part of search. Usually, $0 < \eta < 1$, and parameter tunning is required to get the best performance.

Once we have assign weights to each delivery location, the probability that one delivery location is chosen to generate the neighborhood solution is calculated in the following equation:

$$\begin{aligned} Prob(v_i) = \frac{w_i}{\sum _{j = 1}^{N} w_j} \end{aligned}$$

(2)

where N is the number of delivery locations, $w_i$ the weight of $v_i$.

Similar to the delivery locations, operators are also not equally effective. Therefore, we apply a similar idea to the operators. Because of the space limitation, we omit the details here.

3.5 Eliminating Data-Preparation

When dealing with vehicle routing problem, existing OR based methods assume that the travel costs between each pair of delivery locations are calculated in advance, or can be calculated in O(1) time (e.g., in Euclidean space). Usually, the calculated travel cost is stored in a matrix-like structure (referred as cost matrix).

Although the cost matrix can be calculated in static cases, it is far more time-consuming to do this precomputation in time-dependent road network. This is because it has to calculate the time-dependent travel costs between every point pair in each time interval. This process involves $O(TN^2)$ time-dependent shortest path calculation, where T is the number of time intervals, N is the number of delivery locations. Note that the shortest path calculation in time-dependent road network is costly [4].

Table 2. Percentage of accessed cells in cost matrix

Observation 3

Most of the precomputed travel cost is not required.

To analyze the effectiveness of the data preparation step, we record the number of cells in cost matrix that is accessed by the algorithm for at least once. If the algorithm used the travel cost from location $v_i$ to location $v_j$ at the t-th time interval. then the corresponding cell, e.g., cost[i][j][t], will be accessed. Table 2 shows the percentage of accessed cells in the cost matrix (neighbor size $\sigma = 40$) with different number of delivery locations. As shown in Table 2, most of the cells in the cost matrix have never been accessed. For example, less than 5 % of the cells in the matrix are accessed when the number of delivery locations is 1000. This could be explained via the following reasons:

• Most of the effective local moves are those applied to a delivery location and its nearby locations, which means that the shortest path is only required between a location and some of its close neighbors.

• For a certain pair of delivery locations, only a small portion of the time intervals is accessed. For example, suppose the vehicle departs from depot at $t_0$, and the minimum travel time between the depot $v_d$ and a delivery location $v_i$ is $c(v_d, v_i, t_0)$, then it is possible that the time-dependent travel cost between $v_d$ and $v_i$ with start time earlier than $t_0 + c(v_d, v_i, t_0)$ are not accessed. This is because the path from depot to $v_i$ which bypasses other delivery location may yield a later arrival time than the path which directly passes the location $v_d$.

Based on the above observation, we argue that data preparation process can be eliminated and replaced by an on-demand calculation strategy. The main idea is to compute shortest path only when it is needed, and at the same time the partial results are cached from the expansion of shortest path computation for future usage. Algorithm 3 shows our proposed on-demand-calculation approach to evaluate the routes of a candidate solution. When one route of the solution is changing, we recalculate the travel cost from the beginning of this route (lines 4–10). In this process, if the travel cost between two delivery locations $v_i$ and $v_j$ during a time interval is not cached previously, function TDSPAndCache is called on-the-fly to calculate the travel cost (line 9). Meanwhile, the travel cost from $v_i$ to its $\sigma$ nearest neighbors is also calculated and cached through the expansion of $v_i$ because these neighbors are usually close to the current delivery location and caching them could facilitate the future search process. We use the time-dependent incremental network expansion algorithm described in [10].

4 Experimental Evaluation

4.1 Experimental Settings

Datasets. The experiments are conducted in Los Angeles(LA) road network dataset which contains 111,532 vertices and 183,945 edges. The time-varying edge patterns(i.e., time-dependent edge weights) of LA road network are generated from the sensor dataset we have been collecting in the past three years: we split the day time into 60 intervals from 6am to 9pm, and for each interval we assign the aggregated sensor data travel times to the corresponding network segment. In terms of the delivery locations, they are obtained from a delivery company in Los Angeles, each delivery locations corresponds to a node in the LA road network. We generate 40 test cases from these real delivery locations, which contains 100, 200, 500 and 1000 delivery locations separately, each has 10 test cases².

Baseline Approaches. We compare our proposed algorithm with the following algorithms:

• Sweep: a cluster-first and route-second approach [11].

• Clarke-Wright: a saving heuristic based approach [9] that is widely used in most industries.

• TDRTR: we extend RTR to support time-dependent road network. Specifically, we pre-compute the cost matrix and evaluate the travel cost using time-dependent edge weights.

Accuracy Evaluation Method. For accuracy comparison, TDRTR is treated as the benchmark as it usually generates the best result.Thus, we compute the gap between the travel time from the current solution and the solution returned by TDRTR. Formally, for a problem instance, suppose the travel time of a solution generated by another algorithm (e.g., Sweep) is $c'$, and the travel time of the solution generated by TDRTR is c, then the gap $\epsilon = \frac{c'- c}{c}$.

Smaller gap means smaller travel cost and thus yields higher accuracy. Note that the value of gap can be negative, because sometimes an algorithm could achieve better solution than TDRTR.

Configuration. We first compare our proposed algorithm(SSBLS) with Sweep, Clarke-Wright and TDRTR. For SSBLS, we use the parameters $\sigma$ and $\eta$ which produces the best solution tuned in the experiment. To show the effectiveness of using time-dependent road network, we also apply RTR in the static road network and evaluate the retrieved solution on the time-dependent road network. The steps are listed as follows: (1) generate a static road network by averaging the travel cost of each edge during the day. (2) run RTR in the generated averaged static road network, and generate a routing plan. (3) evaluate the travel cost of the routing plan in the time-dependent road network.

We then vary the neighbor size $\sigma$, and the learning rate $\eta$ in the adaptive delivery location and operator selection process. All algorithms were implemented using Java, and all the experiments were performed on a Linux machine with 3.5 GHz CPU and 16 GB RAM.

4.2 Comparisons of Different Algorithms

Figure 4 shows the accuracy comparison between algorithms with respect to number of delivery locations. As illustrated, SSBLS achieves a similar accuracy with TDRTR and performs better than RTR. In general, local search based algorithms (e.g., SSBLS, TDRTR and RTR) are much more accurate than Sweep and Clarke-Wright. For example, SSBLS is 15 % to 27 % more accurate than Sweep or Clarke-Wright algorithm. In addition, with increasing number of delivery locations, the benefit tends to grow larger.

Fig. 4.

Accuracy comparison

Fig. 5.

Efficiency comparison

At the same time, with comparing RTR with TDRTR, we observe that time-dependent road network based apoproach can save 6 % to 8 % travel cost. This is because in real world road network, the travel cost between two delivery locations may be quite different during rush hours and non-rush hours. Failing to consider traffic information leads to congestion, and thus larger travel cost.

Figure 5 shows the comparison of efficiency between different algorithms. We also show the precomputation (i.e., data preparation) time for TDRTR. As classic heuristics are much faster, and they can generate a feasible schedule within 1 min even for more than 1000 delivery locations. However, these heuristic algorithms suffer from low accuracy, which makes them less promising in practice. Although SSBLS is less efficient than Sweep and Clarke-Wright, SSBLS is much more faster than TDRTR. For example, SSBLS solves a problem instance with 1000 delivery locations in 20 min, which is 8 times faster than TDRTR. This is because (1) data preparation step is eliminated in SSBLS, which takes more than half of the total running time for TDRTR, as shown in Fig. 5, (2) SSBLS prefers to choose promising delivery locations and operators to generate neighborhood solution, thus reduce the unnecessary search of the solution space.

Note that although RTR is less accurate than SSBLS, RTR is a little faster than SSBLS. This is mainly because RTR is performed in the static road network. Compared to the time-dependent road network, (1) data preparation process in static road network is much faster, i.e., the number of interval is only 1 rather than 60, (2) travel cost evaluation in static network is also much faster.

In summary, considering the balance between accuracy and efficiency, SSBLS is best suitable for fast delivery with large scale delivery locations.

Fig. 6.

Neighbor size v.s. efficiency

Fig. 7.

Neighbor size v.s. accuracy

4.3 Effect of Neighbor Size

Figures 6 and 7 show the effect of neighbor size $\sigma$ in terms of efficiency and accuracy when the number of delivery locations N are 100 and 500. For $N=100$, $\sigma \in [10, 100]$ , and for $N=500$, $\sigma \in [10, 500]$. We use the number of evaluations to describe the relative speed. Generally, with decreasing $\sigma$, the algorithm tends to be more efficient but less accurate. For example, by setting $\sigma = 10$, the number of evaluated moves is reduced to 10 % compared with the case where $\sigma =100$, however it suffers from a considerable drop of accuracy. In the following experiment, we set $\sigma = 40$ to balance accuracy and efficiency.

Table 3. Effect of adaptive delivery location selection ($\sigma =40, N=100$)

4.4 Effect of Adaptive Delivery Location Selection

Table 3 shows the effect of adaptive delivery location selection. “–” means adaptive delivery location selection is not used. With increasing $\eta$, the accuracy first increases and then decreases. Thus, parameter tuning is required to achieve a good result. In addition, using adaptive delivery location selection also increases the efficiency. We use the number of evaluated moves to compare the relative efficiency of using different value of $\eta$. With adaptive delivery location selection, the algorithm prefers to conduct local moves on promising delivery locations, thus it is more likely to generate a better neighbor solution and reach the (local) optimal solution with less number of iterations. From Table 3, we find that by setting the learning rate $\eta =0.02$, the algorithm reduces the number of evaluated moves to half while achieves a better accuracy compared with treating all the delivery locations with equal importance.

4.5 Effect of Adaptive Operator Selection

Table 4 shows the performance of different operator selection strategy. The number of evaluations describe the relative speed, and the gap represents the accuracy. In this set of experiment three operators are used: i.e., One-Point(OP), Two-Point(TP) and Two-Opt(TO). We compare the performance of using different operators, “X” in the cell means one corresponding operator is used.

Table 4. Effect of adaptive operator selection ($\sigma =40, N=100$)

As shown in Table 4, different operator strategies result in different efficiency and accuracy. Generally, the more operators we use, the more accurate results and the more number of evaluations will be conducted. However, by adaptively selecting operators in the local search process, the algorithm manages to be 3 times faster than using all three operators, while not compromising the accuracy. This is because by applying promising operators, i.e. those who have good performance in the previous iterations, the algorithm is more likely to generate a better neighborhood solution, thus quickly reaching a (local) optimal, i.e., meet the stop condition with less number of evaluations.

5 Related Work

Vehicle Routing Problem (VRP)  [1] is a well studied combinatorial optimization problem with different variants such as vehicle routing problem with time windows (VRPTW) [6, 12], the capacitated vehicle routing problem (CVRP) [13]. Recently, the delivery and courier services are entering a period of rapid change enabled by recent technologies. On-time and fast delivery is becoming a significant differentiator for both delivery and E-commerce companies (e.g., Amazon), and hence same-day delivery or even 2-hour delivery become increasingly popular. To enable this new type of delivery, the efficiency and the accuracy are two of the most important factors. Previous methods focus either on efficiency or quality, but not both. Among the heuristic algorithms on the VRP problem, there are two main categories: classic heuristics and meta-heuristics. Classic heuristics (e.g., Clarke-Wright [9], Sweep algorithms [14]) emphasize more on quickly obtaining a feasible solution: for example, Clarke-Wright algorithm starts with an initial solution where each route only contains one delivery location, it continuously merges two routes into one route which generates the largest savings whenever it is feasible. The drawback with classic heuristics is that the solution could exists more than 20 % deviation with the best-known solution. This means that even in a small delivery instance with around 30 delivery locations, the solution calculated by classic heuristics could take 1 hour more delivery time than the best solution. In contrast, meta-heuristics perform a more thorough search of the solution space and hence gain more in solution quality but at the expense of speed. For example, even for a small delivery instance with around 100 delivery locations, some meta-heuristics [1] take more than one hour to calculate a routing plan with gap of less than 1 % with the best solution. In addition, this time usually increases exponentially when the number of delivery locations grows larger (e.g., more than 500 delivery locations), which is quite common in the real applications [7]. Compared with previous methods, our SSBLS algorithm strikes a balance between the accuracy and efficiency through restricting the neighbor size and adaptively selecting the delivery locations and local search operators.

Previous approaches mainly assume that the problem instance is defined on a complete directed graph. However, in practice, most of the VRPs take place on real road networks. Although, it is possible to transform a VRP instance on a road network into an instance on a complete directed graph, it involves large amount of shortest path computation [15, 16]. The problem becomes even more challenging when dealing with real world time-dependent road network. Previous works on time dependent VRP [17, 18] mainly use the synthetic time-varying edge weights in which they assume for each delivery pair, there exists a few fixed number (e.g., 3 or 4) of time intervals and the travel time between the delivery locations at each time interval is a constant, thus they could pre-compute a distance matrix for each delivery pair at every time interval. However, the real world time-dependent road network has a much larger number of time intervals (e.g., 60), and the travel cost between a pair of delivery locations at certain time interval is not known in advance, which usually requires a costly shortest path computation on road network. In [4, 10], a time-dependent bidirectional A* shortest path algorithm is proposed, which builds indexes and calculates tight bound in the A* search process based on the lower/upper bound graph. Even with these optimization, shortest path computation on time-dependent road network takes several hundred milliseconds on Los Angeles road network. Moreover, in the on-line delivery business, the requests may not be known in advance, which also prohibits the pre-computation of the distance matrix for each delivery problem. In this paper, we eliminate the data-preparation step via an on-demand calculation procedure, which significantly reduces the total running time of the algorithm.

6 Conclusion

In this paper, we studied the problem of Vehicle Routing in time-dependent road network. To enable fast and accurate results, we proposed a new local search framework, which eliminates the time-consuming data-preparation step required by the Operation Research methods via an on-demand-calculation strategy from the field of spatial databases. We further improved the efficiency by leveraging a guided search process to reduce the unnecessary exploration of the solution space. Our experiments with real-world dataset verified that our algorithm strikes a good balance between efficiency and accuracy, which makes it practical for the future delivery business in large-scale and dynamic environment.