Keywords

1 Introduction

In recent decades, robot manipulators were applied widely in various fields, in which many tasks require high-speed and high-precision trajectory tracking. However, robotic manipulators are generally nonlinear and involve many uncertainties and external disturbances in their dynamics, such as payload variations, friction, external disturbances, and sensor noise etc. Therefore, designs of a controller that can attenuate the effects of robotic uncertainties have become the subject of many researches. In order to deal with this problem, many control approaches have been proposed such as proportional-integral-derivative (PID) control [1], robust control [2, 3], adaptive control [4, 5], sliding mode control [6–11], and neural network control [12–16].

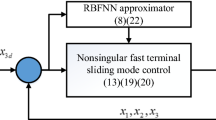
In this paper, an adaptive terminal sliding mode control based on local approximation method is proposed for trajectory tracking of uncertain robotic manipulators. At first, the controller is developed based on terminal sliding mode technique. Then, in order to improve the system performance and attenuate the effects of uncertainties, the RBFNNs are used to directly approximate individual element of the inertial matrix, the Coriolis matrix and gravity torques vector. Finally, a simulation study is performed on a two-link robot manipulator to prove the effectiveness of the proposed control method.

The rest of this paper is arranged as follows. The system dynamics and problem formulation are described in Sect. 2. The structure of terminal sliding mode neural networks controller is presented in Sect. 3. In Sect. 4, simulation results for a two-link robot manipulator are provided to demonstrate the performance of the proposed controller. Finally, some important remarks are concluded in Sect. 5.

2 System Dynamics and Preliminaries

The dynamics of a serial n-links robot manipulator can be written as [17]

$$ M(q)\mathop q\limits^{..}+\,C(q,\dot{q})\dot{q} + G(q) + \tau_{d} = \tau $$
(1)

where \( q(t),\dot{q}(t),\mathop q\limits^{..} (t) \in {\mathbf{R}}^{n} \) are the vector of joint accelerations, velocities and positions, respectively. \( M(q) \in {\mathbf{R}}^{n \times n} \) is the inertial matrix, \( C(q,\dot{q}) \in {\mathbf{R}}^{n \times n} \) expresses the centripetal and Coriolis matrix, \( G(q) \in {\mathbf{R}}^{n} \) represents the gravity torques vector, \( \tau \in {\mathbf{R}}^{n} \) is the control torque, and \( \tau_{d} \in {\mathbf{R}}^{n} \) is the bounded external disturbance vector.

For convenience, the above dynamic equation has the following useful structural properties;

Property 1:

\( M(q) \) is a symmetric positive definite matrix.

$$ m_{1} \left\| x \right\|^{2} \le x^{T} M(q)x \le m_{2} \left\| x \right\|^{2} ;\forall x \in R^{n} $$
(2)

where \( m_{1} ,m_{2} \) are known positive scalar constants, \( x \in R^{n} \) is a vector, \( \left\| {} \right\| \) denotes the Euclidean vector norm.

Property 2:

\( M(q) - 2C(q,\dot{q}) \) is a skew symmetric matrix.

$$ x^{T} [\dot{M}(q) - 2C(q,\dot{q})]x = 0 $$
(3)

for any vector \( x \in {\mathbf{R}}^{n} \).

The control objective of this paper is to design a stable control law to ensure that the tracking error between joint position vector \( q \) and desired joint position vector \( q_{d} \) converge to zero in finite time.

3 Controller Design

In order to apply the terminal sliding mode control, it is necessary to define the terminal sliding surface \( s(t) \) for n-link robot manipulator as

$$ s = \dot{e} + \beta sig(e)^{\varphi } $$
(4)

where \( \beta = diag(\beta_{1} ,\beta_{2} , \ldots ,\beta_{n} ) \), \( \beta_{1} ,\beta_{2} , \ldots \beta_{n} \) are positive constants, \( 0 < \varphi < 1 \), \( sig(\dot{e})^{\varphi } = \left( {\left| {\dot{e}_{1} } \right|^{\varphi } sign(\dot{e}_{1} ),\left| {\dot{e}_{2} } \right|^{\varphi } sign(\dot{e}_{2} ), \ldots ,\left| {\dot{e}_{n} } \right|^{\varphi } sign(\dot{e}_{n} )} \right) \), \( s = \left[ {s_{1} ,s_{2} , \ldots, s_{n} } \right] \), \( e(t) = q(t) - q_{d} (t) \), \( \dot{e}(t) = \dot{q}(t) - \dot{q}_{d} (t) \).

According to the sliding mode design procedure, the control input \( u \) consists of the components

$$ \tau = u_{eq} - K_{SW} sign(s) $$
(5)

where \( K_{SW} = diag(k_{SW1} ,k_{SW2} , \ldots ,k_{SWn} ) \), \( k_{SW1} ,k_{SW2} , \ldots, k_{SWn} \) are positive constants. The equivalent control can be interpreted as the continuous control law that is obtained by equation \( \dot{s} = 0 \) for nominal system in the absence of the uncertainties and external disturbances.

$$ \dot{s} = \mathop e\limits^{..} +\,\varphi \beta \left| e \right|^{\varphi - 1} \dot{e} $$
(6)

From (1), the \( \mathop e\limits^{..} \) is given by

$$ \mathop e\limits^{..} = \mathop {q_{d} }\limits^{..} - \mathop q\limits^{..} = \mathop {q_{d} }\limits^{..} - \frac{{\tau - \tau_{d} - C(q,\dot{q})\dot{q} - G(q)}}{M(q)} $$
(7)

Multiplying both sides of Eq. (6) by \( M(q) \) and substituting (7) into it yields

$$ M(q)\dot{s} = M(q)\mathop {q_{d} }\limits^{..} +\,C(q,\dot{q})\dot{q} + G(q) + \varphi \beta M\left| e \right|^{\varphi - 1} \dot{e} - \tau + \tau_{d} $$
(8)

Define \( \dot{q}_{s} = s + \dot{q} \), then \( \mathop {q_{s} }\limits^{..} = \dot{s} + \mathop q\limits^{..} \), \( \dot{q}_{s} = \dot{q}_{d} + \beta sig(e)^{\varphi } \), \( \mathop {q_{s} }\limits^{..} = \mathop {q_{d} }\limits^{..} +\,\varphi \beta \left| e \right|^{\varphi - 1} \dot{e} \). From (8), we have

$$ M(q)\dot{s} = - C(q,\dot{q})s - \tau + \tau_{d} + M(q)\mathop {q_{s} }\limits^{..} +\,C(q,\dot{q})\dot{q}_{s} + G(q) $$
(9)

If the nonlinear robot dynamic functions \( M(q) \), \( C(q,\dot{q}) \), \( G(q) \) are clearly known, then the equivalent control can be defined as

$$ u_{eq} = M(q)\mathop {q_{s} }\limits^{..} +\,C(q,\dot{q})\dot{q}_{s} + G(q) + Ks $$
(10)

where \( K = diag(k_{1} ,k_{2} , \ldots ,k_{n} ) \), \( k_{1} ,k_{2} , \ldots, k_{n} \) are positive constants.

The stability of the close loop system (10) can be easily proved by Lyapunov theory if the gains of the switching controller are bigger than the upper bounds of uncertainties. However, robot manipulators are complex nonlinear systems which involve many uncertainties and external disturbances. Therefore, the RBFNNs are used to directly approximate individual element of the inertial matrix, the Coriolis matrix and gravity torques vector of the robot. Therefore Eq. (9) becomes.

$$ M(q)\dot{s} = - C(q,\dot{q})s - \tau + \tau_{d} + \hat{M}(q)\mathop {q_{s} }\limits^{..} +\,\hat{C}(q,\dot{q})\dot{q}_{s} + \hat{G}(q) $$
(11)

where \( \hat{M}(q) \), \( \hat{C}(q,\dot{q}) \), and \( \hat{G}(q) \) be the estimates of \( M(q) \), \( C(q,\dot{q}) \), and \( G(q) \), respectively. For the system (11), the proposed controller is expressed by the following equation

$$ u_{eq} = \hat{M}(q)\mathop {q_{s} }\limits^{..} + \hat{C}(q,\dot{q})\dot{q}_{s} + \hat{G}(q) + Ks $$
(12)

where \( \hat{M}(q) = \left[ {\hat{W}_{M}^{T} \bullet \sigma_{M} (q)} \right] \), \( \hat{C}(q,\dot{q}) = \left[ {\hat{W}_{C}^{T} \bullet \sigma_{C} (q,\dot{q})} \right] \), \( \hat{G}(q) = \left[ {\hat{W}_{G}^{T} \bullet \sigma_{G} (q)} \right] \). The neural network weight vectors are designed as follows.

$$ \dot{\hat{W}}_{Mk} = \varGamma_{Mk} .\left\{ {\sigma_{Mk} (q)} \right\}\mathop {q_{s} }\limits^{..} s_{k} $$
(13)
$$ \dot{\hat{W}}_{Ck} = \varGamma_{Ck} .\left\{ {\sigma_{Ck} (q,\dot{q})} \right\}\dot{q}_{s} s_{k} $$
(14)
$$ \dot{\hat{W}}_{Gk} = \varGamma_{Gk} .\left\{ {\sigma_{Gk} (q)} \right\}s_{k} $$
(15)

where \( k = 1,2, \ldots, n \). \( \varGamma_{Mk} \), \( \varGamma_{Ck} \), and \( \varGamma_{Gk} \) are constant symmetric positive definite matrices. \( \hat{W}_{Mk} \),\( \hat{W}_{Ck} \), and \( \hat{W}_{Gk} \) are column vectors with their elements being \( W_{Mkj} \), \( W_{Ckj} \), \( W_{Gkj} \), respectively.

4 Simulation Results

In this section, to verify the validity and effectiveness of the proposed method, the performance of the proposed controller is tested via simulation on a two-link planar robotic manipulator. The simulations are performed in the MATLAB-Simulink environment using ODE 4 solver with a fixed-step size of \( 10^{ - 4} \,s \).

The dynamic equation of the two-link robot is described as follows

$$ \left[ {\begin{array}{*{20}c} {M_{11} (q)} & {M_{12} (q)} \\ {M_{12} (q)} & {M_{22} (q)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\mathop {q_{1} }\limits^{..} } \\ {\mathop {q_{2} }\limits^{..} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {C_{11} (q,\dot{q})} & {C_{12} (q,\dot{q})} \\ {C_{12} (q,\dot{q})} & {C_{22} (q,\dot{q})} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{q}_{1} } \\ {\dot{q}_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {G_{1} (q)} \\ {G_{2} (q)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\tau_{{d_{1} }} } \\ {\tau_{{d_{2} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tau_{1} } \\ {\tau_{2} } \\ \end{array} } \right] $$
(16)

where the inertia matrix \( M_{ij} (q) \) is given by

$$ \begin{aligned} M_{11} (q) & = (m_{1} + m_{2} )l_{1}^{2} + m_{2} l_{2}^{2} + 2m_{2} l_{1} l_{2} \cos (q_{2} ), \\ M_{12} (q) & = M_{21} (q) = m_{2} l_{2}^{2} + m_{2} l_{1} l_{2} \cos (q_{2} ), \\ M_{22} (q) & = m_{2} l_{2}^{2} , \\ \end{aligned} $$

The Coriolis and centrifugal matrix \( C_{ij} (q,\dot{q}) \) is given by

$$ \begin{array}{*{20}c} {C_{11} (q,\dot{q}) = - m_{2} l_{1} l_{2} \sin (q_{2} )\dot{q}_{2} } & {C_{12} (q,\dot{q}) = - m_{2} l_{1} l_{2} \sin (q_{2} )(\dot{q}_{1} + \dot{q}_{2} )} \\ {C_{21} (q,\dot{q}) = m_{2} l_{1} l_{2} \sin (q_{2} )\dot{q}_{1} } & {C_{22} (q,\dot{q}) = 0} \\ \end{array} $$

The gravity torques vector \( G_{i} (q) \) is given by

$$ \begin{aligned} G_{1} (q) & = (m_{1} + m_{2} )l_{1} g\cos (q_{2} ) + m_{2} l_{2} g\cos (q_{1} + q_{2} ), \\ G_{2} (q) & = m_{2} l_{2} g\cos (q_{1} + q_{2} ), \\ \end{aligned} $$

The parameters values employed to simulate the robot are given as of \( l_{1} = 1\,{\text{m}} \), \( l_{2} = 0.8\,{\text{m}} \), \( m_{1} = 1\,{\text{kg}} \), \( m_{2} = 1\,{\text{kg}} \), \( \beta = diag(12,12) \), \( \varphi = 0.8 \), \( K = diag(150,50) \), \( K_{SW} = diag(5,5) \). The external disturbances are selected as

$$ \tau_{d} = \left[ {\begin{array}{*{20}c} {\tau_{{d_{1} }} } \\ {\tau_{{d_{2} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {1.7\sin (2t)} \\ {1.3\cos (2t)} \\ \end{array} } \right] $$
(17)

The reference trajectories are given by

$$ \begin{aligned} q_{1d} & = 0.3\sin (\pi t) \\ q_{2d} & = 0.5\sin (\pi t) \\ \end{aligned} $$
(18)

The initial states are chosen as

$$ q_{1} (0) = 0.4,\text{ }q_{2} (0) = - 0.5,\text{ }\dot{q}_{1} (0) = 0,\text{ }\dot{q}_{2} (0) = 0 $$
(19)

The simulation results are shown in Figs. 1 and 2. It can be observed that the controller can track the desired trajectory very well, the controller brings very small tracking errors, and the state trajectories reach to the origin in a finite amount of time. Thus, the simulation results demonstrate that the proposed controller can effectively control the unknown nonlinear dynamic system.

Fig. 1.
figure 1

Responses at joint 1: (a) Output tracking, (b) Tracking error.

Full size image
Fig. 2.
figure 2

Responses at joint 2: (a) Output tracking, (b) Tracking error.

Full size image

5 Conclusion

In this paper, an adaptive terminal sliding mode control based on local approximation method is proposed for trajectory tracking of uncertain robotic manipulators. The controller is developed based on the combination of terminal sliding mode control technique and radian basis function neural networks (RBFNNs). Adaptive learning laws have been derived to adjust on-line the output weights of the RBFNNs during the trajectory tracking control of robot manipulators without any offline training phases. In the simulation example, the proposed control is applied to a two-link robotic manipulator. The simulation results are given to demonstrate the effectiveness of the proposed method.