Efficient Card-Based Protocols for Generating a Hidden Random Permutation Without Fixed Points

Abstract

Consider the holiday season, where there are n players who would like to exchange gifts. That is, we would like to generate a random permutation having no fixed point. It is known that such a random permutation can be obtained in a hidden form by using a number of physical cards of four colors with identical backs, guaranteeing that it has no fixed point (without revealing the permutation itself). This paper deals with such a problem and improves the known result: whereas the known protocol needs $O(n^2)$ cards of four colors, our efficient protocol uses only $O(n \log n)$ cards of two colors.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Consider the holiday season, where there are n players who would like to exchange gifts. We wish to avoid the undesirable situation in which a player must buy a present for himself/herself. That is, we need to produce a random permutation $\pi \in S_n$ that has no fixed point, where $S_n$ denotes the symmetric group of degree n (throughout this paper). There is an unconventional solution to the “no fixed point” problem, i.e., it is known that such a random permutation can be obtained in a hidden form by using a number of physical cards of four colors, say  ,  ,  , and  ,¹ with identical backs  , guaranteeing that it has no fixed point (without revealing the permutation itself) [3]. This paper deals with such a problem and proposes an efficient approach that improves the known result.

1.1 Known Method for Generating a Random Permutation

In 1993, Crépeau and Kilian gave a card-based protocol for generating a random permutation $\pi \in S_n$ without any fixed point [3]. Their protocol produces a pile of n cards that consists of $(n-1)$  s and one with their faces down (on the table) for every player $p_i, 1 \le i \le n$:

The position of card   corresponds to the value of $\pi (i)$ when all the n cards are revealed:

Thus, if player $p_i$ looks at his/her pile privately, then the information about who $p_i$ is going to buy a present for will be kept secret.

Because the protocol produces a pile of such cards for each of the n players, as seen above, it uses $n(n-1)$  s and n  s. In addition, it requires a number of cards of different colors, namely $n^2/2$  s and $n^2/2$  s. Thus, the known method needs $2n^2$ cards of four colors in total². Further details are given in Sect. 2.

1.2 Our Results and Related Work

Table 1 summarizes both the known result and our results. As mentioned above, to generate a random permutation without fixed points, the known method [3] requires $2n^2$ cards of four colors. In this paper, we reduce the number of required colors and cards. First, we devise a new shuffling operation called a “pile-scramble shuffle” in Sect. 3. Using this new shuffle, we can enhance the efficiency of the known protocol, and consequently, we can show that $n^2$ cards of two colors are sufficient. We then show in Sect. 4 that $(2n \lceil \log n \rceil +6)$ cards³ of two colors are sufficient to solve the “no fixed point” problem by considering another expression of each player’s index.

Table 1. Performance of each protocol

Before presenting our protocols, we present a complete description of the known protocol [3] in Sect. 2. Section 5 concludes this paper with some discussion.

Card-based cryptography allows us not only to generate a random permutation, but also to have various kinds of cryptographic protocols such as secure multiparty computations and zero-knowledge proof. For example, there are known protocols for securely computing AND [1, 3, 7, 8, 10, 13], XOR [3, 8, 9], adder [6], 3-variable symmetric functions [12], and so on. Furthermore, the relationship between playing cards and cryptography has been explored in the literature (e.g., [2, 4, 5, 14]).

2 Known Protocol

In this section, we present a complete description of the Crépeau-Kilian protocol [3] that generates a hidden random permutation having no fixed point.

Assume that n players $p_1, p_2, \dots , p_n$ would like to produce a random permutation $\pi \in S_n$ without any fixed point. Their protocol consists of two phases, the Random-Permutation Generating phase and the Fixed-Point Checking phase, as follows.

[ Random-Permutation Generating phase ]

• 1-1. Using $n(n-1)$  s and n  s, arrange the cards as below (putting each on the diagonal), and insert a “marker” after each row, where a marker consists of n / 2  s and n / 2  s (for simplicity, n is assumed to be an even number):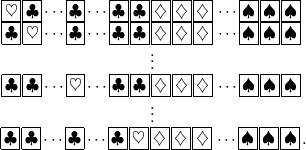

  

• 1-2. Turn over the cards so that they are all face down, and apply a random cut, i.e., a cyclic shuffle, to the sequence of $2n^2$ cards (obtained by row-wise concatenation).

• 1-3. Reveal the first card. If the face-up card is either or  , go back to step (1–2). If it is either or  , i.e., a marker, then proceed to the next step. Note that the probability of returning to step (1–2) is exactly 1 / 2.

• 1-4. Assume that the face-up card is  :

  

  Its right-hand card must also be a marker. Reveal the markers right next to it one by one. After all the makers on the right side (which are $\ell$   s for some $\ell$ and n / 2  s) are face up, reveal the remaining markers on the left side (where the first card’s “left” is the last card), namely ($n/2 - \ell -1$)  s. For the case where the first card is  , we manipulate the sequence of cards similarly to the case. Note that in this case, we start revealing the markers toward the left side first. Remove all of the (face-up) n markers.

• 1-5. After all of the n markers are removed, we regard the first n cards as the value of $\pi (1)$. That is, the pile of these n cards is assigned to player $p_1$ and corresponds to $\pi (1)$:

  

• 1-6. Similarly, for the remaining cards, repeat steps (1-2)–(1-4) so that we obtain piles corresponding to $\pi (2), \pi (3), \dots , \pi (n)$.

[ Fixed-Point Checking phase ]

• 2-1. To verify that the generated permutation $\pi$ has no fixed point, arrange the piles of cards assigned to $p_1, p_2, \dots , p_n$ as below:

  

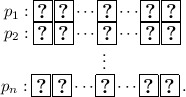
• 2-2. Reveal all the cards on the diagonal to determine if they are all . If so, $\pi$ has no fixed point. If one of them is , then the pile corresponds to a fixed point and in this case, we must return to the Random-Permutation Generating phase.

Thus, the first phase of this protocol produces a random permutation $\pi \in S_n$, and then the second phase checks that $\pi$ has no fixed point. In the first phase, we need to repeat the steps until markers are found, and hence it is a Las Vegas algorithm taking 2n trials on average. With respect to the second phase, note that in general, the probability that a random permutation $\pi \in S_n$ has no fixed point is $\sum _{i=0}^{n} (-1)^i/i!$, which is approximately 1 / e, where e is the base of the natural logarithm [3]. Therefore, the average number of how many times we need to execute the Fixed-Point Checking phase is approximately $e \approx 2.7$.

This is the existing protocol for solving the “no fixed point” problem. It uses $2 n^2$ cards of four colors, as detailed above. We improve on this efficiency in the succeeding sections.

3 Pile-Scramble Shuffle

In this section, we focus on the process of producing a random permutation and propose an efficient method for achieving this.

Remember that the known protocol [3] uses random cuts and markers to generate a random permutation, as shown in the preceding section. That is, in order to shuffle n piles (each of which consists of n cards and is assigned to a player), we repeatedly apply a random cut to create each value of $\pi (i)$ one by one, while markers are used as “delimiters.” Here, instead of using markers, we consider a somewhat more direct way of shuffling piles.

Assume that there are a number of face-down cards that are divided into n piles of the same size. We denote each pile by $pile_i$, $1 \le i \le n$. Given a sequence of piles $(pile_1, pile_2, pile_3, ..., pile_n)$, consider a shuffle operation that outputs $(pile_{\pi (1)}, pile_{\pi (2)}, pile_{\pi (3)}, ..., pile_{\pi (n)})$, where $\pi \in S_n$ is a random permutation. As we now have n piles, a permutation is randomly chosen from the n! possibilities. We call such a shuffling operation a pile-scramble shuffle. We believe that the pile-scramble shuffle can be easily implemented by human beings using rubber bands, clips, envelopes, or something similar.

If steps (1-2)–(1-6) in the Random-Permutation Generating phase of the known protocol [3] introduced in Sect. 2 are replaced with the pile-scramble shuffle, it is obvious that $n^2$ cards of two colors are sufficient to produce a random permutation. That is, we can generate a random permutation without any marker, meaning that we do not require any trials, and hence can output a random permutation after exactly one pile-scramble shuffle. Therefore, taking the Fixed-Point Checking phase into account, such an improved protocol needs only $n^2$ cards of two colors and takes an average number of about 2.7 trials to generate a random permutation having no fixed point. Thus, we are able to reduce the numbers of required cards and colors by half (see Table 1 again).

In the next section, we further reduce the number of required cards.

4 Our Main Protocol

In this section, we propose a more efficient method than those mentioned previously. Our main protocol requires only $(2 n \lceil \log n \rceil +6)$ cards to generate a random permutation having no fixed point.

First, in Sect. 4.1, we show that considering a binary representation of players’ indices dramatically reduces the number of required cards. Next, in Sect. 4.2, we present a sub-protocol to check for fixed points under such a binary representation. Finally, in Sect. 4.3, by combining these components, we present a complete description of our protocol.

4.1 Binary Representation

In the Crépeau-Kilian protocol [3] presented in Sect. 2, each player’s index $i \in \{1,2, \dots ,n\}$ and its permuted position $\pi (i)$ are represented by a pile of n cards, i.e., $(n-1)$  s and one  , say

In contrast, we represent this information using a binary representation with $2 \lceil \log n \rceil$ cards as follows.

To deal with Boolean values, following the previous studies (e.g., [1, 3, 10, 13]), we use the encoding rule with a pair of cards:

(1)

For a bit $x \in \{0,1\}$, when two face-down cards have a value equaling x according to encoding (1) above, the pair of these face-down cards is called a commitment to x, and is written as

Under such an encoding rule, each player’s index can be represented by $\lceil \log n \rceil$ commitments, namely $2 \lceil \log n \rceil$ cards. Therefore, n players’ indices are represented naturally by $2n \lceil \log n \rceil$ cards. Thus, we can greatly reduce the number of required cards to express players’ indices.

It is obvious that we can easily produce a random permutation by applying a pile-scramble shuffle (explained in Sect. 3) to these n piles that are based on this binary expression.

4.2 How to Check for Fixed Points

In this subsection, we present a sub-protocol to check that a random permutation in the form of binary representation has no fixed point.

Assume that a random permutation $\pi \in S_n$ has been generated by a pile-scramble shuffle, as shown in Sect. 3, based on the binary representation shown in Sect. 4.1. That is, a pile of $\lceil \log n \rceil$ commitments is assigned to each player $p_i$:

where and hereafter, $\log n$ in the subscript means $\lceil \log n \rceil$. Because the pile above corresponds to $\pi (i)$, we have

$$\begin{aligned} (\pi (i)-1)_{10} = (a_{\log n} \cdots a_{2} a_1)_2. \end{aligned}$$

In order to verify that the pile is not a fixed point, namely $\pi (i) \ne i$, we check whether the equation below holds:

$$\begin{aligned} (a_1 \oplus \overline{b_1}) \wedge (a_2 \oplus \overline{b_2}) \wedge \cdots \wedge (a_{\log n} \oplus \overline{b_{\log n}}) = 0\, , \end{aligned}$$

(2)

where $\oplus$ denotes the exclusive-or (XOR) operation and bits $b_1, b_2, \cdots , b_{\log n}$ are defined as

$$\begin{aligned} (i-1)_{10} = (b_{\log n} \cdots b_{2} b_1)_2 . \end{aligned}$$

Aiming to compute Eq. (2) efficiently without revealing values $a_i$, $1 \le i \le \lceil \log n \rceil$, we first introduce the existing copy protocol [8], and then present a “one-input-preserving” AND protocol. Finally we describe a sub-protocol for checking that Eq. (2) holds.

Copy Protocol. Give a commitment to a bit x together with four additional cards, the known copy protocol [8] generates two copied commitments to x, as follows.

• 1. Arrange two commitments to 0:

  

• 2. Rearrange the order of the sequence as:

  

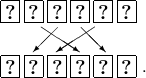
• 3. Bisect the sequence of six cards and switch the two portions randomly (we call this a random bisection cut [8] and denote it by $\left[ \, \cdot \, | \, \cdot \, \right]$ ):

  

• 4. Rearrange the order of the sequence as:

  

  We then have

  

  where r is a (uniformly distributed) random bit because of the random bisection cut.

• 5. Reveal the first two cards from the left. We then have

  

  Thus, we obtain two copied commitments to x. In the latter case, we can easily convert $\overline{x}$ to x using the NOT operation that swaps the left and right cards. In addition, the two face-up cards are available for another computation.

One-input-preserving AND Protocol. We present a one-input-preserving AND protocol that can keep one of input commitments after the AND computation. The protocol can be constructed immediately based on two known ideas: the AND protocol [8] and the half-adder protocol [6].

First, we present some notation. For a pair of bits (x, y), define operations $\mathsf {get}$ and $\mathsf {shift}$ as

Note that

$$\begin{aligned} a \wedge b = \mathsf {get}^{a \oplus r}(\mathsf {shift}^{r}(0,b)) \end{aligned}$$

(3)

for an arbitrary bit $r \in \{0, 1\}$. In addition, for two bits x and y, the expression

means

The following is a one-input-preserving AND protocol that produces not only a commitment to $a \wedge b$ but also a commitment to the input a using eight cards.

• 1. In addition to the input commitments to a and b, arrange two commitments to 0 as follows:

  

• 2. Rearrange the order of the sequence as:

  

• 3. Apply a random bisection cut:

   .

• 4. Rearrange the order of the sequence as:

  

  We then have

  

  where r is a (uniformly distributed) random bit.

• 5. Reveal the first two cards. If they are  , we have $a \oplus r = 0$, i.e., $r = a$. Therefore, the output is (see Eq. (3)):

  

  If they are  , we have $a \oplus r = 1$, i.e., $r = \bar{a}$. Therefore, the output is:

  

In this way, we can obtain commitments to both $a \wedge b$ and a. The two face-up cards are still available for another computation. In addition, the two cards of the remaining commitment can also be available after they are shuffled.

Sub-protocol for Checking Eq. ( 2 ). Given the discussion above, we are ready to present a procedure for checking Eq. (2) to determine if there are fixed points. Given a pile

the following sub-protocol computes the value of

$$\begin{aligned} (a_1 \oplus \overline{b_1}) \wedge (a_2 \oplus \overline{b_2}) \wedge \cdots \wedge (a_{\log n} \oplus \overline{b_{\log n}}), \end{aligned}$$

where

$$\begin{aligned} (i-1)_{10} = (b_{\log n} \cdots b_{2} b_1)_2. \end{aligned}$$

• 1. Arrange $\lceil \log n \rceil$ input commitments and six additional cards as follows:

  

• 2. Copy the commitment to $a_1$ using the copy protocol [8] mentioned above:

  

• 3. Apply the NOT computation depending on the values of $b_1$ and $b_2$ so that we have

  

  Note that each value of $b_i$ is public.

• 4. Apply the one-input-preserving AND protocol presented above to obtain commitments to $(a_1 \oplus \overline{b_1}) \wedge (a_2 \oplus \overline{b_2})$ and $(a_2 \oplus \overline{b_2})$. Furthermore, apply the NOT computation to the latter commitment depending on the value of $b_2$. We then have

  

• 5. Similarly, obtain commitments to $(a_1 \oplus \overline{b_1}) \wedge (a_2 \oplus \overline{b_2}) \wedge (a_3 \oplus \overline{b_3})$ and $a_3$:

  

  Repeat this until we have

  

• 6. Reveal the commitment to $(a_1 \oplus \overline{b_1}) \wedge (a_2 \oplus \overline{b_2}) \wedge \cdots \wedge (a_{\log n} \oplus \overline{b_{\log n}})$. If the value is 1, then this is a fixed point. Otherwise, it is not a fixed point. It should be noted that in either case, any commitments to $a_1,a_2,\dots ,a_{\log n}$ are not lost.

4.3 Description of Our Proposed Protocol

We are now ready to present an efficient protocol for generating a random permutation having no fixed point. Our protocol uses $(2n \lceil \log n \rceil +6)$ cards to produce n piles corresponding to this random permutation.

• 1. Using $n \lceil \log n \rceil$  s and $n \lceil \log n \rceil$  s, arrange $n \lceil \log n \rceil$ commitments according to players’ indices based on the binary representation:

  

• 2. Regarding each row as a pile, apply a pile-scramble shuffle to the n piles; we then obtain a random permutation $\pi$ in which the i-th pile corresponds to $\pi (i)$:

  

• 3. Using six additional cards, apply the sub-protocol presented in Sect. 4.2 to confirm that $\pi$ has no fixed point, that is, to verify that $p_i$ is not a fixed point for every i, $1 \le i \le n$, in turns. If we find a fixed point, then we go back to step (2). If we confirm that there is no fixed point, the permutation $\pi$ is a desired one.

This is our main protocol for solving the “no fixed point” problem with $O(n \log n)$ cards.

5 Conclusions

The known protocol [3] requires $2 n^2$ cards of four colors to generate a random permutation having no fixed point. In this paper, we first devised a new shuffle operation called a pile-scramble shuffle that immediately enabled us to achieve the same task using only $n^2$ cards of two colors. Furthermore, we showed that using a binary representation dramatically reduces the number of required cards, that is, $(2n \lceil \log n \rceil +6)$ cards of two colors are sufficient.

In our protocol, the $2n \lceil \log n \rceil$ cards are used to hold each players’ index, and the remaining six cards correspond to the additional cards required to execute the sub-protocol for checking fixed points. This comes from the fact that the one-input-preserving AND protocol given in Sect. 4.2 requires four additional cards. Recently, it was shown that such a one-input-preserving AND computation can be done with only two additional cards [11]. Therefore, applying this recently invented protocol [11], we can reduce the number of required cards to $2n \lceil \log n \rceil +4$.

In addition to the protocol solving the “no fixed point” problem, Crépeau and Kilian designed a general protocol for producing a random permutation that satisfies a predetermined condition such as having no short cycle of length at most k, and showed that it can be applied to the “Discreet Solitary Games” [3]. Thus, it is intriguing future work to design an efficient way to determine whether a given permutation based on our binary representation has k-cycles.

Although the card-based protocol is an unconventional way to secure multiparty computations, this approach has many advantages. The most important feature is that even nonspecialists are able to easily understand why the computation is secure.