Moving Discrete Breathers in 2D and 3D Crystals

Abstract

Discrete breathers (DB), also known as intrinsic localized modes, are spatially localized large-amplitude vibrational modes in defect-free anharmonic lattices. Crystals can be regarded as anharmonic lattices and it is natural to expect that they support DB. The role of DB in the solid state physics is not yet well understood because their experimental detection is difficult. Nevertheless there exist a large number of theoretical works where the existence conditions and properties of DB in crystals have been analyzed. The key issue actively discussed in the literature is the mobility of DB. Moving DB can be a carrier of energy, momentum, electric charge, etc. A DB can localize energy of the order of 1 eV, while collision of propagating DB can result in even higher energy localization. The high energy density regions in crystals can act as the sources of crystal lattice defects, they can initiate fracture or phase transitions. In this chapter the anzats for generating moving discrete breathers in monatomic crystals is offered and successfully tested in molecular dynamics simulations for the 2D Morse crystal and hcp cobalt and magnesium. It is then demonstrated that two colliding DB can produce a DB with greater amplitude. Gap DB wandering in an ionic crystal with NaCl structure are described.

1 Introduction

Discrete breathers (DB), as exact solutions to a number of model nonlinear systems possessing translational symmetry, were a hot topic in the nonlinear science in the last decade of the past century [13, 20, 21, 44, 50, 57]. An overwhelming majority of those theoretical studies on DB dealt with the idealized one- or two-dimensional nonlinear lattices of coupled oscillators interacting via oversimplified pairwise potentials. In the last years, DB-mediated effects in solid state physics and materials science have been the focus of a rapidly growing number of studies based on more realistic atomistic models of crystals.

Let us recall some basic properties of DB important for the following discussion. DB frequency lies outside the small amplitude vibration spectrum of the lattice and thus, DB does not excite the small amplitude waves and remains localized forever radiating no energy. The DB frequency can leave the linear vibration spectrum because of the anharmonicity of the lattice. Indeed, it is well-known that the frequency of a nonlinear oscillator is amplitude-dependent. In the case of the so-called hard (soft) anharmonicity, DB frequency increases (decreases) with increase in its amplitude and can cross the upper edge of the spectrum (can enter the spectrum gap, if it exists). Most of the studies on DB have been done in frame of the strongly idealized models of low dimensions and with simple types of anharmonicity. In real physical systems DB are not single-frequency modes and they are not exactly time-periodic. The concept of quasi-breathers, developed by Chechin with co-authors [8], legitimizes the long-lived, spatially localized objects in defect-free crystal lattices, even though they are not exact solutions to the dynamical equations.

During the last few years, the concept of DB (more precisely, quasi-breathers) has been actively penetrating the solid state physics and materials science. Velarde with co-authors have offered the concept of solectron [9–12, 60] which is the bound state of DB and electron, the reaction rate theory in solids has been recently modified to take into account the contribution from DB [2, 16, 18], the DB mediated mechanism of defect annealing deep inside Ge single crystal has been proposed [1], the possible role of DB in thermally activated dehydrogenation of graphane [43] has been discussed in the works [7, 42], molecular dynamics simulation of the DB-induced defect formation in strained carbon nanotube has been reported [55]. Xiong et al. have demonstrated that DB can contribute to thermal conductivity of 1D lattices [65–67].

There exist several reports on experimental observation of DB in crystals. DB have been detected by the resonant Raman scattering measurements in a complex compound termed as PtCl [27, 58, 62], from inelastic x-ray and neutron scattering data in $\alpha$-uranium [46, 49], and from inelastic neutron scattering spectra in NaI [29, 47, 48]. The existence of DB in NaI in thermal equilibrium has been debated [28, 56] because the contribution from DB to the vibrational density of states is masked by the contribution from thermal lattice vibrations. This discussion suggests the importance of numerical studies on DB. Molecular dynamics based on empirical interatomic potentials was used to identify DBs in NaI [30, 34], in Si and Ge [61], in Ni and Nb [24], in C$_{60}$ fullerite nanocrystals [54], in carbon nanotubes [55], in graphene [3, 32, 39, 40], and in graphane [42]. In the work [7] the existence of DB in graphane was demonstrated for the first time with the use of the ab initio simulations based on DFT theory.

The question of whether DB can move through crystal lattice is important for understanding their role in the formation of physical properties of crystals. Often DB are pinned to lattice sites, but in some cases they can be mobile [24]. Moving DB, also known as quodons, are quasi-particles propagating along close-packed crystallographic directions [53]. Their collisions with crystal defects can result in various effects such as the anomalously accelerated diffusion and related phenomena [16]. Moving DB can collide with each other resulting in significant energy localization at the collision point. This energy can be spent on the creation of crystal lattice defects or on the triggering of phase transitions or fracture.

In this contribution we discuss moving DB in 2D Morse crystal (Sect. 8.2), moving DB in 3D metallic crystals (Sect. 8.3) and wandering DB in the ionic crystals with NaCl structure (Sect. 8.4). A brief summary with the outline of some open problems is given in Sect. 8.5.

2 Moving DB in 2D Hexagonal Lattice with Long-Range Morse Potentials

In the theoretical work by Kiselev et al. [33] it has been shown that the 1D chains with atoms interacting via classical pairwise potentials (Toda, Born-Mayer, Lennard-Jones and Morse) cannot support DB with frequency above the phonon spectrum. Let us demonstrate that introduction of the on-site potential in that model makes the existence of DB with frequency above the phonon spectrum possible by suppressing the dc displacements of the atoms and increasing the contribution of the hard core of the potential into atomic dynamics.

We consider the 1D chain of identical atoms of unit mass whose dynamics is described by the following equations of motion

$$\begin{aligned} \ddot{u}_n=U'(u_{n+1}-u_n)-U'(u_{n}-u_{n-1})-V'(u_n)\,, \end{aligned}$$

(8.1)

U(r) is the potential energy of the two particles at the distance r and $V(u_n)$ is the on-site potential. Interatomic interactions are described by the empirical Morse potential

$$\begin{aligned} U(r)=D(e^{-2\alpha (r-r_m)}-2e^{- {\alpha } (r-r_m)})\,, \end{aligned}$$

(8.2)

where r is the distance between two atoms, D, $\alpha$, $r_m$ are the potential parameters. The function U(r) has a minimum at $r=r_m$, the depth of the potential (the binding energy) is equal to D and $\alpha$ defines the stiffness of the bond. We take $D=1$, $r_m=1$ and $\alpha =5$. For the considered case of the nearest-neighbor interactions the equilibrium interatomic distance is unity. The on-site potential is taken in the sinusoidal form,

$$\begin{aligned} V(u_n)=-A\cos (2\pi u_n)\,, \end{aligned}$$

(8.3)

with the amplitude $A=4$.

A DB excited by the try and error method is presented in Fig. 8.1. Shown are the displacements of the central atom of the DB, $u_0$, and its three neighbors as the functions of time. DB frequency is $\omega _{DB}=21.33$ which is above the upper edge of the phonon spectrum $\omega _{\max }=18.92$.

Fig. 8.1

Displacements of the central atom of the DB, $u_0$, and its three neighbors as the functions of time. The DB is excited in the chain (8.1) with the parameters $D=1$, $r_m=1$ and $\alpha =5$ in (8.2) and $A=4$ in (8.3). Results for the 1D chain of particles (8.1) interacting via Morse potential (8.2) in the sinusoidal on-site potential (8.3)

2.1 Simulation Setup and Moving DB Ansatz

In 2D crystal with Morse interatomic interactions, and without any on-site potential, DB with frequency above the phonon spectrum are possible [36–38] because the close-packed atomic row, in which the DB is excited, experiences the action of the effective on-site potential induced by the rest of the crystal.

Fig. 8.2

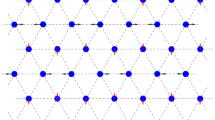
a Stroboscopic picture of atomic motion showing the moving DB excited in a close-packed atomic row with the help of (8.4) for the parameters $A=0.128$, $B=0.015$, $\beta =\gamma =0.25$, $x_0=0$, $\omega =19.5$, $\varphi _0=0.1\pi$, $\delta =0.04\pi$. b DB frequency as the function of amplitude. The upper edge of the phonon band is shown by the horizontal line. Results for the 2D hexagonal lattice with long range Morse potential

A two-dimensional (2D) close packed lattice with the interatomic distance (lattice constant) equal to a is considered. Interatomic interactions are described by the empirical Morse potential (8.2). In the following, we choose scales of time, energy and distance such that $D=1$, $r_m=1$ and the atom mass is unity. We take $\alpha =5$, for which the equilibrium interatomic distance is $a=0.98813$. The cut-off radius is chosen to be $r_c=5$. Due to the long-range interaction $a<r_m$.

The computational cell, generated by the translation vectors $\mathbf {a}$ $_1=a(1,0)$, $\mathbf {a}$ $_2=(a/2)(1,\sqrt{3})$ consists of $160\times 160$ atoms. The cell is subjected to the periodic boundary conditions. Discrete breathers are excited in the middle part of the computational cell. In order to absorb the small-amplitude waves emitted by the DB, an ad hoc viscosity term is introduced into the equations of motion for the atoms close to the borders of the computational cell. The atoms in a close-packed row are numbered by the index n as shown in Fig. 8.2a.

To excite a moving DB in a close-packed row of atoms the following moving DB ansatz [38] is used

$$\begin{aligned} x_n(t)= & {} S_n^0+(-1)^n T_n^0\cos (\omega t+\varphi _0+\delta ), \nonumber \\ y_n(0)= & {} 0, \quad \dot{y}_n(0)=0, \end{aligned}$$

(8.4)

where $\omega$ is the DB frequency, $\varphi _0$ is the initial phase, $\delta$ is the parameter indicating the phase difference for neighboring atoms, the atom vibration amplitudes, $T_n^0$, and the displacements of the atom vibration centers, $S_n^0$, are defined as follows

$$\begin{aligned} T_n^0=\frac{A}{\cosh [\beta (n-x_0)]}, \quad S_n^0=\frac{-B(n-x_0)}{\cosh [\gamma (n-x_0)]}\,, \end{aligned}$$

(8.5)

where A is the DB amplitude, B defines the amplitude of displacements of the vibration centers of the atoms, $\beta$ and $\gamma$ define the degree of spatial localization of DB, $x_0$ is the DB initial position. For $x_0=0$ the DB is centered on a lattice site, while for $x_0=1/2$ midway between two neighboring lattice sites. The DB velocity depends on $\delta$, and for $\delta =0$ it is equal to zero. Thus the functions ${T_n^0}$ and ${S_n^0}$ in (8.5) describe the amplitudes and the displacements of the vibration centers of the atoms at $t=0$, respectively. These quantities will be calculated for each period of DB oscillation as

$$\begin{aligned} T_n=\frac{x_{n,\max }-x_{n,\min }}{2}, \quad S_n=\frac{x_{n,\max }+x_{n,\min }}{2}, \end{aligned}$$

(8.6)

where $x_{n,\max }$ and $x_{n,\min }$ are the maximal and minimal values of the quasiperiodic function $x_n(t)$ that describes the motion of nth atom of a close-packed atomic row. For atoms in the atomic rows where DB is not excited we set $x_n(0)=y_n(0)=0$ and $\dot{x}_n(0)=\dot{y}_n(0)=0$.

The proposed ansatz is based on the data from [24] and takes into account the fact that the DB is exponentially localized in space owing to hyperbolic functions in (8.5). In addition, the frequency of the DB should lie above the phonon spectrum of the crystal, which can be implemented only for the shortest wavelength vibrational modes, when the neighboring atoms move in antiphase. This requirement is fulfilled owing to the introduction of the factor $(-1)^n$ in (8.4) in front of the amplitudes of atoms $T_n$. The term $S_n$ in (8.4) takes into account the effect of dilation in the vicinity of the DB caused by the asymmetric anharmonicity of the interatomic forces, when the centers of vibrations of atoms of the close-packed row are displaced away from the center of the DB. Finally, the motion of the discrete breather over the crystal is provided by the introduction of a small phase difference $\delta$ in the vibrations of the neighboring atoms in (8.4).

It should be noted that the ansatz (8.4, 8.5) is not an exact solution to the equations of motion for the considered 2D crystal. That is why a part of the energy given to the system at $t=0$ is radiated in the form of small-amplitude extended waves and then a stable and robust moving DB emerges, if the parameters in (8.4, 8.5) are properly chosen.

In Fig. 8.2a the moving DB excited in a close-packed atomic row is depicted by the stroboscopic picture of atomic motion. The DB is shown at $t=10$. The following parameter values were used for setting the initial conditions $A=0.128$, $B=0.015$, $\beta =\gamma =0.25$, $x_0=0$, $\omega =19.5$, $\varphi _0=0.1\pi$, $\delta =0.04\pi$. The frequency used to excite the DB is above the phonon spectrum of the crystal. As it can be seen in Fig. 8.2b, the DB frequency, $\omega _\mathrm{DB}$, increases with the increase in the DB amplitude A revealing the hard-type anharmonicity of this vibrational mode. The upper edge of the phonon band, $\omega _{\max }=18.9$, is shown in (b) by the horizontal line.

Fig. 8.3

Head-on collision of DB moving in a close-packed atomic row. Panels from the top to the bottom are presented with the time step of 10 time units. $T_n$ is the oscillation amplitude of nth atom. As a result of the collision the two DB merge into one having the amplitude larger than the initial DB. Results for the 2D hexagonal lattice with long range Morse potential

2.2 Head-On Collision of Moving DB

Here we present an illustrative example of head-on collision of two identical DB moving toward each other with equal velocities along the x axis in the same atomic row of the 2D Morse crystal [36]. The initial velocity of DB for the chosen parameter values is 0.35a in one time unit. Fig. 8.3 shows the outcome of the head-on collision where two DB merge forming a single DB with amplitude greater than the initial DB.

Head-off collisions of DB moving toward each other in parallel close-packed atomic rows were also studied [36] and it was demonstrated that in some cases DB were destroyed as a result of the collision, while in other cases one of them took a part of energy from another.

Clearly a mechanism of energy gain by DB becomes available since two colliding DB can produce a DB with the amplitude greater than the initial amplitudes of the colliding DB. This is important because the concept of DB is used to explain various effects observed in crystalline solids [1, 4, 18, 22, 45].

3 DB in Pure Metals

Very recently the hard-type anharmonicity DB were identified in pure metals with fcc lattice (Ni) and bcc lattice (Nb, Fe) [24, 25]. The latter studies have inspired the development of the ansatz for the initial conditions to excite DBs with hard-type nonlinearity [38]. The ansatz has been used to simulate the interaction of DBs with a vacancy [37]. Note that the moving DB studied here are qualitatively different from the soliton-like waves called crowdions (kinks), analyzed recently in [9–12, 26].

Fig. 8.4

Computational cell in the form of a cuboid used to simulate DBs in hcp metals. To excite a moving DB, initial positions and initial velocities of atoms belonging to a close-packed atomic row (shown in light color) are calculated from (8.4, 8.5). All other atoms have zero initial positions and initial velocities

Here, with the use of the molecular dynamics simulations, we demonstrate that moving DB can also be excited in hcp metals Co and Mg.

The simulations are performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) package [51] with the embedded atom method (EAM) interatomic potentials [52].

Fig. 8.5

Merger of two symmetric DB moving toward each other in Co in the same close-packed atomic row with equal velocities. $T_n$ is the oscillation amplitude of nth atom. The resulting standing DB has the amplitude higher than the initial ones. Parameters of the ansatz used for excitation of the DB see in the text

Fig. 8.6

Same as in Fig. 8.5 but for the DB having different initial phases. As a result of collision DB are reflected

Hard-type nonlinearity DB in Co and Mg is excited in a close-packed atomic row (see Fig. 8.4) with the help of the ansatz (8.4, 8.5) [38].

3.1 Collision of Moving DB

In Figs. 8.5 and 8.6 collision of two DB moving in the same close-packed atomic row in Co are presented by the time evolution of the functions $T_n$ representing the amplitudes of atomic vibrations. In Fig. 8.5 two symmetric DB moving toward each other with equal velocities collide to create a standing DB with the amplitude larger than the initial DB amplitudes. The following parameters of the ansatz were used to excite the DB: $A=0.3$ Å, $B=0.08$ Å, $\beta =0.5$, $\gamma =0.6$, $\omega =14.8$ THz, $x_0=1/2$, $\delta =\pm 0.1\pi$, $\phi _0= \pi /2$. In Fig. 8.6 both DB have the same parameters except for the initial phase, which is equal to $\phi _0= \pi /2$ and $\phi _0= \pi /4$ for the DB moving from the left and from the right, respectively. In this case DB are reflected after the collision.

Fig. 8.7

Merger of two symmetric DB moving toward each other in Mg in the same close-packed atomic row with equal velocities. $T_n$ is the oscillation amplitude of nth atom. Parameters of the ansatz used for excitation of the DB see in the text

Fig. 8.8

Same as in Fig. 8.7 but for the DB having different initial phases. As a result of collision one DB emerges and moves from the left to the right with the velocity greater than the initial DB velocity

Similar results are presented in Figs. 8.7 and 8.8 for DB collisions in Mg. In Fig. 8.7 symmetric DB collide. Parameters of the ansatz (8.4, 8.5) are $A=0.5$ Å, $B=0.08$ Å, $\beta =0.5$, $\gamma =0.6$, $\omega =125$ THz, $x_0=1/2$, $\delta =\pm 0.03\pi$, $\phi _0= \pi /2$. In Fig. 8.8 both DB have the same parameters except for the initial phase, which is equal to $\phi _0= \pi /2$ and $\phi _0= \pi /4$ for the DB moving from the left and from the right, respectively. Collision of DB with different initial phases in this case produces one DB moving from the left to the right with the velocity greater than the initial DB velocity.

It can be concluded that at 0 K the moving DB in pure hcp metals such as Co and Mg are very robust, they can travel very long distances and can survive head-on collisions with each other. Energy exchange between colliding DB is possible and it strongly depends on the mutual phase of colliding DB.

3.2 Application to Radiation Effects

Crystal lattice defects play a very important role in solid state physics and materials science. It is interesting to study the effect of DB scattering on the natural defects (e.g. vacancies, voids, dislocations, and grain boundaries) [14–17, 30, 56]. In this respect, the ability of DB to move in pure metals, demonstrated in the present chapter, is very important since it greatly enhances the range of their interaction with the lattice defects. This interaction may be responsible for the long-range interaction between the defects resulting in their spatial ordering. A prominent example is the ordering of vacancy voids into three-dimensional super-lattices under neutron and heavy-ion irradiation of a number of bcc metals (Mo, W, Nb, Ta) and fcc Ni and Al [41], where they copy the host lattice of the metal, and in hcp metals Zr and Mg [5]. The void super-lattice copies the host lattice of the metal in bcc and fcc metals, while voids are aligned in bands parallel to the basal planes in hcp metals. Irradiation may cause continuous generation of DBs inside material due to external lattice excitation, thus pumping the material with a gas of DBs propagating along close-packed lattice directions. A scattering of DB on the void surfaces excites the surface atoms [59], which enhances the rate of the vacancy emission from voids. As a result, the vacancy solubility, $C_V^{irr}$, also known as the dynamic equilibrium concentration of vacancies in the vicinity of the void surface, start to depend on the irradiation flux $F_{irr}$ of fast particles that generate DB [14, 16]:

$$\begin{aligned} C_V^{irr}(F_{irr},T)= & {} C_V^{th}(T)\exp \left( \frac{\varDelta \phi _q(F_{irr},T)}{k_B T}\right) , \nonumber \\ \varDelta \phi _q(F_{irr},T)\equiv & {} \frac{\langle E_{st}(F_{irr},T) \rangle ^2}{k_B T}, \end{aligned}$$

(8.7)

where $C_V^{th}(T)$ is the thermal vacancy solubility, $k_B$ is the Boltzmann constant, T is the temperature, and $\langle E_{st}(F_{irr},T) \rangle$ is the standard deviation of the vacancy formation energy from the ground value caused by the DB-induced excitation, which is given by the product of the frequency of DB-void collisions, the excitation amplitude and lifetime. It is positive by definition, which means that $C_V^{irr}>C_V^{th}$. The void growth rate is proportional to the difference between the net flux of vacancies from the bulk to the void, $J_V^{in}$, and the flux of vacancies from the void to the bulk, $J_V^{out}$. The former flux $J_V^{in}$ is determined by the difference between the fluxes of vacancy and self-interstitial atoms (SIAs) produced by irradiation in the bulk, while the latter flux $J_V^{out}$ is proportional to the vacancy solubility at the void surface, $C_V^{irr}/J_V^{out} \sim D_V C_V^{irr}$, where $D_V$ is the vacancy diffusivity.

Fig. 8.9

Illustration of the dissolution of a void in the interstitial position due to the absorption of DB coming from larger distances as compared to locally ordered voids that shield each other from the breather fluxes along the close packed directions [15]

Radiation-induced DB can move along the close-packed directions until they decay or collide with a void. If the DB propagating range is larger than the void spacing, the voids can shield each other from DB fluxes along the close packed directions, and so, the vacancy emission rate for voids, which have more immediate neighbors along the close packed direction, becomes smaller than that for other voids, and so they have some advantage in growth (Fig. 8.9). Quantitatively, it means that $C_V^{irr}$ for the locally ordered voids is lower that for the locally interstitial voids. If the void number density is sufficiently high, the competition between them can be shown to make the interstitial voids shrink away resulting in the void lattice formation, in which the nearest neighbors are arranged along the close-packed directions of the host lattice [15]. For cubic metals this means the void lattice copes the host lattice, while in hcp metals, the alignment of voids in bands parallel to the basal planes (in which DB propagate) is expected, in agreement with experimental data [5, 41]. This driving force for the void ordering was proposed by Dubinko [15] well before the existence of DB in metals was demonstrated. Subsequent results on the DB mobility in bcc metals [59] and the present results on the DB mobility in hcp metals strongly support this model, although further work is needed to demonstrate that DBs can be robust at the elevated temperatures.

Another prominent phenomenon that can be expected from the anisotropy of DB propagation in hcp metals is the irradiation growth (IG). IG is the name given to the volume-conserved shape deformation that occurs in non-cubic crystalline materials under irradiation in the absence of an applied stress [6, 19, 23, 63, 64]. The best known examples of irradiation growth are found in graphite, uranium, zirconium and its alloys (see [6, 19] for the review). In most cases, IG corresponds to an expansion along the a-direction and a contraction along the c-direction in its constituent grains [19]. Available models of IG are based on the anisotropy of migration of point defects (usually, self-interstitial atoms—SIAs) produced by irradiation [63, 64] or mobile SIA-clusters produced by cascade damage [23]. However, diffusion anisotropy in hcp is yet a subject of debates, while the IG related effects are observed also under electron irradiation, which does not produce cascades, and hence, in-cascade SIA-clusters cannot explain these effects. So, it becomes evident that the mechanisms involved in the irradiation growth of hcp metals may be more complicated than those that can be understood within the conventional rate theory models.

Fig. 8.10

DB propagate within the basal planes in hcp metals. Accordingly, the DB-induced vacancy emission from prismatic grains is enhanced as compared to that from the basal grains, which should result in an expansion along the a-direction and a contraction along the c-direction

Here we note that IG can be based on a principally new mechanism related to the anisotropy of DB propagation in hcp metals, where all the close-packed directions lie within the basal plane (Fig. 8.10). Accordingly, the DB-induced vacancy emission from prismatic grains, $J_V^{out} \sim D_V C_V^{irr}$, is enhanced as compared to that from the basal grains, $J_V^{out} \sim D_V C_V^{th}$ at which only thermally activated vacancy emission takes place. This should result in a relative expansion along the a-direction and a contraction along the c-direction at a rate IGR given by

$$\begin{aligned} IGR\approx \frac{D_V}{l_G^2}(C_V^{irr}-C_V^{th}), \end{aligned}$$

(8.8)

where $l_G$ is the grain size. This mechanism is similar to the Nabarro-Herring creep mechanism, in which the vacancy concentration difference at different grains is induced by the applied external stress. In the IG case, the concentration gradient is induced by irradiation and by the anisotropy of DB propagation. This mechanism predicts that IGR decreases with increasing grain size, which agrees with experimental data [6, 19]. With increasing grain size, dislocations become the dominant sinks and sources of vacancies, and the model should take into account interaction of DBs with dislocations of different orientations, which could result in a more efficient emission of vacancies from a-component dislocations as compared to c-component dislocations. That would explain a break-away growth of Zr at high neutron fluences caused by the generation of vacancy at the c-component dislocations loops, that would lead to shrinkage along the c-axis much in the same way as the vacancy loops on basal planes that were originally proposed by Buckley to explain the observed growth in uranium [19]. However, consideration of the DB-dislocation interaction in hcp metals is beyond the scope of the present chapter and will be done elsewhere.

4 Wandering DB in an Ionic Crystal

In this section we give an example of a special type of DB motion when it moves not along a straight line but wanders over the crystal changing the direction of motion.

4.1 Simulation Details

NaCl structure consists of two face-centered cubic lattices with lattice parameter a, one occupied by anions and another one by cations, displaced one with respect to another by the vector (a / 2, 0, 0) so that one falls in the body centered position of the other. Each atom has six neighbors of the opposite type which are at the vertices of a regular octahedron. Thus, each cubic translational cell consists of four anions and four cations as shown in Fig. 8.11a.

Interactions between atoms are described by the pairwise potentials that include Coulomb interaction, Born-Mayer-type repulsion, and dispersive interaction. The potentials and their parameters are given in [30]. For chosen parameters of potentials the equilibrium lattice parameter of the NaCl structure was found to be $a = 6.25$ Å. The atomic weight of the heavy atom was fixed to $M = 100$ g/mol and for the light atom we took $m = 10$ g/mol. Large difference in the atomic weight of the anions and cations ensures the existence of a wide gap in the phonon spectrum of the crystal [30, 35]. Computational cell used in our simulations included $8\times 8 \times 8$ cubic translational cells, and it was subjected to periodic boundary conditions.

Fig. 8.11

a The NaCl crystal structure. Light (heavy) atoms are shown by filled (open) circles. b Stroboscopic picture of atomic motion showing a pair of DBs in the crystal with the NaCl structure. The atoms A and C oscillate out-of-phase along [110] direction with equal, large amplitudes

Fig. 8.12

a Density of phonon states (DOS) for the considered crystal with the NaCl structure. The gap in the phonon spectrum ranges from 4.4 to 11.8 THz. b Frequency of DB pair of AC-type (see Fig. 8.11b) as the function of DB amplitude (dots connected with the line). Horizontal lines show the edges of the phonon spectrum gap

DB in the considered crystal model is highly localized on a light atom. The light atom can vibrate with a large amplitude along one of the high-symmetry directions, $\langle 100\rangle$, $\langle 110\rangle$, or $\langle 111\rangle$ [30, 34, 35]. Excitation of DB with $\langle 111\rangle$ polarization requires a special procedure [35], while DB with the other two polarizations can be easily excited by displacing one light atom away from its equilibrium position in the desired direction by about 0.3–0.5 Å. After a short transient period, a stable DB emerges, while a part of the energy initially given to the exited atom spreads over the computational cell in the form of small-amplitude vibrations. Magnitude of the initial displacement defines the DB amplitude.

In Fig. 8.12 a the density of phonon states (DOS) for the considered crystal with the NaCl structure is presented. The spectrum features a wide gap that is the necessary condition for the existence of gap DB, i.e., DB having frequency within the phonon gap.

4.2 Pairs of Discrete Breathers

Three types of DB pairs were considered, namely, the atoms A and B oscillating along [100] direction, the atoms A and C oscillating along [110] direction, and the atoms A and D oscillating along [111] direction (see Fig. 8.11a).

Fig. 8.13

Displacements $u_x=u_y$ for atom a A and c C in the NaCl structure crystal. b Phase difference for atoms A and C. Initially only A and C atoms were excited with the amplitudes $A_x=A_y=0.45$ Å with the phase difference $\varDelta \phi =\pi$. Here $\theta$ is the DB oscillation period

Fig. 8.14

Same as in Fig. 8.13 but for the case of small initial difference in the amplitudes of the atoms A and C. Initially only A and C atoms were excited with the amplitudes $A_x=0.45$ Å, $A_y=0.47$ Å, with the phase difference $\varDelta \phi =\pi$

The AB and AD pairs are easy to excite. However, for these two pairs, a heavy atom is in between the two nearest light atoms oscillating with large amplitudes. The heavy atom precludes from the energy exchange between the light atoms and this makes the AB and AD pairs not interesting for the present study which focuses on the energy exchange between DBs. On the other hand, in the AC pair the two nearest light atoms are not separated by a heavy atom and it was found that they can exchange by their energies. In the following the results will be presented only for the AC pairs of DB.

In Fig. 8.12b, frequency of the DB pair of AC-type (see Fig. 8.11b) is plotted as the function of DB amplitude (dots connected with the line). The DB in the pair oscillate out of phase without energy exchange between them. Horizontal lines show the edges of the phonon spectrum gap. Reduction of the DB frequency with the increase in DB amplitude suggests that this vibrational modes demonstrate soft type anharmonicity.

An example of AC-type DB pair is presented in Fig. 8.11b as a stroboscopic picture of atomic motion. It can be seen that only two neighboring light atoms, A and C, oscillate out-of-phase with large amplitudes, while the other atoms oscillate with much smaller amplitudes.

In Figs. 8.13 and 8.14 two examples of AC-type DB pairs are given by plotting the displacements $u_x=u_y$ as the functions of dimensionless time $t/\Theta$ of the atoms (a) A and (c) C. Here $\Theta$ is the oscillation period of DB. In (b) the phase difference is shown for the atoms A and C. In Fig. 8.13 the atoms A and C oscillate out of phase, while in Fig. 8.14 they oscillate with a phase shift. In the former case the amplitudes of both atoms do not change in time, while in the latter case, the energy exchange between two DBs can be observed. The energy exchange is not exactly time periodic. The possibility of energy exchange between neighboring light atoms suggests the possibility of DB motion.

Fig. 8.15

Schematic picture of atomic motion for the case when two atoms, a and c, were initially excited in the NaCl structure crystal with the amplitudes $A_x=A_y=0.455$ Åand phase difference $\varDelta \phi =0.9\pi$. Vibration amplitudes of the atoms (a–e) as the functions of dimensionless time are shown in Fig. 8.16

Fig. 8.16

a–e Vibration amplitudes for the atoms labeled (a–e) in Fig. 8.15, respectively, as the functions of dimensionless time. Here $\theta$ is the DB oscillation period

The next example shows the possibility of complex energy transmission from one atom to neighboring atoms so that even vibration polarization of atoms can be changed. The light atoms a and c were initially excited to oscillate along $\langle 110\rangle$ crystallographic direction with the initial amplitudes $A_x=A_y=0.455$ Åand phase difference $\varDelta \phi =0.9\pi$ (see Fig. 8.15 for the schematic presentation of the energy transmission and the changes in vibration polarization of atoms). More detailed information is presented in Fig. 8.16a–e where the displacements of atoms a to e are presented, respectively. Note that for the atoms b and c the x and y components of the displacements are shown on separate panels because they are not equal and thus, the vibration polarization differs from $\langle 110\rangle$.

This example shows that the energy initially given only to the atoms a and c wanders over the neighboring light atoms, the vibration polarization of atoms changes and nevertheless the energy remains in the spatially localized form for a very long time. Panel (c) of Fig. 8.16 reveals a large-amplitude vibration of the atom c along $\langle 100\rangle$ crystallographic direction for $t>500\theta$. Partial energy exchange between atom c and atom b can be observed. The simulation till $t=750\theta$ did not reach the energy dissipation of the excited DB over the computational cell.

5 Summary

Molecular dynamics simulations based on the empirical interatomic potentials have demonstrated that movable DB can be excited in 2D and 3D crystal models. In monatomic crystals with one atom in a primitive translational cell, such as 2D Morse crystal and pure fcc and bcc metals, phonon spectra cannot have gaps. hcp metals typically do not feature a gap in the phonon spectrum even though they have two atoms in a primitive cell. In such crystals only hard-type anharmonicity DB with frequencies above the phonon gap can exist. In complex crystals possessing gaps in the phonon spectrum in addition to the hard-type anharmonicity DB, also soft-type anharmonicity DB with frequencies within the gaps can exist.

Hard-type anharmonicity breathers studied here for 2D Morse crystal and for 3D models of hcp metals can move along a close-packed atomic row with the velocities of the order of 0.1 of the sound velocity [24]. Soft-type anharmonicity breathers in the alkali-halide crystals with NaCl structure demonstrate the ability of random wandering over the neighboring light atoms. Polarization of atomic vibrations can change but the energy stays in the spatially localized form for hundreds and thousands of vibration periods.

As an open problem let us mention the analysis of the DB concentration and lifetime in different crystals at thermal equilibrium. Preliminary study for the 2D crystal of the A$_3$B composition was carried out in [31].