Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Modern financial mathematics is based on the theory of semimartingales and Markov processes. Nevertheless there is a process of fractional Brownian motion introduced by Mandelbrot and van Ness in [4] which is often used in practice. There is no equivalent martingale measure for models which use fractional Brownian motion (see [1]). Cheridito in [1] showed that even if fractional Brownian motion market assumes arbitrage strategies these strategies cannot be realized in practice since there is always a time delay between transactions in practice. Guasoni in [3] considered that if transaction costs exist then an opportunity of arbitrage vanishes as well.

A problem of optimal stopping time is of our interest. In financial sense this problem can be interpreted as follows: if an investor has a set of assets he has to make a decision: at which time he should sell these assets. In paper [5] a problem of optimal stopping time has been considered as a problem of maximization expectation value of a utility function. A process considered was a process of Brownian motion with a drift. The solution of a problem derived in that paper can be represented as “Buy and Hold” rule.

In this paper we will show that for fractional Brownian motion “Buy and Hold” rule cannot be applied. We will discuss a class of stopping times which can be claimed to be optimal and easy to model.

The paper is organized as follows: in Sect. 2 we will discuss properties of fractional Brownian motion, a problem of optimal stopping time will be introduced and some stopping time classes will be shown. In Sect. 3 we will show an example of non optimality of these stopping times and results of numerical modeling showing non triviality of these stopping times.

2 Optimal Stopping Problem

First of all we should introduce an optimal stopping problem. Consider an asset which price changes corresponding to a stochastic process X. An owner of this asset should sell this asset till time T in the best way. This problem is called optimal stopping time problem. Mathematically this problem is formulated as follows: we should find a time τ ∗:

$$\displaystyle{\tau ^{{\ast}} = argmax(\mathsf{E}U(X_{\tau })),0 \leq \tau \leq T}$$

where U(x) is an utility function, τ is a stopping time.

In [5] authors have shown that for classical Brownian motion a solution of this problem can be represented as “Buy and hold” rule. An owner of an asset should sell it either at time t = 0 or at time t = T. In this paper we will show that for fractional Brownian motion a solution of this problem is more complex.

Definition 1 (see [4])

Fractional Brownian motion is a gaussian stochastic process B H (t) with the following properties:

  • B H (0) = 0 and E[B H (t)] = 0;

  • \(cov(B_{H}(t),B_{H}(s)) = \frac{1} {2}(t^{2H} + s^{2H} -\vert t - s\vert ^{2H}).\)

Parameter H is called Hurst parameter.

Remark 1

If \(H = \frac{1} {2}\) then this process is a classical Brownian motion.

Remark 2

Having \(H < \frac{1} {2}\) this process has negative autocorrelation. Having \(H > \frac{1} {2}\) this process has a positive autocorrelation.

Remark 3

Fractional Brownian motion has a self-similarity property with Hurst parameter equal to H. This means that if a process B H (t) is a process of fractional Brownian motion, then the following processes have the same distributions

$$\displaystyle{\left \{B_{H}(at): 0 \leq t < \infty \right \}\stackrel{d}{=}\left \{a^{H}B_{ H}(t): 0 \leq t < \infty \right \}.}$$

Using Remark 3 and a property of continuity of fractional Brownian motion we can study properties of this process for discrete times and then rescale it for any time interval.

There are several different ways of fractional Brownian motion modeling. In this paper we will use a model proposed by Dieker in [2]. Fractional Brownian motion has the following covariation function:

$$\displaystyle{\gamma (s) = cov(X_{H}(t),X_{H}(t + s)) = \frac{1} {2}(\vert s - 1\vert ^{2H} + \vert s + 1\vert ^{2H} - 2\vert s\vert ^{2H}).}$$

Let \(\varGamma (n) =\{\gamma (i - j)_{(i,j=1,n)}\}\) be a covariation matrix, and c(n) is a vector of size (n + 1), where \(c(n)_{k} =\gamma (k + 1)\). Then \(X_{n+1} = B_{h}(n + 1) - B_{h}(n)\) is a random value with normal distribution with expectation μ n and variance σ n 2, where \(\mu _{n} = d(n)^{T}\left (\begin{array}{*{10}c} X_{n} \\ X_{n-1}\\ \vdots \\ X_{0} \end{array} \right )\), \(\sigma _{n}^{2} = 1 - c(n)^{T}\varGamma (n)^{-1}c(n)\). Dieker shows that there is an iterative algorithm for modeling μ n and σ n 2 with no need of matrix inversion as well.

An optimal stopping time problem is a following problem:

$$\displaystyle{f(h) =\sup _{\tau \leq 1}\mathsf{E}B_{H}(\tau ),\tau (h) = \mathrm{arg}\max _{\tau \leq 1}\mathsf{E}B_{H}(\tau ).}$$

Using self similar property this problem is equivalent to the following problem:

$$\displaystyle{f_{N}(h) = \frac{1} {N^{h}}\sup _{\tau \leq N}\mathsf{E}\sum _{i=0}^{\tau }X_{ H}(i),\tau _{N}(h) = \frac{1} {N^{h}}\mathrm{arg}\max _{\tau \leq N}\mathsf{E}\sum _{i=1}^{N}X_{ H}(i).}$$

In this problem a following class of stopping times τ is considered: \(\tau _{c} = \frac{1} {N^{h}}min(t:\mu _{t} < c(N - t) {\ast} t^{H}),\) where \(\mu _{t} = \mathsf{E}(X_{h}(t + 1)\vert X_{h}(1),\ldots,X_{h}(t)).\)

Example 1

Consider the case of c = 0. From financial point of view this means that we don’t sell assets till the moment when the next increment has a negative average.

Here we have following limit cases:

  • H = 0. 5. In this case μ t  = 0 ∀t, i.e. E B τ  = 0. 

  • H = 1 In this case X(t) = X(1) ∀t. This means

    $$\displaystyle{\sup _{\tau \in [0,1]}\mathsf{E}B_{\tau } =\int _{ 0}^{\infty }x \frac{1} {\sqrt{2\pi }}e^{-\frac{x^{2}} {2} }dx = \frac{1} {\sqrt{2\pi }},}$$

    but the optimal moment cannot be reached.

It can be shown that

$$\displaystyle\begin{array}{rcl} & \mathsf{E}(\mu _{n+1}\vert F_{n}) = \mathsf{E}(d_{0}^{n+1}X_{n+1}\vert F_{n}) +\sum _{ i=1}^{n+1}d_{n-i+1}^{n+1}X_{i} = d_{0}^{n+1}\mu _{n} +\sum _{ i=1}^{n+1}d_{n-i+1}^{n+1}X_{i},& {}\\ & \mathsf{E}(\mu _{n+2}\vert F_{n}) = \mathsf{E}(d_{0}^{n+2}X_{n+2}\vert F_{n}) + \mathsf{E}(d_{1}^{n+2}X_{n+1}\vert F_{n}) +\sum _{ i=2}^{n+2}d_{i}^{n+2}X_{n-i+2} = & {}\\ & = d_{0}^{n+2}\mathsf{E}(\mu _{n+1}\vert F_{n}) + d_{1}^{n+2}\mu _{n} +\sum _{ i=2}^{n+2}d_{i}^{n+2}X_{n-i+2}. & {}\\ \end{array}$$

And for any k we have \(\mathsf{E}(\mu _{n+k}\vert F_{n}) =\sum _{ j=0}^{k-2}\mathsf{E}(d_{j}^{n+k}X_{n+k-j}\vert F_{n}) + d_{k-1}^{n+k}\mu _{n} +\sum _{ i=k}^{n+k}d_{i}^{n+k}X_{n-i+k},\) i.e. an average for any future values of fractional Brownian motion according to the information available for current moment is linear combination of values of discretization of fractional Brownian motion.

Example 2

We consider the following stopping times class as τ:

$$\displaystyle{\tau _{k} = \frac{1} {N^{h}}min(n:\mu _{n} < 0,\sum _{i=0}^{j}E(\mu _{ n+i}\vert F_{n}) < 0,\forall j \leq k).}$$

From financial point of view this means that we do not sell assets if there is a tendency to growth for at least any interval from 0 to k.

3 Modeling Results

In this section we will consider modeling results for different stopping times.

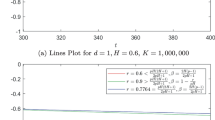
On (Fig. 1) modelling results of τ c for different c are presented. As we see, for quite small negative c we have quite good results for H > 0. 5. As we see when H tends to 1 we have a result that was shown before: \(\frac{1} {\sqrt{2\pi }}\). For H < 0. 5 we do not consider small H because we have problems with continuity of a process. But we see that for H < 0. 5 we have non trivial results as well. As we see when H > 0. 5 stopping time corresponding to c = 0 is not optimal.

Fig. 1
figure 1

Modeling results for τ c for different c. T=1000. On X-Axis—H, on Y-axis—corresponding values of \(EX_{\tau _{c}}\) for different c. Since it’s difficult to model fractional Brownian motion when H is small we discuss only H > 0. 2

Full size image

Example 3

It can be shown that E(μ n+k  | F n ) can be positive even if E(μ n  | F n ) < 0, where F n is a filtration of \(X_{0},X_{1},\ldots,X_{n}\). We shall assume H = 0. 7,

$$\displaystyle\begin{array}{rcl} X_{0}& =& 1,X_{1} = 1,X_{2} = 2,X_{3} = -1 {}\\ d^{4}& =& (0.278596,0.0728796,0.0540914,0.0507365) {}\\ d^{5}& =& (0.276542,0.07069,0.0511412,0.0394588,0.0404806) {}\\ \mu _{3}& =& -0,0280089 < 0 {}\\ \end{array}$$

But in this case,

$$\displaystyle{E(\mu _{4}\vert X_{0},X_{1},X_{2},X_{3}) = 0,0526450 > 0}$$

Moreover,

$$\displaystyle{E(\mu _{4}\vert X_{0},X_{1},X_{2},X_{3}) > -\mu _{3}}$$

This means that there exists stopping time which is even better than \(\tau = \frac{1} {N^{h}}min(t:\mu _{t} < 0)\).

We see that proposed stopping times give us non trivial results as well. The results of modeling of τ k can be shown on the previous figure (Fig. 2). As we see on it for H > 0. 5 we have bigger values of \(EB_{\tau _{k}}\) for bigger k. When H tends to 1 we have the same value that we have got for τ c . We see that for H > 0. 5 τ k gives better results than τ c and it can claim to be optimal.

Fig. 2
figure 2

Modeling results for τ k for different k (N = 1000). On X-Axis—H, on Y-axis—corresponding values of \(EX_{\tau _{k}}\) for different k. Since it’s difficult to model fractional Brownian motion when H is small we discuss only H > 0. 2

Full size image