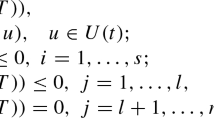Keywords

1 Introduction

The generalized variational problem proposed by Herglotz in 1930 [3, 4] can be formulated as follows:

figure a

It consists in the determination of trajectories \(x(\cdot )\) and corresponding trajectories \(z(\cdot )\) that extremize (maximize or minimize) the value z(b), where \(L \in C^1([a,b]\times \mathbb {R}^{2n}\times \mathbb {R};\mathbb {R})\). While in [3, 4, 6] the admissible functions are \(x(\cdot ) \in C^2([a,b];\mathbb {R}^n)\) and \(z(\cdot ) \in C^1([a,b];\mathbb {R})\), here we consider (\(P_{H}\)) in the wider class of functions \(x(\cdot ) \in PC^1([a,b];\mathbb {R}^n)\) and \(z(\cdot ) \in PC^1([a,b];\mathbb {R})\).

It is obvious that Herglotz’s problem (\(P_{H}\)) reduces to the classical fundamental problem of the calculus of variations (see, e.g., [13]) if the Lagrangian L does not depend on the z variable: if \(\dot{z}(t)=L(t,x(t),\dot{x}(t))\), \(t \in [a,b]\), then (\(P_{H}\)) is equivalent to the classical variational problem

$$\begin{aligned} \int _a^b L(t,x(t),\dot{x}(t))dt \longrightarrow \text {extr}, \quad x(a) = \alpha . \end{aligned}$$
(1)

Herglotz proved that an Euler–Lagrange optimality condition for a pair \(\left( x(\cdot ),z(\cdot )\right) \) to be an extremizer of the generalized variational problem (\(P_{H}\)) is given by

$$\begin{aligned} \frac{\partial L}{\partial x}\left( t,x(t),\dot{x}(t),z(t)\right)&-\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}\left( t,x(t),\dot{x}(t),z(t)\right) \nonumber \\&+\frac{\partial L}{\partial z}\left( t,x(t),\dot{x}(t),z(t)\right) \frac{\partial L}{\partial \dot{x}}\left( t,x(t),\dot{x}(t),z(t)\right) = 0, \end{aligned}$$
(2)

\(t \in [a,b]\). The Eq. (2) is known as the generalized Euler–Lagrange equation. Observe that for the fundamental problem of the calculus of variations (1) one has \(\frac{\partial L}{\partial z}=0\) and the differential Eq. (2) reduces to the classical Euler–Lagrange equation

$$ \frac{\partial L}{\partial x}\left( t,x(t),\dot{x}(t)\right) -\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}\left( t,x(t),\dot{x}(t)\right) =0. $$

Since the celebrated work [5] by Pontryagin et al., the calculus of variations is seen as part of optimal control. One of the simplest problems of optimal control, in Bolza form, is the following one:

$$\begin{aligned} \begin{array}{c} \mathcal {J}(x(\cdot ),u(\cdot ))=\displaystyle \int _a^b f(t,x(t),u(t))dt+\phi (x(b))\longrightarrow \text {extr} \\ \text {subject to } \dot{x}(t)=g(t,x(t),u(t)) \text { and } x(a)=\alpha , \quad \alpha \in \mathbb {R}, \end{array} \end{aligned}$$
(P)

where \(f \in C^1([a,b]\times \mathbb {R}^{n}\times {\varOmega };\mathbb {R})\), \(\phi \in C^1(\mathbb {R}^{n};\mathbb {R})\), \(g \in C^1([a,b]\times \mathbb {R}^{n}\times {\varOmega };\mathbb {R}^n)\), \(x \in PC^1([a,b]; \mathbb {R}^n)\) and \(u\in PC([a,b];{\varOmega })\), with \({\varOmega }\subseteq \mathbb {R}^r\) an open set. In the literature of optimal control, x and u are called the state and control variables, respectively, while \(\phi \) is known as the payoff or salvage term. Note that the classical problem of the calculus of variations (1) is a particular case of problem (P) with \(\phi (x) \equiv 0\), \(g(t,x,u)=u\) and \({\varOmega }=\mathbb {R}^n\). In this work we show how the results on Herglotz’s problem of the calculus of variations (\(P_{H}\)) obtained in [2, 6] can be generalized by using the theory of optimal control. The main idea is simple and consists in rewriting the generalized variational problem of Herglotz (\(P_{H}\)) as a standard optimal control problem (P), and then to apply available results of optimal control theory.

The paper is organized as follows. In Sect. 2 we briefly review the necessary concepts and results from optimal control theory. In particular, we make use of Pontryagin’s maximum principle (Theorem 1); the DuBois–Reymond condition of optimal control (Theorem 2); and the Noether theorem of optimal control proved in [8] (cf. Theorem 3). Our contributions are then given in Sect. 3: we generalize the Euler–Lagrange equation and the transversality condition for problem (\(P_{H}\)) found in [6] to admissible functions \(x(\cdot ) \in PC^1([a,b];\mathbb {R}^n)\) and \(z(\cdot ) \in PC^1([a,b];\mathbb {R})\) (Theorem 4); we obtain a DuBois–Reymond necessary optimality condition for problem (\(P_{H}\)) (Theorem 5); and a generalization of the Noether theorem [2] (Theorem 6) as a corollary of the optimal control results of Torres [7–9]. We end with Sect. 4 of conclusions and future work.

2 Preliminaries

The central result in optimal control theory is given by Pontryagin’s maximum principle, which is a first-order necessary optimality condition.

Theorem 1

(Pontryagin’s Maximum Principle for Problem (P) [5]). If a pair \((x(\cdot ),u(\cdot ))\) with \(x \in PC^1([a,b]; \mathbb {R}^n)\) and \(u\in PC([a,b];{\varOmega })\) is a solution to problem (P), then there exists \(\psi \in PC^1([a,b];\mathbb {R}^n)\) such that the following conditions hold:

  • the optimality condition

    $$\begin{aligned} \frac{\partial H}{\partial u}(t, x(t),u(t), \psi (t))=0; \end{aligned}$$
    (3)

  • the adjoint system

    $$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=\frac{\partial H}{\partial \psi }(t, x(t),u(t), \psi (t))\\ \dot{\psi }(t)=-\frac{\partial H}{\partial x}(t, x(t),u(t), \psi (t)); \end{array}\right. } \end{aligned}$$
    (4)

  • and the transversality condition

    $$\begin{aligned} \psi (b)=\nabla \phi (x(b)); \end{aligned}$$
    (5)

where the Hamiltonian H is defined by

$$\begin{aligned} H(t,x,u,\psi )=f(t,x,u)+\psi \cdot g(t,x,u). \end{aligned}$$
(6)

Definition 1

(Pontryagin Extremal to (P)). A triplet \((x(\cdot ),u(\cdot ), \psi (\cdot ))\) with \(x \in PC^1([a,b]; \mathbb {R}^n)\), \(u\in PC([a,b];{\varOmega })\) and \(\psi \in PC^1([a,b];\mathbb {R}^n)\) is called a Pontryagin extremal to problem (P) if it satisfies the optimality condition (3), the adjoint system (4) and the transversality condition (5).

Theorem 2

(DuBois–Reymond Condition of Optimal Control [5]). If \((x(\cdot ),u(\cdot ), \psi (\cdot ))\) is a Pontryagin extremal to problem (P), then the Hamiltonian (6) satisfies the equality

$$\begin{aligned} \frac{d H}{dt}(t,x(t),u(t),\psi (t))=\frac{\partial H}{\partial t}(t,x(t),u(t),\psi (t)), \end{aligned}$$

\(t \in [a,b]\).

Noether’s theorem has become a fundamental tool of modern theoretical physics [1], the calculus of variations [10, 11], and optimal control [7–9]. It states that when an optimal control problem is invariant under a one parameter family of transformations, then there exists a corresponding conservation law: an expression that is conserved along all the Pontryagin extremals of the problem [7–9, 12]. Here we use Noether’s theorem as found in [8], which is formulated for problems of optimal control in Lagrange form, that is, for problem (P) with \(\phi \equiv 0\). In order to apply the results of [8] to the Bolza problem (P), we rewrite it in the following equivalent Lagrange form:

$$\begin{aligned} \mathcal {I}(x_0(\cdot ),x(\cdot ),u(\cdot )&) =\int _a^b \left[ f(t,x(t),u(t))+ x_0(t)\right] dt \longrightarrow \text {extr},\nonumber \\&{\left\{ \begin{array}{ll} \dot{x}_0(t)=0,\\ \dot{x}(t)=g\left( t,x(t),u(t)\right) , \end{array}\right. }\\&x_0(a)= \frac{\phi (x(b))}{b-a}, \ x(a)=\alpha .\nonumber \end{aligned}$$
(7)

The notion of invariance for problem (P) is obtained by applying the notion of invariance found in [8] to the equivalent optimal control problem (7). In Definition 2 we use the little-o notation.

Definition 2

(Invariance of Problem (P)). Let \(h^s\) be a one-parameter family of \(C^1\) invertible maps

$$\begin{aligned}&\qquad \ h^s:[a,b]\times \mathbb {R}^n\times {\varOmega }\rightarrow \mathbb {R}\times \mathbb {R}^n\times \mathbb {R}^r,\\&\quad h^s(t,x,u)=\left( \mathcal {T}^s(t,x,u), \mathcal {X}^s(t,x,u),\mathcal {U}^s(t,x,u)\right) ,\\&h^0(t,x,u)=(t,x,u) \text { for all } (t,x,u)\in [a,b]\times \mathbb {R}^n\times {\varOmega }. \end{aligned}$$

Problem (P) is said to be invariant under transformations \(h^s\) if for all \((x(\cdot ),u(\cdot ))\) the following two conditions hold:

  1. (i)
    $$\begin{aligned} \Big [f \circ h^s(t,x(t),u(t))+\frac{\phi (x(b))}{b-a} + \xi s + o(s&)\Big ]\frac{d\mathcal {T}^s}{dt}(t,x(t),u(t))\nonumber \\&= f(t,x(t),u(t)) + \frac{\phi (x(b))}{b-a} \end{aligned}$$
    (8)

    for some constant \(\xi \);

  2. (ii)
    $$\begin{aligned} \frac{d\mathcal {X}^s}{dt}\left( t,x(t),u(t)\right) =g\circ h^s(t,x(t),u(t))\frac{d\mathcal {T}^s}{dt}(t,x(t),u(t)). \end{aligned}$$
    (9)

Theorem 3

(Noether’s Theorem for the Optimal Control Problem (P)). If problem (P) is invariant in the sense of Definition 2, then the quantity

$$\begin{aligned} (b-t) \xi + \psi (t) \cdot X(t,x(t),u(t)) -\left[ H(t,x(t),u(t),\psi (t)) + \frac{\phi (x(b))}{b-a}\right] \cdot T(t,x(t),u(t)) \end{aligned}$$

is constant in t along every Pontryagin extremal \((x(\cdot ),u(\cdot ), \psi (\cdot ))\) of problem (P), where

$$\begin{aligned}&T(t,x(t),u(t))=\frac{\partial \mathcal {T}^s}{\partial s}(t,x(t),u(t))\biggm \vert _{s=0},\\&X(t,x(t),u(t))=\frac{\partial \mathcal {X}^s}{\partial s}(t,x(t),u(t))\biggm \vert _{s=0}, \end{aligned}$$

and H is defined by (6).

Proof

The result is a simple exercise obtained by applying the Noether theorem of [8] and the Pontryagin maximum principle (Theorem 1) to the equivalent optimal control problem  (7) (in particular using the adjoint equation corresponding to the multiplier associated with the state variable \(x_0\) and the respective transversality condition).

3 Main Results

We begin by introducing some basic definitions for the generalized variational problem of Herglotz (\(P_{H}\)).

Definition 3

(Admissible Pair to Problem (\(P_{H}\))). We say that \((x(\cdot ),z(\cdot ))\) with \(x(\cdot ) \in PC^1([a,b];\mathbb {R}^n)\) and \(z(\cdot ) \in PC^1([a,b];\mathbb {R})\) is an admissible pair to problem (\(P_{H}\)) if it satisfies the equation

$$\begin{aligned} \dot{z}(t)=L(t,x(t),\dot{x}(t),z(t)), \quad t \in [a,b], \end{aligned}$$

and the initial conditions \(x(a)=\alpha \) and \(z(a)=\gamma \), \(\alpha , \gamma \in \mathbb {R}\).

Definition 4

(Extremizer to Problem (\(P_{H}\))). We say that an admissible pair \((x^*(\cdot ),z^*(\cdot ))\) is an extremizer to problem (\(P_{H}\)) if \(z(b)-z^*(b)\) has the same signal for all admissible pairs \((x(\cdot ),z(\cdot ))\) that satisfy \(\Vert z-z^* \Vert _0< \epsilon \) and \(\Vert x-x^* \Vert _0< \epsilon \) for some positive real \(\epsilon \), where \(\Vert y\Vert _0=\displaystyle \mathop {\max _{a\le t \le b}}|y(t)|\).

We now present a necessary condition for a pair \((x(\cdot ),z(\cdot ))\) to be a solution (extremizer) to problem (\(P_{H}\)). The following result generalizes [3, 4, 6] by considering a more general class of functions. To simplify notation, we use the operator \(\langle \cdot ,\cdot \rangle \) defined by

$$ \langle x, z \rangle (t):=(t,x(t),\dot{x}(t),z(t)). $$

When there is no possibility of ambiguity, we sometimes suppress arguments.

Theorem 4

(Euler–Lagrange Equation and Transversality Condition for Problem (\(P_{H}\))). If \((x(\cdot ),z(\cdot ))\) is an extremizer to problem (\(P_{H}\)), then the Euler–Lagrange equation

$$\begin{aligned} \frac{\partial L}{\partial x}\langle x, z \rangle (t) -\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{x}}\right) \langle x, z \rangle (t) +\frac{\partial L}{\partial z}\langle x, z \rangle (t) \frac{\partial L}{\partial \dot{x}}\langle x, z \rangle (t) = 0 \end{aligned}$$
(10)

holds, \(t \in [a,b]\). Moreover, the following transversality condition holds:

$$\begin{aligned} \frac{\partial L}{\partial \dot{x}}\langle x,z\rangle (b)=0. \end{aligned}$$
(11)

Proof

Observe that Herglotz’s problem (\(P_{H}\)) is a particular case of problem (P) obtained by considering x and z as state variables (two components of one vectorial state variable), \(\dot{x}\) as the control variable u, and by choosing \(f\equiv 0\) and \(\phi (x,z)=z\). Note that since \(x(t)\in \mathbb {R}^n\), we have \(u(t)\in \mathbb {R}^n\) (i.e., for Herglotz’s problem (\(P_{H}\)) one has \(r=n\)). In this way, the problem of Herglotz, described as an optimal control problem, takes the form

$$\begin{aligned}&\qquad \qquad z(b) \longrightarrow \text {extr},\nonumber \\&\ {\left\{ \begin{array}{ll} \dot{x}(t)=u(t),\\ \dot{z}(t)=L(t,x(t),u(t),z(t)), \end{array}\right. }\\&x(a)=\alpha , \ z(a)=\gamma , \quad \alpha , \gamma \in \mathbb {R}.\nonumber \end{aligned}$$
(12)

It follows from Pontryagin’s maximum principle (Theorem 1) that there exists \(\psi _x \in PC^1([a,b];\mathbb {R}^n)\) and \(\psi _z \in PC^1([a,b];\mathbb {R})\) such that the following conditions hold:

  • the optimality condition

    $$\begin{aligned} \frac{\partial H}{\partial u}(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t))=0; \end{aligned}$$
    (13)

  • the adjoint system

    $$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=\frac{\partial H}{\partial \psi _x}(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t))\\ \dot{z}(t)=\frac{\partial H}{\partial \psi _z}(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t))\\ \dot{\psi }_x(t)=-\frac{\partial H}{\partial x}(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t))\\ \dot{\psi }_z(t)=-\frac{\partial H}{\partial z}(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t)); \end{array}\right. } \end{aligned}$$
    (14)

  • and the transversality conditions

    $$\begin{aligned} {\left\{ \begin{array}{ll} \psi _x(b)=0,\\ \psi _z(b)=1, \end{array}\right. } \end{aligned}$$
    (15)

where the Hamiltonian H is defined by

$$ H(t,x,u,z,\psi _x,\psi _z)=\psi _x \cdot u+\psi _z \cdot L(t,x,u,z). $$

Observe that the adjoint system (14) implies that

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\psi }_x=-\psi _z\frac{\partial L}{\partial x}\\ \dot{\psi }_z=-\psi _z\frac{\partial L}{\partial z}. \end{array}\right. } \end{aligned}$$
(16)

This means that \(\psi _z\) is solution of a first-order linear differential equation, which is solved using an integrand factor to find that \(\psi _z=ke^{-\int _a^t\frac{\partial L}{\partial z}d\theta }\) with k a constant. From the second transversality condition in (15), we obtain that \(k=e^{\int _a^b\frac{\partial L}{\partial z}d\theta }\) and, consequently,

$$ \psi _z=e^{\int _t^b\frac{\partial L}{\partial z}d\theta }. $$

The optimality condition (13) is equivalent to \(\psi _x+\psi _z\frac{\partial L}{\partial u}=0\) and, after derivation, we obtain that

$$\begin{aligned} \dot{\psi }_x=-\frac{d}{dt}\left( \psi _z\frac{\partial L}{\partial u}\right) =-\dot{\psi }_z\frac{\partial L}{\partial u}-\psi _z\frac{d}{dt}\left( \frac{\partial L}{\partial u}\right) =\psi _z\frac{\partial L}{\partial z}\frac{\partial L}{\partial u} -\psi _z\frac{d}{dt}\left( \frac{\partial L}{\partial u}\right) \!\!. \end{aligned}$$

Now, comparing with (16), we have

$$ -\psi _z\frac{\partial L}{\partial x} =\psi _z\frac{\partial L}{\partial z}\frac{\partial L}{\partial u} -\psi _z\frac{d}{dt}\left( \frac{\partial L}{\partial u}\right) \!\!. $$

Since \(\psi _z(t)\ne 0\) for all \(t \in [a,b]\) and \(\dot{x}=u\), we obtain the Euler–Lagrange Eq. (10):

$$ \frac{\partial L}{\partial x}-\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{x}}\right) +\frac{\partial L}{\partial z}\frac{\partial L}{\partial \dot{x}} = 0. $$

Note that from the optimality condition (13) we obtain that \(\psi _x=-\psi _z\frac{\partial L}{\partial u}=-\psi _z\frac{\partial L}{\partial \dot{x}}\), which together with transversality condition (15) for \(\psi _x\) leads to the transversality condition (11):

$$\begin{aligned} \frac{\partial L}{\partial \dot{x}}(b,x(b),\dot{x}(b),z(b))=0. \end{aligned}$$

This concludes the proof.

Definition 5

(Extremal to Problem (\(P_{H}\))). We say that an admissible pair \((x(\cdot ), z(\cdot ))\) is an extremal to problem (\(P_{H}\)) if it satisfies the Euler–Lagrange Eq. (10) and the transversality condition (11).

Theorem 5

(DuBois–Reymond Condition for Problem (\(P_{H}\))). If \((x(\cdot ), z(\cdot ))\) is an extremal to problem (\(P_{H}\)), then

$$\begin{aligned} \frac{d}{dt}\left( -\psi _z(t)\frac{\partial L}{\partial \dot{x}}\langle x, z \rangle (t) \dot{x}(t)+\psi _z(t) L\langle x, z \rangle (t)\right) =\psi _z(t)\frac{\partial L}{\partial t}\langle x, z \rangle (t), \end{aligned}$$

\(t \in [a,b]\), where \(\psi _z(t)=e^{\int _t^b\frac{\partial L}{\partial z}\langle x,z \rangle (\theta )d\theta }\).

Proof

The result follows from Theorem 2, rewriting problem (\(P_{H}\)) as the optimal control problem (12).

We define invariance for (\(P_{H}\)) using Definition 2 for the equivalent optimal control problem (12).

Definition 6

(Invariance of Problem (\(P_{H}\))). Let \(h^s\) be a one-parameter family of \(C^1\) invertible maps

$$\begin{aligned}&\qquad \qquad \ h^s:[a,b]\times \mathbb {R}^n \times \mathbb {R} \rightarrow \mathbb {R}\times \mathbb {R}^n \times \mathbb {R},\\&h^s(t,x(t),z(t))=(\mathcal {T}^s\langle x,z \rangle (t),\mathcal {X}^s\langle x,z \rangle (t), \mathcal {Z}^s\langle x,z \rangle (t)),\\&\quad h^0(t,x,z)=(t,x,z), \quad \forall (t,x,z) \in [a,b]\times \mathbb {R}^n \times \mathbb {R}. \end{aligned}$$

Problem (\(P_{H}\)) is said to be invariant under the transformations \(h^s\) if for all admissible pairs \((x(\cdot ),z(\cdot ))\) the following two conditions hold:

  1. (i)
    $$\begin{aligned} \left( \frac{z(b)}{b-a}+\xi s + o(s)\right) \frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t) =\frac{z(b)}{b-a} \end{aligned}$$
    (17)

    for some constant \(\xi \);

  2. (ii)
    $$\begin{aligned}&\frac{d \mathcal {Z}^s}{dt}\langle x,z \rangle (t)\nonumber \\&= L\left( \mathcal {T}^s\langle x,z \rangle (t),\mathcal {X}^s\langle x,z \rangle (t), \frac{d\mathcal {X}^s}{d\mathcal {T}^s}\langle x,z \rangle (t), \mathcal {Z}^s\langle x,z \rangle (t)\right) \frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t), \end{aligned}$$
    (18)

where

$$ \frac{d\mathcal {X}^s}{d\mathcal {T}^s}\langle x,z \rangle (t) =\frac{\frac{d\mathcal {X}^s}{dt}\langle x,z \rangle (t)}{\frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t)}. $$

Follows the main result of the paper.

Theorem 6

(Noether’s Theorem for Problem (\(P_{H}\))). If problem (\(P_{H}\)) is invariant in the sense of Definition 6, then the quantity

$$\begin{aligned} \psi _z(t)\biggl [\frac{\partial L}{\partial \dot{x}}\langle x,z \rangle (t) X\langle x,z \rangle&(t) -Z\langle x,z \rangle (t)\nonumber \\&\ +\left( L\langle x,z \rangle (t)-\frac{\partial L}{\partial \dot{x}}\langle x, z \rangle (t) \dot{x}(t)\right) T\langle x,z \rangle (t)\biggr ] \end{aligned}$$
(19)

is constant in t along every extremal of problem (\(P_{H}\)), where

$$\begin{aligned} T\langle x,z \rangle (t)=\frac{\partial \mathcal {T}^s}{\partial s}\langle x,z \rangle (t)\biggm \vert _{s=0},\\ X\langle x,z \rangle (t)=\frac{\partial \mathcal {X}^s}{\partial s}\langle x,z \rangle (t)\biggm \vert _{s=0},\\ Z\langle x,z \rangle (t)=\frac{\partial \mathcal {Z}^s}{\partial s}\langle x,z \rangle (t)\biggm \vert _{s=0} \end{aligned}$$

and \(\psi _z(t)=e^{\int _t^b\frac{\partial L}{\partial z}\langle x,z \rangle (\theta )d\theta }\).

Proof

As before, we rewrite problem (\(P_{H}\)) in the equivalent optimal control form (12), where x and z are the state variables and u the control. We prove that if problem (\(P_{H}\)) is invariant in the sense of Definition 6, then (12) is invariant in the sense of Definition 2. First, observe that if Eq. (17) holds, then (8) holds for (12): here \(f \equiv 0\), \(\phi (x,z) = z\) and (8) simplifies to \(\left[ \frac{z(b)}{b-a} + \xi s + o(s)\right] \frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t) = \frac{z(b)}{b-a}\). Note that the first equation of the control system of problem (12) (\(u(t) = \dot{x}(t)\)) defines \(\mathcal {U}^s:=\frac{d\mathcal {X}^s}{d\mathcal {T}^s}\), that is,

$$\begin{aligned} \frac{d \mathcal {X}^s}{dt}\langle x,z \rangle (t) =\mathcal {U}^s\langle x,z \rangle (t)\frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t). \end{aligned}$$
(20)

Hence, if Eqs. (18) and (20) holds, then there is also invariance of the control system of (12) in the sense of (9) and consequently problem (12) is invariant in the sense of Definition 2. We are now in conditions to apply Theorem 3 to problem (12), which guarantees that the quantity

$$\begin{aligned} (b-t)\xi&+ \psi _x(t)\cdot X(t,x(t),u(t),z(t)) + \psi _z(t)\cdot Z(t,x(t),u(t),z(t))\\&-\left( H(t,x(t),u(t),z(t),\psi _x(t),\psi _z(t)) + \frac{z(b)}{b-a}\right) \cdot T(t,x(t),u(t),z(t)) \end{aligned}$$

is constant in t along every Pontryagin extremal of problem (12), where

$$\begin{aligned} H(t,x,u,z,\psi _x,\psi _z)=\psi _x u +\psi _z L(t,x,u,z). \end{aligned}$$

This means that the quantity

$$\begin{aligned} (b-t)\xi + \psi _x(t) X\langle x,z \rangle&(t) + \psi _z(t) Z\langle x,z \rangle (t)\\&\ -\left( \psi _x(t) \dot{x}(t) +\psi _z(t) L\langle x,z \rangle (t) + \frac{z(b)}{b-a}\right) T\langle x,z \rangle (t) \end{aligned}$$

is constant in t along all extremals of problem (\(P_{H}\)), where

$$ \psi _x(t)=-\psi _z(t) \frac{\partial L}{\partial u}\langle x,z \rangle (t) =-\psi _z(t) \frac{\partial L}{\partial \dot{x}}\langle x,z \rangle (t). $$

Equivalently,

$$\begin{aligned} (b-t)\xi - \frac{z(b)}{b-a}T\langle x,z \rangle (t) -\psi _{z}&(t)\biggl [\frac{\partial L}{\partial \dot{x}}\langle x,z \rangle (t) X\langle x,z \rangle (t) -Z\langle x,z \rangle (t)\\&+\left( L\langle x,z \rangle (t)-\frac{\partial L}{\partial \dot{x}}\langle x, z \rangle (t) \dot{x}(t)\right) T\langle x,z \rangle (t)\biggr ] \end{aligned}$$

is a constant along the extremals. To conclude the proof, we just need to prove that the quantity

$$\begin{aligned} (b-t)\xi - \frac{z(b)}{b-a}T\langle x,z \rangle (t) \end{aligned}$$
(21)

is a constant. From the invariance condition (17) we know that

$$\begin{aligned} \left( z(b)+\xi (b-a) s + o(s)\right) \frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t) =z(b). \end{aligned}$$

Integrating from a to t, we conclude that

$$\begin{aligned} \Big (z(b)+\xi (b-a) s&+ o(s)\Big )\mathcal {T}^s\langle x,z \rangle (t)\nonumber \\&\ =z(b)(t-a)+\left( z(b)+\xi (b-a) s + o(s)\right) \mathcal {T}^s\langle x,z \rangle (a). \end{aligned}$$
(22)

Differentiating (22) with respect to s, and then putting \(s=0\), we obtain

$$\begin{aligned} \xi (b-a) t + z(b) T\langle x,z \rangle (t) =\xi (b-a)a+z(b)T\langle x,z\rangle (a). \end{aligned}$$
(23)

We conclude from (23) that expression (21) is the constant \((b-a)\xi - \frac{z(b)}{b-a}T\langle x,z\rangle (a)\).

4 Conclusion

We introduced a different approach to the generalized variational principle of Herglotz, by looking to Herglotz’s problem as an optimal control problem. A Noether type theorem for Herglotz’s problem was first proved by Georgieva and Guenther in [2]: under the condition of invariance

$$\begin{aligned} \frac{d}{ds}\left[ L\left( \mathcal {T}^s\langle x,z \rangle (t),\mathcal {X}^s\langle x,z \rangle (t), \frac{d\mathcal {X}^s}{d\mathcal {T}^s}\langle x,z \rangle (t),z(t)\right) \frac{d\mathcal {T}^s}{dt}\langle x,z \rangle (t)\right] \bigg \vert _{s=0}=0, \end{aligned}$$
(24)

they obtained

$$\begin{aligned} \lambda (t) \Biggl [\frac{\partial L}{\partial \dot{x}}\langle x,z \rangle (t) X\langle x,z \rangle (t) +\left( L\langle x,z \rangle (t)-\frac{\partial L}{\partial \dot{x}}\langle x,z \rangle (t) \dot{x}(t)\right) T\langle x,z \rangle (t)\Biggr ], \end{aligned}$$
(25)

where \(\lambda (t)=e^{-\int _a^t\frac{\partial L}{\partial z}\langle x,z \rangle (\theta )d\theta }\), as a conserved quantity along the extremals of problem (\(P_{H}\)). Our results improve those of [2] in three ways: (i) we consider a wider class of piecewise admissible functions; (ii) we consider a more general notion of invariance whose transformations \(\mathcal {T}^s\), \(\mathcal {X}^s\) and \(\mathcal {Z}^s\) may also depend on velocities, i.e., on \(\dot{x}(t)\) (note that if (18) holds with \(\mathcal {Z}^s\langle x,z \rangle = z\), then (24) also holds); (iii) the conserved quantity (25), up to multiplication by a constant, is a particular case of (19) when there is no transformation in z (\(Z=\left. \frac{\partial \mathcal {Z}^s}{\partial s}\right| _{s=0}=0\)). The results here obtained can be generalized to higher-order variational problems of Herglotz type. This is under investigation and will be addressed elsewhere.