Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Supply chain management deals with the organization of the flows of products and information throughout the supply chain structure so as to ensure the requirements of customers, while minimizing operating costs. To attain such goal inventory management is, within supply chains, a key activity since it ensures the continuity and balance between supply and demand. Beamon [3] characterized inventory management through the different activities in the chain and enhanced the importance of developing correct inventory management policies. In order to avoid such problem there is a need of an integrated approach for the planning and control of inventory throughout the entire supply chain. In this context inventory management appears as an important and challenging problem, since decisions made by a chain member may affect, with different impacts, the remaining supply chain entities.

Krautter [6] presented new perspectives for corporative management on the inventory theory area and stated that inventories appear as the result of mismanagement of the different supply chain processes. The need to fully control the processes was identified by the author as a way of optimizing inventories. Giannoccaro and Pontrandolfo [4] studied the integration and coordination of inventory policies adopted by different supply chain actors so as to smooth material flow and minimize costs while responsively meeting customer demand.

Later on, [2] proposed a method to determine control parameters on a one-warehouse/N-retailer network. An approximate optimization of reorder points for a continuous review installation stock (R, Q) policy was considered in a two-echelon distribution inventory system with stochastic demand. All orders are placed at the retailers and the retailers replenish their stock from the warehouse that, in turn, replenishes its stock from an outside supplier with infinite supply.

Abdul-Jalbar et al. [1] dealt with the classic deterministic one-warehouse multi-retailer inventory/distribution system where customer demand rates were assumed to be known and constant and there was no backlog or lost sales. The retailers placed orders to satisfy customer demands generating demands at the warehouse. Order lead times were assumed to be instantaneous, so no lead time was considered. Costs at each facility consisted of a fixed charge per order and of a holding cost.

Ozdemir et al. [8] studied the multi-location transshipment problem with capacitated transportation. They used a simulation based approach that incorporates transportation capacity such that transshipment quantities between stocking locations are bounded due to transportation media capacity or the location’s transshipment policy.

Hsiao [5] investigated the classic deterministic one-warehouse multi-retailer inventory/distribution system. In this study the customer demand rates were assumed to be known and constant. Shortages were not permitted and lead times were assumed negligible. A method that reached the optimal solution in most of the instances studied was proposed.

In the same year, [7] also developed an inventory control system for a one-warehouse multiple-retailers supply chain. They considered only one product. A mixed integer linear model was proposed to determine the optimal inventory and distribution plan that minimized total related costs. The efficiency of the inventory control system was compared to a periodic review policy.

More recently, [9] researched and reviewed inventory models with lateral transshipments. Models of many different systems have been considered. This paper provides a literature review which categorizes the research to date on lateral transshipments, so that these differences can be understood and gaps within the literature can be identified. Yousuk and Luong [10] present a model of two-retailer inventory system with preventive lateral transshipment. Each retailer employs base stock periodic review policy.

Most of these studies dealt with a supply chain management structure formed by a single warehouse that supplies multiple retailers with a single product item. A single period of analysis also characterizes most of the models proposed. Based on this analysis it is clear that some research space still exists to generalize the inventory management models proposed. In particular, new models should be developed to deal with more generic supply chain structures. Aspects that will allow a closer description of the real problems should be explored namely: (i) generic structure with links between the different entities present (e.g. transshipment); (ii) inclusion of supply lead times; (iii) safety stock considerations and finally (iv) inclusion of lost sales at all retailers.

The present work follows this need and develops an Inventory Management (IM) policy that may support in an optimized way, by minimizing total operational costs, the definition of the product flows through a multi-warehouse/multi-retailer/multi-product and multi-period supply chain. Costs include ordering, holding in stock and in transit, transportation, transshipping and lost sales. The system in study and the associated IM policy are modeled through a MILP model. The classical Continuous Review (CR) and the Periodic Review (PR) policies are also modeled by means of mathematical programming models that act in the same system, so as to compare the results of the three studied policies.

The remainder of this paper is organized as follows. The problem definition is given in Sect. 2. Section 3 describes the IM mathematical model and the CR and PR mathematical models are presented respectively in Sects. 4 and 5. An inventory management case study is presented in Sect. 6. Finally the conclusions are drawn in Sect. 7.

2 Problem Definition

A generic supply chain is considered in this current study. It comprises multiple regional warehouses and multiple retailers as depicted in Fig. 1, where multiple products are distributed over a given time horizon.

Fig. 1
figure 1

Supply chain structure

Full size image

The structure considered assumes that retailers replenish their inventories from the regional warehouses, these replenish their inventories from a central warehouse and customer demand is observed at the retailers. Each retailer has a normally distributed demand with a mean and a standard deviation in each unit of time, which is independent of demands of the other retailers. It is also assumed that storage and transportation capacities, in regional warehouses and retailers, are limited and that transportation occurs after orders have been placed. Also the storage and transportation capacity from the central warehouse is unlimited.

Lateral transshipment between regional warehouses or between retailers is allowed. If the demand in a given time period and at a given retailer is not satisfied, this is considered as a lost sale. Different cost types are included. These are related to the ordering process, holding in storage and holding in-transit, transportation, transshipping and lost sale. Fixed ordering costs occur each time a regional warehouse or a retailer places an order and are related to the ordering activity, being independent of the quantity ordered. Holding costs are defined for both storage and in-transit inventory. The first ones are defined per unit stored and per time period on each regional warehouse or retailer. The second ones are defined per unit of product transported and are dependent of the lead times. Transportation costs are considered per unit of material transported between the different stages of the supply chain. Related to these are the transshipment costs that represent the costs of transporting items between two locations belonging to the same echelon. Finally, lost sale costs are associated to the demand that cannot be satisfied and are defined per unit of product. Thus, it is important to effectively represent and optimize the flows of products through the entire supply chain so as to minimize costs. These aspects are included in the problem under study and the relevant decision that needs to be modeled is then to determine the shipping quantity to be sent from the regional warehouses to each retailer in each time period so as to minimize the total system costs. The problem in study can be generally defined as follows:

Given:

  • The planning time horizon and a defined discrete time scale;

  • The number of regional warehouses and retailers;

  • The number of products;

  • Initial inventory level of each product at each regional warehouse and retailer;

  • Customer demands for each product in all time periods;

  • Storage capacities in each regional warehouse and retailer per time period;

  • Transportation capacities between entities;

  • Safety stock by product in each regional warehouse and retailer;

  • Transportation lead times between entities;

  • Ordering costs per order of each product at each regional warehouse and retailer (independent of order quantity);

  • Unitary holding cost per time period per product at each regional warehouse or retailer;

  • Unitary holding cost per time period per product in transit (dependent of lead time);

  • Unitary transportation and transshipping cost per product;

  • Unitary lost sale cost per product and per each time period.

Determine:

  • The inventory profiles for each product throughout the time horizon in each regional warehouse and retailer;

  • The flows of products across the supply chain for each time period. These involve shipping quantities between entities on different supply chain levels and transshipment quantities between entities on the same supply chain level;

  • The lost sale quantities of each product at each retailer at each time period.

So as to minimize the total costs over the time horizon considered. A mathematical programming formulation is proposed for the problem, which will be presented in the subsequent section.

3 Inventory Management Model (IM Model)

The supply chain inventory management problem presented is formulated as a MILP model. As referred, it aims to minimize the total costs during the time horizon in study. The MILP model considers time through a discretized time scale, where the time intervals have equal durations.

The indices, sets, parameters and variables (binary and continuous) used in the model formulation are defined using the following notation:

Indices

  • i   productj, k, l, m   entity nodet   time period

Sets

  • \(i \in P =\{ 1,2,\ldots,NP\}\)   products\(j,k,l,m \in I =\{ 0,1,2,\ldots,NW,NW + 1,NW + 2,\ldots,NW + NR\}\)  supply chain nodes\(t \in T =\{ 1,2,\ldots,NT\}\)   time periods\(W =\{ 1,2,\ldots,NW\},W \subset I\)   regional warehouses\(R =\{ 1,2,\ldots,NR\},R \subset I\)   retailers\(W_{o} =\{ 0\},W_{o} \subset I\)   central warehouse\(DN =\{ 1,2,\ldots,NW,NW + 1,NW + 2,\ldots,NW + NR\},DN \subset I\)   demand nodes (regional warehouses and retailers)\(SN =\{ 0,1,2,\ldots,NW\},SN \subset I\)   supply nodes (central warehouse and regional warehouses)Note that \(W_{o} \cup W \cup R = I\)

Parameters

  • BGM   a large positive numberCD ijt   customer demand of the product i at node j ∈ R in time period t (note that customer demand occurs only at the retailers, but not at the warehouses)HOC ij   unitary holding cost of the product i at node j ∈ DN per time periodHTCR ijk   unitary holding cost of the product i in transit from a regional warehouse j ∈ W to a retailer k ∈ R per time periodHTCW ijk   unitary holding cost of the product i in transit from a central warehouse j ∈ W o to a regional warehouse k ∈ W by time periodIto ij   initial inventory level of the product i at node j ∈ DNLSC ijt   unitary lost sale cost of the product i at node j ∈ R in time period tLTT jk   transportation lead time from node j ∈ I to node k ∈ IOC ij   ordering cost of the product i at node j ∈ DN (note that ordering cost is independent of quantity of product i)SS ij   safety stock of the product i at node j ∈ DNSTC jt   storage capacity at node j ∈ DN in time period tTRACMAX jk   maximum transportation capacity from node j ∈ DN to node k ∈ DNTRACMIN jk   minimum transportation capacity from node j ∈ DN to node k ∈ DNTRCR ijk   unitary transportation cost of product i from a regional warehouse j ∈ W to a retailer k ∈ RTRCW ijk   unitary transportation cost of product i from a central warehouse j ∈ W o to a regional warehouse k ∈ WTSCW ijl   unitary transshipment cost of product i from a regional warehouse j ∈ W to another regional warehouse l ∈ WTSCR ikm   unitary transshipment cost of product i from a retailer k ∈ R to another retailer m ∈ R

Continuous variables

  • FI ijt   inventory of product i at node j ∈ DN at the end of time period tLS ijt   lost sales of product i at node j ∈ R during time period t (note that lost sales only occur at the retailers)SQ ijkt   shipping quantity of product i from node j ∈ I to node k ∈ I during time period t

Binary variable

  • BV 1 ijt   equal to 1 if an order of product i is placed by node j ∈ DN in time period t; 0 otherwise

Objective function

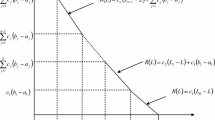
The objective function consists of the minimization of the total cost is given as follows:

$$\displaystyle{ minimize\;total\;cost =\sum _{i\in P}\sum _{j\in DN}\sum _{t\in T}OC_{ij}\times BV 1_{ijt}+\sum _{i\in P}\sum _{j\in DN}\sum _{t\in T}HOC_{ij}\times FI_{ijt} }$$
$$\displaystyle{ +\sum _{i\in P}\sum _{j\in W_{o}}\sum _{k\in W}\sum _{t\in T}HTCW_{ijk}\times LTT_{jk}\times SQ_{ijkt}+\sum _{i\in P}\sum _{j\in W}\sum _{k\in R}\sum _{t\in T}HTCR_{ijk}\times LTT_{jk}\times SQ_{ijkt} }$$
$$\displaystyle{ +\sum _{i\in P}\sum _{j\in W_{o}}\sum _{k\in W}\sum _{t\in T}TRCW_{ijk} \times SQ_{ijkt} +\sum _{i\in P}\sum _{j\in W}\sum _{k\in R}\sum _{t\in T}TRCR_{ijk} \times SQ_{ijkt} }$$
$$\displaystyle{ +\sum _{i\in P}\sum _{j\in W}\sum _{l\in W}\sum _{t\in T}TSCW_{ijl} \times SQ_{ijlt} +\sum _{i\in P}\sum _{k\in R}\sum _{m\in R}\sum _{t\in T}TSCR_{ikm} \times SQ_{ikmt} }$$
$$\displaystyle{ +\sum _{i\in P}\sum _{j\in R}\sum _{t\in T}LSC_{ijt} \times LS_{ijt} }$$
(1)

The first term of objective function (1) is the ordering cost. The second term expresses the holding costs at both stages of the supply chain, regional warehouses and retailers. The third and the fourth terms are the holding cost in transit at both supply chain stages. The holding cost in transit is lead time dependent. The fifth and the sixth terms are the transportation costs at both supply chain stages. The transshipping cost, between regional warehouses and between retailers, is given by the seventh and eighth terms and, finally, the last term represents the lost sale cost.

Constraints

The model developed consists of different types of constraints. These are grouped into: inventory constraints; shipping constraints; storage capacities; transportation capacities; safety stock policy and non-negativity and binary conditions.

Inventory constraints

Inventory constraints have to be defined for both the regional warehouses and retailers, taking into account all inputs and outputs at each time period.

Regional warehouses:

The total incoming quantity at each regional warehouse is equal to the shipping quantity from the central warehouse to the regional warehouse, plus the transshipping quantity from the others regional warehouses, considering the transportation lead time through the introduction of a time lag.

The total outgoing quantity at each regional warehouse is equal to the sum of shipping quantity from the regional warehouse to the retailers plus the transshipping quantity to the others regional warehouses, at time period t. For t = 1 the inventory of product i at the end of this time period at regional warehouses is given by constraints (2), which takes into account the initial inventory level at each regional warehouse Ito im .

$$\displaystyle{ FI_{imt} = Ito_{im} + SQ_{i,0,m,t-LTT_{0m}\vert _{LTT_{ 0m}=0}} -\sum _{k\in R}SQ_{imkt} -\sum _{l\in W\wedge l\neq m}SQ_{imlt} }$$
$$\displaystyle{ +\sum _{l\in W\wedge l\neq m}SQ_{i,l,m,t-LTT_{lm}}\vert _{LTT_{lm}=0},\quad i \in P,m \in W,t = 1 }$$
(2)

For the remaining time periods the inventory at the end of these time periods at regional warehouses is given by constraints (3).

$$\displaystyle{ FI_{imt} = FI_{i,m,t-1}+SQ_{i,0,m,t-LTT_{0m}}\vert _{LTT_{0m}<t}-\sum _{k\in R}SQ_{imkt}-\sum _{l\in W\wedge l\neq m}SQ_{imlt} }$$
$$\displaystyle{ +\sum _{l\in W\wedge l\neq m}SQ_{i,l,m,t-LTT_{lm}}\vert _{LTT_{lm}<t},\quad i \in P,m \in W,t \in T\setminus \{1\} }$$
(3)

Retailers:

At each retailer, the incoming quantity is equal to the sum of the shipping quantity from the regional warehouses to that retailer, plus the transshipping quantity from the others retailers, at time period t, considering the transportation lead time.

At each retailer the outgoing quantity is equal to the customer demand minus the lost sale of that retailer plus the transshipping quantity to the others retailers, at time period t.

For t = 1 the inventory of product i at the end of this time period at the retailers is given by constraints (4), which accounts for the initial inventory of product i at retailer k (Ito ik ) whereas constraints (5) is applicable for the remaining time periods.

$$\displaystyle{ FI_{ikt} = Ito_{ik}+\sum _{j\in W}SQ_{i,j,k,t-LTT_{jk}}\vert _{LTT_{jk}=0}-(CD_{ikt}-LS_{ikt})-\sum _{m\in R\wedge m\neq k}SQ_{ikmt} }$$
$$\displaystyle{ +\sum _{m\in R\wedge m\neq k}SQ_{i,m,k,t-LTT_{mk}}\vert _{LTT_{mk}=0},\quad i \in P,k \in R,t = 1 }$$
(4)
$$\displaystyle{ FI_{ikt} = FI_{i,k,t-1}+\sum _{j\in W}SQ_{i,j,k,t-LTT_{jk}}\vert _{LTT_{jk}<t}-(CD_{ikt}-LS_{ikt})-\sum _{m\in R\wedge m\neq k}SQ_{ikmt} }$$
$$\displaystyle{ +\sum _{m\in R\wedge m\neq k}SQ_{i,m,k,t-LTT_{mk}}\vert _{LTT_{mk}<t},\quad i \in P,k \in R,t \in T\setminus \{1\} }$$
(5)

Shipping constraints

Since transportation occurs after an order has been placed from a destination to its source, it is assumed that the fixed ordering cost is always incurred when the transportation occurs. Hence, if the transportation amount is not zero the binary variable BV 1 ikt equals 1, as implied in constraints (6). The left hand side of this constraint represents the quantity received by a regional warehouse, which can come from the central warehouse (first term) or any other regional warehouse (second term).

$$\displaystyle{ SQ_{i0kt} +\sum _{l\in W\wedge l\neq k}SQ_{ilkt} \leq BGM \times BV 1_{ikt},\quad i \in P,k \in W,t \in T }$$
(6)

Equivalents constraints are defined for retailers, constraints (7). The BGM value will have a value that is valid as an upper bound of any quantity that can be ordered by a regional warehouse or retailer.

$$\displaystyle{ \sum _{j\in W}SQ_{ijkt} +\sum _{l\in R\wedge l\neq k}SQ_{ilkt} \leq BGM \times BV 1_{ikt},\quad i \in P,k \in R,t \in T }$$
(7)

Storage capacities

The total inventory stored at any node, given by the sum of the inventory level of each product i must respect the storage capacity in each demand node j at any time period t, which is enforced by constraints (8). In this formulation we consider storage capacities time dependent to illustrate that, depending on the time period, capacities may vary since we are dealing on an operational perspective. Also the storage capacity of the central warehouse is unlimited.

$$\displaystyle{ \sum _{i\in P}FI_{ijt} \leq STC_{jt},\quad j \in DN,t \in T }$$
(8)

Transportation capacities

At any time period t, the sum of the shipping quantity of each product i must respect the transportation lower and maximum limits between each two nodes j and k, as stated in constraints (9) and (10). Note that the quantities in transit were not considered for the usage of transportation capacity, but for the total transportation capacity. Also the transportation capacity from the central warehouse is unlimited.

$$\displaystyle{ \sum _{i\in P}SQ_{ijkt} \leq TRACMAX_{jk},\quad j \in DN,k \in DN,j\neq k,t \in T }$$
(9)
$$\displaystyle{ TRACMIN_{jk} \leq \sum _{i\in P}SQ_{ijkt},\quad j \in DN,k \in DN,j\neq k,t \in T }$$
(10)

Safety stock policy

Constraints (11) ensure that the inventory of each product i at each node j at each time period t must be higher than the required safety stock level for that product in that node.

$$\displaystyle{ SS_{ij} \leq FI_{ijt},\quad i \in P,j \in DN,t \in T }$$
(11)

Non-negativity and binary conditions

As defined above, the model uses both positive continuous variables (12) and binary variables (13).

$$\displaystyle{ SQ_{ijkt},FI_{ijt},LS_{ijt} \geq 0,\quad i \in P,j \in I,k \in I,t \in T }$$
(12)
$$\displaystyle{ BV 1_{ijt} \in \{ 0,1\},\quad i \in P,j \in I,t \in T }$$
(13)

The above model is formed by constraints (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), and (13), using the objective function (1) that describes the proposed IM model. In order to compare the performance and adequacy of this model with classical inventory policies, two other models are developed: the continuous review inventory model (CR, Sect. 4) and the periodic review inventory model (PR, Sect. 5).

4 Continuous Review Inventory System Model (CR Model)

In the CR policy, the inventory level is continuously reviewed over the time horizon. Thus, whenever the inventory level is at or below a given reorder point level s, an order is placed that has a fixed quantity. Since inventory is tracked and the order is made when necessary, this inventory management policy is characterized by a fixed order quantity requested at variable time intervals. In order to represent this policy through a MILP model, two more parameters must be added to the list proposed in Sect. 3:

  • RSC ik reference stock level of product i at node k (used for regional warehouses and retailers)

  • s ik reorder point level of product i at node k (used for regional warehouses and retailers)

The fixed order quantity is then given by \((RSC_{ik} - s_{ik})\) since at the moment that an order is placed the inventory position (inventory level plus inventory in transit) must reach the reference stock level. In terms of model representation, the reference stock value can replace the BGM value used in constraints (6) and (7), since that value also works as an upper bound of any SQ variable. The MILP model that represents the continuous review policy consists of constrains (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), and (13), with the change in constraints (6) and (7), while the objective function (1) remains equal.

5 Periodic Review Inventory System Model (PR Model)

In this policy, the inventory level is reviewed at fixed time points, determined by a fixed review period. If at that time the inventory level is below a reference stock RS, an order is placed. The order quantity is determined by the difference between the reference stock and the current inventory level, to bring the inventory position up to level RS; otherwise, nothing is done until the next review point. A periodic inventory system uses variable order sizes at fixed time intervals. We add a subset of T that includes all the time periods for which there will be orders.

\(ST \subset T\) all the time periods for which there will be orders due to the periodic review policy.

As in Sect. 4 also in here is necessary to add an extra parameter to the initial list of Sect. 3.

RSP ik reference stock level of product i at node k (used for regional warehouses and retailers)

The original constraints (6) and (7) are now replaced by constraints (14) and (15).

$$\displaystyle{ SQ_{i0kt} +\sum _{l\in W\wedge l\neq k}SQ_{ilkt} \leq (RSP_{ik} - FI_{ikt}) \times BV 1_{ikt},\quad i \in P,k \in W,t \in ST }$$
(14)
$$\displaystyle{ \sum _{j\in W}SQ_{ijkt} +\sum _{l\in R\wedge l\neq k}SQ_{ilkt} \leq (RSP_{ik} -FI_{ikt})\times BV 1_{ikt},\quad i \in P,k \in R,t \in ST }$$
(15)

In order to solve the non-linearity on the right end-side of constraints (14) and (15), we define the auxiliary variable Y ikt (positive continuous variable) that represents the inventory of product i at node k at the end of time period t. Thus, the non-linear term FI ikt × BV 1 ikt is replaced by the continuous variable Y ikt in constraints (14) and (15). The value of this auxiliary variable is given by Eq. (16):

$$\displaystyle{ Y _{ikt} = FI_{ikt} \times BV 1_{ikt},\quad i \in P,k \in I,t \in T }$$
(16)

Using the definition of variable Y ikt it is possible to impose the logical conditions (17) and (18). If the binary variable BV 1 ikt is 0, then the auxiliary variable Y ikt is also 0 (condition (17)). If, on the other hand, the binary variable BV 1 ikt is equal to 1, we want to ensure that the new auxiliary variable takes the value of the inventory in the current time interval (FI ikt ), as expressed in condition (18).

$$\displaystyle{ BV 1_{ikt} = 0\Rightarrow Y _{ikt} = 0,\quad i \in P,k \in I,t \in T }$$
(17)
$$\displaystyle{ BV 1_{ikt} = 1\Rightarrow Y _{ikt} = FI_{ikt},\quad i \in P,k \in I,t \in T }$$
(18)

To translate these logical conditions into the MILP model representation of the periodic review policy, we need to add the extra constraints (19), (20) and (21).

$$\displaystyle{ Y _{ikt} - RS_{ik} \times BV 1_{ikt} \leq 0,\quad i \in P,k \in I,t \in T }$$
(19)
$$\displaystyle{ -FI_{ikt} + Y _{ikt} \leq 0,\quad i \in P,k \in I,t \in T }$$
(20)
$$\displaystyle{ FI_{ikt} - Y _{ikt} + RS_{ik} \times BV 1_{ikt} \leq RS_{ik},\quad i \in P,k \in I,t \in T }$$
(21)

where RS ik is the upper bound for FI ikt (and hence also for Y ikt ). Constraints (19) and (20) ensure that the auxiliary variable takes the value of 0 if the binary variable is equal to 0 (constraints (19)). If this variable is equal to 1, then the auxiliary variable takes, at most, the value of FI ikt (constraints (20)). In order to ensure that in this situation the auxiliary variable takes exactly the value of FI ikt , we add constraints (21). Note that this equation only becomes active whenever BV 1 ikt  = 1. Finally, we add constraints (22) and (23) that are applied for time periods where no orders are to be placed. They impose that no transportation activity occurs at these time periods.

$$\displaystyle{ SQ_{i0kt} +\sum _{l\in W\wedge l\neq k}SQ_{ilkt} = 0,\quad i \in P,k \in W,t\notin ST }$$
(22)
$$\displaystyle{ \sum _{j\in W}SQ_{ijkt} +\sum _{l\in R\wedge l\neq k}SQ_{ilkt} = 0,\quad i \in P,k \in R,t\notin ST }$$
(23)

The periodic review policy MILP model consists of constraints (2), (3), (4), and (5), (8),(9), (10), (11), (12), and (13), (16) and constraints (19), (20), (21), (22), and (23), using objective function (1).

6 Inventory Management Case Study

In this section we present a case study based on a Portuguese Company that we use to compare the three inventory management policies modeled, and to test the proposed IM policy. Due to confidentiality reasons the data provided has been changed but still describes the real operation. Please note that the products amounts involved in the present case study although referred as units they correspond to euro-pallets. The models were implemented in GAMS 23.5 modeling language and solved using the CPLEX 12.2.0.0 solver in an Intel CORE i5 CPU 2.27 GHz and 4 GB RAM. The stopping criterion was either a computational time limit of 3600 s or the determination of the optimal solution.

6.1 Data and Parameters

The supply chain considered involves one central warehouse, three regional warehouses and four retailers. Three families of products are considered, which for sake of simplicity will be modeled aggregated per family. The available storage capacity of all warehouses and retailers is of 500 SKU units and the transportation capacity is between 0 and 500 SKU units. We consider that demand at retailers is represented by a normal distribution, with parameters presented in Table 4. These values are given by the company forecast process. A 7-period planning horizon was assumed to test the three different inventory management policies. The first scenario considers the IM policy (modeled in Sect. 3), which uses a variable order quantity at variable time intervals. The second scenario explores the CR policy (Sect. 4) that uses a fixed order quantity at variable time intervals. Finally, the third scenario explores the PR policy (Sect. 5) where a variable order quantity at fixed time intervals is considered. Tables from 1 to 5 present all the parameters.

Table 1 Models parameters (euro)
Full size table
Table 2 Unit transportation cost for all products (euro)
Full size table
Table 3 Initial inventory level (Ito)/safety stock (SS) on warehouses and retailers (unit)
Full size table
Table 4 Customer demand (CD) parameters for product1/product2/product3 (unit)
Full size table
Table 5 Transportation lead time (LTT) for all products (time period)
Full size table

Table 6 illustrates the reference stock level for the CR and PR policies for the warehouses and retailers. The reorder point value is assumed equal to the safety stock. In the PR policy that implies a review period taking place every three time periods, the first time period with revision is time period 3. The initial inventory level, the customer demand, reference stock level for warehouses and retailers and the supply chain structure are the same for the three policies.

Table 6 Reference stock level for CR policy (RSC)/reference stock level for PR policy (RSP) on warehouses and retailers (unit)
Full size table

6.2 Experimental Results

The costs per nature of the objective function analyses for all three policies are present below, although computational statistics are shown in appendix.

6.2.1 Initial Inventory as a Parameter Given by the Portuguese Company

The costs per nature of the objective function for all three inventory policies are shown in Table 7. For the IM policy the holding cost, of 557.60 euro, is the highest cost term. The objective function reaches a value of 1955.46 euro. For the CR policy the objective function has a higher cost value than the observed for the IM policy, being the cost with highest contribution the lost sales cost. Holding costs also increase when compared to the IM policy. The PR policy has the lowest ordering costs. On the other hand, since inventory levels are not replenished frequently, the highest cost becomes associated with the lost sales. The objective function value is 10,286.23 euro, being the highest one amongst the three policies. In conclusion the IM policy appears as more flexible than the CR or PR policies, which is then confirmed by the lower operational costs. This is explained by the policy flexibility in terms of managing the flows allowing for an order occurrence strictly when necessary. This leads to a less costly system operation.

Table 7 Costs per nature for all three inventory policies (euro)
Full size table

The costs per nature for CR policy for three different reference stock levels are shown in Table 8. The ordering and lost-sales costs are the same for all situations, while that the remaining costs increase with the reference stock level increase. Note that the scenario with less 10 % yielded better solutions without increasing the lost sales, therefore as a recommendation, the company should reduce the reference stock level in 10 %.

Table 8 Costs per nature for CR policy for three different reference stock levels (euro)
Full size table

Table 9 shows the costs per nature for PR policy for three different review periods. When the review period length increases, we have in general a decrease of the costs per nature except lost-sales. This is due to the fact that we do not have enough stock to satisfy the customers during the review period.

Table 9 Costs per nature for PR policy for three different review periods (euro)
Full size table

6.2.2 Initial Inventory as an Optimization Variable

Now we run the same analyses, but considering that the initial inventory is subject to optimization, in order to analyze the possibility of having zero lost-sales and consequently maximum service level in all retailers. The costs per nature of the objective function for all three inventory policies are shown in Table 10. As expected the most significant value is the holding cost to face demand in the initial time periods, in order to avoid lost-sales.

Table 10 Costs per nature for all three inventory policies (euro)
Full size table

The costs per nature for CR policy for three different reference stock levels are shown in Table 11. The holding costs are the most representative for all situations. This results confirm that the company should reduce the reference stock level in 10 %.

Table 11 Costs per nature for CR policy for three different reference stock levels (euro)
Full size table

Table 12 shows the costs per nature for PR policy for three different review periods. With the review period increase, we have a generally decrease of the costs per nature except holding cost. This is due to the fact that we must have enough products to satisfy the customers during the review period.

Table 12 Costs per nature for PR policy for three different review periods (euro)
Full size table

7 Conclusions

This paper proposes a generic inventory management policy applied to a multi-period and multi-product supply chain, which provides an inventory and distribution plan that minimizes the total operation costs. Based on the experimental results, it could be concluded that the proposed IM policy proved to be more flexible since the total costs are lower when compared to the classical policies for the same network and under the same conditions.

The classical policies are very commonly used in companies that control more than one echelon even though they were designed to be applied to a single entity. These policies are well spread in most ERPs and commonly used by decision makers. Given this fact, it is important to show why incorporating all the costs in the optimal policy is important as well as when capacities are disputed by more than one product.

In the real world there are thousands of SKUs, but simplifying techniques are used, such as grouping in specific families. Nevertheless, a tighter formulation should be deigned in future.

The lost sales represent a large value that reflects somewhat the impact of those lost sales for our test company, thus other model driving force should be used, namely profit or even to balance costs with service level. Our future work also will focus on optimizing the safety stock as well to reduce lost sales.

The results obtained and consequent conclusions are related with the test company. In future works, more instances should be studied so as to show the potential generalization of our conclusions.