Compact Indexes for Flexible Top-$k$ Retrieval

Abstract

We design and engineer a self-index based retrieval system capable of rank-safe evaluation of top-$k$ queries. The framework generalizes the GREEDY approach of Culpepper et al. (ESA 2010) to handle multi-term queries, including over phrases. We propose two techniques which significantly reduce the ranking time for a wide range of popular Information Retrieval (IR) relevance measures, such as ${\textsc {TF}\times \textsc {IDF}}$ and ${\textsc {BM25}}$. First, we reorder elements in the document array according to document weight. Second, we introduce the repetition array, which generalizes Sadakane’s (JDA 2007) document frequency structure to document subsets. Combining document and repetition array, we achieve attractive functionality-space trade-offs. We provide an extensive evaluation of our system on terabyte-sized IR collections.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Calculating the $k$ most relevant documents for a multi-term query $Q$ against a set of documents $\mathcal {D}$ is a fundamental problem – the top-$k$ document retrieval problem – in Information Retrieval (IR). The relevance of a document $d$ to $Q$ is determined by evaluating a similarity function $\mathcal {S}$ such as BM25. Exhaustive evaluation of $\mathcal {S}$ generates scores for all $d$ in $\mathcal {D}$. The top-$k$ scored documents in the list are then reported. Algorithms which guarantee production of the same top-$k$ results list as the exhaustive process are called rank-safe.

The inverted index is a highly-engineered data structure designed to solve this problem. The index stores, for each unique term in $\mathcal {D}$, the list of documents containing that term. Queries are answered by processing the lists of all the query terms. Advanced query processing schemes [2] process lists only partially while remaining rank-safe. However, additional work during construction time is required to avoid scoring non-relevant documents at query time. Techniques used to speed up query processing include sorting lists in decreasing score order, or pre-storing score upper bounds for sets of documents which can then safely be skipped during query processing. These pre-processing steps introduce a dependency between $\mathcal {S}$ and the stored index. Changing the $\mathcal {S}$ requires at least partial reconstruction of the index, which in turn reduces the flexibility of the retrieval system.

Another family of retrieval systems is based on self-indexes [16]. These systems support functionality not easily provided by inverted indexes, such as efficient phrase search, and text extraction. Systems capable of single-term top-$k$ queries have been proposed [17, 20] and work well in practice [8, 13].

Hon et al. [12] investigate top-$k$ indexes which support different scoring schemes such as term frequency or static document scores. They also extended their framework to multi-term queries and term proximity. While the space of the multi-term versions is still linear in the collection size the query time gets dependent on the root of the collection size. At CPM 2014, Larson et al. [14] showed that it is not expected to improve their result significantly by reducing the boolean matrix multiplication problem to a relaxed version of Hon et al.’s problem, i.e. just answering the question whether there is a document which contains both of the query times. While the single-term version of Hon et al.’s framework was implemented and studied by several authors [5, 19] there is not yet an implementation of a rank-safe multi-term version.

Our Contributions. We propose, to the best of our knowledge, the first flexible self-index based retrieval framework capable of rank-safe evaluation of multi-term top-$k$ queries for complex IR relevance measures. It is based on a generalization of GREEDY [4]. We suggest two techniques to decrease the number of evaluated nodes in the GREEDY approach. The first is reordering of documents according to their length (or other suitable weight), the second is a new structure called the repetition array, $R$. The latter is derived from Sadakane’s [25] document frequency structure, and is used to calculate the document frequency for subsets of documents. We further show that it is sufficient to use only $R$ and a subset of the document array if query terms, which can also be phrases, are length-restricted. Finally, we evaluate our proposal on two terabyte-scale IR collections. This is, to our knowledge, three orders of magnitudes larger than previous self-index based studies. Our source code and experimental setup is publicly available.

2 Notation and Problem Definition

Let $\mathcal {D} '=\{d_1,\ldots ,d_{N \!-\!1}\}$ be a collection of $N \!-\!1$ documents. Each $d_i$ is a string over an alphabet (words or characters) $\varSigma '=[2,\sigma ]$ and is terminated by the sentinel symbol ‘$1$’, also represent as ‘#’. Adding the one-symbol document $d_{0}=0$ results in a collection $\mathcal {D}$ of $N$ documents. The concatenation $\mathcal {C} =d_{\pi (0)}d_{\pi (1)}\ldots d_{\pi (N \!-\!1)}$ is a string over $\varSigma =[0,\sigma ]$, where $\pi$ is a permutation of $[0,N \!-\!1]$ with $\pi (N \!-\!1)=0$. We denote the length of a document $d_i$ with $|d_i|=n_{d_i}$, and $|\mathcal {C} |=n$. See Fig. 1 for a running example. In the “bag of words” model a query $Q=\{q_0,q_1,\ldots ,q_{m-1}\}$ is an unordered set of length $m$. Each element $q_i$ is either a term (chosen from $\varSigma '$) or a phrase (chosen from ${\varSigma '}^p$ for $p>1$).

Fig. 1.

$\mathcal {C}$ is the concatenation of a document collection $\mathcal {D}$ for $\pi =[1,3,2,0]$. We use both words (as in $\mathcal {C} ^{word}$) or integer identifiers (as in $\mathcal {C}$) to refer to document tokens.

Top-$k$ Document Retrieval Problem. Given a collection $\mathcal {D}$, a query $Q$ of length $m$, and a similarity measure $\mathcal {S} \!:\!\mathcal {D} \!\times \! \mathcal {P}_{=m}(\varSigma ')\rightarrow \mathbb {R}$. Calculate the top-$k$ documents of $\mathcal {D}$ with regard to $Q$ and $\mathcal {S}$, i.e. a sorted list of document identifiers $\mathrm {T}=\{\tau _0,\ldots ,\tau _{k-1}\}$, with $\mathcal {S} (d_{\tau _i},Q)\ge \mathcal {S} (d_{\tau _{i+1}},Q)$ for $i<k$ and $\mathcal {S} (d_{\tau _{k-1}},Q)\ge \mathcal {S} (d_{j},Q)$ for $j\not \in \mathrm {T}$.

A basic similarity measure used in many self-index based document retrieval systems (see [16]), is the frequency measure $\mathcal {S} ^{freq}$. It scores $d$ by accumulating the term frequency of each term. Term frequency $f_{d,q}$ is defined as the number of occurrences of term $q$ in $d$; e.g.

in Fig. 1. In IR, more complex ${\textsc {TF}\times \textsc {IDF}}$ measures also include two additional factors. The first is the inverse of the document frequency (${{\mathrm{{\textsc {df}}}}}$), which is the number of documents in $\mathcal {D}$ that contain $q$, defined $F_{\mathcal {D},q}$; e.g.

The second is the length of the document $n_d$. Due to space limitations, we only present the popular Okapi BM25 function:

(1)

where $n_{\tiny {\text {avg}}}$ is the mean document length, and $w_{d,q}$ and $w_{Q,q}$ refer to components that we address shortly. Parameters $k_1$ and $b$ are commonly set to $1.2$ and $0.75$ respectively. Note that the $w_{Q,q}$ part is negative for $F_{\mathcal {D},q}>\frac{N}{2}$. To avoid negative scores, real-world systems, such as Vigna’s MG4J [1] search engine, set $w_{Q,q}$ to a small positive value ($10^{-6}$), in this case. We refer to Zobel and Moffat [29] for a survey on IR similarity measures including ${\textsc {TF}\times \textsc {IDF}}$, BM25, and LMDS.

3 Data Structure Toolbox

We briefly describe the two most important building blocks of our systems, and refer the reader to Navarro’s survey [16] for detailed information. A wavelet tree (WT) [10] of a sequence $X[0,n\!-\!1]$ over alphabet $\varSigma [0,\sigma \!-\!1]$ is a perfectly balanced binary tree of height $h=\lceil \log \sigma \rceil$, referred to as $\text {WT-X}$. The $i$-th node of level $\ell \in [0,h\!-\!1]$ is associated with symbols $c$ such that $\lceil c/2^{h-1-\ell }\rceil =i$. Node $v$, corresponding to symbols $\varSigma _v=[c_b,c_e] \subseteq [0,\sigma -1]$, represent the subsequence $X_v$ of $X$ filtered by symbols in $\varSigma _v$. Only the bitvector which indicates if an element will move to the left or right subtree is stored at each node; that is, $\text {WT-X}$ is stored in $n\lceil \log \sigma \rceil$ bits. Using only sub-linear extra space it is possible to efficiently navigate the tree. Let $v$ be the $i$-th node on level $\ell <h\!-\!1$, then method ${{expand}}(v)$ returns in constant time a node pair $\langle u,w\rangle$, where $u$ is the $(2\cdot i)$-th and $w$ the $(2\cdot i+1)$-th node on level $\ell +1$. A range $[l,r]\subseteq [0,n\!-\!1]$ in $X$ can be mapped to range $[l,r]_{v}$ in node $v$ such that the sequence $X_v[l,r]_{v}$ represents $X[l,r]$ filtered by $\varSigma _v$. Operation ${{expand}}(v,[l,r]_{v})$ then returns in constant time a pair of ranges $\langle [l,r]_{u},[l,r]_{w}\rangle$ such that the sequence $X_u[l,r]_{u}$ (resp. $X_w[l,r]_{w}$) represents $X[l,r]$ filtered by $\varSigma _u$ (resp. $\varSigma _w$). Figure 2 provides an example.

Fig. 2.

Wavelet tree over document array $D$. Method ${{expand}}(v_{root},[4,9])$ maps range $[4,9]$ (locus of

) to range $[2,3]$ in the left and range $[2,5]$ in the right child.

The binary suffix tree (BST) of string $X[0,n\!-\!1]$ is the compact binary trie of all suffixes of $X$. For each path $p$ from the root to a leaf, the concatenation of the edge labels of $p$, corresponds to a suffix. The children of a node are ordered lexicographically by their edge labels. Each leaf is labeled with the starting position of its suffix in $X$. Read from left to right, the leaves form the suffix array ($SA$), which is a permutation of $[0,n-1]$ such that $X[SA[i],n\!-\!1]<_{lex} X[SA[i\!+\!1],n\!-\!1]$ for all $0\le i < n\!-\!1$. We refer to Fig. 3 for an example. Compressed versions of $SA$ and ST – the compressed $SA$ (CSA) and compressed ST (CST) – use space essentially equivalent to that of the compressed input, while efficiently supporting the same operations [23, 24]. For example, given a pattern $P$ of length $m$, the range $[l,r]$ in $SA$ containing all suffixes start with $P$ or the corresponding node, that is the locus of $P$, in the BST is calculated in $\mathcal {O}(m\log \sigma )$.

Fig. 3.

Top: BST of the example in Fig. 1. The leaves form $SA$, the gray numbers below form $D$. Bottom: Bitvector $H[0,2n\!-N\!-1]$ and repetition array $R$.

4 Revisiting and Generalizing the GREEDY Framework

The GREEDY framework [4] consists of two parts: a CSA built over $\mathcal {C}$, and a WT over the document array $D[0..N-1]$; with each $D[i]$ specifying the document in which suffix $SA[i]$ starts. A top-$k$ query using $\mathcal {S} ^{ freq }$ with $m=1$ is answered as follows. For term $q=q_0$ the CSA returns a range $[l,r]$, such that all suffixes in $SA[l,r]$ are prefixed by $q$. The size of the range corresponds to $f_{\mathcal {D},q}$, the number of occurrences of $q$ in $\mathcal {D}$. In $\text {WT-D}$ the alphabet $\varSigma _v$ of each node represents a subset $\mathcal {D} _v\subseteq \mathcal {D}$ of documents of $\mathcal {D}$; and the size of the mapped interval $[l,r]_{v}$ equals $f_{\mathcal {D} _v,q}$, the number of occurrences of $q$ in the subset $\mathcal {D} _v$. Each leaf $v$ in $\text {WT-D}$ corresponds to a $d\in \mathcal {D}$, such that the size of $[l,r]_{v}$ equals term frequency $f_{d,q}$.

To calculate the documents with maximal $f_{d,q}$, i.e. maximizing $\mathcal {S} ^{ freq }_{q,d}$, a max priority queue stores $\langle v,[l,r]_{v}\rangle$-tuples sorted by interval size. Initially, $\text {WT-D}$’s root node and $[l,r]$ is enqueued. The following process is repeated until $k$ documents are reported or the queue is empty: dequeue the top element $\langle v,[l,r]_{v}\rangle$. If $v$ is a leaf, the corresponding document is reported. Otherwise the interval is expanded and the two tuples $\langle u,[l,r]_{u}\rangle$ and $\langle w,[l,r]_{w}\rangle$ containing the expanded ranges are enqueued.

This process returns the correct result if $f_{\mathcal {D},q}$ at a parent is never smaller than that of a child ($f_{\mathcal {D} _u,q}$ or $f_{\mathcal {D} _w,q}$). The interval size $f_{\mathcal {D},q}$ is never smaller than the maximum $f_{d,q}$ value in the subtree. Thus, in general the algorithm is correct, if (1) the score estimate $s_v$ at any node $v$ is larger than or equal to the maximum document score in $v$’s subtree and (2) the score estimates $s_u$ and $s_w$ of the children of $v$ are not larger than $s_v$. For many similarity measures (e.g. ${\textsc {TF}\times \textsc {IDF}}$, BM25, and LMDS) theses conditions hold true if $s_v$ is computed as follows: first, all document-independent parts, such as query weight $w_{Q,q}$ are determined. Then $n_d$ is estimated with the smallest document length $n_{min}$ in $\mathcal {D}$ if $v$ is an inner node. Last, the maximal term frequency $f_{d,q}$ of each term $q_i$ is set to $f_{\mathcal {D},q_i}$, the size of interval $[l_i,r_i]_{v}$. Since each interval size is non-increasing when traversing down $\text {WT-D}$ the algorithm is correct, but not necessarily efficient. Instead of processing only one range, wavelet tree based algorithms can be process multiple ranges simultaneously [6]. In this case, the queue stores states $\langle s_v, v, \{[l_0,r_0]_{v},\ldots ,[l_{m-1},r_{m-1}]_{v}\}\rangle$ sorted by $s_v$. Processing a state takes $\mathcal {O}(m)$ time as $m$ intervals are expanded.

5 Improving Score Estimation

The runtime of GREEDY is dependent on the process time of a state and the number of states evaluated, which is determined by the quality of the score estimations.

Length Estimation by Document Relabelling. We improve document length estimation in $\mathcal {D} _v$ by replacing the collection-wide value $n_{min}$ by the smallest document length $n_{\tilde{d}}$ in the sub-collection $\mathcal {D} _v$. The computation of $n_{\tilde{d}}$ can be performed in constant time if the document identifiers are assigned in documents length order. Thus, the smallest document corresponds to smallest symbol in $\mathcal {D} _v$ which is $\varSigma _v[0]$ which can be computed in constant time. Let $v$ be the $i$-th node of level $\ell$ in $\text {WT-D}^n$ then $\varSigma _v[0]=i\cdot 2^{\lceil \log N \rceil -\ell -1}$. The document lengths are stored in an array $L[0,N-1]$. In Figs. 1 and 2 the documents are reordered using the permutation $\pi =[1,3,2,0]$. The additional space of $N\log N+N\log n_{max}$ bits is negligible compared to the size of the CSA and $D$.

Improved Term Frequency Estimation. Until now we use the range size $f_{\mathcal {D} _{v},q}$ of term $q$ in $v$ to estimate an upper bound for the maximal term frequency in a document $d\in \mathcal {D} _v$. Knowing the number of distinct documents in $\mathcal {D} _v$, called $F_{\mathcal {D} _{v},q}$, helps to improve the upper bound to the number of repetitions plus one: $\delta _{\mathcal {D} _{v},q}=f_{\mathcal {D} _{v},q}-F_{\mathcal {D} _{v},q}+1$. In this section, we present a method that computes $\delta _{\mathcal {D} _{v},q}$ in constant time during $\text {WT-D}$ traversal. The solution is built on top of Sadakane’s [25] document frequency structure (DF), which solves the problem solely for $\mathcal {C} _v=\mathcal {C}$. We briefly revisit the structure: first, a BST is built over $\mathcal {C}$, see Fig. 3. The leaves are labeled with the corresponding documents, i.e. from left to right $D$ is formed. The inner nodes are numbered from $1$ to $n-1$ in-order. Each node $w_i$ holds a list $\mathcal {R}_{i}$, containing all documents which occur in both subtrees of $w_i$. We refer to elements in $\mathcal {R}_i$ as repetitions. Let $w_i$ be the locus of a term $q$ in the BST and let $[l,r]$ be $w_i$’s interval. Then the total number of repetitions in $D[l,r]$ can be calculated by accumulating the length of all repetition lists in $w_i$’s subtree. To achieve this, Sadakane generated a bitvector $H$ that concatenates the unary coding of the lengths of all $\mathcal {R}_i$: $H=10^{|\mathcal {R}_{0}|}10^{|\mathcal {R}_{1}|}1\ldots 0^{|\mathcal {R}_{n-1}|}1$. The subtree interval $[l,r]$ can be mapped into $H$ via select operations: $[l',r']=[select_1(l,H),select_1(r,H)]$, since the accumulation of the list lengths equals the number of zeros in $[l',r']$. The following example illustrates the process: interval $[4,9]$ corresponds to term $q=$

and is mapped to $[l',r']=[select_1(4,H),select_1(9,H)]=[7,15]$ in $H$. It follows that there are $z_l=l'\!-\!l=3$ zeros in $H[0,l']$ and $z_r=r'\!-\!r=6$ in $H[0,r']$; thus there are $6\!-\!3=3$ repetitions in $D[4,9]$. We can overestimate the maximal term frequency by assuming that all repetitions belong to the same document $d_x$ and add one for $d_x$ itself. So $\delta _{\mathcal {D} _{v},q}=4$ in this case. This overestimates the maximal term frequency, which is $f_{d_3,q}= 3$, by one. The interval size estimate would have been $6$.

We now extend Sadakane’s solution to work on all subsets $\mathcal {D} _v$. First, we concatenate all $\mathcal {R}_i$ and form the repetition array $R[0,n\!-\!N-1]$ (again, see Fig. 3), containing the actual repetition value for each zero in $H$. As above, using $H$ and $select_1$, we can map $[l,r]$ to the corresponding range $[l'',r'']=[z_l,z_r-1]$ in $R$. To calculate $\delta _{\mathcal {D} _{v},q}$ for $\mathcal {D} _v$ we represent $R$ as a WT. Now, we can traverse $\text {WT-D}$ and ${\text {WT}\hbox {-}R}$ simultaneously, mapping $[l'',r'']$ to $[l'',r'']_{v}$ in ${\text {WT}\hbox {-}R}$. The size of $[l'',r'']_{v}\!+\!1$ equals $\delta _{\mathcal {D} _{v},q}$ since node $v$ contains only repetitions of $\mathcal {D} _v$.

6 Space Reduction

The space of $R$ can be reduced to array $\hat{R}$ by omitting all elements belonging to the root $v_{ST}$ of the non-binary ST since we will never query the empty string. In Fig. 3 all nodes with empty path labels correspond to $v_{ST}$, i.e. $v_1, v_4,$ and $v_{10}$. Hence $\hat{R}=\{3,3,1,2\}$ and we use a bitvector to map from the index domain of $R$ into $\hat{R}$.

Second, we note that the space of $\text {WT-D}$ and $\text {WT}\hbox {-}\hat{R}$ can be reduced if the length of query phrases is restricted to length $\ell$. In this case, we can sort ranges in $\hat{R}$ which belong to nodes $v_i$, where $v_i$ are the loci of patterns of length $\ell$. Since all query ranges are aligned at borders of sorted ranges, the interval sizes during processing will not be affected. In our example, if $\ell =1$, we sort the elements of $v_9$’s subtree, resulting in $\hat{R}^{1}=\{1,3,3,2\}$. The sorting will result in $H_0(T)$-compression of $\text {WT}\hbox {-}\hat{R}^{\ell }$ for $\ell =1$.

Third, we observe that when using $\text {WT}\hbox {-}\hat{R}^{\ell }$ only a part of $\text {WT-D}$ is necessary to calculate $\delta _{\mathcal {D} _{v},q}$. If $q$ occurs more than once in $\mathcal {D} _v$, $\text {WT}\hbox {-}\hat{R}^{\ell }$ can be used to get $\delta _{\mathcal {D} _{v},q}$. Hence, $\text {WT-D}$ is only used to determine the existence of $q$ in $\mathcal {D} _v$, and we only need to store the unique values inside ranges corresponding to loci of $\ell$-length patterns. In addition, values in these ranges can be sorted, since this does not change the result of the existence queries. In our example we get $D^1=\{3,0,1,2,0,1,2,0,1,2\}$; one increasing sequence per symbol. A bitvector is again used to map into $D^{\ell }$.

7 Experimental Study

Indexes and Implementations. To evaluate our proposals we created the SUccinct Retrieval Framework (surf) which implements document retrieval specific components, like Sadakane’s DF structure. These components can be parametrized by structures provided by the sdsl library [7]. We assembled three self-index based systems, corresponding to different functionality-space trade-offs. All systems use the same CSA and DF structure. The CSA is a FM-index using a WT. The WT as well as DF use RRR bitvectors [18, 22] to minimize space.

Our first index (i-d $^n$) adds $\text {WT-D}^n$, which uses plain bitvectors to allow fast WT traversal. Our second structure

adds $\text {WT}\hbox {-}\hat{R}^n$. A RRR bitvectors compresses the increasing sequences in $\hat{R}^n$. A variant of the latter index is

, which restricts the phrase length to one, and will show a functionality-space trade-off. In this version $\text {WT-D}^1$ is also compressed by using RRR vectors.

As a reference point we also implemented a competitive inverted index (invidx) which stores block-based postings lists compressed using OptPFD [15, 28]. For each block, a representative is stored to allow efficient skipping. The top-$k$ documents are calculated using two processing schemes. The first scheme – invidx-w – uses the efficient Wand list processing algorithm [2]. However, Wand requires pre-computation specific to $\mathcal {S}$ at construction time. A more flexible, but less efficient algorithm – invidx-e – exhaustively evaluates all postings in document-at-a-time order without either the burden or benefit of score pre-computation.

Fig. 4.

Collection statistics for Gov2 and ClueWeb09.

Fig. 5.

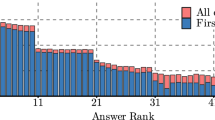
Left: Memory breakdown of our indexes. $|\mathcal {C} ^{raw}|$ denotes the original size of the collection, while $|\mathcal {C} ^{word}|$ denotes the size after parsing it. A more detailed space breakdown of the indexes is available at http://go.unimelb.edu.au/6a4n. Right: Percentage of states evaluated for $k=10, 100,$ and $1000$ during Ranked-OR retrieval using BM25 for queries on Gov2.

Data Sets and Environment. We use two standard IR test collections: (1) the Gov2 test collection of the TREC 2004 Terabyte Track and (2) the ClueWeb09 collection consists of “Category B” subset of the ClueWeb09 dataset. To ensure reproducibility we extract the integer token sequence $\mathcal {C}$ from Indri [26] using default parameters. We selected $1000$ randomly sampled queries from both the TREC 2005 and 2006 Terabyte tracks efficiency queries, ensuring all query terms are present in both collections. Statistics of our datasets (see Fig. 4) are in line with other studies [27]. We support ranked disjunctive (Ranked-OR, at least one term must occur) and ranked conjunctive (Ranked-AND, all terms must occur) retrieval. All indexes were loaded into RAM prior to query processing. Our machine was equipped with $256$ GiB RAM and one Intel E5-2680 CPU.

Space Usage. The space usage of our indexes is summarized in Fig. 5 (right). All indexes are much larger than our inverted index, which uses $7.3$ GiB for Gov2 and $22.8$ GiB for ClueWeb09. The space of the compressed docid and frequency representations is $5.1$ GiB and $17.6$ GiB respectively which is comparable to other recent studies [21]. However, an inverted index supporting phrase queries would require additional positional information, which would significantly increase its size. The size of our integer parsing of size $n\lceil \log \sigma \rceil$ is shown as a horizontal line. The CSA for both collections compresses to roughly $30\,\%$ of the size of the integer parsing. The space for DF is negligible. The $\text {WT-D}^n$ has the size of the integer parsing plus $5\,\%$ overhead for a rank structure. The size reduction from $R$ to $\hat{R}$ is substantial. For example, storing $R$ for ClueWeb09 requires $123$ GiB, whereas $\hat{R}$ requires only $74$ GiB. Restricting the phrase length to one

, which makes it equivalent to a non-positional inverted index, shrinks the structure below the original input size.

Processed States. First, we measure the quantitative effects of our improved score estimation during GREEDY processing. We compare the range size ($f_{\mathcal {D} _{v},q}$)-only estimation to (a) range size estimation including document length estimation and (b) repeats estimation ($\delta _{\mathcal {D} _{v},q}$) including document length estimation. Figure 5 shows the percentage of processed states for all methods and $k=\{10, 100, 1000\}$ for both query sets on Gov2 using BM25 Ranked-OR processing. The percentage is calculated as the fraction of states processed compared to the exhaustive processing of each query ($k=N$). For all $k$, range size only estimation evaluates the most states on average. For $k=10$, the median percentage of evaluated states for range size only estimation is $1.6\,\%$. Adding document length estimation reduces the number of evaluated states to $0.8\,\%$. Using $\delta _{\mathcal {D} _{v},q}$ instead of $f_{\mathcal {D} _{v},q}$ to estimate the frequency further improved the percentage of evaluated states to $0.06\,\%$. Similar effects can be observed for $k=100$ and $k=1000$. For $k=1000$, document length estimation reduces the percentage from $5.1\,\%$ to $3.2\,\%$. Frequency estimation using $\delta _{\mathcal {D} _{v},q}$ again marginally improves the number of evaluated nodes to $2.8\,\%$. Overall, document length estimation has a larger impact on GREEDY than better frequency estimation via $\delta _{\mathcal {D} _{v},q}$.

Disjunctive Ranked Retrieval. Next we evaluate the performance of i-d $^n$,

for BM25 Ranked-OR query processing. Figure 6 (left) shows runtime on Gov2 and both query sets for $k=\{10, 100, 1000\}$. We additionally included invidx-w as a reference point for an efficient inverted index. The latter uses additional similarity measure dependent information and clearly outperforms all self-index based indexes. For $k=10$, it achieves a median runtime performance of less than 20 ms, and performs well for other test cases. However, if an additional $k+1$-th item is to be retrieved with the inverted index, the computation has to be restarted, whereas returning additional results using GREEDY is efficient. Our fastest index, i-d $^n$, is roughly $15$ times slower, achieving a median runtime of 300 ms for $k=10$. The indexes

and

are approximately two times slower than i-d $^n$. This can be explained by the fact that i-d $^n$ uses an uncompressed WT, whereas the other indexes use compressed WTs to save space. Also note that

is faster than

as ranges in $\hat{R}^1$ can be sorted, which creates runs in the WT which in turn allows faster state processing. The mean time per processed state – depicted in Fig. 6 (right) – highlights this observation. For i-d $^n$, the time linearly increases from $2$ to $5$ microseconds. While there is a correlation to the number of query terms, rank operations occur in close proximity – cache friendly – within $\text {WT-D}^n$, which increases performance. For the other indexes, we simultaneously access two WTs to evaluate a single state. This doubles the processing time per state.

Fig. 6.

Runtime (left) and WT state process time for $k\!=\!100$ (right) for BM25 Ranked-OR.

Efficient Retrieval Using Multi-Word Expressions. Multi-word queries often contain mutli word expressions (MWE), i.e. sequences of words which describe one concept; e.g. the terms “saudi” and “arabia” are strongly associated [3] in our collections and would be recognized as one concept “saudi arabia”. Using our index we can efficiently parse a query into MWE [9] (the problem of parsing MWE is also know as the query segmentation problem in IR; see e.g. [11]). Figure 7 (left) explores the runtime of MWE queries generated from Trec2006 for Gov2 using i-d $^n$. The runtime is reduced by an order of magnitude. This experiment shows how our system would support retrieval tasks where the vocabulary does not consist of words but a large number of entities. Supporting MWE does not increase the size of our index, but vastly increases the size of an inverted index.

Flexible Document Retrieval. Our indexes efficiently support a wide range of similarity measures, which can be changed and tuned after the index is built, while optimized inverted indexes require pre-computation depending on $\mathcal {S}$ at construction time [2]. If ranking functions are only chosen at query time, inverted indexes require exhaustive list processing. Figure 7 (right) shows the benefits of scoring flexibility. We compare our index structures to invidx-e using three ranking formulas: ${\textsc {TF}\times \textsc {IDF}}$, BM25, and LMDS on Gov2. Our index structures significantly outperform the exhaustive inverted index for ${\textsc {TF}\times \textsc {IDF}}$. This can be attributed to the influence of the document length $n_d$ on $\mathcal {S} ^{{\textsc {TF}\times \textsc {IDF}}}$. Unlike BM25 or LMDS, the final document score is linearly proportional to the actual size of the document, thus document length estimation significantly reduces the number of evaluated states. For BM25, the document length contribution to the final document score is normalized by the average document length, and thus has a smaller effect on the overall score of each document.

Fig. 7.

BM25 runtime for MWE queries (left) Ranked-OR runtime for different $\mathcal {S}$ (right).

8 Conclusions

We presented a self-index based retrieval framework which allows rank-safe top-$k$ retrieval on multi-term queries using complex scoring functions. The proposed estimation methods have improved the query speed compared to frequency-only score estimation. We found that top-$k$ document retrieval is still solved more efficiently by inverted indexes, if augmented by similarity measure-dependent pre-computations. However, self-index based systems provide can be used in scenarios where the inverted index is not applicable or slower such as phrase retrieval or query segmentation.