Keywords

1 Introduction

For many years researchers discusses influence of random number generator into speed of evolutionary process. There it is hard to recognize significant behaviors and features of the optimal random number generator [1–3]. The work [1] studies influence of choice of different pseudo-random generators onto performance of selected genetic algorithms. The works [2, 3] discuss impact of the Random Number Generator quality on Particle Swarm Optimization Algorithm. PSO algorithms are not GA or ES algorithms, but they also strongly depend on randomness. On the opposite side, they are not applying natural selection principle. There is accessible study of random number generator to genetic algorithm produced by another authors group too in [4].

Studies concluding the possibility to replace the random number generator by deterministic chaos system [15, 16] are now in works [5–8]. But the pseudo-random number generators are only long period functions with specific properties; especially they have constrained magnitudes and large number of crossing of any value in the output interval during one period. Typically, this requirement is known in the much stronger form as requirement of uniformity.

There is also the second significant requirement – requirement of independence, which tells that the generated numbers has no correlation with each other. Thus there is correct to form question if it is possible to replace random number generator by any non periodic or long period function?

It is also interesting to mention that any periodical continuous function might be transformed into non periodic discrete one if the length of period is not integer multiple of sampling period. This is the alternative way how to satisfy the third requirement – maximal cycle length. Maximal cycle length is significant especially in situations when large populations, big number of evolutionary steps and highly dimensional problems occurs. This fact might be demonstrated e.g. by increasing popularity of Mersenne-Twister algorithm [9]. This algorithm has extremely long period, e.g. its implementation MT19937 has period \( 2^{19937} - 1 \). Applicability of this algorithm in evolutionary algorithms is presented e.g. in [10].

Problem of non periodic functions created from periodic ones is that they satisfy requirement of independence only partially, in contrary to some deterministic chaos systems.

On the base of this background, the idea of evolutionary system not using random number generator nor even deterministic chaos system was formulated. As the test bed, simple evolutionary strategy algorithm described in the Chap. 2 was used. The random number generator was replaced by \( \sin \left( {kx} \right) \) function, as it is described in the Chap. 3. As test cases, the identification of parameters of equations describing Lorenz attractor and Rabinovich-Fabrikant system is applied. The results are outlined in the Chaps. 4 and 5.

2 Used Evolutionary Strategy Algorithm

The simple evolutionary strategy algorithm is outlined at Fig. 1. It is used as test bed in herein presented experiments for its simplicity and well known behavior.

Fig. 1
figure 1

Used evolutionary strategy algorithm

Full size image
\( n \) :

number of individuals

S :

maximal number of iterations

X :

vector of individuals

\( X' \) :

vector of new population candidates

\( f\left( x \right) \) :

fitness function

Errlimit:

Required error magnitude

3 Replacement of Random Number Generator by Non Periodic or Long-Periodic Functions

Random number generators, both natural and artificial, described by specific equations should satisfy the following properties:

  • Uniformity: The numbers generated appear to be distributed uniformly on interval <0, 1>;

  • Independence: The numbers generated show no correlation with each other within interval of given cycle length;

  • Cycle length: It should take long before numbers start to repeat.

Above mentioned works, especially [5–8] demonstrate that it is possible to replace random number generator by deterministic chaos system equations. These results are significant, because studied systems do not guarantee the property of uniformity in common. So, there occurs question, if it is needed to use deterministic chaos system equations or if it is possible to extend the group of applicable equations? Before answering of this question, it is useful to reason why evolutionary algorithms need to use random number generators?

The evolutionary algorithms use the random numbers in two different situations – initialization population formulation and processing of evolution. The first case points especially uniformity of generated numbers. The second one uses random numbers to achieve diverse modifications, to test big number of different possible solutions if the number of evolutionary cycles is high. Thus, the cycle length is significant, because it is the parameter giving the chance to test more values, more solution candidates.

Probably, there is no reason that avoids us to replace random number generator by any long periodic or non-periodic function. Even it is possible to sample any periodic continuous function defined on domain of real numbers and analogous infinite co-domain such way, that resulting discrete sequence of numbers will have endless period. E.g. if sin(x) with period of 2π will be sampled with period 1, we obtain such infinite non-periodic sequence because there does not exist any integers n and m different from 0, that \( n\pi = m \). The next chapters will be denoted to testing of applicability of two such functions (1) and (2) in above described evolutionary strategy algorithm on the place of standard random number generator. As test examples, the identification of parameters of non-linear differential equations of deterministic chaos will be used. These equations will represent Lorenz attractor (3) described by [11] and Rabinovich-Fabrikant system (4) described in [12]. Identification means in the case of Lorenz attractor determining of parameters \( \sigma ,{\kern 1pt} \rho ,\,and \;{\kern 1pt} \beta \) magnitudes to fit the modeled data. In the case of Rabinovich-Fabricant system these parameters are \( \alpha \,and\,\gamma \). Training data set consisted in the case of Lorenz attractor 400 samples and 2000 samples in the case of Rabinovich-Fabricant system. These two systems have been chosen for its nonlinearity, which forces the need of uniformity and independence of the tested generator and the transformation of Rabinovich-Fabricant system into more complicated form (6) increases the significance of cycle length requirement. Bigger number of parameters with similar influence to final behavior of the identified equation complicated identification and thus increases needed number of evolutionary algorithm cycles. Increasing of this number forces the need of longer cycle of number generator together with the larger genes (more parameters are optimized simultaneously, thus the larger number of magnitudes must be generated by the generator).

$$ \sin \left( {kn} \right) $$
(1)
$$ \sin \left( {a\,\;\sin \left( {nx} \right)} \right) $$
(2)

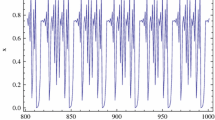
The property of this function is illustrated by Fig. 2.

Fig. 2
figure 2

Property of sin(y sin(x)) function

Full size image
$$ \begin{aligned} x' = & \sigma \left( {{\text{y}} - {\text{x}}} \right), \\ y' = & {\text{x}}\left( {\rho - \text{z}} \right) - {\text{y}}, \\ z' = & {\text{xy}} - \beta {\text{z}} \\ \end{aligned} $$
(3)
$$ \begin{aligned} x' & = y(z - 1 + x^{2} ) + \gamma x \\ y' & = x\left( {3z + 1 - x^{2} } \right) + \gamma y \\ z' & = - 2z\left( {\alpha + xy} \right) \\ \end{aligned} $$
(4)

4 Identification of Lorenz Attractor Equations Parameters

Average number of the used Evolutionary Strategy algorithm in the case of population of 1000 individuals (this number of individuals is used in all experiments presented in this contribution) for identification of Lorenz equations parameters \( \sigma \) and \( \beta \) are outlined in Table 1 for each variable x, y and z, when standard C++ rand() and sin() number generators are used. All average results were obtained by 1000 times repetition of experiments:

Table 1 The average number of cycles of Lorenz attractor equations parameter identification depending on different number generators
Full size table

The Fig. 3 presents numbers of iterations when standard rand() function is replaced by sin(k x) function. These numbers are also similar for all three variables x, y and z, but they are approximately five times worse than for standard rand function.

Fig. 3
figure 3

Number of iterations for x, y and z variables, sin(k x) is used on the place of random number generator

Full size image

Figures 4 and 5 then display the analogous dependency for random number generator in the form of Eq. (2) with parameter a equal to 1 and 10 respectively.

Fig. 4
figure 4

Number of iterations for x, y and z variables, sin(sin(k x)) is used on the place of random number generator

Full size image
Fig. 5
figure 5

Number of iterations for x, y and z variables, sin(10sin(k x)) is used on the place of random number generator

Full size image

Above presented results demonstrate that function (2) gives better results than (1), as it is summarized in Table 1. This result is in relation to self-correlation of time series produced by rand function and sin(t) function (rand gives much smaller than sin(kn), but sin(sin(t)) and especially function sin(sin(10t)) gives competitive results), but the Lorenz system consist of equations where is only one parameter to identify. Self-correlation is measure of independence condition of number generator.

The sin(a sin(kn)) function gives results comparable to rand() function while sin(kn) produces significantly worse convergence of ES algorithm. It is probably given by higher self-correlation of sin(x) function in comparison to the rest ones.

Table 2 presents correlations of sin(akt) and sin(ak(t + 1)) functions and Table 3 outlines correlations of sin(sin(kt)) and sin(sin(k(t + 1)) or sin(sin(10 kt)) and sin(sin(10 k(t + 1)) functions.

Table 2 The self-correlation of sin(akt) and sin(ak(t + 1)) functions
Full size table
Table 3 The correlations of sin(sin(kt)) and sin(sin(k(t + 1)) or sin(sin(10 kt)) and sin(sin(10k(t + 1)) functions
Full size table

5 Identification of Rabinovich-Fabrikant System Attractor Parameters

Problem of n-dimensional system is the problem of independence of random time sub-series influencing each particular parameter. In the case on multidimensional system the independence is required in more complex manner than in the case of one dimensional one.

Def. 1: Let is given reasoned number of samples n. Let used Evolutionary algorithm optimizes m dimensional problem and it need 1 random number to each parameter to be optimized. Symbol r i denotes i-th number of time series generated by random number generator or alternative function. Then there is need to investigate mutual independence and self-independence (independence of data taken in t and t + d) of all following data sub-series separated from the original series r:

$$ \forall k \in \left\langle {1,m} \right\rangle ,\forall l \in \left\langle {0,m - 1} \right\rangle ,\forall i \in \left\langle {1,n{\kern 1pt} \,div\,m} \right\rangle ,\;\;s_{k,l,i} = k + l, \ldots ik + l.$$
(5)

Rabinovich-Fabrikant system is described by three equations as Lorenz one, but these equations are strongly non-linear, where e.g. the first equation contains expression \( x^{2} y \) and the second one contains \( x^{3} \) one. These equations were transformed into the form (6), which is much complicated to ES algorithm (they contains additional parameters \( \alpha_{1} , \ldots ,\alpha_{4} \)):

$$ \begin{aligned} x' & = y(z - \alpha_{1} + x^{2} ) + \gamma x \\ y' & = x\left( {\alpha_{2} z + \alpha_{3} - x^{2} } \right) + \gamma y \\ z' & = - \alpha_{4} z\left( {\alpha + xy} \right) \\ \end{aligned} $$
(6)

It means that these equations contain 2, 3 and 2 parameters respectively in contrary to Eq. (3), where each differential equation contains one parameter to be identified only. Such situation is avoided by GPA algorithms frequently because these algorithms have no preventive mechanism against creation of overcomplicated structures. The solution of this problem is difficult and it is partially solved e.g. by GPA-ES algorithm [13].

For each number generator it was the most difficult to identify the second equation (equation describing variable y) with tree parameters. The best results for each category of functions are summarized in Table 4.

Table 4 The average number of cycles of Rabinovich – Fabrikant equations parameters identification depending on different number generators
Full size table

These results point interesting fact that for identification of the first and last equations, the rand() function is the best random number generator, but from the viewpoint of the second one sin(k n) or sin(sin(k n)) are better, non looking that both the first and the second equations both contain nonlinearities in the form of multiplication of three variables and two or three parameters respectively. To colorate this paradox, it is need to mention previous work [14], where it is presented, that symbolic regression of expression \( x^{3} \) is much more complicated than regression of other expression occurring in Eq. (5). In fact, in herein discussed case the increase of needed computational complexity is given by presence of three parameters which masks each other.

6 Conclusion

Presented paper discusses the possibility to replace standard random number generator by continuous periodic function. This replacement is possible, when the requirements of uniformity, independence and cycle length are satisfied. Such functions as sin(kt) or sin(a sin(kt)), which solve as examples in this paper might be carefully applied, but the results are applicable to much wider group of functions. Analysis of the next types of functions and the next function features influencing the speed of convergence of evolutionary algorithms will be subjects of future works.

The conclusion of above presented work is that nonstandard number generators as sin(kt) function and composed sin(a sin(kt)) are not significantly worse than standard rand() random number generator in presented situation. There is chance, that the random number generators may be replaced by any continuous aperiodic function satisfying conditions of uniformity, independence and (maximal) cycle length in application in evolutionary algorithms. Future tests with other functions with smaller self-correlation will give information about its influence to evolutionary algorithm behaviors. Presented short work is not able to give complete answer on the question, which random number generator parameters are significant to evolutionary algorithms, but it points to above mentioned tree conditions. On the opposite side, while in the case of single parameter equations describing Lorenz attractor, the sin(k sin(nx)) functions were comparable to rand() generator, in the case of Rabinovich-Fabrikant system these functions were worse than rand() generator. Thus there is probably undiscovered some more deep, or it is possible to say more complicated, property than above discussed three conditions.