Granular Geometry

Abstract

Many approaches have been proposed in the fuzzy logic research community to fuzzifying classical geometries. From the field of geographic information science (GIScience) arises the need for yet another approach, where geometric points and lines have granularity: Instead of being “infinitely precise”, points and lines can have size. With the introduction of size as an additional parameter, the classical bivalent geometric predicates such as equality, incidence, parallelity or duality become graduated, i.e., fuzzy. The chapter introduces the Granular Geometry Framework (GGF) as an approach to establishing axiomatic theories of geometries that allow for sound, i.e., reliable, geometric reasoning with points and lines that have size. Following Lakoff’s and Núñez’ cognitive science of mathematics, the proposed framework is built upon the central assumption that classical geometry is an idealized abstraction of geometric relations between granular entities in the real world. In a granular world, an ideal classical geometric statement is sometimes wrong, but can be “more or less true”, depending on the relative sizes and distances of the involved granular points and lines. The GGF augments every classical geometric axiom with a degree of similarity to the truth that indicates its reliability in the presence of granularity. The resulting fuzzy set of axioms is called a granular geometry, if all truthlikeness degrees are greater than zero. As a background logic, Łukasiewicz Fuzzy Logic with Evaluated Syntax is used, and its deduction apparatus allows for deducing the reliability of derived statements. The GGF assigns truthlikeness degrees to axioms in order to embed information about the intended granular model of the world in the syntax of the logical theory. As a result, a granular geometry in the sense of the framework is sound by design. The GGF allows for interpreting positional granules by different modalities of uncertainty (e.g. possibilistic or veristic). We elaborate the framework for possibilistic positional granules and exemplify it’s application using the equality axioms and Euclid’s First Postulate.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

Many approaches have been proposed in the fuzzy logic research community to fuzzify classical geometries. From the field of geographic information science (GIScience) arises the need for yet another approach, where geometric points and lines have granularity: Instead of being “infinitely precise”, points and lines can have size. With the introduction of size as an additional parameter, the classical bivalent geometric predicates such as equality, incidence, parallelity or duality become graduated, i.e., fuzzy.

The chapter introduces the Granular Geometry Framework as an approach to establishing an axiomatic theory of geometry that allows for reliable geometric reasoning with points and lines that have size: In the presence of granularity, classical geometric statements are often wrong, and and it depends on the specific geometric configuration “how wrong” they are [35, 72, 73]. A granular geometry in the sense of the framework augments every classical geometric statement with a degree of reliability, and the reliability degree is propagated in geometric reasoning. The Granular Geometry Framework extends the work of Roberts [51] and Katz [32] by using Łukasiewicz Fuzzy Logic with Evaluated Syntax [41], $FL_{ev}$(Ł$\forall$), as a background logic for representing and propagating the degree of reliability. $FL_{ev}$(Ł$\forall$) allows for treating the reliability degree as an intrinsic part of the syntax of a logical formula and guarantees that reasoning in granular geometry is sound.

Following L. Zadeh’s Restriction Centered Theory of Truth and Meaning [83] (RCT), points and lines with size can be seen as positional restrictions of the geographic space, and, in the style of Zadeh’s theory of Z-valuations [82], a granular geometry can be seen as a precisiation of a reliability calculus for positional restrictions. In RCT, restrictions can have different modalities of uncertainty, and this is also the case for granular geometries. For instance, a “positional restriction of type point” may be precisiated by a possibility distribution, a probability distribution, or a verity distribution, and the Granular Geometry Framework provides a guideline for precisiating the geometric theory accordingly.

As a first step towards a possibilistic granular geometry, we apply the Granular Geometry Framework to the equality axioms and to Euclid’s first postulate. We show exemplarily how the introduction of size in classical geometries causes a fuzzification of classic geometric predicates. Borrowing a terminology commonly used in the GIScience literature, we call the resulting theory an Approximate Tolerance Geometry [73–75].

The chapter is structured as follows: Sect. 6.2 gives a motivation for the introduction of granular geometries for geographic information systems (GIS) and reviews related work from the GIScience community and related fields. Section 6.3 introduces similarity logic as the underlying idea and main tool for incorporating a reliability measure in classical geometry, and—on this basis—develops the Granular Geometry Framework. Section 6.4 applies a possibilistic instantiation of the Granular Geometry Framework to the equality axioms and to Euclid’s First Postulate, thus elaborating a first step towards an Approximate Tolerance Geometry. In Sect. 6.5, we briefly discuss the Granular Geometry Framework in the context of Zadeh’s RCT. Section 6.6 finally gives a summery of results and discusses current limitations of the framework. We also give an outlook to future directions and further work.

6.2 Background

In Sect. 6.2.1, we briefly discuss the rationale of introducing a granular geometry, which stems from the area of geographic information science (GIScience) and gives simple examples of granular geometric configurations. Section 6.2.2 reviews existing approaches to handle granular geometric objects withing the GISience community and related research fields. Section 6.2.3 reviews related work from computer science and mathematics, with a special focus on axiomatic approaches.

Fig. 6.1

An example of a a veristic, b a possibilistic, and c a probabilistic interpretation of a granular point that is more or less incident with a granular line ((a) after [77])

6.2.1 Motivation

As a motivation for the introduction of granular geometries for spatial analysis in geographic information systems (GIS), Fig. 6.1 illustrates three typical geographic scenarios: Part (a) shows a boat floating on a river. While the boat may be seen as a granular point, the river may be conceptualized as a granular line. We can say that the granular point approximately “sits on” the granular line. Using a geometric terminology, the granular point is more or less incident with the granular line. Part (b) shows a similar configuration. Here, a metro station building is shown, which is more or less incident with railway tracks. Part (c) shows a highway and a highlighted area that indicates an increased freuquency of car accidents in this sector of the road. All three scenarios can be interpreted geometrically, namely as approximate incidence of a (granular) point with a (granular) line. The difference between the them is the modality of imperfection with which the granular features are modeled: The statement “The boat is on the river” refers to the boat as an indivisible entity, and we can model this by a (crisp) verity distribution. Here, every coordinate pair in the black rectangle is considered part of the boat with a degree of 1. In contrast, when I say “I am at the metro station”, the metro station in (b) indicates the (crisp) set of coordinate pairs that possibly coincide with my true exact location at the time of speaking. Finally, in (c), the shaded area provides a color indication of the probability that I encounter a car accident when driving through this section of the highway.

The need for geometric reasoning with extended objects in GIS stems from a paradigm change that took place in GIScience in the recent years. While traditionally, imprecision in geographic data was considered an error, the proliferation of location based applications and crowd-sourced geographic data¹ raised the general awareness for the value of human-centered and perception based interaction with GIS applications. Today, it is considered a feature to offer GIS functionality for imprecise input. Since geometric reasoning lies at the core of the GIS vector data model and thereby also at the core of all derived spatial analysis capabilities, it is desirable to provide a geometric calculus for granular features in GIS. While most current approaches in the community are based on heuristics that where originally designed to deal with small imprecisions in traditional, well-maintained datasets, the proposed Granular Geometry Framework aims at providing a reliable granular geometric calculus that is reliable, even if the position granules involved are potentially very large.

Existing heuristic algorithms in GIS often map classical geometric predicates to the approximate geometric relations between granular points and lines. Yet, when classical geometric reasoning is applied to position granules, i.e., to points and/or lines with size, the result may be wrong. In other words, geometric reasoning with position granules is not reliable. A classical example of this fact is the Poincaré Paradox [46], which states that the equality of sensations and measurements in the physical continuum is not transitive. An instance of the Poincaré Paradox is illustrated in Fig. 6.2a.

Fig. 6.2

a Poincaré Paradox, b approximate direction

A test person whose skin is stimulated in the spots $P$ and $Q$, e.g. by a sharp object, may not be able to distinguish the two approximate locations on their skin. In other words, in the person’s perception, the two spots are equal. For the same reason, the person will also not be able to distinguish $Q$ and $R$, and therefore, they will also consider them as equal. Yet, since the spots $P$ and $R$ are not very close together, they can be distinguished easily, and the person will identify the relation between $P$ and $R$ as not equal. In other words, perceived equality is not always transitive. When we model the relation of perceived equality (i.e., of indistinguishability) by the classical (transitive) geometric equality relation, the result of the query “$P=R$?” may be wrong. In geographic information systems, these kind of problems arise as a result of, e.g., measurement inaccuracy, mapping error or overlay errors.² To the knowledge of the author a generic solution to the problem of sound, i.e., reliable, geometric reasoning with position granules in GIS has not been found as of yet.

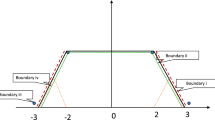
With the introduction of size to classical geometries, classical crisp geometric notions become fuzzy. As an example, Fig. 6.2b shows two granular points $P$ and $Q$. The granular line $L$ is approximately incident with both, $P$ and $Q$, and so is the granular line $M$. What we observe is that, in contrast to classical geometry, “the” connecting line is not unique, and the direction specified by the two granular points $P$ and $Q$ is only an approximate direction.

Fig. 6.3

The “degree of uniqueness” of an approximate connection depends on the distance between the involved granular points [73]

Fig. 6.4

The “degree of uniqueness” of the approximate connection depends on the sizes of the involved granular points [73]

Figure 6.3 illustrates exemplarily that the “degree of uniqueness” of “the” connecting granular line depends on the distance between the involved granular points. Figure 6.4 illustrates that it also depends on their size.

Notice that the fuzziness of geometric predicates is a result of the fact that the size of objects varies: If granular points have fixed size, there is a bijection from granular to exact geometry. The Granular Geometry Framework assumes variabel size of positional granules. It is an approach to parametrizing the fuzziness of classical geometric statements as a function of size and distance parameters.

Figure 6.5 illustrates exemplarily the fuzzification of the classic geometric notion of duality in granular geometries: In classical logic, every point can be seen as a pencil of lines, and every line can be interpreted as a range of points. In granular geometry, every (approximate) range of granular points specifies an approximate direction, i.e., it is more or less (granular) linear. Conversely, every (approximate) pencil of granular lines specifies a an approximate location, which is more or less (granular) punctual.

Fig. 6.5

a–c Classical duality, a $\mathbf {'}$–c $\mathbf {'}$ Fuzzyfied duality [73]

6.2.2 Granulated Space in Geographic Information Science

We discuss the increasing need for granular geometries in GIScience and give a brief overview over existing approaches from the community that relate to the problem.

GIScience as a Mapping Science

The representation and propagation of error and uncertainty in measurement sciences like surveying is based on a well-developed mathematical foundation in measurement theory [23, 64]. Here, measurement inaccuracy can often be disregarded, “because it has been possible to devise increasingly more careful or refined methods of comparison for properties like weight and distance” [65, p. 299f.]. As opposed to surveying, which deals with physical measurements, geographic information science is not a measurement science, but a mapping science [25]. Mapping errors that arise, e.g., from geocoding [84], and the superposition of different data layers with different lineage and quality leads to geometrical discordance: different data layers represent what is meant to refer to the same entity in reality by different coordinate representations, thus introducing positional uncertainty of coordinate points and lines. The resulting uncertainty can often only be subsumed as possibilistic uncertainty and cannot be propagated with established statistical methods of Gaussian error propagation.

The need to deal with large positional uncertainties has been drastically increasing in the last years as lay users became prosumers by collecting geographic data (known as “volunteered geographic data”, VGI [25]) in participatory GIS projects such as OpenStreetMap (OSM³). Here, the strict quality control of traditional mapping agencies does not apply, and the expert use of scale as a means to balance the granularity of representation with the sampling frequency of the available measurement points can not be taken for granted. Still, it is paramount to provide positional information that is sufficiently reliable for the end users, e.g., of OSM-based car navigation systems. To guarantee that the positional information that is derived by geometric construction from the original VGI measurement data is reliable enough for the respective application, a sound error calculus for possibilistic uncertainty is needed.

Besides possibilistic positional uncertainty, veristic uncertainty also becomes an issue in GI Science as the need for geometric reasoning with extended objects increases: A verity distribution [82] specifies the set of all positions, where a certain property applies, such as, e.g., the property of belonging to a certain registered place such as Picadilli Circus. With the proliferation of mobile computing, cheap GPS sensors, and natural language user interfaces such as Siri,⁴ it is considered a feature to allow users of location based services to specify location on an appropriate level of detail instead of forcing them to be as precise and accurate as possible. An example is the natural language statement “My house is in the middle between Picadilli Circus and Leicester Square”. Here, the geographic information system should be able to derive the approximate center point of the approximate line segment that connects Picadilli Circus and Leicester Square, including the corresponding uncertainty.

In the following, we describe approaches from the GI Science community towards handling positional uncertainty in geometric reasoning. Most of these approaches are heuristics that are not geared towards handling large uncertainties and/or soundness of reasoning. When used in longer sequences of geometric constructions, they may produce highly unreliable or even completely wrong results.

Models of Positional Granularity in GIScience

One of the earliest error models for representing point and line features with positional uncertainty is the epsilon band model introduced by J. Perkal [43, 44]. Here, every feature is associated with a zone of width epsilon around it. The zone can be associated with different modalities of imperfections, e.g., it may refer to the area in which the true feature possibly sits, or to a probability distribution for the position of the true feature with standard error epsilon. The epsilon band model gave rise to a huge amount of research in this direction, which today mainly focuses on statistical treatment of positional imperfection.⁵ Another classical error model for line features is Peucker’s ‘Theory of the Cartographic Line’ [45], which postulates thickness as an intrinsic characteristic of cartographic lines. The theory derives from research on the generalization of line features by D. Douglas and T.K. Peucker [15]. The Douglas-Peucker algorithm, which was independently suggested by U. Ramer [49], is still in use today.

In the GIS community, the representation of geographic regions such as mountains or informally defined places in a city as fuzzy sets is usually referred to by the term vague regions or regions with broad boundaries.⁶ An approaches to reasoning with vague regions have been proposed, e.g., by A. Dilo [14]. Her work is based on fuzzy sets theory and defines topological and metrical operations for vague regions. In terms of geometric notions, these approaches use vague regions as point-like objects that have a fuzzy size, and extend point-operations to them. E. Clementini [13] extends the existing models for vague regions to linear (line-like) features that have extension. He defines the boundary of a line feature (i.e., a line segment) as its zero-dimensional boundary in $\mathbb {R}$, and broadens it by assigning to it a two dimensional extent in $\mathbb {R}^{2}$. Clementini’s approach is not limited to fuzziness, but integrates different modalities of imperfections of positional information. From the field of remote sensing stems the approach of S. Heuel. His work is concerned with augmenting Grassmann-Cayley algebra (an algebraic approach to projective geometry that is widely used in remote sensing) with Gaussian probability density functions (pdfs). Heuel’s calculus provides an error-propagation calculus for probabilistic uncertainty, yet, it does not represent the incomplete knowledge about geometric relations as an intrinsic part of the calculus, and soundness can not be shown directly.

Research on the quality of volunteered geographic information has not gained much interest yet, and the research on positional accuracy of VGI is even more sparse. One of the first papers that carried out a systematic analysis of VGI data quality is [28]. It is partly based on the work of N. Zulfiqar [86] on the positional accuracy of motorways in the UK using a buffer overlap analysis. C. Amelunxen [1] investigates the positional accuracy of OpenStreetMap data for the purpose of geocoding. M. Haklay [29] show that the positional accuracy of Open Street Map data increases with the number of contributors to the data set.

6.2.3 Fuzzy and Granular Geometries

We review related literature from other research communities, in particular from computer science and mathematics. Here, we put particular emphasis on axiomatic approaches. We briefly introduce Robert’s tolerance geometry and Katz’ inexact geometry that both provide the basis for approximate tolerance geometry and the generic Granular Geometry Framework.

Digital Geometry

In the field of computer science, a predominant source of granulation of positional information is the discretization error that stems from the discrete representation and finite precision arithmetic used in digital image processing. From this problem field stems the research area of digital geometry. Digital geometry deals with the representation of geometric configurations as subsets of the discrete digital 2D and 3D space, and devises according geometric constructions and tests. It’s main areas of application is digital image analysis and digital image processing. A prominent approach in digital geometry is the cell complex model of the digital plane that defines “digital points” as equivalence classes of points in $\mathbb {R}^{2}$. Derived from digital points are “digital lines”, and problems of unsound reasoning arise from it: “The intersection of two digitized lines is not necessarily a digital point, and two digital points do not define a unique digital straight line, unless we introduce additional criteria to select such a line” [71, p. 100]. Based on the cell complex model, P. Veelaert [71] provides a mathematical framework that addresses the affine geometric relations of parallelism, collinearity, and concurrency in the digital plane. In contrast to the Granular Geometry Framework introduced here, Veelaert does not use an axiomatic approach, but instead shows that the digitized versions of affine geometric relations “can be verified by constructions that are still purely geometric, though slightly more complicated [...]” [71, p. 100]. He replaces the geometric relations by Helly-type properties, whose characteristic is to be not in general transitive and introduces a notion of thickness of digital points and lines to parametrize positional imprecision. Veelaert’s approach differs from the one presented here in two main points: First, granular geometries are defined axiomatically and therefore meta-mathematical properties like soundness can be investigated. Second, Veelaert’s approach is tailored to digital image processing, and consequently only applicable to positional error that results from discretization. In contrast to that, positional error in GIS stems from a large variety of sources, and it is necessary to provide a more general approach, where points and lines with size are not restricted to the constraints imposed by the structure of the digital plane. Yet another approach to capture a notion of granularity in geometric reasoning from the field of digital geometry is the ‘Epsilon Geometry’ proposed by D. Salesin, J. Stolfi, and L. Guibas.⁷ Epsilon geometry is not only a model for error representation, but implements geometric constructions and tests.

Fuzzy Geometry as a Part of Fuzzy Mathematics

In the mathematical literature, different approaches to fuzzifying classical geometry can be found, and we list some of them. One prominent field is fuzzy geometry as a subfield of fuzzy mathematics. Much of the early work in this area has been done by K. C. Gupta [26], A. Rosenfeld [53–56] J. J. Buckley and E. Eslami [8, 9], S.-C. Cheng and J. N. Mordeson [12]. Later work in this line is, e.g., H. Liu’s and G. M. Coghill’s fuzzy trigonometry [37]. An approach to propagating incomplete positional information in geometric reasoning that is based on fuzzy sets theory has been proposed by S. Dutta [16]. Following Zadeh’s approach [79] of defining mathematical and logical operators on the semantic level, all these approaches have the disadvantage that metamathematical properties such as soundness of reasoning cannot be verified easily.

Axiomatic Approaches to Fuzzy Geometry

In contrast to that, axiomatic approaches also exist that define a geometric theory on the syntactic level and provide corresponding models on the semantic level. An example is L. Kuijken’s and H. Van Maldeghem’s “fibered” projective geometry [33, 34]. Here, every point $x$ in $\mathbb {R}^{2}$ is a base point for several uncertain points. T. Topaloglou [68] axiomatizes one and two dimensional discrete space “with a built-in concept for imprecision” in a first order language. The axiom system is based on two sorts, point and scale, and two predicates, haze and precedence, where the haze relation is a reflexive and symmetric indistinguishability relation that is not necessarily transitive. In two dimensions, a theory of haze rectangles is constructed: A haze rectangle is a pair of haze points, where “haze points refer to points of space which are surrounded by a haze area, the smallest distinguishable quantity in the representation” [68, p. 47f.]. In 1971 T. Poston published his PhD thesis under the title of “Fuzzy Geometry” [47]. Yet, the term “geometry” in the title of Poston’s thesis mostly refers to topological and not to geometric notions. The word “fuzzy” in the title of Poston’s thesis can be misleading as well: Poston replaces the terms “physical continuum” and “tolerance space”, with the term fuzzy space, but the term “fuzzy” in his work is not directly related to notion of “fuzzy set” as introduced by L. A. Zadeh [79].

Y. Rylov discusses axiomatic approaches to multivaraint geometries in physics, which he defines as geometries with an “equivalence” relation that is not transitive in general. This definition corresponds to the relation of “possible equality “ in Approximate Tolerance Geometry (cf. Sect. 6.4), which is an instance of granular geometry as introduced in this chapter. Rylov discusses that multivaraint geometries are granular geometries in the sense that they are partly continuous and partly discrete.

Region based geometries, or point-free geometries, are axiomatic theories of geometry that—instead of using the abstract concept of point as a primitive object—are based on the region primitive. Similar to granular geometries, region based geometries are motivated by the fact that the interpretation of a point as an infinitely small entity is counter-intuitive, whereas regions have extension and are cognitively more adequate. The difference between the two approaches is that granular geometries axiomatize a new form of geometric reasoning, namely geometric reasoning with regions, while region based geometries axiomatize classical geometric reasoning, with exact points, only using a different object primitive, namely the region primitive, to do that. As in granular geometry, the regions in region based geometries are considered to be location constraints for exact points. The literature on region-based geometries has a long history, starting with N. I. Lobacevskij [38]. A historical overview is given by G. Gerla [18], and recent results are summarized by D. Vakarelov [70]. Many newer approaches build upon A. Tarski’s Geometry of Solids [67]. In particular, the work of Gerla and co-workers [6, 17, 21, 22], is relevant for granular geometry, because some of Gerla’s results are used as a basis for it; The work of B. Bennett et al. [2–5], relates to the field of GIS.

The Granular Geometry Framework introduced in this chapter and, in particular, its possibilistic version, Approximate Tolerance Geometry, is based on F. S. Roberts’ tolerance geometry [51], and M. Katz’ inexact geometry [32]. The basis for Roberts’ tolerance geometry was laid with the work of Zeeman [85] and Roberts and Suppes [52] on the granular nature of visual perception. Zeeman described as a distinguishing property of the geometry of visual perception the fact that the identity relation is reflexive and symmetric, but not in general transitive, and he calls such a relation a tolerance relation. Tolerance relations are often also called indistinguishability relations [40, 46, 47, 50, 69, 85]. Other examples of tolerance relations are the nearness relation and the relation of possible equality, as we use it in Approximate Tolerance Geometry. The observation that transitivity is often violated when dealing with identity in the physical continuum is usually attributed to H. Poincaré [46], and is also known as the Poincaré Paradox. Amongst others, it motivated the work of K. Menger [39] on ensemble flou (probabilistic equivalence relations) and was further continued by L. Zadeh [80] with the introduction of fuzzy similarity relations (fuzzy equivalence relations).

Roberts tolerance geometry is an axiomatic theory of one dimensional Euclidean geometry, where the notion of identity (i.e., equality or equivalence) is replaced by tolerance, i.e., by a tolerance relation. He derives his theory of tolerance geometry in an iterative process: First, he chooses an existing axiomatization of a classical geometry. Second, he chooses a specific model of the axiom system, i.e., an interpretation that complies with the axioms. Third, in this model, he substitutes the equality relation with an interpretation of the tolerance relation, namely with the closeness relation. In other words, he defines an “intended interpretation” of the equality relation. As a consequence of the changed interpretation, the interpretation does not comply with all of the axioms of the theory. In a fourth step, he modifies the respective axioms in such a way that the intended interpretation is a model again. Robert’s iterative approach is the basis for the generic Granular Geometry Framework introduced in Sect. 6.3, where an “intended interpretation” of the geometric primitives point and line as position granules and their relations is the starting point for the fuzzy extension of an axiom system of classical geometry.

Roberts interprets the tolerance relation as a closeness relation with an arbitrary, but fixed distance threshold $\varepsilon$: Here, two points, $p$ and $q$, are considered close to each other if their distance is smaller than or equal to $\varepsilon$. In other words, the granularity of the position granules is fixed. Katz [32] shows that modeling variable granularity (i.e., variable size of position granules) requires a graduated, i.e., fuzzy version of the tolerance relation. As a consequence, he uses a fuzzy logical system for the axiomatization of his theory of inexact geometry instead of the classical crisp logical system used by Roberts. More specifically, Katz uses Łukasiewicz fuzzy predicate logic Ł$\forall$, and Approximate Tolerance Geometry adopts his choice. A big drawback of Katz’ theory is the fact that his definition of graduated tolerance is in fact not an extension of the crisp tolerance relation, but an extension of a crisp equivalence relation (i.e., its kernel is transitive). It was only in 2008—18 years after Katz’ introduction of inexact geometry—that Gerla [20] introduced the notion of an approximate fuzzy equivalence relation, which is a true fuzzy extension of both, tolerance and equivalence relations. Approximate fuzzy equivalence relations lay the basis for approximate tolerance geometry as introduced in this chapter.

6.3 The Granular Geometry Framework

Before introducing the Granular Geometry Framework itself in Sects. 6.3.2 and 6.3.1 introduces similarity logic as the basic idea and main tool for axiomatizing geometric reasoning with granular points and lines as proposed in the framework.

6.3.1 Similarity Logic

Soundness of Geometric Reasoning

Granular geometry is intended to provide a calculus for geometric reasoning with position granules that is sound, i.e., reliable. A logical theory is sound, if all formulas that can be derived from the theory with its inference rules are valid with respect to its semantics. In other words, the rules of a corresponding calculus do not produce wrong or erroneous output. This is clearly not the case for heuristic approaches towards geometric reasoning with position granules. For this reason, the Granular Geometry Framework adopts a logical and axiomatic approach to the problem, where soundness is provable. Yet, the classical logical definition of soundness only applies in the context of perfect information (i.e., information that is precise, complete and certain). Outside this context, we cannot speak of soundness or unsoundness. To solve this problem, the Granular Geometry Framework uses a fuzzy logical system in the narrow sense, i.e., a graduated logical system that allows for treating imperfections of data as an integral part of the logical theory, allowing for the definition of soundness despite the presence of imperfections. More specifically, we use Łukasiewicz Fuzzy Logic with Evaluated Syntax as a similarity logic.

Similarity Logic

“In classical logic, falsity entails any statement. But, in many occasions, we may want to use ‘false’ theories, for instance, Newton’s Gravitational Theory.” [24, p. 80] These are theories that are not self-contradictory, but empirically or factually false. The problem can be solved by attaching to statements degrees of approximate truth, measured as proximity, or closeness, to the truth. The proximity of a statement $\varPhi$ to the truth is measured as a “distance”, or, dually, a similarity, between models of $\varPhi$ and models of “reality”. Logical formalisms that represent and reason with proximity to truth are usually subsumed under the name similarity logics or similarity based reasoning. They aim at “studying which kinds of logical consequence relations make sense when taking into account that some propositions may be closer to be true than others. A typical kind of inference which is in the scope of similarity-based reasoning responds to the form ‘if $\varPhi$ is true then $\varPsi$ is close to be true’, in the sense that, although $\varPsi$ may be false (or not provable), knowing that $\varPhi$ is true leads to infer that $\varPsi$ is semantically close (or similar) to some other proposition which is indeed true [24, p. 83].”

Research in similarity-based reasoning is mainly divided in two major approaches: The first approach uses similarity relations between models (or “worlds”) of a logical statement or theory. I.e., it defines similarity semantically. From the similarity relation a notion of approximate semantic entailment is derived which allows to draw approximate conclusions from approximate premises. The main reference in this area is Ruspini [57]. The second approach was proposed by Ying [78]. It uses similarity relations between formulas, i.e. it defines similarity syntactically. A notion of approximate proof is developed “by allowing the antecedent clause of a rule to match its premise only approximately” [78, p. 830], which again allows for drawing conclusions in an approximate setting. As shown by Biacino and Gerla [7], a generalization of Ying’s apparatus can be reduced to Rational Pavelka Logic [42], which extends Łukasiewicz fuzzy predicate logic ($FL_{ev}$(Ł$\forall$)) by adding additional truth constants [27]. Rational Pavelka Logic has been further generalized to Łukasiewicz fuzzy predicate Logic with Evaluated Syntax ($FL_{ev}$(Ł$\forall$)) by V. Novák and I. Perfilieva [41] and G. Gerla [19]. $F$ Ł $_{ev}$ is the main tool used in the Granular Geometry Framework to define an approximate geometric calculus.

Godo’s and Rodríguez’ Ontology of Imperfections

L. Godo and R. O. Rodríguez [24] propose an ontology of imperfections that is based on a formal logical viewpoint and allows for assigning appropriate classes of approximate reasoning tools. They distinguish three types of imperfections: vagueness, uncertainty and truthlikeness (cf. Fig. 6.6).

Fig. 6.6

Ontology of Imperfections after Godo and Rodríguez [73]

In classical logics, vagueness can not be expressed, since a classical logical interpretation function as proposed by A. Tarski [66] is bivalent. Fuzzy logic solves the problem. Uncertainty stems from the problem of incomplete information: In classical logic, there is no means of deciding the truth value of a statement in case neither the statement nor it’s negation can be deduced. The problem can be solved by attaching belief degrees to the truth values of statements, and examples of corresponding approximate reasoning tools are, e.g., probability theory, possibility theory or Dempster-Shafer theory of evidence. Finally, truthlikeness refers to the fact that classical logic has no means of expressing how close a false theory or statement comes to being true, and the problem can be solved by similarity based reasoning.

Contributing Imperfections: Possibility and Truthlikeness

According to this ontology of imperfections, two types of imperfections contribute to geometric reasoning with position granules. These are (positional) uncertainty and truthlikeness. Positional uncertainty stems from the positional granulation of exact points and lines. Truthlikeness stems from the assumption that classical geometry is false but close to the truth, which we adopt from Lakoff’s and Nunez’ cognitive theory of mathematics [35]. For a given modality of uncertainty, the Granular Geometry Framework describes a generic way of defining and propagating truthlikeness in granular geometry. More specifically, it provides guidance of

• 1. how to define a truthlikeness measure for granular geometry based on a given modality of uncertainty (e.g., possibilistic or probabilistic),

• 2. how to axiomatize granular geometry in Fuzzy Logic with Evaluated Syntax (as a similarity logic) based on a given axiomatization of classical geometry.

The result is an axiomatic theory of granular geometry that treats reliability (truthlikeness) as an intrinsic part of the theory. Fuzzy Logic with Evaluated Syntax allows for propagating the integrated reliability degree, and geometric reasoning with position granules is sound by design.

6.3.2 The Granular Geometry Framework

The Granular Geometry Framework provides a step-wise approach to axiomatize granular geometry based on an existing axiomatization of a classical geometry and for a given modality of uncertainty. It consists of four steps:

• 1. Choose a classical geometry and a corresponding axiomatization $\left\{ \varphi _{i}\right\} _{i}$.

• 2. Define an intended interpretation of

  • the primitive geometric objects of the axiomatization by positional granules (such as points and lines with size) with a fixed modality of uncertainty (such as possibilistic, probabilistic, or veristic).

  • the equality relation between positional granules that is semantically consistent with the chosen modality of uncertainty (e.g., if points with size are interpreted as sets of possible exact points, a sensible interpretation of the equality predicate is the overlap relation, cf. Sect. 6.4.2).

  • the primitive geometric relations between these positional granules that is semantically consistent with the chosen modality of uncertainty.

• 3. Define a truthlikeness measure for all predicates in the intended interpretation.

• 4. Fuzzify the chosen axiomatization $\left\{ \varphi _{i}\right\} _{i}$ in $FL_{ev}$(Ł$\forall$):

  • (a) For every axiom $\varphi _{i}$ of the chosen axiomatization $\left\{ \varphi _{i}\right\} _{i}$ use the truth-functional operators and quantifiers of Łukasiewicz fuzzy predicate logic ($FL_{ev}$(Ł$\forall$))⁸ to derive the truthlikeness degree $a_{i}$ of $\varphi _{i}$ from the truthlikeness measures of the involved predicates.

  • (b) For every axiom $\varphi _{i}$ assign the truthlikeness degree $a_{i}$ to $\varphi _{i}$ as a fuzzy degree of membership to the truth.

  • (c) Check if the truthlikeness degrees of all axioms $\varphi _{i}$ are greater than zero:

    • If yes, $\left\{ \left( \varphi _{i};a_{i}\right) \right\}$ defines an axiomatization of a granular geometry.

    • If no, extend the corresponding axioms (if possible), such that a positive truthlikeness degree results. The fuzzy extension must be consistent with the classical axiom. (I.e., for positional granules of size zero, fuzzy extension must coincide with the respective classical axiom).

Section 6.3.1 discussed the rationale of steps 1–3. In step 4, the classical axiomatization is fuzzified by attaching to every classical axiom its degree of truthlikeness. The result is a fuzzy set of axioms, $\left\{ \left( \varphi _{i};a_{i}\right) \right\}$, where the truthlikeness degrees (signs) $a_{i}$ attached to the classical axioms $\varphi _{i}$ indicate their fuzzy membership degrees to “real world geometry”. The truthlikeness is interpreted as a measure of reliability of the respective axiom in the presence of positional granularity. It may happen that the truthlikeness of one or several of the axioms is zero,⁹ which is equivalent to absolute falsity. In $FL_{ev}$(Ł$\forall$)—as in classical (crisp) logical theories—it is not useful to list an absolutely false formula as an axiom of a fuzzy theory: from an absolutely false formula, the graded deduction apparatus of $FL_{ev}$(Ł$\forall$) can only deduce absolutely false formulas, and absolutely false formulas are completely unreliable, i.e., useless. For this reason, it is necessary to ensure in step 4b that all fuzzified classical axioms have a positive truthlikeness degree. Only if this is the case, we call the resulting fuzzy theory a granular geometry.

Remark 1

Notice that the steps 3 and 4a derive the truthlikeness measure semantically in the interpretation domain, while it is used in step 4b as part of the syntax. As a result, the intended interpretation is by design a model of the fuzzy theory $\left\{ \left( \varphi _{i};a_{i}\right) \right\}$. In $FL_{ev}$(Ł$\forall$), a pair $(\varphi _{i},a_{i})$ is called a signed formula, and $a_{i}$ is called the sign or syntactic evaluation of $\varphi _{i}$.¹⁰

In the subsequent section, we apply the Granular Geometry Framework exemplarily to some axioms of projective plane geometry, based on a possibilistic interpretation of granular geometric objects.

6.4 Towards an Approximate Tolerance Geometry

Wilke [73, 75] developed the Granular Geometry Framework for a special case of possibilistic uncertainty, where possibilistic position granules are (crisp) neighborhoods of possible positions of an exact point or line. The uncertain geometric relation between these possibilistic position granules as they occur in GIScience community is often referred to as positional tolerance, and Wilke calls the developed possibilistic granular geometry an approximate tolerance geometry (ATG). In step 1 of the Granular Geometry Framework, she chooses a standard axiomatization of projective plane geometry, and elaborates in steps 2–3 the definition of the intended interpretation of possibilistic position granules and their truthlikeness. In step 4 (the fuzzification step), she applies the fuzzification procedure only to a subset of the chosen axiomatization, and a complete fuzzy axiomatization of approximate tolerance geometry in $FL_{ev}$(Ł$\forall$) is subject to further work.

Wilke shows that step 4(c) of the framework (validation of non-zero truthlikeness) is indeed necessary: In ATG, some of the axioms have a truthlikeness degree of zero. She proposes fuzzy extensions of these axioms that have positive truthlikeness degrees and are consistent with the corresponding classical axioms.

6.4.1 Step 1: Choose an Axiomatization

Wilke [73, 74], chooses the following standard axiomatization of projective plane geometry¹¹ that uses points and lines as primitive objects, and equality and incidence as primitive relations:

(Pr1) For any two distinct points, at least one line is incident with them.

(Pr2) For any two distinct points, at most one line is incident with them.

(Pr3) For any two lines, at least one point is incident with both lines.

(Pr4) Every line is incident with at least three distinct points.

(Pr5) There are at least three points that are not incident with the same line.

The axioms (Pr1) and (Pr2) are usually called Euclid’s First Postulate. They state that two distinct points can always be connected by a unique line. The projective axioms (Pr1)–(Pr5) can be formalized in classical predicate logic as follows:

(Pr1) $\mathtt {\forall p,q.\exists \mathtt {l}.\left[ \lnot E(p,q)\,\rightarrow \, I(p,\mathtt {l})\, \& \, I(q,\mathtt {l})\right] },$

(Pr2) $\mathtt {\forall p,q,l,m.\left[ \lnot E(p,q)\, \& \, I(p,l)\, \& \, I(q,l)\, \& \, I(p,m)\, \& \, I(q,m)\rightarrow E(l,m)\right] ,}$

(Pr3) $\mathtt {\forall l,m.\exists \mathtt {p}.\left[ I(p,\mathtt {l})\, \& \, I(p,m)\right] },$

(Pr4) $\mathtt {\forall \mathtt {l}.\exists p,q,r.\left[ \lnot E(p,q)\, \& \,\lnot E(q,r) \& \lnot E(r,p) \& I(p,l) \& I(q,l) \& I(r,l)\right] ,}$

(Pr5) $\mathtt {\exists p,q,r.\forall l.\lnot \left[ I(p,l)\, \& \, I(q,l)\, \& \, I(r,l)\right] .}$

Here, $\forall$ (“for all”) denotes the the universal quantifier, and $\exists$ (“exists”) denotes the existential quantifier. Connectives are used to formulate compound statements: stands & for a logical AND operator (conjunction),$\rightarrow$ denotes implication, $\lnot$ denotes negation. We use the symbol $\mathtt {E}$ to denote the equality predicate and the symbol $\mathtt {I}$ to denote the incidence predicate. Predicates can assume Boolean truth values, i.e. the value $1$ (true) or the value $0$ (false). E.g., $\mathtt {\mathtt {I}\mathtt {(p,l)}}=1$ says that $\mathtt {p}$ is incident with $\mathtt {l}$. The axioms employ two sorts of object variables, namely points and lines. Points are denoted by $\mathtt {p,q,r,\ldots }$, lines are denoted by $\mathtt {l,m,n,\ldots }$ In logical theories, equality (equivalence) is usually treated as part of the background logic. Yet, in the context of uncertainty, equality can not be recognized with certainty in general. The Granular Geometry Framework accounts for this fact, and treats the axioms of geometric equality as part of the logical theory. They are axiomatized as follows:

(E1) $\mathtt {\quad \forall x.\left[ E(x,x)\right] },$

(E2) $\mathtt {\quad \forall x,y.\left[ E(x,y)\;\rightarrow \; E(y,x)\right] ,}$

(E3) $\mathtt {\quad \forall x,y,z.\left[ E(x,y)\; \& \; E(y,z)\;\rightarrow \; E(x,z)\right] .}$

Here, $\mathtt {x,y,z}$ are either all points or all lines. (E1) is called reflexivity, (E2) is called symmetry, and (E3) is called transitivity.

6.4.2 Step 2: Define the Intended Interpretation

Step 2 of the framework requires the definition of the intended interpretation of the primitive geometric objects and relations of the chosen axiomatization in the context of granularity. For the axiom system (Pr1)–(Pr5), primitive objects are points and lines, and the primitive relations are equality and incidence.

The Intended Interpretation of Primitive Objects

According to Lakoff and Núñez, granules of positional information are the primitives of geometry as we perceive it in our interaction with the world around us, and we call them position granules (PGs).

Definition 1

Let $\left( X,d_{X}\right)$ be a metric space, and let $\tau _{d_{X}}$ be the induced metric topology on $X$. We call $P\subseteq X$ a position granule of type approximate point in $X$, if $P$ is either a $\tau _{d_{X}}$-topological neighborhood of a point $p\in X$ or a singleton, $P=\{p\}$. We denote the set of approximate points in $X$ by $\mathcal {P}_{X}$.

The definition of a PG $P$ as a neighborhood in a metric space (or a singleton) is motivated by examples from the GIS domain, cf., e.g., Fig. 6.1. Here, a PG is given as a crisp point set. Since Wilke address the possibilistic modality of uncertainty, she interprets a PG $P$ as the crisp set of possible positions of an exact point, i.e. as a possibilistic position granule (PPG). I.e., a PPG of type approximate point can be specified by the simple possibility distribution

$$\begin{aligned} pos(x)&= {\left\{ \begin{array}{ll} 1 &{} \text{ if } x\in P,\\ 0 &{} \text{ if } x\notin P. \end{array}\right. } \end{aligned}$$

(6.1)

In many axiomatizations of geometry, both, points and lines are primitive objects. In the vector based representation model of GIS, geometric lines are not considered primitive objects, yet they are sometimes obtained as original measurements. It is therefore reasonable that the ATG framework adopts the approach of treating lines as primitives. A line feature in GIS consists of a number of connected line segments and is represented as a tuple $(p_{1},\ldots ,p_{n})$ of coordinate points. Each pair $\left( p_{i},p_{i+1}\right)$, $i\in 1,\ldots ,n-1$, of consecutive coordinate points of the tuple defines a line segment, together with its corresponding geometric line $l_{i}=p_{i}\vee p_{i+1}$, cf. Fig. 6.7a. If the points $p_{i},p_{i+1}$ have positional tolerance, they can be represented by position granules $P_{i},P_{i+1}$ of type approximate point. As a consequence, the corresponding line $l_{i}$ inherits positional tolerance from $p_{i},p_{i+1}$, and it can be represented as a set $L=\{L_{i}\}_{i}$ of geometric lines, cf. Fig. 6.7b. It is consequently reasonable to interpret a geometric line with positional tolerance by a set $L_{i}$ of geometric lines that are possible candidates for an assumed ideal “true” line $l_{i}$.

Fig. 6.7

a A line feature and a geometric line. b Points with tolerance induce a geometric line with tolerance [75]

Similar to the definition of PGs of the type approximate point, we call $L$ a PG of type approximate line. It is a set of geometric lines, which are “close” to the unknown “true” line and constrains its position:

Definition 2

Let $L_{X}$ denote the set of geometric lines in a domain $X$. For a given geometric line $l\in L_{X}$, denote by $l'$ its dual point in a dual line parameter space $Y=X'$. Let $d_{Y}$ be a metric on $Y$, and let $\tau _{d_{Y}}$ be the induced metric topology on $Y$. $L\subseteq L_{X}$ is called a position granule of type approximate line in$X$, if $L'=\{l'|l\in L\}$ is a position granule of type approximate point in $Y$. We denote the set of approximate lines in $X$ by $\mathcal {L}_{X}$.

In analogy to the possibilistic semantic of approximate points, we attribute a possibilistic semantic to approximate lines, i.e., we consider PPGs of type approximate line. The definition of approximate points and lines extends the (corresponding) classical interpretation of geometric points and lines: An approximate point is a set $P$ of points that possibly coincide with the coordinates of an assumed “true” point $p$. If there is no uncertainty about the coordinates of $p$, $P=\{p\}$ holds. Similarly, if there is no uncertainty about the parameters of an exact line $l$, the set of possible coordinates of $l$ coincide with the one-element set containing $l$, i.e. $L=\{l\}$.

The Intended Interpretation of Primitive Relations

Since PPGs represent the set of possible positions of an exact point or line, geometric relations between PPGs can not be recognized with certainty. In order to guarantee a correct representation of the available information, the primitive geometric relations between approximate points and lines are interpreted as possible relations of exact points and lines. More specifically, the geometric equality predicate is interpreted by possible equality (often also called indistinguishability [46, 47, 80, 85]) of the corresponding “true” points, cf. Fig. 6.8. It can be represented by overlapping neighborhoods of equal sort, i.e. the overlapping of an approximate point with an approximate point, or the overlapping of an approximate line with an approximate line. Notice that by “overlapping approximate lines”, we mean that the approximate lines have a line (and not only a point) in common.

Fig. 6.8

The exact points $\bar{p},\bar{q}$ (the exact lines $\bar{l},\bar{m}$) are a certainly distinct; b possibly equal [73]

Definition 3

The intended interpretation of the geometric equality predicate in ATG in a metric space $X$ is given by the Boolean overlap relations

$$\begin{aligned} e_{\mathbb {B}}:\mathcal {P}_{X}\times \mathcal {P}_{X}\rightarrow \{0,1\},&\; e_{\mathbb {B}}(P,Q)=\left( P\cap Q\ne \varnothing \right) ,\end{aligned}$$

(6.2)

$$\begin{aligned} e_{\mathbb {B}}:\mathcal {L}_{X}\times \mathcal {L}_{X}\rightarrow \{0,1\},&\; e_{\mathbb {B}}(L,M)=\left( L'\cap M'\ne \varnothing \right) . \end{aligned}$$

(6.3)

The relation $e_{\mathbb {B}}$ is called equality with tolerance.

Following the same semantic as for equality, the geometric incidence predicate is interpreted by possible incidence of an exact point with an exact line. In terms of neighborhoods, possible incidence of exact objects translates into the overlap relation between constraints of different sort, i.e. into the overlapping of an approximate point with an approximate line, cf. Fig. 6.9.

Fig. 6.9

An exact point $\bar{p}$ and an exact line $\bar{l}$ are a certainly not incident; b possibly incident [73]

Definition 4

The intended interpretation of the incidence predicate in ATG in a metric space $X$ is given by the Boolean relation

$$\begin{aligned} i_{\mathbb {B}}:\mathcal {P}_{X}\times \mathcal {L}_{X}\rightarrow \{0,1\},\quad i_{\mathbb {B}}(P,L)=\left( P\cap L\ne \varnothing \right) . \end{aligned}$$

(6.4)

The relation $i_{\mathbb {B}}$ is called incidence with tolerance.

6.4.3 Step 3: Define Truthlikeness

Step 3 of the Granular Geometry Framework requires the definition of a truthlikeness measure of all predicates in the intended interpretation.

Truthlikeness of Primitive Relations

The relations equality with tolerance, $e_{\mathbb {B}}$, and incidence with tolerance, $i_{\mathbb {B}}$, are Boolean relations that specify the intended interpretation of the corresponding logical predicates geometric equality and incidence in an ATG. The interpretations specify what we intend to accept as truth. Similarity of $e_{\mathbb {B}}$ and $i_{\mathbb {B}}$ to the intended truth (truthlikeness) can be represented by fuzzy relations, that extend the corresponding Boolean relations. The fuzzy relations are chosen such that they assume the value $1$ if the corresponding Boolean relations hold and their values decrease “the more wrong” it is to assume that the corresponding Boolean relations hold. The fuzzy membership degrees are understood as truthlikeness degrees. I.e. the fuzzy relations are graduated extensions of the intended truth.

We first quantify the similarity of the statement $e_{\mathbb {B}}(P,Q)=1$ to the truth (i.e., the statement “$P$ and $Q$ are equal with tolerance”). The spatial setting of the problem statement suggests that a similarity measure that is dual to a spatial distance measure is appropriate. More specifically, Definition 3 of equality with tolerance, $e_{\mathbb {B}}(P,Q):=\left( P\cap Q\ne \varnothing \right)$, suggests using the following set distance measure, which is illustrated in Fig. 6.10:

$$\begin{aligned} d_{(d_{X})}(P,Q)=\inf \left\{ d_{X}(\bar{p},\bar{q})|\bar{p}\in P,\bar{q}\in Q\right\} , \quad P,Q\subseteq X. \end{aligned}$$

(6.5)

Fig. 6.10

The set distance measure (6.5) [75]

Here, $d_{X}$ denotes the metric in the underlying metric space $X$. $d_{(d_{X})}(P,Q)$ is an extensive distance (cf. Wilke [74], Gerla [20]), and measures the shortest distance between the subsets $P$ and $Q$: It quantifies the semantic distance of the statement $d_{(d_{X})}(P,Q)=0$ from the truth. Since

$$\begin{aligned} d_{(d_{X})}(P,Q)=0\quad \Leftrightarrow \quad P\cap Q\ne \varnothing \quad \Leftrightarrow \quad e_{\mathbb {B}}(P,Q)=1 \end{aligned}$$

(6.6)

holds, $d_{(d_{X})}(P,Q)$ is a dual measure of the of similarity of $e_{\mathbb {B}}(P,Q)=1$ to the truth: The greater the distance $d_{(d_{X})}(P,Q)$, the smaller the truthlikeness of $d_{(d_{X})}(P,Q)=~0$. Similarly, the set distance

$$\begin{aligned} d_{(d_{Y})}(L,M)=\inf \left\{ d_{Y}(\bar{l}',\bar{m}')|\bar{l}'\in L',\bar{m}'\in M'\right\} \end{aligned}$$

(6.7)

quantifies the semantic distance of the statement $d_{(d_{Y})}(L,M)=0$ from the truth, and is a dual measure of truthlikeness of $d_{(d_{Y})}(L,M)=0$. Here, $d_{Y}$ denotes the metric in the underlying line parameter space.

Similarity measures are often normalized to the interval $[0,1]$, and we adopt this. We assume that the distance measures (6.5) and (6.7) are normalized to the interval $[0,1]$ as well. As a result of this assumption, the degree of truthlikeness of a statement $e_{\mathbb {B}}(P,Q)=1$, or $e_{\mathbb {B}}(L,M)=1$, can be defined by $1-d_{(d_{X})}(P,Q)$ and $1-d_{(d_{Y})}(L,M)$, respectively. The assumption that $d_{X}$, and consequently $d_{(d_{X})}$, can be normalized, i.e. that a maximal distance exists, is reasonable in the context of GIS, since all maps are bounded.

Definition 5

The fuzzy interpretation of the geometric equality predicate in ATG is given by the fuzzy relations

$$\begin{aligned} e_{(d_{X})}:\mathcal {P}_{X}\times \mathcal {P}_{X}\rightarrow [0,1],&\quad e_{(d_{X})}(P,Q):=1-d_{(d_{X})}(P,Q),\quad and\end{aligned}$$

(6.8)

$$\begin{aligned} e_{(d_{Y})}:\mathcal {L}_{Y}\times \mathcal {L}_{Y}\rightarrow [0,1],&\quad e_{(d_{Y})}(L,M):=1-d_{(d_{Y})}(L,M). \end{aligned}$$

(6.9)

$P,Q$ and $L,M$ are called approximately equal with tolerance to the degree $e_{(d_{X})}$ $(P,Q)$ and $e_{(d_{Y})}(L,M)$, respectively. Here, $d_{X}$ and $d_{Y}$ are a normalized metrics in $X$ and $Y$, respectively.

The fuzzy relations $e_{(d_{X})}$ and $e_{(d_{Y})}$ extend the Boolean relations $e_{\mathbb {B}}$ and $e_{\mathbb {B}}$, respectively, because they coincide at the value $1$:

$$\begin{aligned} e_{(d_{X})}(P,Q) =1-d_{(d_{X})}(P,Q)=1 \quad&\Leftrightarrow \nonumber \\ e_{\mathbb {B}}(P,Q)&= \left( P\cap Q=\varnothing \right) =1,\end{aligned}$$

(6.10)

$$\begin{aligned} e_{(d_{Y})}(L,M) =1-d_{(d_{Y})}(L,M)=1 \quad&\Leftrightarrow \nonumber \\ e_{\mathbb {B}}(L,M)&= \left( L'\cap M'=\varnothing \right) =1. \end{aligned}$$

(6.11)

As a second step, we quantify the similarity of the statement $i_{\mathbb {B}}(P,L)=1$ to the truth (i.e., the statement “$P$ and $L$ are incident with tolerance”). A measure of truthlikeness for the primitive relation of incidence with tolerance is a measure that quantifies the distance of the statement $i_{\mathbb {B}}(P,L)=\left( P\subset L\right) =1$ from the truth. The set distance measure used for specifying truthlikeness of equality with tolerance can not be used here: While the Boolean interpretation of equality with tolerance is the overlap relation between location constraints of the same sort, incidence with tolerance is interpreted by the overlap relation between location constraints of different sorts. The trivial solution for this problem is to keep the Boolean relation $\left( P\subset L\right)$ and interpret it as a discrete similarity measure. In order to simplify the modeling task at hand, [73] adopts this solution, and we keep with it. The integration of a more realistic graduated definition of truthlikeness of incidence with tolerance is a task for future work. In analogy to the definition of $e_{\mathbb {B}}$, we may understand $\left( P\subset L\right)$ as an inverse distance measure, $\left( P\subset L\right) =1-\varDelta (P,L)$, where $\varDelta$ denotes the discrete distance measure

$$\begin{aligned} \varDelta (P,L)=1-\left( P\subset L\right) ={\left\{ \begin{array}{ll} 1 &{} \text {if }(P\subset L)=0,\\ 0 &{} \text {if }(P\subset L)=1. \end{array}\right. } \end{aligned}$$

(6.12)

Definition 6

The fuzzy interpretation of the incidence predicate in ATG coincides with Definition 4. It is a Boolean relation and it is given by

$$\begin{aligned} i_{\varDelta }:\mathcal {P}_{X}\times \mathcal {L}_{X}\rightarrow \{0,1\}\subset [0,1],\quad i_{\varDelta }(P,L):=1-\varDelta (P,L)=P\subset L, \end{aligned}$$

(6.13)

$P$ and $L$ are called approximately incident with tolerance to the degree $i_{\varDelta }(P,L)\in \{0,1\}$.

Since the fuzzy relation is chosen such that it coincides with the Boolean relation, it trivially extends the Boolean relation.

Remark 2

A possible candidate for a graded definition of truthlikeness is the distance measure $d_{(d_{X})}^{\perp }(P,L)=\inf \left\{ d_{X}^{\perp }(\bar{p},\bar{l})|\bar{p}\in P,\bar{l}\in L\right\}$, where $d_{X}^{\perp }(\bar{p},\bar{l})$ denotes the orthogonal distance between Cartesian points and lines $\bar{p},\bar{l}$. In order to integrate this measure in ATG, it is necessary to investigate if it works in concert with the definition of truthlikeness of the possible equality predicate in the sense that, together, they allow for a modification of classical geometric axioms such that a model of the modified axioms exists that complies with the properties of the intended interpretation.

6.4.4 Step 4: Fuzzification

In the fourth step of the Granular Geometry Framework, the truthlikeness measure derived in step 3 is used to fuzzify the classical axioms (E1)–(E3) and (Pr1)–(Pr5). As a first step towards an approximate tolerance geometry, Wilke [73] did this exemplarily for the equality axioms (E1)–(E3) and for Euclid’s First Postulate, (Pr1) and (Pr2).

Step 4a: Truthlikeness of the Classical Axioms

Geometric axioms are compound geometric statements: they are composed of atomic formulas, connectives and quantifiers. In the present work, atomic formulas are statements that involve one of the predicates geometric equality $\mathtt {E}$, incidence $\mathtt {I}$, and in ATG, these are interpreted by the fuzzy relations approximate equality with tolerance $e_{(d_{X})}$, approximate incidence with tolerance $i_{(d_{X})}$, respectively. A truth-functional fuzzy logical system provides fuzzy interpretations of connectives and quantifiers, and since Łukasiewicz fuzzy predicate logic (L$\forall$) is truthfunctional, it can be used to evaluate the truthlikeness degree of the classical axioms (E1)–(E3) and (Pr1)–(Pr2) from the truthlikeness degrees of the involved atoms. Attaching the derived truthlikeness degrees to the classical axioms results in a fuzzy set of axioms, and the truthlikeness degree of an axiom indicates its degree of membership to granular geometry. Wilke [73, 74] shows that in the intended interpretation of ATG and with the definition of truthlikeness given in the foregoing subsection, the axioms(E1), (E2) and (Pr1) have a truthlikeness degree of 1, while the transitivity axiom (E3) and the “uniqueness axiom” (Pr2) have a truthlikeness of zero, i.e., they are useless for geometric reasoning with position granules. The subsequent paragraph lists the resulting fuzzy set of axioms in $FL_{ev}$(Ł$\forall$) that includes the “useless” fuzzy axioms, and the remainder of the subsection discusses fuzzy extensions of the two axioms that yield a positive truthlikeness degree.

Step 4b: Fuzzification of the Classical Axioms

Attaching the derived truthlikeness degrees to the axioms (E1), (E2), (E3), (Pr1) and (Pr2) yields the following fuzzy set of axioms in $FL_{ev}$(Ł$\forall$):

(E1) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x.\left[ E(x,x)\right] }$; $1\;\Bigr )$,

(E2) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x,y.\left[ E(x,y)\;\rightarrow \; E(y,x)\right] }$; $1\;\Bigr )$,

(E3) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x,y,z.\left[ E(x,y)\; \& \; E(y,z)\;\rightarrow \; E(x,z)\right] }$; $0\;\Bigr )$,

and

(Pr1) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall p,q.\exists l.\left[ \lnot E(p,q)\;\rightarrow \; I(p,l)\; \& \; I(q,l)\right] }$; $1\;\Bigr )$,

(Pr2) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall p,q,l,m.\Bigl [\lnot E(p,q)\; \& \; I(p,l)\; \& \; I(q,l)\; \& \;}$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathtt {I(p,m)\; \& \; I(q,m)\;\rightarrow \; E(l,m)\Bigr ]}$; $0\;\Bigr )$,

respectively. Here, we write a fuzzy axiom in the form $(\varphi ;a)$, where $\varphi$ is a classical axiom and $a$ is its truthlikeness degree [41]. Since the classical axioms (E3) and (Pr2) have a truthlikeness degree of zero, the corresponding evaluated axioms $(E3)_{ev}$ and $(Pr2)_{ev}$ are useless for geometric reasoning in granular geometry. The following subsection introduces fuzzy extensions of (E3) and (Pr2) that have a positive truthlikeness degree.

Step 4c: A Consistent Extension of the Fuzzified Axioms

Following Gerla [20], Wilke [73, 74] shows that a truthlikeness degree of 1 can be achieved for “weak transitivity”. Weak transitivity (E3x) extends the classical transitivity axiom (E3) with a unary exactness predicate $\mathtt {X}$ that is an inverse measure of the size of position granules:

$\mathsf {(E3x)}\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x,y,z.\left[ E(x,y)\; \& \; X(y)\; \& \; E(y,z)\;\rightarrow \; E(x,z)\right] }$; $1\;\Bigr )$.

The weak transitivity axiom is a fuzzy extension of the classical transitivity axiom, i.e., in particular, it coincides with classical transitivity when only exact points and lines are involved. In this case, $\mathtt {X(y)=1}$ for arbitrary $\mathtt {y}$, and $\mathsf {(E3x)}\equiv \mathsf {(E3)}$.

Wilke [73] also shows that a truthlikeness degree of 1 can be achieved for a “weak uniqueness axiom”: We mentioned in Sect. 6.2.1 that the connection of two approximate points $P,Q$ by an approximate line $L$ is not unique, and that, intuitively, the “degree of uniqueness” depends on the size and distance of the involved granular points $P,Q$, cf. Figs. 6.4 and 6.3. The weak uniqueness axiom (Pr2x) extends the classical uniqueness axiom (Pr2) with a binary directionality predicate $\mathtt {Dir(p,q)}$ that captures the influence of the size and extensive distance on of the involved approximate points $\mathtt {p}$ and $\mathtt {q}$ on the uniqueness of $L$, and can be seen as a measure of the directionality of the approximate connection:

(Pr2x) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall p,q,l,m.\Bigl [\lnot E(p,q)\; \& \; Dir(p,q)\; \& \; I(p,l)\; \& \; I(q,l)\; \& \;}$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathtt {I(p,m)\; \& \; I(q,m)\;\rightarrow \; E(l,m)\Bigr ]}$; $1\;\Bigr )$,

The weak uniqueness axiom is a fuzzy extension of the classical uniqueness axiom, i.e., in particular, it coincides with the classical uniqueness axiom when only exact points and lines are involved. In this case, two distinct points always define an exact direction that is given by the unique connecting line. Here, $\mathtt {Dir(p,q)=1}$ for arbitrary distinct points $\mathtt {p,q}$, and $\mathsf {(Pr2x)}\equiv \mathsf {(Pr2)}$.

In the remaining paragraphs of this section, we give definitions of the exactness and directionality predicates, and briefly show how they can be derived from the intended interpretation introduced in Sect. 6.4.2.

The Exactness Predicate

We first define a Boolean version of the exactness predicate as part of the intended interpretation, and then discuss its fuzzy extension to define a corresponding truthlikeness measure. The Boolean version of the exactness predicate $\mathtt {X}$ is intended to single out the exact classical points and lines from the set of approximate points and lines.

Definition 7

The intended interpretation of exactness of PGs of the type approximate point in a domain $X$ is the set

$$\begin{aligned} x_{\mathbb {B}}:\mathcal {P}_{X}\rightarrow \{0,1\},\quad x_{\mathbb {B}}(P)=\left( \left| P\right| =1\right) . \end{aligned}$$

(6.14)

Here, $\left| P\right|$ denotes the cardinality of the set $P$. If $x_{\mathbb {B}}(P)=1$, $P$ is called exact. Similarly, the intended interpretation of exactness of PGs of the type approximate line in a domain $X$ is the set

$$\begin{aligned} x_{\mathbb {B}}:\mathcal {L}_{X}\rightarrow \{0,1\},\quad x_{\mathbb {B}}(L)=\left( \left| L'\right| =1\right) . \end{aligned}$$

(6.15)

If $x_{\mathbb {B}}(L)=1$, $L$ is called exact.

The exactness predicate $x_{\mathbb {B}}$ can be seen as an inverse bivalent size measure, $x_{\mathbb {B}}=1-s_{\mathbb {B}}$, where the size

$$\begin{aligned} s_{\mathbb {B}}(P):=\max \left\{ \varDelta (p,q)|p,q\in P\right\} \end{aligned}$$

(6.16)

of an approximate point $P$ is measured based on the discrete metric $\varDelta$,

$$\begin{aligned} \varDelta (a,b)={\left\{ \begin{array}{ll} 1 &{} \text { if }a\ne b,\\ 0 &{} \text { if }a=b. \end{array}\right. } \end{aligned}$$

(6.17)

To measure the truthlikeness of the exactness of a granular point or line, we quantify the similarity of the statement “$X(P)=1$” (i.e., the statement “$P$ is exact”) to the truth. Points (or lines) that have non-zero positional tolerance are not exact. In this case $x_{\mathbb {B}}(P)=0$ holds. Since we represent positional tolerance by position granules, the size (diameter) of a position granule $P$ can be used to quantify “how much” positional tolerance is involved: It measures the error made when assuming that all points $p\in P$ are equal. In terms of the exactness relation $x_{\mathbb {B}}$, the size of $P$ measures “how wrong” it is to assume that the statement $x_{\mathbb {B}}(P)=1$ holds.

Definition 8

For an approximate point $P\in \mathcal {P}_{X}$, and an approximate line $L\in \mathcal {L}_{X}$, define the size of $P$ and $L$, respectively, by

$$\begin{aligned} s_{(d_{X})}(P):=&\sup \left\{ d_{X}(\bar{p},\bar{q})|\bar{p},\bar{q}\in P\right\} \quad \text { and }\end{aligned}$$

(6.18)

$$\begin{aligned} s_{(d_{Y})}(L):=&\sup \left\{ d_{Y}(\bar{l}',\bar{m}')|\bar{l}',\bar{m}'\in L'\right\} . \end{aligned}$$

(6.19)

The size measures $s_{(d_{X})}(P)$ and $s_{(d_{Y})}(L)$ quantify the semantic distance of the assumptions

$$\begin{aligned} \left[ d_{X}(\bar{p},\bar{q})=0\quad \forall \bar{p},\bar{q}\in P\right] ,\quad \text {and}\quad \left[ d_{Y}(\bar{l}',\bar{m}')=0\quad \forall \bar{l}',\bar{m}'\in L'\right] \end{aligned}$$

(6.20)

from the truth, respectively. Conversely, the truthlikeness degree of $x_{\mathbb {B}}(P)$ is intended to measure the similarity of the statement $x_{\mathbb {B}}(P)=1$ to the truth. We define the truthlikeness degree $x_{(d_{X})}(P)$ of $x_{\mathbb {B}}(P)=1$ as an inverse size measure:

Definition 9

The fuzzy interpretations of the exactness predicate in ATG are given by the fuzzy sets

$$\begin{aligned} x_{(d_{X})}:\mathcal {P}_{X}\rightarrow [0,1],\quad&x_{(d_{X})}(P):=1-s_{(d_{X})}(P),\;\text { and}\end{aligned}$$

(6.21)

$$\begin{aligned} x_{(d_{Y})}:\mathcal {L}_{Y}\rightarrow [0,1],\quad&x_{(d_{Y})}(L):=1-s_{(d_{Y})}(L), \end{aligned}$$

(6.22)

respectively. Here, $d_{X}$ and $d_{Y}$ are a normalized metrics in $X$ and $Y$. $P$ and $L$ are called approximately exact to the degree $x_{(d_{X})}(P)$ and $x_{(d_{Y})}(L)$, respectively.

Approximate exactness $x_{(d_{X})}$ is a fuzzy extension of exactness $x_{\mathbb {B}}$: The fuzzy set $x_{(d_{X})}:\mathcal {P}_{X}\rightarrow [0,1]$ is an extension of the classical set $x_{\mathbb {B}}:\mathcal {P}_{X}\rightarrow \{0,1\}$, because both coincide at the value $1$:

$$\begin{aligned} x_{(d_{X})}(P)=1\;\Leftrightarrow \; s_{(d_{X})}(P)=0\;\Leftrightarrow \;\left| P\right| =1\;\Leftrightarrow \; x_{\mathbb {B}}(P)=1. \end{aligned}$$

(6.23)

This holds analogously for the second object sort, approximate lines: The fuzzy set $x_{(d_{Y})}:\mathcal {L}_{X}\rightarrow [0,1]$ is an extension of the classical set $x_{\mathbb {B}}:\mathcal {L}_{X}\rightarrow \{0,1\}$. because $x_{(d_{Y})}(L)=1\;\Leftrightarrow \; x_{\mathbb {B}}(L)=1$ holds for all $L\in \mathcal {L}_{X}$.

The Directionality Predicate

In classical projective geometry, the join of two distinct points is the unique line that is incident with them. Inspired by the classical terminology, we give the following definition of an approximate join:

Definition 10

Let $P,Q\in \mathcal {P}_{X}$ be two approximate points in $(X,d_{X})$. An approximate line $L\in \mathcal {L}_{X}$ that is approximately incident with both, $P$ and $Q$, is called an approximate join of $P$ and $Q$.

In the intended interpretation, we may define a pencil of approximate joins as follows:

Definition 11

The pencil of approximate lines through two approximate points $P,Q\in \mathcal {P}_{X}$ is the set of approximate joins of $P$ and $Q$,

$$\begin{aligned} P\star Q:=\left\{ L\in \mathcal {L}_{X}|P,Q\subset L\right\} . \end{aligned}$$

(6.24)

For short, we call $P\star Q$ the pencil of approximate joins of $P$ and $Q$. We call

$$\begin{aligned} S_{(d_{X'})}(P\star Q):=s_{(d_{(d_{X'})})}(P\star Q)=\sup \left\{ d_{(d_{X'})}(L,M)|L,M\in P\star Q\right\} \;\in [0,1] \end{aligned}$$

(6.25)

the extensive size of $\left( P\star Q\right) \subseteq \mathcal {L}_{X}$, and we call

$$\begin{aligned} X_{(d_{X})}(P\star Q):=1-S_{(d_{X})}(P\star Q)\;\in [0,1] \end{aligned}$$

(6.26)

the extensive approximate exactness degree of $P\star Q$.

We mentioned in Sect. 6.2.1 that the connection of two approximate points $P,Q$ by an approximate line $L$ is not unique, and that, intuitively, the “degree of uniqueness” depends on the size and distance of the involved granular points $P,Q$, cf. Figs. 6.4 and 6.3. This intuition is formalized by the uniqueness axiom

$\mathsf {(Pr2)} \, \mathtt {\forall p,q,l,m.\left[ \lnot E(p,q)\, \& \, I(p,l)\, \& \, I(q,l)\, \& \, I(p,m)\, \& \, I(q,m)\rightarrow E(l,m)\right] .}$

This can be seen as follows: According to the Granular Geometry Framework, we determine the truthlikeness degree of (Pr2) by determining its value when interpreted in $FL_{ev}$(Ł$\forall$). Following Gerla, Wilke [73] shows that the interpretation of $\mathsf {(Pr2)}$ in $FL_{ev}$(Ł$\forall$) is equivalent with

$$\begin{aligned} \underset{P,Q\in \mathcal {P}_{X}}{\inf }\Bigl [d_{(d_{X})}(P,Q)\Rightarrow X_{(d_{x})}(P\star Q)\Bigr ], \end{aligned}$$

(6.27)

where

$$\begin{aligned} \Bigl [d_{(d_{X})}(P,Q)\Rightarrow X_{(d_{x})}(P\star Q)\Bigr ] \end{aligned}$$

(6.28)

is the extension of the formula

$$\begin{aligned}&\mathtt {\forall l,m.\Bigl [\lnot E(p,q)\wedge I(p,l)\wedge I(q,l)\wedge }\end{aligned}$$

(6.29)

$$\begin{aligned}&\qquad \qquad \qquad \qquad \qquad \mathtt {I(p,m)\wedge I(q,m)\;\rightarrow \; E(l,m)\Bigr ]}. \end{aligned}$$

(6.30)

Equation (6.28) measures the truthlikeness of the assumption “Whenever the extensive distance of $P$ and $Q$ is large, the extensive exactness of $P\star Q$ is also large”. Loosely formulated we may say that it measures the truthlikeness of the assumption “The larger the distance, the closer is the approximate join to being unique”. We call (6.28) the directionality degree of $P$ and $Q$, and define the corresponding directionality measure and directionality predicate as follows:

Definition 12

For $e_{(d_{X})}:\mathcal {P}_{X}\times \mathcal {P}_{X}\rightarrow [0,1]$ and $i_{:\varDelta }\mathcal {P}_{X}\times \mathcal {L}_{X}\rightarrow \{0,1\}$, the directionality measure induced by $e_{(d_{X})}$ and $i_{\varDelta }$ is the fuzzy relation $dir:\mathcal {P}_{X}\times \mathcal {P}_{X}\rightarrow [0,1]$,

$$\begin{aligned} dir(P,Q):=\Bigl [d_{(d_{X})}(P,Q)\Rightarrow X_{(d_{X})}(P\star Q)\Bigr ]\quad \in [0,1] \end{aligned}$$

(6.31)

We call $dir(P,Q)$ the directionality degree of the pair $P,Q\in \mathcal {P}_{X}$ w.r.t. $e_{(d_{X})},i_{\varDelta }$. The directionality measure $dir$ is the extension of the directionality predicate

$$\begin{aligned}&\mathtt {Dir(p,q)\;:\equiv \;\forall l,m.\Bigl [\lnot E(p,q)\wedge I(p,l)\wedge I(q,l)\wedge }\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathtt {I(p,m)\wedge I(q,m)\;\rightarrow \; E(l,m)\Bigr ]}. \end{aligned}$$

(6.32)

The Extended Axioms

Wilke [73, 74] shows that the following extensions (E3x) and (Pr2x) of the transitivity and uniqueness axioms have a truthlikeness degree of 1. The resulting set of axioms in $F$ Ł $_{ev}$ is the following crisp axiom set:

(E1) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x.\left[ E(x,x)\right] }$; $1\;\Bigr )$,

(E2) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x,y.\left[ E(x,y)\;\rightarrow \; E(y,x)\right] }$; $1\;\Bigr )$,

(E3x) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall x,y,z.\left[ E(x,y)\; \& \; X(y)\; \& \; E(y,z)\;\rightarrow \; E(x,z)\right] }$; $1\;\Bigr )$,

and

(Pr1) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall p,q.\exists l.\left[ \lnot E(p,q)\;\rightarrow \; I(p,l)\; \& \; I(q,l)\right] }$; $1\;\Bigr )$,

(Pr2x) $\mathsf {_{ev}}$ $\Bigl (\mathtt {\forall p,q,l,m.\Bigl [\lnot E(p,q)\; \& \; Dir(p,q)\; \& \; I(p,l)\; \& \; I(q,l)\; \& \;}$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathtt {I(p,m)\; \& \; I(q,m)\;\rightarrow \; E(l,m)\Bigr ]}$; $1\;\Bigr )$,

Consequently, the above axiom set fulfills all requirements of the Granular Geometry Framework.

6.5 Granular Geometries and Zadeh’s Restriction-Centered Theory of Truth and Meaning

In 2011, L. Zadeh [82] introduced the concept of a Z-number as a pair $(A,B)$, where “the first component, $A$, is a restriction (constraint) on the values which a real-valued uncertain variable, $\mathfrak {X}$, is allowed to take. The second component, $B$, is a measure of reliability (certainty) of the first component.” [82, p. 2923]. A position granule in the sense of the Granular Geometry Framework can be seen as a precisiation of a positional restriction in the sense of Zadeh’s restriction-centered theory of truth and meaning (RCT) [81, 83]: Here, Zadeh defines a restriction (or generalized constraint) in its canonical form by $R(X):\; X\ is_{r}\; A$, where X is the restricted variable and A is the restricting relation, both typically expressed in natural language. $r$ specifies the way in which $A$ restricts $X$ (the modality of $R$). Modalities are, for example, $r=blank$ for possibilistic restriction, or $r=p$ for probabilistic restrictions. For $r=blank$, $R(X)$ can be written as $Poss(X=x)=\mu _{A}(x)$.

In Approximate Tolerance Geometry, an approximate point $P$ is a possibilistic restriction of the position of an exact point $p$. It can be written as $R(X):\; X\, \textit{is}\; P$, or, more specifically, $Poss(X=p)=\mu _{P}(p)$, where $\mu _{P}$ is given by the possibility distribution (6.1). To compute the degree to which $X$ satisfies $R$, it is necessary provide a precisiation. In ATG, the restriction is unprecisiated, if $P$ is given in natural language, e.g. $P=$ “Piccadilly Circus”. It is precisiated, if it is given as a subset of a metric space.

The intended interpretations of many of the fuzzy geometric statements $(\varphi ;a)$ in ATG are Z-numbers $(\phi ,a)$, where $\phi$ is the intended interpretation of the classical formula $\varphi$. To see that, observe that a position granule $P\in \mathcal {P}_{X}$ is a restriction of a (possibilistic) uncertain variable $p\in X$. The intended interpretation $\phi$ of a statement $\varphi$ that includes $p$ is in many cases also a restriction of the corresponding domain. As an example consider the statement $\varphi \equiv (\mathtt {p=q})$. Its intended interpretation $\phi$ in ATG is $e_{\mathbb {B}}(P,Q)=1$ (“$P$ and $Q$ are possibly equal”). Since $P$ and $Q$ are restrictions of assumed “true” points $p,q\in X$, respectively, the relation $e_{\mathbb {B}}(P,Q)=1$ can be seen as a restriction of the uncertain variable $(p,q)\in X\times X$ in the sense of RCT. Here, $p$ and $q$ are the assumed “true” exact points associated with the position granules $P$ and $Q$, respectively. Deviating from Zadeh’s definition of a Z-number, $(p,q)$ is not real-valued, and $\phi$ is not a fuzzy number, but, more generally, a fuzzy relation in $X\times X$.¹² The second component, $a$, is the truthlikeness degree associated with $\varphi$. It is a fuzzy number that measures the reliability (certainty) of the information provided by $\phi$.

Zadeh [82] also proposes a generic schema for the computation with Z-numbers. Zadeh’s schema applies on a semantic level, operating on the interpretations of statements and is based on the extension principle. In ATG, the use of fuzzy logic with evaluated syntax allows for the “trick” of evaluating the syntax: Calculations can be done on the syntactic level of logical propositions, while the evaluation component is derived from the “intended” possibilistic interpretation. It thereby allows for metamathematical considerations such as the possibility to guarantee soundness of a theory of granular geometry.

6.6 Conclusions and Outlook

6.6.1 Summary

The introduction of the Granular Geometry Framework is motivated by the intention to provide a geometric calculus for granular geometry that is sound. I.e., geometric reasoning with position granules should be reliable, even if the introduced uncertainty is very big. For a given modality of uncertainty and a given classical axiomatization of geometry, the framework provides a guideline for fuzzifying the classical axioms so that the result is a sound logical theory of granular geometry. Soundness is achieved by augmenting every classical geometric axiom with a degree of reliability (truthlikeness), resulting in a fuzzy set of classical axioms. The reliability degree is derived from the intended interpretation (intended semantic) of granular geometry and incorporated in the logical theory as part of the syntax as a fuzzy membership degree. As a result, any classical geometric theory that is fuzzified based on the Granular Geometry Framework is sound by design. The underlying formal tool for representing and propagating reliability as an intrinsic part of the logical theory is Łukasiewicz Fuzzy Logic with Evaluated Syntax $FL_{ev}$(Ł$\forall$), which is used as a similarity logic.

Approximate Tolerance Geometry is a possibilistic instantiation of the Granular Geometry Framework. We introduced its intended interpretation, derived corresponding truthlikeness (i.e., reliability) measures, and applied them to two fundamental geometric axioms groups, namely the equality axioms and Euclid’s First Postulate. Research [73, 74] shows that some of the fuzzified axioms have a reliability degree of zero, and that a reliable fuzzy extension exists that is consistent with the classical axioms and that even has a reliability degree of 1.

6.6.2 Limitations

In her thesis, Wilke [73] elaborates the interpretation of Approximate Tolerance Geometry introduced in Sect. 6.4.2 for the specific case of the real projective plane $X=\mathbb {P}^{2}$. Her research shows that, in the projective interpretation, the extended uniqueness axiom is always trivially fulfilled, which effectively renders it useless in practical application. She shows that the approximate join $P\star Q$ of two approximate points always has a directionality degree of zero, meaning that $P$ and $Q$, in the worst case, do not constrain the direction of a connecting approximate line at all, cf. Fig. 6.11. The reason for this is that approximate lines are allowed to be “arbitrarily broad”.

With the benefit of the hindsight, this result is not surprising: A theory of granularity is concerned with relating and propagating size restrictionsand if no size restrictions are imposed on some of the objects, results can be arbitrary. In the proposed fuzzy extension of the equality axiom and Euclid’s First Postulate, we introduced size restrictions for some of the involved objects, but not for all of them: In the case of the transitivity axiom (E3x) $\mathsf {_{ev}}$, we restricted (parametrized) the size of the middle element $y$ using the exactness predicate, while the sizes of the other two elements, $x$ and $z$, are arbitrary (cf. Sect. 6.4.4). Here, the sizes of $x,z$ do not impact the truthlikeness degree, which is why it is not necessary to restrict them. This is different in the case of the “uniqueness axiom” (Pr2x) $\mathsf {_{ev}}$: Here, we did not relate the sizes of the involved approximate points and lines to each other, resulting in an arbitrary statement. The following subsection addresses—amongst other topics—possible approaches to avoinding the problem by including further size restrictions.

Fig. 6.11

$P$ and $Q$ behave like one single point w.r.t. $L$. [76]

6.6.3 Further Work

Introducing Size Restrictions

To address the problem of missing size restrictions in ATG, the fuzzified “uniqueness axiom” need to be further extended by also adding exacness predicates for the lines. Wilke [73] also mentiones the presumably simpler solution of introducing global size restriction parameters, i.e., upper and lower bounds on the maximal allowable size of approximate points and lines that can be chosen according to the specific practical application scenario. Its incorporation in ATG, and in the Granular Geometry Framework in general, is subject to future work.

It is expected that the necessity of introducing size restrictions not only applies to ATG, but to granular geometries in general. A test should be added to the Granular Geometry Framework that checks, if an axiom is trivially fulfilled.

Elaborating ATG

In her PhD research, Wilke [73] applied the Granular Geometry Framework to the equality axioms and to Euclid’s First Postulate. To define a full-fledged Approximate Tolerance Geometry of the projective plane, the remaining axioms $\mathsf {(Pr3)}$–$\mathsf {(Pr5)}$ need to be fuzzified as well.

She also simplified the definition of the truthlikeness measure for approximate incidence, cf. Definition 6. The goal was to facilitate the formalization task: Instead of employing the overlap relation, she used the binary subset relation to define the truthlikeness degree of incidence of an approximate point with an approximate line. The formalizations devised in her work should be extended to the overlap relation. It can be expected that this step will add considerable complexity to the formalism.

In order to be able to use approximate tolerance geometry for geometric constructions, e.g. in a geographic information system, it is a precondition that approximate versions of the geometric operators (constructors) join and meet are available. These are not yet defined in Approximate Tolerance Geometry. The reason for that is that the approximate join is not unique in general. As a consequence, an approximate version of the classical join operator is not definable. Instead, only the unique pencil of approximate joins can be assigned to a pair of approximate points. This seems not to be useful in practical application. Wilke suggests to instead use a choice function. Such a function must be defined in the interpretation domain.

Another interesting direction of future work is the elaboration of fuzzy projective notions in ATG, such as approximate direction, approximate angle, or approximate duality. Wilke [73] discusses first considerations in this directions in her thesis.

Finally, the intended interpretation of ATG may be further extended: While the proposed definition of approximate points and lines interprets them by crisp regions, fuzzy regions may be of interest as well. Here as well, it may be expected that considerable complexity will be added to the formalism with this step.

Including Other Modalities of Uncertainty

The Granular Geometry Framework allows for choosing the modality of uncertainty of position granules. In ATG, the intended interpretation of position granules is based on the assumption that location constraints describe possibilistic uncertainty. The Granular Geometry Framework may be applied to other kinds of imperfections in positional information. For example, verity distributions can also be modeled by location constraints. Their interpretation is not possibilistic, but veristic, cf. [81]: Instead of interpreting a location constraint as a set of possible positions of an exact point, it is interpreted as a set of points that are occupied at the same time. Examples are parcels or the footprints of buildings, cf. [72].

Considering Other Gemometries

The Granular Geometry Framework also allows for choosing the classical geometry and its axiomatization. In ATG, we referred to a standard axiomatization of the projective plane. This is sensible for applications in GIS, but for many other applications, e.g., Euclidean geometry is preferable, and the elaboration of a granular Euclidean geometry is desirable.