Keywords

1 Introduction

In contrast to the rigid manipulators, light weight manipulators offer advantages such as higher speed, better energy efficiency, improved mobility, and higher payload-to-arm weight ratio. However, at high operational speeds, inertial forces of moving components become quite large, leading to considerable deformation in the light links, and generating unwanted vibration phenomena. Hence, elastic vibrations of light weight links must be taken into account in the modelling, design, and control of the robot manipulators. In the past decades, significant progresses have been made into the dynamic modeling of manipulators with flexible components [1]. Different discretization techniques, such as the finite element method (FEM) [2, 3], the assumed mode method (AMM) [4, 5], and the lumped parameter method (LPM) [6, 7], have been reported extensively for modeling the dynamics of flexible robot manipulators. However, the matrix size of global dynamic model of a robot manipulator increases with the number of the Degree of Freedom, and therefore heavy computation of dynamic modelling is still a big concern in terms of real-time control.

Alternatively, the transfer matrix method can be used to model linear and continuous parameter systems without discretization [8, 9]. Using the integration procedure, the discrete-time transfer matrix method (DT-TMM) was presented to perform the dynamic analysis of large systems that consists of large subsystems, each of which is a simple dynamic element. The DT-TMM was further developed to model multi-body system dynamics using linearization and integral schemes. With the TD-MM, the local dynamics is transmitted and concatenated through the transfer matrix of each subsystem. As a result, the matrix size of the dynamic equations does not increase with the DOF of multi-body systems as the traditional procedure of establishing the global dynamic equations are avoided. Therefore, the computation efficiency can be significantly improved. In this work, the DT-transfer matrix method is extended to the dynamic modeling of lightweight robot manipulators with the consideration of link flexibility. The procedure of DT-TMM presented in this work for modeling the dynamics of flexible manipulators is: (1) a robot manipulator is decomposed into subsystems or elements: links, motors, and connections between a link and motors; (2) the dynamics model of each element or subsystem is established; (3)the state vector of the input board and the output board of the element is defined, the dynamics of each element is linearized in terms of the defined state vector of the inboard and the outboard, and the transfer matrix is formulated to transform the state vector of the element from the inboard to the outboard; (4) the boundary conditions between the links is applied, and the transformation of the state vector is generated from one link to the neighboring links so that the dynamics of links is connected with motors and fixed mounting; (5) the transformation of the dynamics of the robot manipulator are conducted from the base to the last link, and hence the global transfer matrix is obtained base on the transformation of the input state vector at the base and the output state vector at the tip of the manipulator. The global dynamics is avoided using the proposed method. The matrix size of the robot manipulator dynamics does not increase with the DOF of the robot manipulator, and hence significantly reduce the computation cost.

2 State Vectors and Transformation

The state vector is a column vector that represents the internal forces (force \( q_{x} ,q_{y} ,q_{z} , \) and moment \( M_{x} ,M_{y} ,M_{z} \)) and displacement (rigid motion \( x,y,z,\theta_{x} ,\theta_{y} ,\theta_{z} \) and deformation \( w^{1} ,w^{2} , \ldots ,w^{n} \)) at a particular location within a system. In this work, the acceleration-based integral scheme is selected as

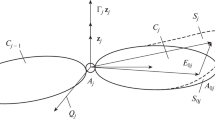
$$ {\mathbf{z}} = [\overbrace {{ \ddot{x} , \ddot{y} , \ddot{z} }}^{\text{acceleration}},\underbrace {{\ddot{\theta }_{x} ,\ddot{\theta }_{y} ,\ddot{\theta }_{z} }}_{{{\text{angular}}\,{\text{acceleration}}}},M_{x} ,M_{y} ,M_{z} ,q_{x} ,q_{y} ,q_{z} ,\overbrace {{ {\ddot{w}^{1} } , {\ddot{w}^{2} } , \ldots , {\ddot{w}^{n} } }}^{{{\text{modal}}\,{\text{acceleration}}}},1]^{T} $$
(1)

The sign convention of the elements in the state vector related to the reference coordinate system is illustrated in Fig. 1. The position coordinates and orientation angles are defined as positive when they are in the positive directions of the coordinate axes. The inboard forces and outboard moments applied on the elements are positive if they are in the positive directions of the coordinate axes, and the outboard forces and inboard moments acted on the elements are negative if they are in the positive directions of the coordinate axes.

Fig. 1
figure 1

State vectors and coordinate system

Full size image

In the DT-TMM, a transfer matrix is formulated to transform the state vector form one end of the component to the other end of the component as

$$ \mathop {{\mathbf{z}}^{O} }\limits_{[n \times 1]} = \mathop {\mathbf{U}}\limits_{[n \times m]} \mathop {{\mathbf{z}}^{I} }\limits_{[m \times 1]} $$
(2)

For a robot manipulator system, the order of the system transfer matrix \( {\mathbf{U}}_{sys} \) depends on the size of the boundary state vectors of the system.

$$ \mathop {{\mathbf{z}}^{O} }\limits_{[n \times 1]} = {\mathbf{U}}_{j} {\mathbf{U}}_{j - 1} \cdots {\mathbf{U}}_{2} {\mathbf{U}}_{1} \mathop {{\mathbf{z}}^{I} }\limits_{[m \times 1]} = \mathop {{\mathbf{U}}_{sys} }\limits_{[n \times m]} \mathop {{\mathbf{z}}^{I} }\limits_{[m \times 1]} $$
(3)

In (3), j is the number of elements divided from the robot manipulator system. It is clear that the order of the system matrix does not increase when the degrees of freedom of the manipulator increase, which results in significant reduction of the computational time and storage requirements. Each component of a robot manipulator has a unique transfer matrix based on the physical behavior it models. The transfer matrices of different elements are established to propagate the state vectors of flexible robot manipulator components in Sect. 4.

3 Linearization and Integration Schemes

The nonlinearity terms may result from 1st and 2nd second order time derivatives, trigonometric terms, multiplications and couplings of variables related to the state vectors. This brings the challenges, if not possible, to formulate the linear transformation between the outboard state vector and the inboard state vector for a subsystem, as shown in Eq. (3). Additionally if no linearization is performed, the transfer matrix may contain some terms related to the current values of the stave vector variables. This would be incompatible with the TMM formulation, as transfer matrices are only allowed to have state vector variables related to the previous time steps. Mathematically, linearization is carried using the method of a Taylor series expansion. The linearization is not detailed in this work due to the limited space. The dynamic equations of the components usually contain terms of the displacement (linear and angular) variables, velocity (linear and angular), and accelerations (linear and angular). To transfer the state vectors with transfer matrices as in Eq. (3), the displacement and velocity variables need to be described as the functions of the variables at the previous time step when the acceleration-based integration scheme. This process can be conducted through an implicit integration method. The principle of an implicit integration is to find a solution by solving an equation consisting of both the current step variables and previous step variables. Assuming i−1 to be the previous time step, and i the current time step, the general form of an implicit scheme can be written as \( \xi = \xi^{(i - 1)} + f(\xi ,t) \), where \( \xi \) and \( \xi^{(i - 1)} \) are the current and previous time stable variables respectively, and f is a function of the current time step variables. Using Newmark-\( \beta \) integration method [10], this implicit equation can be solved and rewritten in terms of TMM parameters as

$$ \xi = \beta \varDelta t^{2} \ddot{\xi } + \xi^{(i - 1)} + \dot{\xi }^{(i - 1)} \varDelta t + \left( {\frac{1}{2} - \beta } \right)\ddot{\xi }^{(i - 1)} \varDelta t^{2} $$
(4)
$$ \dot{\xi } = \gamma \varDelta t\ddot{\xi } + \dot{\xi }^{(i - 1)} + \left( {1 - \gamma } \right)\ddot{\xi }^{(i - 1)} \varDelta t $$
(5)

where the integration parameters \( \gamma \) and \( \beta \) are weighting coefficient in the Newmark method, and the two weighting parameters \( \gamma \) and \( \beta \) play a key role in the stability and convergence of analyses. It was proved that \( \gamma = 0.5 \), or else spurious damping will be added to the system. In general, the Newmark scheme has shown to be unconditionally stable with the following parameters \( 2\beta \ge \gamma \ge \frac{1}{2} \).

4 Transfer Matrix of Components

To establish the system transfer matrix of a robot manipulator, the robot manipulator system is broken down to motors and links. A local transfer matrix is then formulated for each link, motor, and connection between a motor and a link.

4.1 Dynamics and Transfer Matrix of a Flexible Link Element

The lightweight links are assumed as a slender beam, and the state vectors and coordinate system are defined as shown in Fig. 1. The linear transformation is formulated based on the kinematics, the force and moment balance of an Euler-Bernoulli beam. The elastic deformation \( u \) can then be described by the spatial mode shape function \( {\mathbf{N}}(x) \) and the time-dependent modal coordinates \( {\mathbf{w}}(t) \) as \( u(x,t) = {\mathbf{N}}(x){\mathbf{w}}(t) \). In this work, only the first three vibration modes are included to calculated the elastic deformation. The kinematic relation from inboard to outboard end is established, and then is differentiated twice with respect to time as

$$ \left[ {\begin{array}{*{20}c} { \ddot{x} } \\ { \ddot{y} } \\ {\ddot{\theta }} \\ \end{array} } \right]^{O} = \left[ {\begin{array}{*{20}c} { {\ddot{x}^{I} } - \ddot{\theta }\sin \theta L - \dot{\theta }^{2} \cos \theta L - \ddot{u} \sin \theta - 2\dot{u}\dot{\theta }\cos \theta - u\ddot{\theta }\cos \theta_{z} + u\dot{\theta }_{z}^{2} \sin \theta_{z} } \\ { {\ddot{y}^{I} } + \ddot{\theta }\cos \theta L - \dot{\theta }^{2} \sin \theta L + \ddot{u} \cos \theta - 2\dot{u}\dot{\theta }\sin \theta - u\ddot{\theta }_{z} \sin \theta_{z} - u\dot{\theta }^{2} \cos \theta } \\ {\ddot{\theta }^{I} } \\ \end{array} } \right] $$
(6)

The force and moment balance equations of the flexible beam are conducted based on the Newton-Euler equations by including the impact of inertial forces and deformation (the force and moment equations are not detailed due to the limited space). The dynamic equations are then linearized, reorganized, and combined with Eq. (6) to generate the transfer formation equation of a flexible link as

$$ \begin{aligned} {\mathbf{z}}^{O} & = {\mathbf{Uz}}^{I} \\ & = \left[ {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & {u_{1,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{1,7} } \hfill & {u_{1,8} } \hfill & {u_{1,9} } \hfill & {u_{1,10} } \hfill \\ 0 \hfill & 1 \hfill & {u_{2,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{2,7} } \hfill & {u_{2,8} } \hfill & {u_{2,9} } \hfill & {u_{2,10} } \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {u_{4,1} } \hfill & {u_{4,2} } \hfill & {u_{4,3} } \hfill & 1 \hfill & 0 \hfill & 0 \hfill & {u_{4,7} } \hfill & {u_{4,8} } \hfill & {u_{4,9} } \hfill & {u_{4,10} } \hfill \\ {u_{5,1} } \hfill & 0 \hfill & {u_{5,3} } \hfill & 0 \hfill & 1 \hfill & 0 \hfill & {u_{5,7} } \hfill & {u_{5,8} } \hfill & {u_{5,9} } \hfill & {u_{5,10} } \hfill \\ 0 \hfill & {u_{6,2} } \hfill & {u_{6,3} } \hfill & 0 \hfill & 0 \hfill & 1 \hfill & {u_{6,7} } \hfill & {u_{6,8} } \hfill & {u_{6,9} } \hfill & {u_{6,10} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x} } \\ {\ddot{y} } \\ {\ddot{\theta }} \\ {M_{z} } \\ {q_{x} } \\ {q_{y} } \\ {{\ddot{w}^{1} } } \\ { {\ddot{w}^{2} } } \\ { {\ddot{w}^{3} } } \\ 1 \\ \end{array} } \right]^{I} \\ \end{aligned} $$
(7)

The components of the transfer matrix are listed at the Ref. [12].

4.2 Dynamics and Transfer Matrix of a Rotational Motor Joint

Physically, the motor (driven joint) is used to generate the rotation between the mounted inboard and outboard links. The angular acceleration related to the two attached bodies is expressed as \( \ddot{\theta }_{(\kappa + 1)}^{I} = \ddot{\theta }_{(\kappa - 1)}^{I} + \ddot{\theta }^{D} \) where \( \ddot{\theta }^{D} \) is the angle driver. Combining the torque and force relationship at both ends of the motor, the transfer matrix of a motor is given as

$$ {\mathbf{z}}^{O} = {\mathbf{U}}_{\kappa } {\mathbf{z}}^{I} = \left[ {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\ddot{\theta }_{z}^{D} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\mathop x\limits^{..} } \\ {\mathop y\limits^{..} } \\ {\ddot{\theta }} \\ {M_{z} } \\ {q_{x} } \\ {q_{y} } \\ 1 \\ \end{array} } \right]^{I} $$
(8)

4.3 Dynamics and Transfer Matrix of Fixed Mountings

In this work, the connection between a motor and its attached links is modeled as a fixed mounting. The mounting is denoted element \( \kappa \), and inboard and outboard body are denoted \( \kappa - 1 \) and \( \kappa + 1 \), respectively. When both inboard and outboard links are rigid bodies, the transfer matrix of the fixed mounting is an identity matrix. However when a flexible beam is inboard and/or outboard body, the mounting becomes slightly more complex.

4.3.1 Fixed Mounting with Rigid Inboard Body and Flexible Outboard Beam

$$ EI_{2.z} \frac{{\partial^{4} u}}{{\partial x_{2}^{4} }} = \bar{f}_{2.y} - \frac{\partial }{{\partial x_{2} }}\bar{M}_{e} - \rho A\left( {{\ddot{y_{2}}^{{O_{2} }} } + \ddot{\theta }x_{2} - \dot{\theta }^{2} u + \ddot{u} } \right) $$
(9)

Integrating Eq. (9) along the beam length and including the effect of centrifugal stiffening, and then the equation can be rewritten written in a matrix format by the linearization, rearrangement, and matrix partition as

$$ {\mathbf{z}}^{O} = {\mathbf{Uz}}^{I} = \left[ {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ {u_{7,1} } \hfill & {u_{7,2} } \hfill & {u_{7,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{7,7} } \hfill \\ {u_{8,1} } \hfill & {u_{8,2} } \hfill & {u_{8,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{8,7} } \hfill \\ {u_{9,1} } \hfill & {u_{9,2} } \hfill & {u_{9,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{9,7} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x} } \\ { \ddot{y} } \\ {\ddot{\theta }} \\ M \\ {q_{x} } \\ {q_{y} } \\ 1 \\ \end{array} } \right]^{I} $$
(10)

All the items \( u(i,j) \) in Eq. (10) are detailed in Ref. [12].

4.3.2 Fixed Mounting with a Flexible Inboard Body and a Flexible Outboard Body

The relationship between inboard and outboard angle of the inboard body \( \kappa - 1 \) needs to be included and can be described as

$$ \begin{aligned}\varvec{\theta}_{z(\kappa - 1)}^{O} & =\varvec{\theta}_{z(\kappa - 1)}^{I} + \left. {\frac{{\partial u_{y(\kappa - 1)} }}{{\partial x_{2} }}} \right|_{{x_{2} = L}} \\ & =\varvec{\theta}_{z(\kappa - 1)}^{I} + \left. {{\mathbf{N}}_{y}^{\prime } } \right|_{{x_{2} = L}}^{(\kappa - 1)} {\mathbf{w}}_{y(\kappa - 1)} \\ & =\varvec{\theta}_{z(\kappa + 1)}^{I} \\ \end{aligned} $$
(11)

The second order differentiation of Eq. (11) with respect to time is written as

$$ \begin{aligned} \ddot{\theta }_{z(\kappa - 1)}^{O} & = \ddot{\theta }_{z(\kappa - 1)}^{I} + \left. {{\mathbf{N}}_{y}^{'} } \right|_{{x_{2} = L}} {\ddot{\mathbf{w}}_{y(\kappa - 1)} } \\ & = \ddot{\theta }_{z(\kappa + 1)}^{I} \\ \end{aligned} $$
(12)

The calculation of modal coordinates at the outboard link must be based on the actual outboard angle of the inboard link. Combining the equations of the elastic deformation, force, and moment, the transfer matrix is given as

$$ {\mathbf{z}}^{O} = {\mathbf{Uz}}^{I} = \left[ {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{3,7} } \hfill & {u_{3,8} } \hfill & {u_{3,9} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {u_{7,1} } \hfill & {u_{7,2} } \hfill & {u_{7,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{7,7} } \hfill & {u_{7,8} } \hfill & {u_{7,9} } \hfill & {u_{7,10} } \hfill \\ {u_{8,1} } \hfill & {u_{8,2} } \hfill & {u_{8,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{8,7} } \hfill & {u_{8,8} } \hfill & {u_{8,9} } \hfill & {u_{8,10} } \hfill \\ {u_{9,1} } \hfill & {u_{9,2} } \hfill & {u_{9,3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {u_{9,7} } \hfill & {u_{9,8} } \hfill & {u_{9,9} } \hfill & {u_{9,10} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x} } \\ { \ddot{y} } \\ {\ddot{\theta }_{z} } \\ {M_{z} } \\ {q_{x} } \\ {q_{y} } \\ { {\ddot{w}^{1} } } \\ {\mathop {\ddot{w}^{2} } } \\ {\mathop {\ddot{w}^{3} } } \\ 1 \\ \end{array} } \right]^{I} $$
(13)

All the items \( u(i,j) \) in Eq. (13) are detailed in Ref. [12].

5 Case Studies and Simulations

The simulations of a single link manipulator are carried out using parameters identical to those used by Shabana and Berzeri in Ref. [11]. The comparison, as shown in Fig. 2, is made to verify the proposed model in this work. Figure 2 shows that the tip displacement of the rotating flexible beam calculated from the model in this work is very close the the result in Ref. [11]. Figure 3 compares the results based on the DT-TMM method and the traditional Lagrange-Euler method. The comparison demonstrates that the results of the two methods agree well with each other.

Fig. 2
figure 2

Tip-displacement from a simulation by Shabana using ANCF elements with centrifugal stiffening [11]

Full size image
Fig. 3
figure 3

Comparison of tip-displacement between TMM and Euler-Lagrange for simulations with \( \varDelta t = 0.001 \) giving a Mean Absolute Percentage Error of \( {\text{MAPE}} = 0.57\% \)

Full size image

6 Conclusion and Discussion

A computationally efficient dynamic modelling approach is presented in this research. With the proposed method, the computation of the large size dynamic equations is avoided by dividing the global dynamics to component dynamics. The methodology of defining state vectors, linearizing the component dynamics, and deriving transfer matrix for different types of components has been presented with details. Numerical simulations of flexible manipulators are conducted to verify the proposed dynamic modelling method.