Keywords

1 Introduction

The joint surface exists in assembling machinery parts such as robotics, NC machine tool etc. It plays an important role to transfer movement, load and energy in the normal operation of mechanical system. The results show that joint surface’s dynamic characteristics affect the stiffness, damping, machining accuracy and stability in robotics, NC machine tool etc. So, studies on dynamic characteristics of joint surface have important significance in theory and practical applications [1].

Many scholars have carried out lots of studies on joint surface [2–4]. In Macroscopic aspect, researches of joint surface’s dynamic characteristics are largely depends on Hertz theory [5], which is mainly study macroscopic properties of joint surface, such as geometric parameters, material parameters and boundary conditions. But the microscopic characteristics are merely considered in it. In microcosmic aspect, stiffness and damping models [6, 7] of joint surfaces are obtained depends on the M-B fractal model [8]. But M-B fractal model is mainly suitable for the contact analysis of two infinite planes, not for finite surfaces. And macroscopic properties are merely considered. A fractal model of two cylinders’ normal contact stiffness is built up by Zhao [9], but the effect of friction is not considered. Actually, friction and gap between joint surfaces has nonlinear vibration characteristics, which can change the topology mechanisms of dynamic systems and cause problems of vibration and noise [10].

Considering the friction and elastic-plastic deformation of joint surface, fractal models of contact stiffness of two cylinders’ joint surfaces are deduced based on Hertz theory and modified M-B fractal model in this paper.

2 Fractal Prediction Model of Contact Stiffness

2.1 Deformation Property Analysis of Elastomer

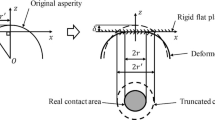
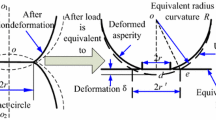
Based on the research of rough-surface contact model by Wang and Komvopoulos [11, 12], the deformation mode of elastomers includes elastic, elastic-plastic and plastic, and the transformation from elastic stage to plastic stage is not mutational. However, the transfer deformation stage, that is to say the elastic-plastic stage, is ignored in M-B fractal model. Moreover, the influence of friction and gap between joint surfaces should be fully considered.

The most basic theory of the contact surface is Hertz theory, and based on the research of elastic deformation and plastic deformation, the critical deformation of micro-bulge from elastic deformation to plastic deformation is Eq. (1).

$$ \delta c = (\frac{{\uppi}{\text{K}} {\upsigma} y}{2E})^{2} R $$
(1)

where, K is the correlation coefficient of hardness H and yield strength \( \sigma y \), and three of them meet the relation \( H = K\sigma y \). E is the integrated elastic modulus got from Hertz analysis.

Based on the M-B fractal model [13], the mathematical model of the surface outline of the micro-bulge can be expressed as Eq. (2), and when \( x = 0 \), it can be expressed as Eq. (3), \( a \) is the actual contact area.

$$ z(x) = G^{D - 1} a^{1 - 0.5D} \cos (\frac{{\uppi} {\text{x}}}{{a^{0.5} }}),\quad - 0.5a^{0.5} < x < 0.5a^{0.5} $$
(2)
$$ \delta = G^{D - 1} a^{1 - 0.5D} $$
(3)

Then, curvature radius of elastomers can be gotten as shown in Eq. (4).

$$ R = a^{0.5D} G^{1 - D} /\uppi $$
(4)

From the Ref. [14], when the relative sliding friction produced in the joint interfaces, the critical average contact pressure of micro-bulge is:

$$ p_{\mu } = 1.1k_{\mu } \sigma_{y} $$
(5)

where, k μ is the friction coefficient correction factor, k μ  \( = \) 1−0.228 μ, 0 ≤ μ ≤ 0.3, k μ  \( = \) 0.932e−1.58(μ−0.3), 0.3 ≤ μ ≤ 0.9.

Based on the Eqs. (1) and (5), while the influence of friction is considered, the critical deformation between the elastic and plastic state of micro-bulge can be expressed as Eq. (6). So the critical area between the elastic and plastic state of micro-bulge can be obtained, and expressed as Eq. (7).

$$ \delta_{\mu c} = \left({\frac{{3{\uppi}p_{\mu } }}{4E}} \right)^{2} R = \left({\frac{{3.3{\uppi}k_{\mu} \sigma_{y}}}{4E}} \right)^{2} R $$
(6)
$$ a_{\mu c} = \left( {\frac{{3.3\uppi^{0.5} k_{\mu } \sigma_{y} }}{4E}} \right)^{2/(1 - D)} G^{2} $$
(7)

The elastic deformation will happen when the contact area is larger than the critical elastic area (\( a_{\mu c} \)), while the influence of the friction is considered. Then we introduce the concept of critical plastic area (\( a_{pt} \)), and the plastic deformation will happen when the contact area is smaller than the critical plastic area. The state is elastic-plastic deformation when the contact area is larger than the critical plastic area and smaller than the critical elastic area.

From the Ref. [15], Eqs. (3) and (4), the critical plastic area can be expressed as follows:

$$ a_{pt} = G^{2} \left( {\frac{E\beta }{{\sigma_{y} }}} \right)^{2/(D - 1)} $$
(8)

where, \( \beta = \frac{{\sqrt\uppi \left( {\frac{2m + 1}{2m}} \right)^{2(m - 1)} }}{{(30 \times 0.2^{1/m} )^{m/(m - 1)} }} \), m is the strain hardening index.

2.2 Model of Normal Contact Stiffness

From the Ref. [16] and other references, the relation of the biggest contact area (\( a_{l} \)) and the distribution of the contact points (\( n^{\prime}(a) \)) is:

$$ n'\left( a \right) = - \frac{{{\text{d}}N'(A > a)}}{{{\text{d}}a}} = \lambda \frac{D}{2}\psi^{(2 - D)/2} a_{l}^{D/2} a^{ - (D + 2)/2} $$
(9)
$$ \lambda = \left( {\frac{{c_{1} \left( {\frac{\varOmega (B,E)}{{X_{h} }}} \right)^{{c_{2} }} }}{\sum S }} \right)^{{X_{h} }} F^{{C_{2} X_{h} }} $$
(10)

where, \( \Sigma S \) is the surface area of two surfaces. \( X_{h} \) is the synthetical curvature radius. B is the width of the contact body. E is the equivalent elastic modulus. \( \Omega (B,E) \) is the function of B and E. C 1, C 2 are the coefficient related to the geometry of surfaces.

With Hertz theory, the normal contact stiffness of single micro-bulge is:

$$ K_{n} = \int {k_{n} } \cdot n'(a){\text{d}}a $$
(11)

Considering the elastic deformation, elastic-plastic deformation and plastic deformation, the fractal model of the normal contact stiffness of the whole joint surfaces can be deviated as follows:

$$ \begin{aligned} K_{n} & = \int\limits_{{a_{\mu c} }}^{{a_{l} }} {k_{n} } \cdot n'(a){\text{d}}a + \int\limits_{{a_{pt} }}^{{a_{\mu c} }} {k_{n} } \cdot n'(a){\text{d}}a \\ & { = }\frac{{2 \cdot \lambda \cdot E \cdot D \cdot \psi^{{1{ - }0.5D}} \cdot a_{l}^{\frac{D}{2}} }}{{\sqrt\uppi (1 - D)}} \cdot (a_{l}^{{\frac{1 - D}{2}}} - a_{\mu c}^{{\frac{1 - D}{2}}} ) + \frac{{2 \cdot \lambda \cdot E' \cdot D \cdot \psi^{{1{ - }0.5D}} \cdot a_{l}^{\frac{D}{2}} }}{{\sqrt\uppi (1 - D)}} \cdot (a_{\mu c}^{{\frac{1 - D}{2}}} - a_{pt}^{{\frac{1 - D}{2}}} ) \\ \end{aligned} $$
(12)

where, \( E' \) is the corresponding elastic modulus.

According to the \( E = \sigma /\varepsilon = Pl/A\Delta l \), the stress decreases with the increase of contact area in the stage of elastic-plastic deformation, and then the deformation amount becomes bigger. So, the corresponding elastic modulus of elastic-plastic stage is smaller than that of elastic stage. The relation of them we make in this paper is \( E' = 0.9E \).

From Eq. (12), it shows that the stiffness of the joint surfaces is combined with the critical plastic area and critical elastic area in friction state. When the fractal characteristic parameters of joint surfaces, such as D, G and E, and the geometric parameters of two cylinders, such as R 1, R 2, F, and B, are obtained, the normal contact stiffness of two cylinders’ joint surfaces can be estimated. The accuracy of estimating the actual contact rigidity will be improved by this method.

2.3 Model of Tangential Contact Stiffness

The relation between tangential force and tangential deformation can be expressed as Eq. (13) when the normal force (P) and tangential force (T) is applied to the contact point of equivalent sphere and rigid plane.

$$ {\text{d}}t = \frac{3(2 - \upsilon )}{{16\overline{G} r}}\mu P\left[ {1 - \left( {1 - \frac{T}{\mu P}} \right)^{2/3} } \right] $$
(13)

where, \( \overline{G} = {E \mathord{\left/ {\vphantom {E {2(1 + \upsilon )}}} \right. \kern-0pt} {2(1 + \upsilon )}} \) is the equivalent shearing elastic modulus. \( \upsilon \) is the poisson ratio. \( \mu \) is the friction coefficient. \( a = {\uppi}r^{2} \), the tangential contact stiffness is:

$$ k_{t} = \frac{{8\overline{G} \sqrt a }}{{\left( {2 - \upsilon } \right)\sqrt\uppi }}(1 - \frac{1}{\mu } \cdot \frac{T}{P})^{1/3} $$
(14)

According to Eqs. (7)–(9) and (14), the tangential contact stiffness can be expressed as follows:

$$ \begin{aligned} K_{t} & = \int\limits_{{a_{\mu c} }}^{{a_{l} }} {k_{t} } \cdot n'(a){\text{d}}a + \int\limits_{{a_{pt} }}^{{a_{\mu c} }} {k_{t} } \cdot n'(a){\text{d}}a \\ & = \frac{{8\lambda \overline{G} D \cdot a_{l}^{\frac{D}{2}} }}{\sqrt \pi (2 - \upsilon )(1 - D)} \cdot \left( {1 - \frac{1}{\mu } \cdot \frac{T}{P}} \right)^{\frac{1}{3}} \cdot \left( {a_{l}^{{\frac{1 - D}{2}}} - a_{\mu c}^{{\frac{1 - D}{2}}} } \right) \\ & \qquad + \frac{{8\lambda \overline{G}^{'} D \cdot a_{l}^{\frac{D}{2}} }}{\sqrt \pi (2 - \upsilon )(1 - D)} \cdot \left( {1 - \frac{1}{\mu } \cdot \frac{T}{P}} \right)^{\frac{1}{3}} \cdot \left( {a_{\mu c}^{{\frac{1 - D}{2}}} - a_{pt}^{{\frac{1 - D}{2}}} } \right) \\ \end{aligned} $$
(15)

3 Feasibility Analysis of Fractal Prediction Model

3.1 Analysis of Normal Contact Stiffness Model

The relation of the dimensionless actual contacting area and single-point maximal contacting area is:

$$ A_{r} = \frac{D}{2 - D}\psi^{{\frac{2 - D}{2}}} a_{l} $$
(16)

When \( \sigma_{y} /E = 0.001 \), µ \( = \) 0.5, D \( = \) 1.45, G \( = \) 1.36 × 10−9, R 1 \( = \) 100 mm, R 2 \( = \) 50 mm, F \( = \) 1000 N, B \( = \) 50 mm, E \( = \) 155,000 Mpa, compared with the research of Ref. [16], the feasibility analysis of the normal contact stiffness model established above considering the influence of friction and elastic-plastic deformation can be studied, the results are shown in Fig. 1.

Fig. 1
figure 1

Contrast curves of normal contact stiffness in different conditions

Full size image

From Fig. 1, we can find that when the effect of friction is taken into consideration, the normal contact stiffness is low. This is mainly because of the existence of friction, the critical elastic area of elastomers will increase, and the proportion of contact point whose contact area is smaller than the critical elastic area will increase. In this condition, the proportion of plastic deformation will increase, while the proportion of elastic deformation will decrease. When both the effect of friction and elastic-plastic deformation is taken into consideration, the normal contact stiffness is high. This is because the proportion of plastic deformation decreases with the consideration of elastic-plastic deformation. Then, the damping of joint surfaces will decrease and the stiffness will increase. The results all proof the normal contact stiffness model we established is feasible.

3.2 Analysis of Tangential Contact Stiffness Model

When \( v = 0.3 \), \( \mu = 0.5 \), \( T/P = 0.02 \), \( D = 1.50 \), \( G = 1.36 \times 10^{ - 9} \), compared with research of Ref. [17], the feasibility analysis of the tangential contact stiffness model established above considering the influence of friction and elastic-plastic deformation can be studied, the results are shown in Fig. 2. The law of curves in Fig. 2 is similar to that in Fig. 1; the results proof the tangential contact stiffness model we established is feasible.

Fig. 2
figure 2

Contrast curves of tangential contact stiffness in different conditions

Full size image

4 Experimental Analysis of Fixed Curved Joint

The fixed curved joint is taken as a research object, shown in Fig. 3. The size of stent is 82 mm × 74 mm × 100 mm, the radius of optical axis is 50 mm, and the length is 150 mm. According to the Ref. [18], the fractal dimension (D) of its profilogram is 1.426 and the fractal scale parameters (G) are 2.34e−5 with the method of experimental determination and data fitting.

Fig. 3
figure 3

Fixed curved joints for experiment

Full size image

By substituting the fractal parameters of steel plate (D), (G), elastic modulus (E), poisson’s ratio (v), density (ρ), and friction coefficient (μ) into Eqs. (12) and (15), the normal contact stiffness (K n ) and tangential contact stiffness (K t ) of joint surfaces are obtained. The parameters are summarized in Table 1. To sake comparison, the normal contact stiffness (K n ) and tangential contact stiffness (K t ) in Ref. [16, 17] are calculated, shown in Table 2.

Table 1 Material constants and fractal parameters
Full size table
Table 2 Stiffness of fixed curved joint’s joint surface under different calculation models
Full size table

Then, the equivalent dynamic model of fixed curved joint is established by the method of spring element. Based on the vibration characteristics of the system, cycles of viscoelastic element are established on the location L 1, L 2, L 3, 4 groups of spring elements are arranged in each cycle, and each group is consist of 3 spring elements separately arranged in the X, Y, Z direction. That is to say, the fixed curved joint is equivalent to a three-degrees-of-freedom model through 36 spring elements. The model has two degrees of freedom in the radial direction and single degree of freedom in the axial direction. Each freedom is a parallel connection of 12 spring elements, and its contact stiffness value is K n/12 or K t/12.

According to the structure of the fixed curved joint, the finite element model is built. In the model, the spring element is simulated by combin14, and each layer material is divided by the Solid-92 element with the simulation soft. Each model shape and natural frequency are obtained through the method of Block Lanczos of modal analysis, the result is shown in Table 3. And the comparison of the results of finite element analysis and modal test are listed in Table 3.

Table 3 Comparisons of the results of finite element analysis and modal test
Full size table

From Table 3, each order natural frequency obtained by finite element analysis is agreement with the results of modal test. The error is lower than 10 %, which proofs the contact stiffness fractal model of two cylinders is correct. Compared with the traditional model, the error of the model considering the effect of friction and elastic-plastic deformation is lower. The results all proves the superiority of the model we establish.

5 Conclusions

Based on Hertz theory and modified M-B fractal model, fractal model of contact stiffness between two cylinders’ joint surfaces is established considering the influence of friction and elastic-plastic deformation. The model has geometric characteristics and scale independence, and it has been proofed by numerical simulation feasible for the reality of the joint surface. The works all lay certain theoretical basis to solve surface contact problems of cylinders and gears in robotics, NC machine tool, etc.

Substituting the fractal parameters, the normal contact stiffness and tangential contact stiffness of joint surfaces are obtained. And the equivalent dynamic model of the joint surface of fixed curved joint is established by the method of spring element. The natural frequencies are gained with finite element analysis, which are agreement with the results of modal test. Compared with the traditional model, the error of the model considering the effect of friction and elastic-plastic deformation is lower. The results all proves the superiority of the model we establish.