Learning in Networked Interactions: A Replicator Dynamics Approach

Abstract

Many real-world scenarios can be modelled as multi-agent systems, where multiple autonomous decision makers interact in a single environment. The complex and dynamic nature of such interactions prevents hand-crafting solutions for all possible scenarios, hence learning is crucial. Studying the dynamics of multi-agent learning is imperative in selecting and tuning the right learning algorithm for the task at hand. So far, analysis of these dynamics has been mainly limited to normal form games, or unstructured populations. However, many multi-agent systems are highly structured, complex networks, with agents only interacting locally. Here, we study the dynamics of such networked interactions, using the well-known replicator dynamics of evolutionary game theory as a model for learning. Different learning algorithms are modelled by altering the replicator equations slightly. In particular, we investigate lenience as an enabler for cooperation. Moreover, we show how well-connected, stubborn agents can influence the learning outcome. Finally, we investigate the impact of structural network properties on the learning outcome, as well as the influence of mutation driven by exploration.

1 Introduction

Understanding the dynamics of networked interactions is of vital importance to a wide range of research areas. For example, these dynamics play a central role in biological systems such as the human brain [10] or molecular interaction networks within cells [4]; in large technological systems such as the word wide web [16]; in social networks such as Facebook [2, 18, 37]; and in economic or financial institutions such as the stock market [12, 22]. Recently, researchers have focused on studying the evolution of cooperation in networks of self-interested individuals, aiming to understand how cooperative behaviour can be sustained in the face of individual selfishness [21, 26, 30, 31].

Many studies have targeted the discovery of structural properties of networks that promote cooperation. For instance, Santos and Pecheco show that cooperation has a higher chance of survival in scale-free networks [31]; Ohtsuki et al. find a relation between the cost-benefit ratio of cooperation and the average node degree of a network that determines whether cooperation can be sustained [27]; and Van Segbroeck et al. investigate heterogeneity and clustering and concludes that these structural properties influence behaviour on the individual rather than the overall network [38]. Others have focused on the role of the particular interaction model between neighbouring nodes in determining the success of cooperation. For example, Hofmann et al. simulate various update rules in different network topologies and find that the evolution of cooperation is highly dependent on the combination of update mechanism and network topology [21].

Cooperation can also be promoted using some incentivising structure in which defection is punishable [9, 32], or in which players can choose beforehand to commit to cooperation for some given cost [19]. Both incentives increase the willingness to cooperate in such scenarios where defection would be individually rational otherwise. Allowing individuals to choose with whom to interact may similarly sustain cooperation, e.g. by giving individuals the possibility to break ties with ‘bad’ neighbours and replacing them with a random new connection. For example, Zimmermann and Eguíluz show how such a mechanism may promote cooperation, albeit sensitive to perturbations [42]. Similarly, Edmonds et al. use a tag-based system through which agents identify whom to interact with [17]. Allowing agents to choose which tag to adopt gives rise to social structures that can enhance cooperation. Finally, control theory is used by Bloembergen et al. to show how external influence on a subset of nodes can drive the behaviour in social networks [7].

Most of these works share one important limitation, in that they consider only imitation-based learning dynamics. Typically in such models, individual agents update their behaviour by replicating the successful behaviour of their peers. In evolution terms, the update process only incorporates selection. However, evolutionary success often stems from the interplay between selection on the one hand, and mutation on the other. Closely related is the exploration/exploitation dilemma that is well-known in the field of reinforcement learning, where exploration plays the role of mutation, and exploitation yield selection.

Here, we bridge these two interpretations by analysing selection-mutation dynamics as a predictive model for multi-agent reinforcement learning, where interaction between agents is modelled as a structured social network. In particular, we investigate lenience [6, 29] as an enabler for cooperation. We report a great difference between pure selection dynamics, and selection-mutation dynamics that include leniency. Moreover, we show how a subset of stubborn agents can influence the learning outcome. We find that well connected agents exert a large influence on the overall network behaviour, and as such can drive the learning process towards a desired outcome. Furthermore, we show how structural network properties, such as size and average degree, influence the learning outcome. Finally, we observe that certain network structures give rise to clusters of cooperators and defectors coexisting.

In contrast to the majority of related work, which almost exclusively focuses on Prisoner’s Dilemma type interactions, we use the Stag Hunt to describe the interaction between agents. The Stag Hunt provides an intuitive model of many real-world strategic (economic) interactions, such as the introduction of potentially beneficial new technologies that require a critical mass of adopters in order to pay off. As such, not switching (defecting) is a safe choice, whereas social cooperation (adoption) may yield higher rewards for all.

This paper proceeds as follows. Firstly, we explain required background knowledge on learning, evolutionary game theory, and networks, in Sect. 2. Secondly, Sect. 3 outlines the methodology used in this work, in particular the formal link between multi-agent learning and the replicator dynamics. We present our model of networked replicator dynamics in Sect. 4, accompanied by a range of experiments in Sect. 5. The paper is closed with main conclusion of this study in Sect. 6.

2 Background

This section gives an overview of relevant background needed for the remainder of this work. The section is split into three main parts. Section 2.1 briefly introduces reinforcement learning; Sect. 2.2 describes basic concepts of evolutionary game theory; and Sect. 2.3 details networks.

2.1 Reinforcement Learning

The reinforcement learning (RL) paradigm is based on the concept of trial-and-error learning, allowing agents to optimise their behaviour without explicitly requiring a model of the environment [34]. The reinforcement learning agent continuously interacts with the environment, perceiving its state, taking actions, and observing the effect of those actions. The agent needs to balance exploration and exploitation in order to ensure good intermediate rewards while avoiding getting stuck in local optima. RL strategies are powerful techniques for optimising control of large scale control problems [15]. Early RL research focused on single-agent problems where the full state knowledge of the agent is known. Later on, RL has been applied to multi-agent domains as well [11]. The computational complexity of multi-agent reinforcement learning (MARL) algorithms is much higher than in single-agent problems, since (near) optimal behaviour of one agent depends on other agents’ policies as well.

Despite this challenge, single-agent RL techniques have been applied successfully to multi-agent settings. Arguably the most famous example of an RL algorithm is the model-free temporal difference algorithm Q-learning [39]. Q-learning¹ maintains a value function over actions, $Q_i$, which is updated at every time step t based on the reward r received after taking action $a_i$:

$$\begin{aligned} Q_i(t+1) \leftarrow Q_i(t) + \alpha \big ( r - Q_i(t) \big ) \end{aligned}$$

(1)

where $\alpha \in [0,1]$ is the learning rate that determines how quickly Q is updated based on new reward information. Choosing which action to take is crucial for the learning process. The Boltzmann exploration scheme is often used as it provides a way to balance exploration and exploitation by selecting an appropriate temperature $\tau$. The policy $\mathbf {x}$ that determines the probability for choosing each action a is computed as

$$\begin{aligned} x_i = \frac{ e^{{Q_i}/{\tau }} }{ \sum _j e^{{Q_j}/{\tau }} } \end{aligned}$$

(2)

A high temperature drives the mechanism towards exploration, whereas a low temperature promotes exploitation.

2.2 Evolutionary Game Theory

The strategic interaction between agents can be modelled in the form of a game, where each player (agent) has a set of actions, and a preference over the joint action space that is captured in the received payoffs. For two-player games, the payoffs can be represented by a bi-matrix $(\mathbf {A}, \mathbf {B})$, that gives the payoff for the row player in $\mathbf {A}$, and the column player in $\mathbf {B}$, see Fig. 1 (left). The goal of each player is to decide which action to take, so as to maximise their expected payoff. Classical game theory assumes that full knowledge of the game is available to all players, which together with the assumption of individual rationality does not necessarily reflect the dynamic nature of real world interaction. Evolutionary game theory (EGT) relaxes the rationality assumption and replaces it by the concepts of natural selection and mutation from evolutionary biology [24, 41]. Where classical game theory describes strategies in the form of probabilities over pure actions, EGT models them as populations of individuals, each of a pure action type, where the population share of each type reflects its evolutionary success.

Fig. 1.

General payoff bi-matrix $(\mathbf {A}, \mathbf {B})$ for two-player two-action games (left) and the Stag Hunt (center), and a typically valued instance of the Stag Hunt (right)

Central to EGT are the replicator dynamics, that describe how this population of individuals evolves over time under evolutionary pressure. Individuals are randomly paired to interact, and their reproductive success is determined by their fitness which results from these interactions. The replicator dynamics dictate that the population share of a certain type will increase if the individuals of this type have a higher fitness than the population average; otherwise their population share will decrease. The population can be described by the state vector $\mathbf {x} = (x_1, x_2, \ldots , x_n)^\text {T}$, with $0 \le x_i \le 1 ~ \forall i$ and $\sum _i x_i = 1$, representing the fractions of the population belonging to each of n pure types. Now suppose the fitness of type i is given by the fitness function $f_i(\mathbf {x})$, and the average fitness of the population is given by $\bar{f}(\mathbf {x}) = \sum _j x_j f_j(\mathbf {x})$. The population change over time can then be written as

$$\begin{aligned} \dot{x_i} = x_i \left[ f_i(\mathbf {x}) - \bar{f}(\mathbf {x}) \right] \end{aligned}$$

(3)

In a two-player game with payoff bi-matrix $(\mathbf {A}, \mathbf {B})$, where the two players use the strategies $\mathbf {x}$ and $\mathbf {y}$ respectively, the fitness of the first player’s $i^{th}$ candidate strategy can be calculated as $\sum _j a_{ij} y_j$. Similarly, the average fitness of population $\mathbf {x}$ is defined as $\sum _i x_i \sum _j a_{ij} y_j$. In matrix form, this leads to the following multi-population replicator dynamics:

$$\begin{aligned} \begin{aligned} \dot{x_i}&= x_i \left[ (\mathbf {A}\mathbf {y})_i - \mathbf {x}^\text {T}\mathbf {A}\mathbf {y} \right] \\ \dot{y_i}&= y_i \left[ (\mathbf {x}^\text {T}\mathbf {B})_i - \mathbf {x}^\text {T}\mathbf {B}\mathbf {y} \right] \end{aligned} \end{aligned}$$

(4)

The Stag Hunt is a game that describes a dilemma between safety and social cooperation [33]. The canonical payoff matrix of the Stag Hunt is given in Fig. 1 (center), where $A > B \ge D > C$. Social cooperation between players is rewarded with A, given that both players choose to cooperate (action C). As the players do not foresee each others’ strategies, the safe choice of players is to defect (action D), since typically $A + C < B + D$ (see Fig. 1, right). Although cooperation pays off more for both players, defection is individually rational when the opponent strategy is unknown. As both players reason like this, they may end up in a state of mutual defection, receiving $D < A$ each, hence the dilemma.

The Stag Hunt is typically said to model individuals that go out on a hunt, and can only capture big game (e.g. a stag) by joining forces, whereas smaller pray (e.g. a hare) can be captured individually. However, it can also be thought of to describe the introduction of a new technology, which only really pays off when more people are using it. Early adopters risk paying the price for this. As such, despite its simplicity the Stag Hunt is an useful model for many real-world strategic dilemmas.

2.3 Networked Interactions

Networks describe collections of entities (nodes) and the relation between them (edges). Formally, a network can be represented by a graph $\mathbb {G} = (\mathcal {V},\mathcal {W})$ consisting of a non-empty set of nodes (or vertices) $\mathcal {V} = \{v_1, \dots ,v_N\}$ and an $N \times N$ adjacency matrix $\mathcal {W}=[w_{ij}]$ where non-zero entries $w_{ij}$ indicate the (possibly weighted) connection from $v_i$ to $v_j$. If $\mathcal {W}$ is symmetrical, such that $w_{ij} = w_{ji}$ for all i, j, the graph is said to be undirected, meaning that the connection from node $v_i$ to $v_j$ is equal to the connection from node $v_j$ to $v_i$. In social networks, for example, one might argue that friendship is usually mutual and hence undirected. This is the approach followed in this work. In general however this need not be the case, in which case the graph is said to be directed, and $\mathcal {W}$ asymmetrical. The neighbourhood, $\mathbb {N}$, of a node $v_i$ is defined as the set of nodes it is directly connected to, i.e. $\mathbb {N}(v_i) = \cup _j v_j : w_{ij} > 0$. The node’s degree $\text {deg}[v_i]$ is given by the cardinality of its neighbourhood.

Several types of networks have been proposed that capture the structural properties found in large social, technological or biological networks, two well-known examples being the small-world and scale-free models. The small-world model exhibits short average path lengths between nodes and high clustering, two features often found in real-world networks [40]. Another model is the scale-free network, characterised by a heavy-tailed degree distribution following a power law [3]. In such networks the majority of nodes will have a small degree while simultaneously there will be relatively many nodes with very large degree, the latter being the hubs or connectors of the network. For a detailed description of networks and their properties, the interested reader is referred to [22].

3 Evolutionary Models of Multi-agent Learning

Multi-agent learning and evolutionary game theory share a substantial part of their foundation, in that they both deal with the decision making process of bounded rational agents, or players, in uncertain environments. The link between these two fields is not only intuitive, but also formally proven that the continuous time limit of Cross learning converges to the replicator dynamics [8].

Cross learning [14] is one of the most basic stateless reinforcement learning algorithms, which updates its policy $\mathbf {x}$ based on the reward r received after taking action j as

$$\begin{aligned} x_i \leftarrow x_i + \bigg \{ \begin{array}{ll} r - x_i r &{}\text {if } i = j \\ -x_i r &{}\text {otherwise} \end{array} \end{aligned}$$

(5)

A valid policy is ensured by the update rule as long as the rewards are normalised, i.e., $0 \le r \le 1$. Cross learning is closely related to learning automata (LA) [25, 35]. In particular, it is equivalent to a learning automaton with a linear reward-inaction ($L_{R-I}$) update scheme and a learning step size of 1.

We can estimate $E \left[ \varDelta x_i \right]$, the expected change in the policy induced by Eq. 5. Note that the probability $x_i$ of action i is affected both if i is selected and if another action j is selected, and let $E_i[r]$ be the expected reward after taking action i. We can now write

$$\begin{aligned} E \left[ \varDelta x_i \right]&= x_i \Big [E_i[r] - x_i E_i[r] \Big ] + \sum _{j \ne i} x_j \Big [ - E_j[r] x_i \Big ] \nonumber \\&= x_i \Big [E_i[r] - \textstyle { \sum _{j} } x_j E_j[r] \Big ] \end{aligned}$$

(6)

Assuming the learner takes infinitesimally small update steps, we can take the continuous time limit of Eq. 6 and write is as the partial differential equation

$$\begin{aligned} \dot{x}_i = x_i \left[ \text {E}_i[r] - \textstyle { \sum _{j} } x_j \text {E}_j[r] \right] \end{aligned}$$

In a two-player normal form game, with payoff matrix $\mathbf {A}$ and policies $\mathbf {x}$ and $\mathbf {y}$ for the two players, respectively, this yields

$$\begin{aligned} \dot{x}_i = x_i \left[ (\mathbf {A}\mathbf {y})_i - \mathbf {x}^\text {T}\mathbf {A}\mathbf {y} \right] \end{aligned}$$

(7)

which are exactly the multi-population replicator dynamics of Eq. 4.

The dynamical model of Eq. 7 only describes the evolutionary process of selection, as Cross learning does not incorporate an exploration mechanism. However, in many scenarios mutation also plays a role, where individuals not only reproduce, but may change their behaviour while doing so. Given a population $\mathbf {x}$ as defined above, we consider a mutation rate $\mathcal {E}_{ij}$ indicating the propensity of species j to mutate into i (note the order of the indices), such that, $\forall i$:

$$ \mathcal {E}_{ij} \ge 0 ~~~\text {and}~~~ \sum _{i} \mathcal {E}_{ij} = 1 $$

Adding mutation to Eq. 7 leads to a dynamical model with separate selection and mutation terms [20], given by

$$\begin{aligned} \dot{x}_i = x_i \underbrace{\Big [ (\mathbf {A}\mathbf {y})_i - \mathbf {x}^\text {T}\mathbf {A}\mathbf {y} \Big ]}_{\text {selection}} + \underbrace{\textstyle {\sum _j}\Big (\mathcal {E}_{ij} x_j - \mathcal {E}_{ji} x_i\Big )}_{\text {mutation}} \end{aligned}$$

(8)

By slightly altering or extending the model of Eq. 7 different RL algorithms can be modelled as well. A selection-mutation model of Boltzmann Q-learning (Eqs. 1 and 2) has been proposed by Tuyls et al. [36]. The dynamical system can again be decomposed into terms for exploitation (selection following the replicator dynamics) and exploration (mutation through randomization based on the Boltzmann mechanism):

$$\begin{aligned} \dot{x}_i = \frac{\alpha x_i}{\tau } \underbrace{\Big [ (\mathbf {A}\mathbf {y})_i - \mathbf {x}^\text {T}\mathbf {A}\mathbf {y} \Big ]}_\text {selection} - \alpha x_i \underbrace{\Big [ \log x_i - \textstyle {\sum _k } x_k \log x_k \Big ]}_\text {mutation} \end{aligned}$$

(9)

Technically, these dynamics model the variant Frequency Adjusted Q-learning (FAQ), which mimics simultaneous action updates [23].

Lenient FAQ-learning (LFAQ) [6] is a variation aimed at overcoming convergence to suboptimal equilibria by mis-coordination in the early phase of the learning process, when mistakes by one agent may lead to penalties for others, irrespective of the quality of their actions. Leniency towards such mistakes can be achieved by collecting $\kappa$ rewards for each action, and updating the Q-value based on the highest of those rewards. This causes an (optimistic) change in the expected reward for the actions of the learning agent, incorporating the probability of a potential reward for that action being the highest of $\kappa$ consecutive tries [29]. The expected reward for each action $\mathbf {A}\mathbf {y}$ in Eq. 9 is replaced by the utility vector $\mathbf {u}$, with

$$\begin{aligned} u_i = \sum _{j} \frac{a_{ij}y_{j} \left[ \left( \sum _{k:a_{ik}\le a_{ij}}y_{k} \right) ^{\kappa } - \left( \sum _{k:a_{ik}<a_{ij}}y_{k} \right) ^{\kappa } \right] }{\sum _{k:a_{ik}=a_{ij}}y_{k}} \end{aligned}$$

(10)

Each of these models approximates the learning process of independent reinforcement learners in a multi-agent setting. Specifically, they are presented for the case of two-agent interacting in a normal-form game. Extensions to n-players are straightforward, but fall outside the scope of this work. In the next section we will describe our extension of networked replicator dynamics.

4 Networked Replicator Dynamics

In this work, agents are placed on the nodes of a network, and interact only locally with their direct neighbours. Assume a graph $\mathbb {G}$ with N nodes as defined in Sect. 2.3, with N agents placed on the nodes $\{v_1,\ldots ,v_N\}$. If we define each agent by its current policy $\mathbf {x}$ we can write the current network state $\mathcal {X} = (\mathbf {x}^1,\ldots ,\mathbf {x}^N)$. The aim of this work is study how $\mathcal {X}$ evolves over time, given the specific network structure and learning model of the agents. For this purpose, we introduce networked replicator dynamics (NRD), where each agent (or node) is modelled by a population of pure strategies, interacting with each if its neighbours following the multi-population replicator dynamics of Eq. 4.

The update mechanism of the proposed networked replicator dynamics is given in Algorithm 1. At every time step, each agent (line 3) interacts with each of its neighbours (line 4) by playing a symmetric normal-form game defined by payoff-matrix $\mathbf {A}$. These interactions are modelled by the replicator dynamics (line 5), where each neighbour incurs a potential population change, $\dot{\mathbf {x}}$, in the agent. Those changes are normalised by the degree, $|\mathbb {N}(v_i)|$, of the agent’s node (line 7). Finally, all agents update their state (line 9).

This model is flexible in that it is independent of the network structure, it can be used to simulate any symmetric normal form game, and different replicator models can easily be plugged in (line 5 of Algorithm 1). This means that we can use any of the dynamical models presented in Sect. 3 as update rule, thereby simulating different MARL algorithms.

5 Experimental Validation

In this section we present experimental results of the networked replicator dynamics model in various setups. In particular, we use Barabási-Albert scale-free [3] and Watts-Strogatz small world [40] networks. The first set of experiments compares the different learning models, focusing in particular on the role of exploration and lenience in the learning process. We then analyse lenience in more detail, investigating the influence of the degree of lenience on the speed of convergence. Hereafter, we look at the relation between network size and degree with respect to the equilibrium outcome. The last set of experiments investigates the role of stubborn nodes, which do not update their strategy, on the resulting network dynamics. All experiments use the Stag Hunt (page 4, Fig. 1, right) as the model of interaction.

5.1 Comparing Different Learning Models

We compare the different dynamical models of multi-agent learning presented before in Sect. 3. We use the following abbreviations: CL is Cross learning (Eq. 7); CL+ is CL with mutation (Eq. 8); FAQ is frequency adjusted Q-learning (Eq. 9); LF-$\kappa$ is lenient FAQ with degree of lenience $\kappa$ (Eq. 10). In order to ensure smooth dynamics we multiply the update $\dot{\mathbf {x}}$ of each model by a step size $\alpha$. CL and CL+ use $\alpha = 0.5$, FAQ uses $\alpha =0.1$, and LF uses $\alpha =0.2$. Moreover, the exploration (mutation) rates are set as follows: CL+ uses $\mathcal {E}_{ij} = 0.01$ for all $i \ne j$, and $\mathcal {E}_{ii} = 1 - \sum _{j \ne i} \mathcal {E}_{ij}$; and FAQ and LF use $\tau =0.1$. We simulate the model on 100 randomly generated networks of $N=50$ nodes (both scale free and small world, the latter with rewiring probability $p=0.5$), starting from 50 random initial states $\mathcal {X} \in \mathbb {R}^N$, and report the average network state $\bar{\mathcal {X}} = \frac{1}{N} \sum _i \mathbf {x}^i$ after convergence. Since the Stag Hunt only has two actions, the full state can be defined by $x_1$, the probability of the first action (cooperate).

Fig. 2.

Dynamics of a networked Stag Hunt game in small world and scale free networks. The figure shows the mean network state in equilibrium (gray scale) for different algorithms (x-axis) and average network degree (y-axis) (Color figure online).

Figure 2 shows the results of this comparison. The gray scale indicates the final network state $\bar{\mathcal {X}}$ after convergence, where black means defection, and white means cooperation. Note the non-linear scale, this is chosen to highlight the details in the low and high ranges of $\bar{\mathcal {X}}$. Several observations can be made based on these results. First of all, there is a clear distinction between non-lenient algorithms, which converge mostly to defection, and lenient algorithms that converge toward cooperation. As expected, lenience indeed promotes cooperation also in a networked interactions. Equally striking is the lack of distinction between pure selection (CL) and selection-mutation (CL+, FAQ) models. Adding mutation (or exploration) in this setting has no effect on the resulting convergence. Increasing the mutation rate does lead to a change at some point, however, this is to the exten that the added randomness automatically drives the equilibrium away from a state of pure defection.

Fig. 3.

Example of the convergence of LF-2 on a Scale Free (top) and Small World (bottom) network with average degree 2 and 4, respectively. The network is split between cooperators (white) and defectors (black) in the final equilibrium state (Color figure online).

The most interesting results of Fig. 2 are those of LF-2. Here, we can observe a range of outcomes, depending on the average network degree. A more strongly connected network yields a higher probability of cooperation in equilibrium. Moreover, LF-2 is the only algorithm that yield an “indecisive” final state, that is significantly removed from pure cooperation or defection. In order to investigate this situation further, we look in detail at the dynamics of a single network. Figure 3a shows the network state $\mathcal {X}$ over time for one specific (randomly drawn) initial state of a scale free network with average degree 2. Clearly, the network is split into clusters of cooperators and defectors, no unanimous outcome is reached. The final state is highlighted in Fig. 3b, depicting the network structure and state of each node, and clearly showing two clusters. Depending on initial conditions, different splits can be observed.

Similar results can be observed in small world networks. Figures 3c and d show the dynamics in an example network with average degree 4. Again, a cluster of defectors is maintained in equilibrium amongst a majority of cooperators. Identifying specific structural network properties that lead to clustering is a main question for future work.

5.2 The Effect of Lenience on Convergence

In this set of experiments, we take a closer look at the influence of leniency on the dynamics and convergence of the network. Using the same set of networks as in the previous section, we zoom in only on the lenient algorithms and compare their convergence speed for the different networks. Table 1 lists the number of time steps to convergence, again averaged over 100 networks with 50 random initial states. Two trends are clearly visible: increasing the degree of lenience decreases the convergence time (most notably for degree 2 networks); and increasing the network degree similarly decreases the convergence time (most notably for LF-2). These results can be explained intuitively, as lenience pushes the learning process in the direction of cooperation, whereas a higher network degree yield more interactions per time step, and hence faster convergence. The fact that no convergence below 33 time steps is observed, independent of the network type, can be explained by the limit that the step size $\alpha$ and the inherent dynamics of the model pose.

Table 1. Time to convergence (mean and std. dev.) of lenient FAQ, for Small World and Scale Free networks of various degree d.

Fig. 4.

The equilibrium state for different network sizes, for Small World and Scale Free networks using LF-2. Fixed degree is 2, proportional degree is 10 % of the network size.

5.3 The Relation Between Network Size and Degree

Here we investigate the role that both network size and average degree play in determining the equilibrium outcome of the learning process. Specifically, we compare networks of different sizes with a fixed degree, with networks which have a degree proportional to their size. Figure 4 shows the results for both small world and scale free networks. For each combination we simulate 100 randomly generated networks, each using 10 randomly drawn initial states, following the LF-2 dynamics. The figure shows that the equilibrium state is independent of the network size if the degree is kept fixed, whereas the probability of cooperation increases when the degree grows with the network. This result shows that a more strongly connected network tends to cooperate more than one with sparse interactions. Intuitively, this can be explained by the inherent dynamics of the Stag Hunt: a critical mass of cooperators is required for cooperation to be a beneficial strategy. In more densely connected networks, this critical mass is reached more easily.

5.4 The Influence of Stubborn Agents

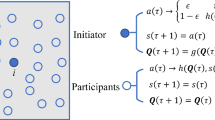
Finally, we look at the influence of stubborn agents on the final state. Stubborn agents are ones that do not update their state, regardless of the actions of their neighbours or the rewards they receive. These agents could be perceived as regulating bodies in financial networks, or politicians in social networks trying to spread their views.

Fig. 5.

The influence of the number of stubborn agents on final network state, for small world and scale free networks of degree 2.

Here, we select the highest degree nodes in the network to be stubborn - future work will investigate this issue further. Figure 5 shows the results of an extensive set of experiments, simulating networks of different sizes $N \in \{20,40,60,80,100\}$ with average degree 2, and varying the percentage of stubborn agents. The stubborn agents keep their state fixed at $x_1 = 0.95$.² Interestingly, the results are independent of the network size when the degree is fixed, and hence the results in Fig. 5 are averaged. We can observe that stubborn agents pull the whole network toward cooperation. Moreover, we see that this effect diminishes as the percentage goes up. Scale free networks in particular show this effect, which can be explained by the fact the in such networks a small number of “hubs” take part in a majority of the connections. Once these hubs are cooperative, the rest follows quickly.

6 Conclusions

We have proposed networked replicator dynamics (NRD) that can be used to model learning in (social) networks. The model leverages the link between evolutionary game theory and multi-agent learning, that exists for unstructured populations, and extends it to settings in which agents only interact locally with their direct network neighbours. We evaluated this model in a range of experiments, showing the effect of various properties of both network and learning mechanism on the resulting equilibrium state. We found that lenience is an enabler for cooperation in a networked Stag Hunt game. A higher degree of lenience yields a higher probability of cooperation in this game; moreover this equilibrium is reached faster. More densely connected networks promote cooperation in a similar way, and stubborn agents can pull the network towards their desired state, in particular when they are well connected within the network. The latter finding is of particular interest to the scenario of adoption of new technologies, as it shows that getting few key players to opt-in may pull the whole network to adopt as well.

There are many interesting avenues for future work stemming from these initial findings. The networked replicator dynamics can be further validated by comparing these findings with the dynamics that would result from placing actual learning agents, rather than their dynamical model, on the network. Moreover, one can look at networks in which different types of learning mechanisms interact. E.g., each agent is modelled by a different dynamical model. This can be easily integrated in the NRD. Furthermore, different games can be studied as the model for various real-world scenarios, such as the N-player Stag Hunt which yields richer dynamics than its two-player counterpart [5, 28]. Finally, an interesting direction for further research would be to extend the NRD model for more complex learning algorithms. For example, it has been shown that adding memory can help sustain cooperation by taking past encounters into account, e.g. by recording the opponent’s intention [1] or by the inclination to stick to previous actions [13].