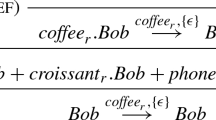Keywords

1 Introduction

Qlock, an abstract version of Dijkstra’s binary semaphore, is a protocol to guarantee exclusive access to a resource. Besides the initial specification and verification in CafeOBJ(see for example [6]), it saw implementations in Coq [12] and Maude [14]. Most of these specifications only consider safety properties, in the current case the mutual exclusion property, that no two agents will have access to the resource at the same time. However, liveness properties are normally left open. These properties ensure that ‘there is progress’. In our particular case, they ensure that agents do not block out other agents from acquiring access to the resource.

We are using CafeOBJ as specification and verification language. CafeOBJ is a many- and order-sorted algebraic specification language from the Obj family, related to languages like Casl and Maude. CafeOBJ allows us to have both the specification and the verification in the same language. It is based on powerful logical foundations (order-sorted algebra, hidden algebra, and rewriting logic) with an executable semantics [8, 10, 11].

The particular interest of the current development is two-fold: Firstly, it extends base specifications in order-sorted and rewriting logics to a meta-level, which requires behavioral logic, thus using the three logics together to achieve the proofs. Secondly, we use a search predicate and covering state patterns that allow us to prove the validity of a property over all possible one-step transitions, by which safety and liveness properties in the base and meta-level can be proven.

1.1 Related Work

Our work is closely related in spirit to [1, 2], where the authors discuss verification and model checking of temporal properties over infinite-state transition systems. Both works discuss variants of a mutual exclusion protocol, but while the main focus of their work is on model checking, we target theorem proving. Furthermore, they use rewriting logic and narrowing, while we are employing behavioral logic to represent infinite data structures. On the other hand, Goguen and Lin [9] use behavioral algebra to specify and verify properties on the Alternating Bit Protocol, but they do not use rewriting logic.

Many of the works done on Unity bear resemblance and relation with our work. Our methodology is closely related to concepts of Unity. Theorem proving over Unity using the Larch prover is the target of [5], while mechanization of Unity in Isabelle is discussed in [15].

Although the approach taken in [3] is similar to ours, there only the progress property (in our words) is discussed, while fairness based on or similar to our concept of fairness of execution sequences allows for stronger properties like the entrance property.

While all the above (and more) related works often deal with similar concepts, we believe that it is the first time that behavioral logic, rewriting logic, and order-sorted logic, are used together for system specification and treatment of liveness properties. This is also the reason why the entrance property introduced here has not been discussed hitherto.

1.2 Layout of the Article

In Sect. 2 we introduce the Qlock protocol and various properties for verification, give a short introduction to the CafeOBJ language, and provide the base specification onto which the current work is building. This section also discusses briefly the proof method by induction and exhaustive search.

In Sect. 3 we extend the base specification to include infinite transition sequences. Here we also discuss the methodology of meta-modeling.

In Sect. 4 we provide (parts) of the proof score verifying the three properties.

In the final section we provide a discussion of the approach with respect to applicability to different problems, and conclude with future research directions.

2 The QLOCK Protocol

The Qlock protocol regulates access of an arbitrary number of agents to a resource by providing a queue (first-in-first-out list). Agents start in the remainder section, henceforth indicated by \(\mathsf{rs }\). The mode of operation is regulated by the following set of rules:

  • If an agent wants to use the resource, it puts a unique identifier into the queue, and by this it transitions into the waiting section (ws).

  • In the waiting section, an agent checks the top of the queue. If it is the agent’s unique identifier, the agent transitions into the critical section (\(\mathsf{cs }\)), during which the agent can use the resource.

  • After having finished with the resource usage, the agent removes the head of the queue and transitions back into the remainder section (\(\mathsf{rs }\)).

See Fig. 1 for a schematic flow diagram.

Fig. 1.
figure 1

Flow diagram of Qlock protocol

Full size image

2.1 Verification Properties

The basic safety property of Qlock is the mutual exclusion property (\(\mathsf{mp }\)):

Property 1

(mutual exclusion property). At any time, at most one agent is in the critical section.

While this is the most important property for safety concerns, it does not guarantee that an agent wanting to use the resource ever gets the chance to use it (for example, in case of denial-of-service attack to a server). To guarantee this, we define two liveness properties: The first concerns the transition from ws to \(\mathsf{cs }\), and is called the progress property (\(\mathsf{pp }\)). This property has already been discussed in [13] as lockout freedom property.

Property 2

(progress property). An agent that has entered into the waiting section (ws), i.e., has put his unique identifier into the queue, will eventually transition into the critical section (\(\mathsf{cs }\)), i.e., progress to the top of the queue and gain access to the resource.

The last one concerns the transition from the remainder section \(\mathsf{rs }\) to the waiting section ws, called entrance property (\(\mathsf{ep }\)):

Property 3

(entrance property). An agent will eventually transition into the queue, i.e., from the remainder section to the waiting section.

Although it might sound counter-intuitive that the entrance property should hold for each agent at all times, we believe that there are good reasons to consider this property: This is motivated by the fact that given any finite run, i.e., finite transition sequence, of the Qlock protocol, we can always extend it to an infinite and fair transition sequence (see later sections for details). Thus, what we are actually proving is that for each agent, either the entrance property holds, or the execution terminates before the agent had a chance. In circumstances of long-running services (like most client-server interaction where a server is practically never stopped), this ensures that agents, or clients, will – given long enough execution time – eventually be served.

As we will see later on, to prove this property we need additional assumptions, in particular fairness, see Sect. 3.2, which makes it conceptually different from the first two properties. To continue with the analogy set forth above, the schedulers used in most operating systems or network hubs try to create a fair execution sequence by using round-robin or similar techniques [20, 21].

2.2 Short Introduction to CafeOBJ

Although we cannot give a full introduction to the CafeOBJ language, to aid readers unfamiliar with it we give a short introduction. Users acquainted with Maude can safely skip this section, as syntaxes of the two languages are very similar.

CafeOBJ is an algebraic specification language, thus the unit of specification is an algebra, in particular an order-sorted algebra. To specify an algebra, the following information have to be given:

  • Signature. Similar to normal algebras, a signature consists of operators and their arities. In the multi-sorted setting we are working in, this means that sorts have to be defined, and for each operator (or function) the number and sorts of the arguments and result have to be specified.

  • Axioms. They provide an equational theory over the (many-sorted) signature defined above. These axioms (or equations) make up the core of any algebraic specification.

We will demonstrate these concepts on a simple definition of natural numbers with successor and addition, but no comparison or subtraction:

figure a

Line 1 begins the specification of the algebra called SIMPLE-NAT with initial semantics (indicated by the ! after mod, which can be replaced with * to indicate loose semantics). The body of the specification consists of two blocks. Lines 2-7 define the signature, lines 8-12 the axioms. In line 3 the sorts and their order are introduced by defining a partial order of sorts between brackets. In case of hidden sorts (of behavioural algebras) we use *[...]*. In this above case there are three sorts, Zero, NzZero, and Nat. The order relation expresses that the former two are a subsort of Nat, but does not specify a relation between themselves. Lines 4-6 give three operators, the constant 0 of sort Zero, the successor function s, and the addition, written in infix notation. Two of the operators are furthermore tagged as constructors of the algebra. Note that in the specification of operators, the _ represents the places of arguments.

The second block defines the equations by first declaring two variables of sort Nat. Axioms are introduced with the eq keyword, and the left- and right-hand side of the equation are separated by =. Thus, the two axioms provided here provide the default inductive definition of addition by the successor function.

Not exhibited here, but used later in the code is the syntax protecting(...), which imports all the sorts and axioms of another module, but does not allow to alter them.

In the following, the signature and axioms block declaration will be dropped, as they are not necessary.

2.3 Base Specification

We are building upon a previously obtained specification and verification of Qlock [6]. Although we are providing the complete source of the specification part, we cannot, due to space limits, include the full verification part. The reader is referred to the full code at [17].

The basic idea of the following specification is to use the natural abstraction of Qlock and its transitions as an Abstract State System (Ass). The usual steps in providing an algebraic specification in this setting are:

  • Define proper abstraction as modules/algebras of the players (e.g., agent, queue) in the protocol.

  • Model the complete state as a module/algebra.

  • Use transitions between terms of the state algebra to describe transitions in the protocol.

  • Specify (and later verify) properties on states (and transitions) to ensure safety and liveness.

Let us start with the most basic item, namely modeling the sections an agent can be in. For literals, i.e., elements of the sort LabelLt, which is a sub-sort of the sort Label, we define identity via the syntactical identity. The second module specification defines an agent, or more specifically, the algebra of agent identifiers AID, without any further axioms, which implies that identifiers are considered different if they are syntactically different.

figure b

In the next step we model a queue, a first-in-first-out storage. Note in the following code, that CafeOBJ allows for parametrized modules. In the present case the parameter X has no further requirements, which is expressed by the fact that it only needs to belong to the trivial algebra. Another important point to note is that we are using associative constructors, which allows us to freely use any way of parenthesizing. Similarly, we introduce a module for parametrized sets, where we use an associative and commutative constructor.

figure c

Concerning agents, we model them as terms of an algebra of agent observers which associates agent identifiers with labels, expressing the fact that the agent is in the current state. More formally, the meaning of the term lb[A]:S is that the agent A is in section S:

figure d

In the final step we instantiate the parametrized queue with agent ids, and define the state algebra as a pair of one queue and an arbitrary set of agent observers. Note that the pairing is done by the syntax l $ r, CafeOBJ allows nearly arbitrary syntax:

figure e

With this we have given a complete definition of the state algebra, but the dynamic aspect of the protocol has been left out till now. We are now providing transition rules over states to express this dynamic aspect. In the following code segments, the two states of the transition are aligned, and changing parts are indicated with a bold font. The three transitions are WaitTrans, where an agent transitions from \(\mathsf{rs }\) to ws, TryTrans, where an agent tries to enter \(\mathsf{cs }\), and ExitTrans, where an agent leaves the critical state:

figure f

Based on the above specification, it is possible to provide a proof score, i.e., a program in CafeOBJ, that verifies the mutual exclusion property \(\mathsf{mp }\). As usual with proofs by induction over the reachable states (see below), the target property by itself does not suffice to work as inductive property, making the introduction of further properties on states necessary. Example properties that have to be used are uniqueness properties (e.g., the same agent identifier cannot appear several times in the queue) or initial state properties (e.g., the queue is empty at the beginning). Obtaining an inductive property (set of properties) is one of the challenging aspects of verifications, and requires an iterative and interactive approach. Readers interested in the details are referred to the code at [17].

We conclude this section with a short discussion on the verification methodology applied here. Details concerning this verification technique and a more generalized methodology will be presented at [18] and the upcoming proceeding.

2.4 Verification by Induction and Exhaustive Search

Verification of properties of an Ass is often done by induction on reachable states, more specifically by induction over the length of transition sequences from initial states to reachable states. That is, we show that a certain property (\( \mathtt{invprop } \)) holds in the set of initial states, characterized by \( \mathtt{init } \). Furthermore, as we proceed through transitions (state changes), the \( \mathtt{invprop } \) is preserved.

But to show liveness properties, considering only invariant properties on states is not enough. We thus use an extended method that does inductive proofs on the reachable state space, and in parallel proves properties (\( \mathtt{transprop } \)) on all transitions between reachable states. To be a bit more specific, assume that \(S \Rightarrow S'\) is a transition from one state (state term, state pattern) \(S\) to a state \(S'\). We show that if \( \mathtt{invprop } (S)\) holds, then also \( \mathtt{invprop } (S')\) (the induction on reachable states), but also that for this transition \( \mathtt{transprop } (S,S')\) holds.

Both of these are done with CafeOBJ’s built-in search predicate (see Sect. 4.2), which exhaustively searches and tests all possible transitions from a given state (pattern). The concepts introduced here are an extension and generalization of transition invariants [16], details can be found in [7].

In the CafeOBJ setting, which means rewrite-based, we have to ensure that both of the following implications reduce to \( \mathsf True \):

$$\begin{aligned} \mathtt{init } (S)&\rightarrow \mathtt{invprop } (S)\\ \mathtt{invprop } (S)&\rightarrow \mathtt{invprop } (S') \qquad \text {where} \;S \rightarrow S' \;\text {is a transition} \end{aligned}$$

where \(S\) and \(S'\) are states (state terms) describing the pre- and post-transition states, respectively. This has to be checked for all possible transitions available in the specification.

If this can be achieved, we can be sure that in all reachable states, i.e., those that can actually occur when starting from an initial state, the required property \( \mathtt{invprop } \) holds.

3 Extended Specification

The starting point of the following discussion is the question of how to verify liveness properties. Initial work by the first author led to a specification which kept track of the waiting time in the queue. Combined with the assumption that there are only finitely (but arbitrary) many agents, we could give a proof score not only for the mutual exclusion property \(\mathsf{mp }\), but also for the progress property \(\mathsf{pp }\). This work was extended by the third author to the currently used base specification.

To verify the last property, \(\mathsf{ep }\), operational considerations alone do not suffice. On the level of observers, we cannot guarantee that an agent will ever enter the queue, since we have no control over which transitions are executed by the system. To discuss (verify) this property, we have to assume a certain meta-level property, in this case the fairness of the transition sequence. A similar approach has been taken in [9] for the Alternating Bit Protocol, where fair event mark streams are considered.

3.1 Fairness

The concept of fairness we are employing here is based on the mathematically most general concept:

Definition 1

(Fairness). A sequence of transitions \(S\) is called fair, if every finite sequence of transitions appears as sub-sequence of \(S\).

A necessary consequence of this definition is that every fair sequence is infinite.

Relation to Other Concepts of Fairness. The methodology of using Ass in CafeOBJ has been strongly influenced by UNITY [4], which builds upon a semantics similar to Ass of sequences of states and temporal operators. It provides an operator ensures, which can be used to model fairness via a measure function.

Another approach to the concept of fairness is taken by LTL logic [19], where two types of fairness, strong and weak, are considered, referring to enabled and applied state of transitions.

$$\begin{aligned} \text {weak}&\qquad \qquad \qquad \Diamond \Box \mathop {enabled}(t) \rightarrow \Box \Diamond applied (t)\\ \text {strong}&\qquad \qquad \qquad \Box \Diamond \mathop {enabled}(t) \rightarrow \Box \Diamond \mathop {applied}(t) \end{aligned}$$

where enabled and applied are properties on transition instances. In the particular case we are considering, enabled is always true, as we can execute every instance of a transition at any time, due to the fact that the wait-state transition can be applied even if the agent is not at the top of the queue. Fairness in this case means that, at some point every transition will be applied.

Both concepts can be represented in suitable way by the definition of fairness, or in other words, the definition used in this setting (every finite sequence is sub-sequence) subsumes these two concepts.

3.2 Transition Sequence

As mentioned above, modeling fairness requires recurring to a meta-assumption, namely that the sequence of transitions is fair, i.e., every instance of a transition appears infinitely often in the sequence. In our case we wanted to have a formalization of this meta-assumption that can be expressed with the rewriting logic of CafeOBJ.

The approach we took models transition sequences using behavioral specification with hidden algebra [9], often used to express infinite entities. Note that we are modeling the transition sequence by an infinite stream of agent identifiers, since the agent uniquely defines the instance of transition to be used, depending on the current state of the agent. This is a fortunate consequence of the modeling scheme at the base level, where, if we pick an agent, we can always apply the transition that is uniquely defined by that agent. Translated into the language of the above mentioned LTL logic it means that all transitions are permanently enabled.

figure g

The transition sequence is then used to model a meta-state, i.e., the combination of the original state of the system as specified in the base case, together with the list of upcoming transitions:

figure h

The dots at the end of the definition refer to a long list of functions on meta-states, we will return to this later on.

In the same way, transitions from the base case are lifted to the meta-level. Here we have to ensure that the semantics of transition sequences and the transition in the original (non-meta level) system do not digress. That means first and foremost, that only the agent at the top of the transition sequence can be involved in a transition.

Let us consider the first transition WaitTrans:

figure i

Due to the structural definition of the meta-transition, we see that it can only be applied under the following conditions that

  • the agent is at the top of the transition sequence, and

  • the agent is in remainder section \(\mathsf{rs }\).

The next transition is TryTrans, where an agent checks whether it is at the top of the queue, and if yes, enters into the critical section. Adding the meta-level requires only that the agent is also at the head of the transition sequence. This transition uses the built-in operator if_then_else_fi, because we want to destructively use up the top element of the transition sequence to ensure that no empty transitions appear.

figure j

The final transition is ExitTrans, where an agent returns into the remainder section:

figure k

Relation between meta-transition and transition. Comparing the transition of the base system (see listing on p. 7), we see that in the meta-transition the part to the left of   \({}^{\widehat{}}\) , the state of the base system, behaves exactly like the corresponding part in the base transition. The only difference is that an additional guard is added, namely that the active agent has to be also at the top of the transition sequence to the right of the \({}^{\widehat{}}\) marker. This can be considered a general procedure of meta-level reflection.

Combining all these algebras provides the specification of the meta system:

figure l

As mentioned above, to express the fairness condition, we recur to an equivalent definition, namely that every finite sequence of agent identifiers can be found as a sub-sequence of the transition sequence, rephrased here in an indirect way in the sense that it cannot happen that we cannot find a (finite) sequence of agent identifiers in a transition sequence:

figure m

3.3 Waiting Times

The axiom shown above uses the function find, which has been defined in the algebra METASTATE. We mentioned that several additional functions are defined, too. These functions are necessary to compute the waiting time for each agent.

Waiting time here refers to the number of meta-transitions until a particular agent is actually changing its section. Here complications arise due to the trial transition from ws to \(\mathsf{cs }\) (by means of the if_then_else_fi usage), where an agent might find itself still in ws due to not being at the head of the queue. This has to be considered while computing waiting times for each agent.

Closer inspection of the transition system provides the following values for waiting times:

For agents in \(\mathsf{rs }\) and \(\mathsf{cs }\). The waiting time is determined by the next occurrence of its agent id in the transition sequence, since there are no further requirements. In CafeOBJ notation, the length of the following sequence:

figure n

For agents in ws. Here we have to ensure that the agent advances to the top of the queue. Thus, each agent higher up in the queue has to appear two times in the transition sequence, once for entering the critical section, and once for leaving it. Let \(Q_A\) be the part of the queue that is above (higher up) the agent id \(a\). Then the waiting time for \(a\) would be determined by doubling \(Q_A\), then searching the transition sequence first for the doubled \(Q_A\), and finally searching for the next appearance of \(a\). Consider for example the state represented in Fig. 2. Assume that initially the queue contains the three agent identifiers \(b\), \(c\), and \(a\) (in this order), and all of them are initially in \(\mathsf{rs }\). To see when the \(a\) at the bottom of the queue can transition into \(\mathsf{cs }\), we first have to bring \(b\) into \(\mathsf{cs }\), which happens at position 2. After that there is a series of trial transitions without success (\(a\), \(c\), \(a\)) until another \(b\) appears, which makes the agent \(b\) transition back into \(\mathsf{rs }\). At this point the queue contains two elements, \(c\) and \(a\). The same repeats for \(c\), until finally \(a\) can enter into \(\mathsf{cs }\). Summing up, what has to be searched within the transition sequence is the sub-sequence 

figure o

, which amounts to (in CafeOBJ notation):

figure p

(The actual code is slightly different, but semantically the same.)

Fig. 2.
figure 2

Computing of waiting time from ws to \(\mathsf{cs }\)

Full size image

Here the doubling of the \(Q_A\) is achieved by first finding the sub-sequence within the queue up to \(A\) (which includes \(A\)), and then dropping the last element, which is \(A\).

The functions mentioned above are exactly those needed to compute this waittime function. Due to the necessity of error handling, the definition becomes a bit lengthy.

4 Verification of Properties

Our aim is to verify the progress property and the entrance property. These properties are now expressed in the following ways:

  • At any transition, the waiting time of agents not changing section decreases.

  • If the waiting time of an agent reaches \(0\), then a section change happens.

Combining these two properties, and assuming fairness, we can show both, that every agent will eventually enter into the queue, and every agent in the queue will eventually gain access to the resource, i.e., enter into the critical section.

In the following let us assume that the following variable definitions are in effect:

figure q

Then the CafeOBJ implementation of the first property is as follows:

figure r

And the one of the second property:

figure s

Here we have to note that the sec operator computes the actual section SS and not the one given by C.

These two properties alone do not function as inductive invariant, so several more have to be included. In addition, we are lifting also the properties used in the original specification to the meta level by making the new operators simply operate on the projections. Again, the interested reader is referred to [17] for the full source.

4.1 Proof Score with Patterns

The method described in Sect. 2.4 is used here in combination with a covering set of patterns. We mention only the definition of cover set here, but details on this methodology will be presented at [18] and a forthcoming article:

Definition 2

(cover set). Assume a set \(\mathcal {S}\subseteq {\mathsf{\textit{State} }}\) of states (ground terms of sort State) is given. A finite set of state patterns \(\mathcal {C}= \{ C_1, \ldots , C_n\}\) is called cover set for \(\mathcal {S}\) if for every \(s\in \mathcal {S}\) there is a substitution \(\delta \) from the variables \(\mathbf {X}\) occurring in \(\mathcal {C}\) to the set of all ground terms, and a state pattern \(C\in \mathcal {C}\) such that \(\delta (C)=s\).

Practically this means, that we give a set of state terms that need to cover all possible ground instances of state terms. For the base case, a set of 13 state patterns has been given. We list only the cases for \(\mathsf{rs }\), the cases for the other sections are parallel.

figure t

For the meta-level we combine these patterns with patterns for the transition sequence, where once b1 is at the head of the transition sequence, and once another identifier b2, amounting to 26 different meta state patterns:

figure u

We conclude this section with a discussion of the search predicate, actually family of search predicates, in CafeOBJ.

4.2 The CafeOBJ Search Predicate

During a proof over reachable states by induction on the transitions, we need a method that provides all possible successors of a certain state. The CafeOBJ search predicate we use is \(S\,\mathtt{= }\mathtt {(*,1)=>+} ~ S'\) suchThat \({{ prop}}(S,S')\), where \(S\) and \(S'\) are states, and \({ prop}(S,S')\) is a Boolean value. This is a tricky predicate and full discussion is available in an upcoming reference manual for CafeOBJ, but in this case it does the following:

  • It searches all successor states \(S'\) that are reachable in exactly one step from the left side state \(S\) (here 1 stands for maximal one step, and + for at least one step). Call the set of successors \( Succ (S)\).

  • It checks all those states determined by the first step whether the property given in Bool holds. If there is at least one successor state where it holds, the whole predicate returns true, i.e., what is returned is \(\exists S'\in Succ (S) : { prop}(S,S')\).

This can be used with a double negation to implement an exhaustive search in all successor states by using the equality:

$$ \forall S'\in Succ (S) : { prop}(S,S') \quad \Leftrightarrow \quad \lnot \exists S'\in Succ (S) : \lnot { prop}(S,S') $$

This leads to the following, admittedly not very beautiful, definition of the inductive invariant condition, where we use SS for the \(S'\) in the above equality:

figure v

Here inv-prop is the set of inductive invariant properties we have mentioned above.

Note that the operator used here has access not only to the original or the successor state, but to both states. This peculiar feature allows us to prove properties like decrease of waiting time, which is impossible if there is no access to both values in the same predicate. As pointed out above, CafeOBJ actually includes a whole set of search predicates which allows searching for arbitrary, but given depth, but verifications making use of these predicates are still to come.

The final step in the proof score is to verify that both the initial condition and the inductive invariant condition do actually hold on all the state patterns by reducing the expressions to true:

figure w

This concludes the discussion of the specification methodology and proof score code.

5 Discussion and Conclusion

Using the method laid out above, we have formally verified the three properties given in the beginning, mutual exclusion property (only at most one agent at a time is in the critical section), progress property (an agent in the queue will eventually gain access to the resource), and entrance property (every agent will eventually enter into the queue). While the original base specification and proof score verified the first two properties, it also required the assumption that the number of agents is finite. In our case, this assumption is superseded by the assumption of fairness of the transition sequence, which is by itself necessary to verify the third property.

This methodology also opens up further options in the specification. By requiring acquisition of the resource within a reasonable time, and providing requirements on the transition sequence that the reasonable-time condition is fulfilled, we believe it is possible to specify and verify time-critical systems.

We have to note that what we call here progress property has already been shown in different settings [1–3, 5, 13]. The key contribution is the change of focus onto behaviour algebras as specification methodology, and as a consequence the extension to the entrance property, meaning that an agent always gets a chance to enter the queue. In addition, we extended the proof of the progress property to infinitely many agents. Of course, every actual instance of the protocol will encompass only finitely many agents, but the proof provided here is uniform for any number of agents. The current work also serves as an example of reflecting meta-properties into specifications, allowing for the verification of additional properties.

Assuming a meta-level fairness property to prove liveness properties of the specification might be considered a circular argument, but without regress to meta-level fairness, no proof of the entrance property can be achieved. Keeping this in mind, our goal is to provide a reasonably simple and intuitive definition of fairness on the meta-level, that can be used for verification of the necessary properties, similar to any axiomatic approach where trust is based on simple axioms.

Future work we are foreseeing centers around the following points:

  • Adaption of the methodology to other protocols: One probable candidate is the already mentioned Alternating Bit Protocol, where proofs for liveness properties are hard to obtain in other systems. We believe that a meta-specification similar to the one given here can be employed for this protocol, as well as others.

  • Automatization of the method: Most of the steps done during lifting the specification to the meta-level are semi-automatic. It might be interesting to provide built-in functionality to extend a given specification based on states with transition sequences.

  • Relation to other methods in the field: As mentioned in the section on related work, targeting liveness properties is an active research area. While our approach seems to be unique in using behavioral algebras, we will compare the methodologies taken by other researchers.

  • Characterization of strength of properties: We have seen that the mutual exclusion property can be proven by only looking at states, that the progress property only needs access to a state and its successor, but the entrance property needs access to all future states. We are working on a formal description of this concept called \(n\)-visibility.

We conclude with recapitulating the major contributions of this work: First of all, it provides an example for the inclusion of meta-concepts in a formal specification. Reflecting these meta-properties allows for the verification of additional properties, in particular liveness properties.

Furthermore, it is an example of a specification that spans all the corners of the CafeOBJ cube, in particular mixing co-algebraic methods, infinite stream representation via hidden sorts, with transition sequence style modeling.