Approximate Shape Gradients for Interface Problems

Abstract

Shape gradients of shape differentiable shape functionals constrained to an interface problem (IP) can be formulated in two equivalent ways. Both formulations rely on the solution of two IPs, and their equivalence breaks down when these IPs are solved approximatively. We establish which expression for the shape gradient offers better accuracy for approximations by means of finite elements. Great effort is devoted to provide numerical evidence of the theoretical considerations.

The work of A. Paganini was partly supported by ETH Grant CH1-02 11-1.

1 Introduction

Optimal control of mathematical models is a core activity of applied mathematics. The goal is to optimize model parameters with respect to target functionals: real mappings on the set of all admissible configurations. In many practical cases the control parameter is the shape of a structure [1, 2]. In this case we speak of shape functionals and, in particular, of PDE constrained shape functionals, when the mapping involves the solution of a PDE, the so-called state problem.

The sensitivity of shape functionals with respect to perturbations of shapes is expressed by the shape gradient: a linear bounded operator on the space of perturbation directions. The knowledge of this mapping is the starting point for gradient based shape optimization [1–6].

Shape gradients of shape differentiable shape functionals can be stated equivalently as an integration over the volume and as an integration on the boundary [7, Chap. 9, Theorem 3.6]. In the case of PDE constrained shape functionals, shape gradients depend on the solution of the state problem and, in general, on the solution of an additional PDE, the so-called adjoint problem. When the state and the adjoint solutions are replaced with numerical approximations, the equivalence of the two representations of the shape gradient breaks down [8].

Several authors suggested that the volume based formulation is better suited, when discretizations by means of finite elements are considered, cf. [7, Chap. 10, Remark 2.3], [8] and [9, Chap. 3.3.7]. However, to our knowledge, thorough convergence analysis and numerical evidence have not been provided. For the case of elliptic boundary value problem constraints, a first theoretical investigation was conducted in [10]. The aim of this work is to extend these results to the case of elliptic interface value problems. In particular, we devote great effort to provide numerical evidence through numerical experiments. For the sake of simplicity, we restrict our considerations to a class of shape functionals and interface problems. Nevertheless, we believe that our test case is representative and that no important aspect is missing.

2 Shape Gradients

A shape functional is a real valued map ${\mathcal J}:{\mathcal A}\rightarrow \mathbb {R}$ defined on a set of admissible domains ${\mathcal A}$, which is usually constructed starting from an initial open bounded domain $\Omega$. In the general approach by Delfour–Zolesio [7, Chap. 4], ${\mathcal A}$ comprises all domains $T_s(\Omega )$ that are generated through the evolution $T_s(\cdot )$ of the flow of a non-autonomous vector field ${\mathcal V}$.

For a fixed perturbation direction ${\mathcal V}$, the Eulerian derivative

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})\mathrel {\mathop :}=\lim _{s\searrow 0} \frac{J\left( T_s(\Omega )\right) -J(\Omega )}{s} \end{aligned}$$

(1)

expresses the sensitivity of the shape functional ${\mathcal J}$ with respect to the perturbation direction ${\mathcal V}$. Without loss of generality, the vector field ${\mathcal V}$ can be assumed to be autonomous [7, Chap. 9, Sect. 3.1]. The shape functional ${\mathcal J}$ is said to be shape differentiable at $\Omega$ if (1) defines a linear bounded mapping

$$\begin{aligned} d{\mathcal J}(\Omega ;\cdot ):W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d) \rightarrow \mathbb {R}, \quad {\mathcal V}\mapsto d{\mathcal J}(\Omega ;{\mathcal V}), \end{aligned}$$

(2)

which is called the shape gradient of ${\mathcal J}$ at $\Omega$. As already mentioned in the Introduction, shape gradients play a key role in shape optimization.

Shape optimization literature mostly deals with PDE constrained shape functionals that can be expressed as an integral on a subdomain $D\subset \Omega$ [1–8]. Here we consider

$$\begin{aligned} {\mathcal J}(\Omega ) = \int _{D} j(u)\,\mathrm {d}\mathbf {x}, \end{aligned}$$

(3)

where $j:\mathbb {R}\rightarrow \mathbb {R}$ is a Lipschitz continuos function and u is the solution the scalar interface problem

$$\begin{aligned}&\left\{ \begin{aligned} -\mathrm {div}(\sigma (\mathbf {x}) \nabla { u})&= f \qquad \text {in } \Omega = \Omega _1\cup \Omega _2,\\ [\![u ]\!]&= 0\qquad \text {on }\Gamma ,\\ \left[ \!\!\left[ \sigma \frac{\partial u}{\partial \mathbf {n}} \right] \!\!\right]&= 0\qquad \text {on }\Gamma ,\\ u&= 0\qquad \text {on }\partial \Omega , \end{aligned}\right. \end{aligned}$$

(4)

with real piecewise constant coefficient

$$\sigma (\mathbf {x}) \mathrel {\mathop :}=\sigma _1\chi _{\Omega _1}(\mathbf {x})+\sigma _2\chi _{\Omega _2}(\mathbf {x}).$$

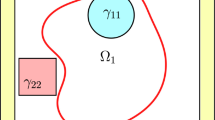
The jump symbol $[\![\cdot ]\!]$ denotes discontinuity across the interface $\Gamma$. Note that for the Neumann jump the vector ${\mathbf {n}}$ points outward, see Fig. 1.

Fig. 1

Computational domain $\Omega$ of (4)

The shape gradient of shape differentiable PDE constrained shape functionals can be expressed both as an integration in volume and as an integration on the boundary (the latter as a result of the Hadamard–Zolésio structure theorem [7, Chap. 9, Theorem 3.6]). For instance, the shape gradient of (3) under the constraint (4) takes the forms¹

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})&= \int _{\Omega }\bigg ( \nonumber \sigma \nabla u \cdot (D{\mathcal V}+ D{\mathcal V}^T) \nabla p + p\nabla f\cdot {\mathcal V}\\&\qquad \qquad +\mathrm{div}({\mathcal V})\left( j(u)-\sigma \nabla u\cdot \nabla p +fp\right) \bigg )\,\mathrm {d}\mathbf {x}\end{aligned}$$

(5)

and

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})= \int _{\Gamma }({\mathcal V}\cdot {\mathbf {n}})\left[ \!\!\left[ 2\sigma \frac{\partial p}{\partial {\mathbf {n}}}\frac{\partial u}{\partial {\mathbf {n}}}-\sigma \nabla u\cdot \nabla p \right] \!\!\right] \,\mathrm {d}S, \end{aligned}$$

(6)

where p is the solution of the adjoint problem

$$\begin{aligned}&\left\{ \begin{aligned} -\mathrm{div}(\sigma (\mathbf {x})\nabla p)&= j'(u)\chi _D&\mathrm {in}\ \Omega ,\\ [\![p ]\!]&= 0&\mathrm {on}\ \Gamma , \\ \left[ \!\!\left[ \sigma \frac{\partial p}{\partial \mathbf {n}} \right] \!\!\right]&= 0&\mathrm {on }\ \Gamma ,\\ p&= 0&\mathrm {on }\ \partial \Omega . \end{aligned}\right. \end{aligned}$$

(7)

Remark 1

Deriving explicit formulas of shape gradients is a delicate and error prone task. Among the several techniques available in literature, the so-called “fast derivation” method of Céa provides a formal shortcut to find the boundary based formulation, cf. [1, Chap. 6.4.3] and [11]. However, great care has to be taken with interface problems. In this case it is worth working out the details in order to overcome the subtle issues induced by the presence of the interface. A thorough derivation of (5) and (6) can be found in [5].

3 Approximation of Shape Gradients

The shape gradient $d{\mathcal J}(\Omega ;{\mathcal V})$ of (3) depends on the solution of the two IPs (4) and (7). To better stress this dependency, as well as to distinguish between Formulas (5) and (6), we refer to them with the notation $d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Vol}}$ and $d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Bdry}}$, respectively.

Lemma 1

Let u and p be exact solutions of (4) and (7), respectively. Then, the following equality holds

$$\begin{aligned} d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Vol}}= d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Bdry}}. \end{aligned}$$

(8)

Proof

Integration by parts on Formula (5) yields

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})&= \int _{\Omega }\bigg ( \nonumber \sigma \nabla u \cdot (D{\mathcal V}+ D{\mathcal V}^T) \nabla p \\ \nonumber&\qquad \qquad -{\mathcal V}\cdot \left( j'(u)\nabla u-\sigma \nabla (\nabla u\cdot \nabla p) +f\nabla p\right) \bigg )\,\mathrm {d}\mathbf {x}\\&\quad +\int _\Gamma [\![{\mathcal V}\cdot {\mathbf {n}}\left( j(u)-\sigma \nabla u\cdot \nabla p +fp\right) ]\!] \,\mathrm {d}S. \end{aligned}$$

(9)

With the vector calculus identity [8, Eq. (44)]

$$\begin{aligned} \nabla u \cdot (D{\mathcal V}+D{\mathcal V}^T)\nabla p + {\mathcal V}\cdot \nabla (\nabla u \cdot \nabla p) = \nabla p\cdot \nabla ({\mathcal V}\cdot \nabla u)+ \nabla u\cdot \nabla ({\mathcal V}\cdot \nabla p), \end{aligned}$$

(10)

Formula (9) can be rewritten as

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})&= \int _{\Omega }\bigg ( \nonumber \sigma \nabla p\cdot \nabla ({\mathcal V}\cdot \nabla u)+ \sigma \nabla u\cdot \nabla ({\mathcal V}\cdot \nabla p)\\ \nonumber&\qquad \qquad -j'(u){\mathcal V}\cdot \nabla u -f{\mathcal V}\cdot \nabla p \bigg )\,\mathrm {d}\mathbf {x}\\&\quad +\int _\Gamma [\![{\mathcal V}\cdot {\mathbf {n}}\left( j(u)-\sigma \nabla u\cdot \nabla p +fp\right) ]\!] \,\mathrm {d}S. \end{aligned}$$

(11)

Then, integration by parts yields

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})&= \nonumber \int _\Gamma \left[ \!\!\left[ \sigma \frac{\partial p}{\partial {\mathbf {n}}}{\mathcal V}\cdot \nabla u \right] \!\!\right] - \int _\Omega \mathrm{div}(\sigma \nabla p)({\mathcal V}\cdot \nabla u)+j'(u)({\mathcal V}\cdot \nabla u)\,\mathrm {d}\mathbf {x}\\ \nonumber&\quad +\int _\Gamma \left[ \!\!\left[ \sigma \frac{\partial u}{\partial {\mathbf {n}}}{\mathcal V}\cdot \nabla p \right] \!\!\right] -\int _{\Omega }\mathrm{div}(\sigma \nabla u)({\mathcal V}\cdot \nabla p)+f({\mathcal V}\cdot \nabla p)\,\mathrm {d}\mathbf {x}\\&\quad +\int _\Gamma [\![{\mathcal V}\cdot {\mathbf {n}}\left( j(u)-\sigma \nabla u\cdot \nabla p +fp\right) ]\!] \,\mathrm {d}S. \end{aligned}$$

(12)

The two domain integrals in (12) vanish because of (4) and (7). Moreover, since $[\![u ]\!]=0$ on $\Gamma$,

$$\begin{aligned} \left[ \!\!\left[ \sigma \frac{\partial p}{\partial {\mathbf {n}}} {\mathcal V}\cdot \nabla u \right] \!\!\right] = {\mathcal V}\cdot {\mathbf {n}}\left[ \!\!\left[ \sigma \frac{\partial p}{\partial {\mathbf {n}}}\frac{\partial u}{\partial {\mathbf {n}}} \right] \!\!\right] \quad \text {and}\quad [\![{\mathcal V}\cdot {\mathbf {n}}j(u) ]\!] = 0, \end{aligned}$$

and since $[\![p ]\!]=0$, $[\![{\mathcal V}\cdot {\mathbf {n}}fp ]\!] = 0$, so that we retrieve

$$\begin{aligned} d{\mathcal J}(\Omega ;{\mathcal V})&= \int _\Gamma {\mathcal V}\cdot {\mathbf {n}}\left[ \!\!\left[ 2\sigma \frac{\partial p}{\partial {\mathbf {n}}}\frac{\partial u}{\partial {\mathbf {n}}}-\sigma \nabla u\cdot \nabla p \right] \!\!\right] \,\mathrm {d}S. \end{aligned}$$

(6)

   $\square$

Remark 2

For $d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Vol}}$ to be well-defined, it is sufficient to assume that $u,\,p\in H^{1}({\Omega })$. On the other hand, higher regularity of u and p is required for $d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Bdry}}$ to be well-defined because the latter is not continuous on $H^{1}({\Omega })$.

Usually, exact solutions of IPs are not available, and one has to rely on numerical approximations $u_h,\,p_h\in W^{1,\infty }(\Omega )$. Equality (8) breaks down when u and p are replaced with their approximate counterparts [8], and both formulas (5) and (6) become approximations

$$\begin{aligned} d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}\approx d{\mathcal J}(\Omega ;{\mathcal V})\approx d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Bdry}}\end{aligned}$$

(13)

of the exact value $d{\mathcal J}(\Omega ;{\mathcal V})$. The natural question is then which among $d{\mathcal J}(\Omega ,u_h,p_h;\cdot )^{\mathrm {Vol}}$ and $d{\mathcal J}(\Omega ,u_h,p_h;\cdot )^{\mathrm {Bdry}}$ is closer to $d{\mathcal J}(\Omega ;\cdot )$.

The answer may depend on the underlying discretization scheme. Although discretization by boundary element method is also possible [2, 4], we focus on discretizations by means of finite elements. This is the most popular choice in shape optimization because of its flexibility, which is much appreciated among engineers.

In applied mathematics several operators that depend on the solution of boundary value problems have equivalent volume and boundary based representations. For instance, this is the case for lift functionals for potential flow [12] and for far field functionals in electromagnetism [13, 14]. When used in the context of finite element approximations, volume based formulations tend to exhibit faster convergence and superior accuracy than their counterparts formulated on the boundary. This can be motivated by volume integrals being continuous in energy norm, whilst boundary integrals involve traces that are not well-defined on the natural variational space. This difference determines whether the formulation displays the superconvergence that holds for the evaluation of continuous functionals on Galerkin solutions [15, Sect. 2].

On account of Remark 2, we heuristically expect the same trend in (13). A rigorous statement can be made in case of smooth interfaces and sufficient regular source function in (4). Following the same lines as for the proofs of Theorems 3.1 and 3.2 in [10], it can be shown that²

$$\begin{aligned} \vert d{\mathcal J}(\Omega ;{\mathcal V})- d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}\vert = C h^2 \Vert {\mathcal V}\Vert _{W^{2,4}(\mathbb {R}^d;\mathbb {R}^d)} \end{aligned}$$

(14)

and that

$$\begin{aligned} \vert d{\mathcal J}(\Omega ;{\mathcal V})- d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Bdry}}\vert = C h \Vert {\mathcal V}\Vert _{L^{\infty }(\mathbb {R}^d;\mathbb {R}^d)}, \end{aligned}$$

(15)

when $u_h$ and $p_h$ are Ritz-Galerkin solutions computed with piecewise linear Lagrangian finite elements on a family of quasi-uniform triangular meshes with nodal basis functions.

Remark 3

The result (14) is restricted to vector fields in $W^{2,4}(\mathbb {R}^d;\mathbb {R}^d)$ because the proof relies on finite element duality techniques [16, Chap. 5.7]. However, the volume based formulation (5) is a continuous linear operator with respect to $W^{1,\infty }(\mathbb {R}^d;\mathbb {R}^d)$, and it can easily be shown that

$$\begin{aligned} \vert d{\mathcal J}(\Omega ;{\mathcal V})- d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}\vert = C h \Vert {\mathcal V}\Vert _{W^{1,\infty }(\mathbb {R}^d;\mathbb {R}^d)}. \end{aligned}$$

(16)

On the other hand, the estimate (15) relies on the nontrivial approximation properties of finite element solutions in $W^{1,\infty }(\Omega )$ [16, Corollary 8.1.12]. We are not aware of a technique to improve the rate in (15) by restricting the space of vector fields.

4 Numerical Experiments

We consider the quadratic shape functional

$$\begin{aligned} {\mathcal J}(\Omega ) = \int _\Omega u^2 \,d\mathbf {x}. \end{aligned}$$

The shape gradient is a linear bounded operator on $W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)$. Hence, the quality of the approximation in (13) should be investigated in the operator norm. Numerically, this is an extremely challenging task, if not impossible. Therefore we have to content ourself with considering convergence with respect to a more tractable operator norm over a finite dimensional space of vector fields.

Since we are mainly interested in contributions of the interface, we select vector fields that vanish on $\partial \Omega$. We set $\Omega =]-2,2[^2$ (a square centered in the origin and with side equal 4), and we restrict ourself to the finite dimensional space of vector fields of the form³

$$\begin{aligned} {\mathcal V}(x,y) = \sum _{\begin{array}{c} m_1+n_1\le 5\\ m_2+n_2\le 5\\ m_1,m_2,n_1,n_2\ge 1 \end{array}} \lambda _{m_1,n_1}\left( {\begin{array}{c}v(x,y,m_1,n_1)\\ 0\end{array}}\right) +\lambda _{m_2,n_2}\left( {\begin{array}{c}0\\ v(x,y,m_2,n_2)\end{array}}\right) \end{aligned}$$

with $v(x,y,m,n) =\sin (mx\pi /2)\sin (ny\pi /2)$ and $\lambda _{m_i,n_i}\in \mathbb {R}$. Moreover, we replace the $W^{1,\infty }$-norm with the more manageable $H^1$-norm.

To investigate the convergence, we monitor the approximate dual norms

$$\begin{aligned} \mathrm {err}^{\mathrm {Vol}} \mathrel {\mathop :}=\left( \max _{{\mathcal V}} \frac{1}{\Vert {\mathcal V}\Vert _{H^{1}({\Omega })}^{2}} \vert d{\mathcal J}(\Omega ;{\mathcal V}) - d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}\vert ^2 \right) ^{1/2} \end{aligned}$$

(17)

and

$$\begin{aligned} \mathrm {err}^{\mathrm {Bdry}} \mathrel {\mathop :}=\left( \max _{{\mathcal V}} \frac{1}{\Vert {\mathcal V}\Vert _{H^{1}({\Omega })}^{2}} \vert d{\mathcal J}(\Omega ;{\mathcal V}) - d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Bdry}}\vert ^2 \right) ^{1/2} \end{aligned}$$

(18)

on different meshes generated through uniform refinement.⁴ The reference value $d{\mathcal J}(\Omega ;{\mathcal V})$ is approximated by evaluating both $d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}$ and $d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Bdry}}$ on a mesh with an extra level of refinement. To avoid biased results we display convergence history both with self- and cross-comparison.

As in [10], we consider finite element discretizations based on linear Lagrangian finite elements on quasi-uniform triangular meshes with nodal basis functions.⁵ Integrals in the domain are computed by 7 point quadrature rule in each triangle, while line integrals by 6 point Gauss quadrature on each segment. In experiment 1, the interface is approximated by a polygon. Nevertheless, the convergence of linear finite elements is not affected by this discretization [17].

In the first numerical experiment the interface $\Gamma$ is a circle centered in (0.1, 0.2) and with radius equal 1, see Fig. 2 (left). The problem data are

$$\begin{aligned} f(\mathbf {x}) = 1 \quad \text {and}\quad \sigma (\mathbf {x}) = 2\chi _{\Omega _1}(\mathbf {x})+1\chi _{\Omega _2}(\mathbf {x}). \end{aligned}$$

(19)

The numerical results are displayed in Fig. 3 (left column). We clearly see that the volume based formulation converges faster and is more accurate than its boundary based counterpart. The convergence rates agree with what has been predicted by (14) and (15). In the cross-comparison plot $d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}$ saturates due to insufficient accuracy of the reference solution computed with $d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Bdry}}$, whereas the boundary based formulation converges with the same rate as for the self-comparison.

Fig. 2

Plot of the solution u of the state problem in the computational domain $\Omega$ for the first (left) and the second (right) numerical experiment. The interface is drawn with a dashed line

In the second numerical experiment the interface $\Gamma$ is a triangle with corners located at $(-1,-1)$, $(1,-1)$ and (0.2, 1), see Fig. 2 (right). Interface corners are known to affect the regularity of the solution of interface problems [18]. Therefore, the estimates (14) and (15) can not be proved in this case, and we expect to observe lower convergence rates. To better stress the impact of the corners we increase the contrast of the diffusion coefficient by setting

$$\begin{aligned} \sigma (\mathbf {x}) = 10\chi _{\Omega _1}(\mathbf {x})+1\chi _{\Omega _2}(\mathbf {x}). \end{aligned}$$

The source function is the same as in (19). From the results displayed in Fig. 3 (right column) we observe that the volume based formulation converges faster and is more accurate then its boundary based counterpart. Again, in the cross-comparison the convergence history of the volume based formulation saturates due to an insufficient accuracy of the reference solution computed with $d{\mathcal J}(\Omega ,u_h,p_h;{\mathcal V})^{\mathrm {Vol}}$. We suspect that this inaccuracy gives rise to the difference in the convergence rates of the boundary based formulation between self- and cross-comparisons.

Fig. 3

Convergence history for the first (left column) and the second (right column) numerical experiment. In the first row the reference value $d{\mathcal J}(\Omega ;{\mathcal V})$ is computed with an extra level of refinement. The second row displays cross-comparisons

In the third numerical experiment we investigate the impact of the choice of the diffusion coefficient $\sigma$ on the results obtained in the first and in the second numerical experiment. For $\sigma _2 = 1$ fixed and $\sigma _1=0.1, 0.5, 0.8, 1.25,2,10$, we monitor the approximate relative error constructed by dividing the approximate dual norms (17) and (18) by

$$\max _{{\mathcal V}} \frac{\vert d{\mathcal J}(\Omega ;{\mathcal V})\vert }{\Vert {\mathcal V}\Vert _{H^{1}({\Omega })}}\,.$$

The reference solution is computed evaluating $d{\mathcal J}(\Omega ,u,p;{\mathcal V})^{\mathrm {Vol}}$ on a mesh with an extra level of refinement. In Fig. 4 (left), we see that the choice of the diffusion coefficient $\sigma$ has no influence on the convergence rates in case of a circular interface. On the other hand, for non-smooth interfaces, the effect of the singularity in the functions u and p is visible only for high contrasts $\sigma _1/\sigma _2$.

Fig. 4

Convergence history for the third numerical experiment. The choice of the diffusion coefficient has no influence on the convergence rates in case of a circular interface (left). On the other hand, for a triangular interface (right), the effect of the singularity in the functions u and p is visible only for high contrasts $\sigma _1/\sigma _2$

5 Conclusion

The shape gradient of shape differentiable PDE constrained shape functionals is a linear bounded operator on $W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)$, and its knowledge is the starting point for gradient based shape optimization. The shape gradient can be stated both as an integration in volume and as an integration on the boundary, both of which depend on the solution of boundary value problems. When used with discrete solutions, these two representations lose their equivalence and become approximations of $d{\mathcal J}(\Omega ;\cdot )$. Theoretical considerations in Sect. 3 and numerical experiments in Sect. 4 convey that volume based approximations of the shape gradient are better suited in the context of finite element discretizations. Although our investigations are conducted on a chosen class of scalar interface problems, we believe that similar conclusions can be drawn for the case of more general PDE constraints stemming from electromagnetism and continuum mechanics.