Keywords

62.1 Introduction

The craze for nanomaterials is expected of their development. Special properties resulting from an increase in surface area and decreased length characteristics are considered. In the case of nanocomposite particulates, in addition to a conventional mixing effect, the addition of nano-sized particles of various matrices cause a change of properties, in particular mechanical, electrical, and of the matrix itself, and simultaneously effect greater capacity especially at low particle sizes. The understanding of phenomena that appear at the interface between the inclusions and the matrix, and the analysis of the influence of the characteristic dimensions of the various phases on the mechanical behavior is found to be of particular interest for the study of these materials.

The improved property of materials is a key industrial performance. More efficient materials reduce the amount of material used to perform a function (stiffness, transmission of current, heat, etc.). One solution is to combine materials with different properties to take advantage of each. These composites consist of two, three, or more elementary materials that each have a role and a function specifies a matrix which gives the overall shape and liaison between the various components and reinforcements that provide the technical functions [1–10].

In the past 10 years, new nanoscale objects also having a fiber-type long winding inspired many works on polymer matrix nanocomposites: carbon nanotubes.

Carbon is an almost essential chemical element that enters into the composition of many organic substances as well (amino acids) and also inorganic (carbides, carbonates). Prior to 1985 there were only two crystalline phases of the rare carbon, hard and insulating the more abundant is called the diamond, the other ductile and conductive called graphite.

Carbon nanotubes are expected and will likely be one of the greatest technological revolution sources. Dice 70, micrographs of nanotubes are visible; they are called hollow cores because they are the central tube on which are deposited layers of carbon to form VGCF (vapor-grown carbon fibers, fiber carbon spray-marks). We paid little attention to detailed analysis of their structure by Iijima [1, 2] in 1991. This study marks the beginning of intensive research on carbon nanotubes The study of composite nanotube is in itself an area of research.

Regarding micromechanical models for electrical percolation properties, we conducted two studies on polyethylene matrix composites reinforced with carbon nanotube monoparpois (SWNTs) in different lengths.

62.2 Physical Model

Elastic constitutive models are developed for nanotube composites/polyethylene with and without functionalization, to predict the functionalization effect of the mechanical stiffness and elastic properties of nanocomposites [3]. We use the equivalent continuum models (molecular dynamics) for predicting the Young’s moduli and shear moduli of the compounds of the amorphous and crystalline polyethylene matrix systems, and various length nanotubes. Figure 62.1 is a model of atomic structure by the functionalization of composite carbon nanotube/polyethylene.

Fig. 62.1
figure 1

Atomic modeling structure by the functionalization of the polyethylene/nanotube composite [8]

Full size image

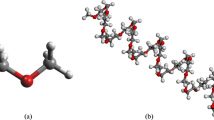
The purpose of the molecular model is to establish the molecular structure of the balanced system. Simulations of the molecular dynamics (MD) were therefore used to determine the equilibrium structures of the nanotube composite and polymer nanocomposites. Carbon nanotube-polymer considered in this work contains nanotubes of large and small lengths as shown in Figs. 62.2 and 62.3. The dashed boxes in the figure contain a representative volume element that is simulated by molecular dynamics [5, 6]. In each compound, the nanotubes are sufficiently separated to prevent the polymer interactions CNT–CNT. The nanotube composite in Fig. 62.1, for example, contains zigzag nanotubes (10.0) that periodically pass through the folded length of the simulation cell. In our model the nanotube is embedded in an amorphous matrix of polyethylene (PE), represented by units CH2-CH2. Specifically, the polyethylene matrix contains six channels of 25-CH2 monomers. For example, Fig. 62.1 shows the application of a stress on the cell simulation for the different directions (x and y). The mechanical response of polymer-nanotube composites submitted to mechanical loading is provided by the stress–strain curves. In the current work, the stress–strain curves of the CNT composite polyethylene obtained by molecular dynamics simulations are presented [2, 13].

Fig. 62.2
figure 2

Diagrams of polymer nanocomposite carbon nanotubes: (a) big length nanotubes (b) small length nanotubes [8]

Full size image
Fig. 62.3
figure 3

Model (VER cell) nanocomposite [8]

Full size image

62.3 Molecular Mechanics and Dynamics

In a molecular dynamics simulation, the infinite crystal is represented by a cell of the same symmetry as the crystal, subject to periodic boundary conditions; individual movements of particles in the cell are studied by integrating Newton’s equations [4].

As part of this work, we consider only the degrees of freedom of the position of Cartesian coordinates of the atoms. In classical simulations, the Hamiltonian molecular system takes the following form [5, 6].

$$ H\left(p,r,m,s\right)=K\left(p,m\right)+v\left(r,s\right) $$
(62.1)

The first term represents the kinetic energy

$$ K\left(p,m\right)={\displaystyle \sum_{i=1}^N\frac{p_i^2}{2{m}_i}}={\displaystyle \sum_{i=1}^N\frac{1}{2}}\ {m}_i{v}_i^2 $$
(62.2)

The potential describing the interaction of the atoms in an organic material is given in many forms. In the system of interactions nanotube/polyethylene carbon involving only carbon and hydrogen, this potential is called the Terssoff–Brenner potential [7, 8] and is widely used for related interactions. It can be expressed by masses and is independent of the coordinates of the particle.

The second term is the potential energy, also called the interaction function (field strength), which describes the interaction energy as a function of particle coordinates r

$$ v\left(r,s\right)=v\left({r}_1,{r}_2,\dots {r}_N;\;{s}_1,{s}_2,\dots {s}_M\right) $$
(62.3)
$$ v={\displaystyle \sum_i{\displaystyle \sum_{j\left(>i\right)}\left[{v}_R\left({r}_{i j}\right)-{B}_{i j}{v}_A\left({r}_{i j}\right)\right]}} $$
(62.4)

Or r ij is the distance between atoms i and j, V R and V A are the attractive and repulsive interactions, and B ij the coupling between the atom i and the atom j for length and angles ENTERED atoms. The force f i acting on a particle i is given by the following equation,

$$ {f}_i=-\frac{\partial }{\partial {r}_i}v\left({r}_1,{r}_2,\dots {r}_N\right) $$
(62.5)

We use Newton’s equations to describe the evolution of atoms in phase space. Other choices exist such as the Lagrange or Hamilton equations. Newton’s equations are used in the form

$$ \frac{d{r}_i(t)}{dt}={v}_i(t) $$
(62.6)

and

$$ \frac{d{v}_i(t)}{dt}=\frac{f_i(t)}{m_i} $$
(62.7)

The atomic velocities are indicated by v i , the force acting on the atom i and the time t by f i (t). Newton’s equations are only valid for the Cartesian coordinates of a particle r i of mass m i . In molecular dynamics simulations, the equations are “integrated” numerically in time.

The integration of these equations is done by dividing the path into a series of discrete states separated by very short intervals of time whose length defines the integration step.

The displacement of an atom during the time interval is thus given by Eq. (62.8).

$${\overrightarrow{r}}_i\left(t+\Delta t\right)={\overrightarrow{r}}_i(t)+{\overrightarrow{V}}_i\left(t+{1}\!\left/ {2}\right.\Delta t\right)\Delta t $$
(62.8)

It is then possible to determine the acceleration from Newton’s second law and for each atom speed:

$$ {\overrightarrow{V}}_i\left(t+ {\Delta t}\!\left/ {2}\right.\right)={\overrightarrow{V}}_i\left(t- {\Delta t}\!\left/ {2} \right.\right)+{\overrightarrow{\gamma}}_i(t)\Delta t $$
(62.9)

The speed determination provides the position of the atom with the equation previously set at the time (t + Δt). Repeating this procedure at discrete time intervals depending on the speed of the identification results in the path [9].

62.3.1 Minimization of Energy

Molecular mechanics allows us to minimize the energy in order to obtain low-energy configurations of our molecular system and reduce too large initial forces that lead to an aberrant trajectory.

We used two methods of gradient and Newton’s method using the potential energy and the following derivative with r. The disadvantage of these methods is that they follow almost exactly the gradient of potential energy by moving in the configuration space.

$$ \Delta {r}_i\approx -\frac{\partial }{\partial {r}_i}v\left({r}_1,{r}_2,\dots {r}_N\right) $$
(62.10)

In this way, it moves almost exclusively down on the energy hypersurface, and the minimum usually reaches the local minimum closest to the initial configuration [14].

62.3.2 Molecular Mechanics

Molecular mechanics and molecular structure are likened to a set of harmonic oscillators (system composed of balls and springs); harmonic functions are associated with a series of potential functions [9]. The sum of these functions is then expressed in the form of a force field molecular.

$$ {E}_{tot}={E}_{li\acute{e} e}+{E}_{non- li\acute{e} e} $$
(62.11)

62.4 Results and Discussion

The composite studied is obtained by grafting the six channels of PE monomers each consisting of 25 (density 0.71 g/cm3) in a zigzag; SWNT has different lengths of a temperature 298 K.

62.4.1 Minimization of Composites with Nanotubes of Different Lengths—Results

For minimization, we use three methods of minimization (steepest gradients, conjugate gradient, Newton) and we obtain the potential energy and the van der Waals energy (repulsive) increase with increasing lengths of carbon nanotubes. Figure 62.4 shows the change in potential energy and the van der Waals energy in the function of the lengths of carbon nanotubes.

Fig. 62.4
figure 4

Energy variation according to the lengths of the nanotubes

Full size image

62.4.2 Molecular Dynamics at Constant Pressure for Composites with Nanotubes of Different Lengths—Results

A molecular dynamics simulation was performed on a model of composite PE/CNT to track changes in the cell over time. The molecular dynamic investigations, subset NPT (number of particles, pressure, and constant temperature), were performed in a simulation box at room temperature 298 K; incorporating Newtonian equations of motion for the simulations was DM done according to the Verlet algorithm [9], with no integration of 1 fs, for a period of 50 ps, and a cutoff number (R c) equal to 8.50. We used the Parnillo Berendsen method for controlling the temperature and pressure.

Figure 62.5 represents the stress–strain curves of the longitudinal and transverse composites of carbon nanotubes/PE of different lengths.

Fig. 62.5
figure 5

Longitudinal and transverse stress–strain curves in a composite with (a) CNT is long (51.12)A; (b) CNT medium length (34.08) A; (c) CNT short length (8.52)A

Full size image

The stress in the transverse direction decreases in the three composites because of the crack of the carbon nanotube; that is, the material is more brittle in this direction than in the other direction and requires a long-term deformation. The alignment of CNTs in the polymer matrix can significantly improve the mechanical performance of the composite. The mechanical properties are not linearly proportional to the deformation of CNT, but there is a performance threshold [10].

According to our calculation results and experimental results from [10, 11], we conclude that the main cause of small deformations is the entanglement of carbon nanotubes and poor dispersion CNT in the polymer matrix, whereas the good dispersion of the carbon nanotubes in the longitudinal direction requires very long CNTs. Our results are comparable to results obtained by [8] (e.g., Figs. 62.5 and 62.6).

Fig. 62.6
figure 6

Curve of Young’s moduli longitudinal and transverse according to the deformation of the composite: (a) carbon nanotubes of high length/PE; (b) carbon nanotubes medium length/PE; (c) carbon nanotubes small length/PE

Full size image

To understand the improvement of the mechanical properties of our composite (polyethylene/SWNT zigzag), we ascend the results of Young’s modulus for the CNT–PE composite of different lengths which are represented by Fig. 62.6.

62.4.2.1 Young Modulus

Figure 62.6 represents the Young’s moduli of the three composites and presents the curves of longitudinal and transverse Young’s moduli for composite carbon nanotube/PE different lengths.

In Fig. 62.6a, the longitudinal Young’s modulus increases with the deformation until reaching a value of 0.035 GPa and 1.2 % strain. The transverse Young’s modulus shows a short-term high value (close to 0.06 GPa) for a deformation of 0.6 %. Then we observe that this module decreases to the value 0.015 GPa; the difference between the two curves shows that the capacity in the longitudinal direction is more resistive with respect to the transverse direction.

In Fig. 62.6b, the longitudinal and transverse Young’s modulus increases with strain up to 1.6 % with a module of 0.009 GPa for the longitudinal direction and up to 0.017 GPa and 1.4 % for the management section. Then we observe that these modules reduce to the values 0.006 GPa and 0.002 GPa, respectively.

Figure 62.6c shows the variation of Young’s modulus in both directions. For the longitudinal direction, we can say that the Young’s modulus increases up to 0.0052 GPa to a deformation of 3.49 % as opposed to the transverse direction where the Young’s modulus increases short term up to 0.035 Gpa and 1.1 % strain deformation. Then, we observe that this module decreases to 0.01 Gpa. The composite that contains short lengths of nanotubes is more fragile than the composite with high nanotube lengths.

From the experimental results of [12], the Young’s modulus decreases due to transverse cracks of the carbon nanotubes, which verifies our results.

Our results show that the Young’s modulus increases with increasing length of the carbon nanotubes; the reinforcement in the longitudinal direction is better than that obtained in the transverse direction. Theoretically, our results are comparable to the experimental results obtained by [12].

62.5 Conclusion

This work has allowed us to present a study of the mechanical behavior of polymer nanocomposites and carbon nanotubes, in order to facilitate their use in electronics knowing that CNTs can be used as reinforcements for drivers or dissipate static electricity in manufacturing equipment hard drives or solid-state, for example. Thus, combining the properties of PMMA and properties of SWNTs, we have an electronically functional reinforced polymer, electrically and thermally conductive applicable to solar cells, LEDs, displays, and so on.

To predict the effect of functionalization on the different properties of nanocomposites, we applied the model to the physical R.V.E. nanocomposite polyethylene (low density amorphous)/SWNT (zigzag).

The simulation of the thermal properties (interaction energy) and lifts (stress–strain and Young’s modulus) of the composite PE/CNT by molecular dynamics is a field for discussion in the literature.

Several results are noteworthy in this work. We have observed that increasing the length of CNTs leads to an increase of the interaction energy as well as Young’s modulus.

Through the results in the literature, our results are explained by the crack of CNTs and the poor dispersion of nanotubes in the polyethylene matrix. These explanations could be a result of this work, trying to bring in a first step CNTs cracked in our model and to study their impact on the mechanical behavior of the nanocomposite obtained.

The effect of the dispersion of CNTs would constitute a second line of research. We can also study the problem of the orientation of CNTs in the polymer matrix and the presences of defects in CNTs. We conclude that the prospects of this work are many and we cannot list them all.