Geostatistical Analysis in Extremes: An Overview

Abstract

Classical statistics of extremes is very well developed in the univariate context for modeling and estimating parameters of rare events. Whenever rain, snow, storms, hurricanes, earthquakes, and so on, happen the analysis of extremes is of primordial importance. However such rare events often present a temporal aspect, a spatial aspect or both. Classical geostatistics, widely used for spatial data, is mostly based on multivariate normal distribution, inappropriate for modeling tail behavior. The analysis of spatial extreme data, an active research area, lies at the intersection of two statistical domains: extreme value theory and geostatistics. Some statistical tools are already available for the spatial modeling of extremes, including Bayesian hierarchical models, copulas and max-stable random fields. The purpose of this chapter is to present an overview of basic spatial analysis of extremes, in particular reviewing max-stable processes. A real case study of annual maxima of daily rainfall measurements in the North of Portugal is slightly discussed as well the main functions in R environment for doing such analysis.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Motivation and Introduction

This chapter is related to a talk presented in a session of the “International Conference Planet Earth. Mathematics of Energy and Climate Change” entitled The role of Statistics of Extremes in Society. Through the ages natural disasters and catastrophes have happened, causing deaths and destruction. Remember, for example, the 1755 Lisbon earthquake and tsunami and the 2005 hurricane Katrina, New Orleans, see Fig. 1.

Fig. 1

The 1755 Lisbon earthquake and tsunami (left) and the 2005 hurricane Katrina, New Orleans (right)

The scientific community has been worried about whether anything could be done for society to be at least better prepared for those occurrences.

On 18.01.12, Nicolas Guerin [22], from École Polytechnique Fédérale de Lausanne, wrote in News Mediacom:

…“The problem of extremes is that there are so few events, by definition…explains EPFL mathematician Anthony Davison. It’s thus necessary to create specific models that are different from those that use innumerable mean values…

For several years now, the scientists have noted that the increase in extreme events associated with climate change appears to be having much more of an impact on society than the increase in mean temperatures. Natural disasters are accompanied by a significant human and economic cost…”

Extreme value theory (EVT) is the branch of probability and statistics dedicated to characterizing the behavior of the extreme observations. An extreme observation is a datum that has low probability of occurrence, but which can be very large (or small).

EVT has its beginnings in the early to middle part of the last century. It formally began with the paper by Dodd [14], followed by papers of Fréchet [18], Fisher and Tippett [17] Gumbel [23] and von Mises [42], to cite the pioneering and most relevant works.

Rare events such as the risk of flooding, potential crop damage from drought, health effects of extreme air pollution, storms, and so on, may cause severe impacts on human life as well as on ecosystems. In weather and climate studies as well as in other fields, often what one wants to characterize is not the usual behavior, but the extreme events.

Assessing the behavior of rare events such as wind speed, precipitation and temperature presents unique statistical challenges, and requires one to characterize the tail of the distribution of the quantity of interest.

Emil Gumbel (1891–1966) was the pioneer in the application of statistics of extremes. He wrote “ …The aim of a statistical theory of extreme values is to analyze observed extremes and to forecast further extremes”. Gumbel [24] presents several applications of EVT on real world problems in engineering and in meteorological phenomena. There appear first applications in hydrology. “…It seems that the rivers know the theory…” is a remarkable expression from Gumbel.

Recently, a special issue of the journal Extremes (2010) 13:2 on Statistics of Extremes in Weather and Climate, shows the relevance of EVT in the area.

Nowadays, extreme value analysis appears in quite diversified areas revealing the importance of statistics of extremes in applications. Many excellent books, presenting both the methodological basis and a great emphasis in the applications must be referred to. Besides Gumbel [24], we can mention Tiago de Oliveira (ed.) [12] that is still a reference today with a wide range of contributions and applications of statistics of extremes. It was the result of a remarkable meeting that took place thirty years ago in Vimeiro and fortunately was remembered in 2013, celebrating that conference and also dedicated to Ivette Gomes, a highly recognized international researcher in Statistics of Extremes. More recently, other books emphasizing the applications appeared and deserve to be mentioned: Coles [4], Finkenstadt and Rootzén (eds.) [16], Castillo et al. [3], Beirlant et al. [1], Reiss and Thomas, [33] and Gomes et al. [21].

Statistical modeling of extremes was based initially on limiting families of distributions for maxima of a sequence, $X_{1},\ldots,X_{n}$, of independent and identically distributed (i.i.d.) random variables from an unknown distribution function (d.f.), F. Given that the distribution of the maxima is highly dependent of the unknown form of F, similar to the central limit theory, researchers tried to obtain sequences {a _n  > 0} and $\{b_{n}\} \in \mathbf{R}$ such that $M_{n}:=\max \{ X_{1},\ldots,X_{n}\}$, linearly normalized by those constants, had a non-degenerate limiting distribution.

Univariate EVT is well developed, but is it well recognized that many extreme events, particularly in the environment, environmental health, climate, hydrology or meteorology occur in a place and/or in a time. In those areas of application we are faced with the task of analyzing data that are geographically referenced and show a correlated structure that needs to be adequately modelled.

Spatial data are measurements or observations taken at specific locations or within specific regions. The dependence structure of those data needs to be adequately captured. Geostatistics is an active area of research with important applications in the environment, agriculture and public health. Classical methods are well known and explored under the Gaussian model.

Regarding extreme values there was thus a need to develop methods for analyzing and characterizing spatial extreme data. Spatial extreme theory is an area that lies at the intersection of EVT and geostatistics. While classical geostatistics is usually applied to situations where only one realization of the process is taken, the spatial extreme approach needs multiple realizations underlying the subset of extreme data analyzed.

After this general motivation and introduction, Sect. 2 introduces the basic notions in EVT and in Standard Geostatistics. In Sect. 3 a background in spatial extremes is given as well as some most common statistical models in the max-stable process approach for spatial extremes. Section 4 is devoted to slightly discuss an application to annual maxima of daily rainfall data, with particular emphasis to the use of R software. Applications to rainfall data have been done recently by Smith and Stephenson [39], Padoan et al. [31] and Davison et al. [8].

2 Fundamental Notions and Basic Results

Classical EVT has been one of the most fast developing areas in the last decades. The underlying mathematical basis is well established, see e.g. Leadbetter et al. [26], Embrechts et al. [15] and de Haan and Ferreira [11], to cite only a few books. To model the tail of a distribution, where extreme events often occur, has been a challenge for researchers. There is now a well established set of methods to model the tail of a distribution.

2.1 Main Limiting Results in EVT

For the univariate EVT the main and well known result is: Let $X_{1},\ldots,X_{n}$ be independent replications from an unknown d.f., F, and define $M_{n}:=\max \{ X_{1},\ldots,X_{n}\}$. Fréchet [18], Fisher and Tippet [17], Gumbel [23], and von Mises [42], in Fig. 2, obtained the first results concerning the existence of a non-degenerate law of the maximum of that series, suitably normalized.

Fig. 2

Fréchet (1878–1973), Gumbel (1891–1966), von Mises (1883–1953) and Weibull (1887–1979) (from left to right)

Gnedenko [20] and later on de Haan [9] gave necessary and sufficient conditions for the existence of sequences {a _n  > 0} and {b _n } ∈ R such that,

$$\displaystyle{\lim _{n\rightarrow \infty }P\left (\frac{M_{n} - b_{n}} {a_{n}} \leq x\right ) =\lim _{n\rightarrow \infty }F^{n}(a_{ n}x + b_{n}) = \mathit{EV }_{\xi }(x),}$$

$\forall x \in \mathbf{R}$, where EV _ξ is a nondegenerate distribution function. This function, called Extreme Value d.f., is given by

$$\displaystyle{ EV _{\xi }(x) = \left \{\begin{array}{lll} \exp [-(1 +\xi x)^{-1/\xi }],\ \ 1 +\xi x > 0&\quad \mbox{ if}&\xi \not =0 \\ \exp [-\exp (-x)],\ \ x \in \mathbf{R} &\quad \mbox{ if}&\xi = 0. \end{array} \right. }$$

(1)

In applications, the d.f. in (1) can also present a more general form with a location parameter λ ∈ R and a scale parameter δ ∈ R ⁺.

The $\mathbf{EV}_{\boldsymbol{\xi }}$ incorporates the three (Fisher-Tippett) types: Gumbel type: $\varLambda (x) =\exp (-\exp (-x)) \equiv \mathit{EV }_{0}(x)$, x ∈ R,  (ξ = 0), the limit for exponential tailed distributions; Fréchet type: $\varPhi _{\xi }(x) =\exp (-(x)^{-1/\xi }) \equiv \mathit{EV }_{\xi }(\frac{x-1} {\xi } )$, x > 0,  ξ > 0, the limit for heavy tailed distribution and Weibull type: $\varPsi _{\xi }(x) =\exp (-(-x)^{1/\xi }) \equiv \mathit{EV }_{\xi }(\frac{-x-1} {\xi } )$, x < 0,  ξ < 0, the limit for short tailed distributions. These three families of models were combined as the d.f. EV _ξ in (1) by von Mises [42].

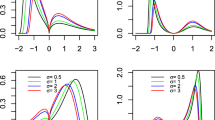
If ξ = 0, the right endpoint, x ^∗: = sup{x: F(x) < 1}, can then be either finite or infinite. If ξ > 0, F has an infinite right endpoint. If ξ < 0, F has a finite right endpoint, x ^∗. The shape parameter, ξ, is then directly related to the weight of the right tail, $\overline{F}:= 1 - F$, of the underlying model F. As ξ increases the right tail becomes heavier. Figure 3 shows the behavior of the right-tails for the three different types of EV models, together with the Gauss model for comparison.

Fig. 3

Gumbel, Fréchet and Weibull p.d.f. (left) and zoom of Gumbel, Fréchet, Weibull and Gauss p.d.f. (right)

Jointly with the knowledge of methodological aspects of extreme values theory, the interest for having free, accurate and simple software has increased tremendously, motivated by the wide range of areas of application of EVT.

R is an environment and a programming language for statistical computing and graphics. It is a free and open source project. Several packages for extreme value analysis are already available, with a large set of functions, among which we mention: evd, Stephenson [40], with functions for statistical analysis of extremes, including multivariate extremes and Bayesian methods; ismev, Stephenson [41], with functions for classical extreme value analysis, fitting extreme value distribution to “block maxima”, as well as generalized Pareto distribution to excesses over a high threshold and extRemes, with a graphical user interface based on ismev, are perhaps the most well known. Other packages are nevertheless available, see Gilleland, et al. [19]. They published a very nice software review, comparing the available statistical software and presenting the main characteristics of the main packages for extreme value analysis.

2.2 Standard Geostatistics

If the quantity of interest, e.g. the rainfall level, is observed at different locations spread over a region, it is necessary to know how to take into account the spatial pairwise dependence among sites, for an adequate analysis of data. There are three types of spatial data:

• Geostatistical data or point referenced data are measurements taken at fixed locations $\mathbf{s} \in \mathbf{K} \subset \mathbf{R}^{d}$. These locations are generally spatial continuous. Data may be modeled as values from a spatial process.

• Lattice data or areal referenced data where K is again a fixed subset but observations are associated with spatial regions and with well defined boundaries.

• Spatial points patterns where locations are now the variable of interest, so K is itself random and observation sites may be treated as random.

We shall consider geostatistical data modeled by a stochastic process {Y(s)} where s ∈ K and K is a compact subset in R ^d. Data are observed at $D =\{ \mathbf{s}_{1},\ldots,\mathbf{s}_{D}\} \subset \mathbf{K} \subset \mathbf{R}^{d}$. Usually d = 2 and we shall assume it throughout. Essential elements for exploring and modeling spatial data are: stationarity, isotropy and the variogram, key elements of the “Matheron school”, see Cressie [7].

Let us consider a spatial process with mean, μ(s) = E[Y(s)] and variance Var[Y(s)] finite for all s ∈ K ⊂ R ².

Usually it is assumed second-order stationarity what implies that covariance relationship between values of the process at any two locations can be summarized by the covariance function $C(\mathbf{h}) = Cov(Y (\mathbf{s}),Y (\mathbf{s + h}))$, for all h ∈ R ², such that s and s + h both lie within K. That function depends only on the separation vector h.

Assuming also that $E\left [\mathbf{Y}(\mathbf{s} + \mathbf{h}) -\mathbf{Y}(\mathbf{s})\right ] = 0$, with s and s +h ∈ K, the variogram is defined as:

$$\displaystyle{E\left [\mathbf{Y}(\mathbf{s} + \mathbf{h}) -\mathbf{Y}(\mathbf{s})\right ]^{2} = V ar\left [\mathbf{Y}(\mathbf{s} + \mathbf{h}) -\mathbf{Y}(\mathbf{s})\right ] = 2\gamma (\mathbf{h}),}$$

where γ(h) is designated as the semivariogram and is a crucial measure for quantifying spatial dependence in the data. If the semivariogram depends only on the length of h, and not on the orientation, $\gamma (\mathbf{h}) =\gamma (\|\mathbf{h}\|)$, the process is said to be isotropic, i.e., roughly speaking “as it looked the same in all directions”. Table 1 summarizes the main models for isotropic semivariograms.

Table 1 Theoretical semivariograms

In an exploratory phase of a geostatistical analysis, the dependence is investigated via an empirical covariogram or empirical semivariogram.

Assuming stationarity and isotropy the simplest semivariogram estimator is the moments estimator, Matheron [27],

$$\displaystyle{\hat{\gamma }(h) = \frac{1} {2\vert N(h)\vert }\sum _{(\mathbf{s}_{i},\mathbf{s}_{j})\in N(h)}\{Y (\mathbf{s}_{i}) - Y (\mathbf{s}_{j})\}^{2},}$$

where $N(h) =\{ (\mathbf{s}_{i},\mathbf{s}_{j}): \vert \vert \mathbf{s}_{i} -\mathbf{s}_{j}\vert \vert = h\}$ and | N(h) | denotes the cardinality of N(h).

A few steps can be summarized for basic geostatistical analysis: remove trends in mean and (perhaps) in variance; transform residuals to standard normal margins; use graphical techniques to assess likely form for the semivariogram function; fit a suitable semivariogram model; make inferences using weighted least squares (kriging), likelihood or Bayes procedures; make predictions using the fitted correlation to obtain a map of predictions, based on a fitted normal model.

In R environment several packages are available for geostatistical analysis. Exploratory analysis, modeling and extrapolating are possible through several functions in spatial, gstat, sp, MASS and geoR, for example.

• gstat includes functions as: variogram—calculates sample (experimental) variograms; plot.variogram—plots an experimental variogram with automatic detection of lag spacing and maximum distance; fit.variogram—iteratively fits an experimental variogram; krige—a generic function to make predictions by inverse distance interpolation, ordinary kriging, OLS regression, regression-kriging and co-kriging; krige.cv—runs krige with cross-validation, see Pebesma [32] and Bivand et al. [2] for a complete overview of gstat functions and examples.

• geoR—extensively described by Diggle and Ribeiro Jr. [13] and Ribeiro Jr. et al. [35], with a series of tutorials.

Usually it is supposed that {Y(s)} follows a Gaussian process, so likelihood inference is realized under this assumption.

3 Geostatistical Analysis in Extremes

As mentioned in the previous section, Gaussian processes play a central role in modeling spatial processes. In this approach relevance is given to studying the central tendencies of the distribution rather than the distribution tails. However in many events already pointed out behind, the extremes are of main interest. The generalization of classical multivariate extreme value distributions to the spatial case is done through max-stable processes. Other statistical approaches have been developed for the spatial modeling of extremes, such as Bayesian hierarchical models and copulas, topics that will not be considered in this brief overview. A recent and very good survey on spatial extremes is Cooley et al. [6].

The purpose of this section is to review some max-stable processes, and mainly to show packages and functions already available in the R environment for the analysis of spatial extremes. First results date back to de Haan [10] and were developed by several authors, such as Smith [38], Schlather [36] and Kabluchko et al. [25], to mention only a few.

Max-stable processes follow a similar asymptotic motivation to the univariate EV distribution, providing a general approach to modeling process extremes incorporating temporal or spatial dependence. For the region K under study and the location s, we will assume $Y _{1}(\mathbf{s}),Y _{2}(\mathbf{s}),\ldots$ as independent replicas of a stochastic process.

Consider that we have daily rainfall data collected in some stations and we are interested in considering the maximum of that quantity over a period of time (e.g. a year) in order to:

• Assess the dependence of the extreme precipitation levels between stations.

• Predict values at unobserved locations.

• Elaborate a map of the distribution of the maximum precipitation levels.

Interest is now to model extremes of a process {Y(s)} over spatial domain K, where data are observed at sites $\mathbf{s}_{d} \in \{\mathbf{s_{1}},\ldots,\mathbf{s}_{D}\}$ within K and at times $\mathbf{T} =\{ t_{1},\ldots,t_{n}\}$. A difference between geostatistics and spatial extremes is that much of geostatistics is applied to situations where one has only one realization of the process {Y(s)}. However to perform an extreme value analysis it is necessary that multiple realizations {Y _i (s)} underlie the subset of extreme data which are analyzed.

An overview on some main max-stable models is here considered and briefly applied to a case study.

3.1 Some Models for Max-Stable Processes

Let us recall the definition of max-stable process by de Haan [10]. Let {Y _i (s)}, $\mathbf{s} \in \mathbf{D},i = 1,\ldots,n$, be independent replicas of a stochastic process {Y(s)} defined in D ⊂ R ².

Definition 1

The stochastic process {Y(s)} is called max-stable if, for all s ∈ D there exist normalizing sequences {a _n (s) > 0} and {b _n (s)} such that, as n → ∞,

$$\displaystyle{\left \{\frac{\max _{i=1,\ldots,n}Y _{i}(\mathbf{s}) - b_{n}(\mathbf{s})} {a_{n}(\mathbf{s})} \right \} \rightarrow _{d}\left \{\mathbf{Y}^{{\ast}}(\mathbf{s})\right \}_{\mathbf{ s}\in \mathrm{\mathbf{R}^{2}}}}$$

where $\left \{\mathbf{Y}^{{\ast}}(\mathbf{s})\right \}$ is identical in law to $\{\mathbf{Y}(\mathbf{s})\}$.

To characterize max-stable processes is a very difficult task. For max-stable processes with Fréchet unit margins de Haan [10] introduced a very useful representation that allowed the construction of parametric models for spatial extremes. Such a general representation is as follows: let $\{Y _{i}(\mathbf{s})\}_{i\in \mathbf{N}}$, be independent realizations of a stochastic process {Y(s)} with E[Y(s)] = 1 and let ζ _i be points of a Poisson process ∏ with intensity d ζ∕ζ ² on (0, ∞). Then

$$\displaystyle{ Z(\mathbf{s}) =\max _{i\geq 1}\zeta _{i}Y _{i}(\mathbf{s}),\quad \mathbf{s} \in \mathbf{D}, }$$

(2)

is a max-stable process with unit-Fréchet margins. and the distribution function is determined by

$$\displaystyle{ P\big(Z(\mathbf{s}) \leq z(\mathbf{s}),\mathbf{s} \in \mathbf{D}\big) =\exp \Bigg (-E\bigg[\sup _{\mathbf{s}\in \mathbf{D}}\bigg\{\frac{Y (\mathbf{s})} {z(\mathbf{s})} \bigg\}\bigg]\Bigg). }$$

Different choices of the process Y _i (s) lead to different models of max-stable processes. As examples let us mention the following models.

• Smith [38] proposed to take $Y _{i}(\mathbf{s}) =\varphi (\mathbf{s} -\mathbf{s}_{i})$, where $\varphi$ is a zero mean multivariate normal density with covariance matriz Σ, where the joint distribution at two sites is given by

  $$\displaystyle\begin{array}{rcl} & & P\left [Z(\mathbf{s}_{1}) \leq z_{1},Z(\mathbf{s}_{2}) \leq z_{2}\right ] = \\ & & \exp \left [-\frac{1} {z_{1}}\varPhi \left (\frac{a} {2} + \frac{1} {a}\log \frac{z_{2}} {z_{1}}\right ) - \frac{1} {z_{2}}\varPhi \left (\frac{a} {2} + \frac{1} {a}\log \frac{z_{1}} {z_{2}}\right )\right ], {}\end{array}$$

  (3)

  where $a = \sqrt{(\mathbf{s} _{1 } - \mathbf{s} _{2 } )^{T } \varSigma ^{-1 } (\mathbf{s} _{1 } - \mathbf{s} _{2 } )}$, is a dependence parameter, and Φ is the standard normal d.f.

• Schlather [36] proposed a more flexible class of max-stable processes by taking Y _i (s) to be any stationary Gaussian random field with finite expectation. He considered

  $$\displaystyle{Z(\mathbf{s}) =\max _{i\geq 1}\zeta _{i}\max \{0,Y _{i}(\mathbf{s})\}}$$

  where $\mu = E\big[\max \{0,Y _{i}(\mathbf{s})\}\big] < \infty$, being the joint distribution at two sites given by

  $$\displaystyle\begin{array}{rcl} & & P\left [Z(\mathbf{s}_{1}) \leq z_{1},Z(\mathbf{s}_{2}) \leq z_{2}\right ] = \\ & & \exp \left [-\frac{1} {2}\left ( \frac{1} {z_{1}} + \frac{1} {z_{2}}\right )\left (1 + \sqrt{1 - \frac{2(\rho (h) + 1)z_{1 } z_{2 } } {(z_{1} + z_{2})^{2}}} \right )\right ], {}\end{array}$$

  (4)

  where $h = \vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert$ and ρ(h) is chosen from Whittle-Matérn, Cauchy and Powered Exponential, see Schlather [36].

• As an example of another model let us consider a more recent proposal, the so-called Brown-Resnick process, studied in Kabluchko et. al. [25], who proposed an alternative specification for the Y _i (⋅ ) process, $Y (\mathbf{s}) =\exp \big (\epsilon _{i}(\mathbf{s}) -\sigma ^{2}(\mathbf{s})/2\big)$, where ε(s) is a Gaussian process with stationary increments, being σ ²(s) the variance of ε(s).

3.2 Spatial Dependence of Extremes

To use max-stable models we need to have information on how the dependence between two locations decreases, when the distance increases. It would be nice to have a kind of variogram for extremes of a stochastic process. However if we assume that Z is a unit Fréchet max-stable process, the variance (and even the mean) might be infinite.

A new function is now needed to reflect how evolves the spatial dependence of extremes. It provides sufficient information about extremal dependence and it is called the extremal coefficient function, Schlather and Tawn [37].

Definition 2

If Z(⋅ ) is a max-stable process with unit Fréchet margins the extremal coefficient function θ() is defined by

$$\displaystyle{P\left [Z(\mathbf{s}_{1}) \leq z,Z(\mathbf{s}_{2}) \leq z\right ] =\exp \left (-\frac{\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert )} {z} \right ),}$$

where $1 \leq \theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) \leq 2$.

The extremal coefficient function has the following meaning: If $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = 1$, we have perfect dependence; if $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = 2$, we have independence.

Extremal coefficient functions for the above models are:

• $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = 2\varPhi \left (\frac{\sqrt{(\mathbf{s} _{1 } -\mathbf{s} _{2 } )^{T } \varSigma ^{-1 } (\mathbf{s} _{1 } -\mathbf{s} _{2 } )}} {2} \right )$, for the Smith model covering the whole range of dependence;

• $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = 1 + \sqrt{\frac{1-\rho (\vert \vert \mathbf{s} _{1 } -\mathbf{s} _{2 } \vert \vert )} {2}}$, for Schlather model that has upper bound of $1 + \sqrt{1/2}$. A drawback of this model is that independence of extremes can not be attained because θ ∈ [1; 1. 8333] and θ = 2 is never attained;

• $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = 2\varPhi \left (\sqrt{\gamma (\vert \vert \mathbf{s} _{1 } - \mathbf{s} _{2 } \vert \vert )/2}\right )$, for the Brown-Resnick process. As $\gamma (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) \rightarrow 0$, we have $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) \rightarrow 1$, while if $\gamma (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert )$ is unbounded, then $\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) \rightarrow 2$ as | | s ₁ −s ₂ | | → ∞.

Another measure of dependence between two locations is given by a “kind” of variogram. The first idea was to consider the madogram, a tool in classical geostatistics, Matheron [28], defined as:

$$\displaystyle{\upsilon (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = E\left [\vert Z(\mathbf{s}_{1}) - Z(\mathbf{s}_{2})\vert \right ].}$$

The madogram requires the finiteness of the first-moment and for stationary max-stable processes with unit Fréchet margins, mean and variance may be not finite and that mean value does not exist theoretically. Consequently, variogram-based approaches, specially designed for extremes, have been proposed:

• the F-Madogram, Cooley et al. [5],

  $$\displaystyle{\upsilon _{F}(\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = \frac{1} {2}E\left [\vert F\{Z(\mathbf{s}_{1})\} - F\{Z(\mathbf{s}_{2})\}\vert \right ].}$$

  The F-madogram is related to the extremal coefficient function as:

  $$\displaystyle{\upsilon _{F}(\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = \frac{\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) - 1} {\theta (\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) + 1}.}$$

• λ-Madogram, Naveau et al. [29].

  $$\displaystyle{\upsilon _{\lambda }(\vert \vert \mathbf{s}_{1} -\mathbf{s}_{2}\vert \vert ) = \frac{1} {2}E\left [\vert F^{\lambda }\{Z(\mathbf{s}_{1})\} - F^{1-\lambda }\{Z(\mathbf{s}_{ 2})\}\vert \right ],\quad 0 \leq \lambda \leq 1,}$$

  where $F(z) =\exp (-1/z)$ is the unit Fréchet d.f.

The F-Madogram is similar to the λ-Madogram when λ = 0. 5. The F-Madogram has the advantage of suggesting an estimator directly from its definition, see Cooley et al. [5].

Naveau et al. [29] discussed the estimation of the madogram. For the F-Madogram it was considered the plug in, $\hat{F}$, an estimate of the d.f., at the specified location and the binned estimate of the F-madogram. For the λ−Madogram, the binned λ−Madogram estimator and the adjusted estimator have been proposed.

4 A Case Study

For 21 different stations, in the North of Portugal, daily precipitation has been recorded. Our data refers to the maximum annual values for 20 years (1977–1996), in each station. A preliminary analysis of these data was done in Neves and Prata Gomes [30]. It would be nice to have more years of observations but surprisingly in recent years some missing values were found.

Figure 4 shows the region of Portugal where data have been collected on the left, and locations of the stations pointed out on the right. In each site and location, the maxima annual values of daily precipitation were considered in our study.

Fig. 4

Map of the North of Portugal (left) and the positions of the stations where data were recorded (right)

We began our analysis by performing marginal analysis and transformation. Daily values of precipitation at a given station x are dependent, however, the maxima values at each hydrological year can be considered almost independent.

As an illustration of the graphical diagnostic GEV fitting, graphics in two locations were chosen and displayed in Figs. 5 and 6.

Fig. 5

GEV model diagnostic for data from Guarda

Fig. 6

GEV model diagnostic for data from Vila Real

The transformation of the data at each station to the unit Fréchet distribution was then performed, through the function gev2frech() of the package SpatialExtremes, Ribatet [34].

To estimate the spatial dependence structure, estimates of values of the extremal coefficient at two stations s ₁ and s ₂ are evaluated. For this, the fitextcoeff() was used considering both Smith, [38], and Schlather-Tawn, [37], estimators. As far as we know only these estimators are available in R package. Work is now in progress for including other functions in R environment. Figure 7 shows pairwise extremal coefficient estimates and lowess curves for Smith and Schlather-Tawn estimators and also the F-madogram, here obtained through fmadogram() function.

Fig. 7

Pairwise extremal coefficient estimates and lowess curves: Smith and Schlather-Tawn (left); F-madogram and binned madogram (right)

Trend surfaces were tried to be estimated in order to capture the spatial dependence structure by describing the marginal parameters as:

$\lambda (x) =\beta _{o,\lambda } +\beta _{1,\lambda }\mathit{lon}(x) +\beta _{2,\lambda }\mathit{lat}(x)$

$\delta (x) =\beta _{0,\delta } +\beta _{1,\delta }\mathit{lon}(x) +\beta _{2,\delta }\mathit{lat}(x)$

ξ(x) = β _o, ξ

where lon(x) and lat(x) denote the longitude and the latitude of the stations.

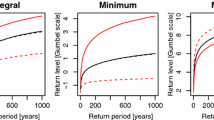
However, for our data, values of λ(x), δ(x) and ξ(x) showed a weak relationship with lon(x) and lat(x). Other trend surfaces need to be considered, but work is now in progress. Even though, considering the estimated matrix for Smith model as well as estimated sill and range for Schlather model, with the powered exponential correlation function, several simulations were performed on a 21 × 21 grid. Figure 8 displays one of those simulations for the Smith model and for the Schlather model.

Fig. 8

One realization of the Smith (left) and Schlather and Tawn (right) models

5 Concluding Remarks

This chapter was intended to introduce spatial models for extreme value analysis as well as to present an overview of functions available in the R software for doing that analysis. Max-stable processes are a natural generalization of multivariate extreme models and the most common way to deal with extreme value data in spatial statistics. Some procedures for estimating the spatial dependence available in the R environment were shown and some simulations using Smith and Schlather models were also performed in the R package SpatialExtremes.

Work is already in progress for including more max-stable models in R, as well as other approaches for modeling spatial dependence.

Some difficulties related to the amount of data available still remain. How to deal with missing values, in a given real situation, is another challenging point.