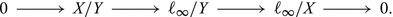Open Problems

Abstract

In this chapter we present and discuss in some detail problems that we encountered in the course of our work. Some of them have already been mentioned in previous chapters, others have appeared under different disguises and a few are new. The contents of the sections may freely overlap.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this chapter we present and discuss in some detail problems that we encountered in the course of our work. Some of them have already been mentioned in previous chapters, others have appeared under different disguises and a few are new. The contents of the sections may freely overlap.

6.1 Characterizations of (Universally) Separably Injective Spaces

Many questions remain unanswered regarding the characterization and basic properties of separably and universally separably injective spaces. Analogously to what happens for injective spaces, it is reasonable to ask:

Problem 1

Is every universally separably injective space isomorphic to a universally 1-separably injective space? Must a $\lambda$-separably injective space, $\lambda < 2$, be isomorphic to a 1-separably injective space?

The second question has an affirmative answer for C-spaces (Proposition 2.34). Recall, however, that 2-separably injective spaces cannot, in general, be renormed to become $\lambda$-separably injective for $\lambda < 2$ (Proposition 2.32 and the fact that c ₀ is 2-separably injective); let alone for $\lambda = 1$ (Proposition 2.31).

Since the first examples of (non-injective) universally separably injective spaces one encounters are $\ell_{\infty }^{c}(\varGamma )$ and $\ell_{\infty }/c_{0}$, it makes sense to ask for a pattern to construct explicit examples of operators into either $\ell_{\infty }^{c}(\varGamma )$ or $\ell_{\infty }/c_{0}$ that cannot be extended to some superspace. In the case of $\ell_{\infty }^{c}(\varGamma )$, the canonical embedding $c_{0}(\varGamma ) \rightarrow \ell_{\infty }^{c}(\varGamma )$ is a reasonable candidate to be a non-extendable operator. Indeed, if some extension $T:\ell _{\infty }(\varGamma ) \rightarrow \ell_{\infty }^{c}(\varGamma )$ would exist, by Rosenthal’s result quoted in Theorem 1.14, this T should be an isomorphism on some copy of $\ell_{\infty }(\varGamma )$. Since

$$\displaystyle{\mathop{\mathrm{dens}}\nolimits \;\ell_{\infty }^{c}(\varGamma ) = \vert \varGamma \vert ^{\aleph _{0} }\quad \mathrm{and}\quad \mathop{\mathrm{dens}}\nolimits \;\ell_{\infty }(\varGamma ) = 2^{\vert \varGamma \vert },}$$

the embedding of $\ell_{\infty }(\varGamma )$ into $\ell_{\infty }^{c}(\varGamma )$ is impossible when $\vert \varGamma \vert ^{\aleph _{0}} < 2^{\vert \varGamma \vert }$. This argument works for, say, $\vert \varGamma \vert = \mathfrak{c}$, while it fails—outside CH—for, say, $\vert \varGamma \vert = \aleph _{1}$ since it is consistent that $\aleph _{1}^{\aleph _{0}} = 2^{\aleph _{1}}$. A similar argument could work to show that no embedding $c_{0}(\varGamma ) \rightarrow \ell_{\infty }/c_{0}$ extends to an operator $\ell_{\infty }(\varGamma ) \rightarrow \ell_{\infty }/c_{0}$.

A different, although akin, topic is the topological characterization of separably injective and universally separably injective C(K)-spaces. The basic problem is:

Problem 2

Characterize the compact spaces K such that C(K) is separably injective or universally separably injective.

Indeed, no known property of compacta seems to provide such characterizations. It is also an open problem to characterize Grothendieck C-spaces in terms of topological properties of the underlying compacta (see Sect. 6.8 for more information on Grothendieck spaces). We have already shown in Theorem 2.14 that K is an F-space if and only if C(K) is 1-separably injective; hence, it is a Grothendieck space and, under CH (see Proposition 2.29), it is universally 1-separably injective. We do not know, however if, in ZFC, the fact that K is an F-space still implies that C(K) is universally separably injective or even must contain $\ell_{\infty }$. When K is $\sigma$-Stonian every non-weakly compact operator C(K) → Y is an isomorphism on some copy of $\ell_{\infty }$ [223, Theorem 3.7] and thus C(K) must necessarily contain $\ell_{\infty }$ (Dashiell [79] extends this result to different C(K), including Baire classes—see last paragraph in Sect. 6.4.2). It is reasonable to conjecture that C(K) is universally separably injective when K is $\sigma$-Stonian (in ZFC). We have even shown in Theorem 2.39 that there is a consistent example of 1-separably injective C(K)-space that is not universally 1-separably injective, but we do not know whether that example is universally separably injective or even if it contains $\ell_{\infty }$. Rosenthal asks in [223] whether there exists an F-space K such that C(K) is injective but K is not $\sigma$-Stonian; and remarks that the answer is affirmative assuming the existence of a measurable cardinal.

It would be interesting to characterize 1-separable injectivity for the most popular classes of Lindenstrauss spaces, namely, M-spaces, G-spaces, and the like. In particular we ask for a characterization of those compact convex sets K for which A(K), the space of continuous affine functions on K, is 1-separably injective. The following condition is sufficient (see Theorem 2.14): Given countable subsets L and U of A(K) such that f ≤ g for every f ∈ L and g ∈ U, there exists h ∈ A(K) such that f ≤ h ≤ g for all f ∈ L and g ∈ U. Is the converse true? What if K is a simplex? (See [97] for the basics on simplex spaces). Related to this we have mentioned that if (S _i ) _i ∈ I is a family of simplices and $\mathcal{U}$ an ultrafilter on I, then $A(S_{i})_{\mathcal{U}} = A(S)$ for some simplex S. Actually, S is unique by results of Rao [220]. It is also interesting to know how S is obtained from (S _i ) _i ∈ I .

The study of $(1,\aleph )$-injectivity in terms of families of balls presented in Propositions 2.30 and 2.62 (for $\aleph = \aleph _{1}$) and Lemma 5.12 has no known analogue for universal injectivity. Precisely:

Problem 3

Can universal $(1,\aleph )$ injectivity be characterized in terms of intersection of families of balls?

6.2 The 3-Space Problem for Universal Separable Injectivity

The main problem we have been unable to solve is the 3-space problem for universal separable injectivity.

Problem 4

Is universal separable injectivity a 3-space property?

This problem has a surprising number of connections and ramifications, as we shall see. An affirmative answer would provide nice characterizations of that property and unexpected examples and counterexamples. As we already mentioned in Sect. 2.1.3, in [20, Proposition 3.7 (3)] it was claimed that universal separable injectivity is a 3-space property; but the proof contains a gap we have been unable to fill and a few statements in [20] and in [21] were infected. Let us clarify the situation about what is actually known:

Proposition 6.1

The following assertions are equivalent:

• 1. Universal separable injectivity is a 3-space property.

• 2. Upper $\ell_{\infty }$ -saturation is a 3-space property.

• 3. $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty },U) = 0$ for every universally separably injective space U.

• 4. $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }/S,U) = 0$ for every universally separably injective space U and every separable space S.

Proof

It is clear that (1) and (2) are equivalent; see Theorem 2.26.

We prove that (1) implies (3) by showing that “$\neg (3) \Rightarrow \neg (1)$”. The idea is to prove that if a nontrivial exact sequence

(6.1)

with U universally separably injective exists, one arrives to another exact sequence

in which X′ lacks Rosenthal’s property (V ) and thus it cannot be universally separably injective by Proposition 2.8.

Partington’s distortion theorem for $\ell_{\infty }$ [210] establishes that any Banach space isomorphic to $\ell_{\infty }$ contains, for every $\varepsilon > 0$, an $(1+\varepsilon )$-isomorphic copy of $\ell_{\infty }$ (see also Dowling [90]). Let Γ be the set of all the 2-isomorphic copies of $\ell_{\infty }$ inside $\ell_{\infty }$. For each E ∈ Γ let $\imath _{E}: E \rightarrow \ell_{\infty }$ be the inclusion map, p _E a projection of $\ell_{\infty }$ onto E of norm at most 2 and let $u_{E}: E \rightarrow \ell_{\infty }$ be a surjective 2-isomorphism.

Assume that (6.1) is a nontrivial exact sequence, with U universally separably injective. There is no loss of generality in assuming that i: U → X is the canonical inclusion map. We consider, for each E ∈ Γ, a copy of (6.1) and form the product of all these copies

Let us consider the operator $J:\ell _{\infty }\rightarrow \ell_{\infty }(\varGamma,\ell_{\infty })$ given by $J(\,f)(E) = u_{E}p_{E}(\,f)$ and then form the pull-back sequence

Let us show that $\;'\!\!p_{\infty }$ cannot be an isomorphism on any copy of $\ell_{\infty }$ inside $\mathop{\mathrm{PB}}\nolimits$. Otherwise, it would have a right inverse on some E ∈ Γ and thus the new pull-back sequence

would split. Therefore, if $\pi _{E}^{U}:\ell _{\infty }(\varGamma,U)\longrightarrow U$ denotes the canonical projection onto the E-th copy of U, and similarly for π _E ^X and $\pi _{E}^{\ell_{\infty }}$, the lower push-out sequence in the diagram

also splits. We want to show that this lower sequence is isomorphically equivalent to the starting sequence (6.1); more precisely, there is an isomorphism $\gamma:\mathop{ \mathrm{PO}}\nolimits \longrightarrow X$ rendering commutative the diagram

In particular, one sequence splits if and only if the other does.

To obtain γ, observe the commutative square

It is commutative since the restriction of $\;'J \circ '\imath _{E}$ to $\ell_{\infty }(\varGamma,U)$ is just the inclusion into $\ell_{\infty }(\varGamma,X)$. Now, the universal property of the push-out construction yields an operator γ making commutative the following diagram:

For the sake of clarity let us display all the data in the same drawing

Let us see that the “horizontal flat” portion of this diagram is commutative. The left square is commutative by the very definition. As for the right square since $\mathop{\mathrm{PB}}\nolimits _{E} \rightarrow \mathop{\mathrm{PO}}\nolimits$ is onto it suffices to check that the composition

is the same as

which is obvious after realizing that $u_{E} =\pi _{ E}^{\ell_{\infty }}\circ J \circ \imath _{E}$. And this is trivial since given f ∈ E one has

$$\displaystyle{\pi _{E}^{\ell_{\infty } }(J(\,f)) = J(\,f)(E) = u_{E}(\,p_{E}(\,f)) = u_{E}(\,f).}$$

That (3) implies (4) is easy: Let S be separable and let U be universally separably injective. The homology sequence (see Appendix A.4.8) obtained from

is the exact sequence

If $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty },U) = 0$, the map $L(S,U)\longrightarrow \mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }/S,U)$ must be surjective and thus every exact sequence $0\longrightarrow U\longrightarrow X\longrightarrow \ell_{\infty }/S\longrightarrow 0$ fits in a push-out diagram

Since U is universally separably injective the operator S → U extends to an operator $\ell_{\infty }\rightarrow U$ and thus the lower sequence splits according to the splitting criterion for push-out sequences (Lemma A.20).

That (4) implies (3) is obvious, so both assertions are equivalent.

We show now that (3) implies (1): Let

be an exact sequence in which both Y, Z are universally separably injective; let $j: S \rightarrow \ell_{\infty }$ be an into isomorphism with S separable, and let t: S → X be an operator. Since Z is universally separably injective, the operator qt admits an extension $T:\ell _{\infty }\rightarrow Z$. We can therefore form the pull-back diagram:

Since $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty },Y ) = 0$, there is an operator $\tau:\ell _{\infty }\rightarrow X$ so that q τ = T. Since $q\tau j - qt = Tj - qt = 0$ the operator t −τ j takes actually values in Y. Let $\theta:\ell _{\infty }\rightarrow X$ be an extension of t −τ j; namely, $\theta j = t -\tau j$. The operator $\theta +\tau:\ell _{\infty }\rightarrow X$ is the desired extension of t:

$$\displaystyle{(\theta +\tau )j = t -\tau j +\tau j = t.}$$

This completes the proof. □ 

The preceding result provides a number of reformulations for Problem 4. A mildly convincing argument to support the idea that universal separable injectivity (i.e., $\ell_{\infty }$-upper-saturation; see Definition 2.25) is a 3-space property is:

Proposition 6.2

c ₀ -upper-saturation is a 3-space property.

Proof

Let $0\longrightarrow Y \longrightarrow X\stackrel{q}{\longrightarrow }Z\longrightarrow 0$ be an exact sequence in which both Y and Z are c ₀-upper-saturated and let S be a separable subspace of X. Pick Z ₀ a subspace of Z isomorphic to c ₀ and containing q[S]. It is a standard fact that there is a separable subspace $X_{S} \subset X$ containing S and such that q[X _S ] = Z ₀. Thus we have a commutative diagram

with $Y _{S} = X_{S} \cap Y$. We want to see that there is a subspace of X isomorphic to c ₀ containing X _S . Let Y ₀ be an isomorphic copy of c ₀ such that $Y _{S} \subset Y _{0} \subset Y$. Making push-out with the inclusion Y _S  → Y ₀ and taking Sobczyk’s theorem into account yields the commutative diagram

which shows that $S \subset Y _{0} \oplus Z_{0} \subset X$. Since $Y _{0} \oplus Z_{0} \sim c_{0}$ we are done. □ 

On the other hand, a serious argument against could be that, analogously to what happens with Pełczyński’s property (V ), which is not a 3-space property (see [61]; see also [68]), one has:

Proposition 6.3

Rosenthal’s property (V) is not a 3-space property.

Proof

We start with a nontrivial exact sequence

(see [54, Sect. 4.2]). Proceeding as in the proof that (1) implies (3) in Proposition 6.1 we construct an exact sequence

in which q cannot be an isomorphism on any copy of $\ell_{\infty }$. Thus, X′ has not Rosenthal’s property (V ). The space $\ell_{\infty }(\varGamma,\ell_{2})$ has Rosenthal’s property (V ) as a quotient of $\ell_{\infty }(\varGamma,\ell_{\infty }) =\ell _{\infty }(\mathbb{N}\times \varGamma )$, since Rosenthal’s property (V ) obviously passes to quotients. □ 

The following consequence of an affirmative answer to the 3-space problem for universal separable injectivity was claimed in [20, Theorem 5.5]:

• A space U would be universally separably injective if and only if $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }/S,U) = 0$ for every separably space S.

The “only if” part is contained in Proposition 6.1. The other part does not depend on the solution to Problem 4:

Proposition 6.4

If $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }/S,X) = 0$ for every separable space S then X is universally separably injective.

Proof

Let S be a separable Banach space, t: S → X an operator and $S \rightarrow \ell_{\infty }$ an embedding. Form the push-out diagram

The lower sequence splits by the assumption $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }/S,X) = 0$ and so t extends to $\ell_{\infty }$, according to the splitting criterion for push-out sequences (Lemma A.20). □ 

In particular, as it was claimed in [20, Proposition 5.6], one would have that $\mathop{\mathrm{Ext}}\nolimits (C(\mathbb{N}^{{\ast}}),C(\mathbb{N}^{{\ast}})) = 0$ since $C(\mathbb{N}^{{\ast}}) =\ell _{\infty }/c_{0}$. This would rank $\ell_{\infty }/c_{0}$ into the exclusive list of spaces X for which $\mathop{\mathrm{Ext}}\nolimits (X,X) = 0$, currently formed by

• c ₀, by Sobczyk’s theorem.

• Injective spaces, by the very definition.

• L ₁(μ)-spaces, by Lindenstrauss’ lifting (Proposition A.18).

It is definitely not true however that $\mathop{\mathrm{Ext}}\nolimits (U,V ) = 0$ for all universally separably injective spaces U and V. For instance, consider the exact sequence $0 \rightarrow \ell_{\infty }^{c}(\varGamma ) \rightarrow \ell_{\infty }(\varGamma ) \rightarrow \ell_{\infty }(\varGamma )/\ell_{\infty }^{c}(\varGamma ) \rightarrow 0$, where Γ is an uncountable set. Since the subspace is universally 1-separably injective (Example 2.4), the quotient is universally separably injective by Proposition 2.11(3). Actually it is even universally 1-separably injective, by Theorem 2.18. The sequence does not split because $\ell_{\infty }^{c}(\varGamma )$ is not injective (Proposition 1.28). Each universally separably injective non-injective space produces a similar counterexample. Moreover, it is easy to see that there exist universally separably injective spaces U such that $\mathop{\mathrm{Ext}}\nolimits (U,U)\neq 0$: if V is a universally separably injective non-injective space then every exact sequence $0 \rightarrow V \rightarrow \ell_{\infty }(\varGamma ) \rightarrow \ell_{\infty }(\varGamma )/V \rightarrow 0$ is not trivial, by Proposition 2.11. The space $W =\ell _{\infty }(\varGamma )/V$ is universally separably injective and, obviously, $\mathop{\mathrm{Ext}}\nolimits (W,V )\neq 0$. The product space U = V ⊕ W is universally separably injective and $\mathop{\mathrm{Ext}}\nolimits (U,U)\neq 0$.

The following problem seems quite interesting to us:

Problem 5

Characterize the C(K) spaces so that $\mathop{\mathrm{Ext}}\nolimits (C(K),C(K)) = 0$.

Probably a step in this direction would be to know whether the following generalization(s) of Problem 4 are possible:

Problem 6

Are there homological characterizations of $\aleph$-injectivity and universal $\aleph$-injectivity? In particular: Is it true that

• A Banach space E is $\aleph ^{+}$-injective if and only if $\mathop{\mathrm{Ext}}\nolimits (c_{0}(\aleph ),E) = 0$?

• A Banach space E is universally $\aleph ^{+}$-injective if and only if $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }(\aleph ),E) = 0$?

• $\mathop{\mathrm{Ext}}\nolimits (\ell_{\infty }(\varGamma ),U) = 0$ for every universally separably injective space U?

Recall that the information we currently have is:

Theorem 6.5

A Banach space E is

• Separably injective if and only if $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$ whenever Q is a quotient of C[0,1].

• Universally separably injective if $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$ whenever Q is a quotient of $\ell_{\infty }$ by a separable subspace (Proposition  6.4).

• [CH] $\aleph _{2}$ -injective if and only if $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$ whenever Q is a quotient of $\ell_{\infty }$ (Corollary  5.6 ).

• [GCH ] $\aleph ^{+}$ -injective if and only if $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$ whenever Q is a quotient of $\ell_{\infty }(\aleph )$ (Corollary  5.6 ).

Proof

Only the first point has not been explicitly done: if E is separably injective, then $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$ for every quotient of C[0, 1]; and conversely, if τ: S → E is an operator from any separable Banach space S, pick an embedding S → C[0, 1] and form the push-out diagram:

Since $\mathop{\mathrm{Ext}}\nolimits (Q,E) = 0$, the lower sequence splits and τ can be extended to an operator C[0, 1] → E, which shows that E is separably injective. □ 

A different way of looking at these questions is the following: A result of Johnson, Rosenthal and Zippin [148], see also [182], asserts that every separable Banach space S fits into an exact sequence

in which both A and B have the BAP. Since a Banach space E is separably injective when $\mathop{\mathrm{Ext}}\nolimits (S,E) = 0$ for all separable Banach spaces S, a 3-space argument yields that a Banach space E is separably injective when $\mathop{\mathrm{Ext}}\nolimits (S,E) = 0$ for all separable Banach spaces S with the BAP. And since there exist a separable space $\mathcal{K}$ with the BAP complementably universal for all separable spaces with the BAP [150, 213], it follows that E is separably injective if and only if $\mathop{\mathrm{Ext}}\nolimits (\mathcal{K},E) = 0$. Therefore, there exist (separable) Banach spaces that “test” the separable injectivity. The question is then whether

• c ₀, or its quotients, could be test spaces for separable injectivity.

• $c_{0}(\aleph )$, or its quotients, could be test spaces for $\aleph ^{+}$-separable injectivity.

• $\ell_{\infty }$, or (some of) its quotients, could be test spaces for universal separable injectivity.

• $\ell_{\infty }(\aleph )$, or (some of) its quotients, could be test spaces for $\aleph ^{+}$-universal injectivity.

And if quotients of c ₀ are a puzzle, quotients of $\ell_{\infty }$ are a conundrum, as we discuss next.

6.3 Subspaces and Quotients of $\ell_{\infty }$

Many results and ideas in this monograph wheel around the question about to what extent universally separably injective spaces are “like” $\ell_{\infty }$. This suggests:

Problem 7

Do there exist universally separably injective subspaces of $\ell_{\infty }$ different from $\ell_{\infty }$?

Nonseparable separably injective subspaces of $\ell_{\infty }$ different from $\ell_{\infty }$ exist: indeed, Marciszewski and Pol show in [193] that there exist at least $2^{\mathfrak{c}}$ non-isomorphic C-spaces arising as twisted sums of c ₀ and $c_{0}(\mathfrak{c})$. These are associated to different choices of almost disjoint families (see Sect. 2.2.4) which yields $2^{\mathfrak{c}}$ non-mutually isomorphic separably injective subspaces of $\ell_{\infty }$. None of them can be universally separably injective since the pull-back space in a diagram of the form

cannot be universally separably injective: otherwise the two sequences above are one pull-back of the other and then the diagonal principles yield

$$\displaystyle{\mathop{\mathrm{PB}}\nolimits \oplus \;(\ell_{\infty }/c_{0}) \sim \ell_{\infty }\oplus c_{0}(\varGamma ),}$$

implying that c ₀(Γ) should also be universally separably injective, which is not.

The same question for quotients has an obvious answer: $\ell_{\infty }/c_{0}$. A further result in this direction follows from Dow and Vermeer [88]: if CH is assumed, every compact F-space of weight $\aleph _{2}$ (or less) embeds as a closed subset of an extremely disconnected compact space. Which implies that, under CH, every 1-separably injective C-space of density character $\aleph _{2}$ (or less) is an isometric quotient of a 1-injective Banach space.

As we have already remarked, there are subspaces G of $\ell_{\infty }$ that are not $\mathcal{L}_{\infty }$ spaces but such that $\ell_{\infty }/G \sim \ell_{\infty }$. No characterization is known of the subspaces X of $\ell_{\infty }$ for which $\ell_{\infty }/X$ is (universally) separably injective. Quotients of $\ell_{\infty }$ must be Grothendieck spaces and quotients $\ell_{\infty }/\mathcal{L}_{\infty }$ of $\ell_{\infty }$ by a unspecified $\mathcal{L}_{\infty }$-space must be of type $\mathcal{L}_{\infty }$ since $\ell_{\infty }^{{\ast}{\ast}}\sim \mathcal{L}_{\infty }^{{\ast}{\ast}}\oplus (\ell_{\infty }/\mathcal{L}_{\infty })^{{\ast}{\ast}}$. We are specially interested in the following case:

Problem 8

Is $\ell_{\infty }/C[0,1]$ separably injective?

Recall that since $\ell_{\infty }$ is separably automorphic the space $\ell_{\infty }/C[0,1]$ is well defined. But we do not know if $\ell_{\infty }/C[0,1]$ is even isomorphic to a (complemented subspace of a) C-space. Additional information is contained in the following proposition.

Proposition 6.6

Let $\mathcal{L}_{\infty }$ denote an arbitrary separable $\mathcal{L}_{\infty }$ space and let $\mathcal{U}$ be a free ultrafilter on $\mathbb{N}$ . Then the following statements are equivalent:

• 1. $\ell_{\infty }/\mathcal{L}_{\infty }$ is separably injective.

• 2. $(\mathcal{L}_{\infty })_{\mathcal{U}}/\mathcal{L}_{\infty }$ is separably injective.

• 3. $[\ell_{\infty }^{n}]_{\mathcal{U}}/\mathcal{L}_{\infty }$ is separably injective.

Proof

We already know that both $[\ell_{\infty }^{n}]_{\mathcal{U}}$ and $(\mathcal{L}_{\infty })_{\mathcal{U}}$ are separably automorphic so there is no need to particularize which embeddings $\mathcal{L}_{\infty }\rightarrow [\ell_{\infty }^{n}]_{\mathcal{U}}$ or $\mathcal{L}_{\infty }\rightarrow (\mathcal{L}_{\infty })_{\mathcal{U}}$ are used. Look at the lower exact sequence in the complete push-out diagram

Since the middle horizontal sequence splits, the lower sequence also splits and

$$\displaystyle{(\mathcal{L}_{\infty })_{\mathcal{U}}/\mathcal{L}_{\infty }\sim (\ell_{\infty }/\mathcal{L}_{\infty }) \oplus ((\mathcal{L}_{\infty })_{\mathcal{U}}/\ell_{\infty }).}$$

Thus, since $(\mathcal{L}_{\infty })_{\mathcal{U}}/\ell_{\infty }$ is separably injective, the space $(\mathcal{L}_{\infty })_{\mathcal{U}}/\mathcal{L}_{\infty }$ is separably injective if and only if $\ell_{\infty }/\mathcal{L}_{\infty }$ is. We draw now the complete pull-back diagram

and recall that $c_{0}^{\mathcal{U}}(\mathbb{N},\ell_{\infty }^{n})$ is separably injective (Theorem 2.21 plus Lemma 4.17). Thus, if $[\ell_{\infty }^{n}]_{\mathcal{U}}/\mathcal{L}_{\infty }$ is separably injective then $\ell_{\infty }/\mathcal{L}_{\infty }$ is separably injective by a 3-space argument applied to the upper sequence. If, however, $\ell_{\infty }/\mathcal{L}_{\infty }$ is separably injective then its quotient $[\ell_{\infty }^{n}]_{\mathcal{U}}/\mathcal{L}_{\infty }$ is separably injective by Proposition 2.11. □ 

Quotients of $\ell_{\infty }$ by separable subspaces are also intriguing. The following question was posted in Mathoverflow (http://mathoverflow.net/questions/148956/quo-tients-of-ell-infty-by-separable-subspaces) by the authors:

Problem 9

Under which conditions on a separable subspace M of $\ell_{\infty }$ is the quotient $\ell_{\infty }/M$ isomorphic to a subspace of $\ell_{\infty }$?

No complete answer to the question above is known, but the following partial results that appeared in that page are due to Bill Johnson, with slightly different proofs:

Proposition 6.7

Let X and Y be subspaces of $\ell_{\infty }$ .

• 1. If X and Y are isomorphic, then $\ell_{\infty }/X$ embeds into $\ell_{\infty }$ if and only if $\ell_{\infty }/Y$ embeds into $\ell_{\infty }$ .

• 2. Suppose that $Y \subset X$ and that $\ell_{\infty }/X$ embeds into $\ell_{\infty }$ . Then $\ell_{\infty }/Y$ embeds into $\ell_{\infty }$ if and only if X∕Y embeds into $\ell_{\infty }$ .

• 3. If X is isomorphic to V ^∗ for some separable space V, then $\ell_{\infty }/X$ embeds into $\ell_{\infty }$ .

• 4. If X is isomorphic to a subspace of a separable dual, then $\ell_{\infty }/X$ embeds into $\ell_{\infty }$ .

• 5. If X contains c ₀ and X∕c ₀ embeds into $\ell_{\infty }$ then $\ell_{\infty }/X$ does not embed into $\ell_{\infty }$ .

• 6. If X embeds into L ₁ [0,1], then $\ell_{\infty }/X$ embeds into $\ell_{\infty }$ .

Proof

 

• 1. Let α: X → Y be an isomorphism and consider the diagram

  

  By the injectivity of $\ell_{\infty }$, both α and α ⁻¹ can be extended to operators $\ell_{\infty }\rightarrow \ell_{\infty }$. Thus, each sequence is a push-out of the other and the diagonal principle (Proposition A.22) yields an isomorphism $(\ell_{\infty }/X) \oplus \ell_{\infty }\sim (\ell_{\infty }/Y ) \oplus \ell_{\infty }.$

• 2. In this case one has an exact sequence

  

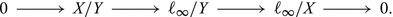
  Since “to be a subspace of $\ell_{\infty }$” is a 3-space property [61, Theorem 3.2.h], the result is clear.

• 3. Let $q:\ell _{1} \rightarrow V$ be a quotient map. Then $V ^{{\ast}}\sim (\ker q)^{\perp }$, so we can assume $X = (\ker q)^{\perp }$ by (1). Hence $\ell_{\infty }/X \sim (\ker q)^{{\ast}}$, which is a subspace of $\ell_{\infty }$.

  Part (4) is a direct consequence of (3), (2), and the fact that separable subspaces embed in $\ell_{\infty }$.

  Part (5) follows from (1), (2) and the fact that $\ell_{\infty }/c_{0}$ does not embed into $\ell_{\infty }$ since it contains an isometric copy of c ₀(Γ) with $\vert \varGamma \vert = 2^{\aleph _{0}}$.

• 6. The case X = L ₁[0, 1] follows from (2) and the fact that L ₁[0, 1] embeds into C[0, 1]^∗ as a complemented subspace: Since $\ell_{\infty }/C[0,1]^{{\ast}}$ and the complement of L ₁[0, 1] in C[0, 1]^∗ embed into $\ell_{\infty }$, so does $\ell_{\infty }/L_{1}[0,1]$. The general case can be proved as (4).

 □ 

Assertion (3) in Proposition 6.7 can be completed with:

Proposition 6.8

Let X be a separable Banach space such that $\mathop{\mathrm{Ext}}\nolimits (X,\ell_{2})\neq 0$ . Then $\ell_{\infty }/j[X^{{\ast}}]$ is not an $\mathcal{L}_{\infty }$ -space for any embedding $j: X^{{\ast}}\longrightarrow \ell_{\infty }$ .

Proof

Let $q:\ell _{1}\longrightarrow X$ be a quotient map. Since $\mathop{\mathrm{Ext}}\nolimits (X,\ell_{2})\neq 0$, there exists a nontrivial exact sequence $0\longrightarrow \ell_{2}\longrightarrow Y \longrightarrow X\longrightarrow 0$, and thus an operator $\ker q\longrightarrow \ell_{2}$ that cannot be extended to ℓ ₁. Since every operator from an $\mathcal{L}_{1}$ into a Hilbert space is 2-summing, it follows that $\ker q$ cannot be an $\mathcal{L}_{1}$-space and thus $(\ker q)^{{\ast}} =\ell _{\infty }/q^{{\ast}}[X^{{\ast}}]$ cannot be an $\mathcal{L}_{\infty }$-space.

Now, let $j: X^{{\ast}}\longrightarrow \ell_{\infty }$ be any embedding. The two sequences in the diagram

are one pull-back of the other since both q ^∗ and j can be extended to operators $\ell_{\infty }\rightarrow \ell_{\infty }$, so the diagonal principle (Proposition A.22) yields that $\ell_{\infty }\oplus \left (\ell_{\infty }/j[X^{{\ast}}]\right )$ is isomorphic to $\ell_{\infty }\oplus (\ker q)^{{\ast}}$; and thus $\ell_{\infty }/j[X^{{\ast}}]$ cannot be an $\mathcal{L}_{\infty }$-space. □ 

In particular, it could be interesting to know if there exists an infinite dimensional separable subspace S of $\ell_{\infty }$ for which $\ell_{\infty }/S \sim \ell_{\infty }$.

6.4 Examples of Separably Injective Spaces

We have seen that there are many natural examples of (universally) separably injective spaces. A few more or less classical spaces could also enjoy separable injectivity properties:

6.4.1 Tensor Products

The fact that when E is separably injective so is $c_{0}(E) = c_{0}\check{ \otimes }_{\varepsilon }E$ suggests:

Problem 10

Must $F\check{ \otimes }_{\varepsilon }E$ be separably injective if both E and F are?

We do not know the answer even if F is a C(K)-space, in which case $C(K)\check{ \otimes }_{\varepsilon }E = C(K,E)$. A particularly interesting test case is that of the space

$$\displaystyle{\ell_{\infty }\check{\otimes }_{\varepsilon }\ell_{\infty } = C(\beta \mathbb{N},C(\beta \mathbb{N})) = C(\beta \mathbb{N} \times \beta \mathbb{N}).}$$

The compact space $\beta \mathbb{N} \times \beta \mathbb{N}$ is not an F-space and it does not contain convergent sequences. However, the space $C(\beta \mathbb{N} \times \beta \mathbb{N}) = C(\beta \mathbb{N},C(\beta \mathbb{N}))$ cannot be even a Grothendieck space as it can be inferred from the following result of Cembranos [72]: If K is an infinite compact and X is an infinite dimensional Banach space, then C(K, X) contains a complemented subspace isomorphic to c ₀. The validity of similar statements for $c_{0}(\aleph _{1})$ under different axioms has been studied by several authors: Galego and Hagler [100] show that under CH there is a compact K so that $c_{0}(\aleph _{1})$ embeds into C(K × K) but not in C(K); Dow et al. [89, Example 2.16] show that in ZFC there exists C(K) spaces with density $2^{\aleph _{0}}$ containing a copy of $c_{0}(\aleph _{1})$ and such that C(K × K) does not contain $c_{0}(\aleph _{1})$ complemented; Candido and Koszmider [59] show that it is consistent that if C(K) has density character $\aleph _{1}$ and contains $c_{0}(\aleph _{1})$ then C(K × K) contains $c_{0}(\aleph _{1})$ complemented.

6.4.2 Baire Classes

The Baire classes of functions on [0, 1] were studied by Bade in [23]. As we shall see, they share some of the properties of the universally separably injective spaces, and therefore can be considered natural candidates to provide new examples of separably injective spaces. We set B ₀ = C[0, 1], and denote by B ₁ the class of all bounded functions which are pointwise limits of functions in B ₀.

Definition 6.9

For each ordinal α with $1 \leq \alpha \leq \omega _{1}$, we define the class of Baire functions of order α, denoted B _α , as the class of all bounded functions which are pointwise limits of functions in $\bigcup _{\beta <\alpha }B_{\beta }$.

Bade shows in [23] that, for 1 ≤ α ≤ ω ₁, the space B _α is linearly isometric to C(K _α ), where K _α is a totally disconnected compact space. He also shows that $B_{\omega _{1}}$ is the space of all bounded Borel measurable functions on [0, 1]. Dashiell shows in [78] (see also [80, Corollary 8]) the following results:

• For $\alpha <\beta \leq \omega _{1}$, B _α is not complemented in B _β .

• The spaces B _α are injective for no α.

• The dual spaces B _α ^∗ are linearly isometric to $\ell_{\infty }^{{\ast}}$, for $1 \leq \alpha \leq \omega _{1}$.

• For $\alpha <\omega _{1}$, B _α is not isomorphic to $B_{\omega _{1}}$.

• B ₁ is not isomorphic to B _α if α > 1.

• For $1 <\alpha <\beta <\omega _{1}$, the spaces B _α and B _β are not isometric. It is apparently unknown whether they are isomorphic.

Passing to separable injectivity affairs, Dashiell also shows that $B_{\omega _{1}} = C(K_{\omega _{1}})$, with $K_{\omega _{1}}$ $\sigma$-Stonean. Since each $\sigma$-Stonean compact is a totally disconnected F-space, $B_{\omega _{1}}$ is 1-separably injective. In Proposition 2.16 it was already shown that the space of all bounded Borel (resp. Lebesgue) measurable functions on the line is 1-separably injective (we do not know however if those spaces are universally 1-separably injective in ZFC). One however has:

Proposition 6.10

The space B ₁ is not 1-separably injective.

Proof

Let $Q = q_{1},q_{2},\ldots$ and $Q' = q_{1}',q_{2}',\ldots$ be two disjoint countable dense subsets of [0, 1]. We consider the following sequences of functions of the first Baire class:

$$\displaystyle{f_{n} = 1_{q_{n}},\quad g_{n} = 1_{[0,1]} - 1_{q_{n}'}.}$$

Then f _n  ≤ g _m for every n, m; hence, if B ₁ were 1-separably injective, then there would exist h ∈ B ₁ such that $f_{n} \leq h \leq g_{m}$ for every n, m. Consider $A = h^{-1}(-\infty,0.4]$ and $B = h^{-1}[0.6,+\infty )$. Then, since h is of the first Baire class, A and B must be $G_{\delta }$ sets, and since $Q \subset B$ and $Q' \subset A$, they are dense sets. But $A \cap B = \varnothing$ while the intersection of two dense $G_{\delta }$ sets is a dense $G_{\delta }$ set. □ 

Thus, while B ₁ is not 1-separably injective, $B_{1} \cap \ell_{\infty }^{c}[0,1]$ is 2-separably injective: see the discussion after Theorem 2.18. Moreover, for all α ≥ 1 the spaces B _α enjoy Rosenthal’s property (V ) and thus, in particular, they are Grothendieck spaces [79, Theorem 3.5].

Problem 11

For which $1 \leq \alpha <\omega _{1}$ is the space B _α (universally) separably injective?

However, the question that motivated our interest in Baire classes is the possibility of having the following type of “surrogate” separable injectivity: Does there exist a function $f:\omega _{1} \rightarrow \omega _{1}$ such that given a separable Banach space X and a subspace $Y \subset X$ every operator $t: Y \longrightarrow B_{\alpha }$ admits an extension $T: X\longrightarrow B_{f(\alpha )}$?

6.4.3 $C(\mathbb{N}^{{\ast}})$ and Its $\aleph$-Injectivity

We know that $C(\mathbb{N}^{{\ast}})$ fails to be $\mathfrak{c}^{+}$-injective (Proposition 2.43) and that it fails to be $(1,\aleph _{2})$-injective (Proposition 5.18). The next question is however open:

Problem 12

Is it consistent that $C(\mathbb{N}^{{\ast}})$ is (universally) $\aleph _{2}$-injective ?

Still, the answer is no for $\mathfrak{c} < 2^{\aleph _{1}}$: since $C(\mathbb{N}^{{\ast}})$ contains $c_{0}(\aleph _{1})$, it contains a $c_{0}(\aleph _{1})$-supplemented copy; so, by Theorem 5.10, $C(\mathbb{N}^{{\ast}})$ should contain $\ell_{\infty }(\aleph _{1})$, which is impossible if $\mathfrak{c} < 2^{\aleph _{1}}$.

It is not difficult to see that a necessary condition for $C(\mathbb{N}^{{\ast}})$ to be universally $\aleph _{2}$-injective is that every operator $c_{0}(\aleph _{1}) \rightarrow C(\mathbb{N}^{{\ast}})$ can be extended to $C(\mathbb{N}^{{\ast}})$. One thus has encountered the notion of space $c_{0}(\aleph _{1})$-extensible (cf. [199]):

Definition 6.11

Let $\mathfrak{M}$ be a class of Banach spaces.

• A Banach space X is said to be $\mathfrak{M}$-extensible if every operator A → X with A a subspace of X in $\mathfrak{M}$ can be extended to an operator X → X.

• A Banach space X is said to be $\mathfrak{M}$-automorphic if every isomorphism between two spaces $A,B \in \mathfrak{M}$ that are subspaces of X and for which X∕A and X∕B have the same density character can be extended to an automorphism of X.

For instance, the choice of $\mathfrak{M}$ as the class of all separable spaces leads to separably automorphic spaces; the choice $\mathfrak{M} =\{ Y \}$ leads to Y -automorphic spaces. When $\mathfrak{M}$ are “all spaces” then we get the notions of extensible and automorphic space. For instance, $\ell_{\infty }$ is extensible but not automorphic while ℓ ₂ is automorphic but not injective. It is proved in [199] that $\mathfrak{M}$-automorphic implies $\mathfrak{M}$-extensible.

We see in this way that the problem of injectivity-like properties of $C(\mathbb{N}^{{\ast}})$ is connected at a deep level with its $c_{0}(\aleph _{1})$-automorphic character: If $C(\mathbb{N}^{{\ast}})$ is not $c_{0}(\aleph _{1})$-extensible then it cannot be (universally) $\aleph _{2}$-injective. Moreover, if all copies of $c_{0}(\aleph _{1})$ in $C(\mathbb{N}^{{\ast}})$ are $c_{0}(\aleph _{1})$-supplemented then by Theorem 5.30 the space $C(\mathbb{N}^{{\ast}})$ is $c_{0}(\aleph _{1})$-automorphic, hence $c_{0}(\aleph _{1})$-extensible. Obviously, we do not know if $C(\mathbb{N}^{{\ast}})$ is $c_{0}(\aleph _{1})$-extensible:

Problem 13

Is $C(\mathbb{N}^{{\ast}})$ a $c_{0}(\aleph _{1})$-automorphic space?

The study of partially automorphic spaces goes beyond the scope of this monograph, and the interested reader is addressed to [17, 19, 63, 67, 199]. A few additional results will help to complete the picture about $C(\mathbb{N}^{{\ast}})$ and will complement Sect. 2.6 We have already shown that $C(\mathbb{N}^{{\ast}})$ is separably automorphic, a property somehow inherited from $\ell_{\infty }$. So, it would be nice to know “how much” automorphic the space is. In any case, it will be partially automorphic in a different sense from $\ell_{\infty }$, since $\ell_{\infty }$ is automorphic for subspaces X so that $\ell_{\infty }/X$ contains $\ell_{\infty }$, while $C(\mathbb{N}^{{\ast}})$ is not since $C(\mathbb{N}^{{\ast}})$ is not $C(\mathbb{N}^{{\ast}})$-automorphic. In contrast with Proposition 2.55 (1), we do not know if the quotient of a separably automorphic space by a separably injective space is separably automorphic.

It is obvious that in a c ₀-automorphic space either all copies of c ₀ are complemented or all of them are uncomplemented. It follows from Lemma 2.48 that C-spaces in which every copy of c ₀ is complemented are c ₀-automorphic. These spaces include C-spaces over Eberlein compacta by Proposition 2.57 or ordinal compacta. The C-spaces in which no copy of c ₀ is complemented are Grothendieck, but their analysis is not so simple. In particular, some are c ₀-automorphic (universally separably injective spaces, for instance) while others are not: if $\mathcal{H}$ denotes Haydon’s Grothendieck C-space without copies of $\ell_{\infty }$, the space $\ell_{\infty }\oplus \mathcal{H}$ is not c ₀-automorphic. Indeed, if $\sigma:\ell _{\infty }\oplus \mathcal{H}\longrightarrow \ell_{\infty }\oplus \mathcal{H}$ is an automorphism sending c ₀ ⊕ 0 to $0 \oplus c_{0}$ and $\pi _{\mathcal{H}}:\ell _{\infty }\oplus \mathcal{H}\longrightarrow \mathcal{H}$ denotes the projection onto the second coordinate, then $\pi _{\mathcal{H}}\sigma _{\vert \ell_{\infty }}:\ell _{\infty }\rightarrow \mathcal{H}$ cannot be weakly compact, hence must be an isomorphism on a copy of $\ell_{\infty }$, which is also impossible.

Copies of c ₀ must also be complemented in any WCG Banach superspace, as it can be proved using the classical Amir-Lindenstrauss Theorem [6]. The natural question of whether the same happens for c ₀(Γ)—must copies of c ₀(Γ) be complemented in every WCG superspace?—has a negative answer, as it was already mentioned in Sect. 2.2.4. More precisely, [13, 192], there exists under GCH an Eberlein compact $\mathcal{E}$ such that $C(\mathcal{E})$ contains an uncomplemented copy of $c_{0}(\aleph _{\omega })$. The C-space $C(\mathcal{E}) \oplus c_{0}(\aleph _{\omega })$ is therefore WCG and it is not $c_{0}(\aleph _{\omega })$-automorphic. This shows that the situation is very different from that for c ₀ and some restrictions in size are necessary. Indeed, if $\mathcal{E}$ is an Eberlein compact of weight $\aleph$ then, by Theorem 4.2 in [35], $C(\mathcal{E})$ contains a copy of $c_{0}(\aleph )$. For $\aleph = \aleph _{n}$, n < ω, all those copies must be complemented in $C(\mathcal{E})$ due to the following result in [13]:

Theorem 6.12

Let K be a Valdivia compact and let Γ be a set with cardinal $\vert \varGamma \vert = \aleph _{n}$ for some n < ω. Then every $\lambda$ -isomorphic copy of c ₀ (Γ) inside C(K) is $2^{n+1}\lambda$ -complemented.

However, we do not know if $C(\mathcal{E})$ is $c_{0}(\aleph _{n})$-automorphic. A positive answer to the following question would imply that $C(\mathcal{E})$ is in fact H-automorphic for all subspaces $H \subset c_{0}(\aleph _{n})$: Let $\mathcal{E}$ be an Eberlein compact and $\aleph < \aleph _{\omega }$. Does every complement of $c_{0}(\aleph )$ in $C(\mathcal{E})$ (having density character at least $\aleph$) contain a copy of $c_{0}(\aleph )$? Recall that it is even unknown if a complement of $c_{0}(\aleph _{n})$ in $C(\mathcal{E})$ must be isomorphic to a C-space.

6.5 Ultraproblems

Since ultrapowers of $\mathcal{L}_{\infty }$ have emerged as unexpected universally separably injective spaces, questions involving ultraproducts are natural. The Henson-Moore classification problem of $\mathcal{L}_{\infty }$-spaces by isomorphic ultrapowers ([134, p. 106], [128, p. 315], [130]) is perhaps the deepest:

Problem 14

How many ultratypes of $\mathcal{L}_{\infty }$-spaces are there?

The results in Chap. 4 show only two different ultra-types of $\mathcal{L}_{\infty }$-spaces: that of C-spaces and that of spaces of almost universal disposition. It would be interesting to add some new classes here. If one is thinking about obtaining a third type, probably the best candidates are “the” quotient $C[0,1]/\mathcal{G}$ (more natural should be thinking about the space $\ell_{\infty }/\mathcal{G}$, which is uniquely defined by the separably automorphic character of $\ell_{\infty }$) or the subspace $\ker \pi$ of a (rightly chosen) quotient map $\pi: C[0,1] \rightarrow \mathcal{G}$ (see Sect. 6.6). Of course that we do not know whether $C[0,1]/\mathcal{G}$ or $\ell_{\infty }/\mathcal{G}$ are C-spaces, whether they have the same ultratype of a C-space, or even if both have the same ultratype.

Even if we would pay for a third ultratype, some of the authors believe that:

Conjecture 1

There is a continuum of different ultratypes of $\mathcal{L}_{\infty }$-spaces.

Reasonable candidates to get such a continuum could then be hereditarily indecomposable $\mathcal{L}_{\infty }$-spaces [12, 240], exotic preduals of ℓ ₁ as in [34, 104], some Bourgain and Pisier [47] or Bourgain and Delbaen [14, 46] spaces, or some of the $\mathcal{L}_{\infty }$-envelopes constructed in [69].

We pass now to problems involving ultraproducts and exact sequences. Recall from [140, 207] that if 0 → Y → X → Z → 0 is an exact sequence and $\mathcal{U}$ is an ultrafilter then $0 \rightarrow Y _{\mathcal{U}}\rightarrow X_{\mathcal{U}}\rightarrow Z_{\mathcal{U}}\rightarrow 0$ is also exact (see [61, Lemma 2.2.g]). No criterion however is known to determine when the ultrapower sequence of a nontrivial exact sequence is again nontrivial.

Definition 6.13

We will say that an exact sequence ultra-splits if some of its ultrapower sequences split.

From the results in Sect. 3.3.4, and more specifically Corollary 4.14, one has:

Proposition 6.14

Any exact sequence $0\longrightarrow Y \longrightarrow X\longrightarrow Z\longrightarrow 0$ in which X is a C-space and either Y or Z are spaces of almost universal disposition does not ultra-split.

Proposition 4.30 shows that the exact sequence

from Example 2.24 in Sect. 2.2.6 yields a nonseparable Lindenstrauss space which is complemented in no C-space, although it does have an ultrapower isomorphic to a C-space (cf. Proposition 4.27). We do not know, however, if the sequence above ultra-splits.

Ultra-splitting problems are connected to the 3-space problem for universal separable injectivity discussed in Sect. 6.2. Indeed, if universal separable injectivity were a 3-space property then one would have $\mathop{\mathrm{Ext}}\nolimits (C(\mathbb{N}^{{\ast}}),C(\mathbb{N}^{{\ast}})) = 0$, which implies, under CH, that all exact sequences of the form (here $\varDelta$ is the Cantor set)

(6.2)

ultra-split no matter whether they are trivial or not. This was claimed in [21, Example 4.5(a)], but we do not know if it is true or not.

Indeed, assuming CH, one has $C(\varDelta )_{\mathcal{U}}\approx C(\mathbb{N}^{{\ast}})$ for all free ultrafilters on the integers $\mathcal{U}$ (Proposition 4.12). Hence the ultrapower sequence of (6.2) has the form

and would split if $\mathop{\mathrm{Ext}}\nolimits (C(\mathbb{N}^{{\ast}}),C(\mathbb{N}^{{\ast}})) = 0$ were true. This could apply to the exact sequence

constructed in [57, Corollary 2.4] which has the form (6.2) since $C[0,1] \sim C(\varDelta )$ by Milutin’s theorem. Thus, if the assertion $\mathop{\mathrm{Ext}}\nolimits (C(\mathbb{N}^{{\ast}}),C(\mathbb{N}^{{\ast}})) = 0$ were true, and under CH, the space $\varOmega _{\mathcal{U}}\sim C(\mathbb{N}^{{\ast}}) \oplus C(\mathbb{N}^{{\ast}})$ would be isomorphic to a C-space, in spite of the fact [57, Corollary 2.4] that Ω is not even isomorphic to a quotient of a Lindenstrauss space.

Some of the authors believe that the following holds:

Conjecture 2

Every exact sequence $0\longrightarrow \mathcal{L}_{\infty }\longrightarrow X\longrightarrow C\longrightarrow 0$ in which $\mathcal{L}_{\infty }$ denotes an arbitrary $\mathcal{L}_{\infty }$-space and C an arbitrary C-space ultra-splits.

We conclude this section with the explicit formulation of several open ends already mentioned though the text:

• Since both $\mathcal{G}$ and C-spaces are Lindenstrauss spaces, it makes sense to ask: Does every $\mathcal{L}_{\infty }$-space have an ultrapower isomorphic to a Lindenstrauss space?

• Does every (infinite-dimensional, separable) Banach space X have an ultrapower isomorphic to its square? What if X is an $\mathcal{L}_{\infty }$-space?

• Are the classes of C ₀-spaces and M-spaces closed under “isometric ultra-roots”?

• Does the Gurariy space have an ultrapower isometric (or isomorphic) to an ultraproduct of finite dimensional spaces? Since spaces of universal disposition cannot be complemented in C-spaces, if $\mathcal{G}_{\mathcal{U}} = (G_{i})_{\mathcal{V}}$ then the spaces G _i cannot be “uniformly injective”.

• Are Lindenstrauss ultraproducts via $\aleph$-good ultrafilters universally $\aleph$-injective spaces in ZFC? In other words, can the conclusion of Theorem 5.15 be strengthened to obtain universal injectivity? Notice that this is sensitive to axioms. The answer is of course affirmative under GCH by Theorem 5.15 and Proposition 5.13.

• Another question regarding a possible generalization of Theorem 5.15 is whether the hypothesis “Lindenstrauss” can be weakened to just “$\mathcal{L}_{\infty }$-space”: Namely, prove or disprove that every ultraproduct built over an $\aleph$-good ultrafilter is $\aleph$-injective as long as it is an $\mathcal{L}_{\infty }$-space.

6.6 Spaces of Universal Disposition

In this section, if no further specification is made, universal disposition means “with respect to finite dimensional spaces”. Up to now, under CH, we have encountered two non-isomorphic spaces of universal disposition: The Grothendieck space $\mathcal{S}^{\omega _{1}}$ and the non-Grothendieck (since it contains c ₀ complemented) space $\mathcal{F}^{\omega _{1}}$.

Problem 7 of Sect. 6.3 can be reformulated here for spaces of universal disposition:

Problem 15

Do there exist subspaces of $\ell_{\infty }$ of universal disposition?

Observe that a space of universal disposition for separable spaces cannot be a subspace of $\ell_{\infty }$ since it must contain copies of all spaces of density character $\aleph _{1}$, such as $\ell_{2}(\aleph _{1})$. It could help to decide whether $\mathcal{F}^{\omega _{1}}$ is a subspace of $\ell_{\infty }$ to know if it contains a subspace isomorphic to $\ell_{2}(\aleph _{1})$.

The same question for quotients of $\ell_{\infty }$ has an affirmative answer, at least under CH: Johnson and Zippin proved in [147] that every separable Lindenstrauss space is a quotient of $C(\varDelta )$, where $\varDelta$ is the Cantor set. So one has an exact sequence

(6.3)

No ultrapower of this sequence splits by the results in Sect. 3.3.4; see also Proposition 6.14. Under CH, the ultrapower sequence with respect to any free ultrafilter $\mathcal{U}$ on $\mathbb{N}$ has the form

and thus $\mathcal{G}_{\mathcal{U}}$ is a quotient of $\ell_{\infty }$. Observe that $\mathcal{F}^{\omega _{1}}$ cannot be a quotient of $\ell_{\infty }$ since c ₀ is not.

Regarding the nature of $\ker \pi$, Pełczyński posed on the blackboard to us the question of whether it is possible to identify the kernel(s) of the sequence(s) (6.3), and in particular if some such kernel can be a C-space. It is not hard to check that $\ker \pi$ is an $\mathcal{L}_{\infty }$-space when π is an “isometric” quotient in the sense that it maps the open unit ball of $C(\varDelta )$ onto that of $\mathcal{G}$. On the other hand, it is possible to get another quotient map $\varpi: C(\varDelta )\longrightarrow \mathcal{G}$ whose kernel is not an $\mathcal{L}_{\infty }$-space: to this end, recall that Bourgain has shown that $\ell_{1}$ contains an uncomplemented copy of itself. An obvious localization argument yields an exact sequence $0\longrightarrow B_{{\ast}}\longrightarrow c_{0}\longrightarrow c_{0}\longrightarrow 0$ in which $\mathcal{B}_{{\ast}}$ cannot be an $\mathcal{L}_{\infty }$-space. See [45, Appendix 1]. “Multiplying” the sequence above by any exact sequence $0\longrightarrow Y \longrightarrow C(\varDelta )\longrightarrow \mathcal{G}\longrightarrow 0$ one gets the exact sequence $0\longrightarrow Y \oplus B_{{\ast}}\longrightarrow C(\varDelta ) \oplus c_{0}\longrightarrow \mathcal{G}\oplus c_{0}\longrightarrow 0$. Since both $C(\varDelta )$ and $\mathcal{G}$ have complemented subspaces isomorphic to c ₀, this sequence can be written as $0\longrightarrow Y \oplus \mathcal{B}_{{\ast}}\longrightarrow C(\varDelta )\longrightarrow \mathcal{G}\longrightarrow 0$ in which the kernel $Y \oplus \mathcal{B}_{{\ast}}$ is not even an $\mathcal{L}_{\infty }$-space.

Again, a positive measure subset of authors believes that the following problem has an affirmative answer:

Problem 16

Is there a continuum of mutually non-isomorphic spaces of universal disposition having density character $\mathfrak{c}$?

The connection between universal disposition and transitivity is not yet clearly understood. In particular is not clear if every space of universal disposition for finite dimensional spaces must be $\mathfrak{F}$-transitive or whether every space of universal disposition for separable spaces must be separably transitive. Ultrapowers are also involved into these affairs: Since it is well known that ultrapowers of almost isotropic spaces are isotropic, one is tempted to believe that the proof for the following question is at hand

Problem 17

Do ultrapowers of almost $\mathfrak{F}$-transitive spaces must be $\mathfrak{F}$-transitive?

More yet: Is every ultrapower of a space of almost universal disposition separably transitive?

In a different direction it would be interesting to know if the class of almost isotropic spaces is “axiomatizable”, equivalently if every Banach space whose ultrapowers are isotropic is itself almost isotropic; see [28] for a related discussion.

6.7 Asplund Spaces

A Banach space is called an Asplund space if every separable subspace has separable dual. One of the referees of this work formulated the problem of whether a classification of Asplund separably injective spaces is possible. More precisely, he asked:

Problem 18

Is it true that every Asplund separably injective space is c ₀-upper-saturated? Does there exist an Asplund separably injective space that contains an infinite dimensional reflexive subspace?

Observe that Proposition 2.10 can be translated into:

Proposition 6.15

A separably injective space is Asplund if and only if it does not contain C[0,1].

Bourgain [43] (see also [105]) proved that any operator $T: C[0,1]\longrightarrow X$ that fixes a subspace of finite cotype also fixes a subspace isomorphic to C[0, 1]. Thus, an Asplund and separably injective space X cannot contain finite cotype (in particular, superreflexive) subspaces: the corresponding embedding would extend to C[0, 1] providing a copy of C[0, 1] inside X. Gasparis [102] showed a similar result for asymptotically $\ell_{1}$ spaces, and therefore an Asplund separably injective space cannot contain asymptotically $\ell_{1}$ spaces. Rosenthal’s conjecture is that any operator $T: C[0,1]\longrightarrow X$ that fixes an infinite dimensional subspace not containing c ₀ would also fix a copy of C[0, 1]. If this were true, an Asplund separably injective space would be c ₀-saturated. Gasparis [103] solves affirmatively Rosenthal’s conjecture under the conditions that the operator is contractive and its restriction to the subspace is an isometry. One therefore has:

Proposition 6.16

Every infinite dimensional Asplund 1-separably injective space is c ₀ -saturated.

It seems very likely that infinite dimensional Asplund 1-separably injective spaces do not exist.

6.8 Grothendieck Spaces

As we have already mentioned, it is an open problem that seems to have been first posed by Lindenstrauss—see [167, 226]—to characterize Grothendieck C(K) spaces in terms of topological properties of K. An obvious necessary condition is that every convergent sequence in K is eventually constant. The condition is insufficient since $C(\beta \mathbb{N} \times \beta \mathbb{N})$ contains complemented copies of c ₀. There is another example due to Schlumprecht [227, 5.4] of a C(K)-space with the Gelfand-Phillips property (something that a Grothendieck space cannot have) without non-stationary convergent sequences in K. Koszmider remarks in [167] that the class of compact spaces where every convergent sequence is eventually constant does not admit a characterization by means of isomorphic properties of the Banach space C(K). To show this, consider an example of Schachermayer in [226] of the Stone compact associated to the Boolean algebra $\mathcal{A}$ of all subsets A of $\mathbb{N}$ such that 2n ∈ A if and only if 2n + 1 ∈ A for all but finitely many $n \in \mathbb{N}$. The compact space $S(\mathcal{A})$ does not contain non-stationary convergent sequences for almost the same reason as $\beta \mathbb{N}$ does not: in fact, $S(\mathcal{A})\setminus \mathbb{N}$ is homeomorphic to $\beta \mathbb{N}\setminus \mathbb{N}$. The space $C(S(\mathcal{A}))$ is not Grothendieck since $T(\,f) = (\,f(2n + 1) - f(2n))_{n}$ defines an operator $C(S(\mathcal{A}))\longrightarrow c_{0}$ which is onto because all the norm one finitely supported sequences are in the image of the closed unit ball. On the other hand $C(S(\mathcal{A})) \sim \ell_{\infty }\oplus c_{0} \sim C(\beta \mathbb{N} \sqcup \alpha \mathbb{N})$, while the compact $\beta \mathbb{N} \sqcup \alpha \mathbb{N}$ has non-stationary convergent sequences.

A Banach space characterization of Lindenstrauss spaces which are Grothendieck spaces is simple: not containing complemented copies of c ₀. A Banach space characterization of Grothendieck $\mathcal{L}_{\infty }$-spaces seems to be unknown. We conjecture

Conjecture 3

Every $\mathcal{L}_{\infty }$ space that contains no complemented separable subspaces is a Grothendieck space.

The next proposition is implicit in Lindenstrauss [177]:

Proposition 6.17

An $\mathcal{L}_{\infty }$ -space X is Grothendieck if and only if every operator T: X → S with S separable can be extended everywhere.

Proof

Let S be a separable space, let $j: X \rightarrow E$ be an embedding and let t: X → S be an operator. Since X is Grothendieck, t must be weakly compact, hence $t^{{\ast}{\ast}}: X^{{\ast}{\ast}}\rightarrow S$ is well defined. Since X is an $\mathcal{L}_{\infty }$-space, $X^{{\ast}{\ast}}$ is injective and thus it is complemented in E ^∗∗. Therefore t ^∗∗ admits an extension $T: E^{{\ast}{\ast}}\rightarrow S$, whose restriction to E is an extension of t. The converse is clear just embed X into some $\ell_{\infty }(\varGamma )$. □ 

We have already mentioned that Grothendieck spaces of type $\mathcal{L}_{\infty }$ do not necessarily contain $\ell_{\infty }$: Talagrand [239] constructed, under CH, a Grothendieck C-space that does not have $\ell_{\infty }$ as a quotient; while Haydon [125] obtained an independent construction, in ZFC, of a Grothendieck C-space that does not admit $\ell_{\infty }$ as a subspace. The density character of Grothendieck spaces was treated in Brech [48] who constructed by forcing an example of a Grothendieck space $C(\mathcal{B}r)$ of density $\aleph _{1}$ in a certain model in which $\mathfrak{c} = \aleph _{2}$. In particular, $C(\mathcal{B}r)$ is a subspace of $\ell: \infty$ and cannot contain $\ell_{\infty }$. More examples of Grothendieck spaces without copies of $\ell_{\infty }$ and additional properties have appeared after Koszmider’s construction of C-spaces with few operators in [166, 167]. The example of Brech shows that the assumption of the existence of a nonreflexive Grothendieck space of density $\aleph _{1}$ is weaker than CH: there are models of ZFC where no nonreflexive Grothendieck space of density $\aleph _{1}$ exists. In particular, if $\mathfrak{s}$ denotes the smallest cardinal κ such that [0, 1]^κ is not sequentially compact then one has:

Proposition 6.18

Every Grothendieck space with density character strictly smaller than $\mathfrak{s}$ must be reflexive.

Proof

Assume that X is a Grothendieck space with density character smaller than $\mathfrak{s}$. Its dual unit ball in the weak* topology will be a compact having weight smaller than $\mathfrak{s}$, hence sequentially compact. By the Grothendieck character, it will also be weakly sequentially compact and X ^∗ should be reflexive, as well as X. □ 

As it is well-known, $\aleph _{0} < \mathfrak{s} \leq \mathfrak{c}$ and $\mathfrak{s} = \mathfrak{c}$ under Martin’s axiom, and in particular $\aleph _{1} < \mathfrak{s}$ is consistent. If $\mathfrak{p}$ is defined as the least cardinality of a family $\mathcal{F}$ of infinite subsets of $\mathbb{N}$ which is closed under finite intersections and such that for every infinite subset A of $\mathbb{N}$ there exists $B \in \mathcal{F}$ such that $A\setminus B$ is infinite (in other words, the smallest cardinal of a filter base in $\mathbb{P}(\mathbb{N})/\mathop{\mathrm{fin}}\nolimits$ whose filter is not contained in a principal filter) then consistently $\mathfrak{p} < \mathfrak{s}$ (see [86]).

The following point regarding the relation between separable injectivity and Grothendieck character remains unsolved:

Problem 19

Is every $\lambda$-separably injective space, with $\lambda < 2$, a Grothendieck space?

This has obvious connections with Problem 1. Another problem connecting Grothendieck spaces and cardinals is the following: Let (E _i ) _i ∈ I be a family of Banach spaces containing no complemented copy of c ₀. Can $\ell_{\infty }(I,E_{i})$ contain a complemented copy of c ₀? Leung and Räbiger show in [174] that if | I | is not real-valued measurable and (E _i ) _i ∈ I is a family of Grothendieck spaces that are Lindenstrauss spaces then $\ell_{\infty }(I,E_{i})$ is a Grothendieck space and so it cannot contain a complemented copy of c ₀. See Sect. 2.2.6.

Although the existence of real-valued measurable cardinals cannot be proved in ZFC, such cardinals, if they exist, need not to be very large: Ulam proved in [243] that if real-valued measurable cardinals do exist then the continuum is one (cf. [142, Theorem 10.1]).