Keywords

1 Introduction

Despite the numerous technology advances in the field of Humanoid Robotics, mobility and ability to move like a human being remains an essential required feature. In that context, gait pattern generation seems to be the key problem to research dedicated to walking robots [1]. Actually, there are two major walking patterns to be found in bipedal robotics: static walking and dynamic walking [2, 3] and several stability criteria may be used depending on the walking pattern selected. The recourse to a given stability criterion ensures the bipedal robot’s balance at every moment in order to avoid falls and collapses. Besides, whether considering the static or dynamic walking pattern, each gait pattern involves the same various phases that are the single support phase, the impacts with the ground and the double support phase. A satisfying control strategy for a gait pattern has to provide good dynamic performances in these different modes in terms of similarity with human gait by guaranteeing at the same time stability, smoothness and safety.

Thus, in this work, to control bipedal robots during the single support stage, we have chosen to focus on Minimum Jerk based control strategy. The main benefit of such approach resides in the generation of smooth trajectories in order to avoid any abrupt motion and consequently limit the robot vibrations [4]. The concept of Jerk Minimization has been developed by Hogan, the pioneer in using the Minimum Jerk principle for robotic systems to reproduce realistic human arm movements [5, 6] and antagonistic muscles [7]. Minimum Jerk Theory comes from the finding that the degree of smoothing of a curve can be quantified by a function counting the number of shocks performed [8]. Hogan named this function Jerk and associated it mathematically to the third time derivative of a given trajectory. Among researchers having recourse to the Minimum Jerk criterion, there are divided opinions between those using trigonometric curves and others using polynomial curves to describe the robot trajectory. Actually, very few research papers consider trigonometric functions to describe the Jerk function [9–11]. They note that all joints involved in the movement are less oscillatory. It seems that most works dealing with the Minimum Jerk criterion are based on polynomial trajectories. As proved by Amirabdollahian et al. [12], the use of polynomial trajectories has some advantages. The control of the movement is easily achievable since the first and second derivatives of the polynomial are known. Also, some studies [13] show that Minimum Jerk control laws based on polynomials of high degrees are more effective because the dynamics of the robot are smoother and the trajectory references are easily followed by the actuators involved. Finally, for applications using real-time control, the trajectories can be corrected or adjusted at any time by simply redefining the polynomials describing the trajectory or by the superposition of a new path to the previous one [14]. Another issue that has also divided opinions among researchers is the space on which reference trajectories must be planed: the Cartesian or the joint space. Actually, Kyriakopoulos and Saridis in [8] are the first to raise the issue of choice of planned trajectories in the Cartesian space or in the joint one. They show that if the minimization problem and its solutions are formulated in the joint space, only physical limitations of the joints actuators will be included in the constraints statement. However, in a realistic environment, obstacles exist and are causing changes in the trajectory direction. Therefore, generating reference trajectories based on the Minimum Jerk criterion may be done whether in the joint or Cartesian space. The space’s choice should only be determined according to the constraints and the shape of the desired trajectory. Finally, it can be noted that very few works using Minimum Jerk criterion were devoted to optimize humanoid motion through gait pattern generation [15–17].

On the other side, to control bipedal robots during the IP and DSP, we have chosen in this work to focus on impedance control strategy. Such control approach was originally proposed by Hogan in [18]. Its goal is to establish a dynamic relation between the end-effector position and the contact force [19]. There are two methodologies stemming from the impedance control law: the classical impedance [6] and dynamic impedance based control laws [20]. The first approach does not take into consideration the dynamic of the robotic system and includes the active stiffness control. In opposition, the dynamic impedance control is based on two assumptions: the consideration of the constraint dynamic model when an external force is applied and the environment characterization by three parameters: inertia, damping and active stiffness. Thus, the dynamic impedance control law represents an efficient control law to overcome difficulties raised in the impact phase. Moreover, it guaranties a stable and safe elastic contact with the ground as it takes into consideration environmental parameters related to the nature of the ground and the contact type. As a result, many research works have recourse to this control law to generate bipedal robots walking gaits as [20–24].

To produce stable, smooth and safe walking cycles for bipedal robots evolving in the 3D space, this chapter proposes the elaboration of appropriate control strategies to be implemented to biped robots. Indeed, during the swing phase, a Minimum Jerk based control law is produced in order to generate a semi-ellipsoidal trajectory for the swing foot while an appropriate impedance control law is proposed to ensure the robot stability and safe balance at foot landings on the ground. Minimum Jerk control is inspired by the human brain cognitive such that trajectories are planned in the Cartesian space system whereas controllers are expressed in the joint space. For the IP and DSP, the impedance control law is designed such that it ensures stable and safe impacts with the ground. Also, it allows the environment characterization through inertia, damping and active stiffness parameters inspired from the recent work [25] where sufficient conditions of stability and discussions about safety during the impacts are given.

This chapter is then organized as follows: in the next section, the novel approach of Jerk optimal control and the impedance control laws are designed. The stability conditions for the two control approaches are rigorously given. Section 3 is dedicated to the application of the proposed approach to a bipedal robot prototype. Indeed, the anthropomorphic model of the Humanoid robot is presented and kinematic and dynamic models of the lower body are developed. Simulations performed on the Humanoid robot do validate both designed control laws and show the generation of a satisfactory walking gait pattern even in presence of measurement noise and uncertainties on the environment stiffness.

2 Stable and Safe Gait Pattern

2.1 The Gait Cycle

A walking gait cycle involves various phases such as single support phase, impacts with the ground and the double support phase [26]. According to Kajita and his colleagues [2, 3], whether considering human or artificial gait, the walking function is based on an alternate displacement of the two legs with a support point permanently in contact with the ground. The leg that is totally in contact with the ground is called the supporting leg whereas the leg starting the foot step is the swinging leg also called free leg. For each lower limb, a human walking cycle is always composed of two phases (see Fig. 1) [27]:

Fig. 1
figure 1

Phases of a walking cycle

Full size image

  • A support phase where the foot remains in contact with the ground. This stage starts at the first foot/ground contact and ends when the foot toe is completely off the ground. This phase represents 60 % of the whole walking cycle.

  • A swinging phase where the foot is free, without any ground contact. This stage starts at the completion of the supporting phase and it ends when the second foot begins its own swinging phase. This phase generally corresponds to the 40 % left of the whole walking cycle.

For a usual walking gait, the lower limb playing the role of supporting leg ensures the three main functions of support, damping and propulsion while the swinging leg is being moved from rear to front [28]. Two distinct phases of double support are often considered:

  • The double support of reception that takes places at the initial foot/ground contact of the previously free leg and is proceeding with the whole weight transfer of the other limb to the current leg.

  • The double support of propulsion occurs at the level of the previously supporting leg at the instant the foot is landing off the ground. This phase also corresponds to the weight transfer from this limb to the other one that becomes the new supporting leg.

Artificial walking aims at reproducing all phases composing a natural walking gait. However, walking bipedal robots are not able to provide a sustained rhythm of walk. Thus, a supplementary phase has to be added and considered. Indeed, a typical walking cycle includes three main stages [26, 29–31]: The single support phase (SSP), the impact phase (IP) and the double support phase (DSP).

The SSP occurs when one limb is pivoted to the ground while the other is swinging from the rear to the front. At the beginning of this stage, the heel of the forward foot is lifted with the toe used as a pivot. When a sufficient rotational motion is done, the foot is to be completely off the ground and swings in the air. The free dynamic model corresponding to the SSP is described by:

$$\begin{aligned} M(\theta )\ddot{\theta }+H(\theta ,\dot{\theta })+G(\theta )=D.U \end{aligned}$$
(1)

where \(\theta \), \(\dot{\theta }\), \(\ddot{\theta } \in R^{n}\) are the joint position vector, the joint velocity vector and the joint acceleration vector of the bipedal robot, respectively. \(M(\theta )\in R^{n\times n}\) is the inertia matrix, \(H(\theta ,\dot{\theta }) \in R^{n}\) is the vector of the Coriolis and centripetal forces \(G(\theta )\in R^{n}\) and is the gravity vector. The matrix \(D\in R^{n\times n} \) is a nonsingular input map matrix whereas \(U\in R^{n}\) is the control input vector.

The IP occurs when the toe of the forward foot starts touching the ground. The impact between the toe of the swing leg and the ground takes place during an infinitesimal length of time [32]. The DSP occurs when both limbs remain in contact with the ground. This phase begins with the heel of the forward foot touching the ground. Then the foot rotational motion continues until the entire sole of the foot becomes in contact with the ground. This stage finally ends with the toe of the rear foot taking off the ground. The length of this phase depends on the walking cycle’s rhythm. The constrained dynamic model during the IP and DSP of the bipedal robot is generally described by [33]:

$$\begin{aligned} M(\theta )\ddot{\theta }+H(\theta ,\dot{\theta })+G(\theta )=DU+\frac{\partial c(\theta )^{T}}{\partial \theta }F \end{aligned}$$
(2)

where \(C(\theta )\in R^{3}\) is the contact point and \(F\in R^{3}\) is the contact force with the ground. During the gait cycle, the supporting foot does not change its position and orientation, and the whole part of its sole is in contact with the ground. As soon as the third phase of the swing foot ends, the foot of the supporting leg goes into its own first stage of the swing motion.

2.2 Minimum Jerk Based Control for the Swing Phase

2.2.1 Minimum Jerk Control: Theoretical Foundations

According to [5], the Jerk is defined as the third time derivative of a given trajectory \(\upbeta (\mathrm{t})\) such that:

$$\begin{aligned} \mathop {\beta }^{\cdots }(t)=\frac{d^{3}\beta {(t)}}{dt^{3}} \end{aligned}$$
(3)

The main benefit of Minimum Jerk based control resides in the generation of smooth trajectories in order to avoid any abrupt motion and consequently limit the robot vibrations [4]. To find among all possible trajectories, the one that allows the achievement of the smoothest motion, a Jerk cost must be assigned. Thus, for a trajectory \(\beta (t)\) describing a particular path starting at and ending at \(t_{f}\), the Minimum Jerk cost criterion is generally defined by [34]:

$$\begin{aligned} C_{\textit{Jerk}}=\textit{min}\, \frac{1}{2}\int _{t=t_{0}}^{t_{f}}{\mathop {\beta }^{\cdots }}(t)^{2}dt \end{aligned}$$
(4)

Even if not essential, some additional terms could be included in the criterion function to minimize a weighted sum of multiple criteria. In [35], for example, the objective function to be minimized is the integral of a weighted sum of squared jerk and the execution time. Among all possible solutions, the following fifth order polynomial trajectories seems to be the most recommended one in the literature [36]:

$$\begin{aligned} \beta (t)=at^{5}+bt^{4}+ct^{3}+dt^{2}+et+f \end{aligned}$$
(5)

where \(a,b,c,d,e,f\) are constants to be determined for each trajectory \(\beta \)(t). The corresponding velocity and acceleration functions are easily deduced as:

$$\begin{aligned} \dot{\beta }(t)=5at^{4}+4bt^{3}+3ct^{2}+2dt+e \end{aligned}$$
(6)
$$\begin{aligned} \ddot{\beta }(t)=20at^{3}+12bt^{2}+6ct+2d \end{aligned}$$
(7)

To compute the parameters \(a,b,c,d,c,e\) and \(f\) two main methods are used in the literature: The Point-to-point method and the Via-point method. The Point-to-point method requires the expression of the function to be minimized and the values of positions, velocities and accelerations of only two points corresponding to the initial and final time of the movement. The control algorithm corresponding to the Point-to-point method only needs to run once. For each a trajectory \(\beta (t)\) the following relation is used to compute the parameters \(a,b,c,d,e\) and \(f\) [37]:

$$\begin{aligned} \left( \begin{array}{l} a\\ b\\ c\\ d\\ e\\ f\end{array}\right) =\left( \begin{array}{llllll} t_{0}^{5}&{} t_{0}^{4}&{} t_{0}^{3} &{}t_{0}^{2}&{} t_{0} &{}1\\ t_{f}^{5}&{}t_{f}^{4}&{}t_{f}^{3} &{}t_{f}^{2} &{}t_{f} &{}1\\ 5t_{0}^{4} &{}4t_{0}^{3} &{}3t_{0}^{2}&{}2t_{0}&{}1&{}0\\ 5t_{f}^{4} &{}4t_{f}^{3} &{}3t_{f}^{2} &{}2t_{f} &{}1&{}0\\ 20t_{0}^{3} &{} 12t_{0}^{2} &{} 6.\,t_{0} &{}2 &{}0&{}0\\ 20t_{f}^{3}&{}12t_{f}^{2} &{}6t_{f} &{}2 &{}0&{}0\end{array}\right) ^{-1} \left( \begin{array}{l} \beta _{0}\\ \beta _{f}\\ \dot{\beta }_{0}\\ \dot{\beta }_{f}\\ \ddot{\beta }_{0}\\ \ddot{\beta }_{f} \end{array}\right) \end{aligned}$$
(8)

where:

\(\beta _{0},\dot{\beta }_{0}\) and \(\ddot{\beta }_{0}\) are respectively the position, velocity and acceleration of the trajectory \(\beta (\mathrm{t})\) at \(t_{0}\).

\(\beta _{f},\dot{\beta }_{f}\) and \(\ddot{\beta }_{f}\) are respectively the position, velocity and acceleration of the trajectory \(\beta (\mathrm{t})\) at \(t_{f}\).

For the Via-point method, such approach is recommended when obstacles occur in the operating space where the robotic system evolves. In such cases, not only the initial and final positions must be specified but also a number of desired intermediate positions characterized by the time at which these positions must be reached. Therefore, the number of intermediate points determines the accuracy of the reference trajectory. This method implies that the algorithm is executed several times. If only one desired intermediate position is specified, the parameters \(a,b,c,d,e\) and \(f\) are computed as follows [38]:

$$\begin{aligned} \left( \begin{array}{llllll} 5t_{0}^{4}&{} 4t_{0}^{3}&{} 3t_{0}^{2} &{}2t_{0}&{} 1 &{}0\\ 5t_{d}^{4}&{} 4t_{d}^{3}&{} 3t_{d}^{2} &{}2t_{d} &{}1 &{}0\\ 5t_{f}^{4} &{}4t_{f}^{3} &{}3t_{f}^{2}&{}2t_{f}&{}1&{}0\\ 20t_{0}^{3} &{}12t_{0}^{2} &{}6t_{0} &{}2 &{}0&{}0\\ 20t_{d}^{3} &{} 12t_{d}^{2} &{} 6t_{d} &{}2 &{}0&{}0\\ 20t_{f}^{3}&{}12t_{f}^{2} &{}6t_{f} &{}2 &{}0&{}0\end{array}\right) \left( \begin{array}{l} a\\ b\\ c\\ d\\ e\\ f\end{array}\right) =\left( \begin{array}{l} \beta _{0}\\ \beta _{d}\\ \beta _{f}\\ \dot{\beta }_{0}\\ \dot{\beta }_{d}\\ \dot{\beta }_{f}\\ \ddot{\beta }_{0}\\ \ddot{\beta }_{d}\\ \ddot{\beta }_{f} \end{array}\right) \end{aligned}$$
(9)

where:

  • \(t_{d}\) is an intermediate instant satisfying \(t_{0}<t_{d}<t_{f}\).

  • \(\beta _{d}, \dot{\beta }_{d}\) and \(\ddot{\beta }_{d}\) are respectively the position, velocity and acceleration of the variable \(\beta _{i}(\mathrm t)\) at \(t_{d}\).

2.2.2 A Novel Approach of a Jerk Optimal Control

To optimize the Jerk for gait pattern generation in the three dimensional space during the swing phase, we propose in this section a new optimal jerk approach different from the Point-to-Point and Via-Point methods. Indeed, the Point-to-Point method implies constraints on positions, velocities and accelerations on boundary conditions whereas the Via-Point method imposes the same boundary constraints in addition to other constraints related to some intermediate desired positions at the instants at which these specific positions have to be reached.

Actually, the proposed approach is based on the generation of reference trajectories specifying at each time iteration not only constraints at boundary conditions or intermediate points but also constraints on the current positions, velocities and accelerations. Furthermore, the proposed method induces three-dimensional reference trajectories involving both trigonometric and polynomial functions. This particular choice provides at the same time benefits of trigonometric functions requiring fewer resources for real time implementation and benefits of polynomial functions giving smoother dynamics and fewer vibrations. Finally, in order to realize an efficient control law, easy to implement, trajectories will be planned in the Cartesian space while the control law is depending on angular variables. Such control design is very close to the human brain cognitive [39].

Considering the swing foot of the bipedal robot, the differential kinematic model of the bipedal robot is given by:

$$\begin{aligned} \dot{X}_{f}(t)=J(\theta )\dot{\theta }(t) \end{aligned}$$
(10)

where \(\dot{X}_{f}\in R^{3}\) is the Cartesian velocity vector for the swing foot and \(J(\theta )\in R^{3\times n}\) is the Jacobian matrix defined by:

$$\begin{aligned} J(\theta )=\frac{\partial X_{f}(\theta )}{\partial \theta }\Big \vert _{\theta _{d}} \end{aligned}$$
(11)

where \(\theta _{d}\in R^{n}\) is the desired joint position vector. The inverse kinematic model is then given by:

$$\begin{aligned} \theta (t)=J(\theta )^{+}\left( X_{f}(t)-X_{f,d}(t)\right) +\theta _{d}(t) \end{aligned}$$
(12)

where \(J(\theta )^{+}\) is the pseudo-inverse of the Jacobian matrix. \(X_{f,d}\in R^{3}\) is the desired Cartesian position vector for the swing foot. The joint velocity vector \(\dot{\theta }(t)\) is obtained using the following equation:

$$\begin{aligned} \dot{\theta }(t)=J(\theta )^{+}\dot{X}_{f}(t) \end{aligned}$$
(13)

where \(\dot{X}_{f}\) is the Cartesian velocity. To get the joint acceleration vector \(\ddot{\theta }(t)\), one just has to determine the first time derivative of the previous equation so that:

$$\begin{aligned} \ddot{\theta }(t)=J(\theta )^{+}\left( \ddot{X}_{f}(t)-\dot{J}(\theta )\dot{\theta }(t)\right) \end{aligned}$$
(14)

where \(\dot{J}(\theta )\) is the first time derivative of the Jacobian matrix \(J(\theta )\). \(\ddot{X}_{f}\) is the Cartesian acceleration. In order to produce a walking gait closed to a human one, the toe of the biped robot has to follow a path similar to the one generated by the human foot when performing a walking step. To reach this goal, we impose to the toe end effector a semi-elliptical trajectory in the sagittal plane such that the three-dimensional Cartesian desired trajectory is described by:

$$\begin{aligned} X_{f,d}=[g+v\; \textit{cos}\,(\alpha \; \beta (t)+\pi ) \quad w \quad h+y \;\textit{sin}\,(\alpha \; \beta (t)+\pi )]^{T} \end{aligned}$$
(15)

where, in this case, \(\beta (t)\in R\) designs the ankle joint trajectory in the sagittal plane defined by the five order polynomial (5) and where its corresponding velocity and acceleration functions are defined by (6) and (7), respectively. Furthermore, the different constant coefficients of the polynomial function (5) are computed using the relation (8) related to the Point-to-point approach. The pair \((g,h)\) represents the initial coordinates of the center of the ellipse in the sagittal plane. Parameter \(v\) represents a half step length whereas \(w\) defines the distance between the two legs and \(y\) represents the maximum height of the step. Parameter \(\alpha \) is a multiplier used in order to increase the variation range of the variable \(\beta (t)\). The first and second derivatives of (15) with respect to time are respectively given by the two following expressions:

$$\begin{aligned} \dot{X}_{f,d}=[-v\alpha \;\dot{\beta }(t)\;\textit{sin}\,(\alpha \;\beta (t)+\pi )\quad 0 \quad y\alpha \dot{\beta }(t)\textit{cos}\,(\alpha \;\beta (t)+\pi )]^{T} \end{aligned}$$
(16)
$$\begin{aligned} \ddot{X}_{f,d}=[\ddot{x}_{f,d}\quad \, \ddot{y}_{f,d}\quad \, \ddot{z}_{f,d}]^{T} \end{aligned}$$
(17)

where:

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_{f,d}=-v\left( \alpha \dot{\beta }(t)\right) ^{2}\textit{cos}\,(\alpha \beta (t)+\pi )-v\alpha \ddot{\beta }(t)\textit{sin}\,(\alpha \beta (t)+\pi )\\ \ddot{y}_{f,d}=0\\ \ddot{Z}_{f,d}=-y\left( \alpha \dot{\beta }(t)\right) ^{2}\textit{sin}\,(\alpha \beta (t)+\pi )+y\alpha \ddot{\beta }(t)\textit{cos}\,(\alpha \beta (t)+\pi ) \end{array}\right. } \end{aligned}$$

During the SSP, the Minimum Jerk criterion is applied to reduce abrupt displacements of the bipedal robot which is controlled via a linearizing control law. Actually, we impose to the bipedal robotic model (1) to follow the following second order linear input-output behavior [40]:

$$\begin{aligned} \left( \ddot{\theta }(t)-\ddot{\theta }_{d}(t)\right) +K_{v,1}\left( \dot{\theta }(t)-\dot{\theta }_{d}(t)\right) +K_{p,1}\left( \theta (t)-\theta _{d}(t)\right) =0 \end{aligned}$$

where \(K_{v,1}\) and \(K_{v,1}\in R^{n\times n}\) are two positive definite diagonal matrices computed offline to ensure global stability, decoupling properties and desired performances [41]. If \(\lambda \) is the desired bandwidth, then to obtain a critically damped closed-loop performance, we must select [16]:

$$\begin{aligned}&K_{v,1}=\textit{diag}\,[2\;\lambda ]\\&K_{p,1}=\textit{diag}\,[\lambda ^{2}]\nonumber \end{aligned}$$
(18)

Using (1) and (18), the control law of the bipedal robot when achieving the swing phase is deduced as:

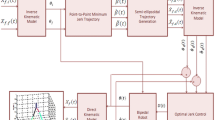
$$\begin{aligned} U(t)&=D^{-1}\Big (M(\theta )\Big [\ddot{\theta }_{d}(t)-K_{v,1}\left( \dot{\theta }(t)-\dot{\theta }_{d}(t)\right) -K_{p,1}\left( \theta (t)-\theta _{d}(t)\right) \Big ]\nonumber \\&\qquad \qquad \quad +H(\theta ,\dot{\theta })+G(\theta )\Big ) \end{aligned}$$
(19)

Figure 2 explains all required steps for the achievement of the novel Jerk optimal control approach.

Fig. 2
figure 2

The novel approach of Minimum Jerk based control during the swing phase

Full size image

The calculus of a control law based on the proposed approach of the Jerk optimal control includes the following steps:

  1. i.

    Computing the initial joint position vector \(\theta _{i}\) and the final joint position vector \(\theta _{f}\) using the inverse kinematic model (12).

  2. ii.

    Generation of \(\beta (t)\), \(\dot{\beta },\ddot{\beta }(t)\) trajectories based on the Point-to-Point method according to Eqs. (5)–(7) applied to the initial and final joint constraints and taking also account of time data \(t_{0}\) and \(t_{f}\).

  3. iii.

    Generation of semi-ellipsoidal reference trajectories in the Cartesian space by computing at each time iteration the reference Cartesian positions, velocities and accelerations \(X_{f,d}(t), \dot{X}_{f,d}(t)\) and \(\ddot{X}_{f,d}(t)\) according to Eqs. (15)–(17), respectively.

  4. iv.

    Generation of the desired joint trajectories \(\theta _{d}(t)\), \(\dot{\theta }_{d}(t)\) and \(\ddot{\theta }_{d}(t)\) using (12)–(14).

  5. v.

    Computing the Jerk optimal control law \(U(t)\) using (19).

  6. vi.

    Implementation of the control law \(U(t)\) to the free robotic system (1) in order to generate joint position and velocity vectors \(\theta (t)\) and \(\dot{\theta }(t)\) using (13) and (14). \(\theta (t)\) and \(\dot{\theta }(t)\) are supposed to be measured via online sensors.

  7. vii.

    Generation of Cartesian trajectories \(X_{f}(t)\) and \(\dot{X}_{f}(t)\) by applying the direct kinematic model (10).

2.3 Impedance Based Control for the Constrained Phases

To control the bipedal robot during the impact and double support stages, we have chosen to implement the impedance based control proposed in [25]. Indeed, the impedance control represents an efficient control law to overcome difficulties raised in the impact phase. Moreover, it guaranties a stable and safe elastic contact with the ground as it takes into consideration environmental parameters related to the nature of the ground and the contact type. Regarding the control law implementation to the bipedal robot, it is simple since the same control expression is used in IP and DSP. During the ground contact, the free end of the biped, at the completion of the step, comes into contact with the ground. This phase is assumed to take place in an infinitesimal time interval [32]. For the constrained model (2), the ground reaction force is given by [25]:

$$\begin{aligned} F=F_{d}-K_{d}(X_{f,d}-X_{f})-B_{d}\left( \dot{X}_{f,d}-\dot{X}_{f}\right) -M_{d}\left( \ddot{X}_{f,d}-\ddot{X}_{f}\right) \end{aligned}$$
(20)

where \(F_{d}\in R^{3}\) is a desired reaction force and \(K_{d}, B_{d}, M_{d}\in R^{3\times 3}\) are the stiffness, the damping and the inertia matrices, respectively. These three parameters characterize the contact type and the environment nature where the contact takes place, under the following control law:

$$\begin{aligned} U&=D^{-1}J(\theta _{c})^{+}[K_{p,2}(X_{f,d}-X_{f})-K_{v,2}\left( \dot{X}_{f,d}-\dot{X}_{f}\right) +K_{f}(F_{d}-F)+F_{d}]\nonumber \\&\quad +D^{-1}G(\theta ) \end{aligned}$$
(21)

where \(J(\theta _{c})^{+}\) is the pseudo-inverse of the Jacobian matrix of the bipedal robotic system at the contact point \(c\) and where \(K_{p,2}, K_{v,2}\) and \(K_{f}\in R^{3\times 3}\) are diagonal matrices representing respectively the position, velocity and force gains related to the impedance control law. Using a Lyapunov approach, the asymptotic stability of the robotic system (2) is guaranteed if the following stability conditions are satisfied [25]:

$$\begin{aligned} K_{p,2}>0\nonumber \\ K_{v,2}>0\\ k_{f}=-I\nonumber \end{aligned}$$
(22)

where \(I \in R^{3\times 3}\) is the identity matrix.

Fig. 3
figure 3

The impedance based control implemented during the constrained phases

Full size image

Figure 3 shows all involved parameters in the impedance control implementation. Parameters \(\mathrm{K}_{\mathrm{p},2}\), \(\mathrm{K}_{\mathrm{v},2}\) and \(\mathrm{K}_\mathrm{f}\) are computed offline to satisfy the Lyapunov asymptotic conditions (22). However and even if a trajectory inside a sagittal plane is imposed, some step parameters like the reference Cartesian positions, velocities and accelerations \(X_{f,d}(t), \dot{X}_{f,d}(t)\) and \(\ddot{X}_{f,d}(t)\) and the desired joint trajectories \(\theta _{d}(t), \dot{\theta }_{d}(t)\) and \(\ddot{\theta }_{d}(t)\) are calculated online at each time iteration. Online sensors are used to measure real joint trajectories \(\theta (t), \dot{\theta }(t)\) and \(\ddot{\theta }(t)\) and the contact forces with the ground \(F\).

3 Application to a Humanoid Robot Prototype

In this section the control laws proposed in the last section will be applied to a Humanoid robot prototype which a particular morphology very close to a human one [41].

3.1 The Anthropomorphic Model of the Humanoid Robot

The Humanoid robot prototype [41] considered in this paper is composed of fifteen links associated to twenty-six degrees of freedom (DOF). The morphological constitution of the humanoid robot corresponds to a human being’s whole anatomy with a weight of 70 kg and a height of 1.73 m. Furthermore, we take account on the following assumptions:

Assumption 1::

The connection between upper and lower bodies is made by a passive joint. Indeed, trunk and pelvis rigid bodies are assumed not to be subject to rotations however their mere presence allows the rigid bodies to move in a correct way. Hence, the upper body’s mass is considered and taken into account during the gait calculation and simulations of the lower body.

Assumption 2::

The vectors of joint position \(\theta \), joint velocity \(\dot{\theta }\), joint acceleration \(\ddot{\theta }\) and contact forces with the ground F are measured via online sensors.

Assumption 3::

During the gait cycle, the humanoid robot is supposed to evolve in a well known environment where no obstacles are encountered. Therefore, no adaptive controls are required.

Assumption 4::

The ground contact surface is assumed to be smooth and regular.

 

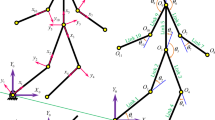
Figure 4 and Table 1 show the involved rotations for each link. The whole humanoid robot is composed of two independent robotic systems: the upper body and the lower body.

Fig. 4
figure 4

The Humanoid robot prototype

Full size image
Table 1 Rigid bodies and articulations
Full size table

Winter statistical model [42] was used to determine all physical parameters corresponding to each link \(\mathrm{C}_\mathrm{i}\). Each rigid body \(\mathrm{C}_\mathrm{i}\) of the humanoid robot is characterized by the following physical parameters (see Fig. 5):

  • \(k_{i}\in \mathfrak {R}\): Proximal distance defined as the distance from the center of gravity to the connect joint of the previous link \(\mathrm{C}_{\mathrm{i}-1.}\)

  • \(l_{i}\in \mathfrak {R}\): Distal distance defined as the distance from the center of gravity to the connect joint of the next link \(\mathrm{C}_{\mathrm{i}+1.}\)

Fig. 5
figure 5

Segmental proportions of rigid bodies

Full size image

Since the kinematic model is elaborated in the three dimensional space, we define \(K_{i}\in \mathfrak {R}^{3\times 1}\) and \(L_{i}\in \mathfrak {R}^{3\times 1}\) as respectively the proximal and distal distance vectors of the link \(\mathrm{C}_\mathrm{i}\) given by:

$$\begin{aligned} K_{i}=[0\quad 0\quad K_{i}]^{T} \qquad \qquad \text {and} \quad \quad L_{i}=[0\quad 0\quad l_{i}]^{T} \end{aligned}$$

Each rigid body \(\mathrm{C}_\mathrm{i}\) of the bipedal robot is characterized by the previous physical parameters plus the following physical parameters:

  • \(m_{i}\in \mathfrak {R}\): Mass of the link \(\mathrm{C}_\mathrm{i}\)

  • \(i_{i}\in \mathfrak {R}\): Inertia about the center of mass of the link \(\mathrm{C}_\mathrm{i}\)

Since the dynamic model is elaborated in the three dimensional space, the following three dimensional parameters are considered:

  • \(M_{i}\in \mathfrak {R}^{3\times 3}\): mass matrix of the link \(\mathrm{C}_\mathrm{i}\) given by:

    $$\begin{aligned} \mathrm{M}_{\mathrm{i}}=\left( \begin{array}{lll} \mathrm{m}_{\mathrm{i}}&{}0 &{}0\\ 0&{} \mathrm{m}_{\mathrm{i}} &{}0\\ 0&{}0&{}\mathrm{m}_{\mathrm{i}}\end{array}\right) \end{aligned}$$

  • \(I_{i}\in \mathfrak {R}^{3\times 3}\): Inertia matrix about the center of mass of link \(\mathrm{C}_\mathrm{i}\) described by:

    $$\begin{aligned} {I}_{i}=\left( \begin{array}{lll} i_{ix}&{}0 &{}0\\ 0&{} i_{iy} &{}0\\ 0&{}0&{} i_{iz}\end{array}\right) \end{aligned}$$

Table 2 gives all segmental physical parameters.

Table 2 Physical parameters obtained via winter model
Full size table

3.2 Kinematic and Dynamic Modelling of the Bipedal Robot

All along this chapter, we focus only on the bipedal part of the humanoid robot presented in the last section. The direct and inverse kinematics of the humanoid robot are obtained using Euler’s transformation principle [43]. Let \(X=[X_{1},\ldots ,X_{7}]^{T}\) be the vector of Cartesian positions for links center of gravity and let \(A_{i}\) be the transformation matrix of link \(\mathrm{C}_\mathrm{i}\) from the body coordinate system to the inertial coordinate one. The robot implicit kinematic model is then described by:

$$\begin{aligned} X_{i}=A_{i}(L_{i}-K_{i})+X_{i-1},\;\mathrm{i}=1,\ldots ,15 \end{aligned}$$
(23)

where \(X_{i}\) is the vector of Cartesian positions of the link \(\mathrm{C}_\mathrm{i}\). An explicit expression of the bipedal robot kinematic model is given here under:

$$\begin{aligned} X_{7}&=A_{7}(L_{7}-K_{7})+A_{6}(L_{6}-K_{6})+A_{5}(L_{5}-K_{5})+A_{4}(L_{4}-K_{4})\\&\quad +A_{3}(L_{3}-K_{3})+A_{2}(L_{2}-K_{2})+A_{1}(L_{1}-K_{1}) \end{aligned}$$

We consider at this level a number of standard scenarios [44–46] to validate the lower body kinematic model. Figure 6 shows validation of standard scenarios for the Humanoid robot lower body. The different postures are represented in both the sagittal and frontal planes.

The three dimensional dynamic modeling of the seven linked bipedal robot has been accurately developed using the Newton-Euler formalism [47] for the SSP, the IP and DSP.

Fig. 6
figure 6

Standard scenarios for the Humanoid robot lower body

Full size image

In order to reach the dynamic model we use Hemami’s works [29, 43] and we suggest a generalized motion equation for the translation as in (24) and the rotation as in (25) of each link \(\mathrm{C}_\mathrm{i}\):

$$\begin{aligned} M_{i}\ddot{X}_{i}=M_{i}g+\varGamma _{i}-\varGamma _{i+1}. \end{aligned}$$
(24)
$$\begin{aligned} I_{i}\dot{w}_{i}=f_{i}+F_{i}+F_{i+1}+G_{i}+G_{i+1}+\tau _{i}+\tau _{i+1} \end{aligned}$$
(25)

where:

\(W_{i}, \dot{W}_{i}\): Angular position and acceleration of the link \(\mathrm{C}_\mathrm{i}\).

\(X_{i}, \ddot{X}_{i}\): Linear position and acceleration of the link \(\mathrm{C}_\mathrm{i}\)

\(F_{i}, \dot{F}_{i+1}\): Torques due to the holonom force applied respectively to the proximal and distal articulation of the link \(\mathrm{C}_\mathrm{i}\) expressed in the body coordinate system

\(G_{i}, G_{i+1}\): Non-holonom torques applied respectively to the proximal and distal articulation of the link \(\mathrm{C}_\mathrm{i}\) expressed in the body coordinate system

\(\tau _{i}, \tau _{i+1}\): Muscular torques applied respectively to the proximal and distal articulation of the link \(\mathrm{C}_\mathrm{i}\) expressed in the body coordinate system

\(\varGamma _{i}, \varGamma _{i+1}\): Holonom forces applied respectively to the proximal and distal articulation of the link \(\mathrm{C}_\mathrm{i}\) expressed in the inertial coordinate system

\(f_{i}\): Intrinsic torque of the link \(\mathrm{C}_\mathrm{i}\) expressed in the body coordinates system \((\mathrm{x}_\mathrm{i},\mathrm{y}_\mathrm{i},\mathrm{z}_\mathrm{i})\) and relating angular velocity to the link inertia.

Human body’s balance of forces and torques reveals that humanoid limbs are subject to three kinds of forces: holonom, non holonom and mechanic forces [43]. Figure 7 shows the applied forces and torques to the humanoid lower body.

Fig. 7
figure 7

Applied forces and torques to the Humanoid robot lower body

Full size image

A clear and sequential methodology to follow in order to establish a reduced and expendable dynamic model is rigorously explained in [47]. Using this method, the dynamic model of the Humanoid robot lower body has been reduced such moving from 42 initial DOFs to only 12 state variables.

3.3 Jerk Optimal Control

Obviously initial conditions have a great influence on the bipedal robot’s trajectory and equilibrium as the robotic system has an inherent nonlinear and very complex dynamical model due to the high number of degrees of freedom involved. To the best of our knowledge, there is no specific methodology that could be used to obtain optimal initial conditions. Therefore, based on previous standard validation scenarios, initial angular conditions are inspired on the one hand by the usual and common posture of a Human being when starting a walking step with a swinging left foot and on the other hand by very intensive simulations. The combination of angular corresponding positions is validated with Fig. 8 and is given by:

$$\begin{aligned} \theta _{i}=\Big [ -\frac{\pi }{11}\quad 0\quad 0\quad 0\quad -\frac{\pi }{9}\quad 0\quad 0\quad \frac{\pi }{9}\quad 0\quad \frac{\pi }{11}\quad -0.0089\quad 0\Big ]^{T} \end{aligned}$$

Indeed, Fig. 8 shows the bipedal robot initial posture in the 3D space.

Fig. 8
figure 8

Initial posture for the bipedal robot

Full size image

Using direct kinematic modelling given, initial Cartesian conditions are given by:

$$\begin{aligned} X_{f,i}=[0\quad 0.53 \quad 0]^{T} \end{aligned}$$

A semi-elliptical trajectory for a walking step of 0.5 s duration is generated using the parameters given in Table 3. It corresponds to a velocity of 0.6 m s\(^{-1}\) which is an acceptable Cartesian velocity when compared to current state of the art gait velocities rates for walking Humanoid robots [48, 49].

The fifth order angular trajectory is given then by:

$$\begin{aligned} \beta (t)=-3.18t^{5}+6.36t^{4}-3.39t^{3}-0.0089 \end{aligned}$$

Position and velocity gains related to the Minimum Jerk control law are chosen so that global stability conditions (18) are satisfied for a desired bandwidth \(\lambda = 12\) such that:

$$\begin{aligned} K_{p,1}&=\textit{diag}\,[24\quad 24 \quad 24]\\ K_{v,1}&=\textit{diag}\,[144\quad 144 \quad 144] \end{aligned}$$
Table 3 Parameters of the Cartesian desired trajectory
Full size table

Figure 9 shows the evolution of the desired and real positions of the swing foot in the 3D Cartesian space while Fig. 10 represents the real Cartesian trajectory of the swing foot during the realization of a walking step.

Fig. 9
figure 9

Desired and real Cartesian positions of the swing foot for a walking step

Full size image
Fig. 10
figure 10

Real Cartesian trajectory of the swing foot during a walking step

Full size image

Figure 11 shows the evolution in time of the position, velocity and acceleration of the swing foot joints. All angular position reach after the step duration their desired values, this is emphasized by the very low values of velocities and accelerations at the step completion.

Fig. 11
figure 11

Evolution of the joint positions, velocities and accelerations of the swing foot during the swing phase

Full size image

Figure 12 emphasizes the control laws involved in the swing foot motion for a walking step of 0.5 s duration.

Fig. 12
figure 12

Evolution of the control laws of the swing foot during the swing phase

Full size image

Simulation results show the efficiency of the Minimum jerk control. Minimum Jerk observed benefits are the smoothness of the foot trajectory and the absence of sudden movements.

3.4 Impedance Based Control

Simulation of the bipedal robot during the IP and DSP is established using the constrained model (2) for the control law (21) and the ground reaction force (20). Environmental parameters used to describe the contact environment are inspired by the Park’s research work [50] as:

$$\begin{aligned} K_{d}&=\textit{diag}\,[10^{4} \quad 10^{4} \quad 10^{4} ]\\ B_{d}&=\textit{diag}\,[630\quad 630\quad 630]\\ M_{d}&=\textit{diag}\,[10^{-2}\quad 10^{-2} \quad 10^{-2}] \end{aligned}$$

Regarding the reference ground reaction force, its role is to allow the free leg located at a height of 0.01 m from the ground to land on the contact area and at the same time to enable a low foot sliding along the \(x\)-axis. The resulting ground reaction force is composed of a vertical component and a normal one. According to [21], the vertical component of the reference external force has to emphasize the weight transfer of the bipedal robot from the right supporting foot to the left free foot. The normal component of the reference ground reaction force is usually a low value but high enough to enable a short translation of the left foot along the \(x\)-axis. Thus, \(F_{d}\) is chosen as follows:

$$\begin{aligned} F_{d}=[30 \quad 0 \quad 300]^{T} \end{aligned}$$

Position, velocity and force gains related to the impedance control law are computed offline so that the Lyapunov asymptotic stability conditions (22) are satisfied:

$$\begin{aligned}&K_{p,2}=\textit{diag}\,[10^{4} \quad 10^{4} \quad 10^{4} ]\\&K_{v,2}=\textit{diag}\,[600\quad 600\quad 600]\\&K_{f}= -\,\textit{diag}\,[1\quad 1 \quad 1] \end{aligned}$$

Actually, the final position reached by the swinging foot while applying a Minimum Jerk control law during the SSP represents the initial position of the robotic system when starting the IP. The duration of the free phase is 0.5 s and the constrained phases’ duration is 0.2 s. Consequently, the swinging foot initial Cartesian position for the impact and double support phases is given by:

$$\begin{aligned} X_{f,i}=[0.3 \quad 0.53 \quad 0.01]^{T} \end{aligned}$$

The final desired Cartesian position of the active foot at the step completion is:

$$\begin{aligned} X_{f,f}=[0.35 \quad 0.53 \quad 0]^{T} \end{aligned}$$

To explore the relevance of the proposed approach, we consider two case studies for simulation.

3.4.1 Case Study 1: Smooth and Regular Ground Surface and No Sensory Noise

This case study validates the proposed methodology of Minimum Jerk control for gait pattern generation under the stated assumptions. The Humanoid robot is supposed then to evolve in a smooth and regular ground contact surface. Furthermore, no sensory noise occurs here. Simulation results show the evolution of the active leg variables when the robot end-effector achieves a complete walking step. The ground reaction force is shown in Fig. 13. The active foot Cartesian components along \(x\) and \(z\) axis are represented in Fig. 14 while the real Cartesian trajectory of the humanoid robot free foot is shown in Fig. 15.

During the SSP, the ground reaction force is null. Then at the impact, it takes the shape of a delta impulse such reaching a maximal value of 750 N. Finally after the impact, the ground reaction force gradually decreases and gets stabilized at the value of 300 N.

Fig. 13
figure 13

Evolution of the ground reaction force during a walking step

Full size image
Fig. 14
figure 14

Real Cartesian components of the active foot during a walking step

Full size image
Fig. 15
figure 15

Real Cartesian trajectory of the active foot during a walking

Full size image

Figure 14 emphasizes the real Cartesian positions evolution for the swinging foot during the achievement of a whole walking step. At the moment of impact, it clearly appears that Cartesian positions along \(x\) and \(z\) axis observe a decrease of their velocity convergence in order to avoid that the foot gets pushed across the floor. Desired Cartesian positions of the free foot are reached \(t_\mathrm{f}=0.7\) s which is the specified time for step completion. The Cartesian trajectory of the moving leg is represented in Fig. 15. During the free stage, the swinging leg follows a semi-ellipsoidal trajectory. This shape is quite close to a human leg motion while achieving a walking step. At the contact point, the trajectory taken by the bipedal robot is similar to a line segment with a negative slope and at the end of the double support phase, the Humanoid robot leg slides along the contact area.

3.4.2 Case Study 2: Uncertain Stiffness of the Ground Surface and Sensory Noise

In this case, the objective is to analyze the robustness of the proposed approach to the environment uncertainties and sensory noise. Actually, the Humanoid robot evolves in an unknown environment as we consider an uncertainty on stiffness in the environment model. Furthermore, sensory noise is introduced. Indeed we consider a Gaussian noise of \(0.01^{\circ }\) mean and \(0.01^{\circ }\) standard deviation for the joint position measurements and \(0.05^{\circ }\,\mathrm{s}^{-1}\) mean and \(0.05^{\circ }\,\mathrm{s}^{-1}\) standard deviation for the joint velocity measurements. Damping and inertia environmental parameters previously given are used while the stiffness parameter is subject to uncertainties such that:

$$\begin{aligned} K_{d}=[1+2000 * \sin (\mathrm{t})]* \textit{diag}\,[10^{4} \quad 10^{4} \quad 10^{4}] \end{aligned}$$

Simulation results show the effect of sensory noise and stiffness uncertainties on the contact force and torques during the impact and double support phases. Hence, the ground reaction force is represented in Fig. 16 while Fig. 17 shows the control laws involved in the swing foot motion.

Fig. 16
figure 16

Evolution of the ground reaction force during a walking step

Full size image
Fig. 17
figure 17

Evolution of the control laws of the swing foot during the swing phase

Full size image

The active foot Cartesian components along \(x\) and \(z\) axis are represented in Fig. 18.

Even if the noise and environment uncertainties are not modeled in the design of the controller, simulation results emphasize the efficiency of the control law and the robustness of the proposed method as perturbations have no effect on the bipedal robot trajectory. We must however note that the effects of vibration are observed in control laws.

Fig. 18
figure 18

Real Cartesian components of the active foot during a walking step

Full size image

3.5 Walking Cycle Generation

To show the walking gait pattern generation during a whole walking cycle, the different rigid bodies composing the bipedal robot are represented in the Cartesian three dimensional space in Fig. 19. Figure 20 gives the evolution in time of the z coordinate of the two feet and the ground reaction force during the achievement of three alternate walking steps.

Fig. 19
figure 19

The 3D gait pattern generation during a walking cycle

Full size image
Fig. 20
figure 20

The two feet z coordinate and the contact force during a walking cycle

Full size image

In Fig. 19, the several postures taken by the bipedal robot emphasize its motion along the time and shows well the achievement of three alternate footsteps starting with a step initiated by the left foot (in blue). Two steps initiated by the left foot are alternate with one step by the right foot. Thus, the alternation of the Minimum Jerk and impedance based control laws represents an efficient control combination for the achievement of a stable walking cycle. Actually, it combines benefits of both control laws a smooth motion during the swing phase and a stable and safe elastic contact with the ground in the constrained phases.

In order to realize the whole Humanoid motion, we adopt two separate controls for the upper and lower bodies where position, velocity and time objectives allow the synchronization of movements between upper and lower limbs during gait. Thus, using the same strategy of linearizing control law (19), we impose to the arms a movement from the inside to the outside according to the walking cycle phase considered. Figure 21 represents in the Cartesian 3D space the several postures taken by the robot during the achievement of two alternate footsteps. We notice that only the two arms, forearms and hands are moving from the inside to the outside in a motion that is alike a human being’s one.

Fig. 21
figure 21

Intermediate positions of the whole Humanoid robot during a walking cycle

Full size image

4 Future Works

Even if stability conditions are guaranteed, tuning control parameters remains a difficult issue considering the complexity of models (1) and (2). The optimization of the controller parameters using multi-objective criteria and biological-inspired optimization techniques known for their global convergence and good performances and also using results of [51] will be addressed in future works. On the other hand, safety is mostly ensured through control software level during the SSP and DSP. Actually, the current control system is designed in order to authorize corrective forces and torques to the ground characteristics through suitable choice of stiffness, damping and inertia parameters for the impedance control approach. In future works, a quantitative index must be established to evaluate the safety criterion [52]. Furthermore, robust safe motion under unknown environment and in presence of obstacles will be addressed based on [53, 54].

5 Conclusion

In this chapter, satisfying control laws have been proposed to provide good dynamic performances in terms of stability, smoothness and safety for bipedal robots during a gait cycle resembling as much as possible to a Human being one. Indeed, during the swing phase a novel Minimum Jerk control strategy is produced to generate a stable semi-ellipsoidal motion trajectory without dynamic vibrations and control shakings while an appropriate impedance control law is proposed to ensure stable and safe elastic contact balance at foot landings on the ground even in presence of sensory noise and uncertainties on the environment stiffness. Simulation results performed on a 15 link/26 DOF Humanoid robot with a weight of 70 kg and a height of 1.73 m walking at a velocity of 0.6 m s\(^{-1}\) show the effectiveness of the proposed strategy and better performances compared to related approaches. Future works will focus on optimizing tuning controller parameters to ensure faster speed for the SSP and better safety performances and robustness for the IP and DSP.