Large-Eddy Simulation of Flow and Heat Transfer Around a Low-Mach Number Turbine Blade

Abstract

If flowines has been In the ideal Brayton cycle, an increase of the pressure ratio directly leads to an increase of the thermodynamic efficiency and subsequently to a decrease of the specific fuel consumption. Unfortunately, this pressure ratio growth causes a direct increase of the temperature ratio through the turbine stages, which may impact the design of turbine blades.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the last decades, the compression ratio in aeronautical gas turbines has been in constant increase. In the ideal Brayton cycle, an increase of the pressure ratio directly leads to an increase of the thermodynamic efficiency and subsequently to a decrease of the specific fuel consumption. Unfortunately, this pressure ratio growth causes a direct increase of the temperature ratio through the turbine stages, which may impact the design of turbine blades. Large-Eddy Simulation (LES) is a promising tool for the prediction of heat transfer on turbine blades. However, wall treatment in LES is a well-known issue mainly related to the high resolution required to capture near-wall phenomena. Several strategies have been proposed to tackle this issue. In the thin-boundary layer (TBL) model [1] or in detached-eddy simulations (DES) [8], a different set of equations is solved in the near-wall region. Another solution is to impose the viscous and thermal fluxes at the wall assuming that the velocity and the temperature in the near-wall region follow the law-of-the-wall. However, the model choice may have a dramatic influence on local pressure losses and heat transfer and as a consequence improvements are still needed to achieve a better reliability of the closures. The present study relies on the creation of a highly refined LES database, in order to gain insight into the flow physics of heat transfer in turbine blades.

Table 1 Description of the computational database

Fig. 1

Side view of the mesh topology of the T7.2 blade

2 Construction of the Database

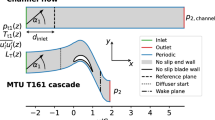
In the present work, highly-refined simulations of a low-Mach number turbine blade, namely the T7.2 blade designed by MTU Aero Engines, are performed. A detailed experimental investigation of this blade was conducted by Ladisch et al. [4]. Measurements were performed in an atmospheric linear cascade facility, which allowed for a variation of the free-stream Reynolds number and turbulence intensity. The Reynolds number based on the chord is 150,000 with a turbulence injection rate of 6 %. The blade, which is immersed in a hot turbulent flow at $T_{in}=350$ K, is internally liquid-cooled in order to maintain a nearly constant wall temperature of $T_w=290$ K. The chosen turbine blade design is typical of a cooled low-pressure turbine blade with moderate to nearly high loading. The intent of the design was to generate a large flow separation zone on the blade pressure side.

The computations are carried out with the YALES2 solver [5] with a variable-density low-Mach number formulation of the Navier-Stokes equations. The dynamic Smagorinsky model [6] has been used to close the subgrid transport for the velocity, and a constant turbulent Prandtl number is assumed (Pr$_t$ = 0.7). A fourth-order finite-volume spatial scheme for unstructured meshes has been used. The temporal advancement is fourth-order in time, implicit for diffusion and explicit for advection. The simulation database consists of LES with increasing resolutions that are summarized in Table 1. All the meshes are tetrahedron-based. Figure 1 presents the topology followed by all the meshes. One node of thirty-five of the first mesh is shown.

$y^+$ is the nondimensional distance from the wall defined as

$$\begin{aligned} y^+ = \frac{y_n u_{\tau }}{\nu } = \frac{y_n}{\sqrt{\nu }} \sqrt{{\left. \frac{\partial u}{\partial y_n} \right| }_w }\, \end{aligned}$$

(1)

with $y_n$ the distance from the wall in the wall normal direction, $u_{\tau }$ the friction velocity, $\nu$ the kinematic viscosity and $u$ the streamwise velocity in the local blade coordinates.

As illustrated in Fig. 2, where coherent structures are represented by an iso-contour of Q-criterion on the M4 mesh, the flow around the blade features a transition of the boundary layer from laminar to turbulent on the suction side, due to the adverse pressure gradient met in this area of the blade. The large separation zone on the pressure side is also clearly visible.

Fig. 2

Turbulent structures around the blade with the M4 mesh. iso-$Q$ criterion $1.5625\times 10^9\, \mathrm{s}^{-2}$

3 Comparison Between Computations and Experimental Results

In order to assess the mesh resolution of the computations for heat transfer prediction, a Nusselt number based on the resolved fields is investigated and compared to the experimental values. This Nusselt number plotted in Fig. 3 is computed using the resolved temperature gradient, i.e. the value of the temperature $\widetilde{T}$ provided by the resolution of the LES equations at the first node in the fluid from the wall,

$$\begin{aligned} Nu=\frac{(\nabla \widetilde{T})C}{T_{in}-T_w} \end{aligned}$$

(2)

where $T_{in}$ and ${T_w}$ are the inlet and wall temperatures, respectively. This Nusselt number is used here as a resolution indicator, as it is computed without taking into account the sub-grid scale contribution of the temperature flux. The evolution of the Nusselt number for the four levels of mesh refinement is depicted in Fig. 3.

Fig. 3

Evolution of the Nusselt number based on the resolved gradient with the level of refinement of the meshes

The Nusselt number is plotted as a function of $s/C$, $s$ being the curvilinear abscissa and $C$ the chord length equal to 7.39 cm for this blade. $s/C=0$, $s/C<0$, $s/C>0$ correspond to the stagnation point, the pressure side and the suction side, respectively. For the two finest meshes that have been converged, i.e. M3 and M4, the resolution of the temperature gradient is good enough to capture the heat transfer in most areas: in the laminar and turbulent layers on the suction side with the correct position of the transition at $s/C=1.1$ and in the recirculation zone on the pressure side. However, at the stagnation point where the strongest gradient is met, even if the $y^+$ is small the experimental value of the Nusselt number is not recovered.

4 Focus on the Turbulent Boundary Layer of the Suction Side

The transition from laminar to turbulent boundary layer flow on the suction side follows features of a by-pass transition scenario. Figure 4 presents an isosurface of the nondimensional temperature $Z=0.5$, with $Z=(T-T_w)/(T_{in}-T_w)$ that can be used as a turbulence marker. This flow visualization allows to understand that the free stream turbulence disturbs the laminar shear layer and, in combination with the streamwise pressure gradient, induces transition.

Fig. 4

Isosurfaces of temperature Z = 0.5 at the suction side of the M4 colored using the magnitude of the instantaneous velocity

The mean streamwise velocity profile in the blade coordinates is plotted in Fig. 5 for the M4 grid. It is compared with the classical analytical laws, namely the linear law for $y^+<10$ and the log-law for $y^+>14$. The values of the constants come from [6]. The velocity profile from our computation is in very good agreement with these laws. We also present a comparison with the law derived by Duprat et al. [2] which takes into account the streamwise pressure gradient via a pressure velocity proposed by Simpson [7]: $u_{p}=\left| \frac{\nu }{\rho }\frac{\partial p}{\partial x} \right| ^{1/3}$. In Fig. 5, the mean velocity is non-dimensionalized by $u_\tau$. The results are in very good agreement with this law, highlighting the fact that on such a configuration the streamwise pressure gradient has a noticeable effect on the dynamics of the boundary layer. Figure 6 presents the temperature profile which shows very good agreement with the classical log-law adapted to temperature via the laminar Prandtl number for the viscous sub-layer, and using a different set of constants, namely $\kappa _\theta =0.47$ and $C_\theta =3.3$ for the log-layer.

Fig. 5

Mean velocity profiles at 98 % of the curvilinear abscissa of the suction side. Mesh M4. Line present LES; dashed $u^+=y^+$; dashed-dotted-dotted $u^+ = ln(y^+)/\kappa + C$; dotted Duprat law

Fig. 6

Mean temperature profiles at 98 % of the curvilinear abscissa of the suction side. Mesh M4. Line present LES; dashed $u^+=Pr~y^+$; dashed-dotted-dotted $u^+ = ln(y^+)/\kappa _\theta + C_\theta$