Keywords

1 Introduction

First applications of the electromagnetic suspension principle have been in experimental physics, and suggestions to use this principle for suspending transportation vehicles for high-speed trains go back to 1937. There are various ways of designing magnetic suspensions for a contact free support—the AMB is just one of them [1]. AMB is a collection of electromagnets used to suspend an object via feedback control. Commercial applications include pumps, compressors, flywheels, milling and grinding spindles, turbine engines, and centrifuges [2].

Magnetic suspension offers advantages over conventional bearings such as lower rotating losses and higher speeds. Bleuler developed a method for designing decentralized proportional derivative (PD) controllers for rigid rotors in 1984, and Salm introduced a control procedure for flexible rotors with collocation and gave stability guarantees for the case of continuous time control in 1988. \({{H}_{\infty }}/\mu \)-synthesis control was first applied to AMB systems around 1990 [3]. A set of decoupled PD controllers was designed and the stability robustness was evaluated via µ-analysis in 2003 [4]. Fault detection and diagnosis were integrated into the active magnetic bearing system to provide reliable information about the system state in 2009 [5].

In the above AMB systems, the controller is one of the key techniques. The performance directly affects the work of magnetic bearing. So this chapter mainly describes the control theories and improves the algorithm.

This chapter shows the difference between the PD controller and proportional integral derivative (PID) controller. By adopting the integrating element in the PID controller, the effects of variation of load on the position of the rotor can be compensated. By selecting the voltage control method instead of current control, the model of the system has better robustness. At the end of the chapter, simulations of different control parameters are given to check the feasibility of the algorithm.

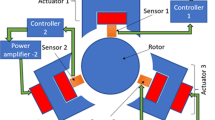
Figure 99.1 presents the main components of a control system of AMB (a controller, a power amplifier, and sensors). A sensor detects the displacement of the rotor from its reference position, and then the controller derives a control signal from the measurements. A power amplifier transforms this control signal into control current, and the control current generates a magnetic field in the actuating magnets, resulting in magnetic force. Then the rotor remains in its hovering position [6–8].

Fig. 99.1
figure 1

Basic composition of active magnetic bearing

Full size image

This chapter is devoted to the research and design of the PID controller of AMB. There are three parts: first, the design and selection of the control methods; second, the analysis of the structure and transfer function of the closed-loop system; and last, simulation and parameter selection.

2 The Principle and Design of the PID Controller

As mentioned before, we discuss the relationships between force and displacement in the electromagnetic field of AMB. When the rotor deviates from the working position, the magnetizing current will change to alter the rotor force, making the rotor return to the operating point and then achieve controlling targets. In order to analyze the system, one direction of AMB controller is studied.

The transient force, a function of displacement and current, is a linear equation:

$$ f(x,i )={{k}_{x}}x+{{k}_{i}}i $$
(99.1)

The control of the rotor is to provide a restoring force, e.g., similar to the mechanical spring. Besides, a damping component should be provided to reduce oscillations. Then the support force f can be calculated as follows [1]:

$$ f=-kx-d\dot{x} $$
(99.2)

where \(k\) is stiffness, \(d\) is damping, \(\dot{x}=dx/dt\) is the rotor speed in the direction of this degree of freedom, force \(f\) and displacement \(x\) are both deviations from the equilibrium point.

According to Eqs. (99.1) and (99.2), the control current \(i(x)\) is as follows:

$$ i(x )=-\frac{(k+{{k}_{x}})x+d\dot{x}}{{{k}_{i}}}$$
(99.3)

Here, let

$$ {{k}_{p}}=-(k+{{k}_{x}})/{{k}_{i}}$$
(99.4)
$$ {{k}_{d}}=-d/{{k}_{i}}$$
(99.5)

and then

$$ i(x )={{k}_{p}}x+{{k}_{d}}\dot{x} $$
(99.6)

Such a control law is named PD control. For an active magnetic bearing with PD control, an external static load will always result in a change in the steady position which is undesired in a technical application.

Thus, an integral part is needed to be introduced to compensate the effect. The inductance L varies in different rotor positions. The rotor motion also generates a coil voltage. This induced voltage is [3]

$$ u=Ri+\frac{Ldi}{dt}+{{k}_{u}}\dot{x} $$
(99.7)

where \(R\) is the coil resistance and \({{k}_{u}}\) is the voltage—the speed factor.

Equation (99.7) is the voltage control; this method maintains the stability of a rotor through a change in voltage, resulting from the signal form sensors.

Figure 99.2 shows the control system diagram of the voltage control scheme.

Fig. 99.2
figure 2

System diagram of the voltage control scheme

Full size image

The system block diagram is shown in Fig. 99.3. \({{G}_{s}}(s )\) is the transfer function of the position sensor, \({{G}_{c}}(s )\) is the transfer function of the PID controller, and \({{G}_{p}}(s )\) is the transfer function of the amplifier.

Fig. 99.3
figure 3

System block diagram of the closed-loop control system

Full size image
$$ {{G}_{c}}(s )={{k}_{p}}+\frac{{{k}_{ic}}}{s}+{{k}_{d}}s $$
(99.8)

where \({{k}_{p}}\), \({{k}_{ic}}\) and \({{k}_{d}}\) are the proportional gain coefficients, the integral gain coefficients, and the differential gain coefficients, respectively.

$$ {{G}_{p}}(s )=\frac{\lambda }{1+s{{T}_{p}}}$$
(99.9)
$$ {{G}_{s}}(s )=\frac{{{A}_{s}}}{1+s{{T}_{s}}}$$
(99.10)

where \(\lambda \) is the gain factor of the amplifier circuit, \({{T}_{p}}\) is the decay time constant of the amplifier circuit, \({{A}_{s}}\) is the gain factor of the displacement sensor, and \({{T}_{s}}\) is the decay time constant of the displacement sensor.

As mentioned above, PID control can compensate the effects of load changes on the steady-state position of the rotor, so this chapter selects PID control.

The motion equation of controlled objects is

$$ m\ddot{x}={{k}_{x}}x+{{k}_{i}}i $$
(99.11)

Combining the formulas above, we get the equation of the system

$$ m{{s}^{3}}+K{{k}_{d}}{{s}^{2}}+(K{{k}_{p}}-{{k}_{x}})s+K{{k}_{ic}}=0 $$
(99.12)

From the above analysis, PID control introduces an integral part, which can compensate for the effects of variation of load on the steady-state position of the rotor. So, PID control is better than PD control at this extent. The voltage control method considers the prevention of magnetic bearing coil inductance on the current changes compared to the current control. It makes the mathematical model of the system more accurate and has better robustness. Besides, the open-loop instability of the system improves. The downsides of the structure are that it is relatively complex, and the controller requires at least two stages. So, for a small-scale system, the current control is available.

3 The Simulation Results

The parameters \({{k}_{p}},\,{{k}_{ic}}\) and \({{k}_{d}}\) are determined by stiffness \(k\) and damping \(d\) in the closed-loop system. In this chapter, MATLAB is used to simulate conditions of a PID controller. We can study the system response of different gain coefficients.

The control function of the PID controller is

$$ u(t )={{k}_{p}}e+{{k}_{ic}}\int_{0}^{t}{edt}+{{k}_{d}}\frac{de}{dt} $$
(99.13)
$$ e=r-{{u}_{1}}(t ) $$
(99.14)

where \(e\) is the input of the controller, \(r\) is a reference value or control objective, and \({{u}_{1}}(t )\) is the output of the sensor.

The transfer function of the PID controller is

$$ {{G}_{c}}(s )={{k}_{p}}+\frac{{{k}_{ic}}}{s}+{{k}_{d}}s $$
(99.15)

The transfer function of the closed-loop system simulated is

$$ H(s)=\frac{{{G}_{c}}(s ){{G}_{p}}(s )G(s )}{1+{{G}_{c}}(s ){{G}_{p}}(s )G(s ){{G}_{s}}(s )} $$
(99.16)

Put Eqs. (99.9) and (99.10) in Eq. (99.16) and we get:

$$ H(s)=\frac{{{k}_{i}}\lambda ({{k}_{d}}{{s}^{2}}+{{k}_{p}}s+{{k}_{ic}})({{T}_{s}}s+1 )}{s(m{{s}^{2}}-{{k}_{x}})({{T}_{p}}s+1 )({{T}_{s}}s+1 )+{{k}_{i}}\lambda {{A}_{s}}({{k}_{d}}{{s}^{2}}+{{k}_{p}}s+{{k}_{ic}})} $$
(99.17)

The relevant parameters used in the simulation are: the quality of the rotor \(m=4.5\,kg\), the bias current of the coil \({{I}_{0}}=0.4\,A\), the displacement stiffness coefficient \({{k}_{x}}=4.211\times {{10}^{5}}\,N/m\), the current stiffness coefficient \({{k}_{i}}=157.9\,N/A\), the gain coefficient of the sensor \({{A}_{s}}={{10}^{4}}\), the time constant \({{T}_{s}}=7.958\times {{10}^{-5}}\,s\), the gain factor of the power amplifier \(\lambda =1\), and time constant \({{T}_{p}}=3.183\times {{10}^{-5}}\,s\).

Figure 99.4 shows the simulation results using the parameters above, with different parameters, \({{k}_{p}},\,{{k}_{ic}}\) and \({{k}_{d}}\).

Fig. 99.4
figure 4

Closed-loop response graphs of different PID parameters of the system

Full size image

The simulation results show that \({{k}_{p}}\) has the greatest impact on the dynamic performance. When \({{k}_{p}}\) is small, the system will oscillate at the beginning. With the increase of \({{k}_{p}}\), the time of convergence increases. So the best range of \({{k}_{p}}\) is 1–15. \({{k}_{ic}}\) has no significant effect at the start, but the time of convergence is significantly reduced when it increases. So, the optimum range is 20–50. \({{k}_{d}}\) has little effect on initial displacement. As \({{k}_{d}}\) increases, the time of convergence increases. Obviously, when \({{k}_{d}}\) is less than 0.001, the system undergoes an oscillation phenomenon. So, the best range of \({{k}_{d}}\) is 0.01–0.1.

Through the analysis above, we carry out multigroup experiments and choose \({{k}_{p}}=5,\,{{k}_{ic}}=40\) and \({{k}_{d}}=0.05\). Fig. 99.5 shows the closed-loop impulse response.

Fig. 99.5
figure 5

Closed-loop response of the system

Full size image

4 Conclusion

A modified AMB control algorithm is designed in this chapter. An integral part is introduced to compensate for the effect of variation of load on the position of the rotor. The voltage control method is adopted to improve the performance of transients of load. Through simulations, the effect of control parameters on the closed-loop response of the system indicates the feasibility of this algorithm.