Abstract
The mathematical modeling of chemically reacting mixtures is investigated. The governing equations, which may be split between conservation equations, thermochemistry, and transport fluxes, are presented as well as typical simplifications often encountered in the literature. The hyperbolic–parabolic structure of the resulting system of partial differential equations is analyzed using symmetrizing variables. The Cauchy problem is discussed for the full system derived from the kinetic theory of gases as well as relaxation toward chemical equilibrium fluids in the fast chemistry limit. The situations of traveling waves and reaction–diffusion systems are also addressed.
Access provided by CONRICYT-eBooks. Download reference work entry PDF
Similar content being viewed by others
1 Introduction
Chemically reacting mixtures are often encountered in nature and industry, notably in astronautics [4, 80], chemical engineering [27, 100, 102], combustion [25, 98, 118], or atmospheric phenomena [104]. This is an important motivation for investigating chemically reacting mixture models and analyzing the mathematical structure and properties of the resulting systems of partial differential equations [39].
Mathematical modeling of multicomponent reactive fluids is first investigated. The equations governing such fluids may be derived from various macroscopic theories like thermodynamics of irreversible processes [59, 90, 99], statistical mechanics [6, 67], or statistical thermodynamics [77], as well as from finer molecular theories like the kinetic theory of gases [16, 26, 33, 44, 85, 110, 116]. The equations derived from the kinetic theory of reactive polyatomic gas mixtures are presented. Such equations may be split between thermodynamics, chemistry, transport fluxes, and coefficients. The structural properties extracted from the underlying kinetic framework are transformed into relevant mathematical assumptions, thereby soundly founding the mathematical model. Typical simplified diffusion fluxes are addressed as well as irreversible chemistry often used in mathematical modeling [34, 36, 37, 57, 58, 97, 113, 117]. The complete fluid model is finally recast into a quasilinear system of partial differential equations.
The mathematical structure of the resulting system of partial differential equations is then analyzed taking into account multicomponent aspects such as complex chemistry and detailed transport phenomena . Symmetrization is a requisite for analyzing systems of partial differential equations of hyperbolic type [8, 18, 20, 35, 56, 103, 105] as well as hyperbolic–parabolic type [45, 50, 66, 70, 73, 74, 106]. Existence of a symmetrized form is related to the existence of a mathematical entropy compatible with convective terms, dissipative terms, and sources. Symmetrizability properties are investigated using entropic variables and next using normal variables [45, 70, 73, 106]. The natural entropic form and the natural normal form of the system of partial differential equations modeling chemically reacting mixtures are finally evaluated.
Existence of strong solutions to the Cauchy problem is then established for the full multicomponent reactive fluid model derived from the kinetic theory of gases [39, 43, 45,46,47]. Global existence theorems of strong solutions around constant equilibrium states are presented as well as asymptotic stability and decay estimates [39, 45, 70, 71, 108]. The method of proof relies on the normal form of the governing equations, on hyperbolic–parabolic estimates , and on the local strict dissipativity of linearized equations [45, 70, 71, 108]. Recent results concerning weak solutions with large data for related nonreactive fluid models [1, 13, 14, 21, 22, 30, 31, 83, 94] as well reactive fluid models [17, 19, 23, 32, 51, 64, 79, 87, 91, 123, 125] are also addressed.
Relaxation toward equilibrium states is an important process of natural phenomena that has been the object of numerous studies [18, 53,54,55, 84, 93, 119]. In the context of reactive flows, relaxation toward chemical equilibrium fluids is discussed. Such chemical equilibrium fluid models are valid when chemical characteristic times are small in comparison with flow characteristic times. The corresponding variables are associated with atomic mass densities, momentum, and energy [39]. Global existence results independent of chemical characteristic times are obtained, and convergence toward the chemical equilibrium fluid model is established [55].
Simplified situations where fluid dynamics remains elementary, namely, traveling waves and reaction–diffusion systems, are next addressed. With traveling waves, fluid dynamics is reduced to a scalar – the mass flow rate – which is an eigenvalue of the system [9,10,11, 38, 61, 62, 101, 114, 115]. With reaction–diffusion systems, the fluid velocity vanishes, and it is investigated when reaction–diffusion systems are exact subsystems of reactive fluid models. Classical reaction–diffusion models from the literature are also addressed [2, 3, 12, 34, 65, 69, 96, 97, 109, 113].
Open problems associated with chemically reacting mixtures and related models are finally mentioned.
2 Mathematical Modeling of Reactive Fluids
The fundamental equations governing chemically reacting mixtures as derived from the kinetic theory of gases are presented in this section.
2.1 Conservation Equations
The governing equations in a multicomponent reactive flow express the conservation of species mass, momentum, and energy and may be written as [39, 59, 102, 118]
where ∂ t denotes the time derivative operator, \(\boldsymbol{\nabla }\) the space derivative operator, ρ k the mass density of the kth species, \(\boldsymbol{v}\) the mass average flow velocity, \(\boldsymbol{\mathcal{J}\ }_{k}\) the diffusion flux of the kth species, m k the molar mass of the kth species, ω k the molar production rate of the kth species, \(\mathfrak{S} =\{ 1,\ldots,n\}\) the set of species indices, \(n\geqslant 1\) the number of species, \(\rho =\sum _{k\in \mathfrak{S}}\rho _{k}\) the total mass density, p the pressure, \(\boldsymbol{I}\) the d-dimensional identity tensor, \(\boldsymbol{\varPi }\) the viscous tensor, \(\boldsymbol{b}\) the force per unit mass acting on the species assumed to be species independent, \(\mathcal{E}\) the internal energy per unit volume, and \(\boldsymbol{Q}\) the heat flux. The spatial dimension is denoted by d and the spatial coordinates by \(\boldsymbol{x} = (x_{1},\ldots,x_{d})^{t}\); the components of \(\boldsymbol{v}\) and \(\boldsymbol{\nabla }\) are written as \(\boldsymbol{v} = (v_{1},\ldots,v_{d})^{t}\) and \(\boldsymbol{\nabla } = (\partial _{1},\ldots,\partial _{d})^{t}\) where v i denotes the velocity in the ith spatial direction and ∂ i the derivation in the ith spatial direction; and bold symbols are used for vector or tensor quantities in the physical space \(\mathbb{R}^{d}\). The mass fluxes and chemical production rates satisfy the mass conservation constraints \(\sum _{k\in \mathfrak{S}}\boldsymbol{\mathcal{J}\ }_{k} = 0\) and \(\sum _{k\in \mathfrak{S}}m_{k}\omega _{k} = 0\), and adding the species conservation equations, the total mass conservation equation \(\partial _{t}\rho +\boldsymbol{ \nabla }\boldsymbol{\cdot }(\rho \boldsymbol{v}) = 0\) is recovered.
These equations have to be completed by the relations expressing the thermodynamic properties like p and \(\mathcal{E}\), the chemical production rates ω k , \(k \in \mathfrak{S}\), and the transport fluxes \(\boldsymbol{\varPi }\), \(\boldsymbol{\mathcal{J}\ }_{k}\), \(k \in \mathfrak{S}\), and \(\boldsymbol{Q}\).
2.2 Thermochemistry
2.2.1 Thermodynamics
The thermodynamics of gas mixtures derived from the kinetic theory of dilute gases coincides with that of ideal mixtures [39, 60, 78, 107]. This thermodynamics is conveniently written using the state variable ρ1, …, ρ n and T where T denotes the absolute temperature and the vector of partial densities is denoted by ϱ = (ρ1, …, ρ n )t [39, 78]. Other state variables could be used as well and may lead to slightly different mathematical formalisms [39, 60, 107]. The internal energy per unit volume \(\mathcal{E}\) and the pressure p may be written as
where e k is the internal energy per unit mass of the kth species and R the gas constant. The internal energy e k of the kth species is given by
where e st k is the standard formation energy of the kth species at the standard temperature Tst, cvk the constant volume specific heat of the kth species, and the formation energy at zero temperature is given by \(e_{k}^{0} = e_{k}(0) = e_{k}^{\mathrm{st}} -\int _{0}^{T^{\mathrm{st}} }\ \ \ c_{\mathrm{v}k}(\tau )\,d\tau\). The (physical) entropy per unit volume \(\mathcal{S}\) can be written in the form
where s k is the entropy per unit mass of the kth species. This quantity is in the form
where s st k is the formation entropy of the kth species at the standard temperature Tst and standard pressure pst and ρ st k = m k pst∕RTst the standard density of the kth species. Similarly, one can introduce the mixture enthalpy per unit volume \(\mathcal{H} =\sum _{k\in \mathfrak{S}}\rho _{k}h_{k}(T)\), the species enthalpies h k (T) = e k (T) + RT∕m k , \(k \in \mathfrak{S}\), the mixture Gibbs function per unit volume \(\mathcal{G} =\sum _{k\in \mathfrak{S}}\rho _{k}g_{k}(\rho _{k},T)\), the species Gibbs functions g k (ρ k , T) = h k (T) − Ts k (ρ k , T), \(k \in \mathfrak{S}\), as well as the reduced chemical potential μ k (ρ k , T) = g k ∕RT, \(k \in \mathfrak{S}\). The mixture energy e, entropy s, enthalpy h, Gibbs function g, and constant volume heat capacity cv per unit mass are naturally defined by \(\mathcal{E} =\rho e\), \(\mathcal{S} =\rho s\), \(\mathcal{H} =\rho h\), \(\mathcal{G} =\rho g\), \(\rho c_{\mathrm{v}} =\sum _{k\in \mathfrak{S}}\rho _{k}c_{\mathrm{v}k}\) and the total energy and enthalpy per unit mass by \(e^{\mathrm{tl}} = e + \tfrac{1} {2}\vert \boldsymbol{v}\vert ^{2}\) and \(h^{\mathrm{tl}} = h + \tfrac{1} {2}\vert \boldsymbol{v}\vert ^{2}\).
The species mass fractions y
k
= ρ
k
∕ρ, \(k \in \mathfrak{S}\), partial pressures p
k
= ρ
k
RT∕m
k
, \(k \in \mathfrak{S}\), and mole fractions x
k
= p
k
∕p, \(k \in \mathfrak{S}\), are introduced as well as the vectors μ = (μ1…, μ
n
)t, y = (y1…, y
n
)t, x = (x1…, x
n
)t, \(\mathfrak{m} = (m_{1}\ldots,m_{n})^{t}\), and  and the mass matrix M = diag(m1, …, m
n
). Denoting by 〈 , 〉 the Euclidean scalar product, the mole fractions may also be evaluated from x
i
= my
i
∕m
i
where m is the mean molar weight given by
and the mass matrix M = diag(m1, …, m
n
). Denoting by 〈 , 〉 the Euclidean scalar product, the mole fractions may also be evaluated from x
i
= my
i
∕m
i
where m is the mean molar weight given by  . The gradients of mole and mass fractions are related through \(\boldsymbol{\nabla }\mathsf{x} = E\boldsymbol{\nabla }\mathsf{y}\) where E is the invertible matrix with components [37]
. The gradients of mole and mass fractions are related through \(\boldsymbol{\nabla }\mathsf{x} = E\boldsymbol{\nabla }\mathsf{y}\) where E is the invertible matrix with components [37]

and \(\det E =\prod _{k\in \mathfrak{S}}(m/m_{k})\), Ey = x,  . Finally, when the components of a vector ϕ = (ϕ1, …, ϕ
n
)t are positive ϕ
i
> 0, respectively nonnegative ϕ
i
≥ 0, it is written for short ϕ > 0, respectively ϕ ≥ 0.
. Finally, when the components of a vector ϕ = (ϕ1, …, ϕ
n
)t are positive ϕ
i
> 0, respectively nonnegative ϕ
i
≥ 0, it is written for short ϕ > 0, respectively ϕ ≥ 0.
The mathematical assumptions concerning thermodynamic properties are the following where ϰ denotes a regularity class of thermodynamic functions [39].
-
(\(\boldsymbol{\mathsf{H_{1}}}\)) The molar masses m k , \(k \in \mathfrak{S}\), and the perfect gas constant R are positive constants. The formation energies e st k , \(k \in \mathfrak{S}\), and entropies s st k , \(k \in \mathfrak{S}\), are real constants. The specific heats cvk, \(k \in \mathfrak{S}\), are Cϰ−1 functions of T ∈ [0, ∞). There exist positive constants \(\underline{c}_{\mathrm{v}}\) and \(\overline{c}_{\mathrm{v}}\) such that \(0 <\underline{c}_{\mathrm{v}}\,\leqslant \,c_{\mathrm{v}k}(T)\,\leqslant \,\overline{c}_{\mathrm{v}}\) for T ≥ 0 and \(k \in \mathfrak{S}\).
Denoting by \(\,\mathbb{D}\) the total derivative, Gibbs’ relation \(T\,\,\mathbb{D}\mathcal{S} =\, \mathbb{D}\mathcal{E}-\sum _{k\in \mathfrak{S}}g_{k}\,\mathbb{D}\rho _{k}\) is obtained by using the expression of thermodynamic functions. Using the conservation equations, one may then obtain the following balance equation for \(\mathcal{S}\)
The transport coefficients and the chemical production rates must ensure that entropy production in the right-hand side of (5) is nonnegative.
Thermodynamics of fluid systems is classically introduced with the concept of local state, that is, the classical laws of thermostatics are applied locally and instantaneously at any point in the fluid system [59]. More satisfactory nonequilibrium thermodynamics are obtained from molecular frameworks like statistical mechanics [59, 77] or the kinetic theory of gases [16, 33, 39, 116] and have a wider range of validity. The physical justification of the existence of a local state indeed arises from the Boltzmann equation which shows that the species distribution functions are essentially Maxwellian distributions when collisions are dominant. Thermodynamics may finally be generalized to encompass the situation of nonideal mixtures which are especially important for supercritical fluids and generally at high pressure [48, 60], but such extension lay out of the scope of the present notes.
2.2.2 Complex Chemistry
Complex chemical networks typically involve a large set of elementary chemical reactions and may be written as [39, 60, 78, 107]
where \(\mathfrak{M}_{k}\) is the chemical symbol of the kth species, ν f ki and ν b ki the forward and backward stoichiometric coefficients of the kth species in the ith reaction, \(\mathfrak{R} =\{ 1,\ldots,n_{\mathrm{r}}\}\) the set of reaction indices, and \(n_{\mathrm{r}}\geqslant 1\) the number of chemical reactions. The overall stoichiometric coefficients are defined by ν ki = ν b ki −ν f ki and the reaction vectors by ν f i = (ν f1i , …, ν f ni )t, ν b i = (ν b1i , …, ν b ni )t, ν i = (ν1i, …, ν ni )t. Note that elementary chemical reactions – representative of molecular events – are reversible as established from statistical mechanics [77] and the kinetic theory of reactive gases [39].
The species of the mixture are assumed to be constituted by atoms, and \(\mathfrak{a}_{kl}\) denotes the number of lth atom in the kth species, \(\mathfrak{A} =\{ 1,\ldots,n_{\mathrm{a}}\}\) the set of atom indices, \(n_{\mathrm{a}}\geqslant 1\) the number of atoms – or elements – in the mixture, and \(\mathfrak{a}_{l} = (\mathfrak{a}_{1l},\ldots,\mathfrak{a}_{nl})^{t}\) the lth atom vector. In order to simplify the presentation of chemical equilibrium limits, it is assumed that the atoms are included in the set of species. Without loss of generality, one may assume that the atoms are the first na species so that \(\mathfrak{a}_{kl} =\delta _{kl}\) for \(k,l \in \mathfrak{A}\). The conservation of atoms in chemical reactions naturally yields that \(\langle \nu _{i},\mathfrak{a}_{l}\rangle = 0\) for \(i \in \mathfrak{R}\) and \(l \in \mathfrak{A}\). The species masses are also given by \(m_{k} =\sum _{l\in \mathfrak{A}}m_{l}\mathfrak{a}_{kl}\) or, in vector form, \(\mathfrak{m} =\sum _{l\in \mathfrak{A}}m_{l}\mathfrak{a}_{l}\). The mass density of the lth atom present in all the species further reads \(\widetilde{\rho }_{l} = m_{l}\langle M^{-1}\mathfrak{a}_{l},\varrho \rangle\) and is distinct from the mass density ρ l of the lth atom as a species. The vectors \(\widetilde{\mathfrak{a}}_{l} = m_{l}M^{-1}\mathfrak{a}_{l}\), \(l \in \mathfrak{A}\), naturally associated with the atom densities \(\widetilde{\rho }_{l} =\langle \widetilde{ \mathfrak{a}}_{l},\varrho \rangle\), \(l \in \mathfrak{A}\), are further introduced, and \(\widetilde{\varrho }= (\,\widetilde{\rho }_{1},\ldots,\widetilde{\rho }_{n_{\mathrm{a}}})^{t}\) denotes the vector of atom mass densities.
The vector spaces spanned by the reaction vectors and by the atom vectors are denoted by \(\mathcal{R} =\mathrm{ Span}\{\,\nu _{i},\ i \in \mathfrak{R}\,\}\) and \(\mathcal{A} =\mathrm{ Span}\{\,\mathfrak{a}_{l},\ l \in \mathfrak{A}\,\}\). Atom conservation then yields \(\mathcal{A}\subset \mathcal{R}^{\perp }\), and in order to simplify the presentation of chemical equilibrium, it is assumed in these notes that \(\mathcal{A} = \mathcal{R}^{\perp }\) or equivalently \(\mathcal{R} =\mathrm{ Span}\{\,\nu _{i},\ i \in \mathfrak{R}\,\} = \mathcal{A}^{\perp }\). This assumption means that the chemical equilibrium states of the reaction mechanism \(M\mu \in \mathcal{R}^{\perp }\) coincide with the natural chemical equilibrium states obtained when all possible chemical reactions are taken into account \(M\mu \in \mathcal{A}\). Keeping in mind that the atomic species have been chosen as the first na species so that \(\mathfrak{a}_{kl} =\delta _{kl}\) for \(k,l \in \mathfrak{A}\), the dimension of \(\mathcal{A}\) is na and the dimension of \(\mathcal{R}\) is n − na. For each species that is not an atom \(k \in \mathfrak{S}\setminus \mathfrak{A} =\{ n_{\mathrm{a}} + 1,\ldots,n\}\), one may further introduce the corresponding formation reaction vector \(\mathfrak{v}_{k} = (-\mathfrak{a}_{k1},\ldots,-\mathfrak{a}_{kn_{\mathrm{a}}},0,\ldots,0,1,0,\ldots,0)^{t}\) where the 1 is at the kth place or equivalently \(\mathfrak{v}_{k} = -\sum _{l\in \mathfrak{A}}\mathfrak{a}_{kl}\mathsf{e}_{l} + \mathsf{e}_{k}\), where e i , 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{n}\). The formation reaction vector \(\mathfrak{v}_{k}\) is associated with the reaction \(\sum _{l\in \mathfrak{A}}\mathfrak{a}_{kl}\;\mathfrak{M}_{l}\ \rightleftarrows \ \mathfrak{M}_{k}\) that may not necessarily be part of the reaction mechanism. It may easily be checked that the reaction vectors may be written as \(\nu _{i} =\sum _{k\in \mathfrak{S}\setminus \mathfrak{A}}\nu _{ki}\mathfrak{v}_{k}\), \(i \in \mathfrak{R}\), in such a way that \(\mathfrak{v}_{k}\), \(k \in \mathfrak{S}\setminus \mathfrak{A}\), form a basis of \(\mathcal{R}\) that is of dimension n − na.
The molar production rates that are considered are the Maxwellian production rates obtained from the kinetic theory [26, 39, 85] when the chemical characteristic times are larger than the mean free times of the molecules and the characteristic times of internal energy relaxation. Letting ω = (ω1, …, ω n )t, these rates are in the form
where τ i is the rate of progress of the ith reaction. The rate of progress τ i is given by
where \(\mathcal{K}_{i}^{\mathrm{s}}\) is the symmetric constant of the ith reaction, as deduced from the kinetic theory [39] as well as thermodynamics or statistical mechanics [57, 77, 86]. Using μ k = μ u k (T) + (1∕m k )log(ρ k ∕m k ) where μ u k (T) = μ k (m k , T) only depends on temperature, the rates of progress (7) are found to be compatible with the law of mass action since they may be written as
The forward and backward rate contants \(\mathcal{K}_{i}^{\mathrm{f}}\) and \(\mathcal{K}_{i}^{\mathrm{b}}\) of reaction i are Maxwellian averaged values of molecular chemical transition probabilities and satisfy the reciprocity relations \(\mathcal{K}_{i}^{\mathrm{f}}(T) = \mathcal{K}_{i}^{\mathrm{b}}(T)\mathcal{K}_{i}^{\mathrm{e}}(T)\) where \(\log \mathcal{K}_{i}^{\mathrm{e}}(T) = -\langle \nu _{i},M\mu ^{\mathrm{u}}\rangle\), \(i \in \mathfrak{R}\), and μu = (μ u1 , …, μ u n )t [24, 39]. These reciprocity relations are closely associated with reciprocity relations between reactive transition probabilities and may be seen as Onsager relations for chemistry. The mass weighted chemical source term Mω may also be written in quasilinear form Mω = −Λμ where Λ is the square matrix of size n
and \(\varLambda _{i} = \mathcal{K}_{i}^{\mathrm{s}}\,\int _{0}^{1}\exp \big(\langle \widetilde{\nu }_{i}^{\mathrm{f}},\mu \rangle +\xi \langle \widetilde{\nu }_{i}^{\mathrm{b}} -\widetilde{\nu }_{i}^{\mathrm{f}},\mu \rangle \big)\,\mathrm{d}\xi\). The coefficients Λ i , \(i \in \mathfrak{R}\), are positive so that the matrix Λ is symmetric positive semi-definite with nullspace \(N(\varLambda ) = M^{-1}\mathcal{A}\) and range \(R(\varLambda ) = M\mathcal{R}\). The mathematical assumptions concerning chemistry are finally the following.
-
(\(\boldsymbol{\mathsf{H_{2}}}\)) The stoichiometric coefficients ν f ki and ν b ki , \(k \in \mathfrak{S}\), \(i \in \mathfrak{R}\), and the atomic coefficients \(\mathfrak{a}_{kl}\), \(k \in \mathfrak{S}\), \(l \in \mathfrak{A}\), are nonnegative integers. The first na species are the atoms and the linear subspaces \(\mathcal{R}\) and \(\mathcal{A}\) are orthogonal complements \(\mathcal{R} = \mathcal{A}^{\perp }\). The vector of species molar masses \(\mathfrak{m}\) is given by \(\mathfrak{m} =\sum _{l\in \mathfrak{A}}m_{l}\,\mathfrak{a}_{l}\). Finally the symmetric reaction constants \(\mathcal{K}_{i}^{\mathrm{s}}\) are Cϰ positive functions of T > 0 for \(i \in \mathfrak{R}\).
Using the expression of the species production rates and of the reaction rates of progress, the entropy production due to chemistry \(-\sum _{k\in \mathfrak{S}}g_{k}m_{k}\omega _{k}/T = -R\langle \mu,M\omega \rangle\) is easily rewritten in the form
Entropy production due to chemistry thus appears as a sum of nonnegative terms in full agreement with the second principle of thermodynamics. The relation (10) also appears as a macroscopic consequence of Boltzman H-theorem involving reactive collisions .
2.2.3 Chemical Equilibrium
Chemical equilibrium points are defined in the following proposition using the expression of entropy production due to chemistry (10) [39, 78, 107].
Proposition 1.
Assume that (H 1 )–(H 3 ) hold and let ϱ > 0 and T > 0. The following statements are equivalent :
-
(i)
The entropy production due to chemistry vanishes − R〈μ, ω〉 = 0.
-
(ii)
The reaction rates of progress vanish τ j = 0, \(j \in \mathfrak{R}\).
-
(iii)
The species production rates vanish ω = 0.
-
(iv)
The vector μ belongs to \((M\mathcal{R})^{\perp }\).
A point T > 0, ϱ > 0, which satisfies these equivalent properties is termed an equilibrium point.
Property (ii) implies that all chemical reactions are equilibrated when the species production rates vanish and is termed the detailed balance property. Only positive equilibrium states with ϱ > 0, i.e., ρ i > 0, \(i \in \mathfrak{S}\), which are in the interior of the composition space are considered in these notes. Spurious points with zero mass fractions where the source terms ω k , \(k \in \mathfrak{S}\), vanish – termed “boundary equilibrium points” – are of a different nature [39]. Properly structured chemical kinetic mechanisms automatically exclude such spurious points unless some atom is missing in the mixture [39].
Proposition 2.
For T e > 0 and \(\tilde{\varrho }> 0\) there exists a unique equilibrium point ϱ e > 0 such that \(\langle \varrho _{\mathrm{e}},\widetilde{\mathfrak{a}}_{l}\rangle =\widetilde{\rho } _{l}\), for \(l \in \mathfrak{A}\). In other words, there exits a unique ϱ e such that \(\mu (\varrho _{\mathrm{e}},T_{\mathrm{e}}) \in M^{-1}\mathcal{A}\) and \(\langle \varrho _{\mathrm{e}},\widetilde{\mathfrak{a}}_{l}\rangle =\widetilde{\rho } _{l}\), for \(l \in \mathfrak{A}\), and the equilibrium partial densities ϱ e are Cϰ function of \((\,\widetilde{\varrho },T_{\mathrm{e}})\).
Proof.
The proof is only sketched and we refer to [39, 48, 78] for more details. For \(\widetilde{\varrho }> 0\), there exists ϱsp > 0 with \(\langle \varrho _{\mathrm{sp}},\widetilde{\mathfrak{a}}_{l}\rangle =\widetilde{\rho } _{l}\) taken as \(\varrho _{\mathrm{sp}} =\sum _{l\in \mathfrak{A}}\widetilde{\rho }_{l}\mathsf{e}_{l} +\delta \sum _{k\in \mathfrak{S}\setminus \mathfrak{A}}M\mathfrak{v}_{k}\) for δ > 0 small enough. The equilibrium point is then investigated in the simplex \(\mathfrak{I} = (\varrho _{\mathrm{sp}} + M\mathcal{R}) \cap (0,\infty )^{n}\), and the Helmholtz free energy \(\mathcal{F} = \mathcal{E}- T_{\mathrm{e}}\mathcal{S}\) is shown to be continuous over the closure \(\overline{\mathfrak{I}} = (\varrho _{\mathrm{sp}} + M\mathcal{R}) \cap [0,\infty )^{n}\) which is a compact set. The function \(\mathcal{F}\) is strictly convex on \(\mathfrak{I}\) and achieves its maximum at ϱe in the interior of the simplex since the proper derivatives have the wrong sign near boundaries [39]. This point ϱe is next shown to be an equilibrium point using that \(\partial _{\varrho }\mathcal{F} = RT_{\mathrm{e}}\mu\) and that \(M\mathcal{R}\) is in the tangent space of the simplex. Uniqueness of the equilibrium point on the simplex is then a consequence of the strict convexity of \(\mathcal{F}\). Finally, the equilibrium partial densities ϱe are Cϰ function of \((\,\widetilde{\varrho },T_{\mathrm{e}})\) as a direct application of the implicit function theorem [39, 78]. □
The energy and entropy per unit volume at equilibrium are defined from
and the specific heat at constant volume by \(\rho _{\mathrm{e}}c_{\mathrm{e}\mathrm{v}} = \partial _{T_{\mathrm{e}}}\mathcal{E}_{\mathrm{e}}(\,\widetilde{\varrho },T_{\mathrm{e}})\). The pressure pe is given by \(p_{\mathrm{e}} = RT_{\mathrm{e}}\sum _{k\in \mathfrak{S}}\rho _{\mathrm{e}k}/m_{k}\), the Gibbs function per unit volume by \(\mathcal{G}_{\mathrm{e}} = \mathcal{E}_{\mathrm{e}} + p_{\mathrm{e}} - T_{\mathrm{e}}\mathcal{S}_{\mathrm{e}}\), and the total density ρe can be written as \(\rho _{\mathrm{e}} =\sum _{k\in \mathfrak{S}}\rho _{\mathrm{e}k} =\sum _{l\in \mathfrak{A}}\widetilde{\rho }_{l}\). The energy and entropy per unit volume at chemical equilibrium \(\mathcal{E}_{\mathrm{e}}\) and \(\mathcal{S}_{\mathrm{e}}\) are a Cϰ functions of the variables \((\,\widetilde{\varrho },T_{\mathrm{e}})\) over the domain Te > 0, \(\widetilde{\varrho }> 0\).
Lemma 1.
The specific heat at chemical equilibrium \(\rho _{\mathrm{e}}c_{\mathrm{e}\mathrm{v}} = \partial _{T_{\mathrm{e}}}\mathcal{E}_{\mathrm{e}}(\,\widetilde{\varrho },T_{\mathrm{e}})\) is positive ρ e c ev > 0 and the map \((\,\widetilde{\varrho },T_{\mathrm{e}}) \rightarrow (\,\widetilde{\varrho },\mathcal{E}_{\mathrm{e}})\) is a Cϰ diffeomorphism from the domain T e > 0, \(\widetilde{\varrho }> 0\) onto an open set. Over this domain, denoting by \(\overline{\partial }\) the derivation with respect to \((\,\widetilde{\varrho },\mathcal{E}_{\mathrm{e}})\), the following relations hold:
where \(g_{\mathrm{e}l} = g_{l}\big(\rho _{\mathrm{e}l}(\,\widetilde{\varrho },T_{\mathrm{e}}),T_{\mathrm{e}}\big)\), for \(l \in \mathfrak{A}\), so that \(T_{\mathrm{e}}\,\,\mathbb{D}\mathcal{S}_{\mathrm{e}} =\, \mathbb{D}\mathcal{E}_{\mathrm{e}} -\sum _{l\in \mathfrak{A}}g_{\mathrm{e}l}\,\mathbb{D}\widetilde{\rho }_{l}\), and moreover \(\mathcal{S}_{\mathrm{e}}\) is a strictly concave function of \((\,\widetilde{\varrho },\mathcal{E}_{\mathrm{e}})\).
The proof of this proposition relies on clever manipulations of equilibrium point constraints and properties as well as their derivatives with respect to Te and \(\widetilde{\varrho }\) [55].
2.2.4 Irreversible Reactions
Even though elementary chemical reactions are always reversible, it may happen that some chemical reactions are approximated or modeled as being irreversible. This is the case in particular for global reactions that typically simplify a complex chemical process into a few reaction paths that are not representative of molecular events. It is thus important to analyze the situation where both reversible and irreversible reactions are present in a given chemical reaction mechanism, and such an analysis has been conducted by Gorban and Yablonski [57] and Gorban, Mirkes, and Yablonski [58].
In this situation, one may introduce the indexing set of reversible reaction \(\mathfrak{R}^{\mathrm{rev}}\), the indexing set of irreversible reactions \(\mathfrak{R}^{\mathrm{irv}}\), the vector space spanned by the reversible reactions \(\mathcal{R}^{\mathrm{rev}} =\mathrm{ Span}\{\,\nu _{i},\ i \in \mathfrak{R}^{\mathrm{rev}}\,\}\), and the convex hull of the set of irreversible reactions \(\mathcal{C}^{\mathrm{irv}} =\mathrm{ Conv}\{\,\nu _{i},\ i \in \mathfrak{R}^{\mathrm{irv}}\,\}\). Systems that are well behaved are obtained as limits of sets of reversible reactions and satisfy two important properties. There is first a geometric structural condition \(\mathcal{R}^{\mathrm{rev}} \cap \mathcal{C}^{\mathrm{irv}} =\emptyset\) that essentially states that irreversible reactions cannot be included in oriented cyclic pathways. There are then algebraic conditions which state that the subset of reversible reactions is structured as in the previous section so that detailed balance holds at equilibrium as established in Proposition 1. In the situation where there is no reversible reaction, a chemical model investigated by Feinberg [29] is recovered. There is no well-defined and satisfactory thermodynamics for such systems with irreversible reactions, however, and different Lyapunov functions have to be used to capture the relaxation of the reversible and of the irreversible parts of the chemical reaction mechanism [58].
2.3 Multicomponent Transport
2.3.1 Transport Fluxes and Coefficients
The transport fluxes \(\boldsymbol{\varPi }\), \(\boldsymbol{\mathcal{J}\ }_{k}\), \(k \in \mathfrak{S}\), and \(\boldsymbol{Q}\) due to spatial gradients may be obtained from various macroscopic and molecular theories, but only the kinetic theory provides the transport coefficients [16, 24, 33, 39, 44, 116]. These fluxes may be written as
where κ denotes the volume viscosity, η the shear viscosity, \(\boldsymbol{I}\) the d dimensional identity tensor, C kl , \(k,l \in \mathfrak{S}\), the multicomponent flux diffusion coefficients, \(\widehat{\boldsymbol{d}}_{k}\), \(k \in \mathfrak{S}\), the unconstrained diffusion driving forces,t the transposition operator, \(\widetilde{\chi }_{k}\), \(k \in \mathfrak{S}\), the rescaled thermal diffusion ratios, and λ the thermal conductivity. The spatial components of the transport fluxes are written in the form \(\boldsymbol{Q} = (Q_{1},\ldots,Q_{d})^{t}\), \(\boldsymbol{\mathcal{J}\ }_{k} = (\mathcal{J}_{k1},\ldots,\mathcal{J}_{kd})^{t}\), and \(\boldsymbol{\varPi }= (\varPi _{ij})_{1\leq i,j\leq d}\). In the expression of the viscous tensor, d′ denotes the dimension of the velocity space in the underlying kinetic framework. It will be assumed in the following that the dimension of the kinetic velocity space d′ is such that 2 ≤ d′ and d ≤ d′. The assumption 1 ≤ d ≤ d′ means that the spatial dimension d of the model has eventually been reduced, so that the equations are considered in \(\mathbb{R}^{d}\) independently from kinetic velocity fluctuations that always have dimension d′. The assumption 2 ≤ d′ is natural since d′ = 3 in the physical world and since \(\boldsymbol{\nabla }\boldsymbol{v} + (\boldsymbol{\nabla }\boldsymbol{v})^{t} - (2/d\prime)(\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{v})\boldsymbol{I}\) is identically zero when d′ = d = 1.
When the mass fractions are nonzero, it is also possible to define the species diffusion velocities v k , \(k \in \mathfrak{S}\), by
where D
kl
= C
kl
∕ρ
k
, \(k,l \in \mathfrak{S}\), are the multicomponent diffusion coefficients. The diffusion coefficients considered in these notes are the symmetric coefficients introduced by Waldmann [116]. Letting \(C = (C_{kl})_{k,l\in \mathfrak{S}}\), \(D = (D_{kl})_{k,l\in \mathfrak{S}}\), and \(\mathcal{Y} =\mathrm{ diag}(\mathsf{y}_{1},\ldots,\mathsf{y}_{n})\), then \(D = (1/\rho )\mathcal{Y}^{-1}C\) is symmetric positive semi-definite with nullspace \(\mathbb{R}\mathsf{y}\). The diffusion driving forces are defined by \(\widehat{\boldsymbol{d}}_{k} = (\boldsymbol{\nabla }p_{k})/p =\boldsymbol{ \nabla }\mathsf{x}_{k} + \mathsf{x}_{k}\boldsymbol{\nabla }\log p\), \(k \in \mathfrak{S}\). The alternative diffusion driving forces \(\boldsymbol{d}_{k} =\boldsymbol{ \nabla }\mathsf{x}_{k} +\big (\mathsf{x}_{k} -\mathsf{y}_{k}\big)\boldsymbol{\nabla }\log p\) that sum up to zero may equivalently be used since Dy = 0 and  where \(\boldsymbol{d} = (\boldsymbol{d}_{1},\ldots,\boldsymbol{d}_{n})^{t}\) and \(\widehat{\boldsymbol{d}} = (\widehat{\boldsymbol{d}}_{1},\ldots,\widehat{\boldsymbol{d}}_{n})^{t}\). We also define for convenience the full constrained diffusion driving forces \(\boldsymbol{d}_{k}\prime =\boldsymbol{ d}_{k} + \mathsf{x}_{k}\widetilde{\chi }_{k}\boldsymbol{\nabla }\log T\), \(k \in \mathfrak{S}\), that sum up to zero and also include Soret effects, as well as \(\boldsymbol{d}\prime = (\boldsymbol{d}\prime_{1},\ldots,\boldsymbol{d}\prime_{n})^{t}\). There exist many alternative forms of multicomponent fluxes that lay out the scope of the present notes [24, 39].
where \(\boldsymbol{d} = (\boldsymbol{d}_{1},\ldots,\boldsymbol{d}_{n})^{t}\) and \(\widehat{\boldsymbol{d}} = (\widehat{\boldsymbol{d}}_{1},\ldots,\widehat{\boldsymbol{d}}_{n})^{t}\). We also define for convenience the full constrained diffusion driving forces \(\boldsymbol{d}_{k}\prime =\boldsymbol{ d}_{k} + \mathsf{x}_{k}\widetilde{\chi }_{k}\boldsymbol{\nabla }\log T\), \(k \in \mathfrak{S}\), that sum up to zero and also include Soret effects, as well as \(\boldsymbol{d}\prime = (\boldsymbol{d}\prime_{1},\ldots,\boldsymbol{d}\prime_{n})^{t}\). There exist many alternative forms of multicomponent fluxes that lay out the scope of the present notes [24, 39].
The transport coefficients for gas mixtures are not given explicitly by the kinetic theory of gases but require solving transport linear systems [16, 24, 33, 39, 116]. These linear systems arise from Galerkin solution of systems of linearized Boltzmann equations obtained from the Chapman-Enskog method. The mathematical properties of transport coefficients may be extracted from the properties of Boltzmann linearized collision operator or from the structure of transport linear systems [16, 24, 33, 36, 37, 44, 116]. The symmetry properties of the transport coefficients are notably inherited from the symmetry properties of the Boltzmann collision operator. The main symmetry properties, mass conservation constraints, as well as positivity properties of transport coefficients may be summarized in the following form.
-
\((\boldsymbol{\mathsf{H_{3}}})\) The flux diffusion matrix \(C = (C_{kl})_{k,l\in \mathfrak{S}}\), the rescaled thermal diffusion ratios vector \(\widetilde{\chi }= (\,\widetilde{\chi }_{1},\ldots,\widetilde{\chi }_{n})^{t}\), the volume viscosity κ, the shear viscosity η, and the thermal conductivity λ are Cϰ functions of y > 0 and T > 0. They satisfy the mass conservation constraints \(N(C) = \mathbb{R}\mathsf{y}\),
 , and \(\widetilde{\chi }\in \mathsf{x}^{\perp }\). The thermal conductivity λ and the shear viscosity η are positive and the volume viscosity κ is nonnegative. The diffusion matrix \(D = (1/\rho )\mathcal{Y}^{-1}C\) is symmetric positive semi-definite, and its nullspace is \(N(D) = \mathbb{R}\mathsf{y}\).
, and \(\widetilde{\chi }\in \mathsf{x}^{\perp }\). The thermal conductivity λ and the shear viscosity η are positive and the volume viscosity κ is nonnegative. The diffusion matrix \(D = (1/\rho )\mathcal{Y}^{-1}C\) is symmetric positive semi-definite, and its nullspace is \(N(D) = \mathbb{R}\mathsf{y}\).
Both the entropy production terms due to viscous phenomena and heat and mass transfer
are then nonnegative where \(\boldsymbol{d}\prime_{k} =\boldsymbol{ d}_{k} + \mathsf{x}_{k}\widetilde{\chi }_{k}\boldsymbol{\nabla }\log T\).
The behavior of transport coefficients for large and small temperature may also be required. This behavior is inherited from that of transport linear systems through collision integrals [38, 39]. One may typically assume that there exists a positive function φ(T) defined for T > 0 such that the reduced coefficients C0(y, T) = C(y, T)∕φ(T), λ0(y, T) = λ(y, T)∕φ(T), and \(\widetilde{\chi }^{0}(\mathsf{y},T) =\widetilde{\chi } (\mathsf{y},T)\) have continuous extensions for T ∈ [0, ∞], \(\mathsf{y}\geqslant 0\), y ≠ 0, that satisfy all previous properties of transport coefficients [38, 39]. The temperature scale for transport coefficients φ depends on the interaction potentials between particles [38], and for rigid spheres one has, for instance, \(\varphi (T) = \sqrt{T}\) [16, 33].
2.3.2 Stefan-Maxwell-Type Equations
The preceding assumptions on the transport coefficients (H 3 ) are a first set of physically realistic assumptions. In a number of situations, however, finer properties may be required, namely, more information about the dependence on species mass or mole fractions of the transport coefficients. As an illustration, finer properties of diffusion coefficients obtained from typical transport linear systems [24, 37] that lead to Stefan-Maxwell-type equations are investigated in this section. For the sake of simplicity, we only discuss diffusion fluxes due to concentration gradients and associated with the diffusion driving forces \(\boldsymbol{d}\). The Soret cross effets may simply be obtained by using the complete driving forces \(\boldsymbol{d}\prime\) instead of \(\boldsymbol{d}\). The situation of positive species is first considered and next the case of nonnegative species. The Stefan-Maxwell matrix \(\varDelta = (\varDelta _{kl})_{kl\in \mathfrak{S}}\) has coefficients
where \(\mathcal{D}_{kl }^{\text{bin} }\) denotes the binary diffusion coefficient of the species pair (k, l) and x
k
the mole fraction of the kth species. The kinetic theory of gases shows that, at first order, the coefficients \(\mathcal{D}_{kl}^{\text{bin}}\) only depend on pressure and temperature \(\mathcal{D}_{kl}^{\text{bin}} = \mathcal{D}_{kl}^{\text{bin}}(p,T)\). More generally, for more accurate multicomponent diffusion coefficients, the quantities \(\mathcal{D}_{kl}^{\text{bin}}\), \(k,l \in \mathfrak{S}\), are Schur complements arising from transport linear systems of size larger than n and are then functions of all state variables [24]. Similarly, with the kinetic theory of dense gases, the binary diffusion coefficients are also functions of the state variables (ρ1, …, ρ
n
, T)t. These binary diffusion coefficients are assumed to be symmetric and smooth functions of the state variable, and it is also assumed in this section that ϱ > 0 or equivalently ρ > 0 and y > 0, that is, y
i
> 0 for \(i \in \mathfrak{S}\). It is not necessarily assumed that  in such a way that the analysis may also be used for other rescaled Stefan-Maxwell type systems of equations. The mole fractions are defined from x
i
= my
i
∕m
i
where
in such a way that the analysis may also be used for other rescaled Stefan-Maxwell type systems of equations. The mole fractions are defined from x
i
= my
i
∕m
i
where  so that
so that  and I
n
denotes the identity matrix in n dimensions. The following properties of the matrix Δ are easily established [36, 37, 39].
and I
n
denotes the identity matrix in n dimensions. The following properties of the matrix Δ are easily established [36, 37, 39].
Proposition 3.
Assume that the coefficients \(\mathcal{D}_{kl}^{\mathit{\text{bin}}}\), \(k,l \in \mathfrak{S}\), k ≠ l, are positive and symmetric and that the species mass fractions are positive. Then Δ is symmetric positive semi-definite,  ,
,  , Δ is irreducible and is a singular M-matrix.
, Δ is irreducible and is a singular M-matrix.
The multicomponent diffusion matrix D may then be obtained as a generalized inverse of Δ [36, 37, 39].
Proposition 4.
Keeping the assumptions of Proposition
3
, there exists a unique generalized inverse D of Δ with prescribed range y⊥ and nullspace \(\mathbb{R}\mathsf{y}\), that is, a unique matrix D such that DΔD = D, ΔDΔ = Δ, R(D) = y⊥, and \(N(D) = \mathbb{R}\mathsf{y}\). This matrix D is positive semi-definite and such that  and
and  . Finally
. Finally  for any positive a, b with
for any positive a, b with  , D is a smooth function of T > 0 and y > 0 and is irreducible.
, D is a smooth function of T > 0 and y > 0 and is irreducible.
The Stefan-Maxwell relations for the diffusion matrix D derived from the kinetic theory are in the form  and must be completed by the mass constraint Dy = 0 or R(D) ⊂ y⊥ [16, 24, 33, 36, 37, 39, 116]. The unique solution to these equations is the generalized inverse matrix D of Proposition 4. In particular, using the matrix D is equivalent to solving the traditional Stefan-Maxwell equations for the diffusion velocities. Denoting indeed by v the vector of diffusion velocities v = (v1, …, v
n
)t where \(\boldsymbol{\mathcal{J}\ }_{k} =\rho _{k}\mathbf{v}_{k}\) for \(k \in \mathfrak{S}\), and \(\boldsymbol{d} = (\boldsymbol{d}_{1},\ldots,\boldsymbol{d}_{n})^{t}\), the vector of constrained diffusion driving forces with
and must be completed by the mass constraint Dy = 0 or R(D) ⊂ y⊥ [16, 24, 33, 36, 37, 39, 116]. The unique solution to these equations is the generalized inverse matrix D of Proposition 4. In particular, using the matrix D is equivalent to solving the traditional Stefan-Maxwell equations for the diffusion velocities. Denoting indeed by v the vector of diffusion velocities v = (v1, …, v
n
)t where \(\boldsymbol{\mathcal{J}\ }_{k} =\rho _{k}\mathbf{v}_{k}\) for \(k \in \mathfrak{S}\), and \(\boldsymbol{d} = (\boldsymbol{d}_{1},\ldots,\boldsymbol{d}_{n})^{t}\), the vector of constrained diffusion driving forces with  , then \(\mathbf{v} = -D\boldsymbol{d}\) so that after a little algebra the traditional Stefan-Maxwell relations with a mass conservation constraint are recovered
, then \(\mathbf{v} = -D\boldsymbol{d}\) so that after a little algebra the traditional Stefan-Maxwell relations with a mass conservation constraint are recovered
In particular, from Proposition 4, the general assumptions (H 3 ) do include diffusion matrices arising from the traditional Stefan-Maxwell equations (18).
In order to investigate finer properties of the diffusion matrix D, the situation where some mass fractions are vanishing must be analyzed. The flux Stefan-Maxwell matrix \(\varGamma = (\varGamma _{kl})_{kl\in \mathfrak{S}}\) has coefficients
is such that \(\varDelta =\rho \varGamma \mathcal{Y}\), and the following properties are easily established [37, 39].
Proposition 5.
Assume that the coefficients \(\mathcal{D}_{kl}^{\mathit{\text{bin}}}\), \(k,l \in \mathfrak{S}\), k ≠ l, are positive and symmetric and that the species mass fractions are nonnegative y ≥ 0 and nonzero y ≠ 0. Then \(N(\varGamma ) = \mathbb{R}\,\mathsf{y}\),  , and Γ is a singular M-matrix.
, and Γ is a singular M-matrix.
The multicomponent flux diffusion matrix C may then be obtained as a generalized inverse of Γ [37, 39].
Proposition 6.
Keeping the assumptions of Proposition
5
, there exists a unique group inverse C of Γ, that is, a unique matrix C such that CΓC = C, ΓCΓ = Γ, and CΓ = ΓC. The matrix C is also the generalized inverse with prescribed range  and nullspace \(\mathbb{R}\mathsf{y}\) so that
and nullspace \(\mathbb{R}\mathsf{y}\) so that  , \(N(C) = \mathbb{R}\mathsf{y}\),
, \(N(C) = \mathbb{R}\mathsf{y}\),  . Moreover,
. Moreover,  for any a, b positive with
for any a, b positive with  . The coefficients of C are smooth functions of T and y ≥ 0, y ≠ 0, and when the mass fractions are positive, C and D are such that \(C =\rho \mathcal{Y}D\).
. The coefficients of C are smooth functions of T and y ≥ 0, y ≠ 0, and when the mass fractions are positive, C and D are such that \(C =\rho \mathcal{Y}D\).
The Stefan-Maxwell relations for the diffusion matrix C derived from the kinetic theory are in the form  and must be completed by the mass constraint Cy = 0 or
and must be completed by the mass constraint Cy = 0 or  [37, 39]. The unique solution to these equations is the generalized inverse matrix C of Proposition 6. Using the matrix C is also equivalent to solving the flux Stefan-Maxwell equations that are in the form \(\varGamma \boldsymbol{\mathcal{J}\ } = -\boldsymbol{d}\) with the constraint
[37, 39]. The unique solution to these equations is the generalized inverse matrix C of Proposition 6. Using the matrix C is also equivalent to solving the flux Stefan-Maxwell equations that are in the form \(\varGamma \boldsymbol{\mathcal{J}\ } = -\boldsymbol{d}\) with the constraint  where \(\boldsymbol{\mathcal{J}\ } = (\boldsymbol{\mathcal{J}\ }_{1},\ldots,\boldsymbol{\mathcal{J}\ }_{n})^{t}\). Using the matrix C, it is further possible to clarify the behavior of the matrix C when some mass fractions are vanishing.
where \(\boldsymbol{\mathcal{J}\ } = (\boldsymbol{\mathcal{J}\ }_{1},\ldots,\boldsymbol{\mathcal{J}\ }_{n})^{t}\). Using the matrix C, it is further possible to clarify the behavior of the matrix C when some mass fractions are vanishing.
Proposition 7.
Let \(\mathsf{y}\geqslant 0\), y ≠ 0, \(\mathfrak{S}^{+} =\{\, k \in \mathfrak{S},\,\mathsf{y}_{k}> 0\,\}\), \(\mathfrak{S}^{0} =\{\, k \in \mathfrak{S},\,\mathsf{y}_{k} = 0\,\}\), and \(\mathrm{P}_{\ \ \mathfrak{S}}\) denote the permutation matrix associated with the reordering of \(\mathfrak{S}\) into \((\mathfrak{S}^{+}\ ,\mathfrak{S}^{0})\). Then the following block structure holds
where C00 is diagonal with positive diagonal coefficients and where D++ defined by ρD ++ kl = C ++ kl ∕y k , \(k,l \in \mathfrak{S}^{+}\), is symmetric positive semi-definite with nullspace \(\mathbb{R}\mathsf{y}^{+}\) where y+ corresponds to the \(\mathfrak{S}^{+}\) mixture, that is, \(\mathsf{y} =\mathrm{ P}_{\ \ \mathfrak{S}}(\mathsf{y}^{+},0)^{t}\).
The flux diffusion matrix C and more generally all the other transport coefficients λ, η, \(\widetilde{\chi }\), and κ have smooth extensions to the domain y ≥ 0 and y ≠ 0 [24]. This is also the case for the nondiagonal coefficients D
ij
for i ≠ j, whereas the coefficient C
ii
= ρ
i
D
ii
has a finite positive limit when ρ
i
→ 0 [24, 37, 39]. This is a direct consequence of Proposition 7 which yields that C
ij
= 0 when i ≠ j and y
i
= 0 in such a way that \(\rho D_{ij} =\int _{ 0}^{1}\ \ \partial _{\mathsf{y}_{i}}C_{ij}\big(\widehat{\mathsf{y}}(\theta )\big)\,\mathrm{d}\theta\) for i ≠ j where \(\widehat{\mathsf{y}}(\theta ) = (\mathsf{y}_{1},\ldots,\mathsf{y}_{i-1},\theta \mathsf{y}_{i},\mathsf{y}_{i+1},\ldots,\mathsf{y}_{n})^{t}\). This generally allows to use the maximum principle in order to establish that the mass fractions remain nonnegative. One may indeed decompose ω
i
in the form ω
i
= a
i
−y
i
b
i
where a
i
and b
i
are nonnegative [39] as well as \(\boldsymbol{\mathcal{J}\ }_{i} = C_{ii}\boldsymbol{\nabla }\mathsf{y}_{i} + \mathsf{y}_{i}\boldsymbol{\mathfrak{f}}_{i}\) for some vector \(\boldsymbol{\mathfrak{f}}_{i}\), and the maximum principle applied to the partial differential equation governing y
i
with proper boundary conditions generally yields that y
i
≥ 0. Entropy production due to diffusive processes and involving the quadratic form associated with the matrix D on the hyperplane  is now investigated [38, 39].
is now investigated [38, 39].
Proposition 8.
There exists a positive constant δ such that

Proof.
Defining \(\widehat{D}_{kk} = C_{kk}\) for \(k \in \mathfrak{S}\), and \(\widehat{D}_{kl} =\rho D_{kl}\sqrt{\mathsf{y} _{k } \mathsf{y} _{l}}\) for \(k,l \in \mathfrak{S}\), k ≠ l, then \(\widehat{D}\) is a continuous function over y ≥ 0,  . The map \((\mathsf{y},x) \rightarrow \langle \widehat{ D}(\mathsf{y},T)x,x\rangle\) over y ≥ 0,
. The map \((\mathsf{y},x) \rightarrow \langle \widehat{ D}(\mathsf{y},T)x,x\rangle\) over y ≥ 0,  , ∥x∥ = 1, \(\langle x,\sqrt{\mathsf{y}}\rangle = 0\) then reaches a minimum that is shown to be positive; otherwise, x = 0 contradicting ∥x∥ = 1. Changing of variable \(z_{k} = x_{k}\sqrt{\mathsf{y} _{k}}\), \(k \in \mathfrak{S}\), finally completes the proof [38]. □
, ∥x∥ = 1, \(\langle x,\sqrt{\mathsf{y}}\rangle = 0\) then reaches a minimum that is shown to be positive; otherwise, x = 0 contradicting ∥x∥ = 1. Changing of variable \(z_{k} = x_{k}\sqrt{\mathsf{y} _{k}}\), \(k \in \mathfrak{S}\), finally completes the proof [38]. □
Entropic estimates for diffusive processes thus typically involve quantities in the form \(\sum _{k\in \mathfrak{S}}\int _{\varOmega }\vert \boldsymbol{d}_{k}\vert _{}^{2}/\mathsf{y}_{k}\,\mathrm{d}x\) as was first used for traveling waves with complex chemistry and detailed multicomponent transport [38]. Letting \(\mathcal{Y} =\mathrm{ diag}(\mathsf{y}_{1},\ldots,\mathsf{y}_{n})\), the nonzero eigenvalues of \(\mathcal{Y}^{1/2}D\mathcal{Y}^{1/2}\) may also directly be estimated from Proposition 8. Indeed if γ is a nonzero eigenvalue of \(\mathcal{Y}^{1/2}D\mathcal{Y}^{1/2}\) with eigenvector x, then \(x = (1/\gamma )\mathcal{Y}^{1/2}D\mathcal{Y}^{1/2}x\) so that  , and one may directly use (20) to deduce that δ ≤ (p∕T)γ. The case of the matrix \(\mathcal{X}^{1/2}D\mathcal{X}^{1/2}\)
where \(\mathcal{X} =\mathrm{ diag}(\mathsf{x}_{1},\ldots,\mathsf{x}_{n})\) may then be deduced from that of \(\mathcal{Y}^{1/2}D\mathcal{Y}^{1/2}\).
, and one may directly use (20) to deduce that δ ≤ (p∕T)γ. The case of the matrix \(\mathcal{X}^{1/2}D\mathcal{X}^{1/2}\)
where \(\mathcal{X} =\mathrm{ diag}(\mathsf{x}_{1},\ldots,\mathsf{x}_{n})\) may then be deduced from that of \(\mathcal{Y}^{1/2}D\mathcal{Y}^{1/2}\).
2.3.3 Simplified Diffusion Models
In order to simplify diffusive processes, one may first neglect the Soret and Dufour cross effects by letting \(\widetilde{\chi }= 0\) in such a way that \(p\mathbf{v} = -D\boldsymbol{\nabla }(p_{1},\ldots,p_{n})^{t}\). Further neglecting barodiffusion – a typical approximation for small Mach number flows – then yields \(\mathbf{v} = -D\boldsymbol{\nabla }\mathsf{x}\), and from \(\boldsymbol{\nabla }\mathsf{x} = E\boldsymbol{\nabla }\mathsf{y}\), one obtains \(\mathbf{v} = -DE\boldsymbol{\nabla }\mathsf{y}\). One may then try to either simplify C and D and use \(p\mathbf{v} = -D\boldsymbol{\nabla }(p_{1},\ldots,p_{n})^{t}\) or \(\mathbf{v} = -D\boldsymbol{\nabla }\mathsf{x}\), or, alternatively, simplify CE and DE and use \(\mathbf{v} = -DE\boldsymbol{\nabla }\mathsf{y}\).
In order to simplify diffusive processes, it is natural to seek for diagonal structures. However, it is established that none of these diffusion matrices may be diagonal because of mass constraints, and when partial densities are positive, it is even established that C and D are irreducible [37]. One may thus seek for the weaker but sufficient property that they coincide with a diagonal matrix on the physical hyperplane  since \(\boldsymbol{d}\), \(\boldsymbol{\nabla }\mathsf{x}\), and \(\boldsymbol{\nabla }\mathsf{y}\) always remain on
since \(\boldsymbol{d}\), \(\boldsymbol{\nabla }\mathsf{x}\), and \(\boldsymbol{\nabla }\mathsf{y}\) always remain on  [37].
[37].
Assuming that y > 0, the diffusion matrices C or D coincide with a diagonal matrix on the physical hyperplane  if and only if the products \(m_{l}m_{l}\mathcal{D}_{kl}^{\text{bin}}\) are equal, and in this situation C coincide with a scalar matrix and all diagonal coefficients are equal [37]. Similarly, still assuming y > 0, the matrices CE and DE coincide with a diagonal matrix on the physical hyperplane
if and only if the products \(m_{l}m_{l}\mathcal{D}_{kl}^{\text{bin}}\) are equal, and in this situation C coincide with a scalar matrix and all diagonal coefficients are equal [37]. Similarly, still assuming y > 0, the matrices CE and DE coincide with a diagonal matrix on the physical hyperplane  if and only if all the binary diffusion coefficients \(\mathcal{D}_{kl}^{\text{bin}}\) are equal, and in this situation CE coincide with a scalar matrix and all diagonal coefficients are equal [37].
if and only if all the binary diffusion coefficients \(\mathcal{D}_{kl}^{\text{bin}}\) are equal, and in this situation CE coincide with a scalar matrix and all diagonal coefficients are equal [37].
Such strong constraints on binary diffusion coefficients are not likely to happen in practice. Therefore, in order to obtain simplified diffusion processes still avoiding constraints on binary diffusion coefficients, it is mandatory to assume that some mass fractions are vanishing, that is, to assume that some species are in trace amounts [37, 39]. In order to obtain a diagonal diffusion process avoiding any constraint between binary diffusion coefficients, a dilution limit must be used and one species has to be discarded. Introducing the pure species state yp = (y1, 0, …, 0)t where y1 > 0 one has the following limit [37]:
where the coefficients \(\delta _{k} = m_{k}\mathcal{D}_{kn}^{\text{bin}}/m_{n}\), 2 ≤ k ≤ n, are positive. As a consequence, in the limit y = yp, one obtains that \(\boldsymbol{\mathcal{J}\ }_{k} = -\delta _{k}\boldsymbol{\nabla }\mathsf{y}_{k}\) for 2 ≤ k ≤ n keeping in mind that \(\boldsymbol{d}_{k} =\boldsymbol{ \nabla }\mathsf{y}_{k} =\boldsymbol{ \nabla }\mathsf{x}_{k}\) when y k = 0. Assuming that the first species is in excess, one may assume that y1 ≃ 1 remains constant and use that \(\boldsymbol{\mathcal{J}\ }_{k} = -\delta _{k}\boldsymbol{\nabla }\mathsf{y}_{k}\) for 2 ≤ k ≤ n and the resulting diffusion process for the reduced set of n − 1 trace species is then diagonal. This is the dilution approximation, and discarding the first species with a new indexing set \(\mathfrak{S}\prime = \mathfrak{S}\setminus \{1\} =\{ 2,\ldots,n\}\), it is obtained that \(\boldsymbol{\mathcal{J}\ }_{k} = -\delta _{k}\boldsymbol{\nabla }\mathsf{y}_{k}\), for \(k \in \mathfrak{S}\prime\).
Finally, with the full transport model derived from the kinetic theory, the fluxes are given by \(\boldsymbol{\mathcal{J}\ }_{k} = -\sum _{l\in \mathfrak{S}}C_{kl}\boldsymbol{\nabla }\mathsf{x}_{l}\) with \(k \in \mathfrak{S}\), and diffusive processes are complex and nondiagonal and couple all species. Moreover, this diffusion model is intrinsically nonlinear since \(N(C) = N(D) = \mathbb{R}\mathsf{y}\) so that it is not possible to assume that C or D is constant since y is varying. But the mass conservation constraint \(\sum _{k\in \mathfrak{S}}\boldsymbol{\mathcal{J}\ }_{k} = 0\) still holds, that is, diffusion is not creating mass and the total mass conservation equation \(\partial _{t}\rho +\boldsymbol{ \nabla }\cdot (\rho \boldsymbol{v}) = 0\) is recovered from the species equations. On the other hand, with the dilution approximation, \(\boldsymbol{\mathcal{J}\ }_{k} = -\delta _{k}\boldsymbol{\nabla }\mathsf{y}_{k}\), for \(k \in \mathfrak{S}\prime\), diffusive processes for the trace n − 1 species lead to uncoupled heat equation operators for the \(\mathfrak{S}\prime\) species, and the diagonal coefficients δ k , \(k \in \mathfrak{S}\prime\), may even be taken as constants. But the mass fluxes \(\sum _{k\in \mathfrak{S}^{{\prime}}}\boldsymbol{\mathcal{J}\ }_{k} = -\sum _{k\in \mathfrak{S}^{{\prime}}}\delta _{k}\boldsymbol{\nabla }\mathsf{y}_{k}\) do not sum to zero for the reduced system of \(\mathfrak{S}^{{\prime}}\) species. In this situation, the diffusion is diagonal with constant coefficients, but diffusion is creating mass for the reduced system of \(\mathfrak{S}^{{\prime}}\) species since \(\sum _{k\in \mathfrak{S}^{{\prime}}}\boldsymbol{\mathcal{J}\ }_{k}\) may differ from zero and a priori estimates of the species mole or mass fractions may be a difficult problem [96].
2.4 Boundary Conditions
A detailed discussion of boundary conditions for multicomponent reactive flows lay out the scope of these notes, and the reader is referred to [8, 39, 76, 95, 98]. Boundary conditions may be complex with subsonic inflow or outflow, free boundaries, elastic interactions, thermal interactions, as well as heterogeneous chemical reactions. The aim of this section is only to present a set of simplified boundary conditions often used at nonreactive impermeable wall boundaries.
A gaseous mixture occupying a domain \(\mathcal{O}_{\boldsymbol{x}} \subset \mathbb{R}^{d}\) in contact with a fixed solid body at the boundary \(\partial \mathcal{O}_{\boldsymbol{x}}\) satisfies the adherence condition
The temperature may either be prescribed at the solid boundary T = Tw where Tw is a given temperature field on \(\partial \mathcal{O}_{\boldsymbol{x}}\), or the wall may be adiabatic
where \(\boldsymbol{\mathfrak{n}}\) denotes the normal vector at the boundary. The species boundary conditions at a nonreactive wall are also of flux type
The set of boundary conditions \(\boldsymbol{v} = 0\), \(\boldsymbol{Q}\boldsymbol{\cdot }\boldsymbol{\mathfrak{n}} = 0\), and \(\boldsymbol{\mathcal{J}\ }_{k}\boldsymbol{\cdot }\boldsymbol{\mathfrak{n}} = 0,\) \(k \in \mathfrak{S}\), at \(\partial \mathcal{O}_{\boldsymbol{x}}\) is often used in the mathematical modelling of reactive mixtures [23, 32, 51, 64, 79, 91, 122].
2.5 Quasilinear Form
2.5.1 Vector Notation
The equations governing multicomponent flows (1), (2), and (3) can be written in vector form

where u is the conservative variable, ∂
i
the spatial derivative operator in the ith spatial direction, \(\mathfrak{D} =\{ 1,\ldots,d\}\) the indexing set of spatial directions, d ∈ {1, 2, 3} the spatial dimension, F
i
the convective flux in the ith direction, F
diss
i
the dissipative flux in the ith direction, and  the source term. Letting n = n + d + 1, the conservative variable \(\mathsf{u} \in \mathbb{R}^{\mathsf{n}}\) is found to be
the source term. Letting n = n + d + 1, the conservative variable \(\mathsf{u} \in \mathbb{R}^{\mathsf{n}}\) is found to be
and the natural variable is defined by \(\mathsf{z} =\big (\rho _{1},\ldots,\,\rho _{n},\,\boldsymbol{v},\,T\big)^{t}\). For convenience, the velocity components of vectors in \(\mathbb{R}_{}^{\mathsf{n}} = \mathbb{R}^{n} \times \mathbb{R}^{d} \times \mathbb{R}\) are written as vectors of \(\mathbb{R}^{d}\), and bold symbols are used for vector or tensor quantities in the physical space \(\mathbb{R}^{d}\).
Proposition 9.
The map z ↦ u is a Cϰ diffeomorphism from the open set \(\mathcal{O}_{\mathsf{z}} = (0,\infty )^{n}\times \mathbb{R}^{d}\times (0,\infty )\) onto an open set \(\mathcal{O}_{\mathsf{u}}\). The open set \(\mathcal{O}_{\mathsf{u}}\) is convex and given by
where \(\phi (u_{1},\ldots,u_{n+d}) = \tfrac{1} {2}(u_{n+1}^{2} + \cdots + u_{ n+d}^{2})/\sum _{ k\in \mathfrak{S}}u_{k} +\sum _{k\in \mathfrak{S}}u_{k}e_{k}^{0}\) and e 0 k is the energy of formation of the kth species at zero temperature.
Proof.
The map z → u is easily shown to be one to one from \(\mathcal{O}_{\mathsf{z}}\) onto \(\mathcal{O}_{\mathsf{u}}\) using the positivity of the constant volume-specific heats. The Jacobian matrix ∂ z u has a triangular structure and is invertible, and one may use the inverse function theorem . □
2.5.2 Directional Fluxes
The convective flux F
i
in the ith direction, the diffusive fluxes F
diss
i
in the ith direction, and the source term  read
read

where \(\boldsymbol{e}_{i}\) denotes the ith basis vector in the physical space \(\mathbb{R}^{d}\), \(\mathcal{J}_{ki}\) the diffusion flux of the kth species in the ith direction, Q i the heat flux in the ith direction, \(\boldsymbol{\varPi }_{i}\) the vector \(\boldsymbol{\varPi }_{i} = (\varPi _{1i},\ldots,\varPi _{di})^{t}\), \(\boldsymbol{0} = (0,\ldots,0)^{t}\), and where it is assumed that the force term \(\boldsymbol{b}\) vanishes. The dissipative fluxes may also be written as \(\mathsf{F}_{i}^{\text{diss}} = -\sum _{j\in \mathfrak{D}}\widehat{\mathsf{B}}_{ij}(\mathsf{u})\partial _{j}\mathsf{z}\) since all transport fluxes are linear expressions in terms of the gradients of the natural variable z. Since z → u is a smooth diffeomorphism, defining \(\mathsf{B}_{ij}(\mathsf{u}) =\widehat{ \mathsf{B}}_{ij}(\mathsf{u})\partial _{\mathsf{u}}\mathsf{z}\), \(i,j \in \mathfrak{D}\), it is obtained that \(\mathsf{F}_{i}^{\text{diss}} = -\sum _{j\in \mathfrak{D}}\mathsf{B}_{ij}(\mathsf{u})\partial _{j}\mathsf{u}\), \(i \in \mathfrak{D}\), where the dissipation matrix B ij relates the dissipative flux in the ith direction to the gradient of the conservative variable in the jth direction. Further denoting by A i = ∂ u F i , \(i \in \mathfrak{D}\), the convective flux Jacobian matrices, a quasilinear system in the conservative variable u is finally obtained. The mathematical structure of such quasilinear systems is discussed in the next section .
3 Hyperbolic–Parabolic Structure
Symmetrization of quasilinear second-order systems of partial differential equations is discussed using entropic variables and normal variables. The hyperbolic–parabolic structure of the resulting systems of partial differential equations is then addressed. The natural entropic symmetrized form as well as the natural normal form for the system of partial differential equations modeling multicomponent reactive fluids are evaluated.
3.1 Entropic Variables
A second-order quasilinear system of conservation laws in the general form

is considered where \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\), \(\mathcal{O}_{\mathsf{u}}\) is an open convex set of \(\mathbb{R}^{\mathsf{n}}\), and n ≥ 1. The system coefficients are such that A
i
= ∂
u
F
i
and the convective fluxes F
i
, \(i \in \mathfrak{D}\), the dissipation matrices B
ij
, \(i,j \in \mathfrak{D}\), and the source term  are assumed to be Cϰ over \(\mathcal{O}_{\mathsf{u}}\) where ϰ ≥ 3.
are assumed to be Cϰ over \(\mathcal{O}_{\mathsf{u}}\) where ϰ ≥ 3.
A mathematical entropy for the system of partial differential equations (26) must be compatible with the convective terms, the dissipative terms, as well as the source terms. The definition presented in [49, 50, 53] is used and simplified to the situation where the set \(\mathcal{O}_{\mathsf{u}}\) is convex. Properties (E 1 ) (E 2 ) concerning the convective terms have been adapted from [35, 56], properties (E 3 ) (E 4 ) associated with the dissipative terms have been adapted from [70, 71, 73, 108], properties (E 5 )– (E 7 ) concerning the source terms have been adapted from [18, 74], and Σd−1 denotes the sphere in d dimensions.
Definition 1.
Consider a Cϰ function u → σ(u) defined over the open convex domain \(\mathcal{O}_{\mathsf{u}}\). The function σ is said to be an entropy function for the system (26) if the following properties hold:
-
\((\boldsymbol{\mathsf{E_{1}}})\) The Hessian matrix ∂ 2 u σ(u) = ∂ u (∂ u σ)t(u) is positive definite over \(\mathcal{O}_{\mathsf{u}}\).
-
\((\boldsymbol{\mathsf{E_{2}}})\) There exist Cϰ functions u → q i (u) such that ∂ u σ(u) A i (u) = ∂ u q i (u) for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\) and \(i \in \mathfrak{D}\).
-
\((\boldsymbol{\mathsf{E_{3}}})\) The reciprocity relations \(\big(\mathsf{B}_{ij}(\mathsf{u})\,\big(\partial _{\mathsf{u}}^{2}\sigma (\mathsf{u})\big)^{-1}\big)^{t} = \mathsf{B}_{ji}(\mathsf{u})\big(\partial _{\mathsf{u}}^{2}\sigma (\mathsf{u})\big)^{-1}\) hold for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\) and \(i,j \in \mathfrak{D}\).
-
\((\boldsymbol{\mathsf{E_{4}}})\) The matrix \(\sum _{i,j\in \mathfrak{D}}\mathsf{B}_{ij}(\mathsf{u})\big(\partial _{\mathsf{u}}^{2}\sigma (\mathsf{u})\big)^{-1}\,\xi _{i}\xi _{j}\) is positive semi-definite for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\) and \(\boldsymbol{\xi }\in \varSigma ^{d-1}\).
-
\((\boldsymbol{\mathsf{E_{5}}})\) There exists a fixed vector space
 such that
such that  for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\) and
for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\) and  if and only if
if and only if  and if and only if
and if and only if  .
. -
\((\boldsymbol{\mathsf{E_{6}}})\) If
 , then the matrix
, then the matrix  is symmetric and its nullspace is given by
is symmetric and its nullspace is given by  .
. -
\((\boldsymbol{\mathsf{E_{7}}})\) The inequality
 holds for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\).
holds for \(\mathsf{u} \in \mathcal{O}_{\mathsf{u}}\).
Existence of an entropy is closely associated with symmetrization properties as established for hyperbolic systems of conservation laws [8, 18, 20, 35, 56, 74, 103] as well as hyperbolic–parabolic systems [45, 50, 66, 70, 106]. The difficulty associated with nonideal fluids where only local symmetrization is feasible and where \(\mathcal{O}_{\mathsf{u}}\) may not be convex [49] is avoided for ideal mixtures. Note also that more general source terms with no symmetry properties at equilibrium have been considered by Chen, Levermore, and Liu [18] and Yong [120].
Definition 2.
Consider a Cϰ−1 diffeomorphism u → v from \(\mathcal{O}_{\mathsf{u}}\) onto an open domain \(\mathcal{O}_{\mathsf{v}}\) and the system in the v variable

where \(\widetilde{\mathsf{A}}_{0} = \partial _{\mathsf{v}}\mathsf{u}\), \(\widetilde{\mathsf{A}}_{i} = \mathsf{A}_{i}\partial _{\mathsf{v}}\mathsf{u}\), \(\widetilde{\mathsf{B}}_{ij} = \mathsf{B}_{ij}\partial _{\mathsf{v}}\mathsf{u}\), and  have at least regularity ϰ − 2. The system is said of the symmetric form if properties (S
1
)–(S
7
) hold.
have at least regularity ϰ − 2. The system is said of the symmetric form if properties (S
1
)–(S
7
) hold.
-
\((\boldsymbol{\mathsf{S_{1}}})\) The matrix \(\widetilde{\mathsf{A}}_{0}(\mathsf{v})\) is symmetric positive definite for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
-
\((\boldsymbol{\mathsf{S_{2}}})\) The matrices \(\widetilde{\mathsf{A}}_{i}(\mathsf{v})\), \(i \in \mathfrak{D}\), are symmetric for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
-
\((\boldsymbol{\mathsf{S_{3}}})\) The reciprocity relations \(\widetilde{\mathsf{B}}_{ij}^{t}(\mathsf{v}) =\widetilde{ \mathsf{B}}_{ji}(\mathsf{v})\) hold for \(i,j \in \mathfrak{D}\) and \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
-
\((\boldsymbol{\mathsf{S_{4}}})\) The matrix \(\widetilde{\mathsf{B}}(\mathsf{v},\boldsymbol{\xi }) =\sum _{i,j\in \mathfrak{D}}\widetilde{\mathsf{B}}_{ij}(\mathsf{v})\xi _{i}\xi _{j}\) is positive semi-definite for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\) and \(\boldsymbol{\xi }\in \varSigma ^{d-1}\).
-
\((\boldsymbol{\mathsf{S_{5}}})\) There exists a fixed vector space
 such that
such that  for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\) and
for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\) and 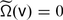 if and only if
if and only if  and if and only if
and if and only if  .
. -
\((\boldsymbol{\mathsf{S_{6}}})\) If
 , then
, then  is symmetric and
is symmetric and  .
. -
\((\boldsymbol{\mathsf{S_{7}}})\) The inequality
 holds for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
holds for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
The manifold  is naturally termed the equilibrium manifold since
is naturally termed the equilibrium manifold since  when
when  . The equivalence between symmetrization (S
1
)–(S
7
) and entropy (E
1
)–(E
7
) for hyperbolic–parabolic systems of conservation laws is obtained with v = (∂
u
σ)t [49].
. The equivalence between symmetrization (S
1
)–(S
7
) and entropy (E
1
)–(E
7
) for hyperbolic–parabolic systems of conservation laws is obtained with v = (∂
u
σ)t [49].
Theorem 1.
Assume that the system (26) admits a Cϰ entropy function σ defined over an open convex domain \(\mathcal{O}_{\mathsf{u}}\). Then the system can be symmetrized with the entropic variable v = (∂ u σ)t. Conversely, assume that the system can be symmetrized with the Cϰ−1 diffeomorphism u → v. Then there exists a Cϰ entropy over the open convex set \(\mathcal{O}_{\mathsf{u}}\) such that v = (∂ u σ)t.
Sketch of the proof.
The equivalence of (S 1 )–(S 2 ) and (E 1 )–(E 2 ) is classical and is essentially obtained with Poincaré lemma. Then (S 3 )–(S 7 ) and (E 3 )–(E 7 ) become identical statements with v = (∂ u σ)t. □
3.2 Normal Variables
In order to split between hyperbolic and parabolic variables, it is necessary to put the system into a normal form, that is, in the form of a symmetric hyperbolic–parabolic composite system [45, 70, 73].
Definition 3.
Consider a symmetrized system as in Definition 2, and let v → w be a Cϰ−1 diffeomorphism from the open set \(\mathcal{O}_{\mathsf{v}}\) onto an open set \(\mathcal{O}_{\mathsf{w}}\). Letting v = v(w) in the symmetrized system (27) and multiplying on the left side by (∂ w v)t, a new system is obtained in the variable w

where \(\overline{\mathsf{A}}_{0} = (\partial _{\mathsf{w}}\mathsf{v})^{t}\,\widetilde{\mathsf{A}}_{0}\,(\partial _{\mathsf{w}}\mathsf{v})\), \(\overline{\mathsf{A}}_{i} = (\partial _{\mathsf{w}}\mathsf{v})^{t}\,\widetilde{\mathsf{A}}_{i}\,(\partial _{\mathsf{w}}\mathsf{v})\), \(\overline{\mathsf{B}}_{ij} = (\partial _{\mathsf{w}}\mathsf{v})^{t}\,\widetilde{\mathsf{B}}_{ij}\,(\partial _{\mathsf{w}}\mathsf{v})\), and  have at least regularity ϰ − 2 and where \(\overline{\mathsf{r}} = -\sum _{i,j\in \mathfrak{D}}\partial _{i}(\partial _{\mathsf{w}}\mathsf{v})^{t}\) \(\widetilde{\mathsf{B}}_{ij}\,(\partial _{\mathsf{w}}\mathsf{v})\partial _{j}\mathsf{w}\) is quadratic in the gradients. This system satisfies the properties (S
1
)–(S
4
) rewritten in terms of overbar matrices. System (28) is said to be of the normal form if there exists a partition of {1, …, n} into I = {1, …, nI} and II = {nI + 1, …, nI +nII} with n = nI +n
II
such that the following properties hold.
have at least regularity ϰ − 2 and where \(\overline{\mathsf{r}} = -\sum _{i,j\in \mathfrak{D}}\partial _{i}(\partial _{\mathsf{w}}\mathsf{v})^{t}\) \(\widetilde{\mathsf{B}}_{ij}\,(\partial _{\mathsf{w}}\mathsf{v})\partial _{j}\mathsf{w}\) is quadratic in the gradients. This system satisfies the properties (S
1
)–(S
4
) rewritten in terms of overbar matrices. System (28) is said to be of the normal form if there exists a partition of {1, …, n} into I = {1, …, nI} and II = {nI + 1, …, nI +nII} with n = nI +n
II
such that the following properties hold.
-
\((\boldsymbol{\mathsf{N_{1}}})\) The matrices \(\overline{\mathsf{A}}_{0}\) and \(\overline{\mathsf{B}}_{ij}\) have the block structure
$$\displaystyle{\overline{\mathsf{A}}_{0} = \left [\begin{array}{cc} \overline{\mathsf{A}}_{0}^\mathrm{I,I}\ & 0_{\mathsf{n}_\mathrm{I},\mathsf{n}_\mathrm{II}}\\ \\ \\ 0_{\mathsf{n}_\mathrm{II},\mathsf{n}_\mathrm{I}}\ & \overline{\mathsf{A}}_{0}^\mathrm{II,II}\end{array} \right ],\qquad \overline{\mathsf{B}}_{ij} = \left [\begin{array}{cc} 0_{\mathsf{n}_\mathrm{I},\mathsf{n}_\mathrm{I}}\ & 0_{\mathsf{n}_\mathrm{I},\mathsf{n}_\mathrm{II}}\\ \\ \\ 0_{\mathsf{n}_\mathrm{II},\mathsf{n}_\mathrm{I}}\ & \overline{\mathsf{B}}_{ij}^\mathrm{II,II}\end{array} \right ].}$$ -
\((\boldsymbol{\mathsf{N_{2}}})\) The matrix \(\overline{\mathsf{B}}^{\mathrm {II,II}}(\mathsf{w},\boldsymbol{\xi }) =\sum _{i,j\in \mathfrak{D}}\overline{\mathsf{B}}_{ij}^{\mathrm {II,II}}(\mathsf{w})\xi _{i}\xi _{j}\) is positive definite for \(\mathsf{w} \in \mathcal{O}_{\mathsf{w}}\) and \(\boldsymbol{\xi }\in \varSigma ^{d-1}\).
-
\((\boldsymbol{\mathsf{N_{3}}})\) The quadratic residual is in the form \(\overline{\mathsf{r}}(\mathsf{w},\boldsymbol{\nabla }\mathsf{w}) =\big (\overline{\mathsf{r}}_{I}(\mathsf{w},\boldsymbol{\nabla }\mathsf{w}_{II}),\overline{\mathsf{r}}_{II}(\mathsf{w},\boldsymbol{\nabla }\mathsf{w})\big)^{t}\).
The vector and matrix block structure induced by the partitioning of \(\mathbb{R}^{\mathsf{n}}\) into \(\mathbb{R}^{\mathsf{n}} = \mathbb{R}^{\mathsf{n}_{I}} \times \mathbb{R}^{\mathsf{n}_{II}}\) has been used in (N 1 )–(N 3 ) so that w = (wI, wII)t, for instance, and 0i, j denotes the zero matrix with i lines and j columns.
The quadratic residual may also be written in the more elegant form
where \(\overline{M}_{ij}(\mathsf{w})\) are third-order tensors that are functions of \(\mathsf{w} \in \mathcal{O}_{\mathsf{w}}\). From the regularity assumptions of the original system (26), the coefficients of both symmetrized systems (27) and (28) have at least regularity ϰ − 2 and the coefficients \(\overline{M}_{ij}\), \(i,j \in \mathfrak{D}\), have at least regularity ϰ − 3. A sufficient condition for system (27) to be recast into a normal form is that the nullspace naturally associated with the dissipation matrix \(\widetilde{\mathsf{B}}\) is a fixed subspace of \(\mathbb{R}^{\mathsf{n}}\). This is Condition (N) introduced by Kawashima and Shizuta [73] which has been strengthened in [45].
-
\((\boldsymbol{\mathsf{N_{}}})\) The nullspace \(N(\,\widetilde{\mathsf{B}})\) of the matrix \(\widetilde{\mathsf{B}}(\mathsf{v},\boldsymbol{\xi }) =\sum _{i,j\in \mathfrak{D}}\widetilde{\mathsf{B}}_{ij}(\mathsf{v})\xi _{i}\xi _{j}\) does not depend on \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\) and \(\boldsymbol{\xi }\in \varSigma ^{d-1}\) and \(\widetilde{\mathsf{B}}_{ij}(\mathsf{v})N(\,\widetilde{\mathsf{B}}) = 0\), for \(i,j \in \mathfrak{D}\).
Let \(\mathsf{n}_{I} =\dim \big (N(\,\widetilde{\mathsf{B}})\big)\), nII = n −nI, and P be an arbitrary constant nonsingular matrix of dimension n such that its first nI columns span the nullspace \(N(\,\widetilde{\mathsf{B}})\). In order to characterize more easily normal forms for symmetric systems of conservation laws satisfying (N), one may introduce the auxiliary variables u′ = Ptu and v′ = P−1v, and the following characterization of normal variables holds [39, 45].
Theorem 2.
Any normal form of the system (27) is given by a change of variable in the form \(\mathsf{w} =\big (\mathcal{F}_\mathrm{I}(\mathsf{u}_\mathrm{I}^{{\prime}}),\mathcal{F}_\mathrm{II}(\mathsf{v}_\mathrm{II}^{{\prime}})\big)^{t}\) where \(\mathcal{F}_\mathrm{I}\) and \(\mathcal{F}_\mathrm{II}\) are two diffeomorphisms of \(\mathbb{R}^{\mathsf{\mathrm{n}}_\mathrm{I}}\) and \(\mathbb{R}^{\mathsf{\mathrm{n}}_\mathrm{II}}\), respectively, and the quadratic residual is in the form
where \(\overline{M}_{ij}^\mathrm{II,II,II}(\mathsf{w})\) are third-order tensors depending on w with regularity at least ϰ − 3. Finally, when \(\mathcal{F}_\mathrm{II}\) is linear, the quadratic residual \(\overline{\mathsf{r}}\) is zero.
The main interest of normal forms is that the resulting subsystem of partial differential equations governing wI is symmetric hyperbolic, whereas the subsystem governing wII is symmetric strongly parabolic [70, 73, 105]. It is further possible to investigate situations where the general structure of the symmetrized source term  is transferred to the source term
is transferred to the source term  of the normal variable
[53].
of the normal variable
[53].
3.3 Hyperbolicity and Parabolicity
Consider a first-order system of partial differential equations written in the general form

where \(\overline{\mathsf{A}}_{0}\), \(\overline{\mathsf{A}}_{i}\), \(i \in \mathfrak{D}\), and  are smooth functions of w over \(\mathcal{O}_{\mathsf{w}}\) and where \(\overline{\mathsf{A}}_{0}\) is assumed to be invertible. The following definition of hyperbolicity
can be found in the book of Denis Serre [105] where i2 = −1.
are smooth functions of w over \(\mathcal{O}_{\mathsf{w}}\) and where \(\overline{\mathsf{A}}_{0}\) is assumed to be invertible. The following definition of hyperbolicity
can be found in the book of Denis Serre [105] where i2 = −1.
Definition 4.
Letting \(\overline{\mathsf{A}}(\mathsf{w},\boldsymbol{\xi }) =\sum _{i\in \mathfrak{D}}\overline{\mathsf{A}}_{i}(\mathsf{w})\xi _{i}\), the system (31) is said to be hyperbolic at a given point w if
When the system (31) is hyperbolic, it is easily established that the matrix \(\big(\overline{\mathsf{A}}_{0}(\mathsf{w})\big)^{-1}\overline{\mathsf{A}}(\mathsf{w},\xi )\) is diagonalizable with real eigenvalues so that it is hyperbolic in the classical sense [20, 105]. Sufficient condition in terms of eigenvalues and eigenvector matrices is presented by Serre [105]. A fundamental property of Definition 4 is its invariance under a change of variable, and one has also the following property for symmetric systems [20, 105].
Proposition 10.
Assume that the system (31) is symmetric at a given point w, that is, assume that \(\overline{\mathsf{A}}_{0}(\mathsf{w})\) is symmetric positive definite and the matrices \(\overline{\mathsf{A}}_{i}(\mathsf{w})\), \(i \in \mathfrak{D}\), are symmetric. Then the system is hyperbolic.
Since the existence of an entropy function implies symmetrizability, it automatically implies hyperbolicity in the sense of Definition 4 as well as in the classical sense [20, 105].
Consider then a second-order system in the form

where \(\overline{\mathsf{A}}_{0}\), \(\overline{\mathsf{B}}_{ij}\), \(i,j \in \mathfrak{D}\), are smooth functions of w over \(\mathcal{O}_{\mathsf{w}}\),  is a smooth function over \(\mathcal{O}_{\mathsf{w}} \times \mathbb{R}^{d\mathsf{n}}\), and \(\overline{\mathsf{A}}_{0}\) is invertible. Such systems are said to be symmetric in the following sense.
is a smooth function over \(\mathcal{O}_{\mathsf{w}} \times \mathbb{R}^{d\mathsf{n}}\), and \(\overline{\mathsf{A}}_{0}\) is invertible. Such systems are said to be symmetric in the following sense.
Definition 5.
The system (33) is said to be symmetric at a given point w when \(\overline{\mathsf{A}}_{0}(\mathsf{w})\) is symmetric positive definite and \(\big(\overline{\mathsf{B}}_{ij}(\mathsf{w})\big)^{t} = \overline{\mathsf{B}}_{ji}(\mathsf{w})\), for \(i,j \in \mathfrak{D}\).
The following definition of strongly parabolic systems of second-order partial differential equations involves the Legendre-Hadamard condition . This definition should only concern the parabolic subsystem in the variable w II , but all II indices have been suppressed in order to simplify the presentation.
Definition 6.
Assume that the system (33) is symmetric at a given point w. This system is said to be strongly parabolic at w if there exists a positive constant δ > 0 such that for any \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) and any x = (x1, …, x n )t,
The definition of strong parabolicity is only given here for symmetric systems and will be applied to the symmetrized forms like (27) or (28), thereby naturally involving entropy Hessians. Indeed, the definition of strong parabolicity in the usual sense, which neither require symmetry properties nor entropy hessians, is not invariant by a change of variable. It only has a meaning for particular forms of systems of partial differential equations under consideration which need to be specified as shown by simple counterexamples [49].
Definition 7.
Denoting \(\overline{\mathsf{B}}(\mathsf{w},\boldsymbol{\xi }) =\sum _{i,j\in \mathfrak{D}}\xi _{i}\xi _{j}\overline{\mathsf{B}}_{ij}(\mathsf{w})\), a system (33) is said to be parabolic in the sense of Petrovsky at a given point w if there exists a positive constant δ such that for any \(\boldsymbol{\xi }\in \mathbb{R}^{d}\), the eigenvalues γ of \(\big(\overline{\mathsf{A}}_{0}(\mathsf{w})\big)^{-1}\overline{\mathsf{B}}(\mathsf{w},\boldsymbol{\xi })\) satisfy
Various other generalized definitions of parabolicity are discussed in the book of Ladyženskaja et al. [81], but these definitions coincide with that of Petrovsky for second-order systems [81] and also coincide with the notion of normal ellipticity. For symmetric systems, Petrovsky parabolicity and strong parabolicity are equivalent [49].
Proposition 11.
Consider a second-order system in the form (33) and assume that the system is symmetric. Then the system is strongly parabolic at w if and only if it is Petrovsky parabolic at w.
Sketch of the proof.
The eigenvalues of \(\big(\overline{\mathsf{A}}_{0}(\mathsf{w})\big)^{-1}\overline{\mathsf{B}}(\mathsf{w},\boldsymbol{\xi })\) are essentially extremal values of Rayleigh quotients with respect to the scalar product \(\langle \ \langle x,y\rangle \ \rangle =\langle \overline{\mathsf{A}}_{0}x,y\rangle\). □
From a practical point of view, for systems of partial differential equations derived from physics, thanks to the existence of a mathematical entropy, one may use symmetrized forms of the systems of partial differential equations and then rely on the proper definition of strongly parabolic systems given in Definition 6. Strong parabolicity is then invariant by a change of variable for symmetric systems after multiplication on the left by the transpose of the Jacobian matrix .
3.4 Natural Entropic Form for Multicomponent Flows
The natural entropic symmetrized form for the system of partial differential equations modeling multicomponent reactive fluids is evaluated in this section. For this particular system of partial differential equations n = n + d + 1, the velocity components of all quantities in \(\mathbb{R}^{n+d+1}\) are denoted as vectors of \(\mathbb{R}^{d}\), and the corresponding partitioning is also used for matrices.
Theorem 3.
Assume that (H 1 )–(H 3 ) hold. Then the function \(\sigma = -\mathcal{S}/R\) is a mathematical entropy for the system governing multicomponent fluids, and the corresponding entropic variable is
The map u → v is a Cϰ−1 diffeomorphism from \(\mathcal{O}_{\mathsf{u}}\) onto \(\mathcal{O}_{\mathsf{v}} = \mathbb{R}^{n} \times \mathbb{R}^{d} \times (-\infty,0)\). The system written in terms of the entropic variable v is

with \(\widetilde{\mathsf{A}}_{0} = \partial _{\mathsf{v}}\mathsf{u}\), \(\widetilde{\mathsf{A}}_{i} = \mathsf{A}_{i}\partial _{\mathsf{v}}\mathsf{u}\), \(\widetilde{\mathsf{B}}_{ij} = \mathsf{B}_{ij}\partial _{\mathsf{v}}\mathsf{u}\), and  , and is of the symmetric form. The matrix \(\widetilde{\mathsf{A}}_{0}\) is given by
, and is of the symmetric form. The matrix \(\widetilde{\mathsf{A}}_{0}\) is given by

where \(\mathcal{M} =\mathrm{ diag}(m_{1}\rho _{1},\ldots,m_{n}\rho _{n})\) and  . Since \(\widetilde{\mathsf{A}}_{0}\) is symmetric, only its left lower triangular part is written and “Sym” is written in the upper triangular part. Denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) an arbitrary vector of \(\mathbb{R}^{d}\) and letting \(\widetilde{\mathsf{A}} =\sum _{i\in \mathfrak{D}}\xi _{i}\widetilde{\mathsf{A}}_{i}\), then
. Since \(\widetilde{\mathsf{A}}_{0}\) is symmetric, only its left lower triangular part is written and “Sym” is written in the upper triangular part. Denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) an arbitrary vector of \(\mathbb{R}^{d}\) and letting \(\widetilde{\mathsf{A}} =\sum _{i\in \mathfrak{D}}\xi _{i}\widetilde{\mathsf{A}}_{i}\), then
Moreover, one may write \(\widetilde{\mathsf{B}}_{ij} =\widetilde{ \mathsf{B}}^{D\lambda }\delta _{ij} +\kappa RT\,\widetilde{\mathsf{B}}_{ij}^{\kappa } +\eta RT\,\widetilde{\mathsf{B}}_{ij}^{\eta }\) with

where  is the matrix of size n with components ρ
k
ρ
l
D
kl
and
is the matrix of size n with components ρ
k
ρ
l
D
kl
and  is the vector of size n with components
is the vector of size n with components  . Moreover, denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) and \(\boldsymbol{\zeta }= (\zeta _{1},\ldots,\zeta _{d})^{t}\) arbitrary vectors of \(\mathbb{R}^{d}\), the matrices \(\widetilde{\mathsf{B}}_{ij}^{\kappa }\) and \(\widetilde{\mathsf{B}}_{ij}^{\eta }\), \(i,j \in \mathfrak{D}\), are given by
. Moreover, denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) and \(\boldsymbol{\zeta }= (\zeta _{1},\ldots,\zeta _{d})^{t}\) arbitrary vectors of \(\mathbb{R}^{d}\), the matrices \(\widetilde{\mathsf{B}}_{ij}^{\kappa }\) and \(\widetilde{\mathsf{B}}_{ij}^{\eta }\), \(i,j \in \mathfrak{D}\), are given by
Finally, the equilibrium manifold is given by  and is spanned by \(\mathsf{a}_{l} = (\,\widetilde{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), \(l \in \mathfrak{A}\), and \(\mathsf{a}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1, where f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). The source term
and is spanned by \(\mathsf{a}_{l} = (\,\widetilde{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), \(l \in \mathfrak{A}\), and \(\mathsf{a}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1, where f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). The source term  is in quasilinear form
is in quasilinear form  with
with
where \(\mathfrak{p}_{i} = (M\nu _{i},\boldsymbol{0},0)^{t}\), \(i \in \mathfrak{R}\), Λ
i
is as in (9) and  .
.
Sketch of the proof.
The proof is lengthy but presents no serious Difficulty, and the reader is referred to [39, 45, 49]. □
For mixtures of ideal gases, there is also a uniqueness theorem for mathematical entropies that are independent of transport coefficients [50]. This result strengthen the representation theorem of normal variable as well as the importance of the natural entropic symmetrized form.
Theorem 4.
Let \(\widetilde{\sigma }\) be a Cϰ function defined on the open set \(\mathcal{O}_{\mathsf{u}}\) satisfying (E 2 ) (E 3 ) and such that \(\partial _{\mathsf{u}}^{2}\widetilde{\sigma }\) is invertible. Assuming that \(\widetilde{\sigma }\) is independent of the mass and heat diffusion parameters, then \(\widetilde{\sigma }\) is in the form \(\widetilde{\sigma }=\alpha _{\mathcal{S}}\mathcal{S} +\sum _{i\in \mathfrak{S}}\alpha _{i}\rho _{i} +\alpha _{\boldsymbol{v}}\rho \boldsymbol{v} +\alpha _{\mathcal{E}}(\mathcal{E} + \tfrac{1} {2}\rho \vert \boldsymbol{v}\vert ^{2})\) where \(\alpha _{\mathcal{S}}\), α i , \(i \in \mathfrak{S}\), \(\alpha _{\boldsymbol{v}}\), and \(\alpha _{\mathcal{E}}\) are constants.
This shows in particular that mathematical entropies independent of transport parameters – a somewhat natural condition – are indeed unique up to an affine transform, once the trivial factors proportional to conserved quantities have been eliminated and the corresponding entropic variables are then proportional .
3.5 Natural Normal Form for Multicomponent Flows
The symmetric system (37) may be rewritten into a normal form, that is, in the form of a symmetric hyperbolic–parabolic composite system, where hyperbolic and parabolic variables are split [45, 46, 73, 106, 121]. The nullspace invariance property has been established for multicomponent flows [39, 45].
Lemma 2.
The nullspace of the matrix \(\widetilde{\mathsf{B}}(\mathsf{v},\boldsymbol{\xi })\) is independent of \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\) and \(\boldsymbol{\xi }\in \varSigma ^{d-1}\) and given by  , and \(\widetilde{\mathsf{B}}_{ij}(\mathsf{v})N(\,\widetilde{\mathsf{B}}) = 0\), \(i,j \in \mathfrak{D}\), for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
, and \(\widetilde{\mathsf{B}}_{ij}(\mathsf{v})N(\,\widetilde{\mathsf{B}}) = 0\), \(i,j \in \mathfrak{D}\), for \(\mathsf{v} \in \mathcal{O}_{\mathsf{v}}\).
Since the nullspace of \(N(\,\widetilde{\mathsf{B}})\) is spanned by  , one may introduce the invertible matrix P obtained by replacing the first column vector of the identity matrix by
, one may introduce the invertible matrix P obtained by replacing the first column vector of the identity matrix by  . The auxiliary variables u′ = Ptu and v′ = P−1v are then given by \(\mathsf{u}^{{\prime}} =\big (\rho,\rho _{2},\ldots,\rho _{n},\rho \boldsymbol{v},\mathcal{E} + \tfrac{1} {2}\rho \vert \boldsymbol{v}\vert ^{2}\big)^{t}\) and \(\mathsf{v}^{{\prime}} =\big (g_{1} -\tfrac{1} {2}\vert \boldsymbol{v}\vert ^{2},g_{ 2} - g_{1},\ldots g_{n} - g_{1},\boldsymbol{v},-1\big)^{t}/RT\). From the representation in Theorem 2, all normal forms of the system (27) are obtained with variables w in the form
. The auxiliary variables u′ = Ptu and v′ = P−1v are then given by \(\mathsf{u}^{{\prime}} =\big (\rho,\rho _{2},\ldots,\rho _{n},\rho \boldsymbol{v},\mathcal{E} + \tfrac{1} {2}\rho \vert \boldsymbol{v}\vert ^{2}\big)^{t}\) and \(\mathsf{v}^{{\prime}} =\big (g_{1} -\tfrac{1} {2}\vert \boldsymbol{v}\vert ^{2},g_{ 2} - g_{1},\ldots g_{n} - g_{1},\boldsymbol{v},-1\big)^{t}/RT\). From the representation in Theorem 2, all normal forms of the system (27) are obtained with variables w in the form
where \(\mathcal{F}_{I}\) and \(\mathcal{F}_{II}\) are diffeomorphisms of \(\mathbb{R}\) and \(\mathbb{R}^{n+d}\). In the following theorem, the normal form corresponding to the natural normal variable is evaluated.
Theorem 5.
Assume that (H 1 )–(H 3 ) hold and consider the normal variable
Then v ↦ w is a diffeomorphism from \(\mathcal{O}_{\mathsf{v}}\) onto \(\mathcal{O}_{\mathsf{w}} = (0,\infty ) \times \mathbb{R}^{n-1} \times \mathbb{R}^{d} \times (-\infty,0)\), and the system of partial differential equations in normal form may be written as

The matrix \(\overline{\mathsf{A}}_{0}\) is given by

where

\((\overline{\mathcal{M}}\,)_{n-1,n-1}\) is the lower right submatrix of size n − 1 of \(\overline{\mathcal{M}}\), and  are the n − 1 last components of
are the n − 1 last components of  , keeping in mind that
, keeping in mind that  and
and  . Denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) an arbitrary vector of \(\mathbb{R}^{d}\), the matrices \(\overline{\mathsf{A}}_{i}\), \(i \in \mathfrak{D}\), are given by
. Denoting by \(\boldsymbol{\xi }= (\xi _{1},\ldots,\xi _{d})^{t}\) an arbitrary vector of \(\mathbb{R}^{d}\), the matrices \(\overline{\mathsf{A}}_{i}\), \(i \in \mathfrak{D}\), are given by

where

and \((\overline{\mathsf{y}})_{n-1}\) are the last n − 1 components of \(\overline{\mathsf{y}}\).
The matrices \(\overline{\mathsf{B}}_{ij}\) have the structure \(\overline{\mathsf{B}}_{ij} =\delta _{ij}\overline{\mathsf{B}}^{D\lambda } + RT\kappa \overline{\mathsf{B}}_{ij}^{\kappa } + RT\eta \overline{\mathsf{B}}_{ij}^{\eta }\) where \(\overline{\mathsf{B}}_{ij}^{\kappa } =\widetilde{ \mathsf{B}}_{ij}^{\kappa }\) and \(\overline{\mathsf{B}}_{ij}^{\eta } =\widetilde{ \mathsf{B}}_{ij}^{\eta }\) for \(i,j \in \mathfrak{D}\), whereas \(\overline{\mathsf{B}}^{D\lambda }\) has its first line and first column composed of zeros and its lower right block \(\overline{\mathsf{B}}^{D\lambda \,\mathrm{II,II}}\) equal to \(\widetilde{\mathsf{B}}^{D\lambda \,\mathrm{II,II}}\) so that

where  is the lower right submatrix of size n − 1 of
is the lower right submatrix of size n − 1 of  and
and  are the n − 1 last components of
are the n − 1 last components of  .
.
The equilibrium linear manifold  with respect to the normal variable is the fixed subspace spanned by the vectors \(\overline{\mathsf{a}}_{1} = \mathsf{f}_{1}\), \(\overline{\mathsf{a}}_{l} = (\overline{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), for \(l \in \mathfrak{A}\setminus \{1\}\), where
with respect to the normal variable is the fixed subspace spanned by the vectors \(\overline{\mathsf{a}}_{1} = \mathsf{f}_{1}\), \(\overline{\mathsf{a}}_{l} = (\overline{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), for \(l \in \mathfrak{A}\setminus \{1\}\), where  , \(l \in \mathfrak{A}\), and \(\overline{\mathsf{a}}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1, where f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). The source term
, \(l \in \mathfrak{A}\), and \(\overline{\mathsf{a}}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1, where f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). The source term  may also be written in quasilinear form
may also be written in quasilinear form  where
where
and \(\mathfrak{p}_{i}^{{\prime}} = (M\nu _{i}^{{\prime}},\boldsymbol{0},0)^{t}\), ν
′
i
= (0, ν2i, …, ν
ni
)t, Λ
i
is as in (9) and  . Moreover, denoting by π the orthogonal projector onto
. Moreover, denoting by π the orthogonal projector onto  , then \(\overline{\mathsf{L}} = \pi \overline{\mathsf{L}} = \overline{\mathsf{L}}\pi\) and πw represents the fast variable or the “reactive” part of w.
, then \(\overline{\mathsf{L}} = \pi \overline{\mathsf{L}} = \overline{\mathsf{L}}\pi\) and πw represents the fast variable or the “reactive” part of w.
Proof.
The proof is lengthy and tedious but presents no serious difficulties. □
4 The Cauchy Problem
The equations governing multicomponent reactive flows derived from the kinetic theory of gases have local smooth solutions [46], global smooth solutions around constant equilibrium states [45], and traveling wave solutions [38]. The dependence on a parameter has also been investigated in [43]. Existence results around equilibrium states and asymptotic stability are investigated in this section. Local strict dissipativity is first addressed, and then the Cauchy problem is discussed [8, 43, 45, 49, 70, 73,74,75, 105, 112]. Weak solutions with large data for related fluid [1, 14, 21, 30, 31, 83, 94] and chemically reacting mixtures are also briefly addressed [19, 23, 32, 51, 64, 79, 87, 123,124,125].
4.1 Strict Dissipativity
Dissipativity
properties around equilibrium states are required in order to establish global existence and asymptotic stability [45, 70, 108]. Consider a symmetrizable quasilinear system (26); assume that the nullspace invariance property (N) holds and that the system has been rewritten in normal form. Assume that there exists an equilibrium state \(\mathsf{u}^{\star } \in \mathcal{O}_{\mathsf{u}}\) with  , and denote by v⋆ and w⋆ the corresponding constant states in the v and w variables, respectively.
, and denote by v⋆ and w⋆ the corresponding constant states in the v and w variables, respectively.
Linearizing the system in normal form (28) around the constant stationary state w⋆, a linear system in the variable δw = w −w⋆ is obtained
By Fourier transform, the spectral problem associated with the linear system (48) reads
where \(\zeta \in \mathbb{R}\), i2 = −1, \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), \(\phi \in \mathbb{C}^{\mathsf{n}}\), \(\overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi }) =\sum _{i\in \mathfrak{D}}\overline{\mathsf{A}}_{i}(\mathsf{w}^{\star })\xi _{i}\), \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi }) =\sum _{i,j\in \mathfrak{D}}\overline{\mathsf{B}}_{ij}(\mathsf{w}^{\star })\xi _{i}\xi _{j}\), and  . The matrix \(\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\) is symmetric positive definite, the matrices \(\overline{\mathsf{A}}_{i}(\mathsf{w}^{\star })\), \(i \in \mathfrak{D}\), are symmetric, the reciprocity relations \(\overline{\mathsf{B}}_{ij}(\mathsf{w}^{\star })^{t} = \overline{\mathsf{B}}_{ji}(\mathsf{w}^{\star })\), \(i,j \in \mathfrak{D}\), hold, the matrix \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi })\) is positive semi-definite for \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), and the matrix \(\overline{\mathsf{L}}(\mathsf{w}^{\star })\) is symmetric positive semi-definite from general symmetrization properties [49] or from the quasilinear form of
. The matrix \(\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\) is symmetric positive definite, the matrices \(\overline{\mathsf{A}}_{i}(\mathsf{w}^{\star })\), \(i \in \mathfrak{D}\), are symmetric, the reciprocity relations \(\overline{\mathsf{B}}_{ij}(\mathsf{w}^{\star })^{t} = \overline{\mathsf{B}}_{ji}(\mathsf{w}^{\star })\), \(i,j \in \mathfrak{D}\), hold, the matrix \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi })\) is positive semi-definite for \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), and the matrix \(\overline{\mathsf{L}}(\mathsf{w}^{\star })\) is symmetric positive semi-definite from general symmetrization properties [49] or from the quasilinear form of  (47). The set of complex numbers γ such that there exists \(\phi \in \mathbb{C}^{\mathsf{n}}\), ϕ ≠ 0, satisfying (49) is denoted by
(47). The set of complex numbers γ such that there exists \(\phi \in \mathbb{C}^{\mathsf{n}}\), ϕ ≠ 0, satisfying (49) is denoted by  . The following equivalent forms of the “Kawashima condition” have been established by Shizuta and Kawashima [108] for (K
1
)–(K
4
) and Beauchard and Zuazua [5] for (K
5
).
. The following equivalent forms of the “Kawashima condition” have been established by Shizuta and Kawashima [108] for (K
1
)–(K
4
) and Beauchard and Zuazua [5] for (K
5
).
Theorem 6.
The system of partial differential equations is said to be strictly dissipative at w ⋆ when any of the following equivalent properties holds:
-
\((\boldsymbol{\mathsf{K_{1}}})\) There exists a C∞ map \(K:\varSigma ^{d-1} \rightarrow \mathbb{R}^{d,d}\) such that for any \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), the product \(K(\boldsymbol{\xi })\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\) is skew symmetric, \(K(-\boldsymbol{\xi }) = -K(\boldsymbol{\xi })\), and \(K(\boldsymbol{\xi })\,\overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi }) + \overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi }) + \overline{\mathsf{L}}(\mathsf{w}^{\star })\) is positive definite.
-
\((\boldsymbol{\mathsf{K_{2}}})\) For any \(\zeta \in \, \mathbb{R}\), ζ ≠ 0, and any \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), the eigenvalues
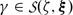 have a negative real part \(\mathfrak{R}(\gamma ) <0\).
have a negative real part \(\mathfrak{R}(\gamma ) <0\). -
\((\boldsymbol{\mathsf{K_{3}}})\) Let \(\phi \in \mathbb{R}^{\mathsf{n}}\setminus \{0\}\) such that \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi })\phi = 0\) and \(\overline{\mathsf{L}}(\mathsf{w}^{\star })\phi = 0\) for some \(\boldsymbol{\xi }\in \varSigma ^{d-1}\). Then \(\gamma \overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\phi + \overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi })\phi \neq 0\) for any \(\gamma \in \mathbb{R}\).
-
\((\boldsymbol{\mathsf{K_{4}}})\) There exists δ > 0 such that for any \(\zeta \in \mathbb{R}\), \(\boldsymbol{\xi }\in \varSigma ^{d-1}\), all eigenvalues
 have their real part majorized by \(\mathfrak{R}(\gamma ) \leq -\delta \vert \zeta \vert ^{2}/(1 +\vert \zeta \vert ^{2})\).
have their real part majorized by \(\mathfrak{R}(\gamma ) \leq -\delta \vert \zeta \vert ^{2}/(1 +\vert \zeta \vert ^{2})\). -
\((\boldsymbol{\mathsf{K_{5}}})\) Letting \(\widehat{\mathsf{A}}^{\star } =\big (\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\big)^{-1}\overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi })\) and \(\widehat{\mathsf{B}}^{\star } =\big (\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\big)^{-1}\big(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi }) + \overline{\mathsf{L}}(\mathsf{w}^{\star })\big)\), the Kalman condition \(\mathrm{rank}\big[\,\widehat{\mathsf{B}}^{\star },\widehat{\mathsf{A}}^{\star }\,\widehat{\mathsf{B}}^{\star },\ldots,(\widehat{\mathsf{A}}^{\star })^{\mathsf{n}-1}\,\widehat{\mathsf{B}}^{\star }\,\big] = \mathsf{n}\) holds.
A physical interpretation of the “Kawashima condition” (K 1 )–(K 5 ) is that the waves \(\phi \exp (\gamma t +\boldsymbol{\xi } \boldsymbol{\cdot }\boldsymbol{x})\) associated with the convective constant coefficient hyperbolic operator \(\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\partial _{t}\ +\sum _{i\in \mathfrak{D}}\overline{\mathsf{A}}_{i}(\mathsf{w}^{\star })\partial _{i}\) lead to dissipation, i.e., entropy production, since they are not in the nullspace of \(\overline{\mathsf{B}}\) or \(\overline{\mathsf{L}}\) as shown by (K 3 ). Only the symmetric part of the product \(K(\boldsymbol{\xi })\,\overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi })\) plays a role in (K 1 ). The traditional Kalman condition involving the n2 ×n matrix with first block \(\widehat{\mathsf{B}}^{\star }\), second block \(\widehat{\mathsf{B}}^{\star }\,\widehat{\mathsf{A}}^{\star }\), and kth block \(\widehat{\mathsf{B}}^{\star }\,(\widehat{\mathsf{A}}^{\star })^{k-1}\) has been rewritten in the form (K 5 ) with a n ×n2 matrix, thanks to the symmetry of \(\overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\), \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi })\), and \(\overline{\mathsf{L}}(\mathsf{w}^{\star })\). It is not known in general if the matrix \(K(\boldsymbol{\xi })\) may be written as \(\sum _{j\in \mathfrak{D}}K_{j}\xi _{j}\) although it is generally possible to obtain compensating matrices in this form in practical applications [45, 70, 108].
4.2 Strong Solutions
Local-in-time solutions may be obtained by using an existence theorem of Volpert and Hujaev [112] together with a normal form [46]. Such an existence result has been presented for chemically reacting mixtures in vibrational desequilibrium [46] but also directly applies to the system of partial differential equations presented in the previous sections.
On the other hand, global solutions around equilibrium states may be obtained using the local strict dissipative properties for multicomponent flows [45]. The existence of equilibrium states is first a consequence of the structural properties of thermochemistry as discussed in previous sections [39].
Proposition 12.
For T⋆ > 0, \(\widetilde{\varrho }^{\star }> 0\), \(\boldsymbol{v}^{\star } \in \mathbb{R}^{d}\), there exists a unique chemical equilibrium point u⋆ associated with \(\mathsf{z}^{\star } =\big (\rho _{1}^{\star },\ldots,\rho _{n}^{\star },\boldsymbol{v}^{\star },T^{\star }\big)^{t}\) such that \(m_{l}\langle \varrho ^{\star },M^{-1}\mathfrak{a}_{l}\rangle =\widetilde{\rho }_{ l}^{\star }\).
The system of partial differential equations governing multicomponent reactive flows written in normal form is then strictly dissipative at w⋆ [45, 49].
Proposition 13.
Consider an equilibrium state w ⋆ as obtained in Proposition 12 . Then the linearized normal form at w ⋆ is strictly dissipative.
Proof.
Using for convenience the characterization (K 3 ), consider \(\boldsymbol{\xi }\in \varSigma ^{d-1}\) and assume that ϕ ≠ 0 is such that \(\overline{\mathsf{B}}(\mathsf{w}^{\star },\boldsymbol{\xi })\phi = \overline{\mathsf{L}}(\mathsf{w}^{\star })\phi = 0\). It is first established that ϕ = α(1, 0, …, 0)t for some α ≠ 0. From the expression of \(\overline{\mathsf{B}}\) in Theorem 5, letting \(\phi = (\phi _{1},\ldots,\phi _{n},\boldsymbol{\phi }_{\boldsymbol{v}},\phi _{T})^{t}\) it is obtained that

where the superscript⋆ is used to denote quantities evaluated at w⋆. This is a sum of nonnegative terms, and if it is zero, it is successively deduced that ϕ
T
= 0 and then that \(\boldsymbol{\phi }_{\boldsymbol{v}} = 0\) and finally that  . This shows that the auxiliary vector (0, ϕ2, …, ϕ
n
)t is in the nullspace
. This shows that the auxiliary vector (0, ϕ2, …, ϕ
n
)t is in the nullspace  given by
given by  (since \(N(D) = \mathbb{R}\mathsf{y}^{\star }\)) so that the auxiliary vector must vanish ϕ2 = … = ϕ
n
= 0. It has thus been established that ϕ is proportional to (1, 0, …, 0)t and such vectors are in the nullspace of \(\overline{\mathsf{L}}\) from (47). A direct calculation then yields
(since \(N(D) = \mathbb{R}\mathsf{y}^{\star }\)) so that the auxiliary vector must vanish ϕ2 = … = ϕ
n
= 0. It has thus been established that ϕ is proportional to (1, 0, …, 0)t and such vectors are in the nullspace of \(\overline{\mathsf{L}}\) from (47). A direct calculation then yields

and \(\gamma \overline{\mathsf{A}}_{0}(\mathsf{w}^{\star })\phi + \overline{\mathsf{A}}(\mathsf{w}^{\star },\boldsymbol{\xi })\phi\) never vanishes since \(\boldsymbol{\xi }\in \varSigma ^{d-1}\) and (K 3 ) holds. □
The local strict dissipativity properties
now imply global existence and asymptotic stability of equilibrium states [43, 45, 70]. The global existence proof mainly consists in a priori estimates for linearized equations, local existence, a priori estimates independent of time intervals using strict dissipativity, and repeated use of local existence [43, 45, 54, 70, 71, 108]. A key property of the source term [45, 49], which may be deduced from (S
5
)–(S
7
) [120], is notably that  for some constant δ > 0 and v in the neighborhood of v⋆. A global existence theorem for the equations governing multicomponent reactive flows in their natural normal form [45] is presented in the following, and | ⋅ |
l
denotes the norm of the Sobolev space
\(H^{l}(\mathbb{R}^{d})\).
for some constant δ > 0 and v in the neighborhood of v⋆. A global existence theorem for the equations governing multicomponent reactive flows in their natural normal form [45] is presented in the following, and | ⋅ |
l
denotes the norm of the Sobolev space
\(H^{l}(\mathbb{R}^{d})\).
Theorem 7.
Let \(d\geqslant 1\), \(l\geqslant [d/2] + 2\), consider the equations governing multicomponent reactive flows with the normal variable w = (wI, wII)t where
and let w⋆ be a chemical equilibrium state as in Proposition 12 . There exist constants \(\bar{b}\) and \(\bar{c}\) such that if the initial condition w0 satisfies \(\Vert \mathsf{w}_{0} -\mathsf{w}^{\star }\Vert _{l} <\bar{b}\), then the Cauchy problem with w(0, x) = w0(x) has a global solution with
This solution w is such that
and \(\sup _{\mathbb{R}^{d}}\vert \mathsf{w}(t) -\mathsf{w}^{\star }\vert\) goes to zero as t → ∞.
From Theorem 7 the equilibrium point w⋆ is asymptotically stable, and with stronger assumptions it is possible to obtain decay estimates [45, 70].
Theorem 8.
Let \(d\geqslant 1\), \(l\geqslant [d/2] + 3\) and assume that the initial condition w0 is such that \(\mathsf{w}_{0} -\mathsf{w}^{\star } \in H^{l}(\mathbb{R}^{d}) \cap L^{p}(\mathbb{R}^{d})\), where p = 1, if d = 1, and p ∈ [1, 2), if \(d\geqslant 2\). There exist constants \(\bar{b}\) and \(\bar{c}\) such that if \(\Vert \mathsf{w}_{0} -\mathsf{w}^{\star }\Vert _{l} +\Vert \mathsf{w}_{0} -\mathsf{w}^{\star }\Vert _{L_{}^{p}} <\bar{b}\) is small enough, the global solution satisfies the decay estimate
for t ∈ [0, ∞), where β is a positive constant and α = d × (1∕2p − 1∕4).
Such theorems for hyperbolic–parabolic systems may be used for various other fluid models. They have been notably used for ambipolar plasmas where Poisson equation is replaced by the zero current limit [43], partial equilibrium flows where some group of chemical reactions is assumed to be infinitely fast [47], as well as for Saint-Venant equations modeling thin viscous layers over fluid substrates [52].
4.3 Weak Solutions and Other Boundary Value Problems
Many results have been devoted to the existence of strong solutions for single-species compressible Navier-Stokes equations [1, 8, 21, 22, 70, 71, 88, 92]. Concerning the Cauchy problem, Nash [92] has proved a local existence result, and global existence around equilibrium states has been established by Matsumura and Nishida [88]. Estimates for strong solutions are generally obtained upon deriving the governing equations, multiplying by the solution derivatives, and integrating in space and time. The Cauchy problem is in particular similar to the case of periodic boundary conditions. Danchin [21, 22] has further established global existence of solutions in critical hybrid Besov spaces with minimum regularity for the isentropic as well as the full compressible model around constant equilibrium states using Littlewood-Paley decompositions . Alazard [1] has investigated the limit of small Mach number flows for inviscid as well as viscous compressible flows with large temperature variations. The Cauchy problem for general hyperbolic systems has been investigated by Dafermos [20], Benzoni and Serre [8], and Serre [105], and for composite hyperbolic–parabolic systems by Kawashima [70, 71] in his pioneering work. Strong solutions for boundary value problems have also been addressed by Matsumura and Nishida [89], Benzoni and Serre [8], and Kawashima, Nishibata, and Zhu [72].
On the other hand, the existence of global-in-time weak solutions with no restriction on initial data is among one of the most difficult problems concerning compressible fluids [8, 13, 30, 31, 83]. Estimates for weak solutions are usually derived from energy and zeroth-order entropy estimates as well as by using renormalized equations. The behavior of compressible fluid models at low/high densities and at low/high temperatures has been a key ingredient in recent advances concerning the existence of global weak solutions with large initial data [13, 14, 30, 83] as well as classical solutions [111]. This requires to adapt and modify both thermodynamics and transport coefficients for extreme values of temperature and density as, for instance, with the introduction of a cold pressure. Fundamental existence results have been obtained by Lions [83] in his pioneering work – both for the Cauchy problem and boundary value problems, as well as Feireisl [30], Bresch, and Desjardins [13, 14], Novotný and Straškraba [94], and Feireisl and Novotný [31] for boundary value problems. Among the difficulties are density oscillations and concentrations in temperature, and a major problem is the compactness properties of weak sequences of approximated solutions [13, 14, 30, 31, 83, 94].
These outstanding difficulties are of course inherited by compressible chemically reacting mixtures which naturally include the compressible Navier-Stokes-Fourier model as a subsystem. Both the Cauchy problem [123, 124] and boundary value problems with boundary conditions typically in the form (21), (22), and (23) have been investigated [17, 23, 32, 51, 64, 79, 91, 122, 125]. In a one-dimensional geometry, for reacting systems with one deficient component, weak solutions with discontinous large initial data have been investigated by Chen, Hoff, and Trivisa [17] and Zlotnik [125], and the multispecies situation with no diffusion has also been investigated by Hoff [64]. In the multidimensional situation, proofs established in the nonreacting single-species situation have been adapted to the reacting case with modified thermodynamics and transport coefficients. Global existence with large data has been obtained in three dimensions with arbitrary complex chemistry and a simplified diffusion model by Feireisl, Petzeltová, and Trivisa [32] using notably weighted oscillation defect measures. Steady solutions have been obtained by Zatorska [122] with pressure laws depending on the species variables. Kwon and Trivisa [79] have analyzed the limit of low Mach numbers in a similar framework. Radiating gases including a transport equation for radiative intensity have been analyzed by Ducomet, Feireisl, and Nečasová [23]. The case of nondiagonal diffusion with cross effects with a special form of the diffusion matrix has also been investigated by Zatorska [123, 124], Giovangigli, Pokorný, and Zatorska [51] and Mucha, Pokorný, and Zatorska [91]. On the other hand, the incompressible case with Stefan-Maxwell-type equations has been investigated by Marion and Temam [87] as well as Chen and Jüngel [19].
5 Relaxation Toward Chemical Equilibrium Fluids
Relaxation is a natural process habitually modeled by systems of partial differential equations with stiff damping terms. This dynamical process has been the object of numerous studies in various physical and mathematical contexts [18, 20, 74, 93, 106, 119]. Relaxation of chemically reacting mixtures toward chemical equilibrium fluids is investigated in this section. To this aim, the multicomponent reactive fluid equations are rewritten in the form [55]

where ε represents the ratio between chemical characteristic times and fluid characteristic times, and the singular limit ε → 0 is investigated. The limiting chemical equilibrium fluid model is of interest for various applications such as flows around space vehicles [4] or diverging nozzle rocket flows [118].
5.1 Chemical Equilibrium Fluids
In order to derive the chemical equilibrium fluid
equations, it is necessary to introduce the proper projectors associated with the slow manifold  . Let \(\mathsf{a}_{1},\ldots,\mathsf{a}_{\mathsf{n}_{\mathrm{e}}}\) denote a basis of the slow manifold
. Let \(\mathsf{a}_{1},\ldots,\mathsf{a}_{\mathsf{n}_{\mathrm{e}}}\) denote a basis of the slow manifold  and \(\mathsf{a}_{\mathsf{n}_{\mathrm{e}}+1},\ldots,\mathsf{a}_{\mathsf{n}}\) a basis of the fast manifold
and \(\mathsf{a}_{\mathsf{n}_{\mathrm{e}}+1},\ldots,\mathsf{a}_{\mathsf{n}}\) a basis of the fast manifold  . The slow manifold
. The slow manifold  is of dimension ne = na + d + 1 and is spanned by the vectors \(\mathsf{a}_{l} = (\,\widetilde{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), \(l \in \mathfrak{A}\), and \(\mathsf{a}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1. The vectors \(\widetilde{\mathfrak{a}}_{l} =\widetilde{ m}_{l}M^{-1}\mathfrak{a}_{l}\), \(l \in \mathfrak{A}\), are associated with atomic densities and f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). In addition, the fast manifold is spanned by \(\mathsf{a}_{\mathsf{n}_{\mathrm{e}}+k-n_{\mathrm{a}}} = (M\mathfrak{v}_{k},\boldsymbol{0},0)^{t}\) for \(k \in \mathfrak{S}\setminus \mathfrak{A} =\{\, n_{\mathrm{a}} + 1,\ldots,n\,\}\), where \(\mathfrak{v}_{k}\) is the formation reaction vector of the kth species. The linear operators \(\Pi _{\mathsf{e}}\) and \(\Pi _{\mathsf{r}}\) are defined in the canonical bases by
is of dimension ne = na + d + 1 and is spanned by the vectors \(\mathsf{a}_{l} = (\,\widetilde{\mathfrak{a}}_{l},\boldsymbol{0},0)^{t}\), \(l \in \mathfrak{A}\), and \(\mathsf{a}_{n_{\mathrm{a}}+l} = \mathsf{f}_{n+l}\), for 1 ≤ l ≤ d + 1. The vectors \(\widetilde{\mathfrak{a}}_{l} =\widetilde{ m}_{l}M^{-1}\mathfrak{a}_{l}\), \(l \in \mathfrak{A}\), are associated with atomic densities and f
i
, 1 ≤ i ≤ n, denote the basis vectors of \(\mathbb{R}^{\mathsf{n}}\). In addition, the fast manifold is spanned by \(\mathsf{a}_{\mathsf{n}_{\mathrm{e}}+k-n_{\mathrm{a}}} = (M\mathfrak{v}_{k},\boldsymbol{0},0)^{t}\) for \(k \in \mathfrak{S}\setminus \mathfrak{A} =\{\, n_{\mathrm{a}} + 1,\ldots,n\,\}\), where \(\mathfrak{v}_{k}\) is the formation reaction vector of the kth species. The linear operators \(\Pi _{\mathsf{e}}\) and \(\Pi _{\mathsf{r}}\) are defined in the canonical bases by
and the metric matrices \(\mathcal{J}_{\mathsf{e}}\) and \(\mathcal{J}_{\mathsf{r}}\) of order ne and n −ne, respectively, are defined by \(\mathcal{J}_{\mathsf{e}}^{-1} = \Pi _{\mathsf{e}}^{t}\Pi _{\mathsf{e}}\) and \(\mathcal{J}_{\mathsf{r}}^{-1} = \Pi _{\mathsf{r}}^{t}\Pi _{\mathsf{r}}\). Each vector \(\mathsf{x} \in \mathbb{R}^{\mathsf{n}}\) admits a unique decomposition  where
where  and
and  . Moreover, it is easily established that \(I_{\mathsf{n}} = \Pi _{\mathsf{e}}\mathcal{J}_{\mathsf{e}}\Pi _{\mathsf{e}}^{t} + \Pi _{\mathsf{r}}\mathcal{J}_{\mathsf{r}}\Pi _{\mathsf{r}}^{t}\) and \(\tilde{\pi } = \Pi _{\mathsf{r}}\mathcal{J}_{\mathsf{r}}\Pi _{\mathsf{r}}^{t}\) where \(\tilde{\pi }\) is the orthogonal projector onto
. Moreover, it is easily established that \(I_{\mathsf{n}} = \Pi _{\mathsf{e}}\mathcal{J}_{\mathsf{e}}\Pi _{\mathsf{e}}^{t} + \Pi _{\mathsf{r}}\mathcal{J}_{\mathsf{r}}\Pi _{\mathsf{r}}^{t}\) and \(\tilde{\pi } = \Pi _{\mathsf{r}}\mathcal{J}_{\mathsf{r}}\Pi _{\mathsf{r}}^{t}\) where \(\tilde{\pi }\) is the orthogonal projector onto  .
.
Since the slow manifold  is orthogonal to the stiff source term
is orthogonal to the stiff source term  , the slow conservative variable is naturally given by \(\mathsf{u}_{\mathsf{e}} = \Pi _{\mathsf{e}}^{t}\mathsf{u}\), and the limiting governing equations as ε → 0 are obtained by applying the projection operator \(\Pi _{\mathsf{e}}^{t}\) to the governing equations in conservative form and by superimposing the chemical equilibrium condition
, the slow conservative variable is naturally given by \(\mathsf{u}_{\mathsf{e}} = \Pi _{\mathsf{e}}^{t}\mathsf{u}\), and the limiting governing equations as ε → 0 are obtained by applying the projection operator \(\Pi _{\mathsf{e}}^{t}\) to the governing equations in conservative form and by superimposing the chemical equilibrium condition  . The conservative variable at equilibrium thus reads
. The conservative variable at equilibrium thus reads
where \(\widetilde{\rho }_{l}\), \(l \in \mathfrak{A}\), are the atomic mass densities and \(\mathcal{E}_{\mathrm{e}}\) the internal energy at chemical equilibrium discussed in Sect. 2.2.3. The natural variable at equilibrium \(\mathsf{z}_{\mathrm{e}} \in \mathbb{R}^{\mathsf{n}_{\mathrm{e}}}\) is defined by \(\mathsf{z}_{\mathrm{e}} =\big (\widetilde{\rho }_{1},\ldots,\,\widetilde{\rho }_{n_{\mathrm{a}}},\,\boldsymbol{v}_{\mathrm{e}},\,T_{\mathrm{e}}\big)^{t}\) and the map ze → ue is a Cϰ diffeomorphism from the open set \(\mathcal{O}_{\mathsf{z}_{\mathrm{e}}} = (0,\infty )^{n_{\mathrm{a}}}\times \mathbb{R}^{d}\times (0,\infty )\) onto an open set \(\mathcal{O}_{\mathsf{u}_{\mathrm{e}}}\) [39]. The open set \(\mathcal{O}_{\mathsf{u}_{\mathrm{e}}}\) can be fully characterized and shown to be convex under stronger assumptions involving the heats of formation at zero temperature [39]. From Proposition 12, for any \(\mathsf{u}_{\mathrm{e}} \in \mathcal{O}_{\mathsf{u}_{\mathrm{e}}}\) there exists a unique u = ueq such that the chemical equilibrium condition holds  and \((\Pi _{\mathsf{e}})^{t}\mathsf{u}_{\mathrm{eq}} = \mathsf{u}_{\mathrm{e}}\). The map ue → ueq is Cϰ and \(\mathsf{v}_{\mathrm{eq}} \in M^{-1}\mathcal{A}\) where veq is the entropic variable associated with ueq. Applying the projector \(\Pi _{\mathsf{e}}^{t}\) to (52) and using the equilibrium condition u = ueq(ue), it is obtained that
and \((\Pi _{\mathsf{e}})^{t}\mathsf{u}_{\mathrm{eq}} = \mathsf{u}_{\mathrm{e}}\). The map ue → ueq is Cϰ and \(\mathsf{v}_{\mathrm{eq}} \in M^{-1}\mathcal{A}\) where veq is the entropic variable associated with ueq. Applying the projector \(\Pi _{\mathsf{e}}^{t}\) to (52) and using the equilibrium condition u = ueq(ue), it is obtained that
where \(\mathsf{A}_{i}^{\mathrm{e}}(\mathsf{u}_{\mathrm{e}}) = \Pi _{\mathsf{e}}^{t}\mathsf{A}_{i}\big(\mathsf{u}_{\mathrm{eq}}(\mathsf{u}_{\mathrm{e}})\big)\,\partial _{\mathsf{u}_{\mathrm{e}}}\mathsf{u}_{\mathrm{eq}}\) and \(\mathsf{B}_{ij}^{\mathrm{e}}(\mathsf{u}_{\mathrm{e}}) = \Pi _{\mathsf{e}}^{t}\mathsf{B}_{ij}(\mathsf{u}_{\mathrm{eq}}(\mathsf{u}_{\mathrm{e}})\big)\,\partial _{\mathsf{u}_{\mathrm{e}}}\mathsf{u}_{\mathrm{eq}}\). These equations express the conservation of atomic mass densities, momentum, and total energy. They are also equivalent to a one term Chapman-Enskog expansion of the conservative variable u in the fast chemistry limit [53]. More accurate equations may be obtained by using a two-term Chapman-Enskog expansion [18, 53, 54, 84] but are not required here and lay out the scope of the present notes.
The entropic symmetrized form as well as a normal form for the system modeling fluids at thermodynamic equilibrium (53) is evaluated [39, 55].
Theorem 9.
Assume that (H 1 )–(H 3 ) hold. Then the function \(\sigma _{\mathrm{e}} = -\mathcal{S}_{\mathrm{e}}/R\) is a mathematical entropy for the system at thermodynamic equilibrium, and the corresponding entropic variable is
where γ l , \(l \in \mathfrak{A}\), are uniquely defined by \((g_{1\mathrm{e}},\ldots,\,g_{n\mathrm{e}})^{t} =\sum _{l\in \mathfrak{A}}\gamma _{l}\,\widetilde{\mathfrak{a}}_{l}\) and in addition \(\mathsf{v}_{\mathrm{eq}} = \Pi _{\mathrm{e}}\mathsf{v}_{\mathrm{e}}\) and \(\mathsf{v}_{\mathrm{e}} = \mathcal{J}_{\mathrm{e}}\Pi _{\mathrm{e}}^{t}\mathsf{v}_{\mathrm{eq}}\). The map ue → ve is a Cϰ−1 diffeomorphism from \(\mathcal{O}_{\mathsf{u}_{\mathrm{e}}}\) onto the open set \(\mathcal{O}_{\mathsf{v}_{\mathrm{e}}} =\{ \mathsf{v} \in \mathbb{R}^{\mathsf{n}_{\mathrm{e}}};\ \mathsf{v}_{n_{ \mathrm{a}}+d+1} <0\}\). The system written in terms of the entropic variable ve is of the symmetric form
where \(\widetilde{\mathsf{A}}_{0}^{\mathrm{e}} = \partial _{\mathsf{v}_{\mathrm{e}}}\mathsf{u}_{\mathrm{e}} = \Pi _{\mathsf{e}}^{t}\,\widetilde{\mathsf{A}}_{0}\Pi _{\mathsf{e}}\), \(\widetilde{\mathsf{A}}_{i}^{\mathrm{e}} = \mathsf{A}_{i}^{\mathrm{e}}\partial _{\mathsf{v}_{\mathrm{e}}}\mathsf{u}_{\mathrm{e}} = \Pi _{\mathsf{e}}^{t}\,\widetilde{\mathsf{A}}_{i}\Pi _{\mathsf{e}}\), \(\widetilde{\mathsf{B}}_{ij}^{\mathrm{e}} = \mathsf{B}_{ij}^{\mathrm{e}}\partial _{\mathsf{v}_{\mathrm{e}}}\mathsf{u}_{\mathrm{e}} = \Pi _{\mathsf{e}}^{t}\,\widetilde{\mathsf{B}}_{ij}\Pi _{\mathsf{e}}\), have regularity ϰ − 1.
The nullspace invariance property
for the symmetrized system (55) modeling fluids at thermodynamic equilibrium has been established with  where
where  [39] and the normal variable
[39] and the normal variable
is used for convenience. The corresponding equations in normal form are investigated in the following theorem where the linear operator associated with the equilibrium manifold  with respect to the normal variable is denoted by \(\overline{\Pi }_{\mathsf{e}} = \left [\overline{\mathsf{a}}_{1},\ldots,\overline{\mathsf{a}}_{\mathsf{n}_{\mathrm{e}}}\right ]\) and \(\overline{\mathsf{a}}_{1},\ldots,\overline{\mathsf{a}}_{\mathsf{n}_{\mathrm{e}}}\) are defined in Theorem 5. The orthogonal projector onto
with respect to the normal variable is denoted by \(\overline{\Pi }_{\mathsf{e}} = \left [\overline{\mathsf{a}}_{1},\ldots,\overline{\mathsf{a}}_{\mathsf{n}_{\mathrm{e}}}\right ]\) and \(\overline{\mathsf{a}}_{1},\ldots,\overline{\mathsf{a}}_{\mathsf{n}_{\mathrm{e}}}\) are defined in Theorem 5. The orthogonal projector onto  is also denoted by π and the metric matrix associated with \(\overline{\Pi }_{\mathsf{e}}\) by \(\overline{\mathcal{J}}_{\mathrm{e}} = \overline{\Pi }_{\mathsf{e}}^{t}\overline{\Pi }_{\mathsf{e}}\).
is also denoted by π and the metric matrix associated with \(\overline{\Pi }_{\mathsf{e}}\) by \(\overline{\mathcal{J}}_{\mathrm{e}} = \overline{\Pi }_{\mathsf{e}}^{t}\overline{\Pi }_{\mathsf{e}}\).
Theorem 10.
Assume that (H 1 )–(H 3 ) hold. Then the map ve → we is a Cϰ−1 diffeomorphism from \(\mathcal{O}_{\mathsf{v}_{\mathrm{e}}}\) onto the open set \(\mathcal{O}_{\mathsf{w}_{\mathrm{e}}}\) given by \(\mathcal{O}_{\mathsf{w}_{\mathrm{e}}} = (0,\infty )\times \mathbb{R}^{n_{\mathrm{a}}-1+d}\times (-\infty,0)\). The system written in the we variable is of the normal form
where \(\overline{\mathsf{A}}_{0}^{\mathrm{e}} = (\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}})^{t}\,\widetilde{\mathsf{A}}_{0}^{\mathrm{e}}\,\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}}\), \(\overline{\mathsf{A}}_{i}^{\mathrm{e}}(\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}})^{t}\,\widetilde{\mathsf{A}}_{i}^{\mathrm{e}}\,\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}}\), \(\overline{\mathsf{B}}_{ij}^{\mathrm{e}} = (\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}})^{t}\,\widetilde{\mathsf{B}}_{ij}^{\mathrm{e}}\,\partial _{\mathsf{w}_{\mathrm{e}}}\ \mathsf{v}_{\mathrm{e}}\), have regularity ϰ − 1. The system coefficients are finally given by \(\overline{\mathsf{A}}_{0}^{\mathrm{e}} = \overline{\Pi }_{\mathsf{e}}^{t}\overline{\mathsf{A}}_{0}\overline{\Pi }_{\mathsf{e}}\), \(\overline{\mathsf{A}}_{i}^{\mathrm{e}} = \overline{\Pi }_{\mathsf{e}}^{t}\overline{\mathsf{A}}_{i}\overline{\Pi }_{\mathsf{e}}\), \(i \in \mathfrak{D}\), and \(\overline{\mathsf{B}}_{ij}^{\mathrm{e}} = \overline{\Pi }_{\mathsf{e}}^{t}\overline{\mathsf{B}}_{ij}\overline{\Pi }_{\mathsf{e}}\), \(i,j \in \mathfrak{D}\).
5.2 Convergence Toward Equilibrium
A global existence result independent of chemical characteristic times for the out of equilibrium model with the source term in quasilinear form is first presented and next a convergence result toward the limiting chemical equilibrium fluid model [55].
Theorem 11.
Let d ≥ 1 and l ≥ [d∕2] + 2 be integers. There exists \(\bar{b}> 0\) and \(\bar{c}\) such that if w0 satisfies \(\vert \mathsf{w}_{0} -\mathsf{w}^{\star }\vert _{l}^{2} + \frac{1} {\epsilon } \vert \pi \mathsf{w}_{0}\vert _{l-1}^{2} <\bar{b}^{2}\); there exists a unique global solution to the Cauchy problem
with initial condition \(\mathsf{w}(0,\boldsymbol{x}) = \mathsf{w}^{0}(\boldsymbol{x})\) and
and w satisfies the estimate
and \(\sup _{\boldsymbol{x}\in \mathbb{R}^{d}}\vert \mathsf{w}(t,\boldsymbol{x}) -\mathsf{w}^{\star }\vert\) goes to zero as t → ∞.
The estimates in the stiff case (58) notably differ from that of the nonstiff case (51) by the inclusion of new terms associated with the fast variables \(\pi \mathsf{w}/\sqrt{\epsilon }\) and πw∕ε as well as the coupling with the estimates for ∂ t w. On the other hand, at chemical equilibrium, there are not anymore sources in (57), and in order to obtain a global existence result, Kawashima’s theory may directly be used [39, 70]. Using estimates of the out of equilibrium solution and stability at chemical equilibrium [54] valid on any finite time interval \([0,\bar{\tau }]\), convergence of the out of equilibrium solution toward the chemical equilibrium solution is then established [55].
Theorem 12.
Let d ≥ 1, l ≥ l0 + 3, l0 = [d∕2] + 1, be integers and let \(\bar{b}\) from Theorem 11 . For any \(\mathsf{w}_{0} \in \overline{\mathcal{O}}_{0}\) with \(\vert \mathsf{w}_{0} -\mathsf{w}^{\star }\vert _{l}^{2} + \frac{1} {\epsilon } \vert \pi \mathsf{w}_{0}\vert _{l-1}^{2} <\bar{b}^{2}\) there exists a unique solution to the out of equilibrium system such that the estimates (58) hold. For \(\bar{b}\) small enough, there exists also a unique global solution of the equilibrium system starting from the equilibrium projection \(\overline{\mathcal{J}}_{\mathrm{e}}\overline{\Pi }_{\mathrm{e}}^{t}\mathsf{w}_{0}\). Then for any time \(\bar{\tau }\), there exists a constant c depending on \(\bar{\tau }\) such that
and the out of equilibrium solution converges toward the chemical equilibrium solution as 𝜖 → 0.
6 Models with Elementary Hydrodynamics
This section is concerned with chemically reacting mixtures whose hydrodynamics remains elementary. Traveling waves, where hydrodynamics is reduced to a single scalar, namely, the wave mass flow rate, are first discussed [9,10,11, 38, 61, 62, 101, 114, 115]. The case of reaction–diffusion systems, where the velocity \(\boldsymbol{v}\) identically vanishes, is next addressed. The situation where solutions of the complete reactive fluid system coincide with that of a reaction–diffusion subsystem is investigated, and typical results obtained in the literature concerning classical reaction–diffusion models are also discussed [2, 3, 12, 34, 63, 65, 69, 96, 97, 109, 113].
6.1 Traveling Waves
Traveling waves in inert or reactive flows can be classified into deflagration waves and detonation waves [118]. The structure of reactive exothermic detonation waves lay out the scope of these notes and the reader is referred to [118], whereas weak deflagration waves typically correspond to plane flames. The existence of solutions for plane flame models with complex chemistry has been investigated [38, 62, 115]. An existence theorem for deflagration waves with an arbitrary number of reversible chemical reactions and the complete transport model derived from the kinetic theory [38] is discussed in this section.
For other existence theorems associated with combustion models, the reader is referred to [9,10,11, 61, 62, 101, 114, 115] and the references therein. The mathematical structure and properties of chemically reacting mixtures and the existence of traveling wave solutions have been investigated by Volpert and Hudjaev [114]. Singular limits in combustion with a single exothermic reaction have been analyzed by Berestycki, Nicolaenko, and Scheurer [9]. Complex networks of exothermic reactions with no cycles have been studied by Heinze [62]. Multidimensional flame fronts have been investigated in cylindrical geometries by Berestycki, Larrouturou, and Lions [10] as well as conical geometries by Hamel, Monneau, and Roquejoffre [61]. Stability of travelling wave solutions of the multidimensional thermodiffusive model for flame propagation with unit Lewis number has been established by Berestycki, Larrouturou, and Roquejoffre [11]. A remarkable survey of traveling wave solutions of parabolic systems has been given by Volpert, Volpert, and Volpert [115].
6.1.1 Plane Flame Equations
The equations governing plane flames can be derived from the equations presented in Sect. 2 upon using the low Mach number limit, stationarity, and the one-dimensional geometry. The conservation of species mass and energy is found in the form
where c denotes the mass flow rate,′ the spatial derivation with respect to the flame normal coordinate x, \(\boldsymbol{\mathcal{J}\ }_{k} = (\mathcal{J}_{k},0,0)^{t}\) the mass flux of the kth species, \(h = \mathcal{H}/\rho\) the enthalpy per unit mass, and \(\boldsymbol{Q} = (Q,0,0)^{t}\) the heat flux. The unknowns are the mass flow rate c – which is a nonlinear eigenvalue – the mass fractions y = (y1, …, y n )t, and the enthalpy h, or equivalently the temperature T. Denoting by \(\boldsymbol{v} = (v,0,0)^{t}\) the velocity vector, the product ρv is the mass flow rate ρv = c that is constant in space from the total mass conservation equation (ρv)′ = 0. The pressure has been decomposed in the form \(p = p_{\mathrm{u}} +\widetilde{ p}\) where pu – the ambient pressure – is a constant and \(\widetilde{p}\) – the pressure corrector – is of the order \(\widetilde{p}/p_{\mathrm{u}} = \mathcal{O}(\mathrm{Ma}^{2})\) where Ma is the Mach number [39]. The state law is then in the form pu = ρRT∕m, and the momentum equation \(\widetilde{p}^{\,{\prime}} = -cv^{{\prime}} +\big ((\tfrac{4} {3}\eta +\kappa )v^{{\prime}}\big)^{{\prime}}\) uncouples and may only be needed in order to evaluate the pressure corrector \(\widetilde{p}\) [38, 39, 118].
The mass fractions are more convenient to use with (59) than the species partial densities. The enthalpy h is written as \(h =\sum _{k\in \mathfrak{S}}\mathsf{y}_{k}h_{k}(T)\) where \(h_{k}(T) = h_{k}^{\mathrm{st}} +\int _{ T^{\mathrm{st}}}^{T}\ \ c_{pk}(t)\,\,dt\) and c pk = c vk + R∕m k , and the specific entropy \(s = \mathcal{S}/\rho\) is rewritten in a similar way [38]. In the small Mach number limit, the transport fluxes \(\mathcal{J}_{k}\), \(k \in \mathfrak{S}\), and Q are in the form \(\mathcal{J}_{k} = -\sum _{l\in \mathfrak{S}}C_{kl}(\mathsf{x}_{l}^{{\prime}} + \mathsf{x}_{l}\widetilde{\chi }_{l}T^{{\prime}}/T)\), \(k \in \mathfrak{S}\) and \(Q =\sum _{k\in \mathfrak{S}}(h_{k} + RT\widetilde{\chi }_{k}/m_{k})\mathcal{J}_{k} -\lambda T^{{\prime}}\). All the species second derivatives are thus coupled through the flux matrix C and are coupled with the temperature second derivative through the thermal diffusion coefficients \(\widetilde{\chi }\).
A typical difficulty associated with traveling waves in infinite reactive media (−∞, +∞) is that reactive source terms generally have a single equilibrium state in atom conservation manifolds. The hot boundary condition, say at + ∞, corresponds to hot combustion products and to a chemical equilibrium state, but then source terms cannot vanish at the cold boundary −∞, and this is traditionally termed the cold boundary difficulty. For steady waves, the most satisfying model is that of anchored waves that represents an idealized adiabatic flame holder located at the origin [38]. The corresponding domain is the half line [0, ∞) and the boundary condition at x = 0 are in the form
where (Tf, yf) is a state out of equilibrium and Ti a temperature such that Tf < Ti. The boundary conditions in the hot gases are
where (Te, ye) is an equilibrium state whose existence and uniqueness can be deduced from the structure of thermochemistry under natural assumptions on (Tf, yf), and it is also assumed that Ti < Te [38]. One may also replace the boundary conditions at the origin by T(−∞) = Tf and y(−∞) = yf with T(0) = Ti. In this situation, it is necessary to replace the source term ω by Hω where H is the Heaviside function. One may establish that this formulation over (−∞, ∞) with the source term Hω is equivalent to that of the anchored flame over [0, ∞). Smooth solutions (y, T, c) of the anchored flame model such that T > 0, \(\mathsf{y}\geqslant 0\), y ≠ 0, and c > 0 are investigated.
A key tool in the analysis is then to use the entropy s, thanks to the properties of the source terms and of the transport coefficients [38]. Denoting by s the specific entropy and \(\psi = (Q -\sum _{k\in \mathfrak{S}}g_{k}\mathcal{J}_{k})/T\) the entropy flux, then
In order to estimate accurately entropy production, it is assumed that the diffusion coefficients are obtained from Stefan-Maxwell-type equations in such a way that Proposition 8 holds and it is also assumed that there is a common temperature scale φ to all transport coefficients as presented in Sect. 2.3.1 [38, 39].
6.1.2 Existence of Solutions
In order to establish the existence of solutions , the anchored flame problem is first considered on a bounded domain [0, a] with the boundary conditions at a written as T(a) = Te and y(a) = ye. The problem is solved by using a fixed point formulation and the Leray-Schauder topological degree . The main difficulty is to establish a priori estimates in order to show that the degree is well defined and to evaluate this degree with suitable homotopy paths. An important issue is to establish that the species remain positive in order to be able to use the entropy estimates (8). This entropic estimate allows to control the integrals of \(\varphi \sum _{k\in \mathfrak{S}}\mathsf{y}_{k}^{{\prime}2}/\mathsf{y}_{k}\) and φ(T′∕T)2 which yields a L∞ estimate on temperature [38]. A priori estimates for the eigenvalue c require similar techniques, and it is next possible to estimate the derivatives of T and y at any order and to establish an existence theorem over [0, a] using the homotopy invariance of the degree [38].
In order to let a → ∞, it is important to derive estimates of the eigenvalue c independent of a. A fundamental tool is the exponential decrease of entropy dissipation rate residuals \(\int _{x}^{a}\mathfrak{v}\,dx\) when (y, T) remains close to the equilibrium state (Te, ye) [38]. This exponential decrease is obtained by using (61) with a stability inequality due to Boillat and Pousin which states that for some δ > 0
Such stability inequalities are established locally around equilibrium states and then globally when chemical reaction mechanisms do not have spurious “boundary equilibrium points” in the atom conservation manifolds associated with (Te, ye) [38]. These exponential decrease rates next allow to prove the asymptotic behavior of the solution at infinity. Finally, passing to the limit a → ∞ and using a priori estimates independent of a, one may establish the following result [38, 39].
Theorem 13.
There exists a Cϰ+2 solution to the anchored flame problem over [0, ∞).
6.2 Reaction–Diffusion Models as Fluid Systems
Chemically reacting fluid models which admit solutions with zero convective velocity \(\boldsymbol{v} =\boldsymbol{ 0}\) are investigated in this section. To this aim, it is first assumed that the species have the same molar mass m1 = … = m n and mole and mass fractions then coincide x = y. It is further assumed that initially the density and temperature are constants \(\rho _{0} = \overline{\rho }\) and \(T_{0} = \overline{T}\) and that the initial velocity is zero \(\boldsymbol{v}_{0} = \overline{\boldsymbol{v}} =\boldsymbol{ 0}\). Since the mixture is constituted by isomass species, it is obtained that the initial pressure p0 is also constant \(p_{0} = \overline{p}\) in such a way that the initial derivative of both density and velocity vanishes (∂ t ρ)0 = 0 and \((\partial _{t}\boldsymbol{v})_{0} =\boldsymbol{ 0}\). In order to obtain a similar property for temperature (∂ t T)0 = 0, it is found after a little algebra that it is sufficient to assume that the heat produced by the chemical reactions vanishes \(\sum _{k\in \mathfrak{S}}h_{k}m_{k}\omega _{k} = 0\) at \(T = \overline{T}\). Since \(\sum _{k\in \mathfrak{S}}h_{k}m_{k}\omega _{k} =\sum _{i\in \mathfrak{R}}(\varDelta H)_{i}\tau _{i}\) where \((\varDelta H)_{i} =\sum _{k\in \mathfrak{S}}h_{k}m_{k}\nu _{ki}\), it is sufficient to ensure that \(\sum _{k\in \mathfrak{S}}h_{k}(\overline{T})m_{k}\nu _{ki} = 0\), \(i \in \mathfrak{R}\), or after a little algebra, that the formation enthalpies of the species that are not atoms are in the form \(h_{k}(\overline{T}) =\sum _{l\in \mathfrak{A}}\mathfrak{a}_{kl}m_{l}h_{l}(\overline{T})/m_{k}\), \(k \in \mathfrak{S}\setminus \mathfrak{A}\). In this situation, considering the subsystem of partial differential equations with unknowns \((\rho,\boldsymbol{v},T)^{t}\), it is readily seen that the solution of the subsystem is the constant solution \((\rho,\boldsymbol{v},T)^{t} = (\overline{\rho },\boldsymbol{0},\overline{T})^{t}\) for all times.
As a consequence, the corresponding solutions of the full reactive fluid system are exact solutions of the reaction–diffusion subsystem
where C satisfies assumptions obtained from the kinetic theory of gases (H 3 ). In particular, previously established existence theorems for chemically reacting fluids also apply to reaction–diffusion systems with complex chemistry described by arbitrary sets of elementary reactions and diffusive models derived from the kinetic theory like, for instance, the Stefan-Maxwell equations [46].
6.3 Traditional Reaction–Diffusion Systems
Traditional reaction-diffusion systems have been the object of many studies in the literature and are briefly addressed in this section. The corresponding governing equations may be obtained starting from the species governing equations, assuming that the system is isothermal, using the dilution approximation, assuming that the diluent species is inert, discarding the diluent species, and typically assuming that the limiting diffusion coefficients are constants in such a way that
where \(\boldsymbol{\nabla }^{2}\) denotes the Laplace operator and \(\mathfrak{S}\prime\) the reduced set of species.
Many studies have been devoted to these systems in various functional settings. [2, 3, 12, 34, 63, 65, 69, 96, 97, 109, 113]. Mathematical modeling of reaction–diffusion systems is discussed in the monograph by Fife [34]. Global existence and uniform boundedness for a class of boundary value problems for binary reaction–diffusion systems has been investigated by Hollis, Martin, and Pierre [65]. A comprehensive mathematical analysis of the existence of strong solutions in an elegant mathematical framework for boundary value problems has been given by Amann [2, 3]. Invariant sets and boundary value problems are also investigated in the well-known monograph by Smoller [109]. Since there is no simple mass conservation result – keeping in mind that chemistry does conserve mass but not diffusion in such models – there may be explosions of some of the species as investigated by Pierre and Schmitt [97], and a priori estimates of the mole fractions are generally difficult to obtain. In this context, there is the traditional entropic estimates as well as the elegant dual estimates of Pierre presented in the remarkable survey [96]. On the other hand, the situation where multicomponent diffusion is modeled from the Stefan-Maxwell relations has been investigated. The local existence result of Giovangigli and Massot [46] for the Cauchy problem applies to reaction–diffusion systems as established in the previous section. Bothe [12] and Herberg et al. [63] have also established local existence theorems on bounded domains, and a remarkable global existence has been established by Jüngel and Stelzer [69]. A detailed survey on reaction–diffusion equations including monotone systems as well as multiscale analysis has also been given by Volpert [113].
7 Index of Notation
The main symbols used in this chapter are listed in this Index. Symbols which only occur in a few consecutive lines, however, are not included in this list since their definition is always very close to the place where they are used. The section title following the description of the meaning of a symbol indicates the first section where the symbol is introduced.
-
\(\mathfrak{a}_{kl}\) atom decomposition of chemical species, Complex Chemistry.
-
\(\mathfrak{a}_{l}\) atom vectors, Complex Chemistry.
-
\(\widetilde{\mathfrak{a}}_{l}\) specific atom vectors, Complex Chemistry.
-
a i basis vectors of
 or
or  , Theorem 3 and Chemical Equilibrium Fluids.
, Theorem 3 and Chemical Equilibrium Fluids. -
\(\overline{\mathsf{a}}_{i}\) basis vectors of
 or
or  , Theorem 5 and Chemical Equilibrium Fluids.
, Theorem 5 and Chemical Equilibrium Fluids. -
\(\boldsymbol{b}\) force per unit mass, Conservation Equations.
-
cvk species specific heat at constant volume, Thermodynamics.
-
cv mixture specific heat at constant volume, Thermodynamics.
-
d spatial dimension, Conservation Equations.
-
d′ dimension of the kinetic velocity space, Transport Fluxes and Coefficients.
-
\(\boldsymbol{d}_{k}\) species constrained diffusion driving forces, Transport Fluxes and Coefficients.
-
\(\boldsymbol{d}\) vector of constrained diffusion driving forces, Transport Fluxes and Coefficients.
-
\(\widehat{\boldsymbol{d}}_{k}\) species diffusion driving force, Transport Fluxes and Coefficients.
-
\(\widehat{\boldsymbol{d}}\) vector of diffusion driving forces, Transport Fluxes and Coefficients.
-
e k species specific internal energies, Thermodynamics.
-
e mixture specific internal energy, Thermodynamics.
-
e k standard basis vectors in \(\mathbb{R}^{n}\), Complex Chemistry.
-
\(\boldsymbol{e}_{i}\) standard basis vectors in \(\mathbb{R}^{d}\), Directional Fluxes.
-
f i standard basis vectors in \(\mathbb{R}^{\mathsf{n}}\), Natural Normal Form for Multicomponent Flows.
-
g k species specific Gibbs function, Thermodynamics.
-
g mixture specific Gibbs function, Thermodynamics.
-
h k species specific enthalpies, Thermodynamics.
-
h mixture specific enthalpy, Thermodynamics.
-
i imaginary unit, Hyperbolicity and Parabolicity.
-
m k species molar masses, Conservation Equations.
-
m mixture molar mass, Thermodynamics.
-
\(\mathfrak{m}\) vector of molar masses, Thermodynamics.
-
n number of species, Conservation Equations.
-
nr number of chemical reactions, Complex Chemistry.
-
na number of atoms, Complex Chemistry.
-
n number of unknown components, Vector Notation.
-
\(\boldsymbol{\mathfrak{n}}\) normal vector at the boundary, Boundary Conditions.
-
p k species partial pressures, Thermodynamics.
-
p pressure, Conservation Equations.
-
q i directional mathematical entropy fluxes, Entropic Variables.
-
\(\overline{\mathsf{r}}\) quadratic residual of a normal form, Normal Variables.
-
s k species specific entropies, Thermodynamics.
-
s mixture specific entropy, Thermodynamics.
-
t time variable, Conservation Equations.
-
u conservative variable, Vector notation and Entropic Variables.
-
v entropic variable, Entropic Variables.
-
\(\boldsymbol{v}\) mass average flow velocity, Conservation Equations.
-
v k species diffusion velocities, Transport Fluxes and Coefficients.
-
v vector of species diffusion velocities, Stefan-Maxwell-Type Equations.
-
w normal variable, Normal Variables.
-
\(\boldsymbol{x}\) spatial coordinates, Conservation Equations.
-
x k species mole fractions, Thermodynamics.
-
x vector of species mole fractions, Thermodynamics.
-
y k species mass fractions, Thermodynamics.
-
y vector of species mass fractions, Thermodynamics.
-
z natural variable, Vector Notation.
-
\(\mathfrak{A}\) indexing set for atoms, Complex Chemistry.
-
\(\mathcal{A}\) vector space spanned by the atom vectors, Complex Chemistry.
-
\(\widetilde{\mathsf{A}}_{0}\) derivative ∂ v u, Entropic Variables.
-
\(\overline{\mathsf{A}}_{0}\) matrix coefficient for a normal form, Normal Variables.
-
A i convective Jacobian ∂ u F i , Directional Fluxes.
-
\(\widetilde{\mathsf{A}}_{i}\) convective Jacobian ∂ v F i , Entropic Variables.
-
\(\overline{\mathsf{A}}_{i}\) convective matrices of a normal form, Normal Variables.
-
B ij dissipation matrices of the natural conservative form, Directional Fluxes.
-
\(\widetilde{\mathsf{B}}_{ij}\) dissipation matrices of the natural entropic form, Entropic Variables.
-
\(\overline{\mathsf{B}}_{ij}\) dissipation matrices of a normal form, Normal Variables.
-
C kl flux multicomponent diffusion coefficients, Transport Fluxes and Coefficients.
-
C flux diffusion matrix, Transport Fluxes and Coefficients.
-
D kl multicomponent diffusion coefficients, Transport Fluxes and Coefficients.
-
D multicomponent diffusion matrix, Transport Fluxes and Coefficients.
-
\(\mathcal{D}_{kl}^{\text{bin}}\) species pair binary diffusion coefficients, Stefan-Maxwell-Type Equations.
-
\(\mathfrak{D}\) indexing set of spatial directions, Vector Notation.
-
E derivative of x with respect to y, Thermodynamics.
-
\(\mathcal{E}\) mixture internal energy per unit volume, Conservation Equations.
-
 equilibrium manifold, Entropic Variables and Theorem 3.
equilibrium manifold, Entropic Variables and Theorem 3. -
 equilibrium manifold for w, Natural Normal Form for Multicomponent Flows.
equilibrium manifold for w, Natural Normal Form for Multicomponent Flows. -
F i directional convective fluxes, Vector Notation.
-
F diss i directional dissipative fluxes, Vector Notation.
-
\(\mathcal{G}\) mixture Gibbs function per unit volume, Thermodynamics.
-
\(\mathcal{H}\) mixture enthalpy per unit volume, Thermodynamics.
-
\(\boldsymbol{I}\) unit tensor in the physical space \(\mathbb{R}^{d}\), Conservation Equations.
-
I n unit tensor in n dimensions, Stefan-Maxwell-Type Equations.
-
\(\boldsymbol{\mathcal{J}\ }_{k}\) species diffusion fluxes, Conservation Equations.
-
\(\boldsymbol{\mathcal{J}\ }\) vector of diffusion fluxes, Stefan-Maxwell-Type Equations.
-
K j directional compensating matrices, Strict Dissipativity.
-
K compensating matrix, Strict Dissipativity.
-
\(\mathcal{K}_{i}^{\mathrm{s}}\) symmetric reaction rate constants, Complex Chemistry.
-
\(\widetilde{\mathsf{L}}\) quasilinear source with respect to v, Theorem 3.
-
\(\overline{\mathsf{L}}\) linearized source term with respect to w, Strict Dissipativity and Theorem 5.
-
M mass matrix, Thermodynamics.
-
\(\mathfrak{M}_{k}\) symbol of chemical species, Complex Chemistry.
-
\(\overline{M}_{ij}\) Third order tensors associated with \(\overline{\mathsf{r}}\), Normal Variables.
-
\(\mathcal{O}_{\mathsf{u}}\) open set associated with the variable u, Entropic Variables.
-
\(\mathcal{O}_{\mathsf{v}}\) open set associated with the variable v, Entropic Variables.
-
\(\mathcal{O}_{\mathsf{w}}\) open set associated with the normal variable w, Normal Variables.
-
\(\mathcal{O}_{\boldsymbol{x}}\) open set associated with the spatial variable \(\boldsymbol{x}\), Boundary Conditions.
-
\(\boldsymbol{Q}\) heat flux, Conservation Equations.
-
\(\mathcal{R}\) vector space spanned by the reaction vectors, Complex Chemistry.
-
R perfect gas constant, Thermodynamics.
-
\(\mathfrak{R}\) real part, Hyperbolicity and Parabolicity.
-
\(\mathcal{S}\) mixture entropy per unit volume, Thermodynamics.
-
\(\mathfrak{S}\) indexing set for chemical species, Conservation Equations.
-
T absolute temperature, Thermodynamics.
-
\(\mathcal{Y}\) diagonal matrix of mass fractions, Transport Fluxes and Coefficients.
-
γ l atomic Gibbs functions, Theorem 9.
-
Γ Flux Stefan-Maxwell matrix, Stefan-Maxwell-Type Equations.
-
δ k diagonal species diffusion coefficients, Simplified Diffusion Coefficients.
-
δ kl Kronecker symbol, Thermodynamics.
-
Δ kl Stefan-Maxwell matrix coefficients, Stefan-Maxwell-Type Equations.
-
Δ Stefan-Maxwell matrix, Stefan-Maxwell-Type Equations.
-
ε ratio of flow time to chemical time, Equation (52).
-
φ temperature scale of transport coefficients, Transport Fluxes and Coefficients.
-
η shear viscosity, Transport Fluxes and Coefficients.
-
κ volume viscosity, Transport Fluxes and Coefficients.
-
ϰ regularity class of thermodynamic functions, Thermodynamics.
-
λ thermal conductivity, Transport Fluxes and Coefficients.
-
Λ matrix of the quasilinear form for ω, Complex Chemistry.
-
μ k species reduced chemical potentials, Thermodynamics.
-
μ vector of reduced chemical potentials, Thermodynamics.
-
ν ki reaction stoichiometric coefficients, Complex Chemistry.
-
ν i reaction vectors, Complex Chemistry.
-
ω k species molar production rates, Conservation Equations.
-
ω vector of molar production rates, Complex Chemistry.
-
 source vector of the conservative quasilinear form, Directional Fluxes.
source vector of the conservative quasilinear form, Directional Fluxes. -
 source vector of the entropic form, Entropic Variables.
source vector of the entropic form, Entropic Variables. -
 source vector of the normal form, Normal Variables.
source vector of the normal form, Normal Variables. -
π orthogonal projector onto
 , Natural Normal Form for Multicomponent Flows.
, Natural Normal Form for Multicomponent Flows. -
\(\Pi _{\mathsf{e}}\) linear operator associated with
 , Chemical Equilibrium Fluids.
, Chemical Equilibrium Fluids. -
\(\Pi _{\mathsf{r}}\) linear operator associated with
 , Chemical Equilibrium Fluids.
, Chemical Equilibrium Fluids. -
\(\overline{\Pi }_{\mathsf{e}}\) linear operator associated with
 , Chemical Equilibrium Fluids.
, Chemical Equilibrium Fluids. -
\(\boldsymbol{\varPi }\) viscous tensor, Conservation Equations.
-
ρ k species partial densities, Conservation Equations.
-
ρ total mass density, Conservation Equations.
-
ϱ vector of species partial densities, Thermodynamics.
-
\(\widetilde{\rho }_{l}\) atom partial densities, Complex Chemistry.
-
\(\widetilde{\varrho }\) vector of atom partial densities, Thermodynamics.
-
σ mathematical entropy, Entropic Variables.
-
Σd−1 sphere in d dimensions, Entropic Variables.
-
τ i reactions rates of progress, Complex Chemistry.
-
\(\widetilde{\chi }_{k}\) rescaled thermal diffusion ratios, Transport Fluxes and Coefficients.
-
\(\boldsymbol{\xi }\) vector of \(\mathbb{R}^{d}\), Entropic Variables.
-
\(\boldsymbol{\zeta }\) vector of \(\mathbb{R}^{d}\), Natural Entropic Form for Multicomponent Flows.
-
 vector of \(\mathbb{R}^{n}\) with unit coefficients, Thermodynamics.
vector of \(\mathbb{R}^{n}\) with unit coefficients, Thermodynamics. -
\(\boldsymbol{\nabla }\) vector derivation operator in \(\mathbb{R}^{d}\), Conservation Equations.
-
e chemical equilibrium subscript, Chemical Equilibrium.
-
f forward superscript, Complex Chemistry.
-
b backward superscript, Complex Chemistry.
-
⋆ equilibrium symbol, Strict Dissipativity.
-
′ derivation with respect to the flame coordinate, Plane Flame Equations.
-
t transposition symbol, Conservation Equations.
8 Conclusion
Mathematical models derived from the kinetic theory describing chemically reacting mixtures and their mathematical structures and properties have been presented in these notes. The hyperbolic–parabolic structure, local-in-time solutions [46], global solutions around equilibrium states [39, 45, 49], as well as traveling wave solutions in the low Mach number limit [38] have been investigated. Weak solutions with large data for related reactive fluid models have also been addressed. In addition, the situation of traveling waves in reactive media as well as reaction–diffusion parabolic systems has been discussed.
Various extensions could also consider initial-boundary value problems with boundary conditions involving complex phenomena like inflow or outflow conditions, heat losses, radiation, surface reactions with detailed heterogeneous chemistry, species surface diffusion, as well as heat surface conduction [39, 42, 76, 95, 98]. Various numerical analysis theoretical results could also be extended to the case of chemically reacting mixtures like convergence results of Petrov-Galerkin “Streamline Diffusion” finite element techniques [66, 68].
On the other hand, models at thermodynamic nonequilibrium with two temperatures for a single gas have been investigated, and the apparition of a volume viscosity term has been justified mathematically [53, 54]. These models could be generalized in order to investigate the relaxation of a whole family of quantum states [15].
The notion of higher-order entropy may also be generalized to the situation of multicomponent flows [14, 28, 40, 41] as well as the singular limit of small Mach number flow [1, 31]. Multiphase flows with sprays governed by Boltzmann-type equations [7, 118], or derived multifluid sectional models for droplets [82], may also be investigated mathematically.
Last but not least, one of the formidable problem concerning multicomponent reactive fluids is the global existence of weak solutions with large data taking into account the full complexity of the models obtained from the kinetic of gases as well as high-pressure models with nonideal thermodynamics.
9 Cross-References
References
T. Alazard, Low mach number limit of the full Navier-Stokes equations. Arch. Ration. Mech. Anal. 180, 1–73 (2006)
H. Amann, Dynamic theory of quasilinear parabolic equations. III. Global existence. Math. Z. 202, 219–250 (1989)
H. Amann, Dynamic theory of quasilinear parabolic equations. II. Reaction-diffusion systems. Diff. Int. Equ. 3, 13–75 (1990)
J.D. Anderson Jr., Hypersonics and High Temperature Gas Dynamics (McGraw-Hill Book Company, New York, 1989)
K. Beauchard, E. Zuazua, Large time asymptotics for partially dissipative hyperbolic systems. Arch. Rat. Mech. Anal. 199, 177–227 (2011)
R.J. Bearman, J.G. Kirkwood, The statistical mechanics of transport processes. XI. Equations of transport in multicomponent systems. J. Chem. Phys. 28, 136–145 (1958)
R. Bendahklia, V. Giovangigli, D. Rosner, Soret effects in laminar counterflow spray diffusion flames. Comb. Theory Mod. 6, 1–17, (2002)
S. Benzoni, D. Serre, Multi-Dimensional Hyperbolic Partial Differential Equations. First Order Systems and Applications (Oxford Mathematical Monographs, Oxford, 2007)
H. Berestycki, B. Nikolaenko, B. Scheurer, Traveling wave solutions to combustion models and their singular limits. SIAM J. Math. Anal. 16, 1207–1242 (1985)
H. Berestycki, B. Larrouturou, P.-L. Lions, Multidimensional travelling wave solutions of a flame propagation model. Arch. Rat. Mech. Anal. 111, 33–49 (1990)
H. Berestycki, B. Larrouturou, J.M. Roquejoffre, Stability of travelling fronts in a model for flame propagation part I: linear analysis. Arch. Rat. Mech. Anal. 117, 97–117 (1992)
D. Bothe, On the Maxwell-Stefan approach to multicomponent diffusion. In: Progress in Nonlinear Differential Equations and Their Applications (Springer, Basel, 2011), pp. 81–93
D. Bresch, B. Desjardins, On the construction of approximate solutions for the 2D viscous shallow water model for compressible Navier-Stokes Models. J. Math. Pure Appl. 86, 362–368 (2006)
D. Bresch, B. Desjardins, On the existence of global weak solutions to the Navier-Stokes equations for viscous compressible and heat conducting fluids. J. Math. Pure Appl. 87, 57–90 (2007)
D. Bruno, E. Esposito, V. Giovangigli, Relaxation of quantum population and volume viscosities in He/H2 mixtures. AIP Conf. Proc. 1628, 1237–1244 (2014)
S. Chapman, T.G. Cowling, The Mathematical Theory of Non-Uniform Gases (Cambridge University Press, Cambridge, 1970)
G.Q. Chen, D. Hoff, K. Trivisa, Global solutions to a model for exothermically reacting, compressible flows with large discontinuous initial data. Arch. Rat. Mech. Anal. 166, 321–358 (2003)
G.Q. Chen, C.D. Levermore, T.P. Liu, Hyperbolic conservation laws with stiff relaxation terms and entropy. Commun. Pure Appl. Math. 47, 787–830 (1994)
X. Chen, A. Jüngel, Analysis of an incompressible Navier-Stokes-Maxwell-Stefan system. Commun. Math. Phys. 340, 471–497 (2015)
C.M. Dafermos, Hyperbolic Conservation Laws in Continuum Physics (Springer, Heidelberg, 2000)
R. Danchin, Global existence in critical spaces for flows of compressible Navier-Stokes equations. Invent. Math. 141, 579–614 (2000)
R. Danchin, Global existence in critical spaces for flows of compressible viscous and heat-conductive gases. Arch. Ration. Mech. Anal. 160, 1–39 (2001)
B. Ducomet, E. Feireisl, Š. Nečasová, On a model in radiation hydrodynamics. Ann. Inst. Henri Poincaré. 28, 797–812 (2011)
A. Ern, V. Giovangigli, Multicomponent Transport Algorithms. Lecture Notes in Physics Monographs, vol. M 24 (Springer, Berlin, 1994)
A. Ern, V. Giovangigli, Thermal diffusion effects in hydrogen/air and methane/air flames. Comb. Theor. Mod. 2, 349–372 (1998)
A. Ern, V. Giovangigli, The kinetic equilibrium regime. Physica-A 260, 49–72 (1998)
A. Ern, V. Giovangigli, M. Smooke, Numerical study of a three-dimensional chemical vapor deposition reactor with detailed chemistry. J. Comput. Phys. 126, 21–39 (1996)
L.C. Evans, A survey of entropy methods for partial differential equations. Bull. AMS 41, 409–438 (2004)
M. Feinberg, The existence and uniqueness of steady states for a class of chemical reaction networks. Arch. Rat. Mech. Anal. 132, 311–370 (1995)
E. Feireisl, Dynamics of Viscous Compressible Fluids (Oxford University press, Oxford, 2004)
E. Feireisl, A. Novotný, Singular Limits in Thermodynamics of Viscous Fluids (Birkhäuser, Basel, 2009)
E. Feireisl, H. Petzeltová, K. Trivisa, Multicomponent reactive flows: global-in-time existence for large data. Commun. Pure Appl. Anal. 7, 1017–1047 (2008)
J.H. Ferziger, H.G. Kaper, Mathematical Theory of Transport Processes in Gases (North Holland Pub. Co., Amsterdam, 1972)
P.C. Fife, Mathematical Aspects of Reacting and Diffusing Systems (Springer, Berlin, 1979)
K.O. Friedrichs, P.D. Lax, Systems of conservation laws with a convex extension. Proc. Nat. Acad. Sci. USA 68, 1686–1688 (1971)
V. Giovangigli, Mass conservation and singular multicomponent diffusion algorithms. IMPACT Comput. Sci. Eng. 2, 73–97 (1990)
V. Giovangigli, Convergent iterative methods for multicomponent diffusion. IMPACT Comput. Sci. Eng. 3, 244–276 (1991)
V. Giovangigli, Plane flames with multicomponent transport and complex chemistry. Math. Mod. Methods Appl. Sci. 9, 337–378 (1999)
V. Giovangigli, Multicomponent Flow Modeling (Birkhäuser, Boston, 1999)
V. Giovangigli, Higher order entropies. Arch. Rat. Mech. Anal. 187, 221–285 (2008)
V. Giovangigli, Higher order entropies for compressible fluid models. Math. Mod. Methods Appl. Sci. 19, 67–125 (2009)
V. Giovangigli, S. Candel, Extinction limits of catalyzed stagnation point flow flames. Comb. Sci. Tech. 48, 1–30 (1986)
V. Giovangigli, B. Graille, Asymptotic stability of equilibrium states for ambipolar plasmas. Math. Mod. Methods Appl. Sci. 14, 1361–1399 (2004)
V. Giovangigli, B. Graille, Kinetic theory of partially ionized reactive gas mixtures II. J. Phys. A 42, 025503 (2009)
V. Giovangigli, M. Massot, Asymptotic stability of equilibrium states for multicomponent reactive flows. Math. Mod. Methods Appl. Sci. 8, 251–297 (1998)
V. Giovangigli, M. Massot, The local Cauchy problem for multicomponent reactive flows in full vibrational nonequilibrium. Math. Methods Appl. Sci. 21, 1415–1439 (1998)
V. Giovangigli, M. Massot, Entropic structure of multicomponent reactive flows with partial equilibrium reduced chemistry. Math. Methods Appl. Sci. 27, 739–768 (2004)
V. Giovangigli, L. Matuszewski, Supercritical fluid thermodynamics from equations of state. Physica D 241, 649–670 (2012)
V. Giovangigli, L. Matuszewski, Mathematical modeling of supercritical multicomponent reactive fluids. Math. Mod. Methods App. Sci. 23, 2193–2251 (2013)
V. Giovangigli, L. Matuszewski, Structure of entropies in dissipative multicomponent fluids. Kin. Rel. Mod. 6, 373–406 (2013)
V. Giovangigli, M. Pokorný, E. Zatorska, On steady flow of reactive gaseous mixture. Analysis 35, 319–341 (2015)
V. Giovangigli, B. Tran, Mathematical analysis of a Saint-Venant model with variable temperature. Math. Mod. Methods Appl. Sci. 20, 1–47 (2010)
V. Giovangigli, W.A. Yong, Volume viscosity and fast internal energy relaxation: symmetrization and Chapman-Enskog expansion. Kin. Rel. Models 8, 79–116 (2015)
V. Giovangigli, W.A. Yong, Volume viscosity and fast internal energy relaxation: error estimates (submitted for publication)
V. Giovangigli, W.A. Yong, Global existence and relaxation for fast chemistry fluids (submitted for publication)
S. Godunov, An interesting class of quasilinear systems. Sov. Math. Dokl. 2, 947–949 (1961)
A.N. Gorban, G.S. Yablonsky, Extended detailed balance for systems with irreversible reactions. Chem. Eng. Sci. 66, 5388–5399 (2011)
A.N. Gorban, E.M. Mirkes, G.S. Yablonsky, Thermodynamics in the limit of irreversible reactions. Physica A 392, 1318–1335 (2013)
S.R. de Groot, P. Mazur, Non-Equilibrium Thermodynamics (Dover Publications Inc., New York, 1984)
E.A. Guggenheim, Thermodynamics (North Holland, Amsterdam, 1962)
F. Hamel, R. Monneau, J.M. Roquejoffre, Stability of travelling waves in a model for conical flames in two space dimensions. Ann. Scient. Éc. Norm. Sup. 37, 469–506 (2004)
S. Heinze, Travelling waves in combustion processes with complex Chemical networks. Trans. Am. Soc. 304, 405–416 (1987)
M. Herberg, M. Meyries, J. Prüss, M. Wilke, Reaction-diffusion systems of Maxwell-Stefan type with reversible mass-action kinetics. Nonlinear Anal. (2016, in press)
D. Hoff, Asymptotic behavior of solutions to a model for the flow of a reacting fluid. Archiv. Rat. Mech. Anal. 196, 951–979 (2010)
S.L. Hollis, R.H. Martin, M. Pierre, Global existence and boundedness in reaction-diffusion systems. SIAM J. Math. Anal. 18, 744–761 (1987)
T.J.R. Hughes, L.P. Franca, M. Mallet, A new finite element formulation for computational fluid dynamics: I. Symmetric forms of the compressible Euler and Navier-Stokes equations and the second law of thermodynamics. Comput. Methods Appl. Mech. Eng. 54, 223–234 (1986)
J.H. Irving, J.G. Kirkwood, The statistical mechanics of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 18, 817–829 (1950)
C. Johnson, A. Szepessy, P. Hansbo, On the convergence of shock-capturing streamline diffusion finite element methods for hyperbolic conservation laws. Math. Comput. 54, 107–129 (1990)
A. Jüngel, I.V. Stelzer, Existence analysis of Maxwell-Stefan systems for multicomponent mixtures. SIAM J. Math. Anal. 45, 2421–2440 (2013)
S. Kawashima, Systems of hyperbolic-parabolic composite type, with application to the equations of magnetohydrodynamics. Doctoral Thesis, Kyoto University, 1984
S. Kawashima, Large-time behavior of solutions to hyperbolic-parabolic systems of conservations laws and applications. Proc. R. Soc. Edinb. 106A, 169–1944 (1987)
S. Kawashima, S. Nishibata, P. Zhu, Asymptotic stability of the stationary solution to the compressible Navier-Stokes equations in the half-space. Commun. Math. Phys. 240, 483–500 (2003)
S. Kawashima, Y. Shizuta, On the normal form of the symmetric hyperbolic-parabolic systems associated with the conservation laws. Tôhoku Math. J. 40, 449–464 (1988)
S. Kawashima, W.-A. Yong, Dissipative structure and entropy for hyperbolic systems of conservation laws. Arch. Ration. Mech. Anal. 174, 345–364 (2004)
S. Kawashima, W.-A. Yong, Decay estimates for hyperbolic balance laws. J. Anal. Appl. 28, 1–33 (2009)
R.J. Kee, M.E. Coltrin, P. Glarborg, Chemically Reacting Flow (Wiley Interscience, Hoboken, 2003)
J. Keizer, Statistical Thermodynamics of Nonequilibrium Processes (Springer, New York, 1987)
F.J. Krambeck, The mathematical structure of chemical kinetics. Arch. Ration. Mech. Anal. 38, 317–347 (1970)
Y.S. Kwon, K. Trivisa, Stability and large-time behavior for multicomponent reactive flows. Nonlinearity 22, 2443–2471 (2009)
B. Laboudigue, V. Giovangigli, S. Candel, Numerical solution of a free-boundary problem in hypersonic flow theory: nonequilibrium viscous shock layers. J. Comput. Phys. 102, 297–309 (1992)
O.A. Ladyženskaja, V.A. Solonikov, N.N. Ural’ceva, Linear and Quasilinear Equations of Parabolic Type. Translations of Mathematical Monographs, vol. 23 (American Mathematical Society, Providence, 1968)
F. Laurent, M. Massot, Multi-fluid modeling of laminar poly-dispersed spray flames: origin, assumptions and comparison of the sectional and sampling methods. Comb. Theor. Mod. 5, 537–572 (2001)
P.L. Lions, Mathematical Topics in Fluid Mechanics, vol. 1/2 (Oxford University press, Oxford, 1996/1998)
T.-P. Liu, Hyperbolic conservation laws with relaxation. Commun. Math. Phys. 108, 153–175 (1987)
G. Ludwig, M. Heil, Boundary layer theory with dissociation and ionization. In: Advances in Applied Mechanics VI (Academic Press, New York, 1960), pp. 39–118
M.R. Marcelin, Sur la mécanique des phénomènes irréversibles. C. R. Acad. Sci. Paris 151, 1052–1055 (1910)
M. Marion, R. Temam, Global existence for fully nonlinear reaction-diffusion systems describing multicomponent reactive flows. J. Math. Pures App. 105, 102–138 (2015)
A. Matsumura, T. Nishida, The initial value problem for the equations of motion of a viscous and heat-conductive fluids. J. Math. Kyoto Univ. 200, 67–104 (1980)
A. Matsumura, T. Nishida, The initial boundary value problem for the equations of motion of a viscous and heat-conductive fluids. Commun. Math. Phys. 89, 445–464 (1983)
J. Meixner, Zur Thermodynamik der irreversiblen Prozesse in Gasen mit chemisch reagierenden, dissoziierenden und anregbaren Komponenten. Ann. Phys. 43, 244–270 (1943)
P.B. Mucha, M. Pokorný, E. Zatorska, Heat-conducting, compressible mixtures with multicomponent diffusion: construction of a weak solution. SIAM J. Math. Anal. 47, 3747–3797 (2015)
J. Nash, Le problème de Cauchy pour les equations d’un fluide général. Bull. Soc. Math. Fr. 90, 487–497 (1962)
R. Natalini, Convergence to equilibrium for the relaxation approximation of conservation laws. Commun. Pure Appl. Math. 49, 795–823 (1996)
A. Novotný, I. Straškraba, Introduction to the Mathematical Theory of Compressible Flows (Oxford University press, Oxford, 2004)
E. Oran, J.P. Boris, Numerical Simulation of Reactive Flows (Elsevier, New York, 1987)
M. Pierre, Global existence in reaction-diffusion systems with control of mass: a survey. Milan J. Math. 78, 417–455 (2010)
M. Pierre, D. Schmitt, Blow up in reaction-diffusion systems with dissipation of mass. SIAM J. Math. Anal. 28, 259–269 (1997)
T. Poinsot, D. Veynante, Theoretical and Numerical Combustion (Edwards, Philadelphia, 2005)
I. Prigogine, Etude thermodynamique des phénomènes irréversibles (Dunod, Paris, 1947)
K.F. Roenigk, K.F. Jensen, Low pressure CVD of silicon nitride. J. Electrochem. Soc. 134, 1777–1785 (1987)
J.M. Roquejoffre, Étude mathématique d’un modèle de flamme plane. C. R. Acad. Sci. Paris Série I 311, 593–596 (1990)
D.E. Rosner, Transport Processes in Chemically Reacting Flow Systems (Butterworths, Boston, 1986)
T. Ruggeri, Thermodynamics and symmetric hyperbolic systems. Rend. Sem. Mat. Univ. Torino. 46, 167–183 (1988)
J.H. Seinfeld, S.N. Pandis, Atmospheric Chemistry and Physics (Wiley, New York, 1998)
D. Serre, Systèmes de Lois de Conservation I and II (Diderot Editeur, Art et Science, Paris, 1996)
D. Serre, The structure of dissipative viscous system of conservation laws. Physica D 239, 1381–1386 (2010)
N.Z. Shapiro, L.S. Shapley, Mass action law and the Gibbs free energy function. SIAM J. Appl. Math. 13, 353–375 (1965)
Y. Shizuta, S. Kawashima, Systems of equations of hyperbolic-parabolic type with applications to the discrete Boltzmann equation. Hokkaido Math. J. 14, 249–275 (1985)
J. Smoller, Shock Waves and Reaction Diffusion Equations (Springer, New York, 1994)
H. Van Beijeren, M.H. Ernst, The modified Enskog equations for mixtures. Physica A 70, 225–242 (1973)
A. Veigant, A. Kazhikov, On the existence of global solution to a two-dimensional Navier-Stokes equations for a compressible viscous flow. Sib. Math. J. 36, 1108–1141 (1995)
A.I. Vol’Pert, S.I. Hudjaev, On the Cauchy problem for composite systems of Nonlinear differential equations. Math. USSR Sbornik. 16, 517–544 (1972)
V.A. Volpert, Elliptic Partial Differential Equations, Volume 2: Reaction-Diffusion Equations. Monographs in Mathematics, vol. 104 (Birkhäuser, Basel, 2014)
A.I. Vol’Pert, S.I. Hudjaev, Analysis in Classes of Discontinuous Functions and Equations of Mathematical Physics. Mechanics: Analysis, vol. 8 (Martinus Nijhoff Publishers, Dordrecht, 1985)
A.I. Volpert, V.A. Volpert, V.A. Volpert, Travelling Wave Solutions of Parabolic Systems. Translations of Mathematical Monographs, vol. 140 (AMS, Providence, 1994)
L. Waldmann, Transporterscheinungen in gasen von mittlerem druck. Handbuch der Physik 12, 295–514 (1958)
F.A. Williams, Elementary derivation of the multicomponent diffusion equation. Am. J. Phys. 26, 467–469 (1958)
F.A. Williams, Combustion Theory (The Benjamin/Cummings Pub. Co. Inc., Menlo park, 1985)
W.-A. Yong, Singular perturbations of first-order hyperbolic systems with stiff source terms. J. Differ. Equ. 155, 89–132 (1999)
W.-A. Yong, Entropy and global existence for hyperbolic balance laws. Arch. Ration. Mech. Anal. 172, 247–266 (2004)
W.-A. Yong, An interesting class of partial differential equations. J. Math. Phys. 49, 033503 (2008)
E. Zatorska, On the steady flow of a multicomponent, compressible, chemically reacting gas. Nonlinearity 24, 3267–3278 (2011)
E. Zatorska, On the flow of chemically reacting gaseous mixture. J. Differ. Equ. 253, 3471–3500 (2012)
E. Zatorska, Mixtures: sequential stability of variational entropy solutions. J. Math. Fluid Dyn. 17, 437–461 (2015)
A. Zltonik, Weak solutions of the equations of motion of a viscous compressible reacting binary mixture: uniqueness and Lipschitz-continuous dependence on data. Mat. Zametki 75, 307–311 (2004)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this entry
Cite this entry
Giovangigli, V. (2018). Solutions for Models of Chemically Reacting Compressible Mixtures. In: Giga, Y., Novotný, A. (eds) Handbook of Mathematical Analysis in Mechanics of Viscous Fluids. Springer, Cham. https://doi.org/10.1007/978-3-319-13344-7_73
Download citation
DOI: https://doi.org/10.1007/978-3-319-13344-7_73
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-13343-0
Online ISBN: 978-3-319-13344-7
eBook Packages: Mathematics and StatisticsReference Module Computer Science and Engineering





 , and
, and  such that
such that  for
for  if and only if
if and only if  and if and only if
and if and only if  .
. , then the matrix
, then the matrix  is symmetric and its nullspace is given by
is symmetric and its nullspace is given by  .
. holds for
holds for  such that
such that  for
for 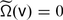 if and only if
if and only if  and if and only if
and if and only if  .
. , then
, then  is symmetric and
is symmetric and  .
. holds for
holds for 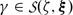 have a negative real part
have a negative real part  have their real part majorized by
have their real part majorized by  or
or  , Theorem
, Theorem  or
or  , Theorem
, Theorem  equilibrium manifold,
equilibrium manifold,  equilibrium manifold for
equilibrium manifold for  source vector of the conservative quasilinear form,
source vector of the conservative quasilinear form,  source vector of the entropic form,
source vector of the entropic form,  source vector of the normal form,
source vector of the normal form,  ,
,  ,
,  ,
,  ,
,  vector of
vector of