A Unified Approach to Piecewise Linear Hopf and Hopf-Pitchfork Bifurcations

Abstract

We propose for symmetric three-dimensional piecewise linear systems with three zones a unified approach to analyze both Hopf and Hopf-pitchfork bifurcations. For the equilibrium at the origin, the crossing of a complex eigenvalue pair through the imaginary axis of complex plane, with the possible simultaneous crossing of a real eigenvalue, is considered. Some results related to the bifurcation of limit cycles are provided, and an illustrative example is included.

1 Introduction

The class of piecewise linear differential (PWL) systems is very important within the realm of nonlinear dynamical systems. In fact, this kind of models is frequent in applications from electronic engineering and nonlinear control systems, where piecewise linear models cannot be considered as idealized ones, see [5] and references therein; they are used in mathematical biology as well, see [14, 15], where they constitute approximate models. On the other hand, since piecewise linear characteristics can be considered as the uniform limit of smooth nonlinearities, the global dynamics of smooth models has been sometimes approximated by piecewise linear models and viceversa, see [9, 16], obtaining a good qualitative agreement between the two modeling approaches. In practice, nonlinear characteristics use to have a saturated part, which is difficult to be approximated by polynomial functions but suitable to be modeled by linear pieces, leading to what we could call a “global linearization.”

The pioneering investigation of piecewise linear systems in a rigorous way was due to Andronov et al. [1]. Their book Theory of Oscillations remains nowadays an obligated reference, still being a source of ideas. More recently, the analysis of piecewise linear systems received growing attention due to the interest on PWL chaotic systems, see for instance [10] and references therein.

While bifurcation theory is rather well established for smooth vector fields, the nonsmooth case and the PWL case in particular are nowadays an area of active research, see [2, 5, 8, 13] among others. It is in this context, where we want to advance in the theory; more precisely, we consider three-dimensional symmetric continuous piecewise linear systems with three zones paying special attention to the bifurcation of limit cycles. Limit cycles are isolated periodic orbits that, after equilibrium points, correspond with the most important solutions of dynamical systems. Their determination is a difficult task, so that new results in this direction are of great relevance in real applications, see [7]. In the case of piecewise smooth systems, there are very few known results about, see again [5].

We study the analogous situation to Hopf bifurcation in smooth systems, allowing that such a bifurcation be simultaneous with a pitchfork bifurcation, and proposing a unified approach for both settings.

To be more specific, we consider the following family of PWL systems written in the Luré form:

$$\dot{\mathbf x}=\mathbf{F}(\mathbf{x})=A_R\mathbf{x}+\mathbf{b}\operatorname{sat}(x),$$

(1)

where $\mathbf{x}=(x,y,z)^{T}\in\mathbb{R}^{3},$ the saturation function is given by

$$\begin{aligned} \text{sat}(u)=\left\{\begin{array}{ll} 1 & \text{if} u> 1,\\ u & \text{if} |u| \leq 1,\\ -1 & \text{if} u < -1,\end{array} \right.\end{aligned}$$

the dot represents derivative with respect to the time τ. Under generic assumptions, see [4], there is no loss of generality in assuming that

$$\begin{aligned}A_R=\left(\begin{array}{lll} t & -1& 0\\ m & 0 & -1\\ d & 0 & 0\end{array}\right) \text{ and} \mathbf{b}=\left(\begin{array}{l} T - t\\ M - m\\ D - d\end{array}\right),\end{aligned}$$

(2)

where the coefficients t, m, d and T, M, D are the linear invariants (trace, sum of principal minors and determinant) of the matrices A _R and A _C , respectively. Note that in the region with $\left\vert x\right\vert \leqslant1$, it becomes the homogeneous system:

$$\begin{aligned}\dot{\mathbf x}(\tau)= A_C\mathbf{x}(\tau) = \left(\begin{array}{lll} T & -1 & 0\\ M & 0 & -1\\ D & 0 & 0\end{array}\right) \mathbf{x}(\tau).\end{aligned}$$

(3)

We observe that $A_C=A_R+\mathbf{b}\mathbf{e}_{1}^{\rm T}$, where $\mathbf{e}_{1}=(1,0,0)^{\rm T}$, and that the considered family of systems is in the generalized Liénard form. Thus, under generic conditions for every system of the form (1) after some change of variables, we can get the matrices in the form given in (2) and (3).

2 Statements of Main Results

In this work, we consider a more general structure of eigenvalues than the one appeared in [6] and [12], which includes both the piecewise linear analogue of Hopf bifurcation and the one of Hopf-pitchfork bifurcation, also called Hopf-zero bifurcation. Let us take ϵ as the main bifurcation parameter and assume the following expressions for the eigenvalues of the linear part at the origin A _C ,

$$\lambda(\varepsilon), \, \sigma(\varepsilon) \pm{\rm i} \omega(\varepsilon),$$

where,

$$\begin{aligned} \lambda(\varepsilon)& = \lambda_0 + \lambda_1\varepsilon + O(\varepsilon^2),\\ \sigma(\varepsilon) &= \sigma_1\varepsilon + O(\varepsilon^2),\\ \omega(\varepsilon) &= \omega_0 + \omega_1\varepsilon + O(\varepsilon^2),\end{aligned}$$

with $\omega_0> 0$. Here we will assume that both $\sigma_1$ and $\lambda_1$ do not vanish; these vanishing cases, much more involved, are left for future work. Clearly, when ϵ passes from negative values to positive ones, a pair of complex eigenvalues crosses the imaginary axis, which is the usual requirement for a Hopf bifurcation.

With this choice of the eigenvalues, the trace, principal minor of order two and determinant must have the following form:

$$\begin{aligned}T(\varepsilon) &= \lambda(\varepsilon) + 2\sigma(\varepsilon),\nonumber\\ M(\varepsilon) &= \sigma^2(\varepsilon) + \omega^2(\varepsilon) + 2\lambda(\varepsilon)\sigma(\varepsilon),\end{aligned}$$

(4)

$$\begin{aligned} D(\varepsilon) &= \lambda(\varepsilon)(\sigma^2(\varepsilon) + \omega^2(\varepsilon)),\nonumber\end{aligned}$$

where

$$\begin{aligned} T_0 &= T(0) = \lambda_0,\\ M_0 &= M(0) = \omega_0^2,\\ D_0 &= D(0) = \lambda_0 \omega_0^2,\end{aligned}$$

so that $D_0 - M_0 T_0 = 0$.

When $\lambda_0 \neq 0$, by moving the parameter ϵ through zero, we reproduce the piecewise linear Hopf or focus-center-limit cycle bifurcation analyzed in [6], by considering M and D constant; thus, we require here less restricted assumptions. Furthermore, when $\lambda_0 = 0$, as it is assumed $\lambda_1 \neq 0$, by moving ϵ we have the simultaneous crossing of a zero eigenvalue and a complex pair, a situation analogous to the Hopf-zero bifurcation in smooth systems. Thus, our analysis unifies the study done in [12], with the one in [6] allowing also to consider new degenerate cases, not yet analyzed.

In particular, the current formulation allows to pave the way for analysing the situations $\lambda_0 = \lambda_1 = 0$, or the case $\omega_0=0$, where we should get a more degenerate case for the focus-center-limit cycle bifurcation or a triple-zero case, respectively; the analysis of such degenerate cases is lacking and far from being solved.

To start with, we emphasize in the next result an invariant property of systems (1)–(2), whose proof is direct and will be omitted.

Proposition 1

Systems ( 1 )–( 2 ) are invariant under the following transformation:

$$ (x,y,z,\tau,t,m,d,\varepsilon) \longrightarrow (x,-y,z,-\tau,-t,m,-d,-\varepsilon).$$

This symmetry property is useful for simplifying the analysis of the family under consideration.

Fig. 1

Structure of periodic orbits in the central zone for $\lambda_0 \neq 0$ and $\varepsilon=0$; the periodic orbits determine a center configuration located at the focal plane $\lambda_0^2 x - \lambda_0 y + z = 0$

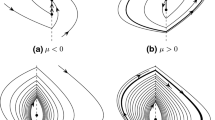
First, we consider the bifurcation for $\varepsilon = 0$ under the hypothesis $\lambda_0 \neq 0$, $\omega_0> 0$, and $\sigma_1 \neq 0$. Under these conditions, it is very easy to show that in the focal plane $\lambda_0^2 x - \lambda_0 y + z = 0$ there exists a center configuration when $\varepsilon = 0$, see Fig. 1. From the periodic orbit of this center that is tangent to the planes $x = \pm 1$, we can assure the bifurcation of one limit cycle as follows.

Theorem 1

Let us consider systems ( 1 )–( 2 ) under condition ( 4 ) where it is assumed $\omega_0> 0$ , $\lambda_0 \neq 0$ , $\sigma_1 \neq 0$ . Thus, we have $MT - D = 0$ for $\varepsilon = 0$ with $M_0> 0$ . Assuming

$$\delta = d -t \omega_0^2 +\lambda_0 (\omega_0^2 - m) \neq 0,$$

for $\varepsilon = 0$ , the system undergoes a focus-center-limit cycle bifurcation, that is, from the linear center configuration in the central zone, which exists for $\varepsilon = 0$ , one limit cycle appears for $\delta\sigma_1\varepsilon> 0$ and $|\varepsilon|$ sufficiently small.

The period P and the amplitude A (measured as the maximum of $\left\vert x\right\vert$ ) of the periodic orbit are analytic functions at 0, in the variable $\varepsilon^{1/3}$ , namely

$$\begin{aligned} P = & \dfrac{2\pi}{\omega_0} + \dfrac{2\pi}{\omega_0^3\delta}\left[\lambda_0\sigma_1(t\omega_0^2 - d) + \omega_0^2\sigma_1(\omega_0^2 - m) - \omega_0\omega_1\delta\right] \varepsilon + O(\varepsilon^{4/3}),\\ A = & 1 + \dfrac{1}{2} \left(\dfrac{3\pi}{2} \dfrac{\sigma_1(\lambda_0^2 + \omega_0^2)}{\delta}\right)^{2/3} \varepsilon^{2/3} + O(\varepsilon^{4/3}).\end{aligned}$$

In particular, if $\lambda_0 < 0$ and $\delta> 0$ , then the limit cycle bifurcates for $\sigma_1\varepsilon> 0$ and is orbitally asymptotically stable.

For sake of brevity, the proof of Theorem 1, being rather similar to the one given in [6], will be omitted.

Fig. 2

Structure of periodic orbits in the central zone for $\lambda_0 = 0$ and $\varepsilon=0$. The two solid cones are completely foliated by periodic orbits surrounding the segment of equilibrium points $\{(x,0,x\omega_0^2)^{\rm T}: \left\vert x\right\vert\leqslant1\}$

The case $\lambda_0 = 0$ with $\lambda_1 \neq 0$ wouldlead to a richer structure of periodic orbits when $\varepsilon = 0$, see Fig. 2, and then the following assertions about possible equilibrium points of the family are relevant.

Proposition 2

For systems ( 1 )and( 2 ) under condition ( 4 ) with $\omega_0> 0$ , $\lambda_0 = 0,$ and $\lambda_1 \neq 0$ , the following statements hold:

(a):

If $d\lambda_1\varepsilon> 0$ , then the unique equilibrium point is the origin.

(b):

If $d\lambda_1\varepsilon < 0$ , then the equilibria are the origin and the two points

$$ \mathbf{x}_{\varepsilon}^+ = \dfrac{1}{d}\left(d- D(\varepsilon), \,d T(\varepsilon) - t D(\varepsilon), \,d M(\varepsilon) - m D(\varepsilon)\right)^{\rm T}, \mathbf{x}_{\varepsilon}^- = -\mathbf{x}_{\varepsilon}^+.$$

(c):

If $\varepsilon = 0$ , then all the points of the segment

$$\{(x,y,z)^{\rm T}\in \mathbb{R}^3: (x,y,z)^{\rm T} = \mu( 1,0,\omega_0^{2})^{\rm T}, \left\vert \mu \right\vert\leqslant 1\}$$

are equilibria for the system. If furthermore $d \neq 0$ , the above segment captures all the equilibrium points.

For a proof of Proposition 2, see the similar result in [12]. From the above statement (c) we see that at $\varepsilon = 0$ systems (1)–(2) have a degenerate pitchfork bifurcation. Note that for $d\lambda_1\varepsilon> 0$, the points $\mathbf{x}_\varepsilon^\pm$ are vanishing points for the vector field corresponding to $|x|> 1$ but they are out of their corresponding zones. They do not constitute real equilibria, although they still organize the dynamics of external regions. This type of equilibrium is usually called a virtual equilibrium point.

Our first result when $\lambda_0 = 0$ concerns the possible bifurcation of symmetrical periodic orbits using the three zones. We note that if $\lambda_0 = 0$, we now have $\delta = d - t\omega_0^2$, which characterizes the criticality of the bifurcation, in a similar way to what happens in the cases considered in [3] and [6].

Theorem 2

Let us consider systems ( 1 )–( 2 ) under condition ( 4 ) where it is assumed $\lambda_0 = 0$ , $\lambda_1 \neq 0$ , $\omega_0> 0$ , and $\delta = d - t\omega_0^2 \neq 0$ . For $\varepsilon = 0$ , the systems ( 1 )–( 2 ) undergo a trizonal limit cycle bifurcation, that is, from the configuration of periodic orbits that exists in the central zone for $\varepsilon = 0$ , one limit cycle appears for $\delta\sigma_1 \varepsilon> 0$ and $|\varepsilon|$ sufficiently small. It is symmetric with respect to the origin and bifurcates from the ellipse $\{(x,y,z)^{\rm T} \in \mathbb{R}^3: \omega_0^2 x^{2} + y^2 = \omega_0^2 \text z = 0\}$ . This limit cycle has period:

$$ P = \dfrac{2\pi}{\omega_0} + 2\pi\dfrac{\omega_0\sigma_1(\omega_0^2 - m) - \omega_1\delta}{\omega_0^2\delta} \varepsilon + O(\varepsilon^{4/3}),$$

and its amplitude in x measured as $\max\{x\} - \min\{x\}$ is

$$\begin{array}{l} A = 1 + \dfrac{1}{2} \left(\dfrac{3\pi}{2} \dfrac{\omega_0^2\sigma_1}{\delta}\right)^{2/3} \varepsilon^{2/3} + O(\varepsilon^{4/3}).\end{array}$$

Furthermore, the bifurcating limit cycle is stable if and only if $t < 0$ , $d < 0$ , and $\delta> 0$ .

By using Proposition 1, we could add a new assertion saying that the bifurcating limit cycle is completely unstable (the two characteristic exponents have positive real part) if and only if $t> 0$, $d> 0$, and $\delta < 0$.

Our last result, which also assumes $\lambda_0 = 0$, gives account of the bifurcation of a symmetrical pair of limit cycles that only use two linearity zones. This result requires extra assumptions, but when they are fulfilled allow us to assure the simultaneous bifurcation of three limit cycles.

Theorem 3

Let us consider system 1 – 2 under conditions ( 4 ) where it is assumed $\delta = d - t\omega_0^2 \neq 0$ , $\lambda_0 = 0$ , $\lambda_1 \neq 0$ , and $\omega_0> 0$ fixed. Thus, if we have $\sigma_1 \neq 0$ ,

$d\sigma_1 - \lambda_1\delta \neq 0$ , and

$$0 < \widehat{z} = \dfrac{d\sigma_1\omega_0^2}{d\sigma_1 - \lambda_1\delta} < \omega_0^2$$

and fixed, a bifurcation takes place for the critical value $\varepsilon = 0$ . Thereby, a symmetrical pair of limit cycles appears when $\delta\sigma_1\varepsilon> 0$ and $|\varepsilon|$ is sufficiently small. They are stable if and only if $t < 0$ and $\lambda_1\sigma_1 < 0$ , or t = 0 and $d\sigma_1 (\lambda_1 + 2\sigma_1) < 0$ . Their common period is

$$\begin{array}{l} P = \dfrac{2\pi}{\omega_0} + \dfrac{2\pi\left[\omega_0\sigma_1(\omega_0^2 - m) - \omega_1\delta\right]}{\omega_0^2\delta} \varepsilon + O(\varepsilon^{5/3}),\end{array}$$

and their common amplitude in x measured as $\max\{x\} - \min\{x\}$ is

$$\begin{array}{l} A = \dfrac{2\lambda_1\delta}{\lambda_1\delta - d\sigma_1} - \dfrac{2(3\pi)^{2/3}}{5} \left(\dfrac{\sigma_1}{\omega_0\delta}\right)^{2/3} \dfrac{d\lambda_1\sigma_1\omega_0^2[2t(\omega_0^2 - m) - 3\delta]}{(\lambda_1\delta - d\sigma_1)^2} \varepsilon^{2/3} + O(\varepsilon).\end{array}$$

For a proof of both Theorems 2 and 3, one can follow the procedure given in [12]. The results included here are similar to the ones in such a quoted paper, but we emphasize that here the number of auxiliary fixed parameters describing the eigenvalue configuration has been increased from two (ρ and ω) to five ($\lambda_0$, $\lambda_1$, $\sigma_1$, $\omega_0$, and $\omega_1$), allowing a unified approach that encompasses both referred bifurcations, including cases not analyzed in [6] nor in [12] and paving the way for future analysis of more degenerate situations.

3 An Illustrative Example: An Electronic Oscillator

In this section, as an illustrative example of the usefulness of above results, we consider an extended Bonhoeffer–van der Pol (BVP) electronic oscillator, which consists of two capacitors, an inductor, a linear resistor, and a nonlinear conductance, as shown in Fig. 3.

Fig. 3

The extended Bonhoeffer–van der Pol (BVP) oscillator proposed in [11]

To obtain more information about this circuit, see [11], where a smooth nonlinearity is assumed for the conductance and a rich variety of dynamical behaviors is found. The circuit equations can be written as:

$$C\dfrac{\text{d}v_1}{\text{d}t} = -i - g(v_1), C\dfrac{\text{d}v_2}{\text{d}t} = i - \dfrac{v_2}{r}, L\dfrac{\text{d}i}{\text{d}t} = v_1 - v_2,$$

where $v_{1}$ and $v_{2}$ are the voltages across the capacitors, the symbol i stands for the current through the inductance L , and the v-i characteristics of the nonlinear resistor is written as $g(v) = -av-b \operatorname{sat}(cv)$, where $a, b, c>0$. Note that, here we adopt a PWL version of the nonlinearity considered in [11].

After some standard manipulations, the normalized equations of the extended BVP oscillator become

$$\begin{aligned} \left\{\begin{array}{lll} \dot{x} = & -z + \alpha x + \operatorname{sat}(\beta x),\\ \dot{y} = & z - \gamma y,\\ \dot{z} = & x - y,\end{array}\right.\end{aligned}$$

where the dot represents derivative with respect to the new time τ, and

$$\begin{aligned} \tau &= \dfrac{1}{\sqrt{LC}}t, \alpha = a\sqrt{\dfrac{L}{C}}, \beta = bc\sqrt{\dfrac{L}{C}}, \gamma = \dfrac{1}{r}\sqrt{\dfrac{L}{C}},\\ \\ x &= \dfrac{v_1}{b}\sqrt{\dfrac{C}{L}}, y = \dfrac{v_2}{b}\sqrt{\dfrac{C}{L}}, z = \dfrac{i}{b}.\end{aligned}$$

Making now the change of variables $X = \beta x$, we obtain the system in its Luré form,

$$\begin{aligned}\dot{\mathbf{x}} = \left(\begin{array}{lll} \alpha & 0 & -\beta\\ 0 & -\gamma & 1\\ 1/\beta & -1 & 0\end{array}\right) \mathbf{x} + \left(\begin{array}{c} \beta\\ 0\\ 0\end{array}\right) \text{sat}(\mathbf{e}_1^{\rm T} \mathbf{x}),\end{aligned}$$

(5)

and we will rename X as x in the sequel, for convenience. Then, it can be written in the form 1–2, and so we will try to apply Theorems 1, 2, and 3 under the corresponding assumptions. Effectively, with a linear change of variables given by the matrix:

$$\begin{aligned} P = \dfrac{1}{\beta} \left(\begin{array}{lll} \beta & 0 & 0\\ \gamma^2 - 1 & \gamma & 1\\ \gamma & 1 & 0\end{array}\right),\end{aligned}$$

we can write system (5) in its Liénard form as

$$\begin{aligned}\dot{\mathbf{x}} = \left(\begin{array}{lll} \alpha-\gamma & -1 & 0\\ 2-\alpha\gamma & 0 & -1\\ \alpha-\gamma & 0 & 0\end{array}\right) \mathbf{x} + \left(\begin{array}{l} \beta\\ -\beta\gamma\\ \beta\end{array}\right) \text{sat}(x),\end{aligned}$$

(6)

where now the trace, the sum of second-order principal minors, and the determinant in the different zones are evident, namely

$$\begin{aligned}\begin{array}{llll} T = & \alpha + \beta - \gamma, & t = & \alpha - \gamma,\\ M = & 2 - \gamma (\alpha + \beta), \ & m = & 2 - \alpha\gamma,\\ D = & \alpha + \beta - \gamma, & d = & \alpha - \gamma.\end{array}\end{aligned}$$

(7)

From (7), we observe that T and D are identically equal, what implies that an extra condition for eigenvalues must be fulfilled. Thus, taking into account the structure of T and D given in (4), we must impose for all values of ϵ,

$$T(\varepsilon)-D(\varepsilon)=\lambda_0 (1 - \omega_0^2) + (\lambda_1 - \lambda_1\omega_0^2 + 2\sigma_1 - 2\lambda_0\omega_1)\varepsilon +O(\varepsilon^2)= 0.$$

We will take γ as the only bifurcation parameter, keeping α and β fixed. In looking for the bifurcations analyzed in Sect. 2 to take place at $\varepsilon = 0$, we need first $\lambda_0(1 - \omega_0^2) = 0$. If we assume $\lambda_0\ne0$, then we must conclude the two conditions

$$\omega_0=1 \text{ and} \sigma_1=\lambda_0\omega_1.$$

Consequently $M(0)=\omega_0^2=1$, and we get for the bifurcation parameter $\gamma(\varepsilon)$ the condition $\gamma(0)=\gamma_0$, with

$$0<\gamma_0=\dfrac{1}{\alpha+\beta}\ne 1,\text{ so that} \lambda_0=\dfrac{1-\gamma_0^2}{\gamma_0}.$$

To apply Theorem 1, we compute for $\varepsilon = 0$,

$$m=2-\dfrac{\alpha}{\alpha+\beta},\text{ and so} \delta=\lambda_0(1-m)\ne0.$$

From (7), writing $\gamma=\gamma_0+\varepsilon$, we also obtain

$$\lambda_1=-\gamma_0^4\dfrac{1+\gamma_0^2}{1+\gamma_0^6}, \sigma_1= \dfrac{\gamma_0^4-1}{2(1+\gamma_0^6)},\text{ and} \omega_1=-\dfrac{\gamma_0(1+\gamma_0^2)}{2(1+\gamma_0^6)}.$$

Thus, the following result is a direct consequence of Theorem 1.

Proposition 3

Let us consider system ( 5 ) or equivalently system ( 6 ) with $\alpha> 0$ , $\beta> 0$ , and $\gamma_0=1/(\alpha+\beta)$ fixed. For $\gamma = \gamma_0$ , the system undergoes a focus-center-limit cycle bifurcation, that is, from the linear center configuration in the central zone, which exists for $\gamma = \gamma_0$ , one limit cycle appears for $\gamma-\gamma_0> 0$ and sufficiently small. In particular, if $\alpha+\beta<1$ , then $\gamma_0> 1$ and the bifurcating limit cycle is asymptotically stable.

On the other hand, if we assume $0<\omega_0 \ne 1$, then to get the consistency between (4) and (7), we need $\lambda_0 = 0$, and therefore,

$$\sigma_1=\dfrac{\lambda_1}{2}(\omega_0^2-1),$$

getting for the bifurcation parameter $\gamma(\varepsilon)$ the condition $\gamma(0)=\gamma_0$, with

$$0<\gamma_0=\alpha+\beta<\sqrt{2},$$

with the additional requirement that $\alpha+\beta\ne 1$; otherwise, $\omega_0=1$ and $\sigma_1=0$, precluding the use of both Theorems 2 and 3. Note that $\omega_0^2=2-\gamma_0^2$ and so when $\gamma_0<1$ we have $\omega_0>1$ and vice versa.

Using 7, we obtain for $\varepsilon = 0$ that $t = d = -\beta$ and $\delta = \beta(\omega_0^2 - 1) \neq 0$. Writing $\gamma=\gamma_0+\varepsilon$, we also obtain

$$\lambda_1=-\dfrac{1}{\omega_0^2}, \sigma_1= \dfrac{1-\omega_0^2}{2\omega_0^2}, \text{ and} \omega_1=-\dfrac{\gamma_0}{2\omega_0}.$$

We note that in Theorem 3,

$$\widehat{z} = \dfrac{d\sigma_1\omega_0^2}{d\sigma_1 - \lambda_1\delta} = \dfrac{\omega_0^2}{3} \in \left(0,\omega_0^2\right).$$

Thus, from Theorems 2 and 3, we get the following result.

Fig. 4

Partial bifurcation set of system (5), showing the two main bifurcation surfaces corresponding to the piecewise linear Hopf and Hopf-pitchfork bifurcations, namely the surface $\gamma=1/(\alpha+\beta)$ and the plane $\gamma = \alpha + \beta$. It is also shown the red straight-line $\gamma = \alpha + \beta = \sqrt{2}$, where $T = M = D = 0$

Proposition 4

Considering system ( 5 ) or equivalently system ( 6 ) with $\alpha> 0$ , $\beta> 0$ and $1 \neq \gamma_0=\alpha + \beta < \sqrt{2}$ and fixed, the following statements hold:

(a):

For $\gamma>\gamma_0$ , the origin is the only equilibrium of the system. Furthermore, if $\gamma\gamma_0 <1$ , then the origin is asymptotically stable.

(b):

For $\gamma = \gamma_0$ , the system undergoes a PWL analogue of the Hopf-zero bifurcation; from the periodic set existing at such critical situation, for $\gamma - \gamma_0 < 0$ and sufficiently small in absolute value, the bifurcation leads to the simultaneous appearance of three limit cycles (one trizonal and two bizonal ones) along with two additional equilibrium points.

Furthermore, if $\gamma_0 < 1$ $(1 < \gamma_0 < \sqrt{2})$ , then the bifurcating trizonal limit cycle is stable (unstable) while the bifurcating bizonal limit cycles are unstable (stable). The bifurcating equilibrium points are stable whenever $\gamma_0 < 1$ and, in the case $1 < \gamma_0 < \sqrt{2}$ , when $\gamma_0 < 1/\alpha$ .

In Fig. 4, we show the two main bifurcation surfaces corresponding to the piecewise linear Hopf and Hopf-pitchfork bifurcations, namely the surface $\gamma=1/(\alpha+\beta)$ and the plane $\gamma=\alpha+\beta$. It is also shown as the straight-line $\gamma=\alpha+\beta=\sqrt{2}$, where $T=M=D=0$ and so, a triple-zero bifurcation is involved. The analysis of such a bifurcation is left for future work.