Linear Rank-Width of Distance-Hereditary Graphs

Abstract

We present a characterization of the linear rank-width of distance-hereditary graphs. Using the characterization, we show that the linear rank-width of every $n$-vertex distance-hereditary graph can be computed in time $\mathcal {O}(n^2\cdot \log (n))$, and a linear layout witnessing the linear rank-width can be computed with the same time complexity. For our characterization, we combine modifications of canonical split decompositions with an idea of [Megiddo, Hakimi, Garey, Johnson, Papadimitriou: The complexity of searching a graph. JACM 1988], used for computing the path-width of trees. We also provide a set of distance-hereditary graphs which contains the set of distance-hereditary vertex-minor obstructions for linear rank-width. The set given in [Jeong, Kwon, Oum: Excluded vertex-minors for graphs of linear rank-width at most k. STACS 2013: 221–232] is a subset of our obstruction set.

Isolde Adler: Supported by the German Research Council, Project GalA, AD 411/1-1.

Mamadou Moustapha Kanté: Supported by the French Agency for Research under the DORSO project.

O-joung Kwon: Supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2011-0011653).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Rank-width [18] is a graph parameter introduced by Oum and Seymour with the goal of efficient approximation of the clique-width [5] of a graph. Linear rank-width can be seen as the linearized variant of rank-width, similar to path-width, which in turn can be seen as the linearized variant of tree-width. While path-width is a well-studied notion, much less is known about linear rank-width. Computing linear rank-width is NP-complete in general (this follows from [10]). Therefore it is natural to ask which graph classes allow for an efficient computation. Until now, the only (non-trivial) known such result is for forests [2]. A graph $G$ is distance-hereditary, if for any two vertices $u$ and $v$ of $G$, the distance between $u$ and $v$ in any connected, induced subgraph of $G$ that contains both $u$ and $v$, is the same as the distance between $u$ and $v$ in $G$. Distance-hereditary graphs are exactly the graphs of rank-width $\le 1$ [17]. They include co-graphs (i.e. graphs of clique-width $2$), complete (bipartite) graphs and forests.

We show that the linear rank-width of $n$-vertex distance-hereditary graphs can be computed in time $\mathcal {O}(n^2\cdot \log (n))$ (Theorem 5). Moreover, we show that a layout of the graph witnessing the linear rank-width can be computed with the same time complexity (Corollary 2). Given that computing the path-width of distance-hereditary graphs is NP-complete [15], this is indeed surprising. We give a new characterization of linear rank-width of distance-hereditary graphs (Theorem 4), which we use for our algorithm. We also provide, for each $k$, a set $\varPsi _k$ of distance-hereditary graphs such that any distance-hereditary graph of linear rank-width at least $k+1$ contains a vertex-minor isomorphic to a graph in $\varPsi _k$. The set $\varPsi _k$ generalizes the set of obstructions given in [14] and we conjecture a subset of it to be the set of distance-hereditary vertex-minor obstructions for linear rank-width $k$.

Our characterization makes use of the special structure of canonical split decompositions [6] of distance-hereditary graphs. Roughly, these decompositions decompose the distance-hereditary graph in a tree-like fashion into cliques and stars, and our characterization is recursive along the subtrees of the decomposition. While a similar idea has been exploited in [2, 9, 16], here we encounter a new problem: The decomposition may have vertices that are not present in the original graph. It is not at all obvious how to deal with these vertices in the recursive step. We handle this by introducing limbs of canonical split decompositions, that correspond to certain vertex-minors of the original graphs, and have the desired properties to allow our characterization. We think that the notion of limbs may be useful in other contexts, too, and hopefully, it can be extended to other graph classes and allow for further new efficient algorithms.

The paper is structured as follows. Section 2 introduces the basic notions, in particular linear rank-width, vertex-minors and split decompositions. In Sect. 3, we define limbs and show some important properties. We use them in Sect. 4 for our characterization of linear rank-width of distance-hereditary graphs. Finally, Sect. 5 presents the algorithm for computing the linear rank-width of distance-hereditary graphs and we discuss vertex-minor obstructions in Sect. 6.

2 Preliminaries

For a set $A$, we denote the power set of $A$ by $2^A$. We let $A{\setminus } B:= \{x\in A\mid x\notin B\}$ denote the difference of two sets $A$ and $B$. For a subset $X$ of a ground set $A$, let $\overline{X} := A{\setminus } X$.

In this paper, graphs are finite, simple and undirected, unless stated otherwise. Our graph terminology is standard, see for instance [8]. Let $G$ be a graph. We denote the vertex set of $G$ by $V(G)$ and the edge set by $E(G)$. An edge between $x$ and $y$ is written $xy$ (equivalently $yx$). If $X$ is a subset of the vertex set of $G$, we denote the subgraph of $G$ induced by $X$ by $G[X]$, and we let $G{\setminus } X:=G[V(G){\setminus } X]$. For a vertex $x\in V(G)$ we let $N_G(x):=\{y\in V(G)\mid x\ne y,\; xy\in E(G)\}$ denote the set of neighbors of $x$ (in $G$). The degree of $x$ (in $G$) is $\deg _G(x):=|N_G(x)|$. A partition of $V(G)$ into two sets $X$ and $Y$ is called a cut in $G$. We denote it by $(X,Y)$.

A tree is a connected, acyclic graph. A leaf of a tree is a vertex of degree one. A path is a tree where every vertex has degree at most two. The length of a path is the number of its edges. A rooted tree is a tree with a distinguished vertex $r$, called the root. A complete graph is the graph with all possible edges. A graph $G$ is called distance-hereditary (or DH for short) if for every two vertices $x$ and $y$ of $G$ the distance of $x$ and $y$ in $G$ equals the distance of $x$ and $y$ in any connected induced subgraph containing both $x$ and $y$ [3]. A star is a tree with a distinguished vertex, called its center, adjacent to all other vertices.

2.1 Linear Rank-Width and Vertex-Minors

Linear rank-width. For sets $R$ and $C$ an $(R,C)$ -matrix is a matrix where the rows are indexed by elements in $R$ and columns indexed by elements in $C$. (Since we are only interested in the rank of matrices, it suffices to consider matrices up to permutations of rows and columns.) For an $(R,C)$-matrix $M$, if $X\subseteq R$ and $Y\subseteq C$, we let $M[X,Y]$ be the submatrix of $M$ where the rows and the columns are indexed by $X$ and $Y$ respectively.

Let $A_G$ be the adjacency $(V(G),V(G))$-matrix of $G$ over the binary field. For a graph $G$, let $x_1,\ldots ,x_n$ be a linear layout of $V(G)$. Every index $i\in \{1,\ldots ,n\}$ induces a cut $(X_i,\overline{X_i})$, where $X_i:=\{x_1,\ldots ,x_i\}$ (and hence $\overline{X_i}=\{x_{i+1},\ldots , x_n\}$). The cutrank of the ordering $x_1,\ldots ,x_n$ is defined as

$$ \mathrm{cutrk }_G(x_1,\ldots ,x_n):=\max \{\mathrm{rank }(A_G[X_i,\overline{X_i}])\mid i\in \{1,\ldots ,n\}\}. $$

The linear rank-width of $G$ is defined as

$$ \mathrm{lrw }(G):=\min \{\mathrm{cutrk }_G(x_1,\ldots ,x_n)\mid x_1,\ldots ,x_n\text { is a linear layout of }V(G)\}. $$

Disjoint unions of caterpillars have linear rank-width $\le 1$. Ganian [11] gives an alternative characterization of the graphs of linear rank-width $\le 1$ as thread graphs. It is proved in [2] that linear rank-width and path-width coincide on trees. It is easy to see that the linear rank-width of a graph is the maximum over the linear rank-widths of its connected components.

Vertex-minors. For a graph $G$ and a vertex $x$ of $G$, the local complementation at $x$ of $G$ consists in replacing the subgraph induced on the neighbors of $x$ by its complement. The resulting graph is denoted by $G*x$. If $H$ can be obtained from $G$ by a sequence of local complementations, then $G$ and $H$ are called locally equivalent. A graph $H$ is called a vertex-minor of a graph $G$ if $H$ is a graph obtained from $G$ by applying a sequence of local complementations and deletions of vertices.

For an edge $xy$ of $G$, let $W_1:=N_G(x)\cap N_G(y)$, $W_2=(N_G(x){\setminus } N_G(y)){\setminus }\{y\}$, and $W_3=(N_G(y){\setminus } N_G(x)){\setminus }\{x\}$. Pivoting on $xy$ of $G$, denoted by $G\wedge xy$, is the operation which consists in complementing the adjacencies between distinct sets $W_i$ and $W_j$, and swapping the vertices $x$ and $y$. It is known that $G\wedge xy=G*x*y*x=G*y*x*y$ [17].

Lemma 1

[17]. Let $G$ be a graph and let $x$ be a vertex of $G$. Then for every subset $X$ of $V(G)$, we have $\mathrm{cutrk }_G(X)=\mathrm{cutrk }_{G*x}(X)$. Therefore, every vertex-minor $H$ of $G$ satisfies $\mathrm{lrw }(H) \le \mathrm{lrw }(G)$.

2.2 Split Decompositions and Local Complementations

Split decompositions. We will follow the definitions in [4]. Let $G$ be a connected graph. A split in $G$ is a cut $(X,Y)$ in $G$ such that $|X|,|Y|\ge 2$ and $\mathrm{rank }(A_G[X,Y]) = 1$. In other words, $(X,Y)$ is a split in $G$ if $|X|,|Y| \ge 2$ and there exist non-empty sets $X'\subseteq X$ and $Y'\subseteq Y$ such that $\{xy\in E(G) \mid x\in X, y\in Y\} = \{xy \mid x\in X', y\in Y'\}$. Notice that not all connected graphs have a split, and those that do not have a split are called prime graphs.

A marked graph $D$ is a connected graph $D$ with a distinguished set of edges $M(D)$, called marked edges, that form a matching, and such that every edge in $M(D)$ is a bridge, i.e., its deletion increases the number of components. The ends of the marked edges are called marked vertices, and the components of $D{\setminus } M(D)$ are called bags of $D$. If $(X,Y)$ is a split in $G$, we construct a marked graph $D$ with vertex set $V(G) \cup \{x',y'\}$ for two distinct new vertices $x',y'\notin V(G)$ and edge set $E(G[X]) \cup E(G[Y]) \cup \{x'y'\} \cup E'$ where we define $x'y'$ as marked and

$$\begin{aligned} E'&:= \{x'x\mid x\in X\ \mathrm{{and~ there~exists}}\ y\in Y \mathrm{{~such~that~}\ xy\in E(G)}\} \cup \\&\quad \;\; \{y'y \mid y\in Y\ \mathrm{{and~there~exists}}\ x\in X \mathrm{{~such~that~}} xy\in E(G)\}. \end{aligned}$$

The marked graph $D$ is called a simple decomposition of $G$. A decomposition of a connected graph $G$ is a marked graph $D$ defined inductively to be either $G$ or a marked graph defined from a decomposition $D'$ of $G$ by replacing a component $H$ of $D'{\setminus } M(D')$ by a simple decomposition of $H$. We call the transformation of $D'$ into $D$ a refinement of $D'$. Notice that in a decomposition of a connected graph $G$, the two ends of a marked edge do not have a common neighbor. For a marked edge $xy$ in a decomposition $D$, the recomposition of $D$ along $xy$ is the decomposition $D':=(D\wedge xy) {\setminus } \{x,y\}$. For a decomposition $D$, we let $\widehat{D}$ denote the connected graph obtained from $D$ by recomposing all marked edges. Note that if $D$ is a decomposition of $G$, then $\widehat{D}=G$. Since marked edges of a decomposition $D$ are bridges and form a matching, if we contract all the unmarked edges in $D$, we obtain a tree called the decomposition tree of $G$ associated with $D$ and denoted by $T_D$. Obviously, the vertices of $T_D$ are in bijection with the bags of $D$, and we will also call them bags.

A decomposition $D$ of $G$ is called a canonical split decomposition if each bag of $D$ is either prime, or a star or a complete graph, and $D$ is not the refinement of a decomposition with the same property. Shortly, we call it a canonical decomposition. The following is due to Cunningham and Edmonds [6], and Dahlhaus [7].

Theorem 1

[6, 7]. Every connected graph $G$ has a unique canonical decomposition, up to isomorphism, that can be computed in time $\mathcal {O}(|V(G)| +|E(G)|)$.

For a given connected graph $G$, by Theorem 1, we can talk about only one canonical decomposition of $G$ because all canonical decompositions of $G$ are isomorphic.

Let $D$ be a decomposition of $G$ with bags that are either primes, or complete graphs or stars (it is not necessarily a canonical decomposition). The type of a bag of $D$ is either $P$, or $K$ or $S$ depending on whether it is a prime, or a complete graph or a star. The type of a marked edge $uv$ is $AB$ where $A$ and $B$ are the types of the bags containing $u$ and $v$ respectively. If $A=S$ or $B=S$, we can replace $S$ by $S_p$ or $S_c$ depending on whether the end of the marked edge is a leaf or the center of the star.

Theorem 2

[4]. Let $D$ be a decomposition of a graph with bags of types P or K or S. Then $D$ is a canonical decomposition if and only if it has no marked edge of type $KK$ or $S_pS_c$.

We will use the following characterization of distance-hereditary graphs.

Theorem 3

[4]. A connected graph is a distance-hereditary graph if and only if each bag of its canonical decomposition is of type K or S.

Local complementations in decompositions. We now relate the decompositions of a graph and the ones of its locally equivalent graphs. Let $D$ be a decomposition. A vertex $v$ of $D$ represents an unmarked vertex $x$ (or is a representative of $x$) if $v=x$ or there is a path from $v$ to $x$ in $D$ starting with a marked edge such that marked edges and unmarked edges appear alternately in the path. Two unmarked vertices $x$ and $y$ are linked in $D$ if there is a path from $x$ to $y$ in $D$ such that unmarked edges and marked edges appear alternately in the path.

Lemma 2

Let $D$ be a decomposition of a graph. Let $v'$ and $w'$ be two marked vertices in a same bag of $D$, and let $v$ and $w$ be two unmarked vertices of $D$ represented by $v'$ and $w'$, respectively. Then $v$ and $w$ are linked in $D$ if and only if $vw\in E(\widehat{D})$ if and only if $v'w' \in E(D)$.

A local complementation at an unmarked vertex $v$ in a decomposition $D$, denoted by $D*v$, is the operation which consists in replacing each bag $B$ containing a representative $w$ of $v$ with $B*w$. Observe that $D*v$ is a decomposition of $\widehat{D}*v$, and that $M(D) = M(D*v)$. Two decompositions $D$ and $D'$ are locally equivalent if $D$ can be obtained from $D'$ by applying a sequence of local complementations.

Lemma 3

[4]. Let $D$ be the canonical decomposition of a graph and let $v$ be an unmarked vertex of $D$. Then $D*v$ is the canonical decomposition of $\widehat{D}*v$.

Let $v$ and $w$ be linked unmarked vertices in a decomposition $D$, and let $B_v$ and $B_w$ be the bags containing $v$ and $w$, respectively. Note that if $B$ is a bag of type S in the path from $B_v$ to $B_w$ in $T_D$, then the center of $B$ is a representative of either $v$ or $w$. Pivoting on $vw$ of $D$, denoted by $D\wedge vw$, is the decomposition obtained as follows: for each bag $B$ on the path from $B_v$ to $B_w$ in $T_D$, if $v', w'\in V(B)$ represent $v$ and $w$ in $D$, respectively, then we replace $B$ with $B\wedge v'w'$. (Note that by Lemma 2, we have $v'w'\in E(B)$, hence $B\wedge v'w'$ is well-defined).

Lemma 4

Let $D$ be a decomposition of a distance-hereditary graph, and let $xy\in E(\widehat{D})$. Then $D\wedge xy=D*x*y*x$.

The proof of Lemma 4, as well as all omitted proofs, can be found in the appendix. As a corollary of Lemmas 3 and 4, we get the following.

Corollary 1

Let $D$ be the canonical decomposition of a distance-hereditary graph and $xy\in E(\widehat{D})$. Then $D\wedge xy$ is the canonical decomposition of $\widehat{D}\wedge xy$.

3 Limbs in Canonical Decompositions

In this section we define the notion of limb that is the key ingredient in our characterization. Intuitively, a limb in the canonical decomposition of a distance-hereditary graph $G$ is a subtree of the decomposition with the property that the linear rank-width of the graph obtained from the subtree by recomposing all marked edges is invariant under taking local complementations.

Let $D$ be the canonical decomposition of a distance-hereditary graph. We recall from Theorem 2 that each bag of $D$ is of type K or S, and marked edges of types KK or $S_pS_c$ do not occur. Given a bag $B$ of $D$, an unmarked vertex $y$ of $D$ represented by some marked vertex $w \in V(B)$, let $T$ be the component of $D{\setminus } V(B)$ containing $y$ and let $v\in V(T)$ be the neighbor of $w$ in $D$. We define the limb $\mathcal {L}:=\mathcal {L}[D,B,y]$ as follows:

• 1. if $B$ is of type $K$, then $\mathcal {L}:=T*v{\setminus } v$,

• 2. if $B$ is of type $S$ and $w$ is a leaf, then $\mathcal {L}:=T{\setminus } v$,

• 3. if $B$ is of type $S$ and $w$ is the center, then $\mathcal {L}:=T\wedge vy {\setminus } v$.

Note that in $T$, $v$ becomes an unmarked vertex, so a limb is well-defined. While $T$ is a canonical decomposition, $\mathcal {L}$ may not be a canonical decomposition at all, because deleting $v$ may create a bag of size $2$. Suppose a bag $B'$ of size $2$ appears in $\mathcal {L}$. If $B'$ has one neighbor bag $B_1$ and a marked vertex $v_1\in B_1$ is adjacent to a marked vertex of $B'$ and $r$ is the unmarked vertex of $B'$ in $\mathcal {L}$, then we can transform the limb into a canonical decomposition by removing the bag $B'$ and replacing $v_1$ with $r$. If $B'$ has two neighbor bags $B_1$ and $B_2$ and two marked vertices $v_1\in B_1$ and $v_2\in B_2$ are adjacent to the marked vertices of $B'$, then we can first transform the limb into a decomposition by removing $B'$ and adding a marked edge $v_1v_2$. However, the new marked edge $v_1v_2$ still could be of type KK or $S_pS_c$. Then by recomposing along $v_1v_2$, we finally transform the limb into a canonical decomposition.

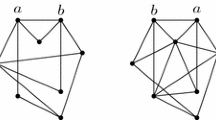
Let $\widetilde{\mathcal {L}}=\widetilde{\mathcal {L}}[D,B,y]$ be the canonical decomposition obtained from $\mathcal {L}[D,B,y]$, and let $\widehat{\mathcal {L}}=\widehat{\mathcal {L}}[D,B,y]$ be the graph obtained from $\mathcal {L}[D,B,y]$ by recomposing all marked edges. See Fig. 1 for an example. If the original canonical decomposition $D$ is clear from the context, we remove $D$ in the notation $\mathcal {L}[D,B,y]$.

Lemma 5

Let $B$ be a bag of $D$. If two unmarked vertices $x$ and $y$ are represented by a marked vertex $w\in V(B)$, then $\widehat{\mathcal {L}}[B,x]$ is locally equivalent to $\widehat{\mathcal {L}}[B,y]$.

For a bag $B$ in $D$ and a component $T$ of $D{\setminus } V(B)$, we define $f(D,B,T)$ as the linear rank-width of $\widehat{\mathcal {L}}[D,B,y]$ for some unmarked vertex $y\in V(T)$. In fact, by Lemma 5, $f(D,B,T)$ does not depend on the choice of $y$. As in the notation $\mathcal {L}[D,B,x]$, if the canonical decomposition $D$ is clear from the context, we remove $D$ in the notation $f(D,B,T)$.

Proposition 1

Let $B$ be a bag of $D$. Let $x\in V(\widehat{D})$ and let $y$ be an unmarked vertex represented in $D$ by $v\in V(B)$. If $y'$ is represented by $v$ in $D*x$, then $\widehat{\mathcal {L}}[D,B,y]$ is locally equivalent to $\widehat{\mathcal {L}}[D*x,B,y']$. Therefore, $f(D,B,T)=f(D*x,B,T_x)$ where $T_x$ is the component of $(D*x){\setminus }V(B)$ containing $y$.

Proposition 2

Let $B_1$ and $B_2$ be two bags of $D$. Let $T_1$ be a component of $D{\setminus } V(B_1)$ such that $T_1$ does not contain the bag $B_2$, and let $T_2$ be the component of $D{\setminus } V(B_2)$ such that $T_2$ contains the bag $B_1$. Then $f(B_1,T_1)\le f(B_2,T_2)$.

Fig. 1.

In $(a)$, we have a canonical decomposition $D$ of a distance-hereditary graph and a bag $B$ of $D$. The dashed edges are marked edges in $D$. In $(b)$, we have limbs $\mathcal {L}$ associated with the components of $D{\setminus } V(B)$. The canonical decompositions $\widetilde{\mathcal {L}}$ associated with limbs $\mathcal {L}$ are shown in $(c)$.

4 Characterizing the Linear Rank-Width of DH Graphs

In this section, we prove the main theorem of the paper, which characterizes distance-hereditary graphs of linear rank-width $k$.

Theorem 4

(Main Theorem). Let $k$ be a positive integer and let $D$ be the canonical decomposition of a distance-hereditary graph. Then $\mathrm{lrw }(\widehat{D})\le k$ if and only if for each bag $B$ of $D$, $D$ has at most two components $T$ of $D{\setminus } V(B)$ such that $f(B,T)=k$, and for all the other components $T'$ of $D{\setminus } V(B)$, $f(B,T')\le k-1$.

To prove the converse direction, we use the following technical lemmas. Let $k$ be a positive integer and let $D$ be the canonical decomposition of a distance-hereditary graph.

Proposition 3

Let $B$ be a bag of $D$ with two unmarked vertices $x$, $y$. If for every component $T$ of $D{\setminus } V(B)$, $f(B,T)\le k-1$, then the graph $\widehat{D}$ has a linear layout of width at most $k$ such that the first vertex and the last vertex of it are $x$ and $y$, respectively.

Lemma 6

Suppose for each bag $B$ of $D$, there are at most two components $T$ of $D{\setminus }V(B)$ satisfying $f(B,T)=k$ and for all the other components $T'$ of $D{\setminus } V(B)$, $f(B,T')\le k-1$. Then $T_D$ has a path $P$ such that for each bag $B$ in $P$ and a component $T$ of $D{\setminus } V(B)$ not containing a bag of $P$, $f(B,T)\le k-1$.

We are now ready to prove Theorem 4.

Proof

(of Theorem 4 ). For the forward direction, it is sufficient to show that if $B$ is a bag of $D$ such that $D{\setminus } V(B)$ has at least three components $T_1, T_2, T_3$ such that $f(B,T_i)=k$, then $\mathrm{lrw }(\widehat{D})\ge k+1$. The proof idea is the same as the one used in [9]. We start from a linear layout assumed to have width $k$ and we prove using Lemmas 1, 3 and Proposition 1 and tools from linear algebra that there exists $i\in \{1,2,3\}$ such that $f(B, T_i)\le k-1$, contradicting that $f(B, T_i)=k$. The details are omitted due to space constraints.

Now we prove the converse direction. Let $P:=B_0-B_1- \cdots -B_n-B_{n+1}$ be the path in $T_D$ such that for each bag $B$ in $P$ and a component $T$ of $D{\setminus } V(B)$ not containing a bag of $P$, $f(B,T)\le k-1$ (such a path exists by Lemma 6). If $B_0$ does not have an unmarked vertex, then we add one unmarked vertex to $B_0$ and we call it $a_0$. Similarly for $B_{n+1}$, but the added unmarked vertex is called $b_{n+1}$.

Now for each $0\le i\le n$, let $b_i$ be the marked vertex of $B_i$ adjacent to $B_{i+1}$ and let $a_{i+1}$ be the marked vertex of $B_{i+1}$ adjacent to $b_{i}$. And for each $0\le i\le n+1$, let $D_i$ be the subdecomposition of $D$ induced on the bag $B_i$ and the components of $D{\setminus } V(B_{i})$ which do not contain a vertex of $P$. Notice that the vertices $a_i$ and $b_i$ are unmarked vertices in $D_i$. Since every component $T$ of $D_i{\setminus } V(B_i)$ is such that $f(D_i,B_i,T) \le k-1$, by Proposition 3, $\widehat{D_i}$ has a linear layout $L_i'$ of width $k$ such that the first vertex of it is $a_i$ and the last vertex of it is $b_i$. For each $1\le i \le n$, let $L_i$ be the linear layout obtained from $L_i'$ by removing $a_i$ and $b_i$. Let $L_1$ and $L_{n+1}$ be obtained from $L_1'$ and $L_{n+1}'$ by removing $b_0$ and $a_{n+1}$, respectively, and also the vertices $a_0$ and $b_{n+1}$, respectively, if they were added. Then we can easily check that $L:= L_0\oplus L_1\oplus \cdots \oplus L_{n+1}$ is a linear layout of $\widehat{D}$ having width at most $k$. Therefore $\mathrm{lrw }(\widehat{D})\le k$.      $\square$

5 Computing the Linear Rank-Width of DH Graphs

In this section, we describe an algorithm to compute the linear rank-width of distance-hereditary graphs. Since the linear rank-width of a graph is the maximum linear rank-width over all its connected components, we will focus on connected distance-hereditary graphs.

Theorem 5

The linear rank-width of any connected graph with $n$ vertices can be computed in time $\mathcal {O}(n^2\cdot \log n)$.

We say that a canonical decomposition $D$ is rooted if we distinguish either a bag of $D$ or a marked edge of $D$, and call it the root of $D$. In a rooted canonical decomposition with the root bag, the parent of a bag is defined analogously as in rooted trees, and when the root is a marked edge, every bag has a parent according to the convention below: if the marked edge between two bags $B_1$ and $B_2$ is the root, then we call $B_2$ the artificial parent of $B_1$, and similarly $B_1$ is also called the artificial parent of $B_2$. We remark that the (artificial) parent will be used to define certain limbs. For two bags $B$ and $B'$ in $D$, $B$ is called a descendant of $B'$ if $B'$ is on the unique path from $B$ to the root in $T_D$. Two bags in $D$ are called comparable if one bag is a descendant of the other bag. Otherwise, they are called incomparable. If two canonical decompositions $D_1$ and $D_2$ are locally equivalent and $B$ is the root bag of $D_1$, then we say $D_2[V(B)]$ is also the root of $D_2$. Similarly, if a marked edge $e$ is the root of $D_1$, then we say $e$ is also the root of $D_2$.

To easy the understanding and to avoid the choice of $y$ in the definition of limbs, we will deal with a set of pairwise locally equivalent canonical decompositions. For a canonical decomposition $D$ of a distance-hereditary graph, we define $\varGamma _D$ as the set of all canonical decompositions locally equivalent to $D$. We remark that for $D_1, D_2\in \varGamma _D$ and $B\subseteq V(D)$, $B$ induces a bag in $D_1$ if and only if $B$ induces a bag in $D_2$. We also have $M(D_1)=M(D_2)$.

For a bag $B$ of a canonical decomposition $D$ and a marked edge $e$ adjacent to $B$ in $D$, let $\mathcal {G}(\varGamma _D, B, e)$ be the set of all canonical decompositions $\widetilde{\mathcal {L}}[D', D'[V(B)], y]$ where $D'\in \varGamma _D$, $T$ is the component of $D'{\setminus } V(B)$ incident with $e$, and $y\in V(T)$ is an unmarked vertex represented by a vertex of $D'[V(B)]$ in $D'$.

Proposition 4

$\mathcal {G}(\varGamma _D, B, e)=\varGamma _{D'}$ for some canonical decomposition $D'$.

Let $D$ be the rooted canonical decomposition of a distance-hereditary graph $G$ with the root $R$. We introduce two ways to take a set of limbs from the decompositions in $\varGamma _D$. Let $B$ be a non-root bag of $D$ and let $B'$ be the (possibly artificial) parent of $B$ and let $e$ be the marked edge connecting $B$ and $B'$ in $D$.

• 1. Let $\varGamma _1(\varGamma _D,B):=\mathcal {G}(\varGamma _D,B',e)$ and ${\mathcal {F}}_1(\varGamma _D, B):=\mathrm{lrw }(\widehat{D'})$ for $D'\in \varGamma _1(\varGamma _D,B)$.

• 2. Let $\varGamma _2(\varGamma _D,B):=\mathcal {G}(\varGamma _D,B, e)$ and $\mathcal {F}_2(\varGamma _D, B):=\mathrm{lrw }(\widehat{D'})$ for $D'\in \varGamma _2(\varGamma _D,B)$.

By Proposition 4, $\varGamma _i(\varGamma _D, B)=\varGamma _{D'}$ for some canonical decomposition $D'$ and so we can apply this function recursively, for instance, $\varGamma _2(\varGamma _1(\varGamma _D,B_1), B_2)$.

In the algorithm, we will compute decompositions in $\varGamma _1(\varGamma _D,B)$ or $\varGamma _2(\varGamma _D,B)$. As explained in Sect. 3, we need sometimes to merge two bags to be able to turn a limb into a canonical decomposition. Whenever a merging operation on two bags $B_1$ and $B_2$ appears, if $B_2$ is a descendant of $B_1$, then we regard the merged bag as $B_1$, and if they are incomparable, then we regard it as a new one.

For $D_i\in \varGamma _i(\varGamma _D,B)$, we define the root $R'$ of $D_i$ as follows. If the root $R$ of $D$ exists in $D_i$, then let $R':=R$. Assume the root $R$ does not exist in $D_i$. In this case, some bag, which was either the root $R$ itself or incident with the root edge $R$, is removed, and two children of it are merged or linked by a marked edge. If two children of the removed bag are merged, then let $R'$ be the merged bag, and if otherwise, let $R'$ be the marked edge between them. We have the following.

Lemma 7

Let $B$ be a non-root bag of $D$ and let $D_i\in \varGamma _i(\varGamma _D,B)$. If $B'$ is a non-root bag of $D_i$, then $B'$ is a non-root bag of $D$ (for $i=1,2$).

Our algorithm uses methods of the algorithm for vertex separation of trees [9]. Our algorithm works bottom-up on $D$, and computes ${\mathcal {F}}_1(\varGamma _D, B)$ for all bags $B$ in $D$ using dynamic programming. Let $B$ be a bag of $D$, and let $B_1, B_2, \ldots , B_m$ be the children of $B$ in $D$. Let $k:=\max _{1\le i\le m}{\mathcal {F}}_1(\varGamma _D, B_i)$. We can easily observe that $k\le {\mathcal {F}}_1(\varGamma _D, B)\le k+1$. We discuss now how to determine ${\mathcal {F}}_1(\varGamma _D, B)$. A bag $B$ of $D$ is called $k$ -critical if ${\mathcal {F}}_1(\varGamma _D, B)=k$ and $B$ has two children $B_1$ and $B_2$ such that ${\mathcal {F}}_1(\varGamma _D, B_1)={\mathcal {F}}_1(\varGamma _D, B_2)=k$. We first observe the following which can be derived from Theorem 4 and Proposition 2.

Proposition 5

Let $k=\max \{{\mathcal {F}}_1(\varGamma _D, B)| \text { B is a non-root bag of D} \}$. Assume that $D$ has neither a bag $B$ having at least three children $B'$ such that ${\mathcal {F}}_1(\varGamma _D, B')=k$ nor two incomparable bags $B_1$ and $B_2$ with a $k$-critical bag $B_1$ and ${\mathcal {F}}_1(\varGamma _D,B_2)=k$. Let $B$ be a $k$-critical bag of $D$. Then $B$ is the unique $k$-critical bag of $D$. Moreover, $\mathrm{lrw }(G)= k+1$ if and only if $\mathcal {F}_2(\varGamma _D, B)= k$.

By Proposition 5, the computation of ${\mathcal {F}}_1(\varGamma _D, B)$ is reduced to the computation of $\mathcal {F}_2(\varGamma _1(\varGamma _D, B), B_c)$ if $D'\in \varGamma _1(\varGamma _D, B)$ has the unique $k$-critical bag $B_c$. In order to compute $\mathcal {F}_2(\varGamma _1(D, B), B_c)$, we can recursively call the algorithm. However, we will prove that these recursive calls are not needed if we compute more than the linear rank-width, and it is the key for the $\mathcal {O}(n^2\cdot \log (n))$ time algorithm (Table 1).

Table 1. Examples of $PD(B, j)$ and $LD(B, j)$.

For each bag $B$ of $D$ and $0\le j\le \lfloor \log |V(G)|\rfloor$, we recursively define a set $D(B,j)$ of canonical decompositions. The integer $j$ will be at most the linear rank-width. The choice of $j\le \lfloor \log |V(G)|\rfloor$ comes from the following fact.

Lemma 8

For a distance-hereditary graph $G$, $\mathrm{lrw }(G)\le \log |V(G)|$.

Let $D(B,\lfloor \log |V(G)|\rfloor ) :=\varGamma _1(\varGamma _D, B)$. For each bag $B$, $j$ and $D'\in D(B, j)$, let $PD(B, j)$ be the maximum ${\mathcal {F}}_1(\varGamma _{D'}, B')$ over all non-root bags $B'$ in $D'$, and let $LD(B, j):=\mathrm{lrw }(\widehat{D'})$.

• 1. Let $D(B,\lfloor \log |V(G)|\rfloor ) :=\varGamma _1(\varGamma _D, B)$.

• 2. For all $1\le j\le \lfloor \log |V(G)|\rfloor$, if $PD(B, j)\ne j$, let $D(B,j-1):=D(B,j)$. If $PD(B, j)= j$, then for $D'\in D(B, j)$,

  • (a) if ($D'$ has a bag with $3$ children $B_1$ such that $LD(B_1,j)=j$) or ($D'$ has two incomparable bags $B_1$ and $B_2$ with a $j$-critical bag $B_1$ and $LD(B_2,j)=j$) or ($D'$ has no $j$-critical bags), then let $D(B,j-1):=D(B,j)$,

  • (b) if $D'$ has the unique $j$-critical bag $B_c$, then let $D(B,j-1):=\varGamma _2( D(B, j) , B_c)$.

The essential cases are when $PD(B, j)=j$, and in these cases, we want to determine whether $LD(B, j)=j$ or $j+1$. We prove the following.

Proposition 6

Let $B$ be a non-root bag of $D$. Let $i$ be an integer such that $0\le i\le \lfloor \log |V(G)|\rfloor$ and $PD(B, i)\le i$. Let $D'\in D(B, i)$ and let $B'$ be a non-root bag of $D'$. Then $B'$ is also a non-root bag of $D$ and $PD(B', i)\le i$. Moreover, $\varGamma _1(D(B, i), B')=D(B',i)$. Therefore, ${\mathcal {F}}_1(D(B, i), B')=LD(B', i)$.

Now we describe the algorithm explicitly. For convenience, we modify the given decomposition as follows. For the canonical decomposition $D'$ of a distance-hereditary graph $G$, we modify $D'$ into a canonical decomposition $D$ by adding a bag $R$ adjacent to a bag $R'$ in $D$ so that $f(D, R, D')=\mathrm{lrw }(G)$. So, if we regard $R$ as the root bag of $D$, then ${\mathcal {F}}_1(\varGamma _D,R')=\mathrm{lrw }(G)=LD(R',\lfloor \log |V(G)|\rfloor )$. The basic strategy is to compute $LD(B, i)$ for all non-root bags $B$ of $D$ and integers $i$ such that $PD(B, i)\le i$. If $B$ is a non-root leaf bag of $D$, then clearly ${\mathcal {F}}_1(\varGamma _D,B)=1$, so let $LD(B, i)=1$ for all $0\le i\le \lfloor \log |V(G)|\rfloor$. For convenience, let $t=\lfloor \log |V(G)|\rfloor$.

• 1. Compute the canonical decomposition $D'$ of $G$, and obtain a canonical decomposition $D$ from $D'$ by adding a root bag $R$ adjacent to a bag $R'$ in $D$ so that $\mathrm{lrw }(G)=LD(R',t)$.

• 2. For all non-root leaf bags $B$ in $D$, set $LD(B, j):=1$ for all $0\le j\le t$.

• 3. While ($D$ has a non-root bag $B$ such that $LD(B, t)$ is not computed).

  • (a) Choose a non-root bag $B$ in $D$ such that for every child $B'$ of $B$, $LD(B', t)$ is computed.

  • (b) Compute a decomposition $D_t$ in $\varGamma _1(\varGamma _D, B)=D(B, t)$.

  • (c) Compute $k:=PD(B,t)$ and set $D_{k}:=D_t$ and $i:=k$.

  • (d) Let $S$ be a stack.

  • (e) While (true) do.

    • i. If either ($D_i$ has a bag with at least $3$ children $B_1$ such that $LD(B_1,i)=i$) or ($D_i$ has two incomparable bags $B_1$ and $B_2$ with $B_1$ an $i$-critical bag and $LD(B_2,i)=i$) or ($D_i$ has no $i$-critical bags), then stop this loop.

    • ii. Find the unique $i$-critical bag in $D_i$.

    • iii. Compute $D_{i-1} \in D(B,i-1)$ and $\mathrm{push }(S,i)$.

    • iv. Set $j:= i-1$ and $i:=PD(B,i-1)$ and $D_i:= D_{j}$.

  • (f) If either ($D_i$ has a bag with at least $3$ children $B_1$ such that $LD(B_1,i)=i$) or ($D_i$ has two incomparable bags $B_1$ and $B_2$ with $B_1$ an $i$-critical bag and $LD(B_2,i)=i$), then set $LD(B,i):=i+1$, else, $LD(B,i) := i$.

  • (g) While $(S \ne \emptyset )$ do.

    • i. Set $j:= \mathrm{pull }(S)$.

    • ii. If $LD(B,i) = j$, then $LD(B,j) := j+1$, else $LD(B,j):= j$.

    • iii. For $\ell =i+1$ to $j-1$, set $LD(B, \ell ):=LD(B, i)$.

    • iv. Set $i:=j$.

  • (h) Set $LD(B,j):=LD(B,k)$ for all $k<j\le t$.

• 4. Return $LD(R', t)$.

Proof

(of Theorem 5 ). By Propositions 5 and 6 the steps of the algorithm outlined above computes the linear rank-width of every connected distance-hereditary graph $G$. Let us now analyze its running time. Let $n$ and $m$ be the number of vertices and edges of $G$. Its canonical decomposition $D'$ can be computed in time $\mathcal {O}(n+m)$ by Theorem 1, and one can of course add a new bag to obtain a new canonical decomposition $D$ and root it in constant time. The number of bags in $D$ is bounded by $\mathcal {O}(n)$ (see [12, Lemma 2.2]). For each bag $B$, $LD(B,j)$ for all $0\le j\le t$ can be computed in time $\mathcal {O}(n\cdot \log (n))$. In fact, Steps 3(a-c) can be done in time $\mathcal {O}(n)$. The loop in 3(e) runs $\log (n)$ times since $k\le \log (n)$, and all the steps in 3(e) can be implemented in time $\mathcal {O}(n)$. Since Steps 3(f-h) can be done in time $\mathcal {O}(n)$, we conclude that this algorithm runs in time $\mathcal {O}(n^2\cdot \log n)$.       $\square$

Corollary 2

For every connected distance-hereditary graph $G$, we can compute in time $\mathcal {O}(n^2\cdot \log (n))$ a layout of the vertices of $G$ witnessing $\mathrm{lrw }(G)$.

6 Obstructions

A graph $H$ is a vertex-minor obstruction for (linear) rank-width $k$ if it has (linear) rank-width $k+1$ and every proper vertex-minor of $H$ has (linear) rank-width at most $k$. The set of pairwise locally non-equivalent vertex-minor obstructions for (linear) rank-width $k$ is not known, but for rank-width $k$ a bound on their size is known [17], which is not the case for linear rank-width $k$. For $k=1$, Adler, Farley, and Proskurowski [1] characterized the distance-hereditary vertex-minor obstructions for linear rank-width at most $1$ by two pairwise locally non-equivalent graphs. For general $k$, Jeong, Kwon, and Oum recently provided a $2^{\varOmega (3^k)}$ lower bound on the number of pairwise locally non-equivalent distance-hereditary vertex-minor obstructions for linear rank-width at most $k$ [14]. Using our characterization, we generalize the construction in [14] and conjecture a subset of the given set to be the set of distance-hereditary vertex-minor obstructions.

We will use the notion of one-vertex extensions introduced in [13]. We call a graph $G'$ an one-vertex extension of a distance-hereditary graph $G$ if $G'$ is a graph obtained from $G$ by adding a new vertex $v$ with some edges and $G'$ is again distance-hereditary. For convenience, if $D$ and $D'$ are canonical decompositions of $G$ and $G'$, respectively, then $D'$ is also called an one-vertex extension of $D$. For example, any one-vertex extension of $K_2$ is isomorphic to either $K_3$ or $K_{1,2}$. For a set $\mathcal {D}$ of canonical decompositions, we define

$$ \mathcal {D}^{+}=\mathcal {D}\cup \{D'|D' \text { is an one vertex extension of }D\in \mathcal {D}\}. $$

For a set $\mathcal {D}$ of canonical decompositions, we define a new set $\varDelta (\mathcal {D})$ of canonical decompositions $D$ as follows:

• Choose three decompositions $D_1, D_2, D_3$ in $\mathcal {D}$ and take one-vertex extensions $D_i'$ of $D_i$ with new vertices $w_i$ for each $i$. We introduce a new bag $B$ of type $K$ or $S$ having three vertices $v_1, v_2, v_3$ and

  • 1. if $v_i$ is in a complete bag, then $D_i''=D_i'*w_i$,

  • 2. if $v_i$ is the center of a star bag, then $D_i''=D_i'\wedge w_iz_i$ for some $z_i$ linked to $w_i$ in $D'$,

  • 3. if $v_i$ is a leaf of a star bag, then $D_i''=D_i'$.

  Let $D$ be the canonical decomposition obtained by the disjoint union of $D_1'', D_2'', D_3''$ and $B$ by adding the marked edges $v_1w_1, v_2w_2, v_3w_3$.

For each non-negative integer $k$, we construct the sets $\varPsi _k$ and $\varPhi _k$ of canonical decompositions as follows.

• 1. $\varPsi _0=\varPhi _0:=\{K_2\}$ ($K_2$ is the canonical decomposition of the graph $K_2$).

• 2. For $k\ge 0$, let $\varPsi _{k+1}:=\varDelta (\varPsi _k^{+})$.

• 3. For $k\ge 0$, let $\varPhi _{k+1}:=\varDelta (\varPhi _k)$.

We prove the following.

Theorem 6

Let $k\ge 0$ and let $G$ be a distance-hereditary graph such that $\mathrm{lrw }(G)\ge k+1$. Then there exists a canonical decomposition $D$ in $\varPsi _k$ such that $G$ contains a vertex-minor isomorphic to $\widehat{D}$.

In order to prove that $\varPsi _k$ is the set of canonical decompositions of distance-hereditary vertex-minor obstructions for linear rank-width at most $k$, we need to prove that for every $D\in \varPsi _k$, $\hat{D}$ has linear rank-width $k+1$ and every of its proper vertex-minors has linear rank-width $\le k$. However, we were not able to prove it, and we showed this property for $\varPhi _k$ instead of $\varPsi _k$.

Proposition 7

Let $k\ge 0$ and let $D\in \varPhi _k$. Then $\mathrm{lrw }(\hat{D}) = k+1$ and every proper vertex-minor of $\hat{D}$ has linear rank-width at most $k$.

One can observe that the obstructions constructed in [1, 14] are contained in $\varPhi _k$ for all $k\ge 1$.

We leave open the question to identify a set $\varPhi _k \subset \varTheta _k \subset \varPsi _k$ that forms the set of canonical decompositions of distance-hereditary vertex-minor obstructions for linear rank-width $k$.