Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Model-based design (MBD) is a mathematical and visual process for designing, implementing, and testing embedded software designs for real-time control systems. MBD is rapidly becoming the pervasive design paradigm in many sectors such as automotive and avionics, but the problem of checking correctness of such designs is a highly challenging task. Of particular interest is the problem of ensuring that the system satisfies safety constraints, which are usually associated with a region of the state space. Analysis techniques from dynamical systems theory can be applied to such designs to verify system properties, such as those for checking stability or estimating performance bounds (see, e.g., Chap. 4 of [3]); however, these are rarely used in any but the earliest stages of the MBD process.

It is well known that a sub level set of a Lyapunov function is a forward invariant set. The existence of a forward invariant set that properly contains the set of initial states, while excluding the unsafe region proves that the system is safe for all time. Thus, it is clear that identifying such invariant sets helps us to address the safety verification problem. A significant obstacle to this approach is that Lyapunov functions of arbitrary (nonlinear or hybrid) systems are notoriously hard to discover. Further, industrial models are often in formats lacking an analytic representation of the dynamics.

We now give a brief overview of our technique. We use an iterative procedure to construct candidate Lyapunov functions using simulation traces. The candidate Lyapunov functions are restricted to the class of polynomial functions, similar to the sum of squares (SoS) techniques described in [5]. This restriction allows us to compute a candidate forward invariant set by solving a linear program (LP). We then verify the validity of the candidate invariant set by testing over a finite number of system states. Note that, alternatively, if an analytic representation of the dynamics is given, one could verify the validity of the candidate invariant set using arithmetic solvers, as we describe in [2].

Our work builds largely on [6], where forward orbits (which are often called simulations or simulation traces) are used to seed a procedure to estimate the region of attraction (ROA) for a dynamical system. We provide the following extensions to that work: (a) we provide a procedure that uses a global optimizer to iteratively improve the quality of the candidate Lyapunov functions (by seeking initial conditions that falsify each intermediate candidate) and (b) Our technique is not restricted to the class of systems with polynomial dynamics.

2 Problem Statement

We consider autonomous nonlinear discrete-time dynamical systems of the form:

$$\mathbf{x}_{k+1} = f({\mathbf{x}}_k).$$
(1)

Here \({\mathbf{x}}\) represents state variables that take values in \({\mathbb{R}}^n\) and f is a nonlinear, locally Lipschitz-continuous vector field. We call \({\hat{\mathbf{x}}}\) the successor of \({\mathbf{x}}\) if \({\hat{\mathbf{x}}}=f({\mathbf{x}})\). We assume that the system has a stable equilibrium point, which is, without loss of generality, at the origin. We address the following problem. Given the dynamical system (1), and a closed and bounded domain of interest \({\mathcal{D}} \subseteq{\mathbb{R}}^n\), identify a forward invariant set \({\mathcal{S}} \subseteq{\mathcal{D}}\) such that for all \({\mathbf{x}} \in{\mathcal{S}}\), \(f({\mathbf{x}})\in{\mathcal{S}}\). We present a procedure that can identify such a set, without explicit knowledge of the vector field \(f(\cdot)\). The following section describes the procedure.

3 Algorithm for Computing Invariant Sets

The procedure consists of three steps: (1) identify a candidate Lyapunov function for (1) within \({\mathcal{D}}\); (2) use the candidate Lyapunov function to compute a candidate invariant set; (3) certify that the candidate invariant set is a forward invariant set. We now describe each step in the process.

Identifying a Candidate Lyapunov Function

Ideally, we want to discover a differentiable function v that \(\forall{\mathbf{x}}\in{\mathcal{D}}\) satisfies:

$$\begin{aligned}&{v}({\mathbf{x}}) \succ 0 \end{aligned}$$
(2)
$$\begin{aligned} &{v}({\mathbf{x}}) - v({\hat{\mathbf{x}}})> 0, ~~~~\forall{\mathbf{x}} \in{\mathcal{D}} \setminus \{0\},\ v(0)=0.\end{aligned}$$
(3)

Here, \({v}({\mathbf{x}}) \succ 0\) means that v is positive definite, i.e., \(\forall{\mathbf{x}}\neq 0\), \({v}({\mathbf{x}})>0\), and \({v}(0)=0\). The problem of identifying such a function v for the general case is of infinite dimension. We relax the problem by restricting the form of v as \({v}({\mathbf{x}})\ =\ {\mathbf{z}}^T{\mathbf{P}}{\mathbf{z}}\), where \({\mathbf{z}}\) is some vector of m monomials in \({\mathbf{x}}\) (e.g., \({\mathbf{z}}=[x_1 x_1^2x_2 x^2_2]^T\)) and \({\mathbf{P}}\in{\mathbb{R}}^m\times{\mathbb{R}}^m\). We use a collection of state/successor pairs to automatically produce candidate Lyapunov functions for the system. Given M pairs of points \({\mathbf{x}}_i, {\hat{\mathbf{x}}}_i\), where \(i\in \{1,2,\ldots,M\}\) and \({\mathbf{x}}_i\neq0\) for all i, we formulate the following LP :

$$\begin{aligned}\underset{\mathbf{P}, \gamma}{\max} & \;\gamma \nonumber\\s.t. & \gamma>0, ~~~ \text{ and} \forall i\in \{1,\ldots,M\}, \nonumber\\& v({\mathbf{x}}_i)>0 \nonumber\\& v({\mathbf{x}}_i)-{v}({\hat{\mathbf{x}}}_i)>\gamma \|{\mathbf{x}}_i \|^2.\end{aligned}$$
(4)

Any feasible solution to (4) results in a candidate Lyapunov function v that satisfies M necessary conditions for (2) and (3). We note that we could strictly enforce (2) by requiring that \({\mathbf{P}}\succ 0\), but this would require that a more expensive semidefinite program (SDP) be solved instead of an LP.

Once a candidate Lyapunov function is obtained from (4), we employ a falsifier to select state/successor pairs that can be used to improve the candidate Lyapunov function. The falsifier is a global optimizer that attempts to solve the following optimization problem:

$$\begin{aligned}\underset{\mathbf{x}\in{\mathcal{D}}}{\min} & \;{v}({\mathbf{x}})-{v}({\hat{\mathbf{x}}}) \nonumber\\s.t. & {\hat{\mathbf{x}}}=f({\mathbf{x}}).\end{aligned}$$
(5)

If the solution to (5) is less than zero, then the optimal \({\mathbf{x}}\) is a witness that falsifies the Lyapunov condition (3). This witness is added to the collection of state/successor pairs and (4) is solved again. This procedure continues until no falsifying witness can be found by solving (5). For our experiments, we use a simulated annealing algorithm to implement the falsifier. Figure 1 illustrates our iterative procedure.

Fig. 1
figure 1

Procedure to create a candidate Lyapunov function for system (1)

Full size image

We note that if both (a) the falsifier is capable of computing a global minimum and (b) the procedure in Fig. 1 halts, then the resulting candidate Lyapunov function \({v}(\cdot)\) is a Lyapunov function for (1). Practical falsifiers cannot reliably find a global minimum in general. Hence, we still need to verify the soundness of the forward invariant set computed using a candidate Lyapunov function obtained from this procedure, and we present a technique to do so later in this section.

Computing a Candidate Invariant Set

Once we obtain a candidate Lyapunov function for (1), we can use it to obtain a forward invariant set. We formulate a convex optimization problem to maximize l such that the sublevel set \({\mathcal{S}} = \{{\mathbf{x}}|{v}({\mathbf{x}})\leq l\}\) is within \({\mathcal{D}}\). If we assume that \({\mathcal{D}}\) is a sublevel set of a polynomial, then standard numerical techniques can be used to obtain the optimal l, as in [1].

Verifying Soundness of the Candidate Invariant Set

Below we show how to verify the soundness of the candidate invariant set computed in the previous step. The technique requires that a Lyapunov-like condition be satisfied at a finite sampling of the points in the set. First, we define a notion of sampling for a set.

Definition

1 [Delta Sampling] Given a \(\delta\in{\mathbb{R}}_{>0}\), a δ-sampling of set \(\mathcal{S}\subset{\mathbb{R}}^n\) is a finite set \(\mathcal{S}_\delta\) such that the following holds: \(\mathcal{S}_\delta \subset \mathcal{S}\); for any \({\mathbf{x}}\in\mathcal{S}\), there exists a \({\mathbf{x}}_\delta\in\mathcal{S}_\delta\) such that \(\|{\mathbf{x}}-{\mathbf{x}}_\delta\|<\delta\).

The following theorem allows us to test whether a given set is forward invariant by testing a finite subset of points within the set.

Theorem 1

[Invariant Soundness] Consider system ( 1 ), where f is locally Lipschitz with constant K f over \({\mathcal{D}}\) . Let \({\mathcal{S}} = \{{\mathbf{x}}|g({\mathbf{x}})\leq l\}\) , where \(g:{\mathbb{R}}^n\rightarrow{\mathbb{R}}_{\geq 0}\) is a \(\mathcal{C}^1\) function that is locally Lipschitz with constant K g over \({\mathcal{S}}\) , and let \({\mathcal{S}}_\delta\) be a δ-sampling of \({\mathcal{S}}\) . If there exists a \(\gamma\in{\mathbb{R}}_{>0}\) such that \(\delta<\frac{\gamma}{K_g\cdot K_f}\) and \(\forall{\mathbf{x}}_\delta\in{\mathcal{S}}_\delta\) , \(g(f({\mathbf{x}}_\delta))\leq l-\gamma\) , then \({\mathcal{S}}\) is a forward invariant set.

Proof

We prove by contradiction. Assume that \(\delta<\frac{\gamma}{K_g\cdot K_f}\) and for all \({\mathbf{x}}_\delta\in{\mathcal{S}}_\delta\), \(g(f({\mathbf{x}}_\delta))\leq l-\gamma\) holds, but \({\mathcal{S}}\) is not forward invariant. Then it is true that for some \({\mathbf{x}}\in{\mathcal{S}}\), \(f({\mathbf{x}})\notin{\mathcal{S}}\). Consider the point \({\mathbf{x}}_\delta\) in \({\mathcal{S}}_\delta\) closest to \({\mathbf{x}}\). The Lipschitz constant for the function composition \(g \circ f\) is \(K_g\cdot K_f\). Applying the definition of Lipschitz continuity, we have \(\|g(f({\mathbf{x}}))-g(f({\mathbf{x}}_\delta))\| \leq K_g\cdot K_f\cdot\|{\mathbf{x}}-{\mathbf{x}}_\delta\|\). By the definition of δ-sampling, \(\|{\mathbf{x}}-{\mathbf{x}}_\delta\| < \delta\), thus we have

$$\|g(f({\mathbf{x}}))-g(f({\mathbf{x}}_\delta))\| < \delta\cdot K_g\cdot K_f.$$
(6)

Since \(f({\mathbf{x}})\notin{\mathcal{S}}\), \(g(f({\mathbf{x}}))>l\), i.e., \(-g(f({\mathbf{x}}))<-l\). By assumption, \(g(f({\mathbf{x}}_\delta)) \leq l-\gamma\); adding the two inequalities, we get \(g(f({\mathbf{x}}_\delta))-g(f({\mathbf{x}})) < -\gamma\). By the triangle inequality, we have \(\| g(f({\mathbf{x}}_\delta))-g(f({\mathbf{x}})) \|> \gamma\). Combining with (6) we get:

$$\begin{aligned}\gamma < \| g(f({\mathbf{x}}_\delta))-g(f({\mathbf{x}})) \| < \delta\cdot K_g\cdot K_f.\end{aligned}$$
(7)

This contradicts our assumption that \(\delta < \frac{\gamma}{K_g\cdot K_f}\). ▪

As both δ and γ cannot be selected simultaneously, we propose an iterative procedure to determine whether the γ thus computed satisfies the condition \(\delta < \frac{\gamma}{K_g\cdot K_f}\). First, a δ value is selected randomly and used to create a δ-sampling of the candidate forward invariant set \({\mathcal{S}}\). Next, the minimum value of \(\gamma=l-{v}(f({\mathbf{x}}_\delta))\) over the finite set \({\mathcal{S}}_\delta\) is computed:

$$\begin{aligned}\gamma^*&={\underset{{\mathbf{x}}_\delta\in{\mathcal{S}}_\delta}{\min}} \;l-{v}(f({\mathbf{x}}_\delta)).\end{aligned}$$
(8)

If the \(\gamma^*<0\), then the candidate \({\mathcal{S}}\) is not a forward invariant set (since the \({\mathbf{x}}_\delta\) that minimizes (8) is such that \({v}(f({\mathbf{x}}_\delta))>l\)). If \(\gamma^*>0\) and \(\delta<\frac{\gamma^*}{K\cdot K_f}\), then by Theorem 1 the candidate \({\mathcal{S}}\) is a forward invariant set. If \(\gamma^*>0\) but \(\delta\not<\frac{\gamma^*}{K\cdot K_f}\), then we select a smaller δ such that \(\delta<\frac{\gamma^*}{K\cdot K_f}\) and repeat the process.

4 Example for Computing an Invariant Set

We now present an example demonstrating the technique in Sect. 3. The following dynamical system was taken from LaSalle [4]:

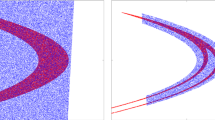
$$\begin{aligned} f({\mathbf{x}}) = \left[\begin{array}{c} \displaystyle\frac{\alpha \cdot x_2}{1+x_1^2} \\ \displaystyle\frac{\beta \cdot x_1}{1+x_2^2}\end{array} \right].\end{aligned}$$

For this exercise, we fix \(\alpha= 1.0\), \(\beta=0.9\). Fig. 2a shows the result of the procedure illustrated in Fig. 1; for the selected quadratic Lyapunov function template (i.e., \({\mathbf{z}} = [x_1\ x_2]^T\)), the procedure terminates in 5.59 s Footnote 1, giving the following candidate Lyapunov function:

$$\begin{aligned} v_{\mathrm{LaSalle}}({\mathbf{x}}) = [x_1\ x_2]\left[\begin{array}{cc} 368.0 & -36.0\\ -36.0 & 396.0\end{array} \right] \left[\begin{array}{c} x_1 \\ x_2\end{array} \right].\end{aligned}$$
Fig. 2
figure 2

LaSalle example results

Full size image

Next, the candidate Lyapunov function is used to candidate invariant \(\mathcal{S} = v_{\mathrm{LaSalle}}({\mathbf{x}}) \leq 343.3\) (as shown in Fig. 2a); the corresponding convex program takes 2.22 s. Finally, \(\mathcal{S}\) is shown to be invariant using the iterative procedure from Sect. 3. The procedure halts after two iterations (i.e., \(\gamma^*\) is computed twice), after 5.82  s and a cumulative total of 57,877 sample points. Fig. 2b shows the results of this step for the example.

5 Conclusions

We describe a numerical technique for discovering forward invariant sets for nonlinear dynamical systems using simulation traces, leveraging techniques from Lyapunov analysis, global optimization, and convex programming. The set of samples from the candidate invariant set required for verifying validity of the candidate can be prohibitively large. In future work, we will investigate satisfiability modulo theories (SMT) and interval constraint propagation solvers to symbolically test the validity of candidate invariants.