Keywords

1 Introduction

Impossible differential attack is a powerful cryptanalysis method introduced by Biham et al. [2] and Knudsen [10] independently. It is often used in cryptanalyzing block ciphers with (generalized) Feistel structures and SPN structures. The main trick of this method is to find an impossible differential path as long as possible and then extend two truncated differentials from it. Then any candidate subkey involved in both truncated differentials, which can lead to the impossible differential path is a wrong key and should be discarded. So long as enough plaintext-ciphertext pairs are collected, an attacker can eliminate all wrong keys and recover the right key.

Due to the requirement of lightweight encryption algorithms which are used in tiny computing devices, such as RFID and sensor network nodes, many lightweight block ciphers have been proposed, for example PRESENT, KATAN, KTANTAN, KLEIN, LED, HIGHT, LBlock, TWINE [4, 5, 7–9, 11–16], and much more. TWINE is a 64-bit lightweight block cipher designed by Suzaki, Minematsu, Morioka and Kobayashi in [15], which has two versions supporting 80-bit and 128-bit keys respectively. Consisting of 36 rounds, TWINE employs Type-2 generalized Feistel structure with 16 nibbles. When TWINE was proposed, the designers presented security evaluation including impossible differential attacks on 23-round TWINE-80 and 24-round TWINE-128 which were the most powerful attacks given by the designers. Unfortunately, the time complexity of their impossible differential attacks may have a flaw and may lead to a complexity of more than exhaustive key search. Besides the designers’ security analysis, Çoban et al. gave an biclique analysis of full round TWINE [6], Boztaş et al. gave an multidimensional meet-in-the-middle attack on reduced-round TWINE-128 [3], Bogdanov et al. gave an key-difference invariant bias attack on reduced-round TWINE-128 [1]. All the results are summarized in Table 1. Note that although our results are not the best considering different cryptanalysis methods, our algorithm which can filter wrong subkeys that have more than 80 bits and 128 bits for TWINE-80 and TWINE-128 respectively shows some novelty. Besides, some observations which may be used to mount other types of attacks are given.

Table 1. Summary of attacks on TWINE
Full size table

Our Contribution. This paper focuses on the security of TWINE against impossible differential attack. The novelty includes the following aspects:

  • Propose an algorithm to filter wrong subkeys which exceeds the master key size;

  • Several observations on key relations and optimization of our algorithm are given;

  • Several tables are precomputed to decrease the time complexity.

This paper is organized as follows. In Sect. 2, we present the necessary notations and a simple description of the TWINE encryption algorithm and the key schedule. Section 3 gives useful observations and the reason for our choice of the impossible differential paths. Section 4 first explains the flaw of attacks in [15], and then shows the impossible differential attack against 23-round TWINE-80. The result of attacking 24-round TWINE-128 is showed in Sect. 5. Section 6 concludes the paper.

2 Preliminaries

Some notations used in this paper and a simple description of the TWINE algorithm are given in this section.

2.1 Notations

 

figure a

2.2 Description of TWINE

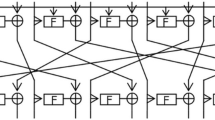
TWINE is a 64-bit block cipher with 80-bit or 128-bit key. The global structure of TWINE is a variant of Type-2 generalized Feistel structure with 16 nibbles. Consisting of 8 4-bit S-boxes and a diffusion permutation \(\pi \) as described in Table 2, the round function of TWINE is showed in Fig. 1. Expressed in a formula form, the round function encrypts an input value of round \(r\) to the input value of round \(r+1\) in the following two steps:

$$\begin{aligned} X^{r}_{2j+1}&\leftarrow s[X^{r}_{2j}\oplus RK^r_j]\oplus X^{r}_{2j+1} (j=0,...,7), \\ X^{r+1}_{\pi (i)}&\leftarrow X^{r}_i. \end{aligned}$$

For both versions of TWINE, the round function is iterated for 36 times and the diffusion permutation is omitted in the last round.

Fig. 1.
figure 1

Round function of TWINE

Full size image
Table 2. S-box and \(\pi \) permutation
Full size table

The key schedules of TWINE-80 and TWINE-128 produce 36 32-bit round subkeys \(RK^r_{[0,...,7]}\) (\(r=1,...,36\)) from the 80-bit master key (denoted as \(k_0,...,k_{19}\)) and 128-bit master key (denoted as \(k_0,...,k_{31}\)) respectively as described in Algorithm D.1. and Algorithm D.2. (Appendix D).

3 Observations and 14-Round Impossible Differentials of TWINE

This section gives several useful observations and the reason for our choice of the impossible differential path. Observation 1 is used in [15]. For the sake of completeness, we describe it here. Observation 2, 3, 4, 5 are about the subkeys. We give the round subkeys of TWINE-80 from round 1 to round 5 and the round subkeys of TWINE-128 from round 1 to round 7 in Table D.1 and Table D.2 (Appendix D).

Observation 1

For any input difference \(a(\ne 0)\) and output difference \(b(\in \triangle s[a])\) of the sbox in TWINE, the average number of pairs that satisfy the differential characteristic \((a\rightarrow b)\) is \(\frac{16}{7}\). Given an 8-bit pair \((X^r_{2i},X^r_{2i+1})\) and \((X^r_{2i}\oplus a,X^r_{2i+1}\oplus b)\), the probability that \(RK^r_i\) leads to the sbox differential characteristic \((a\rightarrow b)\) is \(7^{-1}\).

Observation 2

The round subkeys of TWINE-80 satisfy the following equations among four adjacent rounds.

$$ \begin{array}{l} RK_5^{r+2} = RK_1^r; RK_3^{r+2}=RK_5^r; RK_6^{r+2} = s^{-1}[RK_7^{r+1}\oplus RK_0^r]\oplus C^{r+1}_L, (1\le r\le 34); \\ RK_4^{r+3} = RK_3^r; RK_0^{r+3}=RK_4^r; RK_1^{r+3}=RK_6^r\oplus C_H^{r+2}; RK_2^{r+3}=RK_7^r, (1\le r\le 33);\\ RK_6^{r+3} = RK_2^r \oplus s[RK_7^r] \oplus C^{r+2}_L, (1\le r\le 33). \end{array} $$

Observation 3

The round subkeys of TWINE-80 satisfy the following equations among \(RK^1\), \(RK^2\), \(RK^{21}\), \(RK^{22}\) and \(RK^{23}\).

The precise expression of functions \(f_{i}(i=1,...,8)\) are shown in Appendix A.

Observation 4

The round subkeys of TWINE-128 satisfy the following equations among six adjacent rounds.

$$ \begin{array}{l} RK_7^{r+5} = RK_2^{r+1}\oplus s[RK_6^r]; RK_6^{r+5} = RK_4^r\oplus s[RK_2^{r+1}\oplus s[RK_6^r]], (1\le r\le 31);\\ RK_7^{r+4} = RK_2^r \oplus s[RK_2^{r+3}]; RK_3^{r+4} = RK_7^r \oplus C_L^{r+3}\oplus s[RK_1^{r+1}], (1\le r\le 32); \\ RK_4^{r+4} = RK_0^r ; RK_5^{r+4} = RK_1^r ; RK_0^{r+4} = RK_5^r; RK_2^{r+4} = RK_6^r, (1\le r\le 32);\\ RK_1^{r+3} = RK_3^r \oplus C_H^{r+2}, (1\le r\le 33). \end{array} $$

Observation 5

The round subkeys of TWINE-128 satisfy the following equations among \(RK^1\), \(RK^2\), \(RK^3\), \(RK^4\), \(RK^{21}\), \(RK^{22}\), \(RK^{23}\) and \(RK^{24}\).

$$ \begin{array}{ll} g_{1}(RK^1_1,RK^{22}_{[2,3]}, RK^{23}_5)&{}=0; \\ g_{2}(RK^1_6, RK^2_2, RK^{21}_0, RK^{24}_{[6,7]})&{}=0; \\ g_{3}(RK^3_{[0,1]},RK^{21}_0, RK^{22}_2, RK^{23}_{[5,7]}, RK^{24}_2)&{}=0;\\ g_{4}(RK^1_5, RK^2_3,RK^3_1, RK^{21}_2,RK^{22}_6,RK^{23}_0,RK^{24}_{[2,3]})&{}=0;\\ g_{5}(RK^1_{[0,1]},RK^3_5, RK^4_0, RK^{22}_{[0,2]},RK^{23}_{[1,2,4]}, RK^{24}_{[5,7]}) &{}=0;\\ g_{6}(RK^1_{[0,7]}, RK^2_{[4,5]},RK^3_5, RK^{22}_{[0,2]}, RK^{23}_{[1,2,3,4,7]}, RK^{24}_{[5,7]})&{}=0;\\ g_{7}(RK^1_{[2,4,6]},RK^2_{[0,2,3,7]}, RK^3_{[1,3]}, RK^{21}_2, RK^{22}_6, RK^{23}_{[0,3]}, RK^{24}_{[4,5]})&{}=0;\\ g_{8}(RK^1_{[2,4,6]}, RK^2_{[0,2,6,7]}, RK^3_{[1,3,5]}, RK^{22}_0, RK^{23}_{[0,1,2,4]}, RK^{24}_{[4,5,7]})&{}=0;\\ g_{9}(RK^1_{[2,4,5,6]}, RK^2_{[2,3,7]},RK^3_{[0,1,3]}, RK^{21}_{[0,2]}, RK^{22}_6, RK^{23}_{[0,5]},RK^{24}_{[1,4]}) &{}=0. \end{array} $$

The precise expression of functions \(g_{i}(i=1,...,9)\) are shown in Appendix A.

The 14-Round Impossible Differential Paths. Several 14-round impossible differential paths are given in [15]. This paper uses \((0||\alpha ||\tilde{0}^{14})\overset{14r}{\nrightarrow } (\tilde{0}^{7}||\beta ||\tilde{0}^{8})\) and \((\tilde{0}^{5}||\alpha ||\tilde{0}^{10}) \overset{14r}{\nrightarrow }(\tilde{0}^{11}||\beta ||\tilde{0}^{4})\) in attacking TWINE-80 and TWINE-128 respectively. Our choice of the impossible differential paths is determined by the following two reasons. Making use of the relations in Observation 2 and Observation 4, the truncated differential paths involve the least number of round subkeys. What’s more, the truncated differential paths involve subkeys that have less complicated equations in Observation 3 and Observation 5. Observation 6 is used in [15]. For the sake of completeness, we give a clear description. Observation 6 and 7 are useful in selecting more accurate plaintext/ciphertext pairs for attacking TWINE-80 and TWINE-128 respectively. Observation 8 is used in key recovery phase of our attacking TWINE-80. Its proof gives a detailed computation and analysis of the number of co responding subkeys that passing the differential path.

Observation 6

If the impossible differential \((0||\alpha ||\tilde{0}^{14})\overset{14r}{\nrightarrow } (\tilde{0}^{7}||\beta ||\tilde{0}^{8})\) is extended 4 rounds ahead and 5 rounds behind, then the input difference is of the form

$$ (\alpha _3, \alpha _4, 0, \alpha _2, \tilde{0}^6, \alpha _1, \alpha _2^{''}, \alpha _1^{'}, \alpha _2^{'}, 0, \alpha ) $$

where \(\alpha \ne 0\), \(\alpha _2^{'} \in \triangle s[\alpha _1^{'}]\), \(\alpha _1^{'}\in \triangle s[\alpha ]\), \(\alpha _3\in \triangle s[\alpha _2]\), \(\alpha _2^{''} \in \triangle s[\alpha _1]\), \(\alpha _4\in \triangle s[\alpha _3]\), \(\alpha _2\in \triangle s[\alpha _1]\), \(\alpha _1\in \triangle s[\alpha ]\);

and the output difference is of the form

$$ (0, \beta _1^{'}, 0, \beta _3, \beta ^{'}_2, \beta _3^{'}, \beta , x, \beta _4, \beta _5, \beta _2, \beta _3^{'''}, \beta _2^{''}, \beta _3^{''}, \tilde{0}^2) $$

where \(\beta \ne 0\), \(\beta _3^{'}\in \triangle s[\beta _2^{'}],\beta _5\in \triangle s[\beta _4],\beta _3^{'''}\in \triangle s[\beta _2],\beta _3^{''}\in \triangle s[\beta _2^{''}],\beta _2^{'}\in \triangle s[\beta _1^{'}],\beta _4\in \triangle s[\beta _3],\beta _3\in \triangle s[\beta _2],\beta _1^{'}\in \triangle s[\beta ]\);

\(Pr(\alpha \beta \ne 0, \text{ and } \text{ all } \text{ the } \text{ relations } \text{ hold })=(\frac{15}{16})^2\cdot (\frac{7}{16})^{15} = 2^{-18.08}\).

Observation 7

If the impossible differential \((\tilde{0}^{5}||\alpha ||\tilde{0}^{10})\overset{14r}{\nrightarrow }(\tilde{0}^{11}||\beta ||\tilde{0}^{4})\) is extended 5 rounds on the top and the bottom of it respectively, then the input difference is of the form

$$ (\alpha _4,\alpha _5,0,\alpha _3,\alpha _2^{'},\alpha _3^{'},\tilde{0}^3,\alpha _1^{'},\alpha _2,\alpha _3^{'''},\alpha _2^{''},\alpha _3^{''},\alpha ,y) $$

where \(\alpha \ne 0\), \(\alpha _5 \in \triangle s[\alpha _4]\), \(\alpha _3^{'} \in \triangle s[\alpha _2^{'}]\), \(\alpha _3^{'''} \in \triangle s[\alpha _2]\), \(\alpha _3^{''} \in \triangle s[\alpha _2^{''}]\), \(\alpha _2^{'} \in \triangle s[\alpha _1^{'}]\), \(\alpha _1^{'}\in \triangle s[\alpha ]\), \(\alpha _3\in \triangle s[\alpha _2]\), \(\alpha _4\in \triangle s[\alpha _3]\);

and the output difference is of the form

$$ (\beta _2^{'},\beta _3^{'},\beta _4,\beta _5,0,\beta _1^{'},\beta _2^{''},\beta _3^{''},0,\beta _3,\tilde{0}^2,\beta ,x,\beta _2,\beta _3^{'''}) $$

where \(\beta \ne 0\), \(\beta _3^{'}\in \triangle s[\beta _2^{'}],\beta _5\in \triangle s[\beta _4],\beta _3^{'''}\in \triangle s[\beta _2],\beta _3^{''}\in \triangle s[\beta _2^{''}],\beta _2^{'}\in \triangle s[\beta _1^{'}],\beta _4\in \triangle s[\beta _3],\beta _3\in \triangle s[\beta _2],\beta _1^{'}\in \triangle s[\beta ]\);

\(Pr(\alpha \beta \ne 0, \text{ and } \text{ all } \text{ the } \text{ belonging } \text{ relations } \text{ holds })=(\frac{15}{16})^2\cdot (\frac{7}{16})^{16} = 2^{-19.27}\).

Observation 8

For a plaintext-ciphertext pair satisfying the input-output difference relations in Observation 6, the following can be deduced according to the differential path in attacking TWINE-80:

  1. (1)

    Given \(RK^1_{[1,6,7]},RK^2_6\) that pass the differential path, then \(\frac{16}{7}\) values of \(RK^1_2\) on average can pass the path and be computed;

  2. (2)

    Given \(RK^{23}_{[2,3,4,5]}\) that pass the differential path, then \(\frac{16}{7}\) values of \(RK^{22}_0\) on average can pass the path and be computed;

  3. (3)

    Given \(RK^{23}_{[3,6]}\) that pass the differential path, then \(\frac{16}{7}\) values of \(RK^{22}_4\) on average can pass the path and be computed;

  4. (4)

    Given \(RK^{23}_{[1,3,4,5]},RK^{22}_{[0,5]}\) that pass the differential path, then \((\frac{16}{7})^2\) values of \(RK^{21}_7\) on average can pass the path and be computed.

Proof

  1. (1)

    Compute \(X^4_2\) using \(RK^4_1=RK^1_6\oplus C_H^3\) and \((\triangle X^4_2, \triangle X^4_3)\), where we get \(\#X^4_2=16/7\) for every \(RK^1_6\). Besides, \(X^3_{11}=X^2_{14}\) is computed using \(RK^1_7\) by partial encryption. Then \(X^3_{10}\) is computed using \(RK^3_5=RK^1_1\) by partial decryption, where we get \(\#X^3_{10}=16/7\) for every \(RK^1_{[1,6,7]}\). After that, together with the known \(X^2_{13}=X^1_8\) and \(RK^2_6\), we get the values of \(X^2_{12}\) where \(\#X^2_{12}=16/7\) for every \((RK^1_{[1,6,7]},RK^2_6)\). Finally, with the knowledge of \(X^1_{[4,5]}\), we can compute \(RK^1_2\) with \(\#RK^1_2=16/7\) for every \((RK^1_{[1,6,7]},RK^2_6)\).

  2. (2)

    Compute \(X^{21}_3=X^{20}_6\) using \(RK^{20}_3=RK^{23}_4\) and \((\triangle X^{20}_6, \triangle X^{20}_7)\), where we get \(\#X^{21}_3=16/7\) for every \(RK^{23}_4\). Besides, \(X^{22}_4\) is computed using \(RK^{23}_3\). Then \(X^{22}_1\) is computed using \(RK^{21}_1=RK^{23}_5\), where we get \(\#X^{22}_1=16/7\) for every \(RK^{23}_{[3,4,5]}\). What’s more, \(X^{22}_0\) is computed using \(RK^{23}_2\). Then together with the known \(X^{22}_0=X^{23}_0\), we can compute \(RK^{22}_0\) with \(\#RK^{22}_0=16/7\) for every \(RK^{23}_{[2,3,4,5]}\).

  3. (3)

    Compute \(X^{22}_9=X^{21}_{10}\) using \(RK^{21}_5=RK^{23}_3\) and \((\triangle X^{21}_{10}, \triangle X^{21}_{11})\), where we get \(\#X^{22}_9=16/7\) for every \(RK^{23}_3\). Besides, \(X^{22}_8\) is computed using \(RK^{23}_6\). Then together with \(X^{23}_6\), we can compute \(RK^{22}_4\) with \(\#RK^{22}_4=16/7\) for every \(RK^{23}_{[3,6]}\).

  4. (4)

    As just mentioned, \(16/7\) values of \(X^{22}_9\) is computed for every \(RK^{23}_3\). Since \(X^{22}_9=X^{21}_{10}\), we get \(16/7\) values of \(X^{21}_{10}\) for every \(RK^{23}_3\). Besides, Compute \(X^{20}_{13}=X^{19}_8\) using \(RK^{19}_4=RK^{22}_0\) and \((\triangle X^{19}_8, \triangle X^{19}_9)\), where we get \(\#X^{20}_{13}=16/7\) for every \(RK^{22}_0\). Then \(X^{20}_{12}\) is computed using \(RK^{20}_6=RK^{23}_1\oplus C_H^{22}\), where \(\#X^{20}_{12}=(16/7)^2\) for every \((RK^{23}_{[1,3]},RK^{22}_0)\). Furthermore, compute \(X^{22}_{14}\) using \(RK^{23}_5\), compute \(X^{22}_{10}\) using \(RK^{23}_4\), then compute \(X^{22}_{11}\) using \(RK^{22}_5\). With the knowledge of \(X^{20}_{12}\), \(X^{22}_{14}\) and \(X^{22}_{11}\), we can compute \(RK^{21}_7\) with \(\#RK^{21}_7=(16/7)^2\) for every \((RK^{23}_{[1,3,4,5]}\), \(RK^{22}_{[0,5]})\). \(\quad \Box \)

4 Impossible Differential Cryptanalysis of 23-Round TWINE-80

4.1 Analysis of Suzaki et al.’s Attack on TWINE-80

In the last paragraph of page 9 in the TWINE-80 attack [15], the authors said that In the key elimination we need to COMPUTE some other subkeys (64 bits in total), which is uniquely determined by the key of Eq. (5). These keys contain \(RK^{19}_4\), \(RK^{21}_4\), and \(RK^{23}_6\) and they can cause a contradiction with other keys. Therefore, an attacker has to compute these other subkeys using the 80-bit (\(\mathcal {K}_1,\mathcal {K}_2,\mathcal {K}_3\)), and then check whether there is a contradiction. Unfortunately, it seems that this part is omitted in their time complexity formula \(2^{50.11+10} \cdot 2^{20} \cdot 22/(23\cdot 8) =2^{77.04}\). Because we notice that \(2^{50.11+10}\) means the number of plaintext/ciphertext pairs, \(2^{20}\) stands for the time regarding \(\mathcal {K}_1\), and \(22/(23\cdot 8)\) is the time regarding (\(\mathcal {K}_2,\mathcal {K}_3\)). If the omitted time is considered, the time complexity is supposed to be bigger than exhaustive key search. Take the computation of \(RK^{23}_6 =s[RK^{23}_2] \oplus s[RK^{21}_1] \oplus s^{-1}[RK^2_7 \oplus RK^1_0]\) as an exampleFootnote 1, we know that the numbers of \(RK^{23}_2\), \(RK^{21}_1\), \(RK^2_7\), and \(RK^1_0\) that pass the differential path are all \(16/7\) for one right plaintext/ciphertext pair. Hence the time for checking whether there is a contradiction regarding \(RK^{23}_6\) is \((16/7)^4\). Multiplied by the extra \((16/7)^4\), the time complexity is \(2^{77.04}\cdot (16/7)^4 =2^{81.81}\). It seems that there is a similar problem in the analysis of their attack on TWINE-128.

Table 3. Subkeys involved in the extended head path of attacking 23-r TWINE-80
Full size table
Table 4. Subkeys involved in the extended tail path of attacking 23-r TWINE-80
Full size table
Table 5. \(KT_i\) tables
Full size table

4.2 Impossible Differential Attack on 23-Round TWINE-80

In this section, we present an impossible differential attack on 23-round TWINE-80 using the impossible differential \((0||\alpha ||\tilde{0}^{14})\overset{14r}{\nrightarrow } (\tilde{0}^{7}||\beta ||\tilde{0}^{8})\). This paper uses the same impossible differential as in [15] for TWINE-80, because it leads to the least number of involved round subkeys. The 14-round impossible differential is extended 4 rounds on the top and 5 rounds on the bottom. The extended truncated differential paths are showed in Fig. 2. Making use of Observation 2, eight equations \(RK^3_3=RK^1_5\), \(RK^3_5=RK^1_1\), \(RK^4_1=RK^1_6\oplus C_H^3\), \(RK^{19}_{4}=RK^{22}_{0}\), \(RK^{20}_{3}=RK^{23}_{4}\), \(RK^{20}_{6}=RK^{23}_{1}\), \(RK^{21}_{1}=RK^{23}_{5}\) and \(RK^{21}_{5}=RK^{23}_{3}\) are discovered. Hence the added 9 rounds involve \(44+68 =112\) bits round subkeys (see Tables 3 and 4). Therefore, \(112-80=32\) bits subkey information are redundant, which are described in Observation 3.

The idea of attacking is to discard these \(\mathcal {K}_{112}\) which pass the truncated differential paths under the condition that \(\mathcal {K}_{112}\) is indeed generated from one 80-bit master key according to the key schedule. Denote \(\mathcal {K}_0 = (RK^1_{[1,7]}, RK^{23}_{[0,1,7]})\), \(\mathcal {K}_1 = (RK^1_{[0,2,3,5,6]},RK^2_{[2,4,6,7]},RK^{22}_{[1,3,5]},RK^{23}_{[2,3,5]})\), \(\mathcal {K}_2 = (RK^{21}_{[4,7]}\), \(RK^{22}_{[0,2,4,6]},RK^{23}_{[4,6]})\). The main steps of our attack are as follows. Firstly, some tables are computed in the precomputation phase for the sake of time and memory balance. Secondly, for every guess of \(\mathcal {K}_0\), combine \((\mathcal {K}_1\), \(\mathcal {K}_2)\) which pass the truncated differentials and all the subkeys equations. And then the \(\mathcal {K}_1\) in the combined \((\mathcal {K}_1\), \(\mathcal {K}_2)\) is removed from an initialized subkey table. After all the chosen plaintext-ciphertext pairs are utilized, store \(\mathcal {K}_0\) and the finally remained \(\mathcal {K}_1\). (Notice that once \((\mathcal {K}_0\),\(\mathcal {K}_1)\) is known, \(\mathcal {K}_2\) can be computed uniquely according to the subkey equations.) Finally, do trial encryptions for the remaining keys.

Fig. 2.
figure 2

Attack path for 23-round TWINE-80 (Input (output) values marked with short sloping line and the round subkeys corresponding to black s-box are involved in the attack.)

Full size image

Precomputation. Firstly, two tiny tables are precomputed for sbox. A difference distribution table for sbox is computed to facilitate choosing more accurate plaintext-ciphertext pairs using Observation 6. So that \(\alpha _1\in \triangle s[\alpha ]\) can be examined by looking up the table. Besides, another tiny table is needed in computing round subkeys, which stores the input pairs of sbox with input and output difference as index. Take the computation of \(RK^1_0\) as an example, suppose a plaintext pair satisfies \(\triangle X^1_1 \in \triangle s[\triangle X^1_0]\), looking up this table with index \((\triangle X^1_0\), \(\triangle X^1_1)\) gives the input pair (In1, In2) for sbox, and then \(RK^1_0= In1\oplus X^1_0\).

Secondly, in order to decrease time complexity at the cost of a little memory in key recovery phase, five tables \(KT_i\) (\(i=2\),3,4,5,8) are precomputed for functions \(f_i\). Hence the computation of \(f_i\) can be replaced by one table looking up. A detailed description of these tables is showed in Table 5.

Data Collection. Choose \(2^n\) structures of plaintexts, and each structure contains plaintexts with the following form \((p_0,p_1,\gamma _0,p_2,\gamma _1,\gamma _2,\gamma _3,\gamma _4,\gamma _5,\gamma _6,p_3,p_4,p_5,p_6,\gamma _7,p_7)\), where \(\gamma _i(i=0,...,7)\) are constants in each structure and \(p_i(i=0,...,7)\) take all possible values. As a result, there are \(2^{32}\) plaintexts in each structure and we can get \(2^{n+63}\) plaintext pairs.

Ask for encryptions of the plaintexts in each structure and get the corresponding ciphertexts. The ciphertext is denoted as \((C_0, C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8, C_9, C_{10}, C_{11}, C_{12}, C_{13}, C_{14}, C_{15})\). A hash table with index \(C_{[0,2,14,15]}\) is built to choose the pairs that satisfy the condition \(\triangle C_{[0,2,14,15]} = 0\). The pairs that do not satisfy the condition are discarded. Hence there are \(2^{n+63-16}=2^{n+47}\) pairs remained.

Furthermore, filter the pairs using the plaintext and ciphertext difference relations listed in Observation 6. Therefore, \(2^{n+47-18.08} =2^{n+28.92}\) pairs are finally obtained.

Key Recovery. A detailed key recovery procedure is showed in the following Algorithm 1. It’s main steps are as follows. Firstly, 20-bit \(\mathcal {K}_0\) is guessed. And then for each plaintext-ciphertext pair, substeps \((1.2.1)\) to \((1.2.10)\) compute some round subkeys that pass the differential path. And then substep \((1.2.11)\) combines all the subkeys according to \(f_6\), \(f_7\), \(f_1\), \(f_3\), \(f_5\), \(f_4\), \(f_8\) and \(f_2\) in sequence and the differential characteristic to obtain 92-bit round subkeys. After these done, the combined 112-bit \((\mathcal {K}_0\), \(\mathcal {K}_1\), \(\mathcal {K}_2)\) pass the differential path and contains exactly 80-bit key information which can be expressed by \((\mathcal {K}_0\), \(\mathcal {K}_1)\). Therefore, the obtained \(\mathcal {K}_1\) in the combined 92-bit round Sunkeys are wrong keys and then be discarded in substep \((1.2.12)\). After step 1, the right round subkey is in the remained ones. Hence step 2 aims to recover the right key by trial encryptions. After the candidate master key is computed in substeps \((2.1.1)\) and \((2.1.2)\), a trial encryption is done in substep \((2.1.3)\) to find the right master key.

figure c

Complexity Analysis. As can be seen from Fig. 2, there are 36 active sboxes. Among these sboxes, 17 sboxes with zero input difference let the corresponding subkey pass the truncated differential with probability 1. Any of the 15 sboxes whose input and output difference appeared in the plaintext/ciphertext difference make the corresponding subkey pass the truncated differential with probability \(7^{-1}\). The subkey \(RK^{23}_3\) passes the truncated differential with probability \((\frac{7}{16})^3\) as described in substep (1.2.6). After \(RK^{23}_3\) passing, any of the 3 sboxes who has \(\triangle X^{22}_4\) as its input(output) difference and nonzero output(input) difference let the corresponding subkey pass the truncated differential with probability \(7^{-1}\). Therefore, the proportion of removing wrong subkeys for each pair is \(7^{-18}\cdot (\frac{7}{16})^3 = 2^{-54.11}\). Hence the number of remained 80-bit subkey after analyzing all \(2^{n+28.92}\) pairs is \(\sigma = 2^{80}(1-2^{-54.11})^{2^{n+28.92}} = 2^m\).

figure d

The time complexity of data collection contains: \(2^{n+32}\) to build the hash table, and \(2^{n+47}(\frac{15}{16}\cdot \sum _{i=0}^{7}(\frac{7}{16})^i +(\frac{15}{16})^2\cdot \sum _{i=8}^{14}(\frac{7}{16})^i) =2^{n+47.737}\) looking up difference distribution table to choose the pairs with required ciphertext/plaintext difference, which is \(2^{n+38.628}\) encryptions.

The time complexity of computing the tables in precomputation phase can be omitted compared to the time in key recovery phase.

Notice that the time for substep \((1.2.11)\) dominates the time of step \((1.2)\). Hence the complexity of step \((1.2)\) is \(l_1\cdot (11+2^{-4}\cdot l_2\cdot (9+\frac{16}{7}+1+7^{-1}\cdot (1+\frac{16}{7}+l_3\cdot (7+3+1+7^{-1}\cdot l_4\cdot (1+3+\frac{16}{7}+l_5\cdot (1+1+\frac{16}{7}+1+7^{-1}\cdot (1+l_6\cdot (1+(\frac{16}{7})^2\cdot 2^{-4}\cdot (2+7^{-1}\cdot l_8(2+\frac{16}{7}\cdot 7))))))))))=2^{12.73}\) xor, where the computation of \(f_6\), \(f_7\), \(f_1\) needs 11, 9, 7 xor or looking up sbox respectively. (The computation of values \(l_i\) (i = 1,...,10) and time estimation for substeps (1.2.7) to (1.2.10) is showed in Appendix B.) Hence the time complexity of step 1 in Key Recovery is \(\mathcal {T}_1 =2^{20+n+28.92+12.73}\cdot \frac{1}{23\cdot 24}\) 23-round encryptions \(=2^{n+52.54}\) encryptions.

The time complexity of step 2 in Key Recovery is \(\mathcal {T}_2= 2^{m}\) encryptions, because the time of computing \(\mathcal {K}_2\) and nine partial master key (\(k_2\), \(k_5\), \(k_7\), \(k_9\), \(k_{10}\), \(k_{11}\), \(k_{12}\), \(k_{13}\), \(k_{18}\)) is much less than one encryption for each \(\mathcal {K}_1\) (see Appendix A). Let \(n=25.85\), \(m=77.72\), then the time complexity of this attack is \(\mathcal {T}_1 + \mathcal {T}_2 =2^{79.09}\) encryptions. Hence, the data complexity is \(2^{57.85}\) blocks and the memory complexity is \(2^m\cdot 80/64 + 2^{60}/64=2^{78.04}\) blocks.

5 Impossible Differential Attack on 24-Round TWINE-128

Attack on 24-round TWINE-128 uses the impossible differential \((\tilde{0}^{5}||\alpha ||\tilde{0}^{10}) \overset{14r}{\nrightarrow } (\tilde{0}^{11}||\beta ||\tilde{0}^{4})\), because it involves the least number of round subkeys. What’s more, subkeys involved in the truncated differential paths have less complicated equations which are showed in Observation 5. We extend 5 rounds on the top and the bottom of the 14-round impossible differential respectively. Table 6 and Table 7 show that the top 5 rounds involve 80-bit subkey information and the bottom 5 rounds involve 84-bit subkey information respectively. Therefore, \(80+84-128=36\) bits subkey information are redundant, which are described in Observation 5.

Table 6. Subkeys involved in the extended head path of attacking TWINE-128
Full size table
Table 7. Subkeys involved in the extended tail path of attacking TWINE-128
Full size table

Attacking TWINE-128 is similar to attack on TWINE-80. Suppose \(2^n\) structures are used in this attack, and each structure contains plaintexts with the form \((p_0\), \(p_1\), \(\gamma _0\), \(p_2\), \(p_3\), \(p_4\), \(\gamma _1\), \(\gamma _2\), \(\gamma _3\), \(p_5\), \(p_6\), \(p_7\), \(p_8\), \(p_9\), \(p_{10}\), \(p_{11})\), where \(\gamma _i (i=0,...,3)\) are constants and \(p_i (i=0,...,11)\) take all possible values in each structure. As a result, there are \(2^{48}\) plaintexts in each structure and \(2^{n+95}\) pairs are obtained. And then select the pairs that satisfy Observation 7, \(2^{n+95-16-19.27}=2^{n+59.73}\) pairs are finally obtained. The complexity of data collection is \(2^{n+70.6278}\) encryptions.

Let \(\mathcal {K}_0= (RK^1_{[1,4]}\), \(RK^{24}_{[2,4,5]})\), \(\mathcal {K}_1= (RK^1_{[0,2,3,5,6,7]}\), \(RK^2_{[0,2,3,4,5,6,7]}\), \(RK^3_{[0,1,3,5]}\), \(RK^4_0\), \(RK^{21}_2\), \(RK^{22}_6\), \(RK^{23}_{[0,1,2,4]}\), \(RK^{24}_{[0,6,7]})\), \(\mathcal {K}_2= (RK^{21}_0\), \(RK^{22}_{[0,2,3]}\), \(RK^{23}_{[3,5,7]}\), \(RK^{24}_{[1,3]})\), Since the main idea of key recovery is similar to that in TWINE-80, we give the detailed description of key recovery algorithm in Appendix C. Combining \((\mathcal {K}_0\), \(\mathcal {K}_1\), \(\mathcal {K}_2)\) that pass the truncated differentials and the equations in Observation 5 can be done in \(2^{45.48}\) xor operations according to \(g_1\), \(g_2\), \(g_3\), \(g_4\), \(g_9\), \(g_7\), \(g_8\), \(g_5\), \(g_6\) in sequence (see Appendix C).

Therefore, the time for filtering wrong keys is \(\mathcal {T}_1 =2^{20+n+59.73+45.48}\cdot \frac{1}{24\cdot 24}\) 24-round encryptions \(=2^{n+116.04}\) encryptions, followed by \(\mathcal {T}_2= 2^{m}\) encryptions to do trial encryptions. Since the probability of differential path is Pr\(= (7^{-11}\cdot (\frac{7}{16})^3)^2 =2^{-68.92}\), let \(\sigma = 2^{128}\cdot (1-2^{-68.92})^{2^{n+59.73} }=2^m\). Take \(n=10.1\), \(m=125.29\), then the time complexity is \(\mathcal {T}_1+\mathcal {T}_2= 2^{126.78}\) encryptions. And the memory complexity and data complexity are \(2^m\cdot 80/64 + 2^{108}/64=2^{125.61}\) blocks and \(2^{58.1}\) blocks respectively.

6 Conclusion

This paper gives an impossible differential cryptanalysis of reduced-round TWINE-80 and TWINE-128. In the attacks, we present some key relations, and then an optimal algorithm is proposed to recovery subkeys using these relations, which may be used in other types of attacks. According to the known results, it seems that TWINE currently remains immune to impossible differential attack.