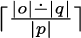Abstract
The development of sophisticated termination criteria for term rewrite systems has led to powerful and complex tools that produce (non)termination proofs automatically. While many techniques to establish termination have already been formalized—thereby allowing to certify such proofs—this is not the case for nontermination. In particular, the proof checker  was so far limited to (innermost) loops. In this paper we present an Isabelle/HOL formalization of an extended repertoire of nontermination techniques. First, we formalized techniques for nonlooping nontermination. Second, the available strategies include (an extended version of) forbidden patterns, which cover in particular outermost and context-sensitive rewriting. Finally, a mechanism to support partial nontermination proofs further extends the applicability of our proof checker.
was so far limited to (innermost) loops. In this paper we present an Isabelle/HOL formalization of an extended repertoire of nontermination techniques. First, we formalized techniques for nonlooping nontermination. Second, the available strategies include (an extended version of) forbidden patterns, which cover in particular outermost and context-sensitive rewriting. Finally, a mechanism to support partial nontermination proofs further extends the applicability of our proof checker.
This research was supported by the Austrian Science Fund (FWF): P22767 and I963.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Program verification aims to establish certain properties of pieces of software, such as termination. But in presence of bugs it is often at least as important to show the negative property by means of a counter-example or, more generally, a disproof, such as a nontermination argument.
In this paper we consider term rewrite systems (TRSs) which constitute a powerful means to express functional programs in a compact way, and are thus a natural input format for program analysis. However, many programming languages employ particular evaluation strategies that are to be considered in program analysis. Thus also TRSs have to be analyzed with respect to specific strategies. In particular, a TRS which is nonterminating when ignoring the strategy may still be terminating when the evaluation respects the strategy.
Sophisticated techniques to analyze termination of TRSs (under strategies) have been developed and implemented in tools for automated termination analysis like AProVE [6] and  [12]. However, these tools are complex and thus one should not blindly trust them: ever so often some tool delivers an incorrect proof, which remains undetected unless another prover gives the opposite answer on the same TRS. Therefore, it is of major importance to independently certify the generated proofs, which can be done using various certifiers [3, 4, 21] that rely on formalizations within some trusted proof assistant. Due to certification, bugs have been revealed in termination tools that have gone unnoticed for years and were easily fixed after they have been detected.
[12]. However, these tools are complex and thus one should not blindly trust them: ever so often some tool delivers an incorrect proof, which remains undetected unless another prover gives the opposite answer on the same TRS. Therefore, it is of major importance to independently certify the generated proofs, which can be done using various certifiers [3, 4, 21] that rely on formalizations within some trusted proof assistant. Due to certification, bugs have been revealed in termination tools that have gone unnoticed for years and were easily fixed after they have been detected.
Our certifier for nontermination techniques is developed in the proof assistant Isabelle/HOL [16], and a preliminary version was already described in [23], which however was quite limited: only looping TRSs \({\mathcal {R}}\) could be treated, i.e., TRSs which admit derivations of the form \(t \rightarrow _{\mathcal {R}}^+ C[t\mu ]\) for some term \(t\), context \(C\), and substitution \(\mu \); and the only supported strategy was innermost. There are even more severe restrictions for the other certifiers: [3] only supports loops without strategy, and [4] does not support nontermination proofs at all.
In the meanwhile, we extended our repertoire of formalized nontermination techniques. It now covers techniques for nonlooping nonterminating TRSs. Moreover, as strategy specification we now support an extended version of forbidden patterns [9], which generalizes many common strategies like (leftmost)-innermost, (leftmost)-outermost, and context-sensitive rewriting [15]. Finally, we also integrated a mechanism to support partial nontermination proofs, which further increases the applicability of our certifier and led to the detection of a severe soundness bug of AProVE, which has now been fixed.
We consider our contributions threefold. First and foremost, our extensions significantly increased the number of certifiable nontermination proofs. Second, on the theory level we could drastically simplify one of the algorithms for checking nontermination using forbidden patterns, and relax the preconditions for applying the technique of rewriting dependency pairs (cf. Theorem 14). Finally, we illustrate how termination checkers can benefit from certification: we used Isabelle’s code generator [10] to integrate the executable functions from our certifier in  , such that this tool is now able to automatically generate nontermination proofs involving general forbidden pattern strategies. This nearly doubled the number of generated nontermination proofs of
, such that this tool is now able to automatically generate nontermination proofs involving general forbidden pattern strategies. This nearly doubled the number of generated nontermination proofs of  .
.
The remainder is structured as follows. In Sect. 2 we give preliminaries. In Sect. 3 we explain our formalization of loop detection involving forbidden patterns. Afterwards, Sect. 4 deals with techniques that allow to disprove termination of nonlooping TRSs, namely the techniques of rewriting and narrowing dependency pairs [7], the switch between innermost termination and termination [8], and a direct technique to disprove termination [5]. Experimental data is provided in Sect. 5 where we also explain how we integrated forbidden patterns in  , and why and how we added support for partial nontermination proofs to
, and why and how we added support for partial nontermination proofs to  . We conclude in Sect. 6.
. We conclude in Sect. 6.
Our formalization is part of the Isabelle Formalization of Rewriting ( ) which also includes our certifier
) which also includes our certifier  [21]. Since
[21]. Since  contains every tiny detail of each proof, in the paper we just highlight some differences between the formalization and the paper proofs. Both
contains every tiny detail of each proof, in the paper we just highlight some differences between the formalization and the paper proofs. Both  and all details on our experiments are available at http://cl-informatik.uibk.ac.at/software/ceta/experiments/ntcert/.
and all details on our experiments are available at http://cl-informatik.uibk.ac.at/software/ceta/experiments/ntcert/.
2 Preliminaries
We refer to [2] for the basics of rewriting. We use \(\ell \), \(r\), \(s\), \(t\), \(u\), \(w\) for terms, \(f\), \(g\) for function symbols, \(x\), \(y\) for variables, \(\sigma \), \(\mu \), \(\tau \), \(\delta \) for substitutions, \(i\), \(j\), \(k\), \(n\), \(m\) for natural numbers, \(o\), \(p\), \(q\) for positions, \(C\), \(D\) for contexts, and \({\mathcal {P}}\), \({\mathcal {R}}\) for TRSs. Here, substitutions are mappings from variables to terms, and \(t\mu \) is the term \(t\) where each variable \(x\) in \(t\) has been replaced by \(\mu (x)\); contexts are terms which contain exactly one hole \({\Box }\), \(t[\cdot ]_p\) is the context that is obtained by replacing the subterm \(t|_p\) of \(t\) at position \(p\) by the hole \(\Box \). The term \(C[t]\) is the term where the hole in \(C\) is replaced by \(t\). We write \(s \unrhd t\) if \(s = C[t]\) for some context \(C\) and \(s \rhd t\) if \(s \unrhd t\) and \(s \ne t\). A position \(p\) is left of \(q\) iff \(p = o \, i \, p'\), \(q = o \, j \, q'\), and \(i < j\). The set of positions in a term \(t\) is written as \({\mathcal {P}}{\mathsf {os}}(t)\) and \(\varepsilon \) denotes the empty position. The set of variables is \({\mathcal {V}}\), and \({\mathcal {V}}(t)\) are the variables within a term \(t\).
A TRS \({\mathcal {R}}\) is a set of rewrite rules \(\ell \rightarrow r\). The rewrite relation of \({\mathcal {R}}\) at position \(p\) is defined by \(t \rightarrow _{{\mathcal {R}},p} s\) iff \(t = C[\ell \sigma ]\) and \(s = C[r\sigma ]\) for some rule \(\ell \rightarrow r \in {\mathcal {R}}\), substitution \(\sigma \), and context \(C\) with \(C|_p = {\Box }\). In this case, the term \(\ell \sigma \) is called a redex at position \(p\). The reduction is outermost iff there is no redex above \(p\), and it is innermost (denoted  ) iff there are no redexes below \(p\). We often omit \(p\) and \({\mathcal {R}}\) in a reduction \(\rightarrow _{{\mathcal {R}},p}\), if \({\mathcal {R}}\) is obvious from the context, and if \(p\) can be chosen freely. A TRS is overlay iff all critical pairs of the TRS are due to root overlaps, i.e., there are no rules \(\ell _1 \rightarrow r_1\) and \(\ell _2 \rightarrow r_2\) such that a non-variable proper subterm of \(\ell _1\) unifies with \(\ell _2\). A TRS is locally confluent if every critical pair \((s,t)\) is joinable, i.e., there is some \(u\) such that \(s \rightarrow _{\mathcal {R}}^* u\) and \(t \rightarrow _{\mathcal {R}}^* u\).
) iff there are no redexes below \(p\). We often omit \(p\) and \({\mathcal {R}}\) in a reduction \(\rightarrow _{{\mathcal {R}},p}\), if \({\mathcal {R}}\) is obvious from the context, and if \(p\) can be chosen freely. A TRS is overlay iff all critical pairs of the TRS are due to root overlaps, i.e., there are no rules \(\ell _1 \rightarrow r_1\) and \(\ell _2 \rightarrow r_2\) such that a non-variable proper subterm of \(\ell _1\) unifies with \(\ell _2\). A TRS is locally confluent if every critical pair \((s,t)\) is joinable, i.e., there is some \(u\) such that \(s \rightarrow _{\mathcal {R}}^* u\) and \(t \rightarrow _{\mathcal {R}}^* u\).
We write \(t \rightarrow ^! s\) if both \(t \rightarrow ^* s\) and \(s\) is in normal form w.r.t. \(\rightarrow \), i.e., there is no \(u\) such that \(s \rightarrow u\). Strong normalization of \(\rightarrow \) is denoted by \({ SN }(\rightarrow )\), and \({ SN }_\rightarrow (t)\) denotes that \(t\) admits no infinite derivation w.r.t. \(\rightarrow \). We sometimes write \({ SN }_{\mathcal {R}}(t)\) instead of \({ SN }_{\rightarrow _{\mathcal {R}}}(t)\). A DP problem is a pair of two TRSs \(({\mathcal {P}},{\mathcal {R}})\) where \({\mathcal {P}}\) is a set of dependency pairs encoding recursive calls, and \({\mathcal {R}}\) is used to evaluate the arguments between two recursive calls. A \(({\mathcal {P}},{\mathcal {R}})\) chain is an infinite derivation of the form \(s_1\sigma _1 \rightarrow _{{\mathcal {P}},\varepsilon } t_1\sigma _1 \rightarrow ^*_{\mathcal {R}}s_2\sigma _2 \rightarrow _{{\mathcal {P}},\varepsilon } t_2\sigma _2 \rightarrow ^*_{\mathcal {R}}\dots \) where each \(s_i \rightarrow t_i \in {\mathcal {P}}\). The chain is an innermost chain, iff additionally  is satisfied for all \(i\). A TRS \({\mathcal {R}}\) is (innermost) nonterminating iff \({ SN }(\rightarrow _{\mathcal {R}})\) (
is satisfied for all \(i\). A TRS \({\mathcal {R}}\) is (innermost) nonterminating iff \({ SN }(\rightarrow _{\mathcal {R}})\) ( ) does not hold. A DP problem \(({\mathcal {P}},{\mathcal {R}})\) is (innermost) nonterminating iff it admits an (innermost) \(({\mathcal {P}},{\mathcal {R}})\) chain or if \({\mathcal {R}}\) is (innermost) nonterminating.Footnote 1
) does not hold. A DP problem \(({\mathcal {P}},{\mathcal {R}})\) is (innermost) nonterminating iff it admits an (innermost) \(({\mathcal {P}},{\mathcal {R}})\) chain or if \({\mathcal {R}}\) is (innermost) nonterminating.Footnote 1
Since the paper describes the formalization on an informal level which does not require deep knowledge of Isabelle, we omit an introduction to this proof assistant here. The logic we are using is classical HOL, which is based on simply-typed lambda-calculus, enriched with a simple form of ML-like polymorphism.
3 Forbidden Patterns
This section deals with checking whether a loop is indeed a loop with respect to a particular evaluation strategy: Given a certificate containing a TRS \({\mathcal {R}}\), a loop and some strategy, our proof checker  can check whether there does indeed exist an infinite \({\mathcal {R}}\)-rewrite sequence which adheres to this strategy.
can check whether there does indeed exist an infinite \({\mathcal {R}}\)-rewrite sequence which adheres to this strategy.
To support a broad variety of strategies we consider forbidden pattern rewriting, which covers for instance innermost, outermost, and context-sensitive rewriting [9, 15]. Hence the formalization of techniques for forbidden pattern strategies has the significant advantage that a wide range of strategies can be treated by the same formalism, so  internally converts all outermost and context-sensitive strategies into forbidden patterns before the certifier for nontermination proofs is invoked, cf. certify-cert-problem in Proof_Checker.thy. We give a motivating example before recalling some preliminaries on forbidden pattern rewriting.
internally converts all outermost and context-sensitive strategies into forbidden patterns before the certifier for nontermination proofs is invoked, cf. certify-cert-problem in Proof_Checker.thy. We give a motivating example before recalling some preliminaries on forbidden pattern rewriting.
Example 1
Consider the following applicative TRS which models a buggy implementation of the \(\mathsf {map}\) function, where \(\mathrel {`}\) denotes a binary infix application symbol, and \({\mathsf {:}}\) the cons operator. In the recursive call one forgot to invoke \({\mathsf {tl}}\) on \(xs\) and hence the TRS does not terminate.

Without strategy there is a loop \({\mathsf {map}}\mathrel {`}f \mathrel {`}{\mathsf {nil}}\rightarrow C[{\mathsf {map}}\mathrel {`}f \mathrel {`}{\mathsf {nil}})]\) for \(C = \mathsf {if}\mathrel {`}({\mathsf {empty}}\mathrel {`}{\mathsf {nil}}) \mathrel {`}{\mathsf {nil}}\mathrel {`}({\mathsf {:}}\mathrel {`}(f \mathrel {`}({\mathsf {hd}}\mathrel {`}{\mathsf {nil}}))\mathrel {`}\Box )\) which definitely does not show the real problem of \({\mathsf {map}}\) to the user: the loop ignores the common evaluation strategy for \(\mathsf {if}\) which disallows reductions in the then and else branches. Note that due to the applicative setting this desired behavior is not expressible by a context-sensitive strategy, but it can be modeled by a forbidden strategy, as shown in Example 3.
3.1 Background
Using forbidden pattern strategies one can specify that the position of any redex may not be below (or above) certain patterns. In this way one can express outermost (or innermost) strategies. We consider the following extended definition of a forbidden pattern which allows for patterns with location \(\mathrm{{R}}\). This admits to also express strategies like leftmost-outermost with special treatment for \(\mathsf {if}\).
Definition 2
A forbidden pattern is a triple \((\ell ,o,\lambda )\) for a term \(\ell \), position \(o \in {\mathcal {P}}{\mathsf {os}}(\ell )\), and \(\lambda \in \{\mathrm{{H}},\mathrm{{A}},\mathrm{{B}},\mathrm{{R}}\}\). For a set \(\varPi \) of forbidden patterns the relation  is defined by
is defined by  iff \(t \rightarrow _p s\) and there is no pattern \((\ell ,o,\lambda ) \in \varPi \) such that there exist a position \(o' \in {\mathcal {P}}{\mathsf {os}}(t)\), a substitution \(\sigma \) with \(t|_{o'} = \ell \sigma \), and
iff \(t \rightarrow _p s\) and there is no pattern \((\ell ,o,\lambda ) \in \varPi \) such that there exist a position \(o' \in {\mathcal {P}}{\mathsf {os}}(t)\), a substitution \(\sigma \) with \(t|_{o'} = \ell \sigma \), and

Example 3
For the TRS in Example 1, the forbidden pattern strategy where \(\varPi \) consists of \((\mathsf {if}\mathrel {`}b \mathrel {`}t \mathrel {`}e, p, \lambda )\) for all \(p \in \{12, 2\}\) and \(\lambda \in \{\mathrm{{H}}, \mathrm{{B}}\}\) has the intended effect that reductions in the then and else branches are not allowed.
A TRS \({\mathcal {R}}\) is forbidden-pattern nonterminating w.r.t. \(\varPi \) iff  , which can be proven via forbidden pattern loops (\(\varPi \)-loops). To succinctly describe infinite derivations that are induced by loops we use context-substitutions.
, which can be proven via forbidden pattern loops (\(\varPi \)-loops). To succinctly describe infinite derivations that are induced by loops we use context-substitutions.
Definition 4
[22]. A context-substitution is a pair \((C,\mu )\) consisting of a context \(C\) and a substitution \(\mu \). The \(n\)-fold application of \((C,\mu )\) to a term \(t\), denoted \(t(C,\mu )^n\), is inductively defined as \(t(C,\mu )^{0} = t\) and \(t(C,\mu )^{n+1} = C[t(C,\mu )^n\mu ]\).
As an example for context-substitutions, we refer to Fig. 1 which illustrates the term \(t(C,\mu )^3\).
Context-substitutions allow to concisely write the infinite derivation induced by a loop \(t \rightarrow _{}^{+} C[t\mu ]\) as \(t = t(C,\mu )^{0} \rightarrow _{}^{+} t(C,\mu )^{1} \rightarrow _{}^{+} \ldots \rightarrow _{}^{+}t(C,\mu )^{n} \rightarrow _{}^{+} \ldots \).
To facilitate the certification of loops under strategies, one needs to analyze its constituting steps. In the remainder of this section we will consider a loop with starting term \(t\), context \(C\) and substitution \(\mu \) with \(C|_p = {\Box }\) of the form
A loop of the form (1) is a \(\varPi \) -loop iff the step \(t_i(C,\mu )^n \rightarrow _{p^nq_i} t_{i+1}(C,\mu )^n\) respects the forbidden pattern strategy induced by \(\varPi \) for all \(i \leqslant m\) and all \(n \in \mathbb {N}\). For instance, assuming that one of the loop’s redexes is \(t|_q\) as illustrated in Fig. 1, we need to know whether this position remains a redex w.r.t. to the strategy, no matter how many contexts and substitutions are applied around \(t\).
The problem of whether a loop constitutes a \(\varPi \)-loop is decidable. To this end, the following notions from innermost and outermost loops are useful.
Definition 5
[20, 22]. A matching problem is a pair \({(u \gtrdot \ell , \mu )}\). It is solvable iff there are \(n\) and \(\sigma \) such that \(u\mu ^n = \ell \sigma \). An extended matching problem is a tuple \({(D \gtrdot \ell ,C,t,{\mathcal {M}},\mu )}\) where \({\mathcal {M}}= \{s_1 \gtrdot \ell _1,\ldots ,s_n \gtrdot \ell _n\}\). It is solvable iff there are \(m\), \(k\), \(\sigma \), such that \(D[t(C,\mu )^m]\mu ^k = \ell \sigma \) and \(s_i\mu ^k = \ell _i\sigma \) for all \(i\). If \({\mathcal {M}}= \varnothing \), we just omit it.
A set of (extended) matching problems is solvable iff some element is solvable. Given a loop, in order to decide whether it indeed constitutes a \(\varPi \)-loop one computes a set of (extended) matching problems which has no solution if and only if the loop is indeed a \(\varPi \)-loop.
3.2 From Forbidden Pattern Loops to Matching Problems
A rewrite step is a \(\varPi \)-step iff it adheres to every single pattern \(\pi \in \varPi \). In fact a loop (1) is a \(\varPi \)-loop if and only if the following key property holds for all choices of \(\pi \in \varPi \), \(t=t_i\), \(t'=t_{i+1}\) and \(q=q_i\) where \(1 \leqslant i < m\) [24]:
Property 6
For a forbidden pattern \(\pi = (\ell ,o,\lambda )\) and \(t \rightarrow _q t'\) all reductions \(t(C,\mu )^n \rightarrow _{p^nq} t'(C,\mu )^n\) are allowed with respect to \(\pi \), i.e., there are no \(n\), \(o'\), and \(\sigma \) such that \(t(C,\mu )^n|_{o'} = \ell \sigma \) and \(p^nq = o'o\) if \(\lambda = \mathrm{{H}}\), \(p^nq < o'o\) if \(\lambda = \mathrm{{A}}\), \(p^nq > o'o\) if \(\lambda = \mathrm{{B}}\), and \(p^nq\) is right of \(o'\) if \(\lambda = \mathrm{{R}}\).
This property can be decided by a case analysis on \(\lambda \), defining suitable sets of (extended) matching problems for each case. In the following paragraphs we give these sets for patterns of type \((\cdot ,\cdot ,\mathrm{{R}})\) and \((\cdot ,\cdot ,\mathrm{{B}})\). The other cases are similar, details can be found in the formalization.
Forbidden Patterns of Type \(\mathbf{( }\cdot ,\cdot ,\mathbf{R }\mathbf{). }\) For patterns \(\pi =(\ell ,o,\mathrm{{R}})\), it has to be checked whether \(p^nq\) occurs to the right of \(o'\). There are four possibilities, as illustrated in Fig. 1: (1) \(o'\) ends in \(t\), (2) \(o'\) ends in a term \(t\mu ^k\), (3) \(o'\) ends in a position of \(C^k\), or otherwise (4) \(o'\) ends in a position of \(C^k\mu ^{k-1}\), for some \(k \leqslant n\). Let \({\mathcal {W}}(t) = \bigcup _{k \in {\mathbb {N}}}{\mathcal {V}}(t\mu ^k)\) denote the set of variables introduced by the substitution \(\mu \) when applied iteratively. Then each case can be covered by a set of matching problems as follows:
Definition 7
Let \({\mathcal {M}}_{\mathrm{{R}},\pi }\) denote the union of the following four sets:

For the formalization of patterns \((\cdot , \cdot , \mathrm{{R}})\), we first had to incorporate support for the left-of relation on positions. However, the most effort was spent on the case analysis, i.e., an induction proof showing that any position in a context-substitution \(t(C,\mu )^n\) fits into one of the four cases.
Forbidden Patterns of Type \(\mathbf{( }\cdot ,\cdot ,\mathbf{B }\mathbf{). }\) For patterns \(\pi =(\ell ,o,\mathrm{{B}})\) the position \(o'o\) has to be strictly above the redex, i.e., \(p^nq > o'o\). Here two cases can be distinguished: \(o'o\) may end in \(t\), so \(o'o \geqslant p^n\), or it may end in some occurrence of \(C\), so \(o'o < p^n\) (similar to cases (1) and (3) in Fig. 1).
In case of the former, \(o'o\) has finitely many possibilities to hit a position in \(t\) above \(q\). Thus, this case reduces to finitely many \((\cdot ,\cdot ,\mathrm{{H}})\) cases.
In the latter case, \(o'o\) is a non-hole position of \(C^n\), i.e., \(p^n > o'o\) (and hence \(p > \varepsilon \)). We consider all possibilities for non-empty subcontexts \(D\), and compute a number \(n_0\) such that it suffices to consider the term \(t(C,\mu )^{n_0}\) in order to account for all loop iterations.Footnote 2 A detailed analysis of these two cases leads to the following sets of matching problems \({\mathcal {M}}_{\mathrm{{B}}}\) and \({\mathcal {E}}_{\mathrm{{B}}}\):
Definition 8
The (extended) matching problems \({\mathcal {M}}_{\mathrm{{B}},\pi } = {\mathcal {M}}_{\mathrm{{B}},1} \cup {\mathcal {E}}_{\mathrm{{B}},2}\) are

where \({\mathcal {M}}_{\mathrm{{H}},(\ell ,\bar{q},\mathrm{{H}})}\) refers to the \(\mathrm{{H}}\) matching problem for \(t\), \(q\), and \((C,\mu )\), and \(n_0\) is, dependent on \(p''\), the minimal number satisfying \(|p''| + n_0|p| > |o|\).
Unsolvability of the respective sets of (extended) matching problems is a sufficient and necessary condition for Property 6:
Theorem 9
[24]. Let \(t \rightarrow _q t'\) and let \((C,\mu )\) be a context-substitution such that \(C|_p = {\Box }\). All reductions \(t(C,\mu )^n \rightarrow _{p^nq} t'(C,\mu )^n\) are allowed with respect to the pattern \(\pi =(\ell ,o,\lambda )\) if and only if \({\mathcal {M}}_{\lambda ,\pi }\) is not solvable.
As to be expected from the technical definitions, the soundness and completeness results for the respective cases required a considerable amount of reasoning about contexts and positions. We preferred contexts over positions whenever possible: position reasoning tends to be tedious because one always needs to ensure that they are valid in the term where they are to be used. For instance,  internally represents forbidden patterns as triples \((\ell [\cdot ]_o,\ell |_o,\lambda )\) rather than \((\ell , o, \lambda )\) to avoid the obvious side condition \(o \in {\mathcal {P}}{\mathsf {os}}(\ell )\). The amount of bureaucracy on valid positions required throughout the formalization was nevertheless substantial. Apart from this, the proofs for all cases could be formalized along the lines of the paper proof. For the case of \(\mathrm{{B}}\) patterns the results crucially rely on the new solving procedure for extended matching problems.
internally represents forbidden patterns as triples \((\ell [\cdot ]_o,\ell |_o,\lambda )\) rather than \((\ell , o, \lambda )\) to avoid the obvious side condition \(o \in {\mathcal {P}}{\mathsf {os}}(\ell )\). The amount of bureaucracy on valid positions required throughout the formalization was nevertheless substantial. Apart from this, the proofs for all cases could be formalized along the lines of the paper proof. For the case of \(\mathrm{{B}}\) patterns the results crucially rely on the new solving procedure for extended matching problems.
3.3 Deciding Solvability of Extended Matching Problems
Solvability of (extended) matching problems is known to be decidable [20, 22], and in [23] we already formalized and simplified the decision procedure for non-extended matching problems. In the remainder of this section we present our algorithm to decide solvability of extended matching problems—these problems originate from the outermost loop checking procedure and are also required in the case of forbidden patterns, cf. Definition 8.
As in [23], our proofs deviate from the paper proofs considerably and result in a simplified decision procedure which we also integrated in termination tools. For example, in AProVE we have been able to delete some sub-algorithms (180 lines) and replace them by a single line of code.
The decision procedure in [22] works in three phases: first, any extended matching problem is simplified to solved form; second, from the simplified matching problem a set of (extended) identity problems is generated, and finally, solvability of the identity problems is decided. We followed this general structure in the formalization, and only report on the first and the third phase, since the second phase was straightforward.
The algorithm for the first phase consists of a set of strongly normalizing inference rules. It contains rules for decomposition and symbol clash as in a standard matching algorithmFootnote 3, but also incorporates rules to apply a (context-)substitution in cases where a standard matching algorithm would fail.
Definition 10
[22, Definition 5]. Let \({{ MP }}= {(D \gtrdot \ell _0,C,t,{\mathcal {M}},\mu )}\) be an extended matching problem where \({\mathcal {M}}= \{s_1 \gtrdot \ell _1, \dots ,s_m \gtrdot \ell _m\}\) and \(C \ne \Box \). Then \({{ MP }}\) is in solved form iff each \(\ell _i\) is a variable. Let \({\mathcal {V}}_{\mathsf{incr },\mu }= \{x \in {\mathcal {V}}\mid \exists n : x\mu ^n \notin {\mathcal {V}}\}\) be the set of increasing variables.
We define a relation \(\Rightarrow \) which simplifies extended matching problems that are not in solved form, so suppose \(\ell _j = f(\ell '_1,\dots ,\ell '_{m'})\).
-
(v)
\({{ MP }}\Rightarrow \bot \) if \(s_j \in {\mathcal {V}}{\setminus } {\mathcal {V}}_{\mathsf{incr },\mu }\)
-
(vi)
\({{ MP }}\Rightarrow {(D\mu \gtrdot \ell _0,C\mu ,t\mu ,\{s_i\mu \gtrdot \ell _i \mid 1 \leqslant i \leqslant m\},\mu )}\) if \(s_j \in {\mathcal {V}}_{\mathsf{incr },\mu }\)
-
(vii)
\({{ MP }}\Rightarrow \top \) if \(j = 0\), \(D = \Box \), and \({({\mathcal {M}}\cup \{t \gtrdot \ell _0\}, \mu )}\) is solvable
-
(viii)
\({{ MP }}\Rightarrow {(C \gtrdot \ell _0,C\mu ,t\mu ,{\mathcal {M}},\mu )}\) if \(j= 0\), \(D = \Box \), and \({({\mathcal {M}}\cup \{t \gtrdot \ell _0\}, \mu )}\)
is not solvable
As in [23], where we formalized the inference rules for simplifying non-extended matching problems, we implemented these rules directly as a function simplify-emp-main using Isabelle’s function package [13]. In this way, we did not have to formalize confluence of \(\Rightarrow \).
Note that for this function one faces the problem of getting it terminating and efficient at the same time: if one has to recompute \({\mathcal {V}}_{\mathsf{incr },\mu }\) in every iteration, the function becomes inefficient; on the other hand, if one passes \({\mathcal {V}}_{\mathsf{incr },\mu }\) using an additional parameter (e.g., \(V_i\)) then the function is not necessarily terminating as it is not guaranteed that \(V_i\) is indeed instantiated by \({\mathcal {V}}_{\mathsf{incr },\mu }\). To see this, suppose the simplification algorithm is invoked on the problem \({(D \gtrdot \ell ,C,t,\{x \gtrdot {\mathsf {c}}\},\mu )}\) where \(\mu \) is the empty substitution but \(V_i\) a set containing \(x\). Then an application of Rule (vi) immediately leads to a recursive call with the same arguments.
To solve this problem, in [23] it was proposed to write two functions: The main soundness result is proven for a terminating but inefficient one where \({\mathcal {V}}_{\mathsf{incr },\mu }\) gets recomputed in every recursive call. A second, possibly nonterminating function has \(V_i\) as additional argument and is proven to be equivalent to the first function if invoked with the right arguments, i.e., in this case with \(V_i = {\mathcal {V}}_{\mathsf{incr },\mu }\).
Although this solution leads to an efficient and sound implementation, it imposes quite some overhead. First, one has to write the simplification algorithm twice, and second one has to perform an equivalence proof of the two functions.
Therefore we propose a different solution for simplify-emp-main. The simple idea is to pass the pair \((\mu ,V_i)\) as an argument to simplify-emp-main, where this pair is encapsulated in a new type with the invariant that \(V_i = {\mathcal {V}}_{\mathsf{incr },\mu }\). Thus, in the implementation one just has to provide selectors from the new type to both \(\mu \) and \(V_i\), where it now suffices to write only one implementation of simplify-emp-main. Moreover, the whole quotient construction—creation of the new type, writing the selectors, reasoning about this new type—can conveniently be done via the lifting and transfer-package of Isabelle [11]. Note that in the meantime we also rewrote the simplification algorithm for matching problems in [23] using the same idea, again by using lifting and transfer.
For the third phase where (extended) identity problems are to be solved, we could of course reuse the algorithm for non-extended identity problems that has been developed in [23]. However, we did not stick to the complicated algorithm of [22] for extended identity problems, since it requires several auxiliary algorithms and the soundness proofs are difficult or tedious to formalize. (The whole description takes 3.5 pages in [22] where these pages do not even cover all proofs.) Instead, we developed a new, partial algorithm which is easy to implement and easy to formalize. In detail, we show that all extended identity problems that are constructed for forbidden patterns via simplify-emp-main belong to a special class of extended identity problems where the context within such a problem is large in comparison to the other terms. This class of problems can easily be translated into non-extended identity problems via the following mini-algorithm: an extended identity problem \({(D \approx s,\mu ,C,t)}\) is solvable iff the identity problem \({(D[t] \approx s, \mu )}\) is solvable, provided there is some \(i\) such that \(C \rhd s\mu ^i\). For more details on (extended) identity problems and our new proofs we refer to [22] and lemmas eident-prob-to-ident-prob and simplify-emp-main-large-C within the theory Outermost_Loops.thy.
4 Nonlooping Nontermination
While in the previous section we restricted ourselves to loops (though for every forbidden pattern strategy), we now aim at possibly nonlooping nonterminating TRSs, but only consider innermost strategies. More precisely, we consider the variant of innermost rewriting which corresponds to  where \(\varPi = \{(\ell ,\varepsilon ,\mathrm{{A}}) \mid \ell \in {\mathcal {Q}}\}\) for some set of terms \({\mathcal {Q}}\). The corresponding rewrite relation is qrstep within
where \(\varPi = \{(\ell ,\varepsilon ,\mathrm{{A}}) \mid \ell \in {\mathcal {Q}}\}\) for some set of terms \({\mathcal {Q}}\). The corresponding rewrite relation is qrstep within  , and it generalizes rewriting without strategy (\({\mathcal {Q}}= \varnothing \)) and innermost rewriting (\({\mathcal {Q}}= \{\ell \mid \ell \rightarrow r \in {\mathcal {R}}\}\)). To ease the presentation, in the paper we just consider the special cases \(\rightarrow _{\mathcal {R}}\) and
, and it generalizes rewriting without strategy (\({\mathcal {Q}}= \varnothing \)) and innermost rewriting (\({\mathcal {Q}}= \{\ell \mid \ell \rightarrow r \in {\mathcal {R}}\}\)). To ease the presentation, in the paper we just consider the special cases \(\rightarrow _{\mathcal {R}}\) and  in the following. In total, we discuss three different techniques which can be used to disprove termination for nonlooping nonterminating TRSs. One disregards the strategy completely (Sect. 4.1), one performs rewrite steps which may violate the strategy (Sect. 4.2), and one directly constructs infinite possibly nonlooping derivations (Sect. 4.3).
in the following. In total, we discuss three different techniques which can be used to disprove termination for nonlooping nonterminating TRSs. One disregards the strategy completely (Sect. 4.1), one performs rewrite steps which may violate the strategy (Sect. 4.2), and one directly constructs infinite possibly nonlooping derivations (Sect. 4.3).
4.1 Switching Between Innermost Termination and Termination
Example 11
Let \({\mathcal {R}}'\) be a confluent overlay TRS which encodes a Turing machine \(\mathcal {A}\) via innermost rewriting. We assume that the computation starts in a constant \({\mathsf {tm}}_{\mathsf {init}}\) which represents the initial configuration of \(\mathcal {A}\). Now consider the TRS \({\mathcal {R}}= {\mathcal {R}}' \cup \{{\mathsf {run\text {-}again}}(x) \rightarrow {\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}})\}\) where \({\mathsf {run\text {-}again}}\) is some fresh symbol.
Obviously, \({\mathcal {R}}\) is not innermost terminating: if \(\mathcal {A}\) terminates in some final configuration represented by a term \(t\), then  is an innermost loop. Otherwise, there is an infinite evaluation of \({\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}})\) when trying to rewrite the argument \({\mathsf {tm}}_{\mathsf {init}}\) to a normal form.
is an innermost loop. Otherwise, there is an infinite evaluation of \({\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}})\) when trying to rewrite the argument \({\mathsf {tm}}_{\mathsf {init}}\) to a normal form.
Observe that in the first case, the derivation may be long and thus hard to find, e.g., \(\mathcal {A}\) may compute the Ackermann function; and in the latter case, there might be no looping derivation at all.
However, disproving termination of \({\mathcal {R}}\) is simple when disregarding the strategy: the loop \({\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}}) \rightarrow _{\mathcal {R}}{\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}})\) is easily detected. Hence, for nontermination analysis one tries to get rid of strategy restrictions, and indeed there are known criteria where  and \({ SN }(\rightarrow _{\mathcal {R}})\) coincide: for example, locally confluent overlay TRSs fall into this class [8]. Thus, the simple loop above constitutes a valid innermost nontermination proof.
and \({ SN }(\rightarrow _{\mathcal {R}})\) coincide: for example, locally confluent overlay TRSs fall into this class [8]. Thus, the simple loop above constitutes a valid innermost nontermination proof.
We formalized the criterion of [8], though we did not follow the original proof structure, but developed a simpler proof via dependency pairs [1]. To this end, we first integrated a similar theorem for DP problems, as it is utilized in AProVE, cf. switch-to-innermost-proc in Innermost_Switch.thy.
Theorem 12
Let \({\mathcal {P}}\) and \({\mathcal {R}}\) be TRSs such that \({\mathcal {R}}\) is locally confluent and such that there is no overlap between \({\mathcal {P}}\) and \({\mathcal {R}}\). Then any \(({\mathcal {P}},{\mathcal {R}})\) chain shows the existence of some innermost \(({\mathcal {P}},{\mathcal {R}})\) chain.
Theorem 12 can not only be used on its own—to switch from innermost termination to termination for DP problems—but it can also be utilized to derive Gramlich’s result to switch from innermost termination to termination for TRSs.
Theorem 13
[8]. Let \({\mathcal {R}}\) be some finite TRS, let there be infinitely many symbols. If \({\mathcal {R}}\) is locally confluent and overlay, then  .
.
Proof
Let \({\mathcal {P}}\) be the set of dependency pairs of \({\mathcal {R}}\). If \({\mathcal {R}}\) is not terminating, then by soundness of dependency pairs there must be some \(({\mathcal {P}},{\mathcal {R}})\) chain. By Theorem 12 we conclude that there also is some innermost \(({\mathcal {P}},{\mathcal {R}})\) chain: \({\mathcal {R}}\) is locally confluent by assumption and there is no overlap between \({\mathcal {P}}\) and \({\mathcal {R}}\) since \({\mathcal {R}}\) is an overlay TRS. Finally, by completeness of dependency pairs we conclude from the innermost chain that \({\mathcal {R}}\) must be innermost nonterminating. \(\square \)
The formalization of this proof was straightforward:  already contained the required results on critical pairs, confluence, and dependency pairs [18, 21], cf. switch-to-innermost-locally-confluent-overlay-finite in Innermost_Switch.thy.
already contained the required results on critical pairs, confluence, and dependency pairs [18, 21], cf. switch-to-innermost-locally-confluent-overlay-finite in Innermost_Switch.thy.
The formalization also reveals side conditions which one never finds in paper proofs: Finiteness of \({\mathcal {R}}\) and an unbounded supply of function symbols are taken for granted, but are crucial to construct fresh function symbols (fresh symbols are required in order to build the set of dependency pairs). With more bureaucracy, one would be able to drop the condition that \({\mathcal {R}}\) is finite—by arguing that in an infinite reduction only countably many symbols can occur, and by implementing Hilbert’s hotel one can always construct enough fresh symbols—but since for certification we are only interested in finite TRSs, we did not spend this additional effort.
In order to guarantee local confluence we had to provide new means for checking joinability. Whereas in [18] the main algorithm was a comparison of normal forms of \(s\) and \(t\), this is no longer the best solution in our setting, since \({\mathcal {R}}\) is usually nonterminating. To this end, we now offer a breadth-first-search algorithm to check joinability. The certificate just has to set a limit on the search depth which ensures termination of the algorithm.
In total, we can now easily certify innermost nontermination proofs like the one for Example 11: the certificate just has to contain the looping derivation \({\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}}) \rightarrow _{\mathcal {R}}{\mathsf {run\text {-}again}}({\mathsf {tm}}_{\mathsf {init}})\) and an indication in how many steps each critical pair of \({\mathcal {R}}\) can be joined.
4.2 Rewriting and Narrowing Dependency Pairs
In this section we consider two techniques of [7] that allow to ignore the strategy for one step. Given a DP problem \(({\mathcal {P}},{\mathcal {R}})\), they replace one of the pairs \(s \rightarrow t\) in \({\mathcal {P}}\) by new ones which result from rewriting or narrowing \(s \rightarrow t\).
One advantage over the result from the previous subsection is that we only need unique normal forms for the usable rules while previously we had to consider the whole TRS. Here, the usable rules of a term \(t\) are any subset \({\mathcal {U}}(t)\) of \({\mathcal {R}}\) such that whenever  for some \(\sigma \) which instantiates all variables by normal forms, then in this derivation all applied rules must be from \({\mathcal {U}}(t)\). There are various estimations of usable rules where the simplest one is provided in [1]. The following theorem already generalizes [7, Theorem 31] which requires non-overlappingness instead of unique normal forms.
for some \(\sigma \) which instantiates all variables by normal forms, then in this derivation all applied rules must be from \({\mathcal {U}}(t)\). There are various estimations of usable rules where the simplest one is provided in [1]. The following theorem already generalizes [7, Theorem 31] which requires non-overlappingness instead of unique normal forms.
Theorem 14
Let \(({\mathcal {P}}\uplus \{s \rightarrow t\},{\mathcal {R}})\) be a DP problem and suppose \(t \rightarrow _{{\mathcal {R}},p} t'\) with rule \(\ell \rightarrow r \in {\mathcal {R}}\) and substitution \(\mu \). If for \({\mathcal {U}}= {\mathcal {U}}(t|_p)\) the rewrite relation  has unique normal forms and there are only trivial critical pairs between \(\ell \rightarrow r\) and \({\mathcal {U}}\) then the following holds: if \(({\mathcal {P}}\uplus \{s \rightarrow t'\},{\mathcal {R}})\) is innermost nonterminating then \(({\mathcal {P}}\uplus \{s \rightarrow t\},{\mathcal {R}})\) is also innermost nonterminating.
has unique normal forms and there are only trivial critical pairs between \(\ell \rightarrow r\) and \({\mathcal {U}}\) then the following holds: if \(({\mathcal {P}}\uplus \{s \rightarrow t'\},{\mathcal {R}})\) is innermost nonterminating then \(({\mathcal {P}}\uplus \{s \rightarrow t\},{\mathcal {R}})\) is also innermost nonterminating.
In the formalization we closely followed the original paper proof where we were able to slightly relax the preconditions: it is sufficient to consider the usable rules with respect to all arguments of \(t|_p\) instead of \(t|_p\) itself. To check that \({\mathcal {U}}\) has unique normal forms we use the following easy but sufficient criterion: if all critical pairs of \({\mathcal {U}}\) at the root level are trivial then  is confluent and thus has unique normal forms. The following TRS can be shown innermost nonterminating via Theorem 14, but it requires the more relaxed preconditions.
is confluent and thus has unique normal forms. The following TRS can be shown innermost nonterminating via Theorem 14, but it requires the more relaxed preconditions.
Example 15
Consider the TRS \({\mathcal {R}}\) consisting of \({\mathcal {R}}'\) of Example 11 and the rules:
Note that the result from the previous subsection is not applicable, since the system is not locally confluent. However, since \({\mathcal {U}}({\mathsf {a}}) = \varnothing \) and \({\mathcal {U}}({\mathsf {tm}}_{\mathsf {init}}) = {\mathcal {R}}'\) is confluent, we can rewrite the dependency pair \({{\mathsf {f}}^\sharp }({\mathsf {a}}) \rightarrow {{\mathsf {f}}^\sharp }({\mathsf {c}}({\mathsf {a}},{\mathsf {tm}}_{\mathsf {init}}))\) to \({{\mathsf {f}}^\sharp }({\mathsf {a}}) \rightarrow {{\mathsf {f}}^\sharp }({\mathsf {a}})\) and obtain an obvious loop.
To certify such a nontermination proof, one only has to provide the rewrite step that is performed and a nontermination proof for the modified problem. All preconditions are automatically checked by  .
.
The second technique considers narrowing of dependency pairs, where a rule \(s \rightarrow t \in {\mathcal {P}}\) is first instantiated to \(s\sigma \rightarrow t\sigma \) and subsequently \(t\sigma \) gets rewritten to \(u\), yielding a new rule \(s\sigma \rightarrow u\). Since instantiation is obviously correct for nontermination analysis, completeness of narrowing is a straightforward consequence of the completeness result for rewriting, cf. Rewriting.thy, Instantiation.thy, and Narrowing.thy.
4.3 Nonterminating Derivations
To finally detect nontermination, one requires a technique which actually finds infinite derivations. As stated before, one can consider loops \(t \rightarrow ^+ C[t\mu ]\), however, there are also techniques which are able to detect a larger class of nonterminating derivations [5, 17] which are both available in  .
.
The idea in [5] is to derive pattern rules of the form \(s\,\sigma ^n\,\tau \hookrightarrow t\,\delta ^n\,\mu \) which state that for each \(n\) there is a rewrite sequence \(s\sigma ^n\tau \rightarrow ^+ t\delta ^n\mu \). To this end, there are several inference rules which allow to derive pattern rules, and there is a sufficient criterion when a pattern rule implies nontermination.
Example 16
Consider the following nonterminating TRS.
It is nonlooping, as in the infinite derivation
it takes more and more steps to rewrite \({\mathsf {s}}^{n+1}({\mathsf {0}}) > {\mathsf {s}}^n({\mathsf {0}})\) to \({\mathsf {true}}\) when \(n\) is increased. However, using the inference rules, one can first derive the pattern rule \(({\mathsf {s}}(x) > {\mathsf {s}}(y))\,\{x/{\mathsf {s}}(x),y/{\mathsf {s}}(y)\}^n\,\{x/{\mathsf {s}}(x),y/{\mathsf {0}}\} \hookrightarrow {\mathsf {true}}\,\varnothing ^n\,\varnothing \) which states that it is possible to rewrite each term \({\mathsf {s}}^{n+2}(x) > {\mathsf {s}}^{n+1}({\mathsf {0}})\) to \({\mathsf {true}}\) (\(\varnothing \) denotes the empty substitution). And afterwards, it is easy to combine this pattern rule with the rule for \({\mathsf {f}}\) to detect nontermination, again using the methods of [5].
To be able to certify this kind of nontermination proofs, in Nonloop.thy we first proved correctness of all inference rules on an abstract level, e.g., where substitutions are modeled as functions from variables to terms. In order to check concrete proofs, in Nonloop_Impl.thy we then introduced a datatype to represent proofs, i.e., sequences of inference steps, where also the type of substitutions was changed from the abstract type to a list based representation.
Using this approach, most of the paper proofs have been easily integrated into Isabelle. We here only report on some issues we had to solve during the formalization. To this end, consider the following two inference rules of [5].


One of the small problems we encountered is the underspecification in Rule (III): the condition “\(z\) is fresh” does not contain the information w.r.t. which other variables \(z\) has to be fresh—in the formalization this is clarified, namely \({\mathcal {V}}(s) \cup {\mathcal {V}}(t) \cup \bigcup _{x : \sigma (x) \ne x} (\{x\} \cup {\mathcal {V}}(\sigma (x)))\).
Moreover, there have been several operations on substitutions which first had to be defined, e.g. for domain renamings [5, Definition 3], one defines substitutions like \(\{x\rho / s\rho \mid x/s \in \sigma \}\) where \(\rho \) has some further properties. Before showing properties of this substitution, in the formalization we first had to prove that this substitution is well-defined, i.e., that the properties of \(\rho \) ensure that \(x\rho \) is always a variable, and that there are no conflicting assignments.
Further operations on substitutions became necessary for certification. For example, in Rule (VII) one has to check equality of substitutions. Here, it turned out that checking equality of the lists which represent the substitutions was not sufficient, as some correct proofs have been rejected by our certifier, e.g., since \([(x,t), (y,s)] \ne [(y,s), (x,t), (x,t)]\), but both lists represent the same substitution \(\{x/t, y/s\}\). Instead, we had to implement a function subst-eq which decides whether two substitutions which are represented by lists are identical.
We finally remark on an extension of the original approach that was required in the formalization: while the technique in [5] is presented on the level of TRSs, the implementation in AProVE also applies the method on DP problems, where in the inference rules one has to distinguish between \({\mathcal {P}}\)- and \({\mathcal {R}}\)-steps. Moreover, AProVE also uses the following inference rule, which was not described in [5].

All these extensions have been integrated in  and
and  .
.
The technique of [17] is quite similar to [5] in the sense that there are also derivation patterns which can be derived via some inference rules, until some pattern is detected which immediately implies nontermination. In fact, [5] is an extension of [17] as the latter only considers string rewrite systems, i.e., TRSs with only unary function symbols. But since it is currently unknown whether [5] can fully simulate [17], we also formalized the technique of [17] directly, which was a relatively easy task: since everything in [17] works on strings, there was no tedious reasoning on substitutions and renamings of variables required, cf. Nonloop_SRS.thy.
For certification we require the full inference tree that derives the final pattern, where in each inference rule all parameters have to be specified. For example, for (III) we explicitly require \(\sigma \), \(p\), and \(z\); and for (VII) the substitution \(\rho \) has to be provided. Moreover, for pretty-printing and early error detection we require that every derived pattern is explicitly stated within the certificate.
5 Experiments and Partial Nontermination Proofs
We tested our certifier using the TRSs from the termination problem database (TPDB 8.0.7). To be more precise, we considered all 596 first-order TRSs where at least one tool in 2013 has generated a nontermination proof. In our experiments, we tested the following termination tools which all print their proofs in a structured proof format (CPF).
-
AProVE ’13 and
 are the versions of AProVE and
are the versions of AProVE and  that participated in the certified category of the termination competition in 2013. Both tools are restricted to nontermination techniques of [23].
that participated in the certified category of the termination competition in 2013. Both tools are restricted to nontermination techniques of [23]. -
AProVE ’14 is the current version of AProVE. It can even apply nontermination techniques that are not supported by
 .
. -
 is the current version of
is the current version of 
Table 1 clearly shows the significance of our formalizations: we doubled the number of certifiable nontermination proofs for AProVE, and can now certify 98 % of the generated proofs.
Since AProVE ’13,  and
and  use only techniques supported by
use only techniques supported by  , it comes as no surprise that all these proofs were certified. In contrast, 12 proofs by AProVE ’14 were refused as the applied nontermination techniques are not available in
, it comes as no surprise that all these proofs were certified. In contrast, 12 proofs by AProVE ’14 were refused as the applied nontermination techniques are not available in  , e.g., proofs for equational rewrite systems (modulo AC).
, e.g., proofs for equational rewrite systems (modulo AC).
To still increase the reliability for these proofs, we added support for partial proofs in  . To be more precise, we added a proof technique called “unknown proof” to CPF which logically states that the certifier may assume the implication \(\lnot { SN }(a_1) \wedge \dots \wedge \lnot { SN }(a_n) \implies \lnot { SN }(a_0)\) where each \(a_i\) may be some arbitrary binary relation, including textual descriptions like “equational rewrite relation of ...” which are not formally specified. As a consequence, every technique that is not supported by
. To be more precise, we added a proof technique called “unknown proof” to CPF which logically states that the certifier may assume the implication \(\lnot { SN }(a_1) \wedge \dots \wedge \lnot { SN }(a_n) \implies \lnot { SN }(a_0)\) where each \(a_i\) may be some arbitrary binary relation, including textual descriptions like “equational rewrite relation of ...” which are not formally specified. As a consequence, every technique that is not supported by  can be exported as an unknown proof, and then
can be exported as an unknown proof, and then  can still check all the proofs for the subgoals \(\lnot { SN }(a_i)\) with \(i > 0\).
can still check all the proofs for the subgoals \(\lnot { SN }(a_i)\) with \(i > 0\).
Using partial certification,  can check in average 70 % of the proof steps within each of the 12 partial proofs. Interestingly, due to the partial certification capabilities of
can check in average 70 % of the proof steps within each of the 12 partial proofs. Interestingly, due to the partial certification capabilities of  , we could even spot and fix one real soundness bug within AProVE. In one example a terminating TRS \({\mathcal {R}}_1\) was transformed into a nonterminating TRS \({\mathcal {R}}_2\) although it was claimed that the termination behavior of \({\mathcal {R}}_1\) and \({\mathcal {R}}_2\) is equivalent. Since AProVE was not able to finally disprove termination of \({\mathcal {R}}_2\)—and hence there was no complete nontermination proof of \({\mathcal {R}}_1\)—this bug was only discovered due to partial certification, where even for incomplete proofs every single nontermination technique could be checked by
, we could even spot and fix one real soundness bug within AProVE. In one example a terminating TRS \({\mathcal {R}}_1\) was transformed into a nonterminating TRS \({\mathcal {R}}_2\) although it was claimed that the termination behavior of \({\mathcal {R}}_1\) and \({\mathcal {R}}_2\) is equivalent. Since AProVE was not able to finally disprove termination of \({\mathcal {R}}_2\)—and hence there was no complete nontermination proof of \({\mathcal {R}}_1\)—this bug was only discovered due to partial certification, where even for incomplete proofs every single nontermination technique could be checked by  .
.
To support partial certification in  , major restructuring was required. Previously, there was a hierarchical structure of nontermination proofs where the hierarchy was given by the input: nontermination proofs for DP problems have been a leaf, proofs for TRSs have been the next layer, and proofs for relative termination have been at the top of the hierarchy. However, now for every input there is the “unknown proof” which may contain subproofs for all other inputs. Therefore, the proof types for every input are modeled via one large mutual recursive datatype (it is the datatype definition ...-nontermination-proof at the beginning of Check_Nontermination.thy), which takes considerably more time to process by Isabelle than the hierarchical sequence of non-mutual recursive datatypes that we had before. Similarly, also all functions and proofs for the overall certification procedure had to be defined and proven simultaneously for all inputs. Whereas most of this adaptation was straightforward, we also encountered problems, that some packages in Isabelle do not support mutual recursion. For example, in order to define our parser for CPF, we first had to add support for mutual recursion to the partial functions package of [14]. We refer to [19] for further details on this extension.
, major restructuring was required. Previously, there was a hierarchical structure of nontermination proofs where the hierarchy was given by the input: nontermination proofs for DP problems have been a leaf, proofs for TRSs have been the next layer, and proofs for relative termination have been at the top of the hierarchy. However, now for every input there is the “unknown proof” which may contain subproofs for all other inputs. Therefore, the proof types for every input are modeled via one large mutual recursive datatype (it is the datatype definition ...-nontermination-proof at the beginning of Check_Nontermination.thy), which takes considerably more time to process by Isabelle than the hierarchical sequence of non-mutual recursive datatypes that we had before. Similarly, also all functions and proofs for the overall certification procedure had to be defined and proven simultaneously for all inputs. Whereas most of this adaptation was straightforward, we also encountered problems, that some packages in Isabelle do not support mutual recursion. For example, in order to define our parser for CPF, we first had to add support for mutual recursion to the partial functions package of [14]. We refer to [19] for further details on this extension.
In order to obtain input examples for  ’s forbidden pattern loop check, we integrated support for forbidden pattern loops into
’s forbidden pattern loop check, we integrated support for forbidden pattern loops into  More precisely, we added a forbidden pattern loop check to the already present unfold strategy which searches for loops. To that end, we exported
More precisely, we added a forbidden pattern loop check to the already present unfold strategy which searches for loops. To that end, we exported  ’s loop checking procedure to OCaml using Isabelle’s code generator. Though interfacing
’s loop checking procedure to OCaml using Isabelle’s code generator. Though interfacing  ’s data structures required some overhead, this proved to be a fast way to integrate a reliable implementation in
’s data structures required some overhead, this proved to be a fast way to integrate a reliable implementation in  Support of forbidden pattern loops allows
Support of forbidden pattern loops allows  to show nontermination of all those TRSs in our test set of 596 problems that feature an innermost, outermost, or context-sensitive strategy (197 problems in total), as well as Example 3. In total, by just integrating
to show nontermination of all those TRSs in our test set of 596 problems that feature an innermost, outermost, or context-sensitive strategy (197 problems in total), as well as Example 3. In total, by just integrating  ’s forbidden pattern loop check, we could nearly double the number of nontermination proofs of
’s forbidden pattern loop check, we could nearly double the number of nontermination proofs of  : from 221 to 417, cf. Table 1.
: from 221 to 417, cf. Table 1.
6 Conclusion
In summary, we formalized several new nontermination techniques which cover nonlooping derivations and looping derivations under strategies. In total this formalization increased the size of  by around 10k lines. Due to our work,
by around 10k lines. Due to our work,  is now able to certify the vast majority of nontermination proofs that are generated by automated tools for TRSs.
is now able to certify the vast majority of nontermination proofs that are generated by automated tools for TRSs.
Notes
- 1.
In the literature (e.g., in [7]) a nonterminating DP problem is also called infinite. This is the reason why in
 this property is defined as infinite-dpp.
this property is defined as infinite-dpp. - 2.
More precisely, \(n_0\) can be set to \(0\) if \(p=\varepsilon \) and to
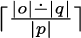
otherwise.
- 3.
Rules (i)–(iv) in [22, Definition 5], which are omitted here for brevity.
References
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theoret. Comput. Sci. 236, 133–178 (2000)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Blanqui, F., Koprowski, A.: \({\sf CoLoR}\): a \({\sf Coq}\) library on well-founded rewrite relations and its application to the automated verification of termination certificates. Math. Struct. Comput. Sci. 4, 827–859 (2011)
Contejean, E., Courtieu, P., Forest, J., Pons, O., Urbain, X.: Automated certified proofs with \({\sf CiME3}\). In: Proceedings of the RTA ’11. LIPIcs, vol. 10, pp. 21–30 (2011)
Emmes, F., Enger, T., Giesl, J.: Proving non-looping non-termination automatically. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS(LNAI), vol. 7364, pp. 225–240. Springer, Heidelberg (2012)
Giesl, J., Schneider-Kamp, P., Thiemann, R.: \({\sf AProVE 1.2}\): automatic termination proofs in the dependency pair framework. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 281–286. Springer, Heidelberg (2006)
Giesl, J., Thiemann, R., Schneider-Kamp, P., Falke, S.: Mechanizing and improving dependency pairs. J. Autom. Reason. 37(3), 155–203 (2006)
Gramlich, B.: Abstract relations between restricted termination and confluence properties of rewrite systems. Fund. Inform. 24, 3–23 (1995)
Gramlich, B., Schernhammer, F.: Extending context-sensitivity in term rewriting. In: Proceedings of the WRS ’09. EPTCS, vol. 15, pp. 56–68 (2010)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010)
Huffman, B., Kunčar, O.: Lifting and transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Heidelberg (2013)
Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean termination tool 2. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 295–304. Springer, Heidelberg (2009)
Krauss, A.: Partial and nested recursive function definitions in higher-order logic. J. Autom. Reason. 44(4), 303–336 (2010)
Krauss, A.: Recursive definitions of monadic functions. In: Proceedings of the PAR ’10. EPTCS, vol. 43, pp. 1–13 (2010)
Lucas, S.: Context-sensitive computations in functional and functional logic programs. J. Funct. Logic Program. 1, 1–61 (1998)
Nipkow, T., Paulson, L.C., Wenzel, M. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002)
Oppelt, M.: Automatische Erkennung von Ableitungsmustern in nichtterminierenden Wortersetzungssystemen. Diploma thesis, HTWK Leipzik, Germany (2008)
Sternagel, C., Thiemann, R.: Formalizing Knuth-Bendix orders and Knuth-Bendix completion. In: Proceedings of the RTA ’13. LIPIcs, vol. 21, pp. 287–302 (2013)
Thiemann, R.: Mutually recursive partial functions. Arch. Formal Proofs, February 2014. Formal Proof Development. http://afp.sf.net/entries/Partial_Function_MR.shtml
Thiemann, R., Giesl, J., Schneider-Kamp, P.: Deciding innermost loops. In: Voronkov, A. (ed.) RTA 2008. LNCS, vol. 5117, pp. 366–380. Springer, Heidelberg (2008)
Thiemann, R., Sternagel, C.: Certification of termination proofs using \({\sf CeTA}\). In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 452–468. Springer, Heidelberg (2009)
Thiemann, R., Sternagel, C.: Loops under strategies. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 17–31. Springer, Heidelberg (2009)
Sternagel, C., Thiemann, R.: Certification of nontermination proofs. In: Beringer, L., Felty, A. (eds.) ITP 2012. LNCS, vol. 7406, pp. 266–282. Springer, Heidelberg (2012)
Thiemann, R., Sternagel, C., Giesl, J., Schneider-Kamp, P.: Loops under strategies ... continued. In: Proceedings of the IWS ’10, vol. 44, pp. 51–65 (2010)
Acknowledgments
The authors are listed in alphabetical order regardless of individual contributions or seniority.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Nagele, J., Thiemann, R., Winkler, S. (2014). Certification of Nontermination Proofs Using Strategies and Nonlooping Derivations. In: Giannakopoulou, D., Kroening, D. (eds) Verified Software: Theories, Tools and Experiments. VSTTE 2014. Lecture Notes in Computer Science(), vol 8471. Springer, Cham. https://doi.org/10.1007/978-3-319-12154-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-12154-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-12153-6
Online ISBN: 978-3-319-12154-3
eBook Packages: Computer ScienceComputer Science (R0)






 are the versions of
are the versions of  that participated in the certified category of the termination competition in 2013. Both tools are restricted to nontermination techniques of [
that participated in the certified category of the termination competition in 2013. Both tools are restricted to nontermination techniques of [ .
. is the current version of
is the current version of 
 this property is defined as infinite-dpp.
this property is defined as infinite-dpp.