Multi-Componential Fluid Flow

Abstract

This chapter deals with mathematical modeling of multi-componential fluid flow and transport processes in a porous media.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

This chapter deals with mathematical modeling of multi-componential fluid flow and transport processes in a porous media. Compare to flow of a pure fluid, interaction of multi-componential fluid flow with other processes is very complex due to the variability of material parameters due to change in pressure, temperature and composition. Numerical simulation helps to understand such complex interaction is arisen from process coupling or variability in the material parameters. Numerical simulation also helps for making a precise prediction the consequences of fluid injection/extraction associated with subsurface. The present modeling is useful for computational investigation of industrial and fundamental problems of mass, momentum and heat transfer through porous media.

1 Basic Equations

This section is concerned with derivation of governing equations for multi-componential fluid flow and transport processes in a porous media. A porous media can be considered as a two-phase system which solid phase is immobile and isotropic material. And the mobile phase is a mixture of different pure fluids filled in the pores of solid skeleton. In this derivation, the concept of Representative Elementary Volume (REV—measurement over a smallest volume represents the whole two phase system) is adopted. In the continuum mechanism, REV concept neglects that a matter is made of atoms. The size of this REV is restricted by inequality $\lambda \le l \le L$ which provides definition of the Knudsen number $K_n = \frac{\lambda }{l}$. $\lambda$ is the average mean free path between two molecules and $l$ is the characteristic length (e.g., diameter of pores).

1.1 Mass Balance Equation

The mass balance equation of a multi-componential fluid flowing with velocity, $\mathbf v$, in a porous media is given by

$$\begin{aligned} \frac{\partial \left( n\rho ^f\right) }{\partial t} + \nabla \cdot \left( \rho ^f n \mathbf v\right) = n \rho ^fQ^f_{\rho } \end{aligned}$$

(5.1)

Here, $\mathbf v = \sum \limits _k\omega ^f_k \mathbf v_k$ is the averaged velocity shared by each component (Bear [1]). $t$ is time, superscript $f$ stands for fluid phase, subscript $k$ stands for component. $\omega ^f_k$ is the mass fraction of $k$th components in the mixture, $\rho ^f$ is mixture density, $\mathbf {k}$ is permeability, $n$ is porosity, $\mu$ is viscosity, $\mathbf {g}$ is gravity vector and $Q^f_{\rho }$ is fluid source/sink term.

According to Helmig [2], sum of the diffusive fluid flux over all components is zero. And the Darcy’s law is used for the advective fluid flux, $F_a$.

$$\begin{aligned} F_a= \rho ^f\mathbf {w} = \rho ^f n \mathbf v = - \frac{ \rho ^f \mathbf k }{\mu } \cdot \left( \nabla p - \rho ^f \mathbf g \right) \end{aligned}$$

(5.2)

Equation (5.1) is expanded in following form

$$\begin{aligned} n\beta ^f \rho ^f \frac{\partial p}{\partial t} - n\alpha ^f_T \rho ^f \frac{\partial T}{\partial t} + \sum \limits _{k} n \rho ^f \gamma _k\frac{\partial \omega ^f_k}{\partial t} + \nabla \cdot \left[ \rho ^f \mathbf w \right] = n \rho ^fQ^f_{\rho } \end{aligned}$$

(5.3)

Here, thermal expansivity $\alpha ^f_T = -\frac{1}{\rho ^f}\left( \frac{\partial \rho ^f}{\partial T}\right) _{p, \omega ^f_k}$, fluid compressibility $\beta ^f = \frac{1}{\rho ^f}\left( \frac{\partial \rho ^f}{\partial p}\right) _{T, \omega ^f_k}$ and solutal expansivity $\gamma _k=\frac{1}{\rho ^f}\left( \frac{\partial \rho ^f}{\partial \omega ^f_k}\right) _{p, T, \omega ^f_i};~~ i\ne k$.

1.2 Fractional Mass Transport Equation

Consider a reaction which affects mass fraction of $k$th chemical component in fluid and solid phases. Rate of this reaction, $R^{\gamma }$, can be decomposed into zero order and $\mathrm {1st~order}$ rates.

$$\begin{aligned} R^{\gamma } = \underbrace{R^{\gamma }_{(0)}}_{\mathrm {zero~order}} + \underbrace{R^{\gamma }_{(1)}}_{\mathrm {1st~order}}; \gamma =f, s \end{aligned}$$

(5.4)

The zero order rate is equivalent to the source/sink term, i.e. $R^{\gamma }_{(0)} = \rho ^{\gamma } Q^{\gamma }$. Whereas, according to the decay process, $\mathrm {1st~order}$ rate is given by relation $R^{\gamma }_{(1)} = - \lambda \rho ^{\gamma } \omega ^\gamma _k$. Choosing the dispersive mass flux in terms of mass fraction, the mass transport equation of the $k$th component for fluid and solid phases are given by

$$\begin{aligned} \frac{\partial \left( n \rho ^f \omega ^f_k \right) }{\partial t} + \nabla \cdot \left( \mathbf w \rho ^f \omega ^f_k \right) - \nabla \cdot \left( n \rho ^f D_{ij}\cdot \nabla \omega ^f_k\right) = - n \lambda \rho ^f \omega ^f_k + n \rho ^f Q^f_{\omega } \quad \end{aligned}$$

(5.5)

and

$$\begin{aligned} \frac{\partial \left[ (1-n)\rho ^s\omega ^s_k\right] }{\partial t} = - (1-n)\lambda \rho ^{s} \omega ^s_k + (1-n) \rho ^s Q^s_{\omega } \end{aligned}$$

(5.6)

The mass fraction of $k$th chemical component in mixture ($\omega ^f_k=\frac{m^f_k}{m^f}$) and solid ($\omega ^s_k=\frac{m^s_k}{m^s}$) phases are related via sorption law i.e., $\omega ^s_k =f(\omega ^f_k) \omega ^f_k$. With considering sorption process, the convective form of the factional mass transport equation is given by

$$\begin{aligned}&n\rho ^f R_1 \frac{\partial \omega ^f_k}{\partial t} + \rho ^f \mathbf w \cdot \nabla \omega ^f_k - \nabla \cdot \left( n\rho ^f D_{ij}\cdot \nabla \omega ^f_k\right) \nonumber \\&\qquad +\, \omega ^f_k\rho ^f \left( n \rho ^f Q^f_{\rho } - n R_0 \lambda \right) = n \rho ^f Q^f_{\omega } + (1-n) Q^s_{\omega } \end{aligned}$$

(5.7)

The retardation coefficient, $R_0$, and its derivative, $R_1$, are given by

$$\begin{aligned} R_0=1+\frac{1-n}{n} \frac{\rho ^s}{\rho ^f} f(\omega ^f_k);~~~\mathrm {and}~~R_1=1+\frac{1-n}{n} \frac{\rho ^s}{\rho ^f} \frac{\partial \left[ f(\omega ^f_k)\omega ^f_k\right] }{\partial \omega ^f_k} \end{aligned}$$

The coefficients of hydrodynamic-dispersion tensor are given by

$$\begin{aligned} D_{ij}=\tau D \delta _{ij}+\alpha _t \left| \mathbf{v }\right| \delta _{ij}+(\alpha _l-\alpha _t ) \frac{\mathbf{v }_i \mathbf{v }_j}{\left| \mathbf{v }\right| } \end{aligned}$$

Here, $\delta _{ij}$ is Kronecker delta, $\tau$ is tortuosity, $D$ is diffusion coefficient, $\alpha _t$ and $\alpha _l$ are transverse- and longitudinal- dispersivity, respectively.

1.3 Heat Transport Equation

Consider an open system with a fluid which internal energy is $e^f$ and density is $\rho ^f$. According to the first law of thermodynamics, energy balance equation for this system is expressed as

$$\begin{aligned} \rho ^f\frac{D e^f}{D t} + \nabla \cdot \mathbf i^f + e^f \rho ^f Q^f_{\rho }= \tau _{ij} \frac{\partial v_i}{\partial x_j} \end{aligned}$$

(5.8)

where, $e^f \rho ^f Q_{\rho }$ is amount of internal energy associated with fluid source/sink term, $Q_{\rho }$, and $\mathbf i^f$ is the fluid heat conduction flux vector. The stress tensor, $\tau _{ij} \frac{\partial v_i}{\partial x_j}$, can be decomposed into pressure term, $p \nabla \cdot \mathbf v$, and viscous term, $\mathbf v\cdot \nabla p$.

$$\begin{aligned} \rho ^f\frac{D e^f}{D t} + \nabla \cdot \mathbf i^f + e^f \rho ^f Q^f_{\rho }= \mathbf v\cdot \nabla p - p \nabla \cdot \mathbf v \end{aligned}$$

(5.9)

For a thermodynamically open system, enthalpy, $h^f$, is preferred over internal energy, $e^f$. Hence, Eq. (5.9) is being transformed in terms of fluid enthalpy with using the mass balance equation.

$$\begin{aligned} p\nabla \cdot \mathbf v = -\frac{p}{\rho ^f}\frac{D\rho ^f}{D t} + p Q^f_{\rho } = \rho ^f\frac{D\left( \frac{p}{\rho ^f}\right) }{D t} - \frac{D p}{D t} + p Q^f_{\rho } \end{aligned}$$

(5.10)

Replacing the pressure term in the Eq. (5.9) by using Eq. (5.10) and relation, $h^f = e^f +\frac{p}{\rho ^f}$, we have

$$\begin{aligned} \rho ^f\frac{D h^f}{D t} + \nabla \cdot \mathbf i^f = \mathbf v\cdot \nabla p + \frac{D p}{D t} - h^f\rho ^f Q^f_{\rho } \end{aligned}$$

(5.11)

The energy balance equation for solid phase in terms of the internal energy, $e^s$, is given by

$$\begin{aligned} \rho ^s\frac{D e^s}{D t} + \nabla \cdot \mathbf i^s = Q^s_e \end{aligned}$$

(5.12)

Replace the total derivative in Eqs. (5.11) and (5.12) with following thermodynamical relations.

$$\begin{aligned} \frac{D h^f}{D t}&= \left( \frac{1}{\rho ^f}-\frac{\alpha ^f_T T^f}{\rho ^f}\right) \frac{D p}{D t}+c^f_p\frac{D T^f}{D t} \nonumber \\ \frac{D e^s}{D t}&= c^s_v\frac{D T^s}{D t} \end{aligned}$$

(5.13)

The heat transport equation for fluid and solid phases in terms of respective phase temperature are

$$\begin{aligned} \rho ^f c^f_p\frac{D T^f}{D t} + \nabla \cdot \mathbf i^f = \mathbf v \cdot \nabla p + \alpha ^f_T T^f\frac{D p}{D t} - h^f\rho ^f Q^f_{\rho } \end{aligned}$$

(5.14)

and

$$\begin{aligned} \rho ^s c^s_v\frac{\partial T^s}{\partial t} + \nabla \cdot \mathbf i^s = Q^s_e \end{aligned}$$

(5.15)

Under the thermal equilibrium ($T^f \cong T^s =T$), total energy conservation equation is preferred which is obtained by averaging the Eqs. (5.14) and (5.15) over fluid and solid phases.

$$\begin{aligned}&\left( \rho c_p\right) _{\textit{eff}} \frac{\partial T}{\partial t} + c^f_p \rho ^f n \mathbf v\cdot \nabla T - \nabla \cdot \left[ \mathbf {\kappa }_{\textit{eff}}\cdot \nabla T\right] \nonumber \\&\qquad = n \alpha ^f_T T \frac{\partial p}{\partial t} + n \mathbf v\cdot \nabla p - \alpha ^f_T T n \mathbf v \cdot \nabla p + c^f_p (T-T_0) n \rho ^f Q^f_{\rho } + Q_T \end{aligned}$$

(5.16)

Here, $Q_T=Q_e$, and heat conduction flux can be represented according to the Fourier’s law.

$$\begin{aligned} \mathbf i^{\gamma } = -\mathbf {\kappa ^{\gamma }} \cdot \nabla T \end{aligned}$$

(5.17)

where $\mathbf {\kappa }_{\textit{eff}}$, is the effective thermal conductivity tensor of the porous media, with coordinates defined as $\mathbf {\kappa }_{\textit{eff}} = (1-n) \mathbf {\kappa }^s + n \mathbf {\kappa }^f$. $\left( \rho c_p\right) _{\textit{eff}}$ is the effective heat capacity of the porous medium defined by $\left( \rho c_p\right) _{\textit{eff}} = (1 - n) \rho ^s c_v^s + n \rho ^f c^f_p$. Here, specific heat capacity and thermal conductivity of the fluid mixture are given in Table 5.1.

Table 5.1 Approximation of material parameters for a mixture

1.4 Equation of State

Tsai and Chen [3] presented the volume translated Peng-Robinson equation of state (VTPR-EoS). In this EoS, molar volume, $v_k$, is corrected by the translated volume, $c$. The translated volume is difference in molar volume obtained by experimental and computation at the reduced temperature $T_r = T/T_c$. Because of this translation, VTPR-EoS approximates the fluid parameters for liquids, gases and supercritical states.

$$\begin{aligned} p=\frac{RT}{(v_k+c-b)}-\frac{a(T)}{(v_k+c)(v_k+c+b)+b(v_k+c-b)} \end{aligned}$$

(5.18)

Here, $R$ is universal gas constant. $a$ and $b$ are attraction and repulsion parameter, respectively.

$$\begin{aligned} a(T)&= 0.4572 \frac{R^2 T_c^2}{p_c} \left[ 1+M_0(1-T_r )+N_0(1-T_r )(0.7-T_r )\right] ^2\\ M_0&= 0.2047+0.8354\omega _a-0.1847\omega _a^2+0.1667\omega _a^3-0.0988\omega _a^4\\ b&= 0.077796 \frac{R T_c}{p_c}\\ c&= \frac{R T_c}{p_c}\left[ k_1 + k_2 \left( 1-T_r^{2/3}\right) + k_3 \left( 1-T_r^{2/3}\right) ^2 \right] \\ k_1&= 0.00185 + 0.00438 \omega _a + 0.36322 \omega _a^2 - 0.90831 \omega _a^3 + 0.55885 \omega _a^4\\ k_2&=-0.00542-0.51112 k_3+0.04533 k_3^2+0.07447 k_3^3-0.03831 k_3^4 \end{aligned}$$

Table 5.2 Constants of the pure fluid

Here, $p_c$ is critical pressure, $T_c$ is critical temperature and $\omega _a$ is acentric parameter. Required parameters for VTPR-EoS are given in Table 5.2. A cubic equation based on VTPR-EoS is obtained by setting $v_k = {z_k R T}{p}$, in Eq. (5.18).

$$\begin{aligned} z^3+ P z^2+ Q z + r&= 0 \nonumber \\ P&=B-1+3C \nonumber \\ Q&=-3B^2+3C^2+2BC-2B-2C+A \nonumber \\ r&=B^3+C^3+B^2-C^2+BC^2-3CB^2-2BC+CA-AB \end{aligned}$$

(5.19)

Here, $A=\frac{a p}{R T}, B = \frac{b p}{R T}$ and $C = \frac{c p}{R T}$. The cubic equation can be easily solved using either Newton-Raphson iteration or analytical method for super compressibility factor, $z_k = z_k(p,T)$. According to the Katz chart, at temperature below to critical point cubic equation has only one real root representing the existence of a single phase. Otherwise, it has two real roots. The maximum root represents gas state, whereas, minimum root represents either liquid or supercritical state.

1.4.1 PVT Derivatives

Two important derivatives, i.e. $\frac{\partial v_k}{\partial p}$ and $\frac{\partial v_k}{\partial T}$ are prerequisite to find other fluid and thermal parameters (particularly, $\beta ^f_k$ and $\alpha ^f_{Tk}$). In this section, we provide expression for these derivative deriving from Eq. (5.18).

$$\begin{aligned} \left( \frac{\partial v_k}{\partial T} \right) _{p, \omega _k}&= \frac{F- \frac{da}{dT} E}{F + 2p\textit{EH} - 2\textit{RTH} + a}\\ \left( \frac{\partial v_k}{\partial p}\right) _{T, \omega _k}&= \frac{\textit{EF}}{pF + 2p\textit{EH} - 2\textit{RTH} + a} \end{aligned}$$

with, $F = (v_k + c)(v_k + c + b) + b(v_k + c - b), E = v_k + c - b$, and $H = v_k + c + b$

$$\begin{aligned} \left( \frac{d a}{d T}\right) = - 0.4572 \frac{R^2 T_c}{p_c} 2 a_0\left[ 1+M(1-T_r )+N(1-T_r )(0.7-T_r )\right] \end{aligned}$$

Here, $a_0 = M_0 + N_0(1.0 - T_r) + N_0(0.7 - T_r)$.

Fig. 5.1

Comparison of carbon dioxide (left) and water (right) parameters with NIST data for pressure from $1.0\times 10^5~\mathrm {Pa}$ to $2.0\times 10^7~\mathrm {Pa}$ at $318.15$ K

1.4.2 Amagt’s Mixing Rule

According to the rule, the molar volume of a mixture is the sum of its component’s partial volumes, i.e. $v = \sum \limits _k v_k$. This mixing rule with the real gas law, we have $p v = \sum \nolimits _k z_k(p, T) R T$. The expression for mixture density is given by

$$\begin{aligned} \frac{1}{\rho ^f} = \sum \limits _k\frac{\omega ^f_k}{\rho ^f_k} \end{aligned}$$

From above relation, expression for the salute expansivity is obtained as

$$\begin{aligned} \gamma _k=\left( \frac{1}{\rho ^f}\frac{\partial \rho ^f}{\partial \omega ^f_k}\right) _{p, T, \omega ^f_i} = -\frac{\rho ^f_k}{\rho ^f};~~ i\ne k \end{aligned}$$

1.4.3 Material Functions for Mixture

We computed density, viscosity, heat conductivity and specific heat capacity for pure fluids according the expression given in the Table 5.1. Figure 5.1 shows that the computed parameters are in close agreement with corresponding data from the National Institute of Standards and Technology (NIST).

2 Examples

2.1 Tracer Test

Tracer is used to characterize the fluid flow through the reservoirs and for estimation of medium parameters. For example, in oil and gas industries (also in hydrology) it is used for indicate mean flow velocity, residual saturation, dispersivities, and etc. For the transport of a contaminant through a porous medium, Genuchten and Alves [4] provided one dimensional analytical solution which is as follow.

$$\begin{aligned}&\omega ^f(x, 0<t\le t_0)=\omega ^f_i + (\omega ^f_0 - \omega ^f_i) A(x, t) \nonumber \\&\omega ^f(x, t\ge t_0)=\omega ^f_i + (\omega ^f_0 + \omega ^f_i) A(x, t) - \omega ^f_0 A(x, t-t_0) \end{aligned}$$

(5.20)

with

$$\begin{aligned} A(x, t)=0.5 \mathrm {erfc}\left[ \frac{n R_0 x - v t}{\sqrt{4 n \tau R_0 D t}}\right] + 0.5 \mathrm {erfc}\left[ \frac{n R_0 x + v t}{\sqrt{4 n\tau R_0 D t}}\right] \exp \left( \frac{v x}{n \tau D}\right) \end{aligned}$$

To consider sorption process in the mass transport, the sorption law can be adapted, e.g. Henry’s law. Extent to which sorption process affects the tracer transport is accounted by the retardation factor, $R_0$. Here, $D$ is the binary diffusion coefficient, $\omega ^f_0$ is the mass fraction of the tracer chemical is used for pulse, $t_0$, injection.

Fig. 5.2

Conceptual model geometry

2.1.1 Definition

Problem of tracer transport in one-dimensional porous column is considered. The pores of the solid skeleton are completely filled with water at a constant pressure and temperature. The tracer chemical is injected from the inlet within short time and computed the tracer breakthrough curve (time evolution of tracer mass fraction) at two different points located at 5 and 10 m from the inlet (see Fig. 5.2). System properties and material parameters used in the simulation (porous medium as well as of fluid and solid phases) are summarized in Table 5.3.

Table 5.3 Model properties and material parameters

2.1.2 Model Geometry and Conditions

• Geometry: The porous column is 1,000 m long in x-direction. Inlet and outlet are located at $x=0$ and 1,000 m, respectively.

• IC: At a constant temperature, 318.15 K, we assume that the pores of solid skeleton are occupied by water at pressure of $1.01325\times 10^5~\mathrm {Pa}$.

• BC: Free boundary condition for pressure and tracer mass fraction is prescribed at the outlet boundary. At the inlet, mass fraction of tracer chemical $\omega ^f_0 = 1$ during pulse tracer injection then altered by free boundary condition.

• ST: From the inlet, the tracer chemical is introduced with rate of 0.83 kg per day for 10 days.

2.1.3 Numerical Solution

For numerical simulation, the numerical module ‘Multi Componential Flow’ embedded in OGS simulator is utilized. This module solves coupled system of mass balance and fractional mass transport equations in monolithic way for pressure and mass fraction of the tracer chemical. For non-linear iterations, it uses the Picard linearization method. Numerical solution is stabilized with mass lumping method. The model geometry is shown in Fig. 5.2 which is discretized into 1,001 line elements. To capture a sharp tracer concentration gradient, a variable spatial step size, i.e. $\Delta x =0.000925289$ m is chosen close to the inlet and it is increased to 10 m far away from it. One year of the reservoir behavior has been simulated using a constant time step size of one day.

Figure 5.3a, b show the tracer breakthrough curves at the observation points. In Fig. 5.3a, sorption process is not included, however, Fig. 5.3b clearly showing that sorption process retards the mass transport significantly. The present finite element solution is in close agreement with the analytical solution, i.e. Eq. (5.20).

Fig. 5.3

Comparison of analytical and finite element solution

2.2 Bottom Hole Pressure

Well control is a technique prevalent in oil and natural gas industries for well drilling or fluid injection. In this technique, hydrostatic pressure (fluid column) is maintained with formation pressure to avoid influx into well. So understanding of the different pressure is important, particularly, Well Head Pressure (WHP) and Bottom Hole Pressure (BHP). Hence, in this benchmark, BHP is simulated with simplified geometry using multi-componential fluid flow approach.

The model geometry is shown in Fig. 5.4. This uses axisymmetric concept to simplify the model, i.e. one-dimensional porous column in r-direction which pores are occupied with water at pressure $6.2\times 10^6~\mathrm {Pa}$ and temperature 318.15 K. From the left point, time dependent injection rate is assigned for $\mathrm {CO_2}$ injection. Required parameters for this numerical simulation are given in Table 5.4. Pressure evolution during injection operation is computed to show that measured pressure data (from real site) could be reproduced by numerical simulation.

Fig. 5.4

Benchmark setup

Table 5.4 Model parameters and geometrical information

2.2.1 System Geometry and Conditions

• Geometry: The porous column is 1,000 m long in the r-direction. The inlet and outlet are located at $r=$ 0.1 and $r=$ 1,000 m, respectively.

• IC: The pores of the solid skeleton are occupied by water at pressure of $6.2\times 10^{6}~\mathrm {Pa}$ and temperature of 318.15 K.

• ST: A time dependent mass source term is assigned at the inlet (see Fig. 5.4) for $\mathrm {CO_2}$ injection.

2.2.2 Numerical Solution

The geometrical model consists 1,001 line elements. To capture the sharp pressure gradient close to the inlet, the spatial step size is refined to $\Delta r=$ 0.000925289 m whereas far from the injection point it is 10 m. The numerical simulation for 19,170 h has been performed using a constant time step size of ten hours. In Fig. 5.5, the pressure evolution is presented which is observed at $r=$ 23 m from the injection point.

Fig. 5.5

BHP evolution at $r=$ 23 m distance from the $\mathrm {CO_2}$ injection point

Fig. 5.6

Semantic of the original experimental

2.3 Plume Migration

Treated wastewater disposal into saline aquifers can rise up to the surface. Due to this, saline aquifers generally are overlain by treated water layers. To make decision for using these layers as a potable drinking water source or not, investigation about plume rising become important. Usually, plume moves away from its source because of density contrast and widens because of entrainment of the surrounding fluid at its edges. Experimental (see Fig. 5.6) investigation of buoyant plume movement is presented by Brakefield [5].

2.3.1 Definition

Geometry of the problem is shown in Fig. 5.6. This two-dimensional plane is assumed a isotropic porous media which pores are completely filled with saltwater at a pressure of $1.01325\times 10^5~\mathrm {Pa}$. Mass rate for treated water (lighter than saltwater) injection is assigned at the injection point. The density of the treated water varies linear with mass fraction, i.e. $\rho ^f_w = \rho ^f_{w0}(1+\gamma _w \omega ^f_w)$. The density of saltwater is used for reference density $\rho ^f_{w0}=$ 1,019 $\mathrm {kg~m^{-3}}$.

2.3.2 Model Geometry and Conditions

• Geometry: The considered plane is 56 cm long and 29 cm high in $x$ and $z$-directions, respectively. From the point ($27, 24~\mathrm {cm}$), treated water is injected.

• IC: At constant temperature, 313.15 K, we assume that the pores of solid skeleton are occupied by saltwater at pressure of $1.01325\times 10^5~\mathrm {Pa}$.

• BC: At the top left and top right point, pressure $p_0 = 1.01325\times 10^5~\mathrm {Pa}$ is assigned. Elsewhere, free boundary conditions for pressure and treated water mass fraction are prescribed.

• ST: A 60 ml volume of treated water is injected by syringe into saltwater for 41 s (Table 5.5).

Table 5.5 Simulation parameters

2.3.3 Numerical Solution

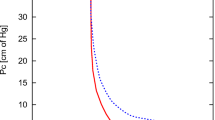
The model geometry is discretized into 24,591 quad elements. For numerical simulation, the numerical module ‘multi componential flow’ is utilized. This solves coupled system of mass balance and fractional mass transport equations in monolithic way for pressure and mass fraction of treated water. For accuracy, a very fine mesh is used in the region of plume rising. 2,671 s of plume rising have been simulated using a constant time step size of ten seconds. For non-linear iterations, the Picard linearization method is applied with the mass lumping method for numerical stabilization. Figure 5.7 shows the development of treated water plume simulated by SUTRA and SEWAT simulators along with the present finite element solution. It is found that plume distribution patter from each simulator is very similar at all-time steps.

Fig. 5.7

Evolution of treated water plume at a 27; b 369; c 685; d 1,385; e 2,631 s after injection completed

2.4 $\mathrm {CO_2}$ Leakage Through Abondoned Well

Leakage is a way for fluid to escape from storage. Leakage of geological storaged $\mathrm {CO_2}$ through natural occurring faults and fractures would have different fatal effects on the nearby environment. So, numerical modeling of the $\mathrm {CO_2}$ leakage is an useful tool for understanding the leakage mechanism. Its understanding helps to estimate fraction of the stored $\mathrm {CO_2}$ that can be retained in a suitable storage for a sufficiently long period of time. In $\mathrm {CO_2}$ capture and storage technology is associated with pressure pulse that move away from the injection point and it is quicker compare to the front of advancing $\mathrm {CO_2}$. The pressure pulse forces the saline water to leak via naturally occurred fractures or existing abondened well. And $\mathrm {CO_2}$ arrives at the leaky point late and boyuncy assists $\mathrm {CO_2}$ leakage and opposes the saline water leakage. The leakage rate is measured in terms of the non-dimensional leakage rate defined by

$$\begin{aligned} {\mathrm{Non}}\text {-}{\mathrm{dimensional\ leakage\ rate}} = \frac{\mathrm {Fluid~flux~through~observation~point}}{\mathrm {CO_2 ~injection~rate}} \end{aligned}$$

(5.21)

The problem of the advective spreading of $\mathrm {CO_2}$ into an aquifer already addressed by Ebigbo et al. [6]. However, they used multi-phase fluid flow approach with assumptions (i) the $\mathrm {CO_2}$ and the brine are two separate and immiscible phases (ii) capillary pressure is negligible. These assumptions help to obtain the similar result using compositional fluid flow approach with neglecting the diffusion-dispersion part of mass transport. We used theirs results in this benchmark for code validation. In this study, we used dada from MUFTE and ELSA simulators

• ELSA code uniquely addresses the challenge of providing quantitative estimation of fluid distribution and leakage rate.

• This problem is came in existence by developer of MUFTE code.

2.4.1 Definition

The problem of $\mathrm {CO_2}$ leakage is modeled using a two-dimensional plane consisting two layers separated by an aquitard. The bottom layer is considered as $\mathrm {CO_2}$ storage and top layer for freshwater body. Both layers share a common hydraulic parameters. To be computationally efficient, the aquitard is omitted from numerical simulation. At a constant temperature, the pores of the solid skeleton of both layers are filled with water at the hydrostatic pressure condition. In the vicinity of the injection point, an inclined fracture is incorporated. The non-dimensional leakage rate is defined in Eq. (5.21) measured at the observation point located at the midpoint of the fracture. The computed $\mathrm {CO_2}$ leakage rate is compared with similar result from ELSA and MUFTE simulators.

2.4.2 Model Geometry and Conditions

• Geometry: A 1,000 m long and 160 m high plane located between 2,860–3,000 m deep to earth surface. This consists two layers each 30 m thick and a 100 m thick aquitard. The $\mathrm {CO_2}$ injection and observation points are located at (0, $-$2,970 m) and (100, $-$2,920 m), respectively.

• IC: At constant temperature, 318.15 K, pores of both layers are filled completely with water under hydrostatic pressure condition $\frac{d p}{d z} =10\text {,}251.45~\mathrm {Pa~m^{-1}}$ with reference depth of 2,840 m.

• BC: At both lateral boundaries, hydrostatic pressure similar to initial condition is assigned. No flow condition is prescribed at top and bottom boundaries.

• ST: $\mathrm {CO_2}$ injection rate is $8.87~\mathrm {kg~s^{-1}}$ for 18 months.

Fig. 5.8

Leakage scenario [6]

2.4.3 Numerical Solution

The layers (see Fig. 5.8) are discretized into 15,231 triangular whereas the fracture is discretized into $52$ line elements. The triangular element closed to fracture are densely distributed is. Within the multi-componential approach, the coupled system of flow and transport equations is solved numerically using monolithic approach for primary variables, i.e. pressure and mass fraction of water and $\mathrm {CO_2}$. Generalized single step scheme is used for time discretization with time step $\Delta t=1~\mathrm {Day}$. For non-linear iterations the Picard linearization method is applied with the mass lumping method for numerical stabilization. Negligence of diffusion-dispersion makes difficult to achieve the desired convergence, but using available techniques (SUPG, FTC, or MASS LUMPPING) we simulate this benchmark problem (Table 5.6).

Figure 5.9 shows the non-dimensional leakage rate of $\mathrm {CO_2}$. To simulate the problem, OGS uses multi-componential fluid flow approach, whereas, other two simulators were used the multi-phase fluid flow approach. This benchmark state that $\mathrm {CO_2}$ leakage rate from both approaches are in close agreement under assumption made earlier in this benchmark.

Table 5.6 Simulation parameters

Fig. 5.9

Comparison of computed leakage rate from three different simulators

2.5 Thermo-Chemical Energy Storage

For a given reaction, amount of product(s) and reactant(s) are varied with reaction time. It also releases/absorbs certain amount of thermal energy, i.e. reaction enthalpy. Therefore, we present numerical modeling approach for investigation of interphase mass and heat transfer.

Consider a $\mathrm {CaO}$ bed which pore is filled with $\mathrm {N_2}$ gas. On introduction of water vapor, $\mathrm {CaO}$ reacts with water produces $\mathrm {Ca(OH)_2}$ and releases heat ($\Delta h$). This system can be considered as a two-phase system which solid phase is composed by $\mathrm {CaO}$ and $\mathrm {Ca(OH)_2}$ and gas phase is a mixture of water vapor and $\mathrm {N_2}$. The reaction rate of this system is modelled with a trigonometric function such that the solid density evolution is sinusoidal (amplitude $a$, angular frequency $f$

$$\begin{aligned} \dot{\rho ^s} (t) = a f \cos (f t) \end{aligned}$$

(5.22)

From this reaction rate, the following composition relations can be derived analytically for solid phase and water vapor densities:

$$\begin{aligned} \rho ^s (t)&= \rho ^s_0 + a \sin (f t)\, , \ \rho ^g (t) = \rho ^g_0 + a \sin (f t)\end{aligned}$$

(5.23)

$$\begin{aligned} \rho _V (t)&= \rho _{V0} + a \sin (f t)\, , \omega _V (t) = \frac{\rho _V (t)}{\rho ^g (t)} \end{aligned}$$

(5.24)

Here, s and g stand for solid and gas phase. The heat transport equation for this system is governed by

$$\begin{aligned} \left[ (1-n)\rho ^s c^s_p + n\rho ^g c^g_p \right] \frac{\partial T}{\partial t} - n \frac{\partial p}{\partial t} = (1-n) \Delta h \frac{\partial \rho ^s}{\partial t} \end{aligned}$$

(5.25)

To obtained the analytical solution of Eq. (5.25), we assumed that $\Delta h \longrightarrow \infty$ and solid and gas phases are in thermodynamical equilibrium. If the gases are ideal and mixing is according to the Amagat’s rule, we find

$$\begin{aligned} \frac{1}{M}&= \sum _i {\frac{\omega _i}{M_i}}, \beta _p = \frac{1}{p}, \alpha _T = -\frac{1}{T}, \gamma _i = -\frac{\rho _i}{\rho }\end{aligned}$$

(5.26)

$$\begin{aligned} \frac{1}{\rho ^g}&= \sum _i {\frac{\omega _i}{\rho _i}}, p = \sum _i {\frac{R T \rho ^g \omega _i}{M_i}}; i=V, N \end{aligned}$$

(5.27)

Here, V and N stand for water vapor and nitrogen. Taking time derivative of gas density function in Eq. (5.27), we have

$$\begin{aligned} \frac{\partial p}{\partial t} = \sum _i {\frac{R T \omega _i}{M_i}} \frac{\partial \rho ^g}{\partial t} + \sum _i {\frac{ R \rho ^g \omega _i}{M_i}} \frac{\partial T}{\partial t} + \sum _i {\frac{R T \rho ^g}{M_i}} \frac{\partial \omega _i}{\partial t} \end{aligned}$$

(5.28)

Again time derivative of pressure function of Eq. (5.27) and considering $\mathrm {N_2}$ is no-reactive ($\dot{\rho ^s}=\dot{\rho _V}=\dot{\rho }$), we find

$$\begin{aligned} \frac{\partial p}{\partial t} = \sum _i {\frac{ R T}{M_i}} \frac{\partial \rho _i}{\partial t} + \sum _i {\frac{ R \rho ^g \omega _i}{M_i}} \frac{\partial T}{\partial t} \end{aligned}$$

(5.29)

the energy balance thus reads

$$\begin{aligned}&\left[ (1-n)\rho ^s c^s_p + n\rho ^g \left( c^g_p - \frac{R}{M}\right) \right] \frac{\partial {T}}{\partial t} = (1-n)\frac{\partial {\rho ^s}}{\partial t} \left( \Delta h - \frac{n T R}{M_V}\right) \end{aligned}$$

(5.30)

If $\delta = \frac{n R}{M_V c^s_p}$, integration yields

$$\begin{aligned} \frac{n R T}{M_V}= \Delta h - \left( \Delta h - \frac{n R T_0}{M_V} \right) \left( \frac{(1-n)\rho ^s c^s_p + n\rho ^g \left( c^g_p - \frac{R}{M}\right) }{(1-n)\rho ^s_0 c^s_{p0} + n\rho ^g_0 \left( c^g_{p0} - \frac{R}{M_0}\right) } \right) ^{-\delta } \end{aligned}$$

(5.31)

2.5.1 Definition

In this example, the behavior of the model when mass transfer occurs between the phases is verified. Consider a closed off system similar to the one described in the previous example. The porous body is filled with a mixture of nitrogen and water vapor modelled as ideal gasses.

2.5.2 Model Geometry and Conditions

• Geometry: Water vapor is introduce from inlet of a 10 cm long bed of $\mathrm {CaO}$.

• IC: Pores are filled with $\mathrm {N_2}$ ($\omega _N =0.5$) at $p_0 = 1.0 \times 10^5\,\mathrm {Pa}$ and $T_0$ 400 K.

• BC: No flow condition is prescribed at inlet and outlet boundaries.

• ST: Injection rate for water vapor $1\times 10^{-10}~\mathrm {kg\cdot s^{-1}}$ is assigned for one second.

Table 5.7 Simulation parameters

Fig. 5.10

Model setup

2.5.3 Numerical Solution

The exemplary parameter set is listed in Table 5.7. The values are chosen such that temperature changes due to mass transfer are visible in both phases. The numerical model was run with the Multi Componential Flow numerical module with a very high number for $\Delta h$. A time step size of $0.001~\mathrm {s}$ was chosen for a time interval of $1~\mathrm {s}$. One dimensional line elements were used for its spatial discretisation (Fig. 5.10).

Fig. 5.11

Comparison of present FEM solution with the analytical solutions of a temperature; b pressure; c water vapor mass fraction; d gas density

The model correctly reproduced the conditions of thermal equilibrium. During the initial stage of the reaction the gas loses mass while the solid (not shown) gains that amount of mass. During the back reaction the opposite effect occurs. An equally good match is obtained for the temperature profiles (Fig. 5.11a). If no heat of reaction is released, the gas simply cools down as its density and pressure drop. The solid phase follows this trend due to the very low density chosen here for demonstration purposes. In the gas pressure profiles this switch of sign can be observed as well along with an increasingly non-sinusoidal trend in the pressure profile (Fig. 5.11b). The numerically obtained water vapor mass fraction and gas density are compared well with the analytical solution (Fig. 5.11c, d and Table 5.8).

Table 5.8 Parameter values for interphase mass transfer verification