Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Chaos is an interesting phenomenon of nonlinear dynamical systems. Chaotic systems are nonlinear dynamical systems which are sensitive to initial conditions, topologically mixing and with dense periodic orbits. Sensitivity to initial conditions of chaotic systems is popularly known as the butterfly effect. Small changes in an initial state will make a very large difference in the behavior of the system at future states. Chaotic behaviour was suspected well over hundred years ago in the study of three bodies problem, but it was established only a few decades ago in the study of 3-D weather models (Lorenz 1963).

The Lyapunov exponent is a measure of the divergence of phase points that are initially very close and can be used to quantify chaotic systems. It is common to refer to the largest Lyapunov exponent as the maximal Lyapunov exponent (MLE). A positive maximal Lyapunov exponent and phase space compactness are usually taken as defining conditions for a chaotic system.

Since the discovery of Lorenz system in 1963, there is a great deal of interest in the chaos literature in finding new chaotic systems. Some well-known paradigms of 3-D chaotic systems in the literature are (Arneodo et al. 1981; Cai and Tan 2007; Chen and Ueta 1999; Chen and Lee 2004; Li 2008; Liu et al. 2004; Lü and Chen 2002; Rössler 1976; Sprott 1994; Sundarapandian and Pehlivan 2012; Tigan and Opris 2008; Vaidyanathan 2013a, b, 2014; Zhou et al. 2008; Zhu et al. 2010).

Chaotic systems have several important applications in science and engineering such as oscillators (Kengne et al. 2012; Sharma et al. 2012), lasers (Li et al. 2014; Yuan et al. 2014), chemical reactions (Gaspard 1999; Petrov et al. 1993), cryptosystems (Rhouma and Belghith 2011; Usama et al. 2010), secure communications (Feki 2003; Murali and Lakshmanan 1998; Zaher and Abu-Rezq 2011), biology (Das et al. 2014; Kyriazis 1991), ecology (Gibson and Wilson 2013; Suérez 1999), robotics (Mondal and Mahanta 2014; Nehmzow and Walker 2005; Volos et al. 2013), cardiology (Qu 2011; Witte and Witte 1991), neural networks (Huang et al. 2012; Kaslik and Sivasundaram 2012; Lian and Chen 2011), finance (Guégan 2009; Sprott 2004), etc.

Synchronization of chaotic systems is a phenomenon that occurs when two or more chaotic systems are coupled or when a chaotic system drives another chaotic system. Because of the butterfly effect which causes exponential divergence of the trajectories of two identical chaotic systems started with nearly the same initial conditions, the synchronization of chaotic systems is a challenging research problem in the chaos literature.

Major works on synchronization of chaotic systems deal with the complete synchronization (CS) which has the goal of using the output of the master system to control the slave system so that the output of the slave system tracks the output of the master system asymptotically. Thus, if \(x(t)\) and \(y(t)\) denote the states of the master and slave systems, then the design goal of complete synchronization (CS) problem is to satisfy the condition

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \Vert x(t) - y(t) \Vert = 0,\quad \forall x(0), y(0) \in \mathrm{I\!\! R}^n \end{aligned}$$
(1)

Anti-synchronization (AS) is an important type of synchronization of a pair of chaotic systems called the master and slave systems. The anti-synchronization characterizes the asymptotic vanishing of the sum of the states of the master and slave systems. In other words, anti-synchronization of master and slave system is said to occur when the states of the synchronized systems have the same absolute values but opposite signs. Thus, if \(x(t)\) and \(y(t)\) denote the states of the master and slave systems, then the design goal of anti-synchronization problem (AS) is to satisfy the condition

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \Vert x(t) + y(t) \Vert = 0,\quad \forall x(0), y(0) \in \mathrm{I\!\! R}^n \end{aligned}$$
(2)

Pecora and Carroll pioneered the research on synchronization of chaotic systems with their seminal papers in 1990s (Carroll and Pecora 1991; Pecora and Carroll 1990). The active control method (Liu et al. 2007; Rafikov and Balthazar 2007; Sundarapandian 2010; Ucar et al. 2007; Vaidyanathan 2012c; Wang and Liu 2006) is commonly used when the system parameters are available for measurement and the adaptive control method (Wu et al. 2008; Huang 2008; Lin 2008; Sarasu and Sundarapandian 2012a, b, c) is commonly used when some or all the system parameters are not available for measurement and estimates for unknown parameters of the systems.

Other popular methods for chaos synchronization are the sampled-data feedback method (Gan and Liang 2012; Li et al. 2011; Xiao et al. 2014; Zhang and Zhou 2012), time-delay feedback method (Chen et al. 2014; Jiang et al. 2004; Shahverdiev et al. 2009; Shahverdiev and Shore 2009), backstepping method (Njah et al. 2010; Tu et al. 2014; Vaidyanathan 2012a; Zhang et al. 2004), etc.

Complete synchronization (Rasappan and Vaidyanathan 2012; Suresh and Sundarapandian 2013; Vaidyanathan and Rajagopal 2011) is characterized by the equality of state variables evolving in time, while anti-synchronization (Vaidyanathan 2011, 2012b; Vaidyanathan and Sampath 2012) is characterized by the disappearance of the sum of relevant state variables evolving in time.

This research work is organized as follows. Section 2 gives a brief introduction about sliding mode control. Section 3 discusses the problem statement for the anti-synchronization of two identical chaotic systems and our design methodology. Section 4 contains the main result of this work, namely, sliding controller design for the global anti-synchronization of identical chaotic systems. Our sliding mode control law is designed by considering constant-plus-proportional sliding law. The main result for the global anti-synchronization of chaotic systems is established using Lyapunov stability theory.

Section 5 introduces the Vaidyanathan–Madhavan chaotic system (Vaidyanathan and Madhavan 2013), which is a seven-term novel 3-D chaotic system with three quadratic nonlinearities. Section details the qualitative properties of the Vaidyanathan–Madhavan 3-D chaotic system. The Lyapunov exponents of the Vaidyanathan–Madhavan chaotic system are found as \(L_1 = 3.2226, L_2 = 0\) and \(L_3 = -30.3406\) and the Lyapunov dimension of the novel chaotic system is found as \(D_L = 2.1095\). The maximal Lyapunov exponent of the Vaidyanathan–Madhavan chaotic system is \(L_1 = 3.2226\).

In Sect. 7, we describe the sliding mode controller design for the global anti-synchronization of identical Vaidyanathan–Madhavan chaotic systems. MATLAB simulations are shown to validate and illustrate the sliding mode controller design for the anti-synchronization of the Vaidyanathan–Madhavan chaotic systems. Section 8 contains a summary of the main results derived in this research work.

2 Sliding Mode Control and Chaos Anti-synchronization

In control theory, the sliding mode control approach is recognized as an efficient tool for designing robust controllers for linear or nonlinear control systems operating under uncertainty conditions (Perruquetti and Barbot 2002; Utkin 1992).

The started steps of sliding mode control theory originated in the early 1950 s and this was initiated by S.V. Emel’yanov as Variable Structure Control (Itkis 1976; Utkin 1978; Zinober 1993). Variable structure control (VSC) is a form of discontinuous nonlinear control and this method alters the dynamics of a nonlinear system by application of a high-frequency switching control.

Sliding mode control method has a major advantage of low sensitivity to parameter variations in the plant and disturbances affecting the plant, which eliminates the necessity of exact modeling of the plant.

In the sliding mode control theory, the control dynamics has two sequential modes, viz. (i) the reaching mode, and (ii) the sliding mode. Basically, a sliding mode controller (SMC) design consists of two parts: hyperplane (or sliding surface) design and controller design.

A hyperplane is first designed via the pole-placement approach in the modern control theory and a controller is then designed based on the sliding condition. The stability of the overall control system is ensured by the sliding condition and by a stable hyperplane. Sliding mode control theory has been used to deal with many research problems of control literature (Bidarvatan et al. 2014; Feng et al. 2014; Hamayun et al. 2013; Lu et al. 2014; Ouyang et al. 2014; Zhang et al. 2014).

3 Problem Statement

This section gives a problem statement of global anti-synchronization of a pair of identical chaotic systems called the master and slave systems.

The master system is taken as the chaotic system

$$\begin{aligned} \dot{x} = A x + f(x), \end{aligned}$$
(3)

where \(x \in \mathrm{I\!\! R}^n\) is the state of the system, \(A\) is the \(n \times n\) matrix of system parameters and \(f\) is a vector field that contains the nonlinear parts of the system and satisfies \(f(0) = 0\).

The slave system is taken as the controlled chaotic system

$$\begin{aligned} \dot{y} = A y + f(y) + u, \end{aligned}$$
(4)

where \(y \in \mathrm{I\!\! R}^n\) is the state of the system, and \(u\) is the controller to be determined.

The anti-synchronization error between the master and slave systems is defined by

$$\begin{aligned} e = y + x \end{aligned}$$
(5)

Differentiating (5) and simplifying, the error dynamics is obtained as

$$\begin{aligned} \dot{e} = A e + \eta (x, y) + u \end{aligned}$$
(6)

where

$$\begin{aligned} \eta (x, y) = f(x) + f(y) \end{aligned}$$
(7)

The design problem is to determine a feedback control \(u\) so that the anti-synchronization error dynamics (6) is globally asymptotically stable at the origin for all initial conditions \(e(0) \in \mathrm{I\!\! R}^n\).

For the SMC design for the global anti-synchronization of the systems (3) and (4), the control \(u\) is taken as

$$\begin{aligned} u(t) = - \eta (x, y) + B v(t), \end{aligned}$$
(8)

where \(B\) is an \((n \times 1)\) column vector chosen such that \((A, B)\) is controllable.

Upon substituting (8) into (6), the closed-loop error system is obtained as

$$\begin{aligned} \dot{e}(t) = A e(t) + B v(t), \end{aligned}$$
(9)

which is a linear time-invariant control system with a single input \(v\).

Hence, by the use of the nonlinear control law (8), original problem of global anti-synchronization of identical chaotic systems (3) and (4) has been converted into an equivalent problem of globally stabilizing the error dynamics (9).

4 Sliding Controller Design for Global Anti-synchronization

This section derives the main result, viz. sliding controller design for the global anti-synchronization of the identical chaotic systems (3) and (4). After applying the control (8) with \((A, B)\) a controllable pair, it is supposed that the nonlinear error dynamics (6) has been simplified as the linear error dynamics (9).

In the sliding controller design, the sliding variable is first defined as

$$\begin{aligned} s(e) = C e = c_1 e_1 + c_2 e_2 + \cdots + c_n e_n, \end{aligned}$$
(10)

where \(C\) is an \((1 \times n)\) row vector to be determined.

The sliding manifold \(S\) is defined as the hyperplane

$$\begin{aligned} S = \{ e \in \mathrm{I\!\! R}^n \ : \ s(e) = C e = 0 \} \end{aligned}$$
(11)

If a sliding motion occurs on \(S\), then the sliding mode conditions must be satisfied, which are given by

$$\begin{aligned} s \equiv 0 \ \ \text{ and } \ \ \dot{s} = C A e + C B v = 0 \end{aligned}$$
(12)

It is assumed that the row vector \(C\) is chosen so that \(C B \ne 0\).

The sliding motion is affected by the so-called equivalent control given by

$$\begin{aligned} v_{\mathrm{eq}}(t) = - (C B)^{-1} C A e(t) \end{aligned}$$
(13)

As a consequence, the equivalent dynamics in the sliding phase is defined by

$$\begin{aligned} \dot{e} = \left[ I - B (C B)^{-1} C \right] A e = E e, \end{aligned}$$
(14)

where

$$\begin{aligned} E = \left[ I - B (C B)^{-1} C \right] A \end{aligned}$$
(15)

It can be easily verified that \(E\) is independent of the control and has at most \((n - 1)\) nonzero eigenvalues, depending on the chosen switching surface, while the associated eigenvectors belong to \(\text{ ker }(C)\).

Since \((A, B)\) is controllable, the matrices \(B\) and \(C\) can be chosen so that \(E\) has any desired \((n - 1)\) stable eigenvalues.

Thus, the dynamics in the sliding mode is globally asymptotically stable.

Finally, for the sliding mode controller (SMC) design, the constant plus proportional rate reaching law is used, which is given by

$$\begin{aligned} \dot{s} = - \beta \mathop {\mathrm {sgn}}(s) - \alpha s \end{aligned}$$
(16)

where \(\mathop {\mathrm {sgn}}(\cdot )\) denotes the sign function and the gains \(\alpha > 0, \beta > 0\) are found so that the sliding condition is satisfied and the sliding motion will occur.

From the Eqs. (12) and (16), sliding control \(v\) is found as

$$\begin{aligned} C A e + C B v = - \beta \mathop {\mathrm {sgn}}(s) - \alpha s \end{aligned}$$
(17)

Since \(s = C e\), the Eq. (17) can be simplified to get

$$\begin{aligned} v = - (C B)^{-1} \left[ C (\alpha I + A) e + \beta \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$
(18)

Next, the main result of this section is established as follows.

Theorem 1

A sliding mode control law that achieves global anti-synchronization between the identical chaotic systems (3) and (4) for all initial conditions \(x(0), y(0)\) in \(\mathrm{I\!\! R}^n\) is given by the equation

$$\begin{aligned} u(t) = - \eta (x(t), y(t)) + B v(t), \end{aligned}$$
(19)

where \(v\) is defined by (18), \(B\) is an \((n \times 1)\) vector such that \((A, B)\) is controllable, \(C\) is an \((1 \times n)\) vector such that \(C B \ne 0\) and that the matrix \(E\) defined by Eq. (15) has \((n - 1)\) stable eigenvalues.

Proof

The proof is carried out using Lyapunov stability theory (Khalil 2001).

Substituting the sliding control law (19) into the error dynamics (6) leads to

$$\begin{aligned} \dot{e} = A e + B v \end{aligned}$$
(20)

Substituting for \(v\) from (18) into (20), the error dynamics is obtained as

$$\begin{aligned} \dot{e} = A e - B (C B)^{-1} \left[ C (\alpha I + A) e + \beta \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$
(21)

The global asymptotic stability of the error system (21) is proved by taking the candidate Lyapunov function

$$\begin{aligned} V(e) = {1 \over 2} \ s^2(e), \end{aligned}$$
(22)

which is a non-negative definite function on \(\mathrm{I\!\! R}^n\).

It is noted that

$$\begin{aligned} V(e) = 0 \ \iff \ s(e) = 0 \end{aligned}$$
(23)

The sliding mode motion is characterized by the equations

$$\begin{aligned} s(e) = 0 \ \ \text{ and } \ \ \dot{s}(e) = 0 \end{aligned}$$
(24)

By the choice of \(E\), the dynamics in the sliding mode given by (14) is globally asymptotically stable.

When \(s(e) \ne 0\), \(V(e) > 0\).

Also, when \(s(e) \ne 0\), differentiating \(V\) along the error dynamics (21) or the equivalent dynamics (16), the following dynamics is obtained:

$$\begin{aligned} \dot{V} = s \dot{s} = - \beta s \, \mathop {\mathrm {sgn}}(s) - \alpha s^2 < 0 \end{aligned}$$
(25)

Hence, by Lyapunov stability theory (Khalil 2001), it is concluded that the error dynamics (21) is globally asymptotically stable for all initial conditions \(e(0) \in \mathrm{I\!\! R}^n\).

This completes the proof. \(\square \)

5 Vaidyanathan–Madhavan 3-D Chaotic System

This section describes the equations and phase portraits of Vaidyanathan–Madhavan 3-D chaotic system (Vaidyanathan and Madhavan 2013).

The Vaidyanathan–Madhavan chaotic system is a described by the 3-D dynamics

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} a (x_2 - x_1) + x_2 x_3, \\ \dot{x}_2 &{} = &{} b x_1 + c x_1 x_3, \\ \dot{x}_3 &{} = &{} - d x_3 - x_1 x_2 - x_1^2, \\ \end{array} \right. \end{aligned}$$
(26)

where \(x_1, x_2, x_3\) are the states and \(a, b, c, d\) are constant, positive, parameters.

The system (26) is a seven-term polynomial chaotic system with three quadratic nonlinearities.

The system (26) depicts a strange chaotic attractor when the constant parameter values are taken as

$$\begin{aligned} a = 22, \quad b = 400, \quad c = 50, \quad d = 0.5 \end{aligned}$$
(27)

For simulations, the initial values of the Vaidyanathan–Madhavan chaotic system (26) are taken as

$$\begin{aligned} x_1(0) = 0.6, \quad x_2(0) = 1.8, \quad x_3(0) = 1.2 \end{aligned}$$
(28)

The novel 3-D chaotic system (26) exhibits a 2-scroll chaotic attractor. Figure 1 describes the 2-scroll chaotic attractor of the Vaidyanathan–Madhavan chaotic system (26) in 3-D view.

Fig. 1
figure 1

Strange attractor of the Vaidyanathan–Madhavan chaotic system in \(\mathrm{I\!\! R}^3\)

Full size image

Figure 2 describes the 2-D projection of the strange chaotic attractor of the Vaidyanathan–Madhavan chaotic system (26) in \((x_1, x_2)\)-plane. In the projection on the \((x_1, x_2)\)-plane, a 2-scroll chaotic attractor is clearly seen.

Fig. 2
figure 2

2-D projection of the Vaidyanathan–Madhavan chaotic system in \((x_1, x_2)\)-plane

Full size image

Figure 3 describes the 2-D projection of the strange chaotic attractor of the Vaidyanathan–Madhavan chaotic system (26) in \((x_2, x_3)\)-plane. In the projection on the \((x_2, x_3)\)-plane, a 2-scroll chaotic attractor is clearly seen.

Fig. 3
figure 3

2-D projection of the Vaidyanathan–Madhavan chaotic system in \((x_2, x_3)\)-plane

Full size image
Fig. 4
figure 4

2-D projection of the Vaidyanathan–Madhavan chaotic system in \((x_1, x_3)\)-plane

Full size image

Figure 4 describes the 2-D projection of the strange chaotic attractor of the Vaidyanathan–Madhavan chaotic system (26) in \((x_1, x_3)\)-plane. In the projection on the \((x_1, x_3)\)-plane, a 2-scroll chaotic attractor is clearly seen.

6 Analysis of the Vaidyanathan–Madhavan Chaotic System

This section gives the qualitative properties of the Vaidyanathan–Madhavan 3-D chaotic system (2013).

6.1 Symmetry and Invariance

The Vaidyanathan system (26) is invariant under the coordinates transformation

$$\begin{aligned} (x_1, x_2, x_3) \rightarrow (-x_1, -x_2, x_3). \end{aligned}$$
(29)

The transformation (29) persists for all values of the system parameters. Thus, the Vaidyanathan system (26) has rotation symmetry about the \(x_3\)-axis.

Hence, it follows that any non-trivial trajectory of the system (26) must have a twin trajectory.

It is easy to check that the \(x_3\)-axis is invariant for the flow of the Vaidyanathan system (26). Hence, all orbits of the system (26) starting from the \(x_3\) axis stay in the \(x_3\) axis for all values of time.

6.2 Equilibria

The equilibrium points of the Vaidyanathan–Madhavan system (26) are obtained by solving the nonlinear equations

$$\begin{aligned} \left. \begin{array}{cclcl} f_1(x) &{} = &{} a (x_2 - x_1) + x_2 x_3 &{} = &{} 0 \\ f_2(x) &{} = &{} b x_1 + c x_1 x_3 &{} = &{} 0 \\ f_3(x) &{} = &{} - d x_3 - x_1 x_2 - x_1^2 &{} = &{} 0 \\ \end{array} \right. \end{aligned}$$
(30)

We take the parameter values as in the chaotic case, viz.

$$\begin{aligned} a = 22, \quad b = 400,\quad c = 50, \quad d = 0.5 \end{aligned}$$
(31)

Solving the nonlinear system of Eqs. (30) with the parameter values (31), we obtain three equilibrium points of the Vaidyanathan–Madhavan system (26) as

$$\begin{aligned} E_0 = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right] , \quad E_1 = \left[ \begin{array}{r} 1.2472 \\ 1.9599 \\ -8.0000 \\ \end{array} \right] \ \ \text{ and } \quad E_2 = \left[ \begin{array}{r} -1.2472 \\ -1.9599 \\ -8.0000 \end{array} \right] . \end{aligned}$$
(32)

The Jacobian matrix of the Vaidyanathan system (26) at \((x_1^\star , x_2^\star , x_3^\star )\) is obtained as

$$\begin{aligned} J(x^\star ) = \left[ \begin{array}{ccc} -22 &{} 22 + x_3^\star &{} x_2^\star \\[1mm] 400 + 50 x_3^\star &{} 0 &{} 50 x_1^\star \\[1mm] - x_2^\star - 2 x_1^\star &{} - x_1^\star &{} - 0.5 \\[1mm] \end{array} \right] \end{aligned}$$
(33)

The Jacobian matrix at \(E_0\) is obtained as

$$\begin{aligned} J_0 = J(E_0) = \left[ \begin{array}{rrr} -22 &{} 22 &{} 0 \\[2mm] 400 &{} 0 &{} 0 \\[2mm] 0 &{} 0 &{} -0.5 \\[2mm] \end{array} \right] \end{aligned}$$
(34)

The matrix \(J_0\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -0.5, \quad \lambda _2 = -105.451, \quad \lambda _3 = 83.451 \end{aligned}$$
(35)

This shows that the equilibrium point \(E_0\) is a saddle-point, which is unstable.

The Jacobian matrix at \(E_1\) is obtained as

$$\begin{aligned} J_1 = J(E_1) = \left[ \begin{array}{ccc} -22 &{} 14 &{} 1.9599 \\[1mm] 0 &{} 0 &{} 62.36 \\[1mm] -4.4543 &{} -1.2472 &{} -0.5 \\[1mm] \end{array} \right] \end{aligned}$$
(36)

The matrix \(J_1\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -26.7022, \quad \lambda _{2, 3} = 2.1011 \pm 14.3283 i \end{aligned}$$
(37)

This shows that the equilibrium point \(E_1\) is a saddle-focus, which is unstable.

The Jacobian matrix at \(E_2\) is obtained as

$$\begin{aligned} J_2 = J(E_2) = \left[ \begin{array}{ccc} -22 &{} 14 &{} -1.9599 \\[1mm] 0 &{} 0 &{} -62.36 \\[1mm] 4.4543 &{} 1.2472 &{} -0.5 \\[1mm] \end{array} \right] \end{aligned}$$
(38)

The matrix \(J_2\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -26.7022, \quad \lambda _{2, 3} = 2.1011 \pm 14.3283 i \end{aligned}$$
(39)

This shows that the equilibrium point \(E_2\) is a saddle-focus, which is unstable.

Hence, \(E_0, E_1, E_2\) are all unstable equilibrium points of the Vaidyanathan–Madhavan chaotic system (26), where \(E_0\) is a saddle point and \(E_1, E_2\) are saddle-focus points.

6.3 Lyapunov Exponents and Lyapunov Dimension

Fig. 5
figure 5

Dynamics of the lyapunov exponents of the Vaidyanathan–Madhavan system

Full size image

We take the initial values of the Vaidyanathan–Madhavan system as in (28) and the parameter values of the Vaidyanathan–Madhavan system as (27).

Then the Lyapunov exponents of the Vaidyanathan system (26) are numerically obtained as

$$\begin{aligned} L_1 = 3.3226, \quad L_2 = 0, \quad L_3 = -30.3406 \end{aligned}$$
(40)

Thus, the maximal Lyapunov exponent of the Vaidyanathan–Madhavan system (26) is \(L_1 = 3.3226\).

Since \(L_1 + L_2 + L_3 = -27.018 < 0\), the system (26) is dissipative.

Also, the Lyapunov dimension of the system (26) is obtained as

$$\begin{aligned} D_L = 2 + {L_1 + L_2 \over | L_3 |} = 2.1095 \end{aligned}$$
(41)

Figure 5 depicts the dynamics of the Lyapunov exponents of the Vaidyanathan–Madhavan system (26).

7 Anti-synchronization of Vaidyanathan–Madhavan Chaotic Systems via SMC

This section details the construction of an anti-synchronizer for identical Vaidyanathan–Madhavan chaotic systems via sliding mode control method.

The master system is taken as the Vaidyanathan–Madhavan system given by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} a (x_2 - x_1) + x_2 x_3 \\[1mm] \dot{x}_2 &{} = &{} b x_1 + c x_1 x_3 \\[1mm] \dot{x}_3 &{} = &{} - d x_3 - x_1 x_2 - x_1^2 \\[1mm] \end{array} \right. \end{aligned}$$
(42)

where \(a, b, c, d\) are constant, positive parameters.

The slave system is also taken as the Vaidyanathan–Madhavan system with controllers attached and given by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{y}_1 &{} = &{} a (y_2 - y_1) + y_2 y_3 + u_1 \\[1mm] \dot{y}_2 &{} = &{} b y_1 + c y_1 y_3 + u_2 \\[1mm] \dot{y}_3 &{} = &{} - d y_3 - y_1 y_2 - y_1^2 + u_3 \\[1mm] \end{array} \right. \end{aligned}$$
(43)

where \(u_1, u_2, u_3\) are sliding controllers to be found.

The anti-synchronization error is defined by

$$\begin{aligned} e = y + x \end{aligned}$$
(44)

Then the error dynamics is obtained as

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_1 &{} = &{} a (e_2 - e_1) + y_2 y_3 + x_2 x_3 + u_1 \\[1mm] \dot{e}_2 &{} = &{} b e_1 + c (y_1 y_3 + x_1 x_3) + u_2 \\[1mm] \dot{e}_3 &{} = &{} -d e_3 - y_1 y_2 - x_1 x_2 - y_1^2 - x_1^2 + u_3 \\[1mm] \end{array} \right. \end{aligned}$$
(45)

The error dynamics (45) can be expressed in matrix form as

$$\begin{aligned} \dot{e} = A e + \eta (x, y) + u \end{aligned}$$
(46)

where

$$\begin{aligned} A = \left[ \begin{array}{ccc} -a &{} a &{} 0 \\[1mm] b &{} 0 &{} 0 \\[1mm] 0 &{} 0 &{} -d \\[1mm] \end{array} \right] , \quad \eta (x, y) = \left[ \begin{array}{c} y_2 y_3 + x_2 x_3 \\[1mm] c ( y_1 y_3 + x_1 x_3 ) \\[1mm] - y_1 y_2 - x_1 x_2 - y_1^2 - x_1^2 \\[1mm] \end{array} \right] , \quad u = \left[ \begin{array}{c} u_1 \\[1mm] u_2 \\[1mm] u_3 \\[1mm] \end{array} \right] \end{aligned}$$
(47)

The parameter values of \(a, b, c, d\) are taken as in the chaotic case, i.e.

$$\begin{aligned} a = 22, \quad b = 400, \quad c = 50, \quad d = 0.5 \end{aligned}$$
(48)

First, the control \(u\) is set as

$$\begin{aligned} u = - \eta (x, y) + B v, \end{aligned}$$
(49)

where \(B\) is chosen such that \((A, B)\) is controllable.

A simple choice for \(B\) is

$$\begin{aligned} B = \left[ \begin{array}{c} 1\\ 1\\ 1\\ \end{array}\right] \end{aligned}$$
(50)

The sliding variable is picked as

$$\begin{aligned} s = C e = \left[ \begin{array}{ccc} 1 &{} 2 &{} -2\\ \end{array} \right] e = e_1 + 2 e_2 - 2 e_3 \end{aligned}$$
(51)

The choice of the sliding variable indicated by (51) renders the sliding mode dynamics globally asymptotically stable.

Next, we choose the SMC gains as

$$\begin{aligned} \alpha = 6 \ \ \ \text{ and } \ \ \beta = 0.2 \end{aligned}$$
(52)

Using the formula (18), the control \(v\) is obtained as

$$\begin{aligned} v(t) = - 784 e_1 - 34 e_2 + 11 e_3 - 0.2 \mathop {\mathrm {sgn}}(s) \end{aligned}$$
(53)

As a consequence of Theorem 1 (Sect. 4), the following result is obtained.

Theorem 2

The control law defined by (49), where \(v\) is defined by (53), renders the Vaidyanathan systems (42) and (43) globally and asymptotically anti-synchronized for all values of the initial states \(x(0), y(0) \in \mathrm{I\!\! R}^3\).

For numerical simulations, the classical fourth-order Runge-Kutta method with step-size \(h = 10^{-8}\) is used in the MATLAB software.

The parameter values are taken as in the chaotic case of the Vaidyanathan systems (42) and (43), i.e.

$$ a = 22, \quad b = 400, \quad c = 50, \quad d = 0.5 $$

The sliding mode gains are taken as \(\alpha = 6\) and \(\beta = 0.2\).

The initial values of the master system (42) are taken as

$$ x_1(0) = 5.2, \quad x_2(0) = 2.7, \quad x_3(0) = -3.2 $$

The initial values of the slave system (43) are taken as

$$ y_1(0) = 3.4, \quad y_2(0) = 3.1, \quad y_3(0) = -8.4 $$

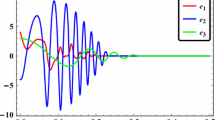
Figures. 6, 7 and 8 show the anti-synchronization of the Vaidyanathan systems (42) and (43). Figure 9 shows the time-history of the anti-synchronization errors \(e_1, e_2\) and \(e_3\).

In Fig. 6, it is seen that the odd states \(x_1(t)\) and \(y_1(t)\) are anti-synchronized in 1 s.

Fig. 6
figure 6

Anti-synchronization of the states \(x_1\) and \(y_1\)

Full size image

In Fig. 7, it is seen that the even states \(x_2(t)\) and \(y_2(t)\) are anti-synchronized in 1 s.

Fig. 7
figure 7

Anti-synchronization of the states \(x_2\) and \(y_2\)

Full size image

In Fig. 8, it is seen that the odd states \(x_3(t)\) and \(y_3(t)\) are anti-synchronized in 1 s.

Fig. 8
figure 8

Anti-synchronization of the states \(x_3\) and \(y_3\)

Full size image
Fig. 9
figure 9

Time-history of the anti-synchronization errors \(e_1, e_2, e_3\)

Full size image

Figure 9 shows the time-history of the anti-synchronization errors \(e_1, e_2\) and \(e_3\). It is seen that the anti-synchronization errors converge to zero in 1 s.

8 Conclusions

A general result has been derived in this work for the anti-synchronization of identical chaotic systems using sliding mode control. The main result has been proved using Lyapunov stability theory. Sliding mode control (SMC) is well-known as a robust approach and useful for controller design in systems with parameter uncertainties. Next, as an application of the main result, anti-synchronizing controller has been designed for Vaidyanathan–Madhavan chaotic systems (2013). The Lyapunov exponents of the Vaidyanathan–Madhavan chaotic system were found as \(L_1 = 3.2226, L_2 = 0\) and \(L_3 = -30.3406\) and the Lyapunov dimension of the novel chaotic system was found as \(D_L = 2.1095\). The maximal Lyapunov exponent of the Vaidyanathan–Madhavan chaotic system was found as \(L_1 = 3.2226\). As an application of the general result derived in this work, a sliding mode controller has been derived for the anti-synchronization of the identical Vaidyanathan–Madhavan chaotic systems. MATLAB simulations have been provided to illustrate the qualitative properties of the novel 3-D chaotic system and the anti-synchronizer results for the identical novel 3-D chaotic systems. As future research, adaptive sliding mode controllers may be devised for the anti-synchronization of identical chaotic systems with unknown system parameters.