Keywords

1 Introduction

The most widely used probabilistic topic model in the field of text mining is pLSI (probabilistic Latent Semantic Indexing) proposed by Hoffman [1] and LDA (Latent Dirichlet Allocation) proposed by Blei [2]. pLSI is a generative model that can be used to discover the mixture weights of topics of documents in a training data set; however, it is limited by the fact that it cannot properly infer the topic mixture weights of unseen documents. Based on the principle of pLSI, Blei proposed LDA that addressed this issue. LDA is a fully generative model that patterns each document m as a distribution \( \overrightarrow{\theta_m} \) over all topics K and each topic k as a distribution \( \overrightarrow{\varphi_k} \) over all words in the vocabulary V. LDA first draws \( \overrightarrow{\theta_m} \) and \( \overrightarrow{\varphi_k} \) from Dirichlet distributions, then samples a topic for each word position in each document m in the corpus according to \( \overrightarrow{\theta_m} \), and finally emits relative words from the topic-word distribution \( \overrightarrow{\varphi_k} \).

LDA has been widely applied to text mining, digital image processing, etc. Usually the current applications of LDA are always “content-based” that process the content of text or pixels in images. To our best knowledge, LDA has not been used to handle social network structure data (in the context of this chapter “social network structure data” means data of friendship or relation between users in a social network; in the following sections “network structure data” and “friendship data” are used interchangeably) to detect the underlying topic communities in a social network. In this chapter, we attempt such a new application by adding a slight modification to LDA.

In the following sections, we first specify the incapability of LDA in handling social networks’ friendship data, and then we introduce our model—Tri-LDA to address it. Lastly we test the effectiveness of our method through an experiment.

2 Tri-LDA Model

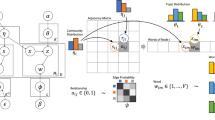
Figure 142.1 (left) displays the Bayesian network of LDA [2]. By borrowing the generation process of documents in the LDA model specified by Blei [1] and Heinrich [3], we interpret LDA’s generation of the friendship data in a social network with N users (each user has arbitrary N u friends) and K topic communities as follows:

Fig. 142.1
figure 1

Bayesian networks of LDA (left) and Tri-LDA (right)

Full size image
  1. i.

    Sampling topic probability mixture \( \overrightarrow{\theta_u} \) for each user u from the Dirichlet distribution with a prior of \( \overrightarrow{a} \), where \( \overrightarrow{\theta_u}={\left\{{\theta}_{u,k}\right\}}_{k=1}^K \) represents the degree to which u likes about each topic k. At the meantime, sampling a distribution \( \overrightarrow{\varphi_k} \) for each topic k over all the users from the Dirichlet distribution with a prior of \( \overrightarrow{\beta} \), where \( \overrightarrow{\varphi_k}={\left\{{\varphi}_{k,u}\right\}}_{u=1}^U \) represents the possibility of each user being added by others as a friend in topic k.

  2. ii.

    For the n th position in user u ’ s friend list that has N u positions for potential friends: firstly, sampling a topic z a   (a = [u, n]) for the n th friend from \( \overrightarrow{\theta_u} \) (this represents that user u will add a new friend who is active in this very topic for this friend position) and secondly, sampling a friend f a according to \( p\left({f}_a\left|\overrightarrow{\varphi_{z_a}},{z}_a\right.\right)={\varphi}_{z_a,{f}_a} \).

  3. iii.

    Repeat step 2 till all friends of all users are generated.

However, it can be easily found that \( \overrightarrow{\theta_u} \) and \( \overrightarrow{\varphi_k} \) are correlated, instead of being independent of each other: for an arbitrary topic k, the more a user likes about it, the more likely this user could be added by other users who also like the topic k to their friend lists. Or, namely, the higher the probability θ u,k , the higher φ k,u is.

We solve this correlation problem by adding a new parameter that is directly proportional to \( \overrightarrow{\theta_u} \): \( \overrightarrow{\pi_u^{(k)}} \) that represents the degree to which u accept other users from the same social network in topic k as his or her friends. In the meantime, we give \( \overrightarrow{\varphi_k} \) a new meaning to make the generation process more natural: the activeness of each user in topic k. The possibility of an arbitrary user u adding another user who is active in topic z a to the n th position in his or her friend list as friend f a is determined by the joint distribution of \( \overrightarrow{\varphi_{z_a}} \) and \( \overrightarrow{\pi_u^{\left({z}_a\right)}} \), which is expressed by the following equation:

$$ p\left({f}_{{}_a}\left|\overrightarrow{\varphi_{z_a}},{z}_a,\overrightarrow{\pi_u^{\left({z}_a\right)}}\right.\right)={\varphi}_{z_a,{f}_a}{\pi}_{u,{f}_a}^{\left({z}_a\right)} $$
(142.1)

By adding this slight modification, we get the modified LDA model—Tri-LDA. Figure 142.1 (right) displays the Bayesian network structure of Tri-LDA. In this chapter we simplify \( \overrightarrow{\pi_u^{(k)}} \) as: \( {\pi}_{u_{{}_1},{u}_2}^k=\left\{\begin{array}{lll}0\hfill & \mathrm{if}\hfill & {u}_1={u}_2\hfill \\ {}{\theta}_{u_{{}_2},k}\hfill & \mathrm{if}\hfill & {u}_1\ne {u}_2\hfill \end{array}\right. \)

That means, firstly, no user would add himself or herself to his or her friend list and, secondly, the degree to which user u 1 accepts another user u 2 as a friend in topic k equals to \( {\theta_{u_2}}_{,k} \), the degree to which user u 2 likes about topic k. Therefore based on the simplification, we can get the following equation:

$$ p\left({f}_a\Big|\overrightarrow{\varphi_{z_a}},{z}_a,\overrightarrow{\pi_u^{\left({z}_a\right)}}\right)={\varphi}_{{}_{z_a,{f}_a}}{\theta}_{{}_{{}_{f_a,{z}_a}}} $$
(142.2)

There are two methods that are commonly used to infer latent parameters for high-dimensional probabilistic models like LDA: EM (Expectation Maximization) and Gibbs sampling. In this chapter, for Tri-LDA, we choose Gibbs sampling to infer \( \overrightarrow{\theta} \), the matrix that represents the degree to which each user likes about each topic in a social network.

Gibbs sampling is a simple implementation of the Monte Carlo algorithm, which is usually used to infer the latent parameters of high-dimensional probabilistic topic models [4]. Gibbs sampling starts from a randomly sampled initial state, then continuously transits to new states based on the current state to build up a Markov chain. After a certain number of transitions, the Markov chain would become stable. The stable state of the Markov chain can be regarded as an approximated observation of the query distribution. In this chapter we run Gibbs sampling methods on the social network to get an approximated observation of \( \overrightarrow{\theta} \): the topic indices \( \overrightarrow{z} \) from which users add their friends to his or her friend list. We specify the implementation of Gibbs sampling on a social network as the following steps:

  1. i.

    Randomly allocate a topic k for every friend in every user’s friend list.

  2. ii.

    In an arbitrary user u ’ s friend list, choose the n th friend position, indexing it with i. Remove the topic k that previously allocated on f i , and then resample a new topic for it based on the following two known conditions: all the friends of all users \( \overrightarrow{f} \) and all the topics of all friends in all users’ friend lists except for the topic of f i : z i .

  3. iii.

    Repeat step ii through all friends in user u ’ s friend list.

  4. iv.

    Repeat step iii through all users in the social network.

In step 2, the posterior probability \( p\left(\overrightarrow{z_i}\Big|\overrightarrow{z_{-i}},\overrightarrow{f}\right) \) needs to be computed. According to Tri-LDA stated above, we can get the following equation:

$$ p\left(\overrightarrow{f},\overrightarrow{z}\Big|\overrightarrow{\theta},\overrightarrow{\varphi},\overrightarrow{\pi}\right)={\displaystyle \prod_{u=1}^U{\displaystyle \prod_{k=1}^K{\theta}_{{}_{u,k}}^{n_u^{(k)}+{n}_{u^{\prime}}^{(k)}}}}{\displaystyle \prod_{k=1}^K{\displaystyle \prod_{u=1}^U{\varphi}_{k,u}^{n_{u^{\prime}}^{(k)}}}} $$
(142.3)

where n k u denotes the number of friends who are allocated with topic k in the friend list of user u and \( {n}_{u^{\prime}}^k \) denotes in the friend lists of other users the number of times that user u is allocated with topic k. Then, we get the following equation:

$$ p\left(\overrightarrow{f},\overrightarrow{z}\Big|\overrightarrow{a},\overrightarrow{\beta},\overrightarrow{\pi}\right)={\displaystyle \prod_{k=1}^K\frac{\Delta \left(\overrightarrow{n_{u^{\prime }}}+\overrightarrow{\beta}\right)}{\Delta \left(\overrightarrow{\beta}\right)}}{\displaystyle \prod_{u=1}^U\frac{\Delta \left(\overrightarrow{n_u}+\overrightarrow{a}+\overrightarrow{n_{u^{\prime }}}\right)}{\Delta \left(\overrightarrow{a}\right)}} $$
(142.4)

where \( \overrightarrow{n_{u^{\prime }}}={\left\{{n}_{u^{\prime}}^{(k)}\right\}}_{k=1}^K \), \( \overrightarrow{n_u}={\left\{{n}_u^{(k)}\right\}}_{k=1}^K \). Assume the i th friend in u ’ s friend list is user u o , and then we get the following posterior distribution \( p\left(\overrightarrow{z_i}\Big|\overrightarrow{z_{-i}},\overrightarrow{f}\right) \):

$$ \begin{array}{l}p\left({z}_i=k\Big|\overrightarrow{z_{-i}},\overrightarrow{f}\right)\propto \frac{p\left(\overrightarrow{f}\Big|\overrightarrow{z}\right)p\left(\overrightarrow{z}\right)}{p\left({\overrightarrow{f}}_{-i}\Big|\overrightarrow{z_{-i}}\right)p\left(\overrightarrow{z_{-i}}\right)}\\ {} \propto \frac{n_{u_o^{\prime },-i}^{(k)}+{\beta}_{u_o}}{{\displaystyle \sum_{u=1}^U{n}_{u^{\prime },-i}^{(k)}+{\beta}_u}}*\left({a}_k+{n}_{u,-i}^{(k)}+{n}_{u^{\prime}}^{(k)}\right)*\left({a}_k+{n}_{u_o}^{(k)}+{n}_{u_o^{\prime },-i}^{(k)}\right)\kern0.1em \end{array} $$
(142.5)

where \( {n}_{u_o^{\prime },-i}^{(k)} \) denotes the number of times that user u o is allocated with topic k excluding i in all other users’ friend lists and n (k) u,− i denotes the number of friends who are allocated with topic k in the friend list of user u excluding i. After running Gibbs sampling on the social network, we get all the topic indices from which all friends of all users are sampled that can be regarded as an approximated observation of \( \overrightarrow{\theta} \). With the approximated observation, we can compute the expectation of the Dirichlet distribution and use it as an estimator for the desirable θ u,k , the degree to which a user u likes about topic k (Table 142.1).

Table 142.1 Pseudocode of Gibbs sampling algorithm for Tri-LDA
Full size table
$$ {\theta}_{u,k}=\frac{n_u^{(k)}+{a}_k+{n}_{u^{\prime}}^{(k)}}{{\displaystyle \sum_{k=1}^K{n}_u^{(k)}+{a}_k+{n}_{u^{\prime}}^{(k)}}} $$
(142.6)

3 Experiment

We collect a data set that includes the connections between 2,315 Sina Weibo users. The friends of each user are limited to be the users in this data set. By reviewing the data set, we find that around 70% of nodes (or users) are richly connected with each other, and around 10% of nodes are relatively isolated. We randomly choose 2,179 of them as the training data set and the remaining as test data set. By manually checking the posts and tags those users posted on the site, we find there are 17 different topics involved in the data set: information technology, business, finance, military, charity, food, education, car, travel, photography, everyday life information, show business, politics, sports, literature, painting, and religion. Based on the contents of each user’s post page, we score the degrees to which each user is interested in those topics. By using the scores, we represent each user’s interest by a vector with 17 elements: \( \overrightarrow{h_u} \). Then the similarity of interests between two users u 1, u 2 can be expressed as:

$$ {\mathrm{Sim}}_{u_1,{u}_2}=\frac{\left|\overrightarrow{h_{u_1}}.\kern0.3em \overrightarrow{h_{u_2}}\right|}{\left|\overrightarrow{h_{u_1}}\left|\kern0.8em \right|\overrightarrow{h_{u_2}}\right|} $$
(142.7)

In this experiment, we first run Gibbs sampling based on the Tri-LDA model to discover the underlying topic communities. We measure the effectiveness of Tri-LDA by computing the fittingness of the outputted result to the actual topic communities manually labeled by us. We also run k-medoid clustering algorithm on the texts and tags posted by the users and see users of each cluster in the output as a topic community [5]. To test the generalization property of Tri-LDA, we compare the predictive perplexity of Tri-LDA with that of k-medoid clustering mentioned above.

In the training process of LDA, we set the prior parameter of a in the range [0.1, 1.5] with an incremental step of 0.1, the prior parameter of β in the range [1.0, 10.0] with an incremental step of 0.1, and the topic number K in the range [5, 20] with an incremental step of 1. We run Gibbs sampling with all the possible parameter combinations and select the one whose output has the best fittingness value. After the learning process, the desirable topic probability mixture θ u. k for every user u, which represented the degree to which user u likes about a topic k, is outputted. We set a threshold value 0.25 for θ u. k : if θ u,k  ≥ 0.25, then we conclude that u is interested in topic k. Denoting T k as the set of users in the k th topic community, then T k  = {u|θ u,k  ≥ 0.25}.

In the real-world social networks, users from the same topic community always have relatively high interest similarities. To measure the credibility of the learning result, we use the interest similarity equation stated above to compute the interest similarity between each two users in a topic community obtained by Tri-LDA and take its averaged value to measure the fittingness of the learning result to the real-world situation. We express the fittingness of the learning result as the following equation:

$$ f=\frac{{\displaystyle \sum_{k=1}^K\mathrm{a}\mathrm{v}\mathrm{g}\left({\mathrm{Sim}}_k\right)}}{K} $$
(142.8)

where avg(Sim k ) denotes the average interest similarity between every two users in a topic community. In the experiment we find that when a = 0.7, β = 8, k = 14, the topic communities outputted by the algorithm have the best fittingness value. Figure 142.2 displays the fittingness value of the learning results under some of the parameter settings in this experiment. The result shows that the average fittingness f under different parameter settings in this experiment is around 0.70, which indicates the learning results can basically reflect the actual interest similarities between users in the selected social network.

Fig. 142.2
figure 2

Fittingness of the Tri-LDA model

Full size image

We denote the degree to which a user d in the test data set likes about topic k as θ d,k , then

$$ {\theta}_{d,k}=\frac{n_d^{(k)}}{N_d} $$
(142.9)

where n (k) d is the number of friends who belong to topic community k in d ’ s friend list and N d is the total number of friends in d ’ s friend list. Use the learning result to predict the interest of users in the test set, and express the predictive perplexity of the predication with the following equation:

$$ \mathrm{perplexity}=\frac{{\displaystyle {\sum}_{d=1}^DH(d)}}{D} $$
(142.10)

where \( H(d)=-{\displaystyle \sum_{k=1}^K{\theta}_{d,k}}\ \log\ {\theta}_{d,k} \) and D is the total number of users in the test data set. A relatively lower predictive perplexity always suggests better generalization property. We compare Tri-LDA’s predictive perplexity, when a = 0.7, β = 8, k = 8, 9, 10, 11, 12, 13, 14, with the predictive perplexity of k-medoid clustering with the medoid number as 8, 9, 10, 11, 12, 13, 14, respectively. Figure 142.3 displays the comparison between the predictive perplexity of Tri-LDA and k-medoid clustering in this experiment. The result indicates that Tri-LDAs have a lower predictive perplexity than k-medoid clustering; therefore Tri-LDA has a better generalization performance that can be used to predict the interests of unseen users than k-medoid clustering in this experiment.

Fig. 142.3
figure 3

Comparison of predictive perplexity between Tri-LDA and k-medoid clustering

Full size image

Conclusion and Future Work

We propose a modified LDA model—Tri-LDA—to detect topic communities in social networks by processing network structure data. The experiment result shows that the learning result is consistent with the realistic topic communities hand-labeled by us in the test data set. Also the experiment result shows that Tri-LDA has a decent generalization performance in predicting the interests of unknown users. In the future we plan to add some further modification to Tri-LDA to allow it to process the combined data of network structure and communications between users to detect the underlying topic communities in a social network.