Open Problems on With-Carry Sequence Generators

Abstract

Pseudorandom sequences are used in a wide range of applications in computing and communications, including cryptography. It is common to use linear feedback shift registers (LFSRs) to generate such sequences, either directly or as components in more complex structures. Much of the analysis of such sequences is done using the algebra of polynomials and power series over finite fields. The subjects of this chapter are feedback with carry shift registers (FCSRs) and algebraic feedback shift registers (AFSRs, generalizations of both LFSRs and FCSRs), sequence generators that are analogous to LFSRs, but whose state update involves arithmetic with a carry. Their analysis is based on algebraic structures with carry, such as the integers and the N-adic numbers. After a brief review of the basics on LFSRs, FCSRs, and AFSRs, we describe several open problems. These include: given part of a sequence, how to find an optimal generator of the sequence; how to construct sequences that cannot be generated by short LFSRs, FCSRs, or AFSRs; and the analysis of various statistical properties related to these generators.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The subject of this chapter is the generation of “pseudorandom” sequences using very high-speed devices. Here pseudorandom means that various statistical properties hold such as (in the binary case) a balance in the numbers of zeroes and ones. Such sequences play critical roles in many applications in communications and computing. Following are some important examples.

• 1. Cryptography: stream ciphers scramble messages by combining them with sequences that are unpredictable from short prefixes.

• 2. CDMA: large families of uncorrelated sequences minimize interference and allow a collection of channels to be shared by users (see Sect. 5.2).

• 3. Radar ranging and GPS: peaks in autocorrelations of a sequence allow delay to be measured.

• 4. Quasi-Monte Carlo: integrals are approximated by sampling integrands at points determined by pseudorandom sequences.

• 5. Built in self-test: test patterns are determined by pseudorandom sequences.

• 6. Wear leveling of storage media: pseudorandom sequences are used to remap the memory locations in a way that distributes the wear evenly across the whole disk.

For some 60 years linear feedback shift registers (LFSRs) (described in Sect. 3) have been used as generators (or components of generators) of pseudorandom sequences for these and other applications. In the form of linear equations modulo N, they have been studied by mathematicians since at least the 1920s [4]. The primary mathematical tools for analyzing these sequences are finite fields and particularly polynomials and power series over finite fields. A great deal is known about these sequences, but there is still much that is unknown.

More recently (since 1993 [6, 20]), researchers have been studying feedback with carry shift registers (FCSRs), a “with-carry” analog of LFSRs (described in Sect. 3). So far they have found a smaller number of applications—cryptanalysis of the summation combiner, quasi-Monte Carlo integration, and the F-FCSR stream cipher. One advantage they have is that the state change is nonlinear, which makes stream ciphers based on them resistant to algebraic attacks.

Much less is known about sequences generated by FCSRs (and algebraic feedback shift registers (AFSRs), a generalization). The purpose of this chapter is to describe some of the open problems in this area. The main focus is on properties of sequences that are of interest cryptographically.

Throughout this chapter, the book by Goresky and the author [10] serves as a reference.

2 Stream Ciphers

In this section we discuss one important application of pseudorandom sequences. The main problem of practical cryptography is how to send a message securely in real time. The common techniques of public key cryptography are too slow for large transmissions (such as video on demand). For example, RSA encrypts by computing $E(m) = m^{e}\mod pq$, where p and q are perhaps 500 bit primes. This is much too slow to encrypt large data sets in real time.

The alternative is to use symmetric key cryptography—block or stream ciphers. The trade-off between these two approaches is that the fastest stream ciphers are somewhat faster than the fastest block ciphers, but stream ciphers seem to be more vulnerable to attack. In this section we are interested in stream ciphers. In their simplest form, a sender and receiver agree on a pseudorandom sequence generator (PSG) G (publicly) and a small shared seed s (privately, perhaps by a slow key agreement protocol). G, initialized with s, generates a pseudorandom sequence $G(s) = \mathbf{a} = a_{0},a_{1},\ldots \in \{ 0,1\}^{\infty }$. A message $m = m_{0},m_{2},\ldots \in \{ 0,1\}^{\infty }$ is encrypted by computing $c_{i} = m_{i} \oplus a_{i}$. See Fig. 1.

Fig. 1

Structure of a stream cipher

Sequence generators used in stream ciphers or other applications mentioned in the introduction must have various properties, depending on the applications. They must operate in (nearly) real time. They must resist known cryptanalytic attacks. They must have good statistical properties, such as the following:

Large period::

A sequence $\mathbf{a} = a_{0},a_{1},\ldots$ is periodic if $\forall i: a_{i} = a_{i+p}$. It is eventually periodic if $\forall i> t: a_{i} = a_{i+p}$ for some t. The period, p, must be large for use in a stream cipher.

Balance::

In one period the numbers of occurrences of different symbols must be nearly equal.

Uniform distribution of small subsequences::

For any r, in one period the numbers of occurrences of different blocks of length r must be nearly equal.

Uncorrelated with shifts::

Let a be a binary sequence with period p. The autocorrelation of a with shift t is

$$\displaystyle{\mathcal{A}_{\mathbf{a}(t)} =\sum _{ i=0}^{p-1}(-1)^{a_{i}+a_{i+t} }.}$$

If t is not a multiple of p, this integer should be close to zero.

Unpredictable from a short prefix::

It should not be possible to determine a knowing only $a_{0},\ldots,a_{k-1}$ for small k using any known methods (e.g., using the Berlekamp–Massey algorithm). This is a critical requirement for stream ciphers.

Since we do not know what requirements will arise in the future, it is useful to have a large pool of high-quality pseudorandom sequences available.

Note that the approach to security described here is different from the complexity theory approach. In that approach one defines a cryptographically strong pseudorandom bit generator (CSPRBG) to be a sequence generator whose output is indistinguishable from a truly random sequence generator by any polynomial time probabilistic distinguisher. Unfortunately this is a strong constraint, and all known CSPRBGs are unable to approach real-time operation (and in fact the security of known CSPRBGs depends on the assumed intractability of certain computational problems such as quadratic residuosity).

3 Sequence Generators

In this section we describe simple, fast devices that satisfy many of the requirements for sequence generators (but not the unpredictability). They are commonly used as building blocks for stream ciphers.

LFSRs, FCSRs, and AFSRs (described in the next three subsections) are special cases of a general model for sequence generators. A PSG is a (not necessarily finite) state machine with output in an alphabet Σ, G = (S, Γ, δ), where the set S is the state space, Γ: S → S is the state change function, and δ: S → Σ is the output function. Such a PSG generates a pseudorandom sequence from a given initial state σ ∈ S by iterating the state change forever. That is

$$\displaystyle{\mathbf{a} = G(\sigma ) = (\delta (\sigma ),\delta (\varGamma (\sigma )),\delta (\varGamma ^{2}(\sigma )),\cdots \,)}$$

It is often desirable that for any given initial state σ, the set of states {Γ ⁱ(σ): i = 0, 1, 2, …} be finite. This implies that G(σ) is eventually periodic.

In what follows, we are concerned with families of PSGs. We may be interested, for example, in finding the most efficient PSG G that generates a given sequence a, where G is in a given family $\mathcal{G}$ of PSGs. In the next few subsections, we describe some interesting families of PSGs.

3.1 LFSRs

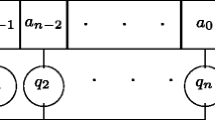
A LFSR of length r over a field F is a finite state PSG whose state set is F ^r and whose state change function is determined by a set of coefficients $g_{1},\ldots,g_{r} \in F$ [10, p. 23]. If the current state is $(a_{0},a_{1},\ldots,a_{r-1})$, then the next state is $(a_{1},\ldots,a_{r-1},a_{r})$, where $a_{r} = g_{r}a_{0} + \cdots + g_{1}a_{r-1}$. The output function is $\delta (a_{0},a_{1},\ldots,a_{r-1}) = a_{0}$. See Fig. 2.

Fig. 2

A length r LFSR

There is a large literature on LFSRs. Some of their salient properties are the following. We assume that the field $F = \mathbb{F}_{q}$ is finite, so the set of states is finite, and the output is eventually periodic:

• 1. The connection polynomial is $g(x) = -1 + g_{1}x + \cdots + g_{r}x^{r}$. The generating function of the output sequence a is $a(x) = a_{0} + a_{1}x + a_{2}x^{2} + \cdots$. There is a polynomial u(x), uniquely determined by the initial state $(a_{0},\ldots,a_{r-1})$, so that $a(x) = u(x)/q(x)$.

• 2. The sequence a is eventually periodic. It’s periodic if and only if deg(u) < deg(g). The maximum possible period is | F | ^r − 1. This is achieved when g(x) is a primitive polynomial, meaning that a root of g is a primitive element in $\mathbb{F}_{q^{r}}$. In this case a is called an m-sequence [10, p. 208]. These sequences are the most commonly used LFSR sequences.

• 3. M-sequences have many good statistical properties. Their shifted autocorrelations are all − 1. They are as balanced as possible for their period, and the distribution of subblocks of fixed size is as uniform as possible. They have the run property [10, p. 172] and the shift and add property [10, p. 191].

• 4. Let E be the unique degree r extension field of F. Let Tr be the trace function from E to F. If the connection polynomial g(x) is irreducible, and the sequence a is periodic, then it can be expressed as $a_{i} = Tr(A\alpha ^{i})$ where α is a root of g(x) and A ∈ E corresponds to the initial state. More generally, if a is periodic, then it can be expressed as

  $$\displaystyle{a_{i} = (\mathit{Ax}^{-i}\mod g)\mod x,}$$

  meaning (1) compute the element $v \equiv \mathit{Ax}^{-i}\mod g$ with deg(v) < r; and (2) a _i is the constant term of v [10, p. 48].

We can form a family of PSGs by fixing F and considering all LFSRs with entries in F.

3.2 FCSRs

Let N ≥ 2 be an integer and $S =\{ 0,1,\ldots,N - 1\}$. A FCSR of length r based on $N$ is a PSG whose state set is $S^{r} \times \mathbb{Z}$ and whose state change function is determined by a set of coefficients $g_{1},\ldots,g_{r} \in \mathbb{Z}$ [10, p. 70]. If the current state is $(a_{0},a_{1},\ldots,a_{r-1};z)$, then the next state is $(a_{1},\ldots,a_{r-1},a_{r};z^{{\prime}})$, where $a_{r} + Nz^{{\prime}} = g_{r}a_{0} + \cdots + g_{1}a_{r-1} + z$. Here the addition and multiplication are in $\mathbb{Z}$. The output function is $\delta (a_{0},a_{1},\ldots,a_{r-1};z) = a_{0}$. See Fig. 3.

Fig. 3

A length r FCSR

FCSRs have many properties that parallel properties of LFSRs. Now, however, the algebra of polynomials and power series is replaced by the algebra of integers and N -adic numbers, which we briefly review [10, p. 72].

An N-adic number is an infinite expression

$$\displaystyle{a =\sum _{ i=0}^{\infty }a_{ i}N^{i},}$$

where a _i  ∈ S. Addition of N-adic numbers is addition with carry. That is,

$$\displaystyle{\sum _{i=0}^{\infty }a_{ i}N^{i} +\sum _{ i=0}^{\infty }b_{ i}N^{i} =\sum _{ i=0}^{\infty }c_{ i}N^{i}}$$

if there are integers $d_{0} = 0,d_{1},d_{2},\ldots$ so that for all i ≥ 0 we have $a_{i} + b_{i} + d_{i} = c_{i} + \mathit{Nd}_{i+1}$. Similarly, we have

$$\displaystyle{\sum _{i=0}^{\infty }a_{ i}N^{i}\sum _{ i=0}^{\infty }b_{ i}N^{i} =\sum _{ i=0}^{\infty }c_{ i}N^{i}}$$

if there are integers $d_{0} = 0,d_{1},d_{2},\ldots$ so that for all i ≥ 0 we have

$$\displaystyle{\sum _{j=0}^{i}a_{ j}b_{i-j} + d_{i} = c_{i} + \mathit{Nd}_{i+1}.}$$

The set of N-adic numbers is thus an algebraic ring, denoted by $\mathbb{Z}_{N}$. Note that

$$\displaystyle{-1 = (N - 1) + (N - 1)N + (N - 1)N^{2} + \cdots }$$

(because adding 1 to the right-hand side gives 0). It can be seen that a sequence $\mathbf{a} = a_{0},a_{1},\ldots \in S^{\infty }$ is eventually periodic if and only if its associated N-adic number

$$\displaystyle{a =\sum _{ i=0}^{\infty }a_{ i}N^{i}}$$

is a rational number u∕g with gcd(g, N) = 1.

The following are some properties of FCSRs and their output sequences:

• 1. The connection integer of an FCSR is $g = -1 + g_{1}N + \cdots + g_{r}N^{r}$. The associated N-adic number of the output sequence a is $a = a_{0} + a_{1}N + a_{2}N^{2} + \cdots$. There is an integer u (uniquely determined by the initial state $(a_{0},\ldots,a_{r-1};z)$) so that $a = u/g$ [10, p. 80].

• 2. The sequence a is eventually periodic [10, p. 88]. This is equivalent to saying that the carry z is bounded in any infinite execution of the FCSR. The sequence a is periodic iff − g ≤ u ≤ 0. The period is at most g − 1. The period equals g − 1 when g is prime and N is a primitive root modulo g, meaning that the multiplicative order of N modulo g is g − 1. In this case a is called an ℓ -sequence [10, p. 264]. These sequences are the most interesting FCSR sequences. It is unknown whether for a fixed N, there are infinitely many primes g such that N is primitive modulo g (Artin’s conjecture). However, Hooley showed that if a certain generalized Riemann hypothesis holds, then for every N there are infinitely many primes g so that N is primitive modulo g [14]. Moreover, it is known that there are at most two values of N for which Artin’s conjecture fails, although it is unknown what these values are [13].

• 3. ℓ-sequences have many good statistical properties. If N = 2, then their shifted arithmetic autocorrelations (defined in Sect. 5.2) are all 0 [10, p. 172]. They are as balanced as possible for their period and the distribution of subblocks of fixed size is as uniform as possible. They have the arithmetic shift and add property [10, p. 204].

• 4. If a is periodic, then it can be expressed as

  $$\displaystyle{a_{i} = (\mathit{AN}^{-i}\mod g)\mod N,}$$

  for some $A \in \mathbb{Z}$, meaning (1) compute the element $v \equiv \mathit{AN}^{-i}\mod g$ with 0 ≤ v < g; and (2) $a_{i} = v\mod N \in S$ [10, p. 87].

We can form a family of PSGs by fixing N and considering all N-ary FCSRs.

3.3 AFSRs

In this section we recall some details on AFSR, a generalization of both LFSRs FCSRs [10, p. 96]. Let R be an algebraic ring. Let π ∈ R be neither a unit and nor a zero divisor, and assume that R∕(π) is finite. Let S ⊆ R be a complete set of representatives for R∕(π). An AFSR of length r based on π is a PSG whose state set is S ^r × R and whose state change function is determined by a set of coefficients $g_{0},\ldots,g_{r} \in R$ with g ₀ invertible modulo π. If the current state is $(a_{0},a_{1},\ldots,a_{r-1};z)$, then the next state is $(a_{1},\ldots,a_{r-1},a_{r};z^{{\prime}})$, where $g_{0}a_{r} + Nz^{{\prime}} = g_{r}a_{0} + \cdots + g_{1}a_{r-1} + z$. Here the addition and multiplication are in R. The output function is $\delta (a_{0},a_{1},\ldots,a_{r-1};z) = a_{0}$. See Fig. 4.

Fig. 4

A length r AFSR

Much of the analysis of AFSRs is based on the algebra of π-adic numbers, which we briefly recall [10, p. 98]. A π-adic number is an infinite expression

$$\displaystyle{a =\sum _{ i=0}^{\infty }a_{ i}\pi ^{i},}$$

where a _i  ∈ S. Addition of π-adic numbers is again addition with carry. That is,

$$\displaystyle{\sum _{i=0}^{\infty }a_{ i}\pi ^{i} +\sum _{ i=0}^{\infty }b_{ i}\pi ^{i} =\sum _{ i=0}^{\infty }c_{ i}\pi ^{i}}$$

if there are elements $d_{0} = 0,d_{1},d_{2},\ldots \in R$ so that for all i ≥ 0 we have $a_{i} + b_{i} + d_{i} = c_{i} +\pi _{i+1}$. Multiplication is defined similarly. The set of π-adic numbers is $d_{i} = c_{i} +\pi d_{i+1}$ thus an algebraic ring, denoted by R _π .

In the case when R = F[x], F a finite field, π = x, S = F, g ₀ = 1, and z = 0, we obtain LFSRs (the carries are all 0 in this case). In the case when $R = \mathbb{Z}$, π = N > 1, $S =\{ 0,1,\ldots,N - 1\}$, and g ₀ = 1, we obtain FCSRs. Other special cases that have been studied include the case when R = F[x] and deg(π) > 1 [10, p. 250], and d-FCSRs, where $R = \mathbb{Z}[\pi ]$ and $\pi = N^{1/d}$ with N square free [10, p. 133]. In the latter case, addition in R is addition with carry where the carry jumps d places ahead.

It is not in general the case that the output from an AFSR is eventually periodic. However, it is known that if R is a ring of integers in a number field, then the output is always eventually periodic iff for every embedding of the fraction field of R in $\mathbb{C}$ the complex norm of π is greater than 1. This is the case, for example, for d-FCSRs.

Following are some properties of AFSRs and their output sequences.

• 1. The connection element of an AFSR is $g = -g_{0} + g_{1}\pi + \cdots + g_{r}\pi ^{r}$. The associated π-adic number of the output sequence a is $a = a_{0} + a_{1}\pi + a_{2}\pi ^{2} + \cdots$. There is an integer u (uniquely determined by the initial state $(a_{0},\ldots,a_{r-1};z)$) so that $a = u/q$.

• 2. The sequence a is eventually periodic if R is a ring of integers in a number field and the complex norm of π is greater than 1 under every embedding of the fraction field of R in $\mathbb{C}$. Otherwise there are AFSRs that do not produce eventually periodic output. There is in general no known condition on the numerator u characterizing the periodic output sequences, even in the case when all output sequences are eventually periodic. However, for d-FCSRs, we have the following.

  Let π ^d = 2. We denote by P the parallelepiped in $R = \mathbb{Z}[\pi ]$ which is spanned by the d linearly independent vectors $-g,-g\pi,\ldots,-g\pi ^{d-1}$,

  $$\displaystyle{P = \left \{\sum _{i=0}^{d-1}v_{ i}g\pi ^{i}\vert \ v_{ i} \in \mathbb{Q}\text{ and } - 1 \leq v_{i} \leq 0\right \} \subset \mathbb{Q}[\pi ].}$$

  Let $\varDelta = P \cap \mathbb{Z}[\pi ]$ be the set of points of the integer lattice $\mathbb{Z}[\pi ]$ in P.

Theorem 3.1 ([9])

Suppose $g \in \mathbb{Z}[\pi ]$ is a unit modulo π. Let a be an output sequence from a d-FCSR with connection element g and let a be the π-adic number associated with a . Suppose that $a = u/g$ . Then a is periodic if and only if u ∈Δ.

The maximum possible period is $\vert R/(q)\vert - 1$. This is achieved when π is a primitive element modulo g, meaning that the multiplicative order of π modulo g is $\vert R/(q)\vert - 1$. In this case a is called a π-adic ℓ -sequence.

• 3. The statistical properties of π-adic ℓ-sequences are not well understood, except in some special cases. For example, for d-FCSRs with d = 2, we have the following. Let $\mathcal{N}_{\mathbb{Q}}^{F}$ denote the rational norm function on F.

Theorem 3.2 ([16])

Let $\pi ^{2} = N \geq 2 \in \mathbb{Z}$ with N square free. Let F be the fraction field of $R = \mathbb{Z}[\pi ]$ . Suppose that $g = y + z\pi \in R$ , with $y,z \in \mathbb{Z}$ , is invertible modulo π, that $h = \mathcal{N}_{\mathbb{Q}}^{F}(g)$ is a prime integer, and that π is primitive modulo g. Let a be an ℓ-sequence defined over $\mathbb{Z}[\pi ]$ with connection element g. If $s \in \mathbb{Z}^{+}$ is even, then the number K of occurrences of any s-tuple in one period of a satisfies

$$\displaystyle{\left \vert K - \frac{h} {N^{s}}\right \vert \leq \frac{h} {N^{s/2}\vert z\vert } + \frac{\vert y\vert + \vert z\vert } {N^{s/2}} + 2.}$$

If $(h/N)^{1/2} \leq \vert z\vert \leq h^{1/2}$ , then

$$\displaystyle{\left \vert K - \frac{h} {N^{s}}\right \vert \leq \frac{(N^{1/2} + (N - 1)^{1/2} + 1)h^{1/2}} {N^{s/2}} + 2.}$$

If N = 2, then

$$\displaystyle{\left \vert K - \frac{h} {2^{s}}\right \vert \leq 3\left ( \frac{h} {2^{s}}\right )^{1/2} + 2.}$$

• 4. It has only been shown that there is an exponential representation of periodic AFSR sequences under special conditions.

We can form a family of PSGs by fixing R, π, and S and considering all AFSRs based on these ingredients. We also may want to impose constraints on the g _i s, such as requiring that they be in S. Note that if we let the g _i s be arbitrary elements of R, then we can take r = 1 and $g = g_{1}\pi + g_{0}$ with g ₀ ∈ S. Thus any π-adic number u∕g can be generated by an AFSR of length one.

4 Register Synthesis Problem

Let $\mathcal{G}$ be a family of PSGs. Suppose that given part of a sequence a we can find the most efficient (in some sense) $G = (S,\varGamma,\delta ) \in \mathcal{G}$ and σ ∈ S so that G(σ) = a. If G is efficient enough, then we have cryptanalyzed a [10, p. 295]. Let us make this more precise.

A register synthesis algorithm for the family $\mathcal{G}$ is an algorithm T that on input $a_{0},a_{1},\ldots,a_{n-1}$, a prefix of a, outputs $G = (S,\varGamma,\delta ) \in \mathcal{G}$ and initial state σ ∈ S so that

• 1. $G(\sigma ) = a_{0},a_{1},\ldots,a_{n-1},?,?,\cdots$.

• 2. If n is large enough, G(σ) = a (convergence).

• 3. T runs in polynomial time in n.

To measure the effectiveness of such an algorithm, we first need a notion of size of a sequence generator G in a family $\mathcal{G}$. This should at least approximate the amount of space needed to store the states that occur in an infinite execution of G. Then we define the $\mathcal{G}$ -complexity $\lambda _{\mathcal{G}}(\mathbf{a})$ of a sequence a to be the minimum size of a generator in $\mathcal{G}$ that outputs a. We typically measure the effectiveness of a $\mathcal{G}$-synthesizing algorithm in terms of $\lambda _{\mathcal{G}}(\mathbf{a})$: for some slowly growing function μ, if the prefix length n is at least $\mu (\lambda _{\mathcal{G}}(\mathbf{a}))$, then T outputs G, σ with G(σ) = a. In all cases we know, μ(λ) is linear in λ.

As a consequence, if $\lambda _{\mathcal{G}}(\mathbf{a})$ is small and $\mathcal{G}$ has an effective register synthesis algorithm, then $\mathbf{a}$ is cryptographically insecure.

We later use the notion of the $\mathcal{G}$-complexity of a finite sequence, the minimum size of a generator in $\mathcal{G}$ that outputs $a_{0},a_{1},\ldots,a_{n-1}$ as its first n output symbols. We denote the $\mathcal{G}$-complexity by $\lambda _{\mathcal{G}}(a_{0},a_{1},\ldots,a_{n-1})$.

4.1 LFSR Synthesis

LFSR synthesis amounts to solving a system of linear equations in the coefficients g _i . There is an efficient algorithm due to Berlekamp and Massey in 1969 [10, p. 296], [22]. This algorithm exploits the special structure of the equations and runs in time O(n ²). Given $a_{0},a_{1},\ldots,a_{n-1}$, the goal is to find relatively prime polynomials u(x) and g(x) so that

$$\displaystyle{a(x) =\sum _{ i=0}^{\infty }a_{ i}x^{i} = \frac{u(x)} {g(x)}.}$$

Then g(x) is the connection polynomial of a minimal size LFSR that generates a, and u(x) determines the initial state. The algorithm proceeds iteratively—at the ith iteration it finds the minimal degree polynomials u _i (x), g _i (x) so that

$$\displaystyle{a(x) \equiv \frac{u_{i}(x)} {g_{i}(x)}\mod x^{i}.}$$

The approximation $u_{i}(x)/g_{i}(x)$ is found by computing a linear combination of two earlier approximations: if $a(x)\not\equiv u_{i}(x)/g_{i}(x)\mod x^{i}$, then

$$\displaystyle{(u_{i+1}(x),g_{i+1}(x)) = (u_{i}(x),g_{i}(x)) + \mathit{bx}^{i-m}(u_{ m}(x),g_{m}(x))}$$

for a certain index m and a certain b.

To measure the effectiveness, we define the linear complexity of a. If $a(x) = u(x)/g(x)$ and gcd(u(x), g(x)) = 1, then

$$\displaystyle\begin{array}{rcl} \lambda _{\mathrm{lin}}(\mathbf{a})& =& \max (\deg (u) + 1,\deg (g)) {}\\ & =& \text{the length of the smallest LFSR that generates }\mathbf{a}. {}\\ \end{array}$$

It can be seen that for the Berlekamp–Massey algorithm, μ(λ) = 2λ. That is, if the sequence a has linear complexity λ and the input to the Berlekamp–Massey algorithm is $a_{0},\ldots,a_{2\lambda -1}$, then the output is the precise rational representation of the generating function of a.

4.2 FCSR and AFSR Synthesis

A first attempt at solving the FCSR synthesis problem is to use the Berlekamp–Massey algorithm but using integer linear combinations instead of $\mathbb{F}_{q}$ linear combinations when finding a new approximation. This doesn’t work—the propagation of carries interferes with convergence.

Instead, for N = 2, Goresky and Klapper developed an FCSR synthesis algorithm based on work of Mahler and De Weger. This Rational Approximation Algorithm iteratively finds a minimal basis for the kth approximation lattice,

$$\displaystyle{L_{k} =\{ (u,g): g\alpha \equiv u\mod 2^{k}\},}$$

by taking linear combinations of earlier bases [10, p. 334].

Subsequently Xu and Klapper solved the problem for any N [10, p. 348], [21, 28]. They modified the Berlekamp–Massey algorithm so that when a new rational approximation is needed, one is found that works for the next three symbols of a. This means that the effect of the carry is overwhelmed by the growth in the number of terms accounted for. This algorithm also works for some classes of AFSRs: if the base ring R is the ring of integers of a number field $F = \mathbb{Q}[N^{1/d}]$ (d-FCSRs) or R is the ring of integers of certain quadratic extensions of $\mathbb{Q}$.

A third approach is due to Arnault et al. [1], [10, p. 338]. For any N, a modified Euclidean algorithm is used. The idea is, given $a_{0},\ldots,a_{n-1}$, to run the extended Euclidean algorithm on input

$$\displaystyle{\left (N^{n},\sum _{ i=0}^{n-1}a_{ i}N^{i}\right )}$$

until the terms are less than N ^n∕2. If n is large enough, this is guaranteed to succeed.

To measure the effectiveness of these algorithms, we must have a clear notion of the size of an FCSR (or more generally of an AFSR). For LFSRs, it is clear that the number of cells is the size, and it can be seen that this is the same as $\max (\deg (u(x)) + 1,\deg (g(x)))$ if u(x)∕g(x) is the corresponding rational representation of the generating function of a. For FCSRs, the “engineering” definition of size would be the number of cells plus the maximum number of N-ary digits needed to store the carry in an infinite execution of the FCSR. We call this the N -adic span. Unfortunately we know of no reasonable algebraic definition of N-adic span. Instead, we define the N -adic complexity of a to be

$$\displaystyle{\lambda _{N}(\mathbf{a}) =\log _{N}(\max (\vert u\vert,\vert g\vert )),}$$

where the N-adic number associated with a has rational representation u∕g and gcd(u, g) = 1. It can be seen that N-adic span and N-adic complexity differ only by a small amount.

The situation is more complicated for AFSRs based on a ring R and an element π ∈ R. There may be multiple competing choices for a size function. For example, represent z ∈ R as $\sum _{i=0}^{k}z_{i}\pi ^{k}$, and let the size of z be k. Or let the size of z be the log (to an appropriate base) of the rational norm of z. The former definition is inadequate in general since not all elements can be represented this way. The latter fails to distinguish the sizes of z and uz where u is a nontrivial unit.

All three algorithms have time complexity O(n ²). For Goresky and Klapper’s rational approximation algorithm, we have $\mu (\lambda ) = \left \lceil 2\lambda \right \rceil + 2$. For Xu and Klapper’s modified Berlekamp–Massey algorithm applied to $R = \mathbb{Z}$, we have $\mu (\lambda ) = \left \lceil 6\lambda \right \rceil + 27$. For the Euclidean approximation algorithm, we have $\mu (\lambda ) = \left \lceil 2\lambda \right \rceil + 3$.

This leaves the following open questions:

• 1. How can we build efficient generators of sequences that have large $\lambda _{\mathcal{G}}$ for all “reasonable” $\mathcal{G}$?

• 2. Are there other “interesting” families $\mathcal{G}$ of PSGs with good register synthesis algorithms?

• 3. Are there families $\mathcal{G}$ of PSGs that provably have no register synthesis algorithm? Or even just no algorithm with μ(λ) linear?

• 4. Can we find effective register synthesis algorithms for other classes of AFSRs?

4.3 Combined and Filtered Generators

In this section we consider two approaches to reducing vulnerability of stream ciphers to synthesis attacks. The general idea is to introduce some nonlinearity to the PSG while maintaining the good statistical properties.

The first approach is to use a set of n simple PSGs, such as LFSRs and FCSRs and to combine their outputs with a nonlinear combiner function $H(x_{1},\ldots,x_{n})$. How can we choose H to maximize security? In particular, how can we choose H to make the linear or N-adic complexity large? In the binary case, suppose the underlying PSGs generate sequences $\mathbf{a}^{1},\ldots,\mathbf{a}^{n}$. Let the overall output sequence be $\mathbf{b} = b_{0},b_{1},\ldots$, with $b_{i} = H(a_{i}^{1},\ldots,a_{i}^{n})$. Then Key showed that the linear complexity of b satisfies

$$\displaystyle{ \lambda _{\mathrm{lin}}(\mathbf{b}) \leq H(\lambda _{\mathrm{lin}}(a^{1}),\ldots,\lambda _{\mathrm{ lin}}(a^{n})), }$$

(1)

where we treat H as a polynomial with integer coefficients that happen to be 0s and 1s [15]. Moreover, Key showed that if the a ^j are m-sequences and their periods are pairwise relatively prime, then we have equality in equation (1).

This leaves several related questions:

• 1. Can we express or bound the 2-adic complexity of b in terms of the 2-adic complexities of the a ⁱ? Similarly for various π-adic complexities.

• 2. Are there conditions under which both the linear and 2-adic complexities of b are large? All π-adic complexities?

• 3. What if we add a small amount of memory to the combiner? Rueppell investigated the summation combiner, where H is binary addition with carry [26]. He gave a heuristic argument that the linear complexity should be large, but gave no actual proof. To our knowledge, no proof has yet been found. On the other hand, it is known that the 2-adic complexity of b is the sum of the 2-adic complexities of the a ⁱ, so the summation combiner is vulnerable to an FCSR synthesis attack. In fact it was this that motivated the invention of FCSRs.

We must point out that even if we achieve large linear and 2-adic complexities (or even large π-adic complexity for all π), this does not make these sequences secure. There are other attacks. For example, combiners tend to be vulnerable to correlation attacks [23].

A second approach to reducing vulnerability of stream ciphers to synthesis attacks is to use a single LFSR or FCSR for the state and state change function, but use a nonlinear function $F(a_{0},\ldots,a_{r-1})$ as the output function. Regarding LFSRs, Key [15] showed that, in the binary case, if d = deg(F), then

$$\displaystyle{ \lambda _{\mathrm{lin}}(\mathbf{b}) \leq \sum _{i=0}^{d}\binom{n}{i}. }$$

(2)

The following questions are open:

• 1. How can F be chosen to achieve equality in inequality (2)?

• 2. What is the N-adic complexity of a filtered FCSR?

• 3. What is the linear complexity of an ℓ-sequence or a filtered FCSR?

• 4. What is the N-adic complexity of an m-sequence or a filtered LFSR?

Similar questions can be asked about π-adic complexity, where π is an element of a ring R. More generally, it is an open problem how to efficiently generate sequences that have both large linear complexity and large 2-adic complexity (or π-adic complexity for any π).

We mention here some additional motivation for studying FCSRs. There is a type of attack on filtered LFSR generators known as algebraic cryptanalysis [5]. The basic idea is to treat each monomial in the filter function F as a variable. Knowing some ciphertext and plaintext gives the attacker some keystream and thus gives an equation in these metavariables. More known keystream gives more equations using the composition of F with iterations of the state change. If the degree of F is small (or if there is a low degree multiple of F), then the number of metavariables is small, and if there are enough equations, we can solve for the metavariables.

Critical to this attack is the fact that F composed with the state change has the same degree as F. However, if we replace the LFSR with an FCSR, this is no longer the case and algebraic cryptanalysis no longer works.

5 Statistics of Sequences

In this section we consider various open questions on statistical properties of shift register sequences.

5.1 Average Behavior

We would like to understand the average behavior of the $\mathcal{G}$-complexity of sequences. Deviation from the average can be used as a measure of nonrandomness (the NIST test suite does this with linear complexity [25]). Moreover, if the average is large, then we know that randomly chosen sequences are likely to have large $\mathcal{G}$-complexity. This is important because many stream ciphers are designed to be hard to analyze. For such ciphers, it is likely to be impossible to determine the $\mathcal{G}$-complexity.

But averaged over what? We can use Haar measure on infinite sequences. However, the eventually periodic sequences are countable, so have measure zero. For most $\mathcal{G}$ of interest only eventually periodic sequences have finite $\mathcal{G}$-complexity, so the average $\mathcal{G}$-complexity is infinite. This tells us nothing.

Instead, we can consider two ways of averaging:

• 1. $E_{n}^{\text{fin},\mathcal{G}} =$ average $\mathcal{G}$-complexity over all finite, length n sequences.

• 2. $E_{n}^{\text{per},\mathcal{G}} =$ average $\mathcal{G}$-complexity over all infinite period n sequences.

Note that these are different. In the first case, the $\mathcal{G}$-complexity of a finite sequence is the minimum $\mathcal{G}$-complexity over all infinite extensions of $(a_{0},\ldots,a_{n-1})$, not just the period n extensions. Thus

$$\displaystyle{E_{n}^{\text{fin},\mathcal{G}}\leq E_{ n}^{\text{per},\mathcal{G}}.}$$

The following averages are known:

• 1. $E_{n}^{\text{fin,lin}} = n/2 + O(1/q)$ for sequences over $\mathbb{F}_{q}$.

• 2. $E_{n}^{\text{per,lin}} \geq n - m/(q - 1).$ for sequences over $\mathbb{F}_{q}$, q a power of p, n = p ^v m, gcd(m, p) = 1 (the exact value can be expressed in terms of cyclotomic numbers).

• 3. $E_{n}^{\text{per,N-adic}} \in n - O(\log (n))$ (the exact value can be expressed in terms of the prime factorization of N ⁿ − 1).

This leaves open the determination of $E_{n}^{\text{fin,N-adic}}$.

For AFSRs over $R = \mathbb{Z}[\pi ]$, we know that if R is a UFD with $\pi ^{2} = -N <0$ or π ^d = N > 0 and n is a multiple of 4 in the former case and is arbitrary in the latter case, then $E_{n}^{\text{per,}\mathcal{G}}\in n - O(\log (n))$ [19]. The average finite π-complexity is unknown, as are both averages for any other R. Note that in these cases, there are reasonable definitions of the size of an AFSR. For example, if $\pi ^{2} = -N$ and F is the field of fractions of R, then we define the size of an element u + vπ ∈ R, $u,v \in \mathbb{Z}$, to be

$$\displaystyle{\phi (u + v\pi ) =\log _{N}(\mathcal{N}_{\mathbb{Q}}^{F}(u + v\pi )) =\log _{ N}(u^{2} + Nv^{2}).}$$

Then the size of an AFSR with a given initial state is $\max (\phi (f),\phi (g))$ if the AFSR has connection element g and outputs a sequence whose associated π-adic number has rational representation f∕g. If π ^d = N > 0, then we let the size of an element be

$$\displaystyle{\phi \left (\sum _{i=0}^{d-1}u_{ i}\pi ^{i}\right ) =\max (d\log _{ N}\vert u_{i}\vert + i),}$$

and we extend this to sequences similarly. In both cases it can be seen that this notion of size approximates the number of N-ary digits needed to represent the state. It seems that the first step in extending these results to more general R is to find a suitable notion of size.

5.2 Correlations

Let a and b be binary sequences of period T. The classical notion of the cross-correlation of a and b is

$$\displaystyle\begin{array}{rcl} \mathcal{C}_{\mathbf{a},\mathbf{b}}(t)& =& \sum _{i=0}^{T-1}(-1)^{a_{i}+b_{i+t} } {}\\ & =& \#\text{zeros} - \#\text{ones in one period of }\mathbf{a} + \text{shift}_{t}(\mathbf{b}). {}\\ \end{array}$$

If a = b, then the cross-correlation is called the autocorrelation of a, denoted $\mathcal{A}_{\mathbf{a}(t)}$.

The cross-correlation is used in code division multiple access (CDMA) communications. Each user has a sequence a that determines how the user’s signal is distributed across a set of T channels. Typically it is necessary that the sequences used by two users have low cross-correlation to prevent interference. Thus the capacity of the system is limited by the size of a family of sequences with low pairwise cross-correlations.

Unfortunately, there are various known constraints on this size. One such constraint is the Welch bound [27]. Let S be a set of n binary sequences of period T. Let $\mathcal{C}_{\max }$ be the maximum cross-correlation between distinct sequences in S (including shifts of sequences and including shifted autocorrelations). Then

$$\displaystyle{\mathcal{C}_{\max }^{2} \geq \frac{T^{2}(n - 1)} {nT - 1}.}$$

Thus, for example, if $n = T^{1/2}$, then

$$\displaystyle{\mathcal{C}_{\max }^{2} \geq T\left (1 - \frac{T - 1} {T^{3/2} - 1}\right ) \sim T.}$$

There is an analogous notion for with-carry algebra. Let −₂ denote subtraction with borrow of binary sequences. That is, to compute $\mathbf{a} -_{2}\mathbf{b}$, find the associated 2-adic numbers a and b, subtract them in $\mathbb{Z}_{2}$, and extract the sequence of coefficients of the result. Note that if a and b have period T, then a −₂ b is only eventually periodic (in fact it is periodic from the Tth term on). We define the arithmetic cross-correlation to be

$$\displaystyle{\mathcal{C}_{\mathbf{a},\mathbf{b}}^{A}(t) = \#\text{zeros} - \#\text{ones in one period of }\mathbf{a} -_{ 2}\text{shift}_{t}(\mathbf{b}).}$$

We next define a set of sequences whose pairwise arithmetic cross-correlations are identically zero. The d-fold decimation of a sequence $\mathbf{a} = a_{0},a_{1},a_{2},\ldots$ is the sequence $\mathbf{a}^{d} = a_{0},a_{d},a_{2d}\ldots$.

Theorem 5.1

Suppose 2 is a primitive root modulo the prime number g. Let a be an ℓ-sequence with connection integer g. Suppose that $\gcd (g,d) =\gcd (g,e) = 1$ and that a ^d is not a shift of a ^e . Then for all t, $\mathcal{C}_{\mathbf{a}^{d},\mathbf{a}^{e}}^{A}(t) = 0$ .

It follows that the set $S_{g} =\{ \mathbf{a}^{d}:\gcd (g,d) = 1\}$ is a set of sequences with identically zero arithmetic cross-correlations. This is in stark contrast to the classical setting. Two questions remain. First, is there an application of this remarkable fact? Second, how large is S? That is, how many shift distinct decimations of an ℓ-sequence are there.

Conjecture 5.2

If $d\not\equiv e\mod q$ and q > 13, then a ^d is not a shift of a ^e.

If true, this would give us sets S _g of period g − 1 sequences with zero arithmetic cross-correlations and $\vert S_{g}\vert =\phi (g - 1)$. Note that ϕ(g − 1) can be as large as $(g - 3)/2$.

It is known that the conjecture is true:

• 1. For 13 < q < 8 × 10⁹ (by brute force search)

• 2. For some special cases (d = 1, $e = q - 2$ [8]; d = 1, $g \equiv 1\mod 4$, and $e = (q + 1)/2$ [11, 12])

• 3. For q > 4. 92 × 10³⁴ [2, 3, 12]

Bourgain’s et al. result is based on recent deep results on bounds for certain exponential sums.

5.3 Asymptotic Complexity

Let $\mathcal{G}$ be a family of PSGs. Typically a sequence a is eventually periodic if and only if it can be generated by some $G \in \mathcal{G}$. Let us call such a $\mathcal{G}$ periodic. The “if” part certainly holds if for any G = (S, Γ, δ) and σ ∈ S, the set of states $\{\varGamma ^{i}(\sigma ): i \in \mathbb{N}\}$ is finite. The “if and only if” holds for LFSRs, FCSRs, and AFSRs based on ring $R = \mathbb{Z}[\pi ]$ and π if | π | > 1 for every embedding of the fraction field of $R$ in $\mathbb{C}$.

Suppose a is not eventually periodic. How can we understand the $\mathcal{G}$-complexity of a? One way is to consider finite prefixes of a and study the growth in their $\mathcal{G}$ complexities as the length increases.

Let $\lambda _{\mathcal{G},n}(\mathbf{a}) =\lambda _{\mathcal{G}}(a_{0},a_{1},\ldots,a_{n-1})$. The $\mathcal{G}$ -complexity profile of a is the sequence $\varLambda _{\mathcal{G}}(\mathbf{a}) = (\lambda _{\mathcal{G},1}(\mathbf{a}),\lambda _{\mathcal{G},2}(\mathbf{a}),\ldots )$. Assume for the remainder of this subsection that $\mathcal{G}$ is a family of periodic PSGs. Then

$$\displaystyle{\lim _{n\rightarrow \infty }\lambda _{\mathcal{G},n}(\mathbf{a}) = \infty,}$$

so the limit tells us nothing. We assume further that for all a, we have $\lambda _{\mathcal{G},n}(\mathbf{a}) \leq n + o(n)$. This is the case for LFSRs, FCSRs, and AFSRs since these families contain pure cycling registers ($g_{1} = \cdots = g_{r-1} = 0,g_{r} = 1$). In this case we can normalize by defining

$$\displaystyle{\delta _{\mathcal{G},n}(\mathbf{a}) =\lambda _{\mathcal{G},n}(\mathbf{a})/n \in [0,1 + o(1)].}$$

Then we can ask about the limiting behavior of $\delta _{\mathcal{G},n}(\mathbf{a})$ as n tends to infinity.

However, it is not in general the case that this sequence has a single limit point. Rather, it has a set of accumulation points T(a) ⊆ [0, 1]. It is this set we want to study. When does there exist a single limit point of the $\delta _{\mathcal{G},n}(\mathbf{a})$? In general what is the structure of T(a)?

The first question was answered by Niederreiter for linear complexity [24]. The answer is that generically a single limit exists and that limit is 1∕2. More precisely, recall that there is a natural measure on the set L = { 0, 1}^∞ of infinite binary sequences, called Haar measure. This is simply the infinite product of the uniform measure on {0, 1}. This is very nearly the uniform measure on the real unit interval [0, 1]. Niederreiter showed that there is a set $U \subseteq L$ with measure one such that if a ∈ U then $T(\mathbf{a}) = [1/2,1/2]$.

It is an open problem to prove this for any other family of PSGs.

Next we mention a theorem that partially answers the second question.

Theorem 5.3 ([17])

If $\lambda _{\mathcal{G},n} \leq \lambda _{\mathcal{G},n+1}$ , then $T(\mathbf{a}) = [B,C] \subseteq [0,1]$ .

But what are the possible values of B and C?

Conjecture 5.4

For all a, we have $T(\mathbf{a}) = [B,1 - B]$. For every B ∈ [0, 1∕2] there are uncountably many sequences a for which $T(\mathbf{a}) = [B,1 - B]$.

The following are the cases when the conjecture is known to be true:

• 1. LFSRs [7].

• 2. 2^k-ary and 3^k-ary FCSRs [17].

• 3. N-ary FCSRs if B < log _N (2) [17].

• 4. π-adic AFSRs with $\pi ^{2} = -2$ if B < log₂(4∕3) [18].

All other cases are open.