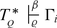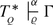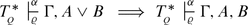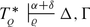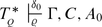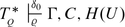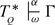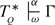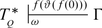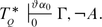Well-Ordering Principles and Bar Induction

Abstract

In this paper we show that the existence of ω-models of bar induction is equivalent to the principle saying that applying the Howard–Bachmann operation to any well-ordering yields again a well-ordering.

1 Introduction

This paper will be concerned with a particular $\Pi _{2}^{1}$ statement of the form

$$\displaystyle\begin{array}{rcl} \mathbf{WOP}(f):& & \;\,\,\;\;\;\forall X\,[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(f(\mathfrak{X}))]{}\end{array}$$

(1)

where f is a standard proof-theoretic function from ordinals to ordinals and $\mathrm{WO}(\mathfrak{X})$ stands for ‘$\mathfrak{X}$ is a well-ordering’. There are by now several examples of functions f familiar from proof theory where the statement WOP(f) has turned out to be equivalent to one of the theories of reverse mathematics over a weak base theory (usually RCA ₀). The first explicit example appears to be due to Girard [7, Theorem 5.4.1] (see also [8]). However, it is also implicit in Schütte’s proof of cut elimination for ω-logic [15] and ultimately has its roots in Gentzen’s work, namely in his first unpublished consistency proof,¹ where he introduced the notion of a “Reduziervorschrift” [6, p. 102] for a sequent. The latter is a well-founded tree built bottom-up via “Reduktionsschritte”, starting with the given sequent and passing up from conclusions to premises until an axiom is reached.

Theorem 1.1

Over $\mathbf{RCA}_{0}$ the following are equivalent:

• (i) Arithmetical comprehension.

• (ii) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(2^{\mathfrak{X}})]$ .

Another characterization from [7, Theorem 6.4.1], shows that arithmetical comprehension is equivalent to Gentzen’s Hauptsatz (cut elimination) for ω-logic. Connecting statements of form (1) to cut elimination theorems for infinitary logics will also be a major tool in this paper.

There are several more recent examples of such equivalences that have been proved by recursion-theoretic as well as proof-theoretic methods. These results give characterizations of the form (1) for the theories $\mathbf{ACA}_{0}^{+}$ and $\mathbf{ATR}_{0}$, respectively, in terms of familiar proof-theoretic functions. ACA ₀ ⁺ denotes the theory ACA ₀ augmented by an axiom asserting that for any set X the ω-th jump in X exists while ATR ₀ asserts the existence of sets constructed by transfinite iterations of arithmetical comprehension. $\alpha \mapsto \varepsilon _{\alpha }$ denotes the usual $\varepsilon$ function while $\varphi$ stands for the two-place Veblen function familiar from predicative proof theory (cf. [16]). Definitions of the familiar subsystems of reverse mathematics can be found in [17].

Theorem 1.2 (Afshari and Rathjen [1]; Marcone and Montalbán [9])

Over $\mathbf{RCA}_{0}$ the following are equivalent:

• (i) $\mathbf{ACA}_{0}^{+}$ .

• (ii) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\varepsilon _{\mathfrak{X}})]$ .

Theorem 1.3 (Friedman [4]; Rathjen and Weiermann [13]; Marcone and Montalbán [9])

Over $\mathbf{RCA}_{0}$ the following are equivalent:

• (i) $\mathbf{ATR}_{0}$ .

• (ii) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\varphi \mathfrak{X}0)]$ .

There is often another way of characterizing statements of the form (1) by means of the notion of countable coded ω-model.

Definition 1.4

Let T be a theory in the language of second order arithmetic, $\mathcal{L}_{2}$. A countable coded ω-model of T is a set $W \subseteq \mathbb{N}$, viewed as encoding the $\mathcal{L}_{2}$-model

$$\displaystyle{\mathbb{M} = (\mathbb{N},\mathcal{S},\in,+,\cdot,0,1,<)}$$

with $\mathcal{S} =\{ (W)_{n}\mid n \in \mathbb{N}\}$ such that $\mathbb{M}\models T$ when the second order quantifiers are interpreted as ranging over $\mathcal{S}$ and the first order part is interpreted in the standard way (where $(W)_{n} =\{ m\mid \langle n,m\rangle \in W\}$ with $\langle \,,\rangle$ being some primitive recursive coding function).

If T has only finitely many axioms, it is obvious how to express $\mathbb{M}\models T$ by just translating the second order quantifiers QX … X … in the axioms by Qx …(W) _x …. If T has infinitely many axioms, one needs to formalize Tarski’s truth definition for $\mathbb{M}$. This definition can be made in RCA ₀ as is shown in [17, Definitions II.8.3 and VII.2]. Some more details will be provided in Remark 1.9.

We write X ∈ W if $\exists n\;X = (W)_{n}$.

The alternative characterizations alluded to above are as follows:

Theorem 1.5

Over $\mathbf{RCA}_{0}$ the following are equivalent:

• (i) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\varepsilon _{\mathfrak{X}})]$ is equivalent to the statement that every set is contained in a countable coded ω-model of $\mathbf{ACA}$ .

• (ii) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\varphi \mathfrak{X}0)]$ is equivalent to the statement that every set is contained in a countable coded ω-model of $\Delta _{1}^{1}\mbox{ -}\mathbf{CA}$ (or $\Sigma _{1}^{1}\mbox{ -}\mathbf{DC}$ ).

Proof

See [12, Corollary 1.8]. □ 

Whereas Theorem 1.5 has been established independently by recursion-theoretic and proof-theoretic methods, there is also a result that has a very involved proof and so far has only been shown by proof theory. It connects the well-known $\Gamma$-function (cf. [16]) with the existence of countable coded ω-models of ATR ₀.

Theorem 1.6 (Rathjen [12, Theorem 1.4])

Over $\mathbf{RCA}_{0}$ the following are equivalent:

• (i) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\Gamma _{\!\mathfrak{X}})]$ .

• (ii) Every set is contained in a countable coded ω-model of $\mathbf{ATR}_{0}$ .

The tools from proof theory employed in the above theorems involve search trees and Gentzen’s cut elimination technique for infinitary logic with ordinal bounds. One could perhaps generalize and say that every cut elimination theorem in ordinal-theoretic proof theory encapsulates a theorem of this type.

The proof-theoretic ordinal functions that figure in the foregoing theorems are all familiar from so-called predicative or meta-predicative proof theory. Thus far a function from genuinely impredicative proof theory is missing. The first such function that comes to mind is of the Bachmann–Howard type. It was conjectured in [14] (Conjecture 7.2) that the pertaining principle (1) would be equivalent to the existence of countable coded ω-models of bar induction, BI. The conjecture is by and large true as will be shown in this paper, however, the relativization of the Bachmann–Howard construction allows for two different approaches, yielding principles of different strength. As it turned out, only the strongest one is equivalent to the existence of ω-models of BI. We now proceed to state the main result of this paper. Unexplained notions will be defined shortly.

Theorem 1.7

Over RCA ₀ the following are equivalent:

• (i) $\mathbf{RCA}_{0} + \mathit{Every\ set}\ \mbox{ $X$}\ \mathit{is\ contained\ in\ a\ countable\ coded}\ \mbox{ $\omega $}\ \mathit{-model\ of }\ \mbox{ $\mathbf{BI}$}$ .

• (ii) $\forall \mathfrak{X}\;[\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\!\mathfrak{X}})]$ .

Below we shall refer to Theorem 1.7 as the Main Theorem.

1.1 A Brief Outline of the Paper

Section 1.2 contains a detailed definition of the theory BI. Section 2 introduces a relativized version of the Howard–Bachmann ordinal representation system, i.e. given a well-ordering $\mathfrak{X}$, one defines a new well-ordering $\vartheta _{\!\mathfrak{X}}$ of Howard–Bachmann type which incorporates $\mathfrak{X}$. Section 3 proofs the direction $(i) \Rightarrow (\mathit{ii})$ of Theorem 1.7. With Sect. 4 the proof of Theorem 1.7 $(\mathit{ii}) \Rightarrow (\mathit{ii})$ commences. It introduces the crucial notion of a deduction chain for a given set $Q \subseteq \mathbb{N}$. The set of deduction chains forms a tree $\mathcal{D}_{Q}$. It is shown that from an infinite branch of this tree one can construct a countable coded ω-model of BI which contains Q. As a consequence, it remains to consider the case when $\mathcal{D}_{Q}$ does not contain an infinite branch, i.e. when $\mathcal{D}_{Q}$ is a well-founded tree. Then the Kleene–Brouwer ordering of $\mathcal{D}_{Q}$, $\mathfrak{X}$, is a well-ordering and, by the well-ordering principle (ii), $\vartheta _{\!\mathfrak{X}}$ is a well-ordering, too. It will then be revealed that $\mathcal{D}_{Q}$ can be viewed as a skeleton of a proof $\mathcal{D}^{{\ast}}$ of the empty sequent in an infinitary proof system $T_{\!_{Q}}^{{\ast}}$ with Buchholz’ $\Omega$-rule. However, with the help of transfinite induction over $\vartheta _{\!\mathfrak{X}}$ it can be shown that all cuts in $\mathcal{D}^{{\ast}}$ can be removed, yielding a cut-free derivation of the empty sequent. As this cannot be, the final conclusion reached is that $\mathcal{D}_{Q}$ must contain an infinite branch, whence there is a countable coded ω-model of BI containing Q, thereby completing the proof of Theorem 1.7 $(\mathit{ii}) \Rightarrow (i)$.

1.2 The Theory BI

In this subsection we introduce the theory BI. To set the context, we fix some notations. The language of second order arithmetic, $\mathcal{L}_{2}$, consists of free numerical variables a, b, c, d, …, bound numerical variables x, y, z, …, free set variables U, V, W, …, bound set variables X, Y, Z, …, the constant 0, a symbol for each primitive recursive function, and the symbols = and ∈ for equality in the first sort and the elementhood relation, respectively. The numerical terms of $\mathcal{L}_{2}$ are built up in the usual way; r, s, t, … are syntactic variables for them. Formulas are obtained from atomic formulas s = t, $s \in U\mbox{ and negated atomic formulas }\neg \,s = t,\neg \,s \in U$ by closing under ∧, ∨ and quantification $\forall x,\exists x,\forall X,\exists X$ over both sorts; so we stipulate that formulas are in negation normal form.

The classes of $\Pi _{2}^{1}$- and $\Sigma _{n}^{1}$-formulae are defined as usual (with $\Pi _{0}^{1} = \Sigma _{0}^{1} = \cup \{\Pi _{n}^{0}: n \in \mathbb{N}\}$). $\neg A$ is defined by de Morgan’s laws; A → B stands for $\neg A\; \vee \; B$. All theories in $\mathcal{L}_{2}$ will be assumed to contain the axioms and rules of classical two sorted predicate calculus, with equality in the first sort. In addition, it will be assumed that they comprise the system $\mathbf{ACA}_{0}$. ACA ₀ contains all axioms of elementary number theory, i.e. the usual axioms for 0, $^{{\prime}}$ (successor), the defining equations for the primitive recursive functions, the induction axiom

$$\displaystyle{\forall X\,[0 \in X\; \wedge \;\forall x(x \in X \rightarrow x^{{\prime}}\in X) \rightarrow \forall x(x \in X)],}$$

and all instances of arithmetical comprehension

$$\displaystyle{\exists Z\,\forall x[x \in Z \leftrightarrow F(x)],}$$

where F(a) is an arithmetic formula, i.e. a formula without set quantifiers.

For a 2-place relation $\prec$ and an arbitrary formula F(a) of $\mathcal{L}_{2}$ we define

• $\text{Prog}(\prec,F):= (\forall x)[\forall y(y \prec x \rightarrow F(y)) \rightarrow F(x)]$ (progressiveness)

• $\mathbf{TI}(\prec,F):= \text{Prog}(\prec,F) \rightarrow \forall xF(x)$ (transfinite induction)

• $\text{WF}(\prec ):= \forall X\mathbf{TI}(\prec,X):=$

• $\forall X(\forall x[\forall y(y \prec x \rightarrow y \in X)) \rightarrow x \in X] \rightarrow \forall x[x \in X])$ (well-foundedness).

Let $\mathcal{F}$ be any collection of formulae of $\mathcal{L}_{2}$. For a 2-place relation $\prec$ we will write $\prec \in \mathcal{F}$, if $\prec$ is defined by a formula Q(x, y) of $\mathcal{F}$ via $x \prec y:= Q(x,y)$.

Definition 1.8

BI denotes the bar induction scheme, i.e. all formulae of the form

$$\displaystyle{\text{WF}(\prec ) \rightarrow \mathbf{TI}(\prec,F),}$$

where $\prec$ is an arithmetical relation (set parameters allowed) and F is an arbitrary formula of $\mathcal{L}_{2}$.

By BI we shall refer to the theory ACA ₀ + BI.

Remark 1.9

The statement of the main Theorem 1.7 uses the notion of a countable coded ω-model of BI. As the stated equivalence is claimed to be provable in RCA ₀, a few comments on how this is formalized in this weak base theory are in order. The notion of a countable coded ω-model can be formalized in RCA ₀ according to [17, Definition VII.2.1]. Let $\mathbb{M}$ be a countable coded ω-model. Since BI is not finitely axiomatizable we have to quantify over all axioms of BI to express that $\mathbb{M}\models \mathbf{BI}$. The axioms of BI (or rather their Gödel numbers) clearly form a primitive recursive set, Ax(BI). To express $\mathbb{M}\models \phi$ for ϕ ∈ Ax(BI) we use the notion of a valuation for ϕ from [17, Definition VII.2.1]. A valuation f for ϕ is a function from the set of subformulae of ϕ into the set {0, 1} obeying the usual Tarski truth conditions. Thus we write $\mathbb{M}\models \phi$, if there exists a valuation f for ϕ such that f(ϕ) = 1. Whence $\mathbb{M}\models \mathbf{BI}$ is defined by $\forall \phi \in Ax(\mathbf{BI})\;\mathbb{M}\models \phi$.

2 Relativizing the Howard–Bachmann Ordinal

In this section we show how to relativize the construction that leads to the Howard–Bachmann ordinal to an arbitrary countable well-ordering. To begin with, mainly to foster intuitions, we provide a set-theoretic definition working in ZFC. This will then be followed by a purely formal definition that can be made in RCA ₀.

Throughout this section, we fix a countable well-ordering $\mathfrak{X} = (X,<_{X})$ without a maximum element, i.e., an ordered pair $\mathfrak{X} = (X,<_{X})$, where X is a set of natural numbers, <  _X is a well-ordering relation on X, and $\forall v \in X\,\exists u \in X\;v <_{X}u$. We write $\vert \mathfrak{X}\vert$ for X.

Firstly, we need some ordinal-theoretic background. Let ON be the class of ordinals. Let $\mathrm{AP}:=\{\xi \in \mathrm{ON}\!: \exists \eta \in \mathrm{ON}[\xi =\omega ^{\eta }]\}$ be the class of additive principal numbers and let $\mathrm{E}:=\{\xi \in \mathrm{ON}\!:\xi =\omega ^{\xi }\}$ be the class of $\varepsilon$-numbers which is enumerated by the function $\lambda \xi.\varepsilon _{\xi }$.

We write $\alpha = _{\mathit{NF}}\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$ if $\alpha =\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$ and $\alpha>\alpha _{1} \geq \cdots \alpha _{n}$. Note that by Cantor’s normal form theorem, for every $\alpha \notin \mathrm{E} \cup \{ 0\}$, there are uniquely determined ordinals α ₁, …, α _n such that $\alpha = _{\mathit{NF}}\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$.

Let $\Omega:= \aleph _{1}$. For $u \in \vert \mathfrak{X}\vert$, let $\mathfrak{E}_{u}$ be the u ^th $\varepsilon$-number $> \Omega$. Thus, if u ₀ is the smallest element of $\vert \mathfrak{X}\vert$, then $\mathfrak{E}_{u_{0}}$ is the least $\varepsilon$-number $> \Omega$, and in general, for $u \in \vert \mathfrak{X}\vert$ with u ₀ <  _X u, $\mathfrak{E}_{u}$ is the least $\varepsilon$-number ρ such that $\forall v <_{X}u\;\mathfrak{E}_{v} <\rho$.

In what follows we shall only be interested in ordinals below $\sup _{u\in X}\mathfrak{E}_{u}$. Henceforth, unless indicated otherwise, any ordinal will be assumed to be smaller than that ordinal.

For any such α we define the set $E_{\Omega }(\alpha )$ which consists of the $\varepsilon$-numbers below $\Omega$ which are needed for the unique representation of α in Cantor normal form recursively as follows:

• 1. $E_{\Omega }(0):= E_{\Omega }(\Omega ):=\emptyset$ and $E_{\Omega }(\mathfrak{E}_{u}):=\emptyset$ for $u \in \vert \mathfrak{X}\vert$.

• 2. $E_{\Omega }(\alpha ):=\{\alpha \},\mbox{ if }\alpha \in E \cap \Omega$.

• 3. $E_{\Omega }(\alpha ):= E_{\Omega }(\alpha _{1}) \cup \cdots \cup E_{\Omega }(\alpha _{n})\;\;\mbox{ if }\;\;\alpha = _{\mathit{NF}}\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$.

Let $\alpha ^{{\ast}}:=\max (E_{\Omega }(\alpha ) \cup \{ 0\})$.

We define sets of ordinals $C_{_{\!\mathfrak{X}}}(\alpha,\beta ),C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )$, and ordinals $\vartheta \alpha$ by main recursion on $\alpha <\sup _{u\in X}\mathfrak{E}_{u}$ and subsidiary recursion on n < ω (for $\beta <\Omega$) as follows.

• (C0) $\mathfrak{E}_{u} \in C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )$ for all $u \in \vert \mathfrak{X}\vert$.

• (C1) $\{0,\Omega \}\cup \beta \;\subseteq \; C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )$.

• (C2) $\gamma _{1},\ldots,\gamma _{n} \in C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )\;\wedge \;\xi = _{\mathit{NF}}\omega ^{\gamma _{1}} + \cdots +\omega ^{\gamma _{n}}\;\Longrightarrow\;\xi \in C_{_{\! \mathfrak{X}}}^{n+1}(\alpha,\beta )$.

• (C3) $\delta \in C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta ) \cap \alpha \;\Longrightarrow\;\vartheta \delta \in C_{_{\!\mathfrak{X}}}^{n+1}(\alpha,\beta )$.

• (C4) $C_{_{\!\mathfrak{X}}}(\alpha,\beta ):=\bigcup \{ C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )\!: n <\omega \}$.

• (C5) $\vartheta \alpha:=\min \{\xi <\Omega \!: C_{_{\!\mathfrak{X}}}(\alpha,\xi ) \cap \Omega \subseteq \xi \;\wedge \;\alpha \in C_{_{\!\mathfrak{X}}}(\alpha,\xi )\}$ if there exists an ordinal $\xi <\Omega$ such that $C_{_{\!\mathfrak{X}}}(\alpha,\xi ) \cap \Omega \subseteq \xi$ and $\alpha \in C_{_{\!\mathfrak{X}}}(\alpha,\xi )$. Otherwise $\vartheta \alpha$ will be undefined.

  We will shortly see that $\vartheta \alpha$ is always defined (Lemma 2.2).

Remark 2.1

The definition of $\vartheta$ originated in [10]. An ordinal representation system based on $\vartheta$ was used in [11] to determine the proof-theoretic strength of fragments of Kripke–Platek set theory and in [13] it was used to characterize the strength of Kruskal’s theorem.

Lemma 2.2

$\vartheta \alpha$ is defined for every $\alpha <\sup _{u\in X}\mathfrak{E}_{u}$ .

Proof

Let $\beta _{0}:=\alpha ^{{\ast}} + 1$. Then $\alpha \in C_{_{\!\mathfrak{X}}}(\alpha,\beta _{0})$ via (C1) and (C2). Since the cardinality of $C_{_{\!\mathfrak{X}}}(\alpha,\beta )$ is less than $\Omega$ there exists a $\;\beta _{1} <\Omega$ such that $C_{_{\!\mathfrak{X}}}(\alpha,\beta _{0}) \cap \Omega \subseteq \beta _{1}$. Similarly there exists for each $\beta _{n} <\Omega$ (which is constructed recursively) a $\beta _{n+1} <\Omega$ such that $C_{_{\!\mathfrak{X}}}(\alpha,\beta _{n}) \cap \Omega \subseteq \beta _{n+1}$. Let $\beta:=\sup \{\beta _{n}\!: n <\omega \}$. Then $\alpha \in C_{_{\!\mathfrak{X}}}(\alpha,\beta )$ and $C_{_{\!\mathfrak{X}}}(\alpha,\beta ) \cap \Omega \subseteq \beta <\Omega$. Therefore $\vartheta \alpha \leq \beta <\Omega$. □ 

Lemma 2.3

• 1. $\vartheta \alpha \in E,$

• 2. $\alpha \in C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha ),$

• 3. $\vartheta \alpha = C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha ) \cap \Omega,$ and $\vartheta \alpha \notin C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha )$ ,

• 4. $\gamma \in C_{_{\!\mathfrak{X}}}(\alpha,\beta )\;\Longleftrightarrow\;\gamma ^{{\ast}}\in C_{_{\!\mathfrak{X}}}(\alpha,\beta )$ ,

• 5. $\alpha ^{{\ast}} <\vartheta \alpha$ ,

• 6. $\vartheta \alpha =\vartheta \beta \; \Longrightarrow\;\alpha =\beta,$

• 7. $\begin{array}{lcl} \vartheta \alpha <\vartheta \beta &\;\Longleftrightarrow\;&(\alpha <\beta \; \wedge \;\alpha ^{{\ast}} <\vartheta \beta )\; \vee \; (\beta <\alpha \; \wedge \;\vartheta \alpha \leq \beta ^{{\ast}}) \\ &\;\Longleftrightarrow\;&(\alpha <\beta \; \wedge \;\alpha ^{{\ast}} <\vartheta \beta )\;\vee \;\vartheta \alpha \leq \beta ^{{\ast}},\end{array}$

• 8. $\beta <\vartheta \alpha \; \Longleftrightarrow\;\omega ^{\beta } <\vartheta \alpha.$

Proof

(1) and (8) basically follow from closure of $\vartheta \alpha$ under (C2).

(2) follows from the definition of $\vartheta \alpha$ taking Lemma 2.2 into account.

For (3), notice that $\vartheta \alpha \subset C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha )$ is a consequence of clause (C1). Since $C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha ) \cap \Omega \subseteq \vartheta \alpha$ follows from the definition of $\vartheta \alpha$ and Lemma 2.2, we arrive at (3).

(4): If $\gamma ^{{\ast}}\in C_{_{\!\mathfrak{X}}}(\alpha,\beta )$, then $\gamma \in C_{_{\!\mathfrak{X}}}(\alpha,\beta )$ by (C2). On the other hand,

$\gamma \in C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )\;\Longrightarrow\;\gamma ^{{\ast}}\in C_{_{\!\mathfrak{X}}}^{n}(\alpha,\beta )$ is easily seen by induction on n.

(5): $\alpha ^{{\ast}}\in C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha )$ holds by (4). As $\alpha ^{{\ast}} <\Omega$, this implies $\alpha ^{{\ast}} <\vartheta \alpha$ by (3).

(6): Suppose, aiming at a contradiction, that $\vartheta \alpha =\vartheta \beta$ and α < β. Then $C_{_{\!\mathfrak{X}}}(\alpha,\vartheta \alpha )\; \subseteq \; C_{_{\!\mathfrak{X}}}(\beta,\vartheta \beta )$; hence $\alpha \in C_{_{\!\mathfrak{X}}}(\beta,\vartheta \beta )\cap \beta$ by (2); thence $\vartheta \alpha =\vartheta \beta \in C_{_{\!\mathfrak{X}}}(\beta,\vartheta \beta )$, contradicting (3).

(7): Suppose α < β. Then $\vartheta \alpha <\vartheta \beta$ implies α ^∗ < ϑ β by (5). If $\alpha ^{{\ast}} <\vartheta \beta$, then $\alpha \in C_{_{\!\mathfrak{X}}}(\beta,\vartheta \beta )$; hence $\vartheta \alpha \in C_{_{\!\mathfrak{X}}}(\beta,\vartheta \beta )$; thus, $\vartheta \alpha <\vartheta \beta$. This shows

$$\displaystyle{(a)\;\;\;\alpha <\beta \; \Longrightarrow\;(\vartheta \alpha <\vartheta \beta \; \Longleftrightarrow\;\alpha ^{{\ast}} <\vartheta \beta ).}$$

By interchanging the roles of α and β, and employing (6) (to exclude $\vartheta \alpha =\vartheta \beta$), one obtains

$$\displaystyle{(b)\;\;\;\beta <\alpha \; \Longrightarrow\;(\vartheta \alpha <\vartheta \beta \; \Longleftrightarrow\;\vartheta \alpha \leq \beta ^{{\ast}}).}$$

(a) and (b) yield the first equivalence of (7) and thus the direction “$\Rightarrow$” of the second equivalence. Since $\vartheta \alpha \leq \beta ^{{\ast}}$ implies $\vartheta \alpha <\vartheta \beta$ by (5), one also obtains the direction “$\Leftarrow$” of the second equivalence. □ 

Definition 2.4

Inductive definition of a set $\mathrm{OT}_{\!_{\mathfrak{X}}}(\vartheta )$ of ordinals and a natural number G _ϑ α for $\alpha \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$.

• 1. $0,\Omega \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta ),\;G_{\vartheta }0:= G_{\vartheta }\Omega:= 0,$ $\mathfrak{E}_{u} \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ and $G_{\vartheta }\mathfrak{E}_{u} = 0$ for all $u \in \vert \mathfrak{X}\vert$.

• 2. If $\alpha = _{\mathit{NF}}\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$ and $\alpha _{1},\ldots,\alpha _{n} \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ then $\alpha \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ and $G_{\vartheta }\alpha:=\max \{ G_{\vartheta }\alpha _{1},\ldots,G_{\vartheta }\alpha _{n}\} + 1$.

• 3. If $\alpha =\vartheta \alpha _{1}$ and $\alpha _{1} \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ then $\alpha \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ and $G_{\vartheta }\alpha:= G_{\vartheta }\alpha _{1} + 1.$

Observe that according to Lemma 2.3 (1) and (6) the function $G_{\vartheta }$ is well-defined. Each ordinal $\alpha \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ has a unique normal form using the symbols $0,\Omega,+,\omega,\vartheta$.

Lemma 2.5

$\mathrm{OT}_{\!_{ \mathfrak{X}}}(\vartheta ) =\bigcup \{ C_{_{\!\mathfrak{X}}}(\alpha,0)\!:\alpha <\sup _{u\in X}\mathfrak{E}_{u}\} = C_{_{\!\mathfrak{X}}}(\sup _{u\in X}\mathfrak{E}_{u},0)$ .

Proof

Obviously $\beta <\sup _{u\in X}\mathfrak{E}_{u}$ holds for all $\beta \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$.

$$\displaystyle{\beta \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta ) \Rightarrow \beta \in C_{_{\!\mathfrak{X}}}(\sup _{u\in X}\mathfrak{E}_{u},0)}$$

is then shown by induction on $G_{\vartheta }\beta$.

The inclusion $C_{_{\!\mathfrak{X}}}(\sup _{u\in X}\mathfrak{E}_{u},0) \subseteq \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ follows from the fact that $\mathrm{OT}_{\!_{\mathfrak{X}}}(\vartheta )$ is closed under the clauses (Ci) for i = 0, 1, 2, 3. Since $\mathfrak{X}$ is an ordering without a maximal element it is also clear that $\bigcup \{C_{_{\!\mathfrak{X}}}(\alpha,0)\!:\alpha <\sup _{u\in X}\mathfrak{E}_{u}\} = C_{_{\!\mathfrak{X}}}(\sup _{u\in X}\mathfrak{E}_{u},0)$. □ 

If for $\alpha,\beta \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ represented in their normal form, we wanted to determine whether α < β, we could do this by deciding α ₀ < β ₀ for ordinals α ₀ and β ₀ that appear in these representations and, in addition, satisfy $G_{\vartheta }\alpha _{0} + G_{\vartheta }\beta _{0} <G_{\vartheta }\alpha + G_{\vartheta }\beta$. This follows from Lemma 2.3 (7) and the recursive procedure for comparing ordinals in Cantor normal form. So we come to see that after a straightforward coding in the natural numbers, we may represent $\langle \mathrm{OT}_{\!_{ \mathfrak{X}}}(\vartheta ),<\upharpoonright \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )\rangle$ via a primitive recursive ordinal notation system. How this ordinal representation system can be directly defined in $\mathbf{RCA}_{0}$ is spelled out in the next subsection.

2.1 Defining $\mathrm{OT}_{\!_{\mathfrak{X}}}(\vartheta )$ in RCA ₀

We shall provide an explicit primitive recursive definition of $\mathrm{OT}_{\!_{ \mathfrak{X}}}(\vartheta )$ as a term structure in RCA ₀. Of course formally, terms or strings of symbols have to be treated as coded by natural numbers since RCA ₀ only talks about numbers and sets of numbers. Though, as it is well-known how to do this, we can’t be bothered with these niceties.

Definition 2.6

Given a well-ordering $\mathfrak{X} = (X,<_{X})$, i.e., an ordered pair $\mathfrak{X}$ in which X is a set of natural numbers and <  _X is a well-ordering relation on X, we define, by recursion, a binary relational structure $\vartheta _{\!_{\! \mathfrak{X}}} = (\vert \vartheta _{\!_{\!\mathfrak{X}}}\vert,<)$, and a function $\;^{{\ast}}:\vert \vartheta _{\!_{\!\mathfrak{X}}}\vert \rightarrow \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$, in the following way:

• 1. $0,\Omega \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$, and $0^{{\ast}}:= 0 =: \Omega ^{{\ast}}$.

• 2. If $\alpha \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ and 0 ≠ α then 0 < α.

• 3. For every u ∈ X there is an element $\mathfrak{E}_{u} \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$. Moreover, $(\mathfrak{E}_{u})^{{\ast}}:= 0$, and $\Omega <\mathfrak{E}_{u}$. If u, v ∈ X and u <  _X v, then $\mathfrak{E}_{u} <\mathfrak{E}_{v}$.

• 4. For every $\alpha \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ there is an element $\vartheta \alpha \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$; and we have $\vartheta \alpha <\Omega$, $\vartheta \alpha <\mathfrak{E}_{u}$ for every u ∈ X, and $(\vartheta \alpha )^{{\ast}}:=\vartheta \alpha$.

• 5. If $\alpha \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ and α is not of the form $\Omega$, $\mathfrak{E}_{u}$, or ϑ β, then $\omega ^{\alpha } \in \vartheta _{\!_{\!\mathfrak{X}}}$ and $(\omega ^{\alpha })^{{\ast}}\,:=\,\alpha ^{{\ast}}$.

• 6. If $\alpha _{1},\ldots,\alpha _{n} \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ and $\alpha _{1} \geq \ldots \geq \alpha _{n}$ with n ≥ 2, then $\omega ^{\alpha _{1}} +\omega ^{\alpha _{2}} +\ldots +\omega ^{\alpha _{n}} \in \vert \vartheta _{\!_{\! \mathfrak{X}}}\vert$ and $(\omega ^{\alpha _{1}} +\omega ^{\alpha _{2}} +\ldots +\omega ^{\alpha _{n}})^{{\ast}}:=\max \{\alpha _{ i}^{{\ast}}: 1 \leq i \leq n\}$.

• 7. Let $\alpha =\omega ^{\alpha _{1}} +\ldots +\omega ^{\alpha _{n}} \in \vert \vartheta _{\!_{\! \mathfrak{X}}}\vert$ and $\beta \in \vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$, where β is of one of the forms ϑ γ, $\Omega$, or $\mathfrak{E}_{u}$.

  • (i) If α ₁ < β, then $\omega ^{\alpha _{1}} +\ldots +\omega ^{\alpha _{n}} <\beta$.

  • (ii) If β ≤ α ₁, then $\beta <\omega ^{\alpha _{1}} +\ldots +\omega ^{\alpha _{n}}$.

• 8. If $\omega ^{\alpha _{1}} +\ldots +\omega ^{\alpha _{n}},\;\omega ^{\beta _{1}} +\ldots +\omega ^{\beta _{m}} \in \vert \vartheta _{\!_{\! \mathfrak{X}}}\vert$ then

  $\omega ^{\alpha _{1}} +\ldots +\omega ^{\alpha _{n}} <\omega ^{\beta _{1}} +\ldots +\omega ^{\beta _{m}}$ iff

  $n <m\: \wedge \:\forall i \leq n\;\,\alpha _{i} =\beta _{i}$ or

  $\exists \,i \leq \min (n,m)\;[(\forall j <i\;\alpha _{j} =\beta _{j}) \wedge (\alpha _{i} <\beta _{i})]$.

• 9. If α < β and α ^∗ < ϑ β then $\vartheta \alpha <\vartheta \beta$.

• 10. If $\vartheta \beta \leq \alpha ^{{\ast}}$ then $\vartheta \beta <\vartheta \alpha$.

Lemma 2.7

• (i) The set $\vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ , the relation <, and the function ^∗ are primitive recursive in $\mathfrak{X} = (X,<_{X})$ .

• (ii) < is a total and linear ordering on $\vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$ .

Proof

Straightforward but tedious. □ 

Of course, RCA ₀ does not prove that < is a well-ordering on $\vert \vartheta _{\!_{\!\mathfrak{X}}}\vert$.

3 A Well-Ordering Proof

In this section we work in the background theory

$$\displaystyle{\mathbf{RCA}_{0} + \forall X\exists Y \;(X \in Y \; \wedge \;\mbox{ $Y $ is an $\omega $-model of $\mathbf{BI}$})}$$

and shall prove the following statement

$$\displaystyle{\forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\mathfrak{X}}))\,,}$$

that is, the part $\mbox{ (i)} \Rightarrow \ (\mathit{ii})$ of the main Theorem 1.7. Some of the proofs are similar to ones in [13, Section 10]. Note that in this theory we can deduce arithmetical comprehension and even arithmetical transfinite recursion owing to [7] and [12], respectively.

Let us fix a well-ordering $\mathfrak{X} = (X,<_{X})$, an arbitrary set Y and a countable coded ω-model $\mathfrak{A}$ of BI which contains both $\mathfrak{X}$ and Y as elements. In the sequel α, β, γ, δ, … are supposed to range over $\vartheta _{\mathfrak{X}}$. < will be used to denote the ordering on $\vartheta _{\mathfrak{X}}$. We are going to work informally in our background theory. A set $U \subseteq \mathbb{N}$ is said to be definable in $\mathfrak{A}$ if $U =\{ n \in \mathbb{N}\mid \mathfrak{A}\models A(n)\}$ for some formula A(x) of second order arithmetic which may contain parameters from $\mathfrak{A}$.

Definition 3.1

• 1. $\mathrm{Acc}:=\{\alpha <\Omega \mid \mathfrak{A}\models \mathrm{WO}(<\upharpoonright \alpha )\},$

• 2. $\mathrm{M}:=\{\alpha \!: E_{\Omega }(\alpha ) \subseteq \mathrm{Acc}\},$

• 3. $\alpha <_{\Omega }\beta:\; \Longleftrightarrow\;\alpha,\beta \in \mathrm{M}\;\wedge \;\alpha <\beta.$

Lemma 3.2

$\alpha,\beta \in \mathrm{Acc}\;\Longrightarrow\;\alpha +\omega ^{\beta } \in \mathrm{Acc}.$

Proof

Familiar from Gentzen’s proof in Peano arithmetic. The proof just requires ACA ₀. (cf. [16, VIII.§ 21 Lemma 1]). □ 

Lemma 3.3

$\mathrm{Acc} = \mathrm{M} \cap \Omega \;(:=\{\alpha \in \mathrm{M}\mid \alpha <\Omega \}).$

Proof

If $\alpha \in \mathrm{Acc}$, then $E_{\Omega }(\alpha ) \subseteq \mathrm{Acc}$ as well; hence, $\alpha \in \mathrm{M} \cap \Omega$. If $\alpha \in \mathrm{M} \cap \Omega$, then $E_{\Omega }(\alpha ) \subseteq \mathrm{M} \cap \Omega$, so α ∈ Acc follows from Lemma 3.2. □ 

Lemma 3.4

Let U be $\mathfrak{A}$ definable. Then

$$\displaystyle{\forall \alpha <\Omega \cap \mathrm{M}\,[\forall \beta <\alpha \ \beta \in U \rightarrow \alpha \in U] \rightarrow \mathrm{Acc} \subseteq U\,.}$$

Proof

This follows readily from the assumption that $\mathfrak{A}$ is a model of BI. □ 

Definition 3.5

Let $\mathrm{Prog}_{\Omega }(X)$ stand for

$$\displaystyle{(\forall \alpha \in \mathrm{M})[(\forall \beta <_{\Omega }\alpha )(\beta \in X)\longrightarrow \alpha \in X].}$$

Let $\mathrm{Acc}_{\Omega }:=\{\alpha \in \mathrm{M}\!:\vartheta \alpha \in \mathrm{Acc}\}.$

Lemma 3.6

If U is $\mathfrak{A}$ definable, then

$$\displaystyle{\mathrm{Prog}_{\Omega }(U) \rightarrow \Omega,\Omega + 1 \in U\,.}$$

Proof

This follows from Lemmas 3.3 and 3.4. □ 

Lemma 3.7

$\mathrm{Prog}_{\Omega }(\mathrm{Acc}_{\Omega }).$

Proof

Assume α ∈ M and $(\forall \beta <_{\Omega }\alpha )(\beta \in \mathrm{Acc}_{\Omega }).$ We have to show that $\vartheta \alpha \in \mathrm{Acc}.$ It suffices to show

$$\displaystyle\begin{array}{rcl} \beta <\vartheta \alpha & \Longrightarrow& \beta \in \mathrm{Acc}.{}\end{array}$$

(2)

We shall employ induction on G _ϑ (β), i.e., the length of (the term that represents) β. If β ∉ E, then (2) follows easily by the inductive assumption and Lemma 3.2. Now suppose $\beta =\vartheta \beta _{0}.$ According to Lemma 2.3 it suffices to consider the following two cases:

Case 1: :

β ≤ α ^∗. Since α ∈ M, we have $\alpha ^{{\ast}}\in E_{\Omega }(\alpha ) \subseteq \mathrm{Acc};$ therefore, $\beta \in \mathrm{Acc}.$

Case 2: :

β ₀ < α and β ₀ ^∗ < ϑ α. As the length of β ₀ ^∗ is less than the length of β, we get $\beta _{0}^{{\ast}}\in \mathrm{Acc};$ thus, $E_{\Omega }(\beta _{0}) \subseteq \mathrm{Acc},$ therefore $\beta _{0} \in \mathrm{M}.$ By the assumption at the beginning of the proof, we then get $\beta _{0} \in \mathrm{Acc}_{\Omega };$ hence, $\beta =\vartheta \beta _{0} \in \mathrm{Acc}$. □ 

Definition 3.8

For every $\mathfrak{A}$ definable set U we define the “Gentzen jump”

$$\displaystyle{U^{j}\;:=\;\{\gamma \mid \forall \delta \,[\mathrm{M}\cap \delta \subseteq U \rightarrow \mathrm{M} \cap (\delta +\omega ^{\gamma }) \subseteq U]\}.}$$

Lemma 3.9

Let U be $\mathfrak{A}$ definable.

• (i) $\gamma \in U^{j} \Rightarrow \mathrm{M} \cap \omega ^{\gamma }\subseteq U$ .

• (ii) $\mathrm{Prog}_{\Omega }(U) \Rightarrow \mathrm{Prog}_{\Omega }(U^{j})$ .

Proof

(i) is obvious. (ii) $\mathrm{M} \cap (\delta +\omega ^{\gamma }) \subseteq U$ is to be proved under the assumptions(a) $\mathrm{Prog}_{\Omega }(U)$, (b) $\gamma \,\in \,\mathrm{M}\, \wedge \,\mathrm{M}\,\cap \,\gamma \subseteq U^{j}$ and (c) $\mathrm{M}\,\cap \,\delta \subseteq U$. So let $\eta \,\in \,\mathrm{M}\,\cap \,(\delta \,+\,\omega ^{\gamma })$.

• 1. η < δ: Then η ∈ U is a consequence of (c).

• 2. η = δ: Then η ∈ U follows from (c) and (a).

• 3. $\delta <\eta <\delta +\omega ^{\gamma }$: Then there exist γ ₁, …, γ _k  < γ such that $\eta =\delta +\omega ^{\gamma _{1}} + \cdots +\omega ^{\gamma _{k}}$ and $\gamma _{1} \geq \cdots \geq \gamma _{k}$. η ∈ M implies $\gamma _{1},\ldots,\gamma _{k} \in \mathrm{M}\cap \gamma$. Through applying (b) and (c) we obtain $\mathrm{M} \cap (\delta +\omega ^{\gamma _{1}}) \subseteq U$. By iterating this procedure we eventually arrive at $\delta +\omega ^{\gamma _{1}} + \cdots +\omega ^{\gamma _{k}} \in U$, so η ∈ U holds.

 □ 

Corollary 3.10

Let $\mathcal{I}(\delta )$ be the statement that $\mathrm{Prog}_{\Omega }(V ) \rightarrow \delta \in \mathrm{M}\; \wedge \;\delta \cap \mathrm{M} \subseteq V$ holds for all $\mathfrak{A}$ definable sets V. Assume $\mathcal{I}(\delta )$ . Let δ ₀ := δ and $\delta _{n+1}:=\omega ^{\delta _{n}}$ . Then

$$\displaystyle{\mathcal{I}(\delta _{n})}$$

holds for all n.

Proof

We use induction on n. For n = 0 this is the assumption. Now suppose $\mathcal{I}(\delta _{n})$ holds. Assume $\mathrm{Prog}_{\Omega }(U)$ for an $\mathfrak{A}$ definable U. By Lemma 3.9 we conclude $\mathrm{Prog}_{\Omega }(U^{j})$ and hence δ _n  ∈ U ^j and $\delta _{n} \cap \mathrm{M} \subseteq U^{j}$. As clearly $\mathrm{M} \cap 0 \subseteq U$ we get $\omega ^{\delta _{n}} \cap \mathrm{M} \subseteq U$. Since $\mathrm{Prog}_{\Omega }(U)$ entails $\delta \in \mathrm{M}$ we also have $\delta _{n+1} \in \mathrm{M}$. Thus $\delta _{n+1} \in \mathrm{M}\; \wedge \;\delta _{n+1} \cap \mathrm{M} \subseteq U$, showing $\mathcal{I}(\delta _{n+1})$. □ 

Let $\omega _{0}(\alpha ):=\alpha$ and $\omega _{n+1}(\alpha ):=\omega ^{\omega _{n}(\alpha )}$.

Proposition 3.11

$\mathcal{I}(\mathfrak{E}_{u})$ holds for all $u \in \vert \mathfrak{X}\vert$ .

Proof

Noting that in our background theory $\mathfrak{X}$ is a well-ordering, we can use induction on $\mathfrak{X}$. Note also that $\mathcal{I}(\mathfrak{E}_{u})$ is a statement about all definable sets in $\mathfrak{A}$ which is not formalizable in $\mathfrak{A}$ itself. However, in our background theory quantification over all these sets is first order expressible and therefore transfinite induction along <  _X is available.

First observe that we have $\mathcal{I}(\Omega + 1)$ by Lemma 3.6. Let u ₀ be the <  _X -least element of $\vert \mathfrak{X}\vert$. We have $\mathfrak{E}_{u_{0}} \in \mathrm{M}$ and for every $\eta <\mathfrak{E}_{u_{0}}$ there exists n such that $\eta <\omega _{n}(\Omega + 1)$. As a result, using Corollary 3.10, we have

$$\displaystyle{\mathrm{Prog}_{\Omega }(U) \rightarrow \mathfrak{E}_{u_{0}} \cap \mathrm{M} \subseteq U}$$

for every $\mathfrak{A}$ definable set U.

Now suppose that $u \in \vert \mathfrak{X}\vert$ is not the <  _X -least element and for all v <  _X u we have $\mathcal{I}(\mathfrak{E}_{v})$. As for every $\delta <\mathfrak{E}_{u}$ there exists v <  _X u and n such that $\delta <\omega _{n}(\mathfrak{E}_{v})$, the inductive assumption together with Corollary 3.10 yields

$$\displaystyle{\mathrm{Prog}_{\Omega }(U) \rightarrow \mathfrak{E}_{u} \cap \mathrm{M} \subseteq U\,.}$$

$\mathfrak{E}_{u} \in \mathrm{M}$ is obvious. □ 

Proposition 3.12

For all α, $\mathcal{I}(\alpha )$ .

Proof

We proceed by the induction on the term complexity of α. Clearly, $\mathcal{I}(0)$. By Lemma 3.6 we conclude that $\mathcal{I}(\Omega )$. Proposition 3.11 entails that $\mathcal{I}(\mathfrak{E}_{u})$ for all $u \in \vert \mathfrak{X}\vert$.

Now let $\alpha =\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{n}}$ be in Cantor normal form. Inductively we have $\mathcal{I}(\alpha _{1}),\ldots,\mathcal{I}(\alpha _{n})$. Assume $\mathrm{Prog}_{\Omega }(U)$. Then $\mathrm{Prog}_{\Omega }(U^{j})$ by Lemma 3.9(ii), and hence $\alpha _{1} \cap \mathrm{M} \subseteq U^{j},\ldots,\alpha _{n} \cap \mathrm{M} \subseteq U^{j}$ and $\alpha _{1},\ldots,\alpha _{n} \in \mathrm{M}$. The latter implies $\alpha _{1} \in U^{j},\ldots,\alpha _{n} \in U^{j}$. Using the definition of U ^j repeatedly we conclude $\alpha \cap \mathrm{M} \subseteq U$. Moreover, α ∈ M since $\alpha _{1},\ldots,\alpha _{n} \in \mathrm{M}$.

Now suppose that $\alpha =\vartheta \beta$. Inductively we have $\mathcal{I}(\beta )$. By Lemma 3.7 we conclude that $\beta \in \mathrm{Acc}_{\Omega }$, and hence $\alpha \in \mathrm{Acc}$. From $\mathrm{Prog}_{\Omega }(U)$ we obtain by Lemma 3.4 that ξ ∈ U for all ξ ≤ α. As a result, $\mathcal{I}(\alpha )$. □ 

Corollary 3.13

$\vartheta _{\mathfrak{X}}$ is a well-ordering.

With the previous Corollary, the proof of Theorem 1.7 (i)$\Rightarrow$(ii) is finally accomplished.

4 Deduction Chains

From now on we will be concerned with the part $\mbox{ (ii)} \Rightarrow \mbox{ (i)}$ of the main Theorem 1.7. An important tool will be the method of deduction chains. Given a sequent $\Gamma$ and a set $Q \subseteq \mathbb{N}$, deduction chains starting at $\Gamma$ are built by systematically decomposing $\Gamma$ into its subformulas, and adding additionally at the nth step the formulas $\neg A_{n}$ and $\neg \bar{Q}(\bar{n})$, where $(A_{n}\mid n \in \mathbb{N})$ is an enumeration of the axioms of the theory BI, and $\bar{Q}(\bar{n})$ is the atom $\bar{n} \in U_{0}$ if n ∈ Q and $\bar{n}\notin U_{0}$ otherwise. The set of all deduction chains that can be built from the empty sequent with respect to a given set Q forms the tree $\mathcal{D}_{Q}$. There are two scenarios to be considered.

• (i) If there is an infinite deduction chain, i.e. $\mathcal{D}_{Q}$ is ill-founded, then this readily yields a model of $\mathbf{BI}$ that contains Q.

• (ii) If each deduction chain is finite, then this yields a derivation of the empty sequent, ⊥ , in a corresponding infinitary system with an ω-rule. The depth of this derivation is bounded by the order-type α of the Kleene–Brouwer ordering of $\mathcal{D}_{Q}$. By the well-ordering principle, transfinite induction up to $\mathfrak{E}_{\alpha +1}$ is available, which allows to transform this proof into a cut-free proof of ⊥ whose depth is less than $\vartheta \mathfrak{E}_{\alpha +1}$.

As the second alternative is impossible, the first yields the desired model.

Definition 4.1

• 1. We let U ₀, U ₁, …, U _m , … be an enumeration of the free set variables of $\mathcal{L}_{2}$ and, given a closed term t, we write $t^{\mathbb{N}}$ for its numerical value.

• 2. Henceforth a sequent will be a finite list of $\mathcal{L}_{2}$-formulae without free number variables.

• 3. A sequent $\Gamma$ is axiomatic if it satisfies at least one of the following conditions:

  • (a) $\Gamma$ contains a true literal, i.e., a true formula of either of the forms $R(t_{1},\ldots,t_{n})$ or $\neg R(t_{1},\ldots,t_{n})$, where R is a predicate symbol in $\mathcal{L}_{2}$ for a primitive recursive relation and $t_{1},\ldots,t_{n}$ are closed terms.

  • (b) $\Gamma$ contains formulae s ∈ U and t ∉ U for some set variable U and terms s,  t with $s^{\mathbb{N}} = t^{\mathbb{N}}$.

• 4. A sequent is reducible if it is not axiomatic and contains a formula which is not a literal.

Definition 4.2

For $Q \subseteq \mathbb{N}$ we define

$$\displaystyle{ \bar{Q}(n) \Leftrightarrow \left \{\begin{array}{@{}l@{\quad }l@{}} \bar{n} \in U_{0}\quad &\mbox{ if }n \in Q, \\ \bar{n}\notin U_{0} \quad &\text{otherwise}. \end{array} \right. }$$

For some of the following theorems it is convenient to have a finite axiomatization of arithmetical comprehension.

Lemma 4.3

$\mathbf{ACA}_{0}$ can be axiomatized via a single $\Pi _{2}^{1}$ sentence $\forall XC(X)$ .

Proof

[17, Lemma VIII.1.5]. □ 

Definition 4.4

In what follows, we fix an enumeration of $A_{1},\,A_{2},\,A_{3},\ldots$ of all the universal closures of instances of ( BI). We also put $A_{0}:= \forall X\,C(X)$, where the latter is the sentence that axiomatizes arithmetical comprehension.

Definition 4.5

Let $Q \subseteq \mathbb{N}$. A Q -deduction chain is a finite string

$$\displaystyle{\Gamma _{0},\,\Gamma _{1},\ldots,\,\Gamma _{k}}$$

of sequents $\Gamma _{i}$ constructed according to the following rules:

• 1. $\Gamma _{0} = \neg \bar{Q}(0),\,\neg A_{0}$.

• 2. $\Gamma _{i}$ is not axiomatic for i < k.

• 3. If i < k and $\Gamma _{i}$ is not reducible, then

  $$\displaystyle{\Gamma _{i+1} = \Gamma _{i},\,\neg \bar{Q}(i + 1),\,\neg A_{i+1}.}$$

• 4. Every reducible $\Gamma _{i}$ with i < k is of the form

  $$\displaystyle{\Gamma _{i}^{{\prime}},\,E,\,\Gamma _{ i}^{{\prime\prime}}}$$

  where E is not a literal and $\Gamma _{i}^{{\prime}}$ contains only literals. E is said to be the redex of $\Gamma _{i}$.

  Let i < k and Γ _i be reducible. $\Gamma _{i+1}$ is obtained from $\Gamma _{i} = \Gamma _{i}^{{\prime}},\,E,\,\Gamma _{i}^{{\prime\prime}}$ as follows:

  • (a) If $E \equiv E_{0} \vee E_{1}$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,E_{ 0},\,E_{1},\,\Gamma _{i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1}.}$$

  • (b) If $E \equiv E_{0} \wedge E_{1}$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,E_{ j},\,\Gamma _{i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1}}$$

    where j = 0 or j = 1.

  • (c) If $E \equiv \exists xF(x)$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,F(\bar{m}),\,\Gamma _{ i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1},\,E}$$

    where m is the first number such that $F(\bar{m})$ does not occur in $\Gamma _{0},\ldots,\,\Gamma _{i}$.

  • (d) If $E \equiv \forall xF(x)$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,F(\bar{m}),\,\Gamma _{ i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1}}$$

    for some m.

  • (e) If $E \equiv \exists XF(X)$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,F(U_{ m}),\,\Gamma _{i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1},\,E}$$

    where m is the first number such that F(U _m ) does not occur in $\Gamma _{0},\ldots,\,\Gamma _{i}$.

  • (f) If $E \equiv \forall XF(X)$, then

    $$\displaystyle{\Gamma _{i+1} = \Gamma _{i}^{{\prime}},\,F(U_{ m}),\,\Gamma _{i}^{{\prime\prime}},\,\neg \bar{Q}(i + 1),\,\neg A_{ i+1}}$$

    where m is the first number such that U _m does not occur in $\Gamma _{i}$.

The set of Q-deduction chains forms a tree $\mathcal{D}_{Q}$ labeled with strings of sequents.

We will now consider two cases.

• Case I: $\mathcal{D}_{Q}$ is not well-founded. Then $\mathcal{D}_{Q}$ contains an infinite path $\mathbb{P}$. Now define a set M via

  $$\displaystyle\begin{array}{rcl} (M)_{i}& =& \{k\mid \mbox{ $\bar{k}\notin U_{i}$ occurs in $\mathbb{P}$}\}. {}\\ \end{array}$$

  Set $\mathbb{M} = (\mathbb{N};\{(M)_{i}\mid i \in \mathbb{N}\},\in,+,\cdot,0,1,<)$.

For a formula F, let $F \in \mathbb{P}$ mean that F occurs in $\mathbb{P}$, i.e. $F \in \Gamma$ for some $\Gamma \in \mathbb{P}$.

Claim: Under the assignment $U_{i}\mapsto (M)_{i}$ we have

$$\displaystyle\begin{array}{rcl} F \in \mathbb{P}& \;\;\;\;\Rightarrow \;\;\;\;& \mathbb{M}\models \neg F.{}\end{array}$$

(3)

The Claim will imply that $\mathbb{M}$ is an ω-model of BI. Also note that (M)₀ = Q, thus Q is in $\mathbb{M}$. The proof of (3) follows by induction on F using Lemma 4.6 below. The upshot of the foregoing is that we can prove Theorem 1.7 under the assumption that $\mathcal{D}_{Q}$ is ill-founded for all sets $Q \subseteq \mathbb{N}$.

Lemma 4.6

Let Q be an arbitrary subset of $\mathbb{N}$ and $\mathcal{D}_{Q}$ be the corresponding deduction tree. Moreover, suppose $\mathcal{D}_{Q}$ is not well-founded. Then $\mathcal{D}_{Q}$ has an infinite path $\mathbb{P}$ . $\mathbb{P}$ has the following properties:

• 1. $\mathbb{P}$ does not contain literals which are true in $\mathbb{N}$ .

• 2. $\mathbb{P}$ does not contain formulas s ∈ U _i and t ∉ U _i for constant terms s and t such that $s^{\mathbb{N}} = t^{\mathbb{N}}$ .

• 3. If $\mathbb{P}$ contains E ₀ ∨ E ₁ , then $\mathbb{P}$ contains E ₀ and E ₁ .

• 4. If $\mathbb{P}$ contains E ₀ ∧ E ₁ , then $\mathbb{P}$ contains E ₀ or E ₁ .

• 5. If $\mathbb{P}$ contains $\exists xF(x)$ , then $\mathbb{P}$ contains $F(\bar{n})$ for all n.

• 6. If $\mathbb{P}$ contains $\forall xF(x)$ , then $\mathbb{P}$ contains $F(\bar{n})$ for some n.

• 7. If $\mathbb{P}$ contains $\exists XF(X)$ , then $\mathbb{P}$ contains F(U _m ) for all m.

• 8. If $\mathbb{P}$ contains $\forall XF(X)$ , then $\mathbb{P}$ contains F(U _m ) for some m.

• 9. $\mathbb{P}$ contains $\neg C(U_{m})$ for all m.

• 10. $\mathbb{P}$ contains $\neg \bar{Q}(m)$ for all m.

Proof

Standard. □ 

Corollary 4.7

If $\mathcal{D}_{Q}$ is ill-founded, then there exists a countable coded ω-model of BI which contains Q.

For our purposes it is important that Corollary 4.7 can be proved in $T_{0}:= \mathbf{RCA}_{0} + \forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\mathfrak{X}}))$. To this end we need to show that the semantics of ω-models can be handled in the latter theory, i.e. for every formula F of $\mathcal{L}_{2}$ there exists a valuation for F in the sense of [17, VII.2.1]. It is easily seen that the principle $\forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\mathfrak{X}}))$ implies

$$\displaystyle{\forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\varepsilon _{\mathfrak{X}}))}$$

(see [1, Definition 2.1]) and thus, by [1, Theorem 4.1], T ₀ proves that every set is contained in an ω-model of ACA. Now take an ω-model containing $\mathcal{D}_{Q}$ and an infinite branch of $\mathcal{D}_{Q}$. In this ω-model we find a valuation for every formula by [17, VII.2.2]. And hence Corollary 4.7 holds in the model, but then it also holds in the world at large by absoluteness.

5 Proof of the Main Theorem: The Hard Direction Part 2

The remainder of the paper will be devoted to ruling out the possibility that for some Q, $\mathcal{D}_{Q}$ could be a well-founded tree. This is the place where the principle $\forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\mathfrak{X}}))$ in the guise of cut elimination for an infinitary proof system enters the stage. Aiming at a contradiction, suppose that $\mathcal{D}_{Q}$ is a well-founded tree. Let $\mathfrak{X}$ be the Kleene–Brouwer ordering on $\mathcal{D}_{Q}$ (see [17, Definition V.1.2]). Then $\mathfrak{X}$ is a well-ordering. In a nutshell, the idea is that a well-founded $\mathcal{D}_{Q}$ gives rise to a derivation of the empty sequent (contradiction) in an infinitary proof system.

5.1 Majorization and Fundamental Functions

In this section we introduce the concepts of majorization and fundamental function. They are needed for carrying through the ordinal analysis of bar induction. More details can be found in [13, Section 4] and [3, I.4] to which we refer for proofs. The missing proofs are actually straightforward consequences of Definition 2.6.

Definition 5.1

• 1. $\alpha \lhd \beta$ means α < β and ϑ α < ϑ β.

• 2. $\alpha \unlhd \beta:\; \Longleftrightarrow\;(\alpha \lhd \beta \vee \alpha =\beta ).$

Lemma 5.2

• 1. $\alpha \lhd \beta \;\wedge \;\beta \lhd \gamma \;\Longrightarrow\;\alpha \lhd \gamma$ .

• 2. $0 <\beta <\varepsilon _{0}\;\Longrightarrow\;\alpha \lhd \alpha +\beta$ .

• 3. $\alpha <\beta <\Omega \;\Longrightarrow\;\alpha \lhd \beta$ .

• 4. $\alpha \lhd \beta \;\Longrightarrow\;\alpha + 1\unlhd \beta.$

• 5. $\alpha \lhd \beta \;\Longrightarrow\;\vartheta \alpha \lhd \vartheta \beta.$

• 6. $\alpha =\alpha _{0} + 1\Longrightarrow\vartheta \alpha _{0}\lhd \vartheta \alpha.$

Lemma 5.3

$\alpha \lhd \beta,\;\beta <\omega ^{\gamma +1}\;\Longrightarrow\;\omega ^{\gamma } +\alpha \lhd \omega ^{\gamma } +\beta.$

Corollary 5.4

$\omega ^{\alpha } \cdot n\lhd \omega ^{\alpha } \cdot (n + 1).$

Lemma 5.5

$\alpha \lhd \beta \;\Longrightarrow\;\omega ^{\alpha } \cdot n\lhd \omega ^{\beta }.$

Definition 5.6

Let $D_{\Omega }:= (\mathrm{OT}_{\!_{\mathfrak{X}}}(\vartheta ) \cap \Omega )\, \cup \,\{ \Omega \}$. A function $f: D_{\Omega } \rightarrow \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ will be called a fundamental function if it is generated by the following clauses:

• F1. $Id: D_{\Omega } \rightarrow D_{\Omega }$ with $Id(\alpha ) =\alpha$ is a fundamental function.

• F2. If f is a fundamental function, $\gamma \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ and $f(\Omega ) <\omega ^{\gamma +1}$, then $\omega ^{\gamma } + f$ is a fundamental function, where $(\omega ^{\gamma } + f)(\alpha ):=\omega ^{\gamma } + f(\alpha )$ for all $\alpha \in D_{\Omega }.$

• F3. If f is a fundamental function, then so is ω ^f with (ω ^f)(α): = ω ^f(α) for all $\alpha \in D_{\Omega }$.

Lemma 5.7

Let f be a fundamental function and $\beta \leq \Omega$.

• (i) If $\alpha <\beta$ , then f(α) < f(β).

• (ii) If $\alpha \lhd \beta$ , then $f(\alpha )\lhd f(\beta )$ .

• (iii) $(f(\beta ))^{{\ast}}\leq \max ((f(0))^{{\ast}},\beta ^{{\ast}})$ .

Proof

• (i) is obvious by induction on the generation of fundamental functions.

• (ii) also follows by induction on the generation of fundamental functions, using Lemmas 5.3 and 5.5.

• (iii) as well follows by induction on the generation of fundamental functions.

 □ 

Lemma 5.8

For every fundamental function f we have $f(\vartheta (f(0)))\lhd f(\Omega )$ .

Proof

Since $\vartheta (f(0)) <\Omega$, we clearly have $f(\vartheta (f(0))) <f(\Omega )$. Since $0\lhd \Omega$ and f is a fundamental function, we have $\vartheta (f(0)) <\vartheta (f(\Omega ))$ by Lemma 5.7 (ii). Invoking Lemma 5.7 (iii), the latter entails that $(f(\vartheta (f(0))))^{{\ast}} <\vartheta (f(\Omega ))$, so that in conjunction with $f(\vartheta (f(0))) <f(\Omega )$ it follows that $\vartheta (f(\vartheta (f(0))))\lhd \vartheta (f(\Omega ))$. As a result, $f(\vartheta (f(0)))\lhd f(\Omega )$. □ 

5.2 The Infinitary Calculus $T_{\!_{Q}}^{{\ast}}$

The calculus $T_{\!_{Q}}^{{\ast}}$ to be introduced stems from [13, Section 6]. We fix a set $Q \subseteq \mathbb{N}$. Let $\mathcal{L}_{2}^{Q}$ be the language of second order arithmetic augmented by a unary predicate $\bar{Q}$. The formulas of $T_{\!_{Q}}^{{\ast}}$ arise from $\mathcal{L}_{2}^{Q}$-formulas by replacing free numerical variables by numerals, i.e. terms of the form $0,0^{{\prime}},0^{{\prime\prime}},\ldots$ Especially, every formula A of $T_{\!_{Q}}^{{\ast}}$ is an $\mathcal{L}_{2}^{Q}$-formula. We are going to measure the length of derivations by ordinals. We are going to use the set of ordinals $\mathrm{OT}_{\!_{\mathfrak{X}}}(\vartheta )$ of Sect. 3.

Definition 5.9

 

• 1. A formula B is said to be weak if it belongs to $\Pi _{0}^{1} \cup \Pi _{1}^{1}$.

• 2. Two closed terms s and t are said to be equivalent if they yield the same value when computed.

• 3. A formula is called constant if it contains no set variables. The truth or falsity of such a formula is understood with respect to the standard structure of the integers.

• 4. $\overline{0}:= 0$, $\overline{m + 1}:= \overline{m}^{{\prime}}$.

In the sequent calculus $T_{\!_{Q}}^{{\ast}}$ below we shall use the following rules of inference:

$$\displaystyle{\begin{array}{ll} (\wedge ) & \vdash \Gamma,A\mbox{ and } \vdash \Gamma,B\;\Longrightarrow\; \vdash \Gamma,A \wedge B, \\ (\vee ) & \vdash \Gamma,A_{i}\;\Longrightarrow\; \vdash \Gamma,A_{0} \vee A_{1}\;\;\;\mbox{ if }i \in \{ 0,1\}, \\ (\forall _{2}) & \vdash \Gamma,F(U)\;\Longrightarrow\; \vdash \Gamma,\forall XF(X), \\ (\exists _{1}) & \vdash \Gamma,F(t)\;\Longrightarrow\; \vdash \Gamma,\exists xF(x), \\ (\mathit{Cut})& \vdash \Gamma,A\mbox{ and } \vdash \Gamma,\neg \;A\;\Longrightarrow\; \vdash \Gamma,\end{array} }$$

where in $(\forall _{2})$ the free variable U is not to occur in the conclusion.

The most important feature of sequent calculi is cut-elimination. To state this fact concisely, let us introduce a measure of complexity, gr(A), the grade of a formula A, for $\mathcal{L}_{2}^{Q}$-formulae.

Definition 5.10

 

• 1. gr(A) = 0 if A is a prime formula or negated prime formula.

• 2. $\mathit{gr}(\forall XF(X)) = \mathit{gr}(\exists XF(X)) =\omega$ if F(U) is arithmetic.

• 3. $\mathit{gr}(A \wedge B) = \mathit{gr}(A \vee B) = \mathit{max}\{\mathit{gr}(A),\mathit{gr}(B)\} + 1$.

• 4. $\mathit{gr}(\forall xH(x)) = \mathit{gr}(\exists xH(x)) = \mathit{gr}(H(0)) + 1$.

• 5. $\mathit{gr}(\forall XG(X)) = \mathit{gr}(\exists XG(X)) = \mathit{gr}(G(U)) + 1,$ if G is not arithmetic.

Definition 5.11

Inductive definition of

for $\alpha \in \mathrm{ OT}_{\!_{\mathfrak{X}}}(\vartheta )$ and ϱ < ω+ω.

• 1. If A is a true constant prime formula or negated prime formula and $A \in \Gamma$, then

  

• 2. If n ∈ Q and t is a closed term with value n and $\bar{Q}(t)$ is in $\Gamma$, then

  

• 3. If n ∉ Q and t is a closed term with value n and $\neg \bar{Q}(t)$ is in $\Gamma$, then

  

• 4. If $\Gamma$ contains formulas A(s ₁, …, s _n ) and $\neg A(t_{1},\ldots,t_{n})$ of grade 0 or ω, where s _i and t _i  (1 ≤ i ≤ n) are equivalent terms, then

  

• 5. If

  

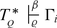
  and $\beta \lhd \alpha$ hold for every premiss $\Gamma _{i}$ of an inference $(\wedge ),(\vee ),(\exists _{1}),(\forall _{2})$ or (Cut) with a cut formula having grade < ϱ, and conclusion $\Gamma$, then

  

• 6. If

  

  holds for some $\alpha _{0}\lhd \alpha$ and a non-arithmetic formula F(U) (i.e., gr(F(U)) ≥ ω), then

  

• 7. (ω-rule). If

  

  is true for every m < ω, $\forall xA(x) \in \Gamma$, and $\beta \lhd \alpha$, then

  

• 8. ($\Omega$-rule). Let f be a fundamental function satisfying

  • (a) $f(\Omega )\unlhd \alpha,$

  • (b)

    , where $\forall XF(X) \in \Pi _{1}^{1}$, and

  • (c)

    implies

    

    for every set of weak formulas $\Xi$ and $\beta <\Omega$.

  Then

  

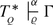
  holds.

Remark 5.12

The derivability relation

is from [13] and is modelled upon the relation

of [3], the main difference being the sequent calculus setting instead of P- and N-forms and a different assignment of cut-degrees. The allowance for transfinite cut-degrees will enable us to deal with arithmetical comprehension.

Remark 5.13

If one ruminates on the definition of the derivability predicate

the question arises whether it is actually a proper inductive definition. The critical point is obviously the condition (c) of the $\Omega$-rule. Note that

occurs negatively in clause (c). However, since $\beta <\Omega$, the pertaining derivation does not contain any applications of the $\Omega$-rule. Thus the definition of

proceeds via an iterated inductive definition. First one defines a derivability predicate without involvement of the $\Omega$-rule via an ordinary inductive definition, and in a second step defines

inductively referring to the first derivability predicate in the $\Omega$-rule.

It will actually be a non-trivial issue how to handle such inductive definitions in a weak background theory.

Lemma 5.14

• 1.
• 2.
• 3.
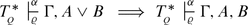
• 4.

  if t and s are equivalent,

• 5.

  for every term s.

• 6. If

  

  and $\mathit{gr}(G(U)) \geq \omega$ , then

  

  .

Proof

Proceed by induction on α. These can be carried out straightforwardly. (5) requires (4). As to (6), observe that $\forall XG(X)$ cannot be the main formula of an axiom. □ 

Lemma 5.15

if $\alpha \geq \mathit{gr}(A(s_{1},\ldots,s_{k}))$ and s _i and t _i are equivalent terms.

Proof

Proceed by induction on gr(A(s ₁, …, s _k )). Crucially note that if gr(A(s ₁, …, s _k )) = ω then $\Gamma,A(s_{1},\ldots,s_{k}),\neg A(t_{1},\ldots,t_{k})$ is an axiom according to Definition 5.11 clause (4). □ 

Lemma 5.16

• 1.
• 2.

Proof

For (1) use induction on m. (2) is an immediate consequence of (1) using Lemma 5.14 (1), the ω-rule, (∨), and $(\forall _{2})$. □ 

Definition 5.17

For formulas F(U) and A(a), F(A) denotes the result of replacing each occurrence of the form e ∈ U in F(U) by A(e). The expression F(A) is a formula if the bound variables in A(a) are chosen in an appropriate way, in particular, if F(U) and A(a) have no bound variables in common.

Lemma 5.18

Suppose $\alpha <\Omega$ and let $\Delta (U) =\{ F_{1}(U),\ldots,F_{k}(U)\}$ be a set of weak formulas such that U doesn’t occur in $\forall XF_{i}(X)\;(1 \leq i \leq k)$ . For an arbitrary formula A(a) we then have:

Proof

Proceed by induction on α. Suppose $\Delta (U)$ is an axiom. Then either $\Delta (A)$ is an axiom too, or

can be obtained through use of Lemma 5.15. Therefore

by Lemma 5.14 (1). If

is the result of an inference, then this inference must be different from $(\exists _{2})$, (Cut), and the $(\Omega -\mathit{rule})$ since $\Delta (U)$ consists of weak formulas, the derivation is cut-free and $\alpha <\Omega$. For the remaining possible inference rules the assertion follows easily from the induction hypothesis. □ 

Lemma 5.19

Let $\Gamma,\forall XF(X)$ be a set of weak formulas. If

and $\alpha <\Omega$ , then

.

Proof

Use induction on α. Note that $\forall XF(X)$ cannot be a principal formula of an axiom, since $\exists X\neg F(X)$ does not surface in such a derivation. Also, due to $\alpha <\Omega$, the derivation doesn’t involve instances of the $\Omega$-rule. Therefore the proof is straightforward. □ 

The role of the $\Omega$-rule in our calculus $T_{\!_{Q}}^{{\ast}}$ is enshrined in the next lemma.

Lemma 5.20

for every arithmetic formula F(U) and arbitrary formula A(a).

Proof

Let $f(\alpha ):= \Omega +\alpha$ with $\mathit{dom}(f):=\{\alpha \in \mathit{OT}(\psi )\!:\alpha \leq \Omega \}.$ Then

(4)

according to Lemma 5.15. For $\alpha <\Omega$ and every set of weak formulas $\Theta$, we have by Lemmas 5.18 and 5.19,

Therefore, by Lemma 5.14 (1),

(5)

The assertion now follows from (4) and (5) by the $\Omega$-rule. □ 

Corollary 5.21

for every arithmetic formula B(a).

Proof

Owing to Lemma 5.20 we have

(6)

As Lemma 5.15 yields

for some k < ω, cutting with (6) yields

. □ 

Corollary 5.22

For every arithmetic relation $\prec$ (parameters allowed) and arbitrary formula A(a) we have

where the quantifiers $\forall \vec{X}\,\forall \vec{x}$ bind all free variables in $\mathrm{WF}(\prec ) \rightarrow \mathrm{TI}(\prec,A)$ .

Proof

By Lemma 5.20 we have

where $^{{\prime}}$ denotes any assignment of free numerical variables to numerals. Hence

by two applications of $(\vee )$. Applying the ω-rule the right number of times followed by the right number of $(\forall _{2})$ inferences, one arrives at the desired conclusion. □ 

5.3 The Reduction Procedure for $T_{\!_{Q}}^{{\ast}}$

Below we follow [13, Section 7].

Lemma 5.23

Let C be a formula of grade ϱ. Suppose C is a prime formula or of either form $\exists XH(X),\;\exists xG(x)$ or A ∨ B. Let $\alpha =\omega ^{\alpha _{1}} + \cdots +\omega ^{\alpha _{k}}$ with $\delta \leq \omega ^{\alpha _{k}} \leq \cdots \leq \omega ^{\alpha _{1}}.$ Then we have

Proof

We proceed by induction on δ.

• 1. Let $\Gamma,C$ be an axiom. Then there are three cases to consider.

• 1.1. $\Gamma$ is an axiom. Then so is $\Delta,\Gamma$. Hence

  

• 1.2. C is a true constant prime formula or negated prime formula. A straightforward induction on α then yields

  

  , and thus

  

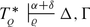
  by Lemma 5.14 (1).

• 1.3. $C \equiv A(s_{1},\ldots,s_{n})$ and $\Gamma$ contains a formula $\neg A(t_{1},\ldots,t_{n})$ where s _i and t _i are equivalent terms. From

  

  one receives

  

  by use of Lemma 5.14 (4). Thence

  

  follows by use of Lemma 5.14 (1), since $\neg A(t_{1},\ldots,t_{n}) \in \Gamma$.

• 2. Suppose $C \equiv A \vee B$ and

  

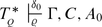
  with $\mathrm{A}_{0} \in \{ A,B\}$ and $\delta _{0}\lhd \delta$. Inductively we get

  

  (7)

  Next use Lemma 5.14 (2) on

  

  to obtain

  

  (8)

  Whence use a cut on (7) and (8) to get the assertion.

• 3. Suppose $C \equiv \exists xG(x)$ and

  

  with $\delta _{0}\lhd \delta$. Inductively we get

  

  (9)

  By Lemma 5.14 (1) and (5), we also get

  

  (10)

  thus (9) and (10) yield

  

  by (Cut).

• 4. Suppose the last inference was $(\exists _{2})$ with principal formula C. Then $C \equiv \exists XH(X)$ and

  

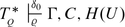
  for some $\delta _{0}\lhd \delta$ and $\mathit{gr}(H(U)) \geq \omega$. Inductively we get

  

  (11)

  By Lemma 5.14 (1) and (6) we also get

  

  (12)

  From (11) and (12) we obtain

  

• 5. Let

  

  be derived by the $\Omega$-rule with fundamental function f. Then the assertion follows from the I. H. by the $\Omega$-rule using the fundamental function α + f.

• 6. In the remaining cases the assertion follows from the I. H. used on the premises and by reapplying the same inference. □ 

Lemma 5.24

Proof

We proceed by induction on α. We only treat the crucial case when

and

, where $\alpha _{0}\lhd \alpha$, and gr(D) = η. Inductively this becomes

and

Since D or $\neg D$ must be one of the forms exhibited in Lemma 5.23, we obtain

by Lemma 5.23. As $\omega ^{\alpha _{0}} +\omega ^{\alpha _{0}}\lhd \omega ^{\alpha }$, we can use Lemma 5.14 (1) to get the assertion. □ 

Theorem 5.25 (Collapsing Theorem)

Let $\Gamma$ be a set of weak formulas. We have

Proof

We proceed by induction on α. Observe that for $\beta <\delta <\Omega$, we always have $\beta \lhd \delta.$

• 1. If $\Gamma$ is an axiom, then the assertion is trivial.

• 2. Let

  

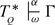
  be the result of an inference other than (Cut) and $\Omega$-rule. Then we have

  

  with $\alpha _{0}\lhd \alpha$ and $\Gamma _{i}$ being the i-th premiss of that inference. $\alpha _{0}\lhd \alpha$ implies $\vartheta \alpha _{0}\lhd \vartheta \alpha$. Therefore

  

  by the I. H., hence

  

  by reapplying the same inference.

• 3. Suppose

  

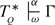
  results by the $\Omega$-rule with respect to a $\Pi _{1}^{1}$-formula $\forall XF(X)$ and a fundamental function f. Then $f(\Omega )\unlhd \alpha$ and

  

  (13)

  and, for every set of weak formulas $\Xi$ and $\beta <\Omega$,

  

  (14)

  The I. H. used on (13) supplies us with

  

  . Hence with $\Xi = \Gamma$ we get

  

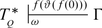  (15)

  from (14). Now Lemma 5.8 ensures that $f(\beta )\lhd f(\Omega )$, where $\beta =\vartheta (f(0))$.

  So using the I. H. on (15), we obtain

  

  (16)

  thus

  

  as $f(\beta )\lhd \alpha$.

• 4. Suppose

  

  and

  

  , where $\alpha _{0}\lhd \alpha$ and $\mathit{gr}(A) <\omega$. Inductively we then get

  

  and

  

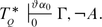
  Let $\mathit{gr}(A) = n - 1$. Then (Cut) yields

  

  (17)

  with $\beta _{1} = (\vartheta \alpha _{0}) + 1$. Applying Lemma 5.24, we get

  

  , and by repeating this process we arrive at

  

  where $\beta _{k+1}:=\omega ^{\beta _{k}}\;(1 \leq k <n)$. Since $\vartheta \alpha _{0} <\vartheta \alpha$, we have $\beta _{n} <\vartheta \alpha;$ thus,

  

   □ 

5.4 Embedding $\mathcal{D}_{Q}$ into $T_{\!_{Q}}^{{\ast}}$

Assuming that $\mathcal{D}_{Q}$ is well-founded tree, the objective of this section is to embed $\mathcal{D}_{Q}$ into $T_{\!_{Q}}^{{\ast}}$, so as to obtain a contradiction. Let $\mathfrak{X}$ be the Kleene–Brouwer ordering of $\mathcal{D}_{Q}$. We write

if $\Gamma$ is the sequent attached to the node τ in $\mathcal{D}_{Q}$.

Theorem 5.26

.

Proof

We proceed by induction on τ, i.e., the Kleene–Brouwer ordering of $\mathcal{D}_{Q}$.

Suppose τ is an end-node of $\mathcal{D}_{Q}$. Then $\Xi$ must be axiomatic and therefore is an axiom of $T_{\!_{Q}}^{{\ast}}$, and hence

.

Now assume that τ is not an end-node of $\mathcal{D}_{Q}$. Then $\Xi$ is not axiomatic.

If $\Xi$ is not reducible, then there is a node τ ₀ immediately above τ in $\mathcal{D}_{Q}$ such that

for some i. Inductively we have

for some k ₀ < ω. We also have

and, using Corollaries 5.21 (if i = 0) and 5.22 (if i > 0),

. Thus, noting that $\Omega \cdot 2 +\omega \lhd \mathfrak{E}_{\tau _{0}} + k_{0}$, and by employing two cuts we arrive at

for some n < ω. By Lemma 5.24 we get

, and hence

since $\omega _{n}(\mathfrak{E}_{\tau _{0}} + k_{0} + 2)\lhd \mathfrak{E}_{\tau }$.

Now suppose that $\Xi$ is reducible. $\Xi$ will be of the form

$$\displaystyle{\Xi ^{{\prime}},\,E,\,\Xi ^{{\prime\prime}}}$$

where E is not a literal and $\Xi ^{{\prime}}$ contains only literals.

First assume E to be of the form $\forall x\,F(x)$. Then, for each m, there is a node τ _m immediately above τ in $\mathcal{D}_{Q}$ such that

for some i. Inductively we have

for all m, where k _m  < ω. We also have

and, using Lemma 5.22,

. Thus, noting that $\Omega \cdot 2 +\omega \lhd \mathfrak{E}_{\tau _{m}} + k_{m}$, and by employing two cuts there is an n such that

holds for all m. By Lemma 5.24 we get

for all m. Whence

since $\omega _{n}(\mathfrak{E}_{\tau _{m}} + k_{m} + 2)\lhd \mathfrak{E}_{\tau }$. A final application of the ω-rule yields

i.e.,

.

If E is a redex of another type but not of the form $\exists XB(X)$ with B(U) arithmetic, then one proceeds in a similar way as in the previous case.

Now assume E to be of the form $\exists X\,B(X)$ with B(U) arithmetic. Then there is a node τ ₀ immediately above τ in $\mathcal{D}_{Q}$ such that

for some i and set variable U. Inductively we have

for some k ₀ < ω. We also have

and, using Lemma 5.22,

. Thus, noting that $\Omega \cdot 2 +\omega \lhd \mathfrak{E}_{\tau _{0}} + k_{0}$, and by employing two cuts there is an n such that

By Lemma 5.24 we get

(18)

Lemma 5.20 yields

(19)

Cutting B(U) and $\neg B(U)$ out of (18) and (19) we arrive at

Since $\omega _{n}(\mathfrak{E}_{\tau _{0}} + k_{0} + 2) + 1\lhd \mathfrak{E}_{\tau }$ we get

, i.e.,

. □ 

Below ∅ stands for the empty sequent and τ ₀ denotes the bottom node of $\mathcal{D}_{Q}$ which is the maximum element of the pertaining Kleene–Brouwer ordering.

Corollary 5.27

If $\mathcal{D}_{Q}$ is well-founded, then

for some n,m < ω.

Proof

We have

. Thus there is a k < ω such that

holds by Theorem 5.26. We also have

and, using Corollary 5.22,

. Thus, noting that $\Omega \cdot 2 +\omega \lhd \mathfrak{E}_{\tau _{0}} + k$, and by employing two cuts we arrive at

for some n < ω. Via Lemma 5.24 we deduce

, so that by Theorem 5.25 we conclude

with $m = k + 2$. □ 

Corollary 5.28

$\mathcal{D}_{Q}$ is not well-founded.

Proof

If $\mathcal{D}_{Q}$ were well-founded, we would have

(20)

for some n, m < ω by Corollary 5.27. But a straightforward induction on $\alpha <\Omega$ shows that

yielding that (20) is impossible. □ 

It remains to show that the result of Corollary 5.28 is provable in $\mathbf{ACA}_{0}$ from

$$\displaystyle{\forall \mathfrak{X}\,(\mathrm{WO}(\mathfrak{X}) \rightarrow \mathrm{WO}(\vartheta _{\mathfrak{X}}))\,.}$$

Let S be the theory ACA ₀ plus the latter axiom. The main issue is how to formalize the derivability predicate

in the background theory S. We elaborated earlier in Remark 5.13 that this seems to require an iterated inductive definition, something apparently not available in S. However, all we need is a fixed point not a proper inductive definition, i.e., to capture the notion of derivability in $T_{\!_{Q}}^{{\ast}}$ without the $\Omega$-rule it suffices to find a predicate $\mathcal{D}$ of α, ρ, Γ such that

• (*) $\mathcal{D}(\alpha,\rho,\Gamma )$ if and only if $\alpha \in \vert \vartheta _{\mathfrak{X}}\vert$, $\rho \leq \omega +\omega$, $\Gamma$ is a sequent, and either $\Gamma$ contains an axiom of $T_{\!_{Q}}^{{\ast}}$ or $\Gamma$ is the conclusion of an inference of $T_{\!_{Q}}^{{\ast}}$ other than $(\Omega )$ with premisses $(\Gamma _{i})_{i\in I}$ such that for every i ∈ I there exists $\beta _{i}\lhd \alpha$ with $\mathcal{D}(\beta _{i},\rho,\Gamma _{i})$, and if the inference is a cut it has rank < ρ.

• (*) can be viewed as a fixed-point axiom which together with transfinite induction for $\vartheta _{\mathfrak{X}}$ defines $T_{\!_{Q}}^{{\ast}}$-derivability (without $(\Omega )$-rule) implicitly.

How can we find a fixed point as described in (∗)? As it turns out, it follows from [12] that S proves that every set is contained in a countable coded ω-model of the theory $\mathbf{ATR}_{0}$. It is also known that ATR ₀ proves the $\Sigma _{1}^{1}$ axiom of choice, $\Sigma _{1}^{1}\mbox{ -}\mathbf{AC}$ (see [17, Theorem V.8.3]). Moreover, in $\mathbf{ACA}_{0} + \Sigma _{1}^{1}\mbox{ -}\mathbf{AC}$ one can prove for every P-positive arithmetical formula A(u, P) that there is a $\Sigma _{1}^{1}$ formula F(u) such that $\forall x[F(x) \leftrightarrow A(x,F)]$, where A(x, F) arises from A(x, P) by replacing every occurrence of the form P(t) in the first formula by F(t). This is known as the Second Recursion Theorem (see [2, V.2.3]). Arguing in S, we find a countable coded ω model $\mathfrak{B}$ with $\mathfrak{X} \in \mathfrak{B}$ such that $\mathfrak{B}$ is a model of ATR. As a result, there is a predicate $\mathcal{D}$ definable in $\mathfrak{B}$ that satisfies (∗). As a result, $\mathcal{D}$ is a set in S. To obtain the full derivability relation

we have to take the $\Omega$-rule into account. We do this by taking a countable coded ω-model $\mathfrak{C}$ of $\mathbf{ATR}$ that contains both $\mathfrak{X}$ and $\mathcal{D}$. We then define an appropriate fixed point predicate $\mathcal{D}_{\Omega }$ using the clauses for defining

and $\mathcal{D}$ for the negative occurrences in the $\Omega$-rule.

The upshot is that we can formalize all of this in $\mathbf{S}$.

Remark 5.29

When giving talks about the material of this article, the first author was asked what the proof-theoretic ordinal of the theories that Theorem 1.7 is concerned with might be. He conjectures that it is the ordinal

$$\displaystyle{\vartheta (\varphi 2(\Omega + 1))}$$

(or $\psi (\varphi 2(\Omega + 1))$ in the representation system based on the ψ-function; see [13, Section 3]), i.e. the collapse of the first fixed point of the epsilon function above $\Omega$.