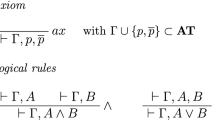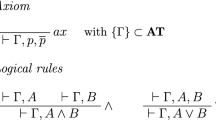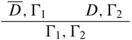Cut Elimination In Situ

Abstract

We present methods for removing top-level cuts from a sequent calculus or Tait-style proof without significantly increasing the space used for storing the proof. For propositional logic, this requires converting a proof from tree-like to dag-like form, but at most doubles the number of lines in the proof. For first-order logic, the proof size can grow exponentially, but the proof has a succinct description and is polynomial time uniform. We use direct, global constructions that give polynomial time methods for removing all top-level cuts from proofs. By exploiting prenex representations, this extends to removing all cuts, with final proof size near-optimally bounded superexponentially in the alternation of quantifiers in cut formulas.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Gentzen’s technique of cut elimination, together with the closely related normalization, is arguably the most important construction of proof theory. The importance of cut elimination lies partly in its connections to constructivity, and indeed cut elimination is algorithmic and can be carried out effectively. The present paper focuses on algorithms for cut elimination in the setting of pure propositional logic and pure first-order logic. We introduce methods for removing top-level cuts from a proof without significantly increasing the space used for generating the proof. Of course, it is well known that eliminating top-level cuts can make proof size grow exponentially, so it requires some special care to describe the resulting proof without any significant increase in space. For propositional logic, our methods require converting a proof from tree-like to dag-like form, but at most double the number of lines in the proof. For first-order logic, the proof size can grow exponentially; in fact, both the number of lines in the proof and the size of the terms can grow exponentially. However, our constructions give polynomial size dag representations for the terms, and succinct descriptions of the proof that give a polynomial time uniform description of the proof and its terms.

Along with the small space usage, our cut elimination methods give direct, global constructions. We define direct, concrete descriptions of the proof that results from eliminating the top-level cuts. Our construction is “global” in that it operates on the entire proof and eliminates all top-level cuts at once.

Our constructions synthesize and generalize a number of prior results from proof complexity and continuous cut elimination. Our immediate motivation arose from the desire to find global versions of the polynomial time algorithms for the continuous cut elimination used by Aehlig-Beckmann [1] and Beckmann-Buss [4]. Continuous cut elimination was developed by Mints [11, 12] for the analysis of higher order logics, and [1] introduced its use for the analysis of bounded arithmetic. In particular, [1, 4] required polynomial time constructions of proofs. Like Mints, they create proofs step-by-step and use a special Rep (for “repetition” or “repeat”) inference to slow down the construction of proofs. In contrast, we shall give direct (not step-by-step) constructions, and avoid the use of a Rep inference.

There is extensive prior work giving upper bounds on the complexity of cut elimination in propositional and first-order logic, including [2, 5–8, 13, 14, 16–18]. Some of the best such bounds measure the complexity of proofs in terms of the height of proofs [5, 7, 13, 16–18]. Loosely speaking, these results work by removing top-level connectives from cut formulas, at the cost of exponentiating the height of the proof, and repeating this to remove all cuts from a proof. Zhang [17] and Gerhardy [7] bound the height of cut free proofs in terms of the nesting of quantifiers in cut formulas; namely, if quantifiers are nested to depth d without any intervening propositional connectives, then cut elimination requires a height increase of only an exponential stack of 2’s of height d + 2. They further show that cut-elimination can remove a top-level block of $\exists$ and ∨ (respectively, $\forall$ and ∧) connectives at the cost of a single exponential increase in proof height.

In contrast, the present paper works with proof size rather than proof height. Somewhat counterintuitively, blocks of arbitrarily nested $\exists$ and ∧ connectives (respectively, $\forall$ and ∨ connectives) can be removed all at once, with a single exponential increase in proof size.

Krajíček [9, 10], Razborov [15], and Beckmann-Buss [3] have given complexity bounds for reducing the depth (alternation of ∨’s and ∧’s) of formulas in constant depth propositional Frege or Tait-style proofs. Reducing the depth of formulas in a proof is essentially equivalent to removing the outermost blocks of like (propositional) connectives from cut formulas. Krajíček [9] and later Beckmann and Buss [3] show that the depth of formulas in a constant depth proof can be reduced from d + 1 to d at the cost of converting the proof from tree-like format to dag-like format with only a polynomial increase in proof size. Our Theorem 3 below is similar to Lemma 6 of [3] in this regard, but gives a more explicitly uniform construction, and works even if there are multiple nested outermost like quantifiers that need to be eliminated.

This paper deals with cut elimination for a Tait-style calculus instead of a Gentzen sequent calculus. In the setting of classical logic, our results all apply immediately to cut elimination in a Gentzen sequent calculus.¹ We assume the reader has some familiarity with sequent calculi or Tait calculi, but Sect. 2 begins with formal definitions of our Tait-style proof system, including definitions of proof size and cut formula complexity. It also describes the basic ideas behind the later constructions. Section 3 shows that, for tree-like propositional proofs, outermost like connectives in cut formulas can be removed at the cost of converting the proof to dag-like form, while at most doubling the number of lines in the proof. Sections 4 and 5 extend this to first-order logic, but now, instead of forming a dag-like proof of the same size, the number of lines in the proof can become exponentially larger. However, the exponentially long proof still has a direct, global, polynomial-time specification. For expository purposes, Sect. 4 first shows how to eliminate all top-level like quantifiers from cut formulas. Section 5 then combines the earlier constructions to show how to eliminate all outermost $\forall$ and ∨ connectives. In light of the duality of the Tait calculus, this is the same as removing all top-level $\exists$ and ∧ connectives. Our constructions use direct methods that reduce the cut-formula complexity for multiple cuts simultaneously.

So far, we have discussed only the problem of removing the top-level connectives from cut formulas. Obviously, the process could be iterated to remove all cuts. Define the alternating quantifier depth of a formula as the maximum number of alternating blocks of existential and universal quantifiers along any branch in the tree representation of the formula (with negations pushed to the atoms, but allowing ∧ and ∨ connectives to appear arbitrarily along the branch). Let $\mathrm{\mathsf{aqd}}(P)$ be the maximum alternating quantifier depth of any cut formula in the proof P. Section 6 proves that it is possible to convert P into a cut free proof of the same end cedent, with the size of P bounded by 2 _d ^| P | for $d =\mathrm{ \mathsf{aqd}}(P) + O(1)$. Here | P | is the number of lines in P, and the superexponential function 2 _d ^a is defined by 2₀ ^a = a and $2_{i+1}^{a} = 2^{2_{i}^{a} }$. This improves on what can be obtained straightforwardly using the constructions of Sects. 3–5 or from the prior bounds obtained by Zhang [17], Gerhardy [7], and Beckmann and Buss [5], since we bound the height of the stack of two’s in terms of the number of alternations of quantifiers without regard to intervening ∧’s or ∨’s. The basic idea for the proof in Sect. 6 is to first modify P so that all cut formulas are in prenex form, and then apply the results of Sect. 4. The results of Sect. 6 do not depend on either Sects. 3 or 5; but we do appeal to constructions of [5, 7, 17] to handle removing cuts on quantifier free formulas.

2 Preliminaries

2.1 Tait Calculus

Our first-order Tait system uses logical connectives ∧, ∨, $\exists$ and $\forall$, and a language of function symbols, constant symbols, and predicate symbols. Terms and atomic formulas are defined as usual. A literal is either an atomic formula $P(\vec{s})$ or a negated atomic formula $\overline{P(\vec{s})}$. Formulas are formed using connectives ∧, ∨, $\forall$ and $\exists$. The negation of complex formulas is inductively defined by defining $\overline{(\overline{p})}$, $\overline{B \wedge C}$, $\overline{B \vee C}$, $\overline{(\exists x)A}$, and $\overline{(\forall x)A}$ to be the formulas p, $\overline{B} \vee \overline{C}$, $\overline{B} \wedge \overline{C}$, $(\forall x)\overline{A}$, and $(\exists x)\overline{A}$, respectively.

We adopt a convention from the Gentzen sequent calculus and assume that first-order variables come in two sorts: free variables (denoted with letters a, b, c, …) and bound variables (denoted with letters x, y, …). Free variables cannot be quantified and must appear only freely. A bound variable x may occur in formulas only within the scope of a quantifier $(\forall x)$ or $(\exists x)$ that binds it.

A line of a Tait calculus proof, called a cedent, consists of a set of formulas. The intended meaning of a cedent is the disjunction of its members. The allowable rules of inference are shown in Fig. 1. It should be noted that an initial cedent $A,\overline{A}$ must have A atomic. We allow Tait proofs to be either tree-like or dag-like. The usual conditions for eigenvariables apply to $\forall$ inferences. The formulas introduced in the lower cedents of inferences are called the principal formula of the inference: these are the formulas A ∧ B, A ∨ B, $(\exists x)A(x)$, and $(\forall x)A(x)$ in Fig. 1. The formulas eliminated from the upper cedent are called auxiliary formulas: these are the formulas A, B, A(s), A(b), A, and $\overline{A}$ in the figure. The auxiliary formulas of a cut inference are called cut formulas. Formulas that appear in the sets $\Gamma$ and Γ _i are called side formulas.

Fig. 1

The rules of inference for a Tait system. The lines of the proof are to be interpreted as sets of formulas. The formula A of the axiom rule must be atomic. The free variable b of the $\forall$ inference is called an eigenvariable and may not occur in the lower cedent

The ∧ and cut inferences have two cedents as hypotheses, which are designated the left and right upper cedents. For a cut inference, we require that the outermost connective of the left cut formula A not be an ∧ or $\exists$ connective; equivalently, the outermost connective of the right cut formula $\overline{A}$ is not ∨ or $\forall$. This restriction on A’s outermost connective causes no loss of generality, since the order of the upper cedents can always be reversed. (We sometimes display cuts with upper cedents out of order, however.) For an ∧ inference, the left–right order of the upper cedents is dictated by the order of the conjunction; except in the case where A and B are the same formula, and then the upper cedents are put in some arbitrary left–right order.

The left–right ordering of upper cedents allows us to define the postordering of the cedents of a tree-like proofs. The postordering of the nodes of a tree T is the order of the nodes output by the following recursive traversal algorithm: Starting at the root of T, the traversal algorithm first recursively traverses the child nodes in left-to-right order, and then outputs the root node. The postorder traversal of the underlying proof tree induces an ordering of the cedents in the proof.

Axioms (initial cedents) and weakening inferences are ignored when measuring the size or height of P. Thus, the size, | P | , of a Tait proof P is defined as the number of ∨, ∧, $\forall$, $\exists$, and cut inferences in P. The height, h(P), of P is the maximum number of these kinds of inferences along any branch of P.

The fact that cedents are sets rather than multisets or sequences means that if a formula is written twice on a line, it appears only once in the cedent. For instance, in the ∨ inference, it is possible that A ∨ B is a member of $\Gamma$. It is also possible that A (say) appears in $\Gamma$, in which case both A and A ∨ B appear in the conclusion of the inference. This latter possibility, however, makes our analysis of cut elimination more awkward, since we will track occurrences of formulas along paths in the proof tree. The problem is that there will be an ambiguity about how to track the formula A in the case where it “splits into two,” for example in an ∨ inference by both being a member of $\Gamma$ and being used to introduce A ∨ B. The ambiguity can be avoided by considering proofs that satisfy the following “auxiliary condition”:

Definition

A Tait proof P satisfies the auxiliary condition provided that no inference has an auxiliary formula also appearing as a side formula. Specifically, referring to Fig. 1, the auxiliary condition requires the following to hold:

• (a) In an ∨ inference, neither A nor B may occur in $\Gamma$.

• (b) In an ∧ inference, neither A nor B may occur in Γ ₁ or Γ ₂.

• (c) In an $\exists$ inference, A(s) may not occur in $\Gamma$.

• (d) In a cut inference, neither A nor $\overline{A}$ may occur in Γ ₁ or Γ ₂.

Note that the eigenvariable condition already prevents A(b) from occurring in the side formulas of a $\forall$ inference.

Lemma 1

Let P be a [tree-like] Tait proof. Then there is a [tree-like] Tait proof  $P^{{\prime}}$ satisfying the auxiliary condition proving the same conclusion as P. Furthermore, $\vert P^{{\prime}}\vert \leq \vert P\vert$ and $h(P^{{\prime}}) \leq h(P)$ .

The proof of the lemma is straightforward using the fact that weakening inferences do not count towards proof size or height.

A path in a proof P is a sequence of one or more cedents occurring in P, with the (i + 1)st cedent a hypothesis of the inference inferring the ith cedent, for all i. A branch is a path that starts at the conclusion of P and ends at an initial cedent.

Suppose P is tree-like and satisfies the auxiliary condition. Also suppose a formula A occurs in two cedents C ₁ and C ₂ in P, and let A ₁ and A ₂ denote the occurrences of A in C ₁ and C ₂, respectively. We call A ₁ a direct ancestor of A ₂ (equivalently, A ₂ is a direct descendant of A ₁) provided there is a path in P from C ₂ to C ₁ such that the formula A appears in every cedent in the path.² If A ₁ is the principal formula of an inference, or occurs in an axiom, that we say A ₁ is a place where A ₂ is introduced. If A ₂ is an auxiliary formula, then we say A ₂ is the place where A ₁ is eliminated. In view of the tree-like property of P, every formula occurring in P either has a unique place where it is eliminated or has a direct descendant in the conclusion of P. However, due to the implicit use of contraction in the inference rules, formulas occurring in P may be introduced in multiple places.

The notions of direct descendant and direct ancestor can be generalized to “descendant” and “ancestor” by tracking the flow of subformulas in a proof. If $\mathcal{I}$ is an ∧, ∨, $\exists$, or $\forall$ inference, then the principal formula of $\mathcal{I}$ is the (only) immediate descendant of each auxiliary formula of $\mathcal{I}$. Then, the “descendant” relation is the reflective, transitive closure of the union of the immediate descendant and direct descendant relations. Namely, a formula $A^{{\prime}}$ occurring in P is a descendant of a formula A occurring in P iff there is a sequence of formula occurrences in P, starting with A and ending with $A^{{\prime}}$ such that each formula in the sequence is the immediate descendant or a direct descendant of the previous formula in the sequence. We also call A an ancestor of $A^{{\prime}}$.

The definitions of descendant and ancestor apply to formulas that appear in cedents. Similar notions also apply to subformulas. Suppose A and B are formulas appearing in cedents with B a descendant of A. Let C be a subformula of A. We wish to define a unique subformula D of B, such that C corresponds to D. This unique subformula is intended to be defined in the obvious way, with each subformula in an upper cedent of an inference corresponding to a subformula in the lower sequent. Assume P is tree-like and satisfies the auxiliary condition. The “corresponds” relation is defined by taking the reflexive, transitive closure of the following conditions.

• The formula A(s) in an $\exists$ inference corresponds to the subformula A(x) in the lower sequent.

• In a $\forall$ inference, the formula A(b) corresponds to the subformula A(x).

• In an ∧ or ∨ inference, the formulas A and B in the upper cedent(s) correspond to the subformulas A and B shown in the lower cedent. Except for an ∨ inference in which A and B are the same formula, the auxiliary formula corresponds to the subformula denoted A in the lower cedent. That is, in this case, the ∨ inference is treated as if it were defined as

  

• If C is a subformula of a side formula, namely of a formula A in $\Gamma$, Γ ₁, or Γ ₂ in Fig. 1, then C corresponds to the same subformula of the occurrence of A in the lower cedent.

• If A and B appear in the upper and lower cedent of an inference and A corresponds to B and if C is the ith subformula of A, then C corresponds to the ith subformula D of B, where the subformulas of C and D are ordered (say) according to the left-to-right positions of their principal connectives.

It is often convenient to assume proofs use free variables in a controlled fashion. The following definition is slightly weaker than the usual definition, but suffices for our purposes.

Definition

A proof P is in free variable normal form provided that each free variable b is used at most once as an eigenvariable, and provided that when b is used as an eigenvariable for inference $\mathcal{I}$, then b appears in P only above $\mathcal{I}$ (that is, each occurrence of b occurs in a cedent reachable from $\mathcal{I}$ by some path in P). The variables c that appear in P but are not used as eigenvariables are called the parameter variables of P.

Any tree-like proof P may be put into free variable normal form without increasing its size or height; furthermore, this can be done while enforcing the auxiliary condition.

2.2 The Basic Constructions

This section describes the basic ideas and constructions used for the cut-elimination results obtained in Sects. 3 and 4.

The first important tool is a generalization of the well-known inversion lemmas for the outermost $\forall$ and ∨ connectives of a formula. Assume we have a tree-like proof P, in free variable normal form, that ends with the cedent Γ, A ∨ B. Then there is a proof $P^{{\prime}}$ of Γ, A, B, with $P^{{\prime}}$ also tree-like, and with $\vert P^{{\prime}}\vert \leq \vert P\vert$ and $h(P^{{\prime}}) \leq h(P)$. Similarly, if P ends with $\Gamma,(\forall x)A(x)$ and t is any term, then there is a proof $P^{{\prime\prime}}$ of Γ, A(t), with $P^{{\prime\prime}}$ also tree-like and satisfying the same conditions on its size and height. The proofs are quite simple: $P^{{\prime}}$ is obtained from P by replacing all direct ancestors of A ∨ B with A, B and removing all ∨ inferences that introduce a direct ancestor of A ∨ B. Likewise, if t does not contain any eigenvariables of P, then $P^{{\prime\prime}}$ is formed by replacing all direct ancestors of $(\forall x)A(x)$ with A(t), and removing the $\forall$ inferences that introduce these direct ancestors and replacing their eigenvariables with t.

Iterating this construction allows us to formulate an inversion lemma that works for the entire set of outermost ∨ and $\forall$ connectives. If B is a subformula of A, we call B an $\vee \forall$ -subformula of A if every connective of A containing B in its scope is an ∨ or a $\forall$. Similarly, a connective ∨ or $\forall$ is said to be $\vee \forall$ -outermost if it is not in the scope of any $\exists$ or ∧ connective. Let P be a tree-like proof of Γ, A, and let B ₁, …, B _k enumerate the minimal $\vee \forall$-subformulas of A in left-to-right order. The subformulas B _i are called the $\vee \forall$ -components of A. Note that each B _i is atomic or has as outermost connective an ∧ or an $\exists$.

Lemma 2

Let P, A, B ₁ ,…,B _k be as above. Let $\sigma$ be any substitution mapping free variables to terms. Then there is a proof $P^{{\prime}}$ of $\Gamma \sigma,B_{1}\sigma,\ldots,B_{k}\sigma$ such that $P^{{\prime}}$ is tree-like and $\vert P^{{\prime}}\vert \leq \vert P\vert$ and $h(P^{{\prime}}) \leq h(P)$ .

The lemma is proved by iterating the inversion lemmas for ∨ and $\forall$.

Section 3 will give the details how to simplify cuts in a propositional Tait calculus proof by removing all outermost ∨ (or, all outermost ∧) connectives from cut formulas. As a preview, we give the idea of the proof, which depends on the inversion lemma for ∨. Namely, suppose the proof P ends with a cut on the formula A ∨ (B ∨ C), as shown in Fig. 2. The right cut formula, in the final line of the subproof R, is in the dual form $\overline{A} \wedge (\overline{B} \wedge \overline{C})$ of course. Now suppose that in the subproof R there are the two pictured ∧  inferences that introduce the formulas $(\overline{B} \wedge \overline{C})$ and then $\overline{A} \wedge (\overline{B} \wedge \overline{C})$.

Fig. 2

A simple example of ∨ cut to be eliminated. Q and R are the subproofs deriving the hypotheses of the cut

By the inversion lemma for ∨, the proof Q can be transformed into a proof $Q^{{\prime}}$ of A, B, C, Γ ₁ with no increase in size or height. The cut in P can thus be removed by replacing the ∧ inferences in R with cuts to obtain the proof $P^{{\prime}}$ shown in Fig. 3. Note that this has replaced the ∧ inference introducing $\overline{B} \wedge \overline{C}$ with two cuts, one on B and one on C, and replaced the ∧ inference introducing $\overline{A} \wedge (\overline{B} \wedge \overline{C})$ with a cut on A. Overall, two ∧ inferences and one cut inference in P have been replaced by three cut inferences in $P^{{\prime}}$. More generally, due to contractions, there can be k ₁ ≥ 1 inferences in P that introduce $\overline{B} \wedge \overline{C}$, and k ₂ ≥ 1 inferences that introduce $\overline{A} \wedge (\overline{B} \wedge \overline{C})$: these k ₁ + k ₂ many ∧ inferences and the cut inference in P are replaced by 2k ₁ + k ₂ many cut inferences in $P^{{\prime}}$. Thus the size of $P^{{\prime}}$ is no more than twice the size of P. The catch though is that $P^{{\prime}}$ may now be dag-like rather than tree-like.

Fig. 3

The proof $P^{{\prime}}$ obtained after eliminating the cut of Fig. 2

Finally, it should be noted that $P^{{\prime}}$ is obtained from P by moving the subproof $Q^{{\prime}}$ and the subproof deriving $\overline{A},\Gamma _{3}$ “rightward and upward” in the proof. This is crucial in allowing us to remove multiple cuts at once. Intuitively, the final cut of P plus all the cuts that lie in the subproofs Q or R can be simplified in parallel without any unwanted “interference” between the different cuts.

Figure 4 shows a proof P from which the outermost ∨ and $\forall$ (dually, ∧ and $\exists$) connectives can be removed from cut formulas. The left subproof Q can be inverted to give a proof $Q^{{\prime}}$ of A(r, s), B(r, t), Γ ₁, and this is used to form the proof $P^{{\prime}}$ shown in Fig. 5. In this simple example, an ∧ inference, three $\exists$ inferences, and the cut inference are replaced by just two cut inferences. As in the ∨ example, the proof $P^{{\prime}}$ is formed by moving (instantiations of) subproofs of P rightward. In particular, the subproof in P ending with $(\exists y)\overline{A(r,y)},\Gamma _{3}$ has become a proof of B(r, t), Γ ₁, Γ ₃ and has been moved rightward in the proof so as to be cut against $\overline{B(r,t)},\Gamma _{6}$.

Fig. 4

A simple example of cuts using ∨ and $\exists$ to be eliminated

Fig. 5

The results of eliminating the cuts in Fig. 4

The general case of removing quantifiers is more complicated, however. For instance, there might be multiple places where the formula $(\exists y)\overline{A(x,y)}$ is introduced, using k ₁ terms $s_{1},\ldots,s_{k_{1}}$. Likewise, there could be k ₂ terms t _j used for introducing the formula $(\exists y)\overline{B(x,y)}$, and k ₃ terms r _ℓ for introducing the $(\exists x)$. In this case we would need k ₁ k ₂ k ₃ many inversions of Q, namely, proofs Q _{i, j, ℓ} of A(r _ℓ , s _i ), B(r _ℓ , t _j ), Γ ₁ for all i ≤ j ₁, j ≤ k ₂, and ℓ ≤ k ₃. The result is that $P^{{\prime}}$ can have size exponential in the size of P; there is, however, still a succinct description of $P^{{\prime}}$ which can be obtained directly from P. This will be described in Sect. 4.

3 Eliminating Like Propositional Connectives

This section describes how to eliminate an outermost block of propositional connectives from cut formulas. The construction applies to proofs in first-order logic.

Definition

Suppose B is a subformula occurring in A. Then B is an ∨-subformula of A iff B occurs in the scope of only ∨ connectives. The notion of ∧-subformula is defined similarly.

An ∨-component (resp., ∧-component) of A is a minimal ∨-subformula (resp., ∧-subformula) of A.

Definition

An $\mbox{ $\vee $/$\wedge $}$-component of a cut formula in P is an ∨-component of a left cut formula in P or an ∧-component of a right cut formula in P.

Theorem 3

Let P be a tree-like Tait calculus proof of  $\Gamma$ . Then there is a dag-like proof  $P^{{\prime}}$ , also of  $\Gamma$ , such that each cut formula of  $P^{{\prime}}$ is an ∨/∧-component of a cut formula of P, and such that $\vert P^{{\prime}}\vert \leq 2 \cdot \vert P\vert$ and hence $h(P^{{\prime}}) \leq 2 \cdot \vert P\vert$ . Furthermore, given P as input, the proof  $P^{{\prime}}$ can be constructed by a polynomial time algorithm.

Note that $P^{{\prime}}$ is obtained by simplifying all the cut formulas in P that have outermost connective ∧ or ∨.

Without loss of generality, by Lemma 1, P satisfies the auxiliary condition. The construction of $P^{{\prime}}$ depends on classifying the formulas appearing in P according to how they descend to cut formulas. For this, each formula B in P can be put into exactly one of the following categories (α)–(γ).

(α) :

B has a left cut formula A as a descendant and corresponds to an ∨-subformula of A, or

(β) :

B has a right cut formula A as a descendant and corresponds to an ∧-subformula of A, or

(γ):

Neither (α) nor (β) holds.

Definition

Let B be an occurrence of a formula in P, and suppose B is in category (β) with a cut formula A as a descendant. The formula A is a conjunction $\mathop{\bigwedge }_{i=1}^{k}C_{i}$ of its k ≥ 1 many ∧-components (parentheses are suppressed in the notation). The formula B is a subconjunction of A of the form $\mathop{\bigwedge }_{i=m}^{\ell}C_{i}$ where 1 ≤ m ≤ ℓ ≤ k. The ∧-components of A to the right of B are C _ℓ+1, …, C _k . The negations of these, namely $\overline{C}_{\ell+1},\ldots,\overline{C}_{k}$, are called the pending implicants for B.

Each formula B in P will be replaced by a cedent denoted ∗(B). For B in category (α), ∗(B) is the cedent consisting of the ∨-components of B. For B in category (β), ∗(B) is the (possibly empty) cedent containing the pending implicants for B. For B in category (γ), ∗(B) is the cedent containing just the formula B.

Definition

The jump target of a category (β) formula B in P is the first cut or ∧ inference below the occurrence of B which has some descendant of B as an auxiliary formula in its right upper cedent. The jump target will be either:

(1)

where the formula D is either equal to B (a direct descendant of B) or is of the form ((⋯(B ∧ B ₁) ∧⋯ ∧ B _k−1) ∧ B _k ) with k ≥ 1 (since only ∧ inferences can operate on B until reaching the jump target). The left upper cedent of the jump target (that is, $\overline{D},\Gamma _{1}$ or C, Γ ₁) is called the jump target cedent. The auxiliary formula of the left upper cedent, that is $\overline{D}$ or C, is called the jump target formula.

We shall consistently suppress parentheses when forming disjunctions and conjunctions. For instance, the formula ((⋯(B ∧ B ₁) ∧⋯ ∧ B _k−1) ∧ B _k ) above would typically be written as just B ∧ B ₁ ∧⋯ ∧ B _k . It should be clear from the context what the possible parenthesizations are.

Lemma 4

Suppose B is category (β) formula in P. Let C ₁ ,…,C _k be as above, so $B = \mathop{\bigwedge }_{i=m}^{\ell}C_{i}$ and the pending implicants of B are $\overline{C}_{\ell+1},\ldots,\overline{C}_{k}$ . Consider B’s jump target, namely one of the inferences shown in (1) , and let E be the jump target formula, that is, either $\overline{D}$ or C. Then ∗(E) is equal to the cedent $\overline{C}_{m},\ldots,\overline{C}_{k}$ .

Proof

If the jump target of B is a cut inference, then D is $\mathop{\bigwedge }_{i=1}^{k}C_{i}$. In this case, $E = \overline{D}$ is the formula $\overline{C}_{1} \vee \cdots \vee \overline{C}_{k}$, and m = 1. It follows that E is category (α), and ${\ast}(E) = \overline{C}_{1},\ldots,\overline{C}_{k}$, so the lemma holds. On the other hand, if the jump target is an ∧ inference, then D equals C _m ∧⋯ ∧ C _r for some r ≤ k, and E = C equals $\mathop{\bigwedge }_{i=j}^{m-1}C_{i}$ for some 1 ≤ j < m. In this case, E is category (β), and ∗(E) again equals $\overline{C}_{m},\ldots,\overline{C}_{k}$. □ 

Proof (of Theorem 3)

The cedents of $P^{{\prime}}$ are formed by modifying each cedent Δ of P to form a new cedent Δ ^∗, called the ∗-translation of Δ. A formula B occurs in or below Δ if it is in Δ or is in some cedent below Δ in P. For each Δ in P, the cedent Δ ^∗ is defined to include the formulas ∗(B) for all formulas B which occur in or below Δ.

Theorem 3 is proved by showing that the cedents Δ ^∗ can be put together to form a valid proof $P^{{\prime}}$. This requires making the following modifications to P: (1) For any inference in P that introduces an ∧-component of a right cut formula, we must insert at that point in $P^{{\prime}}$ a cut on that ∧-component using (the ∗-translation of) its jump target cedent. (2) When forming $P^{{\prime}}$, we remove from P every ∧ inference that introduces an ∧-subformula of a right cut formula, every ∨ inference that introduces an ∨-subformula of a left cut formula, and every cut inference of P. (3) Weakening inferences are added as needed. These changes are described in detail below, where we describe how to combine the cedents Δ ^∗ to form the proof $P^{{\prime}}$. We consider separately each possible kind of inference in P.

For the first case, consider the case where Δ is an initial cedent $B,\overline{B}$. (Surprisingly, this is the hardest case of the proof.) Our goal is to show how the cedent Δ ^∗ is derived in $P^{{\prime}}$. As a first subcase, suppose neither B nor $\overline{B}$ is in category (β), so neither descends to an ∧-component of a right cut formula. Since B is atomic, and B and $\overline{B}$ are each in category (α) or (γ), we have ∗(B) = B and ${\ast}(\overline{B}) = \overline{B}$, respectively. The cedent Δ ^∗ is equal to $B,\overline{B},\Lambda$, where Λ contains the formulas ∗(E) for all formulas E that occur below the cedent $B,\overline{B}$. The proof $P^{{\prime}}$ merely derives $B,\overline{B},\Lambda$ from $B,\overline{B}$ by a weakening inference. (Recall that weakening inferences do not count towards the size or height of proofs.)

For the second subcase, suppose exactly one of B and $\overline{B}$ are in category (β). Without loss of generality, we may assume B is of category (β), and $\overline{B}$ is not. The formula B descends to a right cut formula $\mathop{\bigwedge }_{i=1}^{k}B_{i}$, and corresponds uniquely to one of its ∧-components B _ℓ . We have 1 ≤ ℓ ≤ k, and $\overline{B}_{\ell+1},\ldots,\overline{B}_{k}$ are the pending implicants of B = B _ℓ . Since $\overline{B}$ is atomic and not in category (β), ${\ast}(\overline{B}) = \overline{B} = \overline{B}_{\ell}$. Thus, Δ ^∗ is equal to

$$\displaystyle{ \overline{B}_{\ell+1},\ldots,\overline{B}_{k},\overline{B}_{\ell},\Lambda. }$$

(2)

As before, the cedent Λ is the set of *-translations of formulas that appear below Δ in P.

The jump target for B has the form

(3)

By Lemma 4, the ∗-translation of the upper left cedent has the form

$$\displaystyle{ \overline{B}_{\ell},\ldots,\overline{B}_{k},\Lambda ^{{\prime}} }$$

(4)

where $\Lambda ^{{\prime}}$ contains the formulas ∗(E) for all formulas E occurring in or below the lower cedent of the inference (3). Of course, $\Lambda ^{{\prime}}\subseteq \Lambda$. Thus, in $P^{{\prime}}$, the cedent Δ ^∗ is derived from the cedent (4) by a weakening inference.

In the third subcase, both B and $\overline{B}$ are in category (β). As in the previous subcase, ∗(B) has the form $\overline{B}_{\ell+1},\ldots,\overline{B}_{k}$, and the ∗-translation of its jump target cedent has the form

$$\displaystyle{\overline{B}_{\ell},\ldots,\overline{B}_{k},\Lambda ^{{\prime}}}$$

with B _ℓ  = B. Likewise, ${\ast}(\overline{B})$ has the form $B_{\ell^{{\prime}}+1}^{{\prime}},\ldots,B_{k^{{\prime}}}^{{\prime}}$ and the ∗-translation of $\overline{B}$’s jump target cedent has the form

$$\displaystyle{\overline{B}_{\ell^{{\prime}}}^{{\prime}},\ldots,\overline{B}_{ k^{{\prime}}}^{{\prime}},\Lambda ^{{\prime\prime}}}$$

where $B_{\ell^{{\prime}}}^{{\prime}} = \overline{B}$. These two cedents combine with a cut on the formula B to yield the inference

Since $\Lambda ^{{\prime}},\Lambda ^{{\prime\prime}}\subseteq \Lambda$, the cedent Δ ^∗ is derivable with one additional weakening inference. This completes the argument for the case of an initial cedent. Note that in the first two subcases, the initial cedent is eliminated, while bypassing a cut or ∧ inference. In the third subcase, the initial cedent is replaced with a cut inference on an atomic formula.

For the second case of the proof of Theorem 3, consider a weakening inference

in P. Here, the upper and lower sequents have exactly the same ∗-translations; that is, Γ ^∗ is the same as (Γ, Δ)^∗. Thus the weakening inference can be omitted in $P^{{\prime}}$.

Now consider the case of an ∧ inference in P:

For the first subcase, suppose that A ∧ B is in category (α) or (γ), so ∗(A ∧ B) is just A ∧ B. In this case, A and B are both in category (γ), so also ∗(A) = A and ∗(B) = B. The ∗-translation of the ∧ inference thus becomes

for suitable Λ, and this is still a valid inference. (The formula A ∧ B appears in the upper cedents since the ∗-translations of the cedents A, Γ ₁ and B, Γ ₁ must contain ∗(A ∧ B) = A ∧ B.)

As the second subcase, suppose A ∧ B is category (β), and thus A and B are also category (β). Expressing the formula B as a conjunction of its ∧-components yields B = B ₁ ∧ B ₂ ∧⋯ ∧ B _k for k ≥ 1. Let the pending implicants of A ∧ B be $\overline{C}_{1},\ldots,\overline{C}_{\ell}$ with ℓ ≥ 0. The formula B has the same pending implicants as A ∧ B. Similarly, ∗(A) is $\overline{B}_{1},\ldots,\overline{B}_{k},\overline{C}_{1},\ldots,\overline{C}_{\ell}$. Thus the ∗-translations of the cedents in the ∧ inference become

for suitable Λ. The dashed line is used to indicate that this is no longer a valid inference. However, since the lower cedent is the same as the upper right cedent, this inference can be completely omitted in $P^{{\prime}}$.

Next consider the case of a cut inference in P:

Clearly, A is of category (α), and $\overline{A}$ is of category (β). Since $\overline{A}$ has no pending implicants, ${\ast}(\overline{A})$ is the empty cedent; thus, the ∗-translation of the three cedents has the form

The cut inference therefore can be completely omitted in $P^{{\prime}}$.

Now consider the case of an ∨ inference in P:

There are three subcases to consider. First, if A ∨ B is in category (γ), then so are A and B. The ∗-translation of the two cedents has the form

(5)

This of course is a valid inference, and remains in this form in $P^{{\prime}}$.

The second subcase is when A ∨ B is category (α). Expressing A and B as disjunctions of their ∨-components yields A = A ₁ ∨⋯ ∨ A _k and B = B ₁ ∨⋯ ∨ B _ℓ with k, ℓ ≥ 1. The ∗-translation of the ∨ inference is

and so this inference can be omitted in $P^{{\prime}}$.

The third subcase is when A ∨ B is category (β). In this subcase, A and B are both category (γ). We have ∗(A) = A and ∗(B) = B. And, ∗(A ∨ B) is $\overline{C}_{1},\ldots,\overline{C}_{k}$, where the $\overline{C}_{i}$’s are the pending implicants of A ∨ B, with k ≥ 0. Thus, the ∗-translation of the cedents in the ∨ inference has the form

Of course, this is not a valid inference. Note that the formulas $\overline{C}_{i}$ must be included in the upper sequent since they are part of ∗(A ∨ B). From Lemma 4, the upper left sequent of the jump target of A ∨ B has ∗-translation of the form

$$\displaystyle{\overline{A \vee B},\overline{C}_{1},\ldots,\overline{C}_{k},\Lambda ^{{\prime}},}$$

where $\Lambda ^{{\prime}}\subseteq \Lambda$. The following inferences are used in $P^{{\prime}}$ to replace the ∨ inference:

(6)

This cut is permitted in $P^{{\prime}}$ since A ∨ B is an ∧-component of a right cut formula in P. Note that the ∨ inference in P has been replaced in $P^{{\prime}}$ with two inferences, namely a cut and an ∨ inference.

Now consider the case of a $\forall$ inference in P

This case is handled similarly to the case of an ∨ inference. The formula A(b) is category (γ), so ∗(A(b)) = A(b). If the formula $(\forall x)A(x)$ is category (α) or (γ), then ${\ast}((\forall x)A(x)) = (\forall x)A(x)$. In this case, the ∗-translation of the $\forall$ inference gives

for suitable Λ. This is still a valid inference, and is used as is in $P^{{\prime}}$. Suppose, on the other hand, that $(\forall x)A(x)$ is category (β). In this case, the ∗-translation of the $\forall$ inference has the form

where $\overline{C}_{1},\ldots,\overline{C}_{k}$ are the pending implicants of $(\forall x)A(x)$. Note this is not a valid inference. By Lemma 4, the ∗-translation of the upper left cedent of the jump target of $(\forall x)A(x)$ is equal to

$$\displaystyle{(\exists x)\overline{A(x)},\overline{C}_{1},\ldots,\overline{C}_{k},\Lambda ^{{\prime}},}$$

where $\Lambda ^{{\prime}}\subseteq \Lambda$. The following inferences are used in $P^{{\prime}}$ to replace the $\forall$ inference:

(7)

Note that since P is in free variable normal form, the variable b does not appear in the lower cedent of the new $\forall$ inference. The $\forall$ inference in P has been replaced in $P^{{\prime}}$ with two inferences: a cut and a $\forall$ inference.

The case of an $\exists$ inference in P is handled in exactly the same way as a $\forall$ inference. We omit the details.

The above completes the construction of $P^{{\prime}}$ from P. By construction, the inferences in $P^{{\prime}}$ are valid. To verify that $P^{{\prime}}$ is globally a valid proof, we need to ensure that it is acyclic, so there is no chain of inferences that forms a cycle. This follows immediately from the fact that the inferences in $P^{{\prime}}$ respect the postorder traversal of P. In particular, the upper left cedent of the jump target of a formula B comes before the cedent containing B in the postorder traversal of P. Therefore, $P^{{\prime}}$ is well founded.

It is clear that $P^{{\prime}}$ can be constructed in polynomial time from P. The size of $P^{{\prime}}$ can be bounded as follows. First, each initial sequent in P can add at most one cut inference to $P^{{\prime}}$. Each ∧ inference in P can become at most one ∧ inference in $P^{{\prime}}$. Each ∨, $\forall$, and $\exists$ inference in P can become up to two inferences in $P^{{\prime}}$. Each cut in P is replaced, at least locally, by zero inferences in $P^{{\prime}}$. Let $n_{\text{Ax}}$, $n_{\text{Cut}}$, n _∧, n _∨, $n_{\forall }$, and $n_{\exists }$ denote the numbers of initial sequents, cuts, ∧, ∨, $\forall$, and $\exists$ inferences in P. Then | P | equals $n_{\text{Cut}} + n_{\wedge } + n_{\vee } + n_{\forall } + n_{\exists }$, and $\vert P^{{\prime}}\vert$ is bounded by $n_{\mathrm{Ax}} + n_{\wedge } + 2(n_{\vee } + n_{\forall } + n_{\forall } + n_{\exists })$. Since w.l.o.g. there is at least one cut in P and since $n_{\mathrm{Ax}} = n_{\text{Cut}} + n_{\wedge } + 1$, it follows that $\vert P^{{\prime}}\vert \leq 2 \cdot \vert P\vert$. Q.E.D. Theorem 3. □ 

4 Eliminating Like Quantifiers

We next show how to eliminate the outermost block of quantifiers from cut formulas.

Definition

An $\exists$ -subformula (resp., $\forall$ -subformula) of A is a subformula that is contained in the scope of only $\exists$ (resp., $\forall$) quantifiers. An $\exists$ -component (resp., $\forall$ -component) of A is a minimal $\exists$- or $\forall$-subformula (respectively). A $\mbox{ $\forall $/$\exists $}$ -component of a cut formula in P is a $\forall$-component of a left cut formula in P or an $\exists$-component of a right cut formula in P.

Theorem 5

Let P be a tree-like Tait calculus proof of  $\Gamma$ . Then there is a dag-like proof  $P^{{\prime}}$ , also of  $\Gamma$ , such that each cut formula of  $P^{{\prime}}$ is a $\mbox{ $\forall $/$\exists $}$ -component of a cut formula of P, and such that $\vert P^{{\prime}}\vert \leq 4^{\vert P\vert /5} \leq (1.32)^{\vert P\vert }$ and $h(P^{{\prime}}) \leq \vert P\vert$ . As a consequence of the height bound, $P^{{\prime}}$  can also be expressed as a tree-like proof of size ≤ 2 ^|P| . Similarly, $h(P^{{\prime}}) \leq 2^{h(P)}$ .

Without loss of generality, P is in free variable normal form and satisfies the auxiliary condition. Each formula B in P can be put in one of the following categories (α)–(γ):

(α):

B has a left cut formula A as a descendant and corresponds to a $\forall$-subformula of A, or

(β):

B has a right cut formula A as a descendant and corresponds to an $\exists$-subformula of A, or

(γ):

Neither (α) nor (β) holds.

Definition

An $\exists$ inference as shown in Fig. 1 is critical if the auxiliary formula A(s) does not have an $\exists$ as its outermost connective. The formula A(s) is also referred to as $\exists$ -critical. If A(s) is furthermore of category (β), then the $\exists$ -jump target of A(s) is the cut inference which has a descendant of A(s) as a (right) cut formula. The $\exists$ -jump target cedent of A(s) is the upper left cedent of the jump target of A(s). This is also referred to as the $\exists$-jump target cedent of the cedent Δ containing A(s).

We now come to the crucial new definition for handling cut elimination of outermost like quantifiers. The intuition is that we want to trace, through the proof P, a possible branch in the proof $P^{{\prime}}$. Along with this traced out path, we also need to keep a partial substitution assigning terms to variables: this substitution will track the needed term substitution for forming the corresponding cedent in $P^{{\prime}}$. First we define an “$\exists$-path” and then we define the associated substitution.

Definition

A cut inference is called to-be-eliminated if the outermost connective of the cut formula is a quantifier. An $\exists$ -path π through P consists of a sequence of cedents Δ ₁, Δ ₂,…, Δ _m from P such that Δ ₁ is the endsequent of P and such that for each i < m, one of the following holds:

• Δ _i is the lower cedent of a to-be-eliminated cut inference, and Δ _i+1 is its right upper cedent, or

• Δ _i is the lower cedent of an inference other than a to-be-eliminated cut, and Δ _i+1 is an upper cedent of the same inference, or

• Δ _i  is the upper cedent of an $\exists$-critical inference, and Δ _i+1 is the $\exists$-jump target cedent of Δ _i .

The $\exists$-path is said to lead to Δ _m .

It is easy to verify that, for Δ _i in π, the $\exists$-path π contains every cedent in P below Δ _i .

The cedents in an $\exists$-path are in reverse postorder from P. The effect of an $\exists$-path is to repeatedly traverse up to an $\exists$-critical inference—always going rightward at to-be-eliminated cuts—and then jump back down to the associated $\exists$-jump target cedent. The most important information needed to specify the $\exists$-path is the subsequence of cedents $\Delta _{i_{1}}$, $\Delta _{i_{2}}$,…, $\Delta _{i_{k}}$, i ₁ < i ₂ < ⋯ < i _k which are $\exists$-critical and for which $\Delta _{i_{\ell}+1}$ is the $\exists$-jump target cedent of $\Delta _{i_{\ell}}$. The entire $\exists$-path can be uniquely reconstructed from this subsequence plus knowledge of the last cedent Δ _m in π.

There is a substitution $\sigma _{\pi }$ associated with the $\exists$-path $\pi =\langle \Delta _{1},\ldots,\Delta _{m}\rangle$. The domain of $\sigma _{\pi }$ is the set of free variables appearing in or below Δ _m plus the set of outermost universally quantified variables occurring in the category (α) formulas in Δ _m .

Definition

The definition of $\sigma _{\pi }$ is by induction on the length of π. First, let $(\forall x_{i})\cdots (\forall x_{\ell})A$ be a formula in Δ _m in category (α) with i ≤ ℓ such that A does not have outermost connective $\forall$. Since it is in category (α), this formula has the form $(\forall x_{i})\cdots (\forall x_{\ell})A(b_{1},\ldots,b_{i-1},x_{i},\ldots,x_{\ell})$, and has a descendant of the form $(\forall x_{1})\cdots (\forall x_{\ell})A(x_{1},\ldots,x_{\ell})$ which is the left cut formula of a cut inference. Since the cut is to-be-eliminated, π must reach the upper left cedent by way of a “jump” from an $\exists$-critical cedent Δ _i  ∈ π. As pictured, the associated $\exists$-critical formula must have the form $\overline{A(s_{1},\ldots,s_{\ell})}$:

Note that the terms s ₁, …, s _ℓ are uniquely determined by π, since they are found by following the path from the upper right cedent of the cut inference to the cedent Δ _i , and setting the s _i ’s to be the terms used for $\exists$ inferences acting on the descendants of $A(\vec{s})$.

Let $\pi ^{{\prime}}$ be π truncated to end at $\overline{A(\vec{s}),\Gamma }$. The substitution $\sigma _{\pi }$ is defined to map the bound variables x _i , …, x _ℓ to the terms $s_{i}\sigma _{\pi ^{{\prime}}},\ldots,s_{\ell}\sigma _{\pi ^{{\prime}}}$. (Strictly speaking, the substitution $\sigma _{\pi }$ acts on the occurrences of variables, since the same variable may be used in multiple quantifiers and in different formulas; this is suppressed in the notation, however.)

For b a free variable appearing in or below Δ _m , the value $\sigma _{\pi }(b)$ is defined as follows. If there is a $\forall$ inference, below Δ _m ,

that uses b as an eigenvariable, and if $(\forall x)A(x)$ is category (α), then define $\sigma _{\pi }(b)$ to equal the value of $\sigma _{\pi ^{{\prime}}}(a)$, where $\pi ^{{\prime}}$ is π truncated to end at the lower cedent of the $\forall$ inference. For example, in the proof displayed above, $\sigma _{\pi }(b_{i}) = s_{i}$. Otherwise, if there is no such $\forall$ inference, define $\sigma _{\pi }(b) = b$.

Definition

Let A be a formula appearing in a cedent Δ of P. Let π be an $\exists$-path leading to Δ. Then ∗ _π (A) is defined as follows:

• If A is in category (α) and has the form $A = (\forall x_{1})\cdots (\forall x_{\ell})B$ with ℓ > 0 and B not starting with a $\forall$ quantifier, then define ∗ _π (A) to be the formula $B\sigma _{\pi }$, namely the formula obtained by replacing each x _i with $\sigma _{\pi }(x_{i})$ and each free variable b with $\sigma _{\pi }(b)$.

• If A is in category (β) and has outermost connective $\exists$, then ∗ _π (A) is the empty cedent.

• Otherwise ∗ _π (A) is the formula $A\sigma _{\pi }$, namely obtained by replacing each free variable b with $\sigma _{\pi }(b)$.

For A appearing below Δ, we define ∗ _π (A) to equal ${\ast}_{\pi ^{{\prime}}}(A)$ where $\pi ^{{\prime}}$ is π truncated to end at the cedent $\Delta ^{{\prime}}$ containing A. The ∗ _π -translation, ∗ _π (Δ), of Δ is the cedent containing exactly the formulas ∗ _π (A) for A appearing in or below Δ in P.

We can now give the proof of Theorem 5. The proof $P^{{\prime}}$ will be formed from the cedents ∗ _π (Δ) where Δ ranges over the cedents of P, and π ranges over the $\exists$-paths leading to Δ. The inferences in $P^{{\prime}}$ will respect the postordering of P, and $P^{{\prime}}$ will be a dag.

As before, we must show how to connect up the cedents ∗ _π (Δ) to make $P^{{\prime}}$ into a valid proof. The argument again splits into cases based on the type of inference used to infer Δ in P. The cases of initial cedents, ∨ inferences, ∧ inferences, and weakenings are all immediate. These inferences remain valid after their cedents are replaced by their ∗ _π -translations, since initial cedents contain only atomic formulas, and since the ∗ _π -translations respect propositional connectives.

Consider the case where Δ is inferred by a $\forall$ inference in P:

The $\exists$-path π ends at the lower cedent Δ. Define $\pi ^{{\prime}}$ to be the $\exists$-path that extends π by one step to the upper cedent $\Delta ^{{\prime}}$. If $(\forall x)A(x)$ and A(b) are not in category (α), then $\sigma _{\pi ^{{\prime} }}(b) = b$ and the inference is still valid since the ${\ast}_{\pi ^{{\prime}}}- / {\ast}_{\pi }$-translations of A(b) and $(\forall x)A(x)$ are equal to C(b) and $(\forall x)C(x)$ for C defined by $C(b) = A(b)\sigma _{\pi } = A(b)\sigma _{\pi ^{{\prime}}}$. Thus, in this case, the result is still a valid $\forall$ inference. Otherwise, A(b) and $(\forall x)A(x)$ are both in category (α). In this case, ${\ast}_{\pi }(A(b)) = {\ast}_{\pi }((\forall x)A(x))$; the $\forall$ inference has equal upper and lower cedents and is just omitted from $P^{{\prime}}$.

Now consider the case where Δ is inferred in P with an $\exists$ inference:

Define $\pi ^{{\prime}}$ as in the previous case. If A(s) and $(\exists x)A(x)$ are not in category (β), then the ∗ _π -translation leaves the quantifier on x untouched, and the ${\ast}_{\pi ^{{\prime}}}$-/ ∗ _π -translation of the inference is still a valid inference in $P^{{\prime}}$. Otherwise, both formulas are in category (β). If A(s) has an $\exists$ as its outmost connective, then ${\ast}_{\pi ^{{\prime}}}(A(s))$ and ${\ast}_{\pi }((\exists x)A(x))$ are both empty, and the ${\ast}_{\pi ^{{\prime}}}$- and ∗ _π -translations (respectively) of the upper and lower cedents are identical, and the $\exists$ inference can be omitted in $P^{{\prime}}$. If A does not have an $\exists$ as its outermost connective, then the ${\ast}_{\pi ^{{\prime}}}$-/ ∗ _π -translations of the cedents in the inference are

where Λ contains the formulas ∗ _π (B) for all formulas B, other than A(s), which occur in or below Δ in P. The upper left cedent of the $\exists$-jump target of A(s) has the form

$$\displaystyle{\Gamma _{1},(\forall x_{1})\cdots (\forall x_{\ell})\overline{A(x_{1},\ldots,x_{\ell})},}$$

where x = x _ℓ and A(s) = A(s ₁, …, s _ℓ ) with s corresponding to the term s _ℓ . Let $\pi ^{{\prime\prime}}$ be the $\exists$-path that extends $\pi ^{{\prime}}$ by the addition of this upper left cedent. The ${\ast}_{\pi ^{{\prime\prime}}}$-translation of the upper left cedent has the form

$$\displaystyle{\Lambda _{1},\overline{A(s_{1},\ldots,s_{\ell})}\sigma _{\pi ^{{\prime\prime}}}.}$$

Here $\Lambda _{1} \subseteq \Lambda$, and $\overline{A(s_{1},\ldots,s_{\ell})}\sigma _{\pi ^{{\prime\prime} }}$ is the same as $\overline{{\ast}_{\pi ^{{\prime}}}(A(s))}$. Hence, a cut inference gives

The $\exists$ inference in P is thus replaced with a cut inference in $P^{{\prime}}$, but on a formula of lower complexity than the cut in P.

Finally consider the case of a cut inference in P as shown in Fig. 1 with left cut formula A and right cut formula $\overline{A}$. First suppose it is not a to-be-eliminated cut. Let π ₁ and π ₂ be the $\exists$-paths which extend π by one step to include the upper left or right cedent of the cut, respectively. Then ${\ast}_{\pi _{1}}(A)$ and ${\ast}_{\pi _{2}}(\overline{A})$ are complements of each other, and the cut remains valid in $P^{{\prime}}$. Otherwise, the cut is to-be-eliminated, and π ₂ is again a valid $\exists$-path. The right cut formula $\overline{A}$ is category (β) and has outermost connective $\exists$. Thus ${\ast}_{\pi _{2}}(\overline{A})$ is the empty cedent, so the ${\ast}_{\pi _{2}}$-translation of the right upper cedent and the ∗ _π -translation of the lower cedent are identical. In this case, the cut can be removed completely from $P^{{\prime}}$.

The above completes the construction of $P^{{\prime}}$. The next lemma will be used to bound its size.

Lemma 6

Let Δ be a cedent in P. The number of $\exists$ -paths π to Δ in P is ≤ (1.32) ^|P| .

Proof

Recall that an $\exists$-path π to Δ can be uniquely characterized by its final cedent Δ _m  = Δ and its subsequence $\Delta _{i_{1}},\ldots,\Delta _{i_{k}}$ of cedents which are $\exists$-critical and have $\Delta _{i_{\ell}+1}$ the $\exists$-jump target cedent of $\Delta _{i_{\ell}}$. We will bound the number N of ways to select the $\exists$-critical cedents in this subsequence. For this, we group the $\exists$-critical cedents of P according to their $\exists$-jump target. Let there be m many to-be-eliminated cut inferences in P, and suppose that the ith such cut has n _i  many $\exists$-critical cedents associated with it. The ith cut also has at least one $\forall$ inference associated with it that introduces a $\forall$ quantifier in its left cut formula. Therefore $\vert P\vert \geq \sum _{i=1}^{m}(n_{i} + 2)$. Each $\exists$-path π can jump from at most one of the n _i $\exists$-critical cedents associated with the ith cut. It follows that there are at most $\prod _{i=1}^{m}(n_{i} + 1)$ many $\exists$-paths; namely, there are at most n _i + 1 choices for which one, if any, of ith cut’s associated $\exists$-critical cedents are included in π.

To upper bound the value $N =\prod _{ i=1}^{m}(n_{i} + 1)$, take the logarithm, and upper bound $\sum _{i=1}^{m}\ln (n_{i} + 1)$ subject to $\sum _{i=1}^{m}(n_{i} + 2) \leq \vert P\vert$. For integer values of x, $(\ln x)/(x + 1)$ is maximized at x = 4. Thus, $\ln N \leq \vert P\vert \cdot (\ln 4)/5$; that is, N ≤ | P | ⋅ 4^{| P | ∕5} ≤ (1. 32)^| P |. □ 

The size bound of Theorem 5 follows immediately from the lemma. Namely, $P^{{\prime}}$ contains at most one cedent for each path to each cedent Δ in P, and thus $\vert P^{{\prime}}\vert \leq \vert P\vert \cdot (1.32)^{\vert P\vert }$. The height bound $h(P^{{\prime}}) \leq \vert P\vert$ follows from the construction of P, since paths π traverse cedents of P in reverse postorder, and each ∧, ∨, $\exists$, $\forall$, and cut inference along π contributes at most inference to $P^{{\prime}}$. (Note that cuts contribute an inference only when used as a jump target.) Q.E.D. Theorem 5

The proof $P^{{\prime}}$ was constructed in a highly uniform way from P. Indeed, $P^{{\prime}}$ can be generated with a polynomial time algorithm f that operates as follows: f takes as input a string w of length ≤ | P | many bits, and outputs whether the string w is an index for a cedent Δ _w in $P^{{\prime}}$, and if so, f also outputs: (a) the cedent Δ _w with terms specified as dags, and (b) what kind of inference is used to derive Δ _w , and (c) the index $w^{{\prime}}$ or indices $w^{{\prime}},w^{{\prime\prime}}$ of the cedent(s) from which Δ _w is inferred in $P^{{\prime}}$. For (a), note that the cedent Δ _w can be written out in polynomial length only if terms are written as dags (that is, circuits) rather than as trees (that is, as formulas). This is because the iterated application of substitutions may cause the terms $\sigma _{\pi }(b)$ to be exponentially big when written out as formulas instead of as circuits. Also note that, although some inferences in $P^{{\prime}}$ become trivial and are omitted in $P^{{\prime}}$, we can avoid using Rep inferences in $P^{{\prime}}$ by the simple convention that indices w that would lead to Rep inferences are taken to not be valid indices. (An example of this would be a w encoding an $\exists$-path leading to a to-be-eliminated cut.)

This means of course that there is a polynomial space algorithm that lists out the proof $P^{{\prime}}$.

5 Eliminating and/Exists and or/Forall Blocks

This section gives an algorithm for eliminating outermost blocks of $\mbox{ $\vee $/$\forall $}$ (equivalently, ∧/$\exists$) connectives from cut formulas, where the ∨ and $\forall$ (resp., ∧ and $\exists$) connectives can be arbitrarily interspersed.

Definition

A subformula B of A is an $\vee \forall$ -subformula of A if B is in the scope of only ∨ and $\forall$ connectives. The $\vee \forall$ -components of A are the minimal $\vee \forall$-subformulas of A. The $\wedge \exists$ -subformulas and $\wedge \exists$ -components of A are defined similarly.

An $\vee \forall$/$\wedge \exists$ -component of a cut formula in P is either an $\vee \forall$-component of a left cut formula of P or an $\wedge \exists$-component of a right cut formula of P.

Theorem 7

Let P be a tree-like Tait calculus proof of  $\Gamma$ . Then there is a dag-like proof  $P^{{\prime}}$ , also of  $\Gamma$ , such that each cut formula of  $P^{{\prime}}$ is an $\wedge \exists /\vee \forall$ -component of a non-atomic cut formula of P, and such that $\vert P^{{\prime}}\vert \leq 4^{\vert P\vert /5} \leq (1.32)^{\vert P\vert }$ and $h(P^{{\prime}}) \leq \vert P\vert$ . Consequently, $P^{{\prime}}$  can also be expressed as a tree-like proof of size ≤ 2 ^|P| .

Note that all cuts in P are simplified in $P^{{\prime}}$. The atomic cuts in P are eliminated when forming $P^{{\prime}}$. However, new cuts are added on $\wedge \exists$/$\vee \forall$-components of cuts in P, and some of these might be cuts on atomic formulas. If all cut formulas in P are atomic, then $P^{{\prime}}$ is cut free.

W.l.o.g., P is in free variable normal form and satisfies the auxiliary condition. Each formula B in P can be put in one of the following categories (α)–(γ):

(α):

B has a left cut formula A as a descendant and corresponds to an $\vee \forall$-subformula of A, or

(β):

B has a right cut formula A as a descendant and corresponds to an $\wedge \exists$-subformula of A, or

(γ):

Neither (α) nor (β) holds.

Definition

The jump target of a category (β) formula B occurring in P is the first cut or ∧ inference below the cedent containing B that has some descendant of B as the auxiliary formula D in its right upper cedent. The jump target will again be of the form (1). Its right auxiliary formula D has a unique subformula $B^{{\prime}}$ which corresponds to B. $B^{{\prime}}$ occurs only in the scope of $\exists$ connectives and ∧ connectives, and only in the first argument of ∧ connectives. (The last part holds since otherwise the jump target would be an ∧ inference higher in the proof.) The jump target cedent is defined as before.

Suppose a category (β) formula B has descendant D as the right auxiliary formula of its jump target. Let the $\wedge \exists$-components of D be D _m , …, D _k in left-to-right order. The $\wedge \exists$-components of B in left-to-right order can be listed as B _m , …, B _ℓ , with each B _i corresponding to D _i , with 1 ≤ m ≤ ℓ ≤ k. The formulas $\overline{D}_{\ell+1},\ldots,\overline{D}_{k}$ are the pending implicants of B. The pending quantifiers of B are the quantifiers $(\exists x)$ which appear to the right of the subformula D _ℓ in D and are outermost connectives of $\wedge \exists$-subformulas of D. Let $B^{{\prime}}$ be the subformula of D that corresponds to B; the current quantifiers of B are the quantifiers $(\exists x)$ in D which contain $B^{{\prime}}$ in their scope.

The pending implicants of B will be used similarly as in the proof of Theorem 3, but first we need to define $\wedge \exists$-paths and substitutions $\sigma _{\pi }$ similarly to the proof of Theorem 5. Now, $\sigma _{\pi }$ must also map the pending quantifier variables to terms.

Definition

An upper cedent Δ of an ∧ or $\exists$ inference is critical if the auxiliary formula in Δ is either atomic or has outermost connective ∨ or $\forall$.

Definition

A cut inference in P is non-atomic if its cut formulas are not atomic. An $\wedge \exists$ -path π through P consists of a sequence Δ ₁, …, Δ _m of cedents from P such that Δ ₁ is the end cedent of P and such that, for each i < m, one of the following holds:

• Δ _i is the lower cedent of non-atomic cut inference, and Δ _i+1 is its right upper cedent, or

• Δ _i is the lower cedent of an inference other than a non-atomic cut, and Δ _i+1 is an upper cedent of the same inference, or

• Δ _i  is a critical upper cedent of an ∧ or $\exists$ inference with auxiliary formula A, and Δ _i+1 is the jump target cedent of A.

The next definition of $\sigma _{\pi }$ is more difficult than in the proof of Theorem 5 because the substitution has to act also on the pending implicants of category (β).

Definition

Let π be $\wedge \exists$-path as above. The domain of the substitution $\sigma _{\pi }$ is: the free variables appearing in or below Δ _m , the variables of the $\vee \forall$-outermost quantifiers of each category (α) formula in Δ _m , and the variables of the pending quantifiers of each category (β) formula in Δ _m .³ The definition of $\sigma _{\pi }$ is defined by induction on the length of π. For π containing just the end cedent, $\sigma _{\pi }$ is the identity mapping with domain the parameter variables of P. Otherwise, let $\pi ^{{\prime}}$ be the initial part of π up through the next-to-last cedent Δ _m−1 of π, and suppose $\sigma _{\pi ^{{\prime}}}$ is already defined. There are several cases to consider.

• (a) Suppose Δ _m−1 and Δ _m are the lower cedent and an upper cedent of some inference other than a $\forall$ inference. The $\sigma _{\pi }$ is same as $\sigma _{\pi ^{{\prime}}}$.

• (b) Suppose Δ _m−1 and Δ _m are the lower cedent and an upper cedent of a $\forall$ inference as shown in Fig. 1. If the principal formula $(\forall x)A(x)$ is category (α), then $\sigma _{\pi }$ extends $\sigma _{\pi ^{{\prime}}}$ by letting $\sigma _{\pi }(b) =\sigma _{\pi ^{{\prime}}}(x)$ where $(\forall x)$ is the quantifier introduced by the $\forall$ inference. Otherwise, $\sigma _{\pi }(b) = b$. And, $\sigma _{\pi }$ is equal to $\sigma _{\pi ^{{\prime}}}$ for all other variables in its domain.

• (c) Otherwise, Δ _m is the jump target cedent of Δ _m−1. Suppose the jump target is an ∧ inference

  

  For b a free variable in C, Γ ₁, the value $\sigma _{\pi }(b)$ is defined to equal $\sigma _{\pi ^{{\prime}}}(b)$. Similarly, for any pending quantifier $(\exists x)$ of any category (β) formula in Γ ₁ and for any $\vee \forall$-outermost quantifier $(\forall x)$ of any category (α) formula in Γ ₁, set $\sigma _{\pi }(x) =\sigma _{\pi ^{{\prime}}}(x)$.

  We also must define the action of $\sigma _{\pi }$ on the pending quantifiers of the category (β) formula C. Let D ₁ be the first (leftmost) $\wedge \exists$-component of D. The cedent Δ _m−1 has the form B ₁, Γ ₃ where B ₁ is an ancestor of D and corresponds to D ₁. Write D ₁ = D ₁(x ₁, …, x _j ) where $(\exists x_{1}),\ldots,(\exists x_{j})$ are the current quantifiers for D ₁. Then B ₁ = B ₁(s ₁, …, s _j ) where the s _i ’s are the terms used for $\exists$ inferences acting on descendants of B ₁. The $(\exists x_{i})$’s are pending quantifiers of C, and $\sigma _{\pi }(x_{i})$ is defined to equal $s_{i}\sigma _{\pi ^{{\prime}}}$. The rest of the pending quantifiers of C are the pending quantifiers of B ₁ in the cedent Δ _m−1: for these variables, $\sigma _{\pi }$ is defined to equal the value of $\sigma _{\pi ^{{\prime}}}$.

• (d) Suppose that Δ _m is the left upper cedent of the jump target of Δ _m−1, and the jump target is a cut inference

  

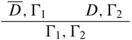
  Let $\pi ^{{\prime}}$ be as before, and set $\sigma _{\pi }(b) =\sigma _{\pi ^{{\prime}}}(b)$ for all free variables of the lower cedent. For any pending quantifier $(\exists x)$ of any category (β) formula in Γ ₁ and for any $\vee \forall$-outermost quantifier $(\forall x)$ of any category (α) formula in Γ ₁, set $\sigma _{\pi }(x) =\sigma _{\pi ^{{\prime}}}(x)$. Now, let D ₁ = D ₁(x ₁, …, x _j ) and B ₁ = B ₁(s ₁, …, s _j ) as in the previous case. Consider any $\vee \forall$-outermost quantifier $(\forall y)$ of $\overline{D}$. If y is one of the x _i ’s, define $\sigma _{\pi }(y) = s_{i}\sigma _{\pi ^{{\prime}}}$. Otherwise, $(\exists y)$ is a pending quantifier of D ₁, and a pending quantifier of B ₁ in Δ _m−1, and we define $\sigma _{\pi }(y) =\sigma _{\pi ^{{\prime}}}(y)$.

Definition

Suppose A is a formula occurring in cedent Δ in P, and π is an $\wedge \exists$-path leading to Δ. The formula ∗ _π (A) is defined as follows:

• If A is category (β), then ∗ _π (A) is the cedent containing the formulas $B\sigma _{\pi }$ for each pending implicant B of A.

• If A is category (α), then ∗ _π (A) is the cedent containing $B\sigma _{\pi }$ for each $\vee \forall$-component B of A.

• Otherwise ∗ _π (A) is $A\sigma _{\pi }$.

The notation ∗ _π (A) is extended to apply also to A appearing in a cedent $\Delta ^{{\prime}}$ below the cedent Δ. Let $\pi ^{{\prime}}$ be the initial subsequence of π leading to Δ′. Then define ${\ast}_{\pi }(A) = {\ast}_{\pi ^{{\prime}}}(A)$. The ∗ _π -translation of Δ consists of the formulas ∗ _π (A) such that A appears in or below Δ in P.

The next lemma is analogous to Lemma 4.

Lemma 8

Suppose B is a category (β) formula in a cedent Δ in P, and let π be an $\wedge \exists$ -path to Δ. Also suppose B does not have outermost connective ∧ or  $\exists$ . Let $\overline{C}_{1},\ldots,\overline{C}_{m}$ be the pending implicants of B. Let $\Delta ^{{\prime}}$ be B’s jump target cedent, and E be the auxiliary formula in  $\Delta ^{{\prime}}$ . Then there is an $\wedge \exists$ -path  $\pi ^{{\prime}}$ to  $\Delta ^{{\prime}}$ such that ${\ast}_{\pi ^{{\prime}}}(E)$ equals the cedent $\overline{B}\sigma _{\pi },\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{m}\sigma _{\pi }$ .

Proof

The jump target of B is either a cut or an ∧ inference as shown in (1), with B corresponding to the first $\wedge \exists$-component C ₀ of D. The remaining $\wedge \exists$-components of D are C ₁,…,C _r where 0 ≤ r ≤ m. Of course, their negations are (some of the) pending implicants of B.

Suppose the jump target is a non-atomic cut inference. Then we have r = m. Since B does not have outermost connective ∧ or $\exists$ and since the cut formula D is non-atomic, B is not the same as D. Consider the lowest direct descendant of B; it appears in a cedent $\Delta ^{{\prime\prime}}$, and is the auxiliary formula of an $\exists$ inference, or the left auxiliary formula of an ∧ inference. In either case, $\Delta ^{{\prime\prime}}$ is critical. Let $\pi ^{{\prime\prime}}$ be the $\wedge \exists$-path consisting of the initial part of π to $\Delta ^{{\prime\prime}}$. Set $\pi ^{{\prime}}$ to be the $\wedge \exists$-path that follows $\pi ^{{\prime\prime}}$ and then jumps from $\Delta ^{{\prime\prime}}$ to the upper left cedent $\Delta ^{{\prime}}$ of the jump target. The left cut formula E is equal to $\overline{D}$, and the $\vee \forall$-components of E are $\overline{C}_{0},\ldots,\overline{C}_{m}$. The cedent ${\ast}_{\pi ^{{\prime}}}(E)$ consists of the formulas $\overline{C}_{i}\sigma _{\pi ^{{\prime}}}$. For i = 0, $\sigma _{\pi ^{{\prime} }}$ was defined so that $C_{0}\sigma _{\pi ^{{\prime}}} = B\sigma _{\pi }$. Likewise, for i > 0, we have $C_{i}\sigma _{\pi ^{{\prime}}} = C_{i}\sigma _{\pi ^{{\prime\prime}}}$. Also, by cases (a) and (b) of the definition of $\sigma _{\pi }$, we have $C_{i}\sigma _{\pi ^{{\prime\prime}}} = C_{i}\sigma _{\pi }$. Thus the lemma holds.

Second, suppose the jump target is a cut on an atomic formula. The right cut formula is equal to B of course; the left cut formula E is equal to $\overline{B}$. Letting $\pi ^{{\prime}}$ be as above, ${\ast}_{\pi ^{{\prime}}}(E)$ is equal to $\overline{B}\sigma _{\pi ^{{\prime}}} = \overline{B}\sigma _{\pi }$ as desired.

Now suppose the jump target is an ∧ inference, as in (1), where E = C. If D is atomic, then D is a direct descendant of B (possibly even the same occurrence as B). In this case, let $\Delta ^{{\prime\prime}}$ be the cedent containing D (the upper right cedent of the ∧ inference), let $\pi ^{{\prime\prime}}$ be the initial part of $\pi ^{{\prime}}$ leading to $\Delta ^{{\prime\prime}}$, and let $\pi ^{{\prime}}$ be $\pi ^{{\prime\prime}}$ plus the upper left cedent $\Delta ^{{\prime}}$. (Note that $\Delta ^{{\prime}}$ is the jump target cedent of D.) Then, the pending implicants of C in $\Delta ^{{\prime}}$ are $\overline{D} = \overline{B}$ and $\overline{C}_{1},\ldots,\overline{C}_{m}$. We have $D\sigma _{\pi ^{{\prime}}} = D\sigma _{\pi ^{{\prime\prime}}} = D\sigma _{\pi }$ and also $C_{i}\sigma _{\pi ^{{\prime}}} = C_{i}\sigma _{\pi ^{{\prime\prime}}} = C_{i}\sigma _{\pi }$, so the lemma holds. Now suppose D is not atomic. Then define $\pi ^{{\prime}}$, $\pi ^{{\prime\prime}}$, and $\Delta ^{{\prime\prime}}$ exactly as in the case above where jump target of B was a cut inference. The pending implicants of C are $\overline{C}_{0},\ldots,\overline{C}_{m}$, and, as before, we have $C_{0}\sigma _{\pi ^{{\prime}}} = \overline{B}\sigma _{\pi ^{{\prime\prime}}} = B\sigma _{\pi }$ and $C_{i}\sigma _{\pi ^{{\prime}}} = C_{i}\sigma _{\pi ^{{\prime\prime}}} = C_{i}\sigma _{\pi }$, satisfying the conditions of the lemma. □ 

Proof (of Theorem 7)

The proof combines the constructions from the proofs of the two previous theorems. For each cedent Δ in P and each $\wedge \exists$-path leading to Δ, form the cedent Δ ^π as the ∗ _π -translation of Δ. Our goal is to show that these cedents can be combined to form a valid proof $P^{{\prime}}$. The proof splits into cases to handle the different kinds of inferences in P separately. In each case, we have a cedent Δ and an $\wedge \exists$-path π leading to Δ, and need to show how Δ ^π is derived in $P^{{\prime}}$.

For the first case, consider an initial cedent Δ of the form $B,\overline{B}$ in P. As the first subcase, suppose neither B nor $\overline{B}$ is category (β). Then Δ ^π is the cedent $B\sigma _{\pi },\overline{B}\sigma _{\pi },\Lambda$ where Λ is the cedent of formulas ∗ _π (E) for E a formula appearing below Δ in P. This is obtained in $P^{{\prime}}$ by applying a weakening to the initial cedent $B\sigma _{\pi },\overline{B}\sigma _{\pi }$.

For the second subcase, suppose B is category (β) and $\overline{B}$ is not. The formula B has a right cut formula as descendant, and corresponds to the ℓth $\wedge \exists$-component D _ℓ of D. Let the pending implicants of B be $\overline{D}_{\ell+1},\ldots,\overline{D}_{k}$. By Lemma 8, there is an $\wedge \exists$-path $\pi ^{{\prime}}$ to the upper left cedent $\Delta ^{{\prime}}$ of the jump target such that the auxiliary formula E in $\Delta ^{{\prime}}$ has ${\ast}_{\pi ^{{\prime}}}(E)$ equal to $\overline{B}\sigma _{\pi },\overline{D}_{\ell}\sigma _{\pi },\ldots,\overline{D}_{k}\sigma _{\pi }$. Thus, Δ ^π and $(\Delta ^{{\prime}})^{\pi ^{{\prime}} }$ are

$$\displaystyle{\overline{B}\sigma _{\pi },\overline{D}_{\ell+1}\sigma _{\pi },\ldots,\overline{D}_{k}\sigma _{\pi },\Lambda }$$

and

$$\displaystyle{\overline{B}\sigma _{\pi },\overline{D}_{\ell+1}\sigma _{\pi },\ldots,\overline{D}_{k}\sigma _{\pi },\Lambda ^{{\prime}}}$$

where $\Lambda ^{{\prime}}\subseteq \Lambda$. In $P^{{\prime}}$, the first cedent is derived from the second by a weakening inference.

In the third subcase, both B and $\overline{B}$ are category (β). We have ∗ _π (B) still equal to $\overline{D}_{\ell+1}\sigma _{\pi },\ldots,\overline{D}_{k}\sigma _{\pi }$, and now ${\ast}_{\pi }(\overline{B})$ is equal to $\overline{D}_{\ell^{{\prime\prime}}+1}^{{\prime\prime}}\sigma _{\pi },\ldots,\overline{D}_{k^{{\prime\prime}}}^{{\prime\prime}}\sigma _{\pi }$ with the $\overline{D}_{i}^{{\prime\prime}}$’s the $k^{{\prime\prime}}$ pending implicants of $\overline{B}$. Using Lemma 8 twice, we have $\wedge \exists$-paths $\pi ^{{\prime}}$ and $\pi ^{{\prime\prime}}$ leading to cedents $\Delta ^{{\prime}}$ and $\Delta ^{{\prime\prime}}$ such that $(\Delta ^{{\prime}})^{\pi ^{{\prime}} }$ and $(\Delta ^{{\prime\prime}})^{\pi ^{{\prime\prime}} }$ (respectively) are

$$\displaystyle{\overline{B}\sigma _{\pi },\overline{D}_{\ell+1},\ldots,\overline{D}_{k}\sigma _{\pi },\Lambda ^{{\prime}}}$$

and

$$\displaystyle{B\sigma _{\pi },\overline{D}_{\ell^{{\prime\prime}}+1}^{{\prime\prime}},\ldots,\overline{D}_{ k^{{\prime\prime}}}^{{\prime\prime}}\sigma _{ \pi },\Lambda ^{{\prime\prime}}}$$

where $\Lambda ^{{\prime}},\Lambda ^{{\prime\prime}}\subseteq \Lambda$. In $P^{{\prime}}$, using a cut and then a weakening gives Δ ^π as desired.

Second, consider the (very simple) case where the cedent Δ is inferred by a weakening inference

where $\Delta \subset \Delta ^{{\prime}}$. The path π to Δ can be extended by one more cedent to be a path $\pi ^{{\prime}}$ to the cedent $\Delta ^{{\prime}}$. The cedents Δ ^π and $(\Delta ^{{\prime}})^{\pi ^{{\prime}} }$ are identical. Thus the weakening inference in P is just omitted in $P^{{\prime}}$.

Now consider the case where Δ is the lower cedent of an ∧ inference in P:

Let Δ ₁ and Δ ₂ be the left and right upper cedents, respectively, and let π ₁ and π ₂ be the $\wedge \exists$-paths obtained by adding Δ ₁ or Δ ₂, respectively, to the end of π. First, suppose A ∧ B is category (α) or (γ), so ∗ _π (A ∧ B) is $(A \wedge B)\sigma _{\pi }$. Then A and B are both category (γ), and ${\ast}_{\pi _{1}}(A) = A\sigma _{\pi _{1}} = A\sigma _{\pi }$ and ${\ast}_{\pi _{2}}(B) = B\sigma _{\pi _{2}} = B\sigma _{\pi }$. Thus, in $P^{{\prime}}$, the ∧ inference becomes

and this is still a valid ∧ inference.

For the second subcase, suppose A ∧ B, thus A and B, are category (β). The formula B in Δ ₂ has the same pending implicants $\overline{C}_{1},\ldots,\overline{C}_{\ell}$ as the formula A ∧ B in Δ. Also, $\overline{C}_{i}\sigma _{\pi _{2}} = \overline{C}_{i}\sigma _{\pi }$. Thus Δ ^π is the same as $(\Delta _{2})^{\pi _{2}}$. This means that the ∧ inference can be omitted in $P^{{\prime}}$.

Next consider the case where Δ is the lower cedent of a cut in P:

Let Δ ₁ and Δ ₂ be the left and right upper cedents, respectively, and π ₁ and π ₂ be the extensions of π to Δ ₁ and Δ ₂. The occurrence of $\overline{A}$ is category (β) of course, and ${\ast}_{\pi _{2}}(\overline{A})$ is the empty cedent. Thus, the cedents Δ ^π and $(\Delta _{2})^{\pi _{2}}$ are identical, and the cut inference may be omitted from $P^{{\prime}}$.

Next consider the case where Δ is the lower cedent of an ∨ inference:

In this, and the remaining cases, let $\Delta ^{{\prime}}$ be the upper cedent of the inference, and let $\pi ^{{\prime}}$ be π extended to the cedent $\Delta ^{{\prime}}$. For the ∨ inference, $\sigma _{\pi ^{{\prime} }}$ is identical to $\sigma _{\pi }$. As a first subcase, suppose A ∨ B is category (γ), and thus A and B are as well. In this subcase, ${\ast}_{\pi }(A \vee B) = (A \vee B)\sigma _{\pi }$, ${\ast}_{\pi ^{{\prime}}}(A) = A\sigma _{\pi }$, and ${\ast}_{\pi ^{{\prime}}}(B) = B\sigma _{\pi }$. The ∗ _π -translation of the two cedents thus forms a valid ∨ inference in $P^{{\prime}}$.

The second subcase is when A ∨ B, A, and B are category (α). Letting A ₁, …, A _k be the $\vee \forall$-components of A, and $B_{1},\ldots,B_{k^{{\prime}}}$ be those of B, the ∗ _π -translation of the ∨ inference has the form

and this can be omitted from $P^{{\prime}}$.

The third subcase is when A ∨ B is category (β). Then A and B are category (γ), and ${\ast}(A) = A\sigma _{\pi }$ and ${\ast}(B) = B\sigma _{\pi }$. Also, ∗(A ∨ B) is $\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{k}\sigma _{\pi }$, where the $\overline{C}_{i}$’s are the pending implicants of A ∨ B. Thus, the ∗ _π -translation of the cedents in the ∨ inference has the form

(8)

Of course, this is not a valid inference. Let $\Delta ^{{\prime\prime}}$ be the upper left cedent of the jump target of A ∨ B. From Lemma 8, there is an $\wedge \exists$-path $\pi ^{{\prime\prime}}$ leading to $\Delta ^{{\prime\prime}}$ so that the ${\ast}_{\pi ^{{\prime\prime}}}$-translation of $\Delta ^{{\prime\prime}}$ is

$$\displaystyle{(\overline{A \vee B})\sigma _{\pi },\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{k}\sigma _{\pi },\Lambda ^{{\prime}}}$$

where $\Lambda ^{{\prime}}\subseteq \Lambda$. In $P^{{\prime}}$, this cedent and the upper cedent of (8) are combined with an ∨ inference and a cut to yield the lower cedent of (8), similarly to what was done in (6).

Now consider the case where Δ is the lower cedent of a $\forall$ inference

First suppose $(\forall x)A(x)$ is category (γ), so ${\ast}_{\pi }((\forall x)A(x)) = (\forall x)A(x)\sigma _{\pi } = (\forall x)A(x)\sigma _{\pi ^{{\prime}}}$. The formula A(b) is category (γ) and $\sigma _{\pi ^{{\prime}}}(b) = b$, thus ${\ast}_{\pi ^{{\prime}}}(A(b)) = A(b)\sigma _{\pi }$. The $\forall$ inference of P becomes

and this forms a valid $\forall$ inference in $P^{{\prime}}$.

For the second subcase, suppose that $(\forall x)A(x)$ is category (β). Hence, A(b) is category (γ). This case is similar to the third subcase for ∨ inferences above. We have ${\ast}_{\pi }((\forall x)A(x))$ equal to $\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{k}\sigma _{\pi }$ where the $\overline{C}_{i}$’s are the pending implicants of $(\forall x)A(x)$. And, ∗ _π (A(b)) equals $A(b)\sigma _{\pi }$; note $\sigma _{\pi }(b) = b$. Thus, the ${\ast}_{\pi ^{{\prime}}}$-/ ∗ _π -translation of the cedents in the $\forall$ inference has the form

(9)

which is not a valid inference. Let $\Delta ^{{\prime\prime}}$ be the upper left cedent of the jump target of $(\forall x)A(x)$. By Lemma 8, there is an $\wedge \exists$-path $\pi ^{{\prime\prime}}$ leading to $\Delta ^{{\prime\prime}}$ so that the ${\ast}_{\pi ^{{\prime\prime}}}$-translation of $\Delta ^{{\prime\prime}}$ is

$$\displaystyle{\overline{(\forall x)A(x)}\sigma _{\pi },\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{k}\sigma _{\pi },\Lambda ^{{\prime}}}$$

where $\Lambda ^{{\prime}}\subseteq \Lambda$. In $P^{{\prime}}$, this cedent and the upper cedent of (9) are combined with an $\forall$ inference and a cut to yield the lower cedent of (9), similarly to what was done in (7).

For the third subcase, suppose that $(\forall x)A(x)$ is category (α), so A(b) is also category (α). By definition, $\sigma _{\pi ^{{\prime}}}(b) =\sigma _{\pi }(x)$. Thus, ${\ast}_{\pi ^{{\prime}}}(A(b)) = A(b)\sigma _{\pi ^{{\prime}}} = A(x)\sigma _{\pi }$. Also, ${\ast}_{\pi }((\forall x)A(x)) = A(x)\sigma _{\pi }$. Therefore, in $P^{{\prime}}$, the $\forall$ inference becomes trivial with Δ ^π and $(\Delta ^{{\prime}})^{\pi ^{{\prime}} }$ equal to each other; so, this inference is omitted from $P^{{\prime}}$.

Finally, consider the case where Δ is the lower cedent of an $\exists$ inference

Note that $\sigma _{\pi ^{{\prime}}}$ is the same as $\sigma _{\pi }$. For the first subcase, suppose $(\exists x)A(x)$ is either category (α) or (γ), so A(s) is category (γ). This gives ${\ast}_{\pi ^{{\prime}}}(A(s)) = A(s)\sigma _{\pi ^{{\prime}}} = A(s)\sigma _{\pi }$. And, since its outermost connective is $\exists$, ${\ast}_{\pi }((\exists x)A(x)) = (\exists x)A(x)\sigma _{\pi }$. The $\exists$ inference in P becomes, in $P^{{\prime}}$,

which is a valid $\exists$ inference.

For the second subcase, suppose $(\exists x)A(x)$ and hence A(s) are category (β). The two formulas have the same pending implicants, $\overline{C}_{1},\ldots,\overline{C}_{k}$, for k ≥ 0. Thus, ${\ast}_{\pi ^{{\prime}}}(A(s))$ and ${\ast}_{\pi }((\exists x)A(x))$ are both equal to the cedent $\overline{C}_{1}\sigma _{\pi },\ldots,\overline{C}_{k}\sigma _{\pi }$. That is to say, Δ ^π and $(\Delta ^{{\prime}})^{\pi ^{{\prime}} }$ are identical, and thus the $\exists$ inference can be omitted from $P^{{\prime}}$.

The above completes the construction of $P^{{\prime}}$ from P. The discussion at the end of the proof of Theorem 5 applies equally well to the $P^{{\prime}}$ just constructed, and $P^{{\prime}}$ is again polynomial time uniform. □ 

6 Bounds on Eliminating All Cuts

This section gives bounds on eliminating all cuts from a proof. The bound obtained has the form 2 _d+O(1) ^| P |, where d is the maximum quantifier alternation of cut formulas in P. The first-order formula classes Σ _i and Π _i are defined as usual by counting alternations of quantifiers, allowing propositional connectives to appear arbitrarily. Namely, Σ ₀ = Π ₀ is the set of quantifier free formulas; and, using Bachus-Naur notation,

$$\displaystyle\begin{array}{rcl} \Sigma _{i}&::=& \Sigma _{i-1}\vert \Pi _{i-1}\vert \Sigma _{i} \wedge \Sigma _{i}\vert \Sigma _{i} \vee \Sigma _{i}\vert \neg \Pi _{i}\vert (\exists x)\Sigma _{i} {}\\ \Pi _{i}&::=& \Pi _{i-1}\vert \Sigma _{i-1}\vert \Pi _{i} \wedge \Pi _{i}\vert \Pi _{i} \vee \Pi _{i}\vert \neg \Sigma _{i}\vert (\forall x)\Pi _{i} {}\\ \end{array}$$

The alternating quantifier depth (aqd) of a cut is the minimum i > 0 such that one cut formula is in Σ _i and the other is in Π _i . The alternation quantifier depth of a proof P, denoted aqd(P), is the maximum aqd of any cut in P.

Theorem 9

Let P be a tree-like proof, and let d = aqd (P). There is a cut free proof  $P^{{\prime}}$ with the same end cedent as P with the size of  $P^{{\prime}}$ bounded by $\vert P^{{\prime}}\vert \leq 2_{d+O(1)}^{\vert P\vert }$ .

The proof of the theorem depends only on Theorem 5, not on Theorems 3 and 7. We also use upper bounds on eliminating cuts on quantifier free formulas as can be found in [5, 7, 17].

Proof

It is helpful to briefly review the well-known fact that the size of formulas appearing in the tree-like proof P can be bounded by the number of inferences in P plus the size of the formulas in the end cedent of P. For this, recall that any formula B appearing in P has a unique descendent A such that A either is a cut formula or is in the end cedent of P. In addition, B corresponds to a unique subformula C of A. Let C be a non-atomic subformula of a formula D in P which has a cut formula as descendant. If there is some ancestor B of D such that B corresponds to C and such that B is a principal formula of a logical inference, then leave C unchanged. If there is no such ancestor D, then mark C for deletion. Now replace every maximal subformula C in P marked for deletion with an arbitrary atomic formula, say with d = d for d some new free variable. The proof remains a valid proof (since only atomic formulas are allowed in initial cedents), and its end cedent is unchanged. Clearly, in the resulting proof, every cut formula has number of logical connectives bounded by the total number of ∧, ∨, $\exists$, and $\forall$ inferences in P. Without loss of generality, we assume this is true of the proof P itself.

The main step in proving Theorem 9 is to convert P into a proof in which all cuts are in prenex form. As a preliminary step, we show that we may assume w.l.o.g. that no cut formula in P has multiple quantifiers on the same bound variable, or in other words, that the bound variables in a cut formula are distinct. Towards this end, for each cut inference in P, with formulas A and $\overline{A}$ as its cut formulas, rename the bound variables in A so that the quantifiers in A use distinct bound variables. This also renames the bound variables of $\overline{A}$ of course. Furthermore, if B is a formula with descendent A or $\overline{A}$, this induces a renaming of the bound variables in B according to the renaming of bound variables in the subformula of A or $\overline{A}$ that corresponds to B. By applying these renamings to all such formulas B, and repeating for all cuts in P, we obtain a proof with the same end cedent as P such that bound variables are never reused in cut formulas.⁴ So, we may assume w.l.o.g. that P satisfies this property.

Now, for each cut in P, with cut formulas A and $\overline{A}$, choose an arbitrary prenex form $A^{{\prime}}$ for A so that the aqd of $A^{{\prime}}$ is ≤ aqd(P). The formula $A^{{\prime}}$ is obtained by choosing an ordering of the quantifiers in A which respects the scope of the quantifiers, and then using standard prenex operations to move the quantifiers out to the front of the formula in the chosen order. The prenex form $(\overline{A})^{{\prime}}$ of $\overline{A}$ is chosen with the same ordering and thus equals $\overline{A^{{\prime}}}$.

Let B be any formula in P with a cut formula A as descendent. The quantifiers of A are ordered as just discussed to form its prenex form $A^{{\prime}}$. Since B corresponds to a subformula of A, this induces an ordering on the quantifiers of B; the prenex form $B^{{\prime}}$ of B is defined using this induced ordering. On the other hand, if B has a descendent in the end cedent of P, the formula $B^{{\prime}}$ is defined to be equal to B. For any cedent Δ in P, define $\Delta ^{{\prime}}$ to contain exactly the formulas $B^{{\prime}}$ for B ∈ Δ.

The proof $P^{{\prime}}$ will contain the cedents $\Delta ^{{\prime}}$ for all Δ ∈ P. However, the ∧ and ∨ inferences in P may no longer be valid in $P^{{\prime}}$. Cuts, weakenings, and quantifier inferences of P do remain valid in $P^{{\prime}}$. In addition, since only atomic formulas are allowed initial cedents, the initial cedents of P are unchanged in $P^{{\prime}}$.

In order to make $P^{{\prime}}$ a valid proof, we must replace the ∧ and ∨ inferences of P with some new subproofs and cuts. The next lemma gives the key construction needed for this.

Lemma 10

Let B ∧ C be the principal formula of an ∧ inference in P with a cut formula as descendent. The auxiliary formulas of the inference are B and C. Let $B^{{\prime}}$ , $C^{{\prime}}$ , and $(B \wedge C)^{{\prime}}$ be their prenex forms in  $P^{{\prime}}$ . Then the cedent

$$\displaystyle{ \overline{B^{{\prime}}},\overline{C^{{\prime}}},(B \wedge C)^{{\prime}} }$$

(10)

has a cut free proof of length linear in the lengths of B and C. Similarly, if B ∨ C is the principal formula of an ∨ inference of P, then the cedents

$$\displaystyle{ \overline{B^{{\prime}}},(B \vee C)^{{\prime}}\qquad \mbox{ and}\qquad \overline{C^{{\prime}}},(B \vee C)^{{\prime}} }$$

(11)

have cut free proofs of length linear in the lengths of B and C.

Proof

Let $B^{{\prime}}$ and $C^{{\prime}}$ have the forms $\mathcal{Q}_{1}B_{0}$ and $\mathcal{Q}_{2}C_{0}$ where $\mathcal{Q}_{1}$ and $\mathcal{Q}_{2}$ denote blocks of zero or more quantifiers and where B ₀ and C ₀ are quantifier free. The formula $(B \wedge C)^{{\prime}}$ or (B ∨ C)^′ will have the form $\mathcal{Q}(B_{0} \wedge C_{0})$ or $\mathcal{Q}(B_{0} \vee C_{0})$. Here the quantifier block $\mathcal{Q}$ is obtained by arbitrarily interleaving (or, “shuffling”) the two blocks $\mathcal{Q}_{1}$ and $\mathcal{Q}_{2}$.

We claim that, for any quantifier blocks $\mathcal{Q}_{1}$ and $\mathcal{Q}_{2}$, and any block $\mathcal{Q}$ obtained as a shuffle of $\mathcal{Q}_{1}$ and $\mathcal{Q}_{2}$, the cedents (10) and (11) have tree-like, cut free proofs with size equal to the number of logical connectives in the cedents being proved. This is proved by induction on the number of quantifiers in $\mathcal{Q}$.

The base case of the induction is when $\mathcal{Q}$ is empty, and B and C are quantifier free. As is well known (and easy to verify) there are proofs of the cedents $\overline{B}_{0},B_{0}$ and $\overline{C}_{0},C_{0}$ with sizes equal to twice the number of logical connectives in B ₀ and C ₀, respectively. These two cedents plus a single ∧ or ∨ inference suffices to derive any of the cedents in (10) or (11).

For the induction step, suppose that $\mathcal{Q}$ contains at least one quantifier. The first quantifier can have the form $(\exists x)$ or $(\forall x)$ and is also the first quantifier of either $\mathcal{Q}_{1}$ or $\mathcal{Q}_{2}$. For instance, suppose $(\exists x)$ is the outermost quantifier of $\mathcal{Q}$ and $\mathcal{Q}_{1}$. Writing B ₀ = B ₀(x) to show the occurrences of the bound variable x, and replacing occurrences of x with a new free variable a, the induction hypothesis gives derivations of the cedents

$$\displaystyle{\overline{\mathcal{Q}_{1}^{-}B_{0}(a)},\mathcal{Q}^{-}(B_{ 0}(a) \vee C_{0})\quad \mbox{ and}\quad \overline{\mathcal{Q}_{2}C_{0}},\mathcal{Q}^{-}(B_{ 0}(a) \vee C_{0})}$$

or

$$\displaystyle{\overline{\mathcal{Q}_{1}^{-}B_{0}(a)},\overline{\mathcal{Q}_{2}C_{0}},\mathcal{Q}^{-}(B_{ 0}(a) \wedge C_{0})}$$

where $\mathcal{Q}_{1}^{-}$ and $\mathcal{Q}^{-}$ are the blocks $\mathcal{Q}_{1}$ and $\mathcal{Q}$ minus the first quantifier $\exists x$. For the ∨ case, the derivation

gives the desired derivation of $\overline{\mathcal{Q}_{2}C_{0}},\mathcal{Q}(B_{0} \vee C_{0})$; and the derivation

gives the desired derivation of $\overline{\mathcal{Q}_{1}B_{0}},\mathcal{Q}(B_{0} \vee C_{0})$. Note that the second inference is a $\forall$ inference; by the assumption of distinctness of bound variables, the eigenvariable a does not appear in C ₀.

A similar argument works for the ∧ case. The cases where outermost quantifier of $\mathcal{Q}$ is $(\forall x)$ are also similar. □ 

We can now complete the proof of Theorem 9. The proof $P^{{\prime}}$ is formed from the cedents $\Delta ^{{\prime}}$ defined above. Using the cedents $\Delta ^{{\prime}}$ maintains the validity of all inferences except for some of the ∨ and ∧ inferences. In $P^{{\prime}}$ these inferences become

and these are no longer valid if their principal formula contains quantifiers and has a cut formula as descendent. However, the ∧ inference can be simulated by using two cuts against the cedent $\overline{B^{{\prime}}},\overline{C^{{\prime}}},(B \wedge C)^{{\prime}}$ given by Lemma 10. Likewise, the ∨ inference can be simulated by using two cuts with the cedents $\overline{B^{{\prime}}},(B \vee C)^{{\prime}}$ and $\overline{C^{{\prime}}},(B \vee C)^{{\prime}}$. This process replaces one inference in P with two cuts in $P^{{\prime}}$; in addition, $P^{{\prime}}$ must contain the derivations of the cedents as given by Lemma 10. Since the formulas $(B \wedge C)^{{\prime}}$ and $(B \vee C)^{{\prime}}$ have cut formulas as descendents, their sizes are bounded by  | P | as discussed at the beginning of the proof. Therefore, the size of $\vert P^{{\prime}}\vert$ can be bounded by $\vert P^{{\prime}}\vert \leq 3\vert P\vert ^{2}$, since the size of the proofs from Lemma 10 is strictly less than 3 | P | .

The proof $P^{{\prime}}$ has all cut formulas in Σ _d or Π _d , where d = aqd(P). It suffices to assume d > 0. Applying Theorem 5 d times gives a tree-like proof $P^{{\prime\prime}}$ with the same end cedent, in which all cut formulas are quantifier free, with $h(P^{{\prime\prime}}) \leq 2_{d-1}^{3\vert P\vert ^{2} }$. Now, applying Theorem 8 of [5] and the discussion from the end of Sect. 4 of [5], we get a proof $P^{{\prime\prime\prime}}$ of the same end cedent with height bounded by $h(P^{{\prime\prime\prime}}) \leq 2^{\vert P\vert }2_{d-1}^{3\vert P\vert ^{2} }$, such that all cut formulas in $P^{{\prime\prime\prime}}$ are atomic. Then, applying Lemma 7 of [5], we get another proof $P^{{\prime\prime\prime}{\prime}}$ again with the same end cedent, which is cut free, and has height bounded by $2^{h(P^{{\prime\prime\prime}})+1 }$. In particular, the size of $P^{{\prime\prime\prime}{\prime}}$ is less than $2_{2}^{h(P^{{\prime\prime\prime}})+1 }$.

Therefore, $\vert P^{{\prime\prime\prime}{\prime}}\vert <2_{d+2}^{\vert P\vert }$, at least for | P | > 7. For d > 0, this gives $\vert P^{{\prime\prime\prime}{\prime}}\vert <2_{d+2}^{\vert P\vert }$ for | P | > 7. This completes the proof of Theorem 9. □ 

The size bound on $P^{{\prime\prime\prime}}$ is not optimal; we expect that even 2 _d+1 ^| P | might work.