Dynamic Analysis and Control of Fully-Constrained Cable Robots with Elastic Cables: Variable Stiffness Formulation

Abstract

In this paper dynamic analysis and control of fully-constrained parallel cable robots are studied in detail. In dynamic analysis, it is assumed that the dominant dynamics of cable can be approximated by linear axial spring. Furthermore, variable stiffness formulation for the cables is employed in modeling process. To overcome vibrations caused by inevitable elasticity of cables, a composite control law is proposed based on singular perturbation theory. Using the proposed control algorithm the dynamics of the cable robot is divided into two subsystems namely slow and fast. Then, based on the results of singular perturbation theory, stability analysis of the total system is performed. Finally, the effectiveness of the proposed composite control law is investigated through several simulations on a planar parallel cable robot.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Although the robots are extensively used in industries, their application in long-reach robotics such as inspection and repair in shipyards, is limited and still is in infancy. Cable robots are a special class of parallel robots in which the rigid links are replaced by cables. Cable robots possess some useful properties such as large workspace capability, transportability and ease of assembly/disassembly, reconfigurability and economical structure and maintenance [1]. Consequently, cable robots are exeptionally suitable for many applications such as, handling of heavy materials [2], high speed manipulation [3, 4], cleanup of disaster areas [5], very large workspace applications [6, 7], and interaction with hazardeous environment [8].

However, replacing the rigid links by cables, introduces many new challenges in the study of cable robots compared to that of conventional robots, amongst them control is the most critical one. Unlike the rigid links, cables can only apply tensile forces and not compressive forces. Due to this physical limitation, well-known control theories can not be used directly for the cable robots and they must be modified so that thay can provide positive tension for the cables. Dynamic behavior of the cables is another major challenge in mechanical design and control of this class of robots. Cables are usually elastic elements and may encounter some unavoidable situations such as elongation and vibration. In applications which require high bandwidth or high stiffness of the system, vibration may be a serious concern [9]. In terms of control, proposed control algorithms for this class of robot shall be designed to damp such vibrations.

Control of cable robots has received limited attention compared to that of conventional robots. With assumption of massless rigid string model for the cable, several efforts have been devoted to finding an efficient control strategy with positive cable tensions. Lyapunov based control [4], PID control [10], computed torque method [11], sliding mode [12] and adaptive PD control [13] are some control schemes being used in the control of cable robots. Kawamura et al. have proposed a PD controller accompanied with gravity compensation and internal forces in the cable-length coordinates [4]. They have analyzed the stability of motion based on Lyapunov theorem and vector closure conditions. Alp and Agrawal used PD control with gravity compensation in task space coordinates and analyzed asymptotic stability of the system [14]. Inverse Dynamics Control (IDC) or computed torque technique is another control scheme which is used in [11]. Fang et al. used nonlinear feed forward control laws in the cable length coordinates [15]. They proposed optimal tension distribution algorithm to compensate dynamic errors.

In these studies cables are treated as ideal massless rigid strings and cables elasticity is not considered. However, in practice especially in high-speed applications, this assumption may affect overal performance of the robot. In these cases, it is important to model both the static and dynamic effects of flexible cables. But, modeling the dynamic effects of elastic cables is an extremely comprehensive task. It is also important to note that the obtained models must not only be sufficiently accurate, they have to be suitable for controller synthesis, as well. Therefore, in practice it is recommended to include only dominant dynamic effects in the dynamic analysis. Ottaviano and Castelli have analyzed the effects of cables’ mass and elasticity and their effects on pose capability of the cable robots [16]. They have shown that cables masses can be neglected if the ratio of the end-effector to cables masses is large or generally, the ratio of the end-effector wrenches to the cables tensions is small. Using natural frequencies of the system, Diao and Ma in [9] have shown that in fully–constrained cable robots transversal vibrations of cables have very limited effects on the total vibration of the end-effector and can be ignored compared to that of axial flexibility. Therefore, dominant dynamic characteristics of the cable can be modeled by an axial spring in dynamic modeling of fully-constrained cable robots. According to these results, in this paper linear axial spring is used to model dominant dynamics of cable and by this means a more precise model of fully-constrained cable robots is derived for the controller design and stability analysis of such robots.

Cables elasticity may affect the precision of the cable robot, requiring appropriate control strategies. Efficient control design for the cable robots is very complicated when cable dynamic characteristics is considered and research on this topic is in infancy. Meunier et al. used multi loop control scheme for a large cable mechanism, in which the inner loop deals with cable model. This loop uses $H_{\infty }$ controller and gain scheduling technique for adaptation of $H_\infty$ with cable lengths, and in the outer loop an inverse dynamics control in addition to a PID controller is used [17]. However, in this research stability analysis of the closed–loop system has not been performed. Using elastic massless model for cable in [1], a new model for the cable robots is derived and a new control algorithm is proposed. This control algorithm is formed in cable length space and uses internal force concept. Stability of the closed-loop system is analyzed through Lyapunov theory and vector closure conditions. Using singular perturbation theory a new control algorithm has been developed in [18]. In this research cables are modeled by linear axial spring but with constant stiffness and stability analysis is performed based on the singular perturbation theory [19].

The structure of this paper is as follows. First, dynamics of cable robot with ideal rigid cables is elaborated and a new control algorithm is proposed for it. In the following sections, dynamics of cable robots with elastic cables is derived using variable stiffness formaulation for the cables. A composite control structure is proposed for this model, which consists of a rigid control term according to corresponding slow or rigid model of the system and a corrective term for vibrational damping. Then, using singular perturbation theory and Tikhonov’s theorem total stability of the system is analyzed and sufficient conditions for the asymptotic stability of the closed-loop system are derived. Finally, to demonstrate the effectiveness of the proposed controller, simulation results on a planar cable robot are examined in details.

2 Control of Rigid Cable Driven Parallel Robots

In this section we assume that the elasticity of cables can be ignored and cables behave as massless rigid strings. Based on this assumption the standard model for the dynamics of n-cable parallel robot with actuators is [1, 10]

$$\begin{aligned} \mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{x}}}+\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}+\mathbf{{G}}_{eq}(\mathbf{{x}})=\mathbf{{J}}^{T}\mathbf{{u}}\end{aligned}$$

(1)

In which,

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf{{M}}_{eq}(\mathbf{{x}})=r\mathbf{{M}}(\mathbf{{x}})+r^{-1}\mathbf{{J}}^{T}\mathbf{{I}}_m\mathbf{{J}}\\ \mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})=r\mathbf{{C}}(\mathbf{{x}},\dot{\mathbf{{x}}})+r^{-1}\mathbf{{J}}^{T}\mathbf{{I}}_m\dot{\mathbf{{J}}}\\ \mathbf{{G}}_{eq}(\mathbf{{x}})=r\mathbf{{G}}(\mathbf{{x}}) \end{array}\right. } \end{aligned}$$

(2)

where $\mathbf{{x}}\in \mathbf{{R}}^6$ is the vector of generalized coordinates, $\mathbf{{M}}(\mathbf{{x}})$ is the inertia matrix, $\mathbf{{I}}_m$ is diagonal matrix of actuator inertias reflected to the cable side of the gears, $\mathbf{{C}}(\mathbf{{x}},\dot{\mathbf{{x}}})$ represents the Coriolis and centrifugal terms, $\mathbf{{G}}(\mathbf{{x}})$ is the gravitational terms, r is radius of cable drums and $\mathbf{{u}}$ represents the input torque. $\mathbf{{J}}$ represents the Jacobian matrix of the system and relates $\dot{\mathbf{{x}}}$ to derivative of the cable length vector $\dot{\mathbf{{L}}}=\mathbf{{J}}\dot{\mathbf{{x}}}$. Although these equations are nonlinear and complex, they have some properties which are beneficial in the controller design [1].

Property 1 Inertia matrix $\mathbf{{M}}_{eq}(\mathbf{{x}})$ is symmetric and positive definite.

Property 2 Matrix $\dot{\mathbf{{M}}}_{eq}(\mathbf{{x}})-2\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})$ is skew symmetric.

2.1 Control Algorithm

Given a two times continuously differentiable reference trajectory $\mathbf{{x}}_d$ for (1), consider the following control law for $\mathbf{{J}}^T \mathbf{{u}}$

$$\begin{aligned} \mathbf{{J}}^T \mathbf{{u}}=\mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{x}}}_d+\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}_d+\mathbf{{G}}_{eq}(\mathbf{{x}}) +\mathbf{{K}}_p(\mathbf{{x}}_d-\mathbf{{x}})+\mathbf{{K}}_v(\dot{\mathbf{{x}}}_d-\dot{\mathbf{{x}}}) \end{aligned}$$

(3)

where $\mathbf{{M}}_{eq}, \mathbf{{C}}_{eq}$ and $\mathbf{{G}}_{eq}$ are defined as (2) and $\mathbf{{K}}_p , \mathbf{{K}}_v$ are diagonal matrices of positive gains for the PD control part of the proposed control scheme. Since in the fully-constrained cable robots the Jacobian matrix of the manipulator is non-square and the system is redundantly actuated, (3) is an underdetermined system of equations and has many solutions if $\mathbf{{J}}^T \mathbf{{J}}$ is invertible. In this case, the general solution of (3) is,

$$\begin{aligned} \mathbf{{u}}=\overline{\mathbf{{u}}}+\mathbf{{Q}}\end{aligned}$$

(4)

Here, $\overline{\mathbf{{u}}}$ is the minimum solution of (3) derived by using the pseudo-inverse of $\mathbf{{J}}^T$ and is given by

$$\begin{aligned} \overline{\mathbf{{u}}}=\mathbf{{J}}(\mathbf{{J}}^T \mathbf{{J}})^{-1} (\mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{x}}}_d+\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}_d+\mathbf{{G}}_{eq}(\mathbf{{x}}) +\mathbf{{K}}_p(\mathbf{{x}}_d-\mathbf{{x}})+\mathbf{{K}}_v(\dot{\mathbf{{x}}}_d-\dot{\mathbf{{x}}})) \end{aligned}$$

(5)

and, $\mathbf{{Q}}$ spans the null space of $\mathbf{{J}}^T$ and must satisfy

$$\begin{aligned} \mathbf{{J}}^T \mathbf{{Q}}=\mathbf 0\end{aligned}$$

(6)

$\mathbf{{Q}}$ can be physically interpreted as internal forces. It means that this term does not contribute into motion of the end-effector and only provides positive tension in the cables. With this notation, the proposed control scheme can be implemented according to Fig. (1a). In this paper we assume that the system always satisfies the vector closure conditions [4] and at all times, positive internal forces can be produced such that the cables are in tension.

Fig. 1

Internal force control structure

2.2 Stability Analysis

Substituting (4) in (1) and using (6), we can write the closed loop system as

$$\begin{aligned} \mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{e}}}+\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{e}}}+\mathbf{{K}}_p \mathbf{{e}}+\mathbf{{K}}_v \dot{\mathbf{{e}}}=\mathbf 0\end{aligned}$$

(7)

where

$$\begin{aligned} \mathbf{{e}}=\mathbf{{x}}_d-\mathbf{{x}}\end{aligned}$$

Consider the following Lyapunov function for the closed loop system (7)

$$\begin{aligned} V_R=\frac{1}{2}\dot{\mathbf{{e}}}^{T}\mathbf{{M}}_{eq}(\mathbf{{x}})\dot{\mathbf{{e}}}+\frac{1}{2}\mathbf{{e}}^{T}\mathbf{{K}}_p\mathbf{{e}}\end{aligned}$$

(8)

$V_R$ is positive for all $\mathbf{{e}}\ne \mathbf 0$ because based on property 1, $\mathbf{{M}}_{eq}$ is positive definite. The time derivative of Lyapunov function V is given by [18]

$$\begin{aligned} \dot{V}_R=-\dot{\mathbf{{e}}}^{T}\mathbf{{K}}_v \dot{\mathbf{{e}}}\,\,\,\,\,\,\,\le 0 \end{aligned}$$

(9)

As it has been fully elaborated in [18] this controller can suitably stabilize the rigid system asymptotically.

3 Robot with Elastic Cables

As mentioned earlier, in practice the overal performance of the cable robot may be affected by vibrations caused by inevitable elasticity of the cables [4, 9]. Thus, elasticity of cables must be considered in the modeling process and control schemes should be designed so that they stabilize the system and damp the vibrations efficiently. New research results show that in fully-constrained cable robots, dominant dynamics of cables are longitudinal vibration [9]. Therefore, axial spring model may suitably used to describe the effects of dominant dynamics of cable.

In order to model a general cable driven robot with n elastic cables assume that: $L_{1i}:i=1,2,...,n$ denotes the length of i-th cable with tension which can be measured by pot-string. $L_{2i}:i=1,2,...,n$ denotes the cable length of the i-th actuator which may be measured by shaft encoder. If the system is rigid, then $L_{1i} = L_{2i} \, ,\forall i$. Let us denote:

$$\begin{aligned} \mathbf{{L}}=(L_{11}, L_{12},\cdots ,L_{1n},L_{21}, L_{22},\cdots ,L_{2n}) =(\mathbf{{L}}_{1}^{T},\mathbf{{L}}_{2}^{T}) \end{aligned}$$

(10)

In a cable driven robot, the stiffness of cables is a function of cable lengths which are changing during the motion of the robot. Using linear axial spring model with Young’s modulus E and cross-sectional area A for the cables, the instantaneous potential energy of i-th cable is

$$\begin{aligned} p_i=\frac{EA(L_{1i}-L_{2i})^2}{2L_{2i}} \end{aligned}$$

With this notation the total potential energy of the system can be expressed by:$\,\,P=P_{0}+P_{1}$, in which, $P_0$ denotes the potential energy of the rigid robot and $P_1$ denotes the potential energy of the cables and can be formulated by:

$$\begin{aligned} P_{1}=\frac{1}{2}(\mathbf{{L}}_{1}-\mathbf{{L}}_{2})^{T}\mathbf{{K}}(\mathbf{{L}}_2)(\mathbf{{L}}_{1}-\mathbf{{L}}_{2}) \end{aligned}$$

(11)

where, $\mathbf{{K}}$ is the stiffness matrix of the cables during the motion which is a function of $\mathbf{{L}}_2$. Assume that all cables have the same Young’s modulus E and cross-sectional area A,¹ then

$$\begin{aligned} \mathbf{{K}}(\mathbf{{L}}_2)=EA \cdot {\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2) \end{aligned}$$

(12)

Furthermore, kinetic energy of the system is

$$\begin{aligned} T=\frac{1}{2}\dot{\mathbf{{x}}}^{T}\mathbf{{M}}(\mathbf{{x}})\dot{\mathbf{{x}}}+ \frac{1}{2}\dot{\mathbf{{q}}}^{T}\mathbf{{I}}_{m}\dot{\mathbf{{q}}} \end{aligned}$$

(13)

In which, $\mathbf{{x}}$ denotes the generalized coordinates in Cartesian space, $\mathbf{{q}}$ is the motor shaft position vector, $\mathbf{{M}}(\mathbf{{x}})$ is the mass matrix and $\mathbf{{I}}_m$ is the actuator moments of inertia. Using Euler-Lagrange formulation and some manipulations, final equations of motion can be written in the following form:

$$\begin{aligned}&\mathbf{{M}}(\mathbf{{x}})\ddot{\mathbf{{x}}}+\mathbf{{N}}(\mathbf{{x}},\dot{\mathbf{{x}}})=EA\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)\cdot (\mathbf{{L}}_{2}-\mathbf{{L}}_{1}) \end{aligned}$$

(14)

$$\begin{aligned}&\mathbf{{I}}_{m}\ddot{\mathbf{{q}}}+r\, EA\cdot \,\,{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)\,\cdot \,(\mathbf{{L}}_{2}-\mathbf{{L}}_{1})+H(\mathbf{{L}}_2,\mathbf{{L}}_1)=\mathbf{{u}} \end{aligned}$$

(15)

in which,

$$\begin{aligned}&\mathbf{{N}}(\mathbf{{x}},\dot{\mathbf{{x}}})=\mathbf{{C}}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}+\mathbf{{G}}(\mathbf{{x}})\,\,\,,\,\,\, \mathbf{{L}}_2-\mathbf{{L}}_0 = r\mathbf{{q}}\\&\mathbf{{H}}(\mathbf{{L}}_2,\mathbf{{L}}_1)=-\frac{r}{2}EA\,\cdot {\mathop {\mathrm {{diag}}}}^{-2}(\mathbf{{L}}_2)\,\cdot {\mathop {\mathrm {{diag}}}}(\mathbf{{L}}_{2}-\mathbf{{L}}_{1})\cdot (\mathbf{{L}}_{2}-\mathbf{{L}}_{1}) \end{aligned}$$

In these equations $\mathbf{{L}}_0$ is the vector of cables length at $\mathbf{{x}}=0$ and $\mathbf{{J}}$ is the Jacobian matrix of the system and relates $\dot{\mathbf{{x}}}$ to derivative of the cable length vector $\dot{\mathbf{{L}}}_{1}=\mathbf{{J}}\dot{\mathbf{{x}}}$, and other parameters are defined as before. For notational simplicity we assumed that all Young’s modulus E and cross-sectional A of cables are the same and EA is large with respect to other system parameters. To idealize the assumption of large cable stiffness and small cable damping, we assume that EA is of order $O(1/\varepsilon ^2)$ ($\varepsilon$ is a small scalar parameter), and furthermore, the damping terms in the cables are neglected.

Equations (14) and (15) represent cable robot as a nonlinear and coupled system. This representation includes both rigid and flexible subsystems and their interactions. The model of cable robot with elastic cables will be reduced to (1) as EA tends to infinity. Furthermore, the new formulation preserves the properties of rigid model (1), such as positive definiteness of inertia matrix and skew symmetry property.

3.1 Control

In this section we show that the control law (3) which is proposed under assumption of perfect rigidity, can be extended for cable robot with elastic cables. First, consider a composite control law by adding a damping term to the control law (3) in the form of

$$\begin{aligned} \mathbf{{u}}=\mathbf{{u}}_r+\mathbf{{K}}_d(\dot{\mathbf{{L}}}_1-\dot{\mathbf{{L}}}_2) \end{aligned}$$

(16)

in which, $\mathbf{{u}}_r$ is given by (3) in terms of $\mathbf{{x}}$. Furthermore, $\mathbf{{K}}_d$ is a constant positive diagonal matrix whose diagonal elements are designed to remain in order of $O(1/\varepsilon )$. Note that

$$\begin{aligned} \mathbf{{L}}_2 = r\mathbf{{q}}+\mathbf{{L}}_0\Longrightarrow \dot{\mathbf{{L}}}_2=r\dot{\mathbf{{q}}}\,\,,\,\,\,\ddot{\mathbf{{L}}}_{2}=r\ddot{\mathbf{{q}}} \end{aligned}$$

(17)

Apply control law (16) in (15) and define variable $\mathbf{{z}}$ as

$$\begin{aligned} \mathbf{{z}}=EA(\mathbf{{L}}_{2}-\mathbf{{L}}_{1}) \end{aligned}$$

(18)

The closed loop dynamic equation reduces to

$$\begin{aligned} r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{z}}}+\mathbf{{K}}_d\dot{\mathbf{{z}}}+r{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2) \cdot \left[ EA\mathbf{{I}}-\frac{1}{2}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)\, {\mathop {\mathrm {{diag}}}}(\mathbf{{z}})\right] \mathbf{{z}}\\\nonumber =EA(\mathbf{{u}}_r-r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{L}}}_1) \end{aligned}$$

(19)

By the assumption on EA and the choice for $\mathbf{{K}}_d$ we may write

$$\begin{aligned} EA=\frac{K_1}{\varepsilon ^2}\,\,\,\,;\,\,\,\,\mathbf{{K}}_d=\frac{\mathbf{{K}}_2}{\varepsilon } \end{aligned}$$

(20)

where, $K_1\,,\,\mathbf{{K}}_2$ are O(1). Therefore, (19) can be written as

$$\begin{aligned} \varepsilon ^{2}r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{z}}}+\varepsilon \mathbf{{K}}_2\dot{\mathbf{{z}}}+r{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2) \cdot \left[ K_1\mathbf{{I}}-\frac{\varepsilon ^2}{2}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2){\mathop {\mathrm {{diag}}}}(\mathbf{{z}})\right] \mathbf{{z}}\\\nonumber =K_1(\mathbf{{u}}_r-r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{L}}}_1) \end{aligned}$$

(21)

Now Eqs. (14) and (21) can be rewritten together:

$$\begin{aligned}&\mathbf{{M}}(\mathbf{{x}})\ddot{\mathbf{{x}}}+\mathbf{{C}}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}+\mathbf{{G}}(\mathbf{{x}})=\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)\mathbf{{z}}\end{aligned}$$

(22)

$$\begin{aligned}&\varepsilon ^{2}r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{z}}}+\varepsilon \mathbf{{K}}_2\dot{\mathbf{{z}}}+r{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2). \left[ K_1\mathbf{{I}}-\frac{\varepsilon ^2}{2}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2){\mathop {\mathrm {{diag}}}}(\mathbf{{z}})\right] \mathbf{{z}}\\\nonumber&=K_1(\mathbf{{u}}_r-r^{-1}\mathbf{{I}}_m\ddot{\mathbf{{L}}}_1) \\\end{aligned}$$

(23)

System (22) and (23) is written in a singularly perturbed form. The variables $\mathbf{{z}}$ and $\dot{\mathbf{{z}}}$ have the interpretation of ‘fast’ variables while the end-effector position variables $\mathbf{{x}}$ and $\dot{\mathbf{{x}}}$ (or $\mathbf{{L}}_1\,,\dot{\mathbf{{L}}}_1$) are representing ‘slow’ variables. Using the results of singular perturbation theory, elastic system (22) and (23) can be approximated by two subsystems, namely the quasi-steady state or slow subsystem and boundary layer or fast subsystem. With $\varepsilon =0$, Eq. (23) yields

$$\begin{aligned} \bar{\mathbf{{z}}}=r^{-1}{\mathop {\mathrm {{diag}}}}(\bar{\mathbf{{L}}}_1)(\bar{\mathbf{{u}}}_r-r^{-1}\mathbf{{I}}_m\ddot{\bar{\mathbf{{L}}}}_1)\;\;\;,\;\;\;\bar{\mathbf{{L}}}_1=\bar{\mathbf{{L}}}_2 \end{aligned}$$

(24)

in which, the overbar variables represent the variables when $\varepsilon =0$. Substitute (24) into (22).

$$\begin{aligned} \mathbf{{M}}(\bar{\mathbf{{x}}})\ddot{\bar{\mathbf{{x}}}}+\mathbf{{C}}(\bar{\mathbf{{x}}},\dot{\bar{\mathbf{{x}}}})\dot{\bar{\mathbf{{x}}}}+\mathbf{{G}}(\bar{\mathbf{{x}}})=r^{-1}\mathbf{{J}}^{T}(\bar{\mathbf{{u}}}_r-r^{-1}\mathbf{{I}}_m \ddot{\bar{\mathbf{{L}}}}_1) \end{aligned}$$

Substitute $\ddot{\bar{\mathbf{{L}}}}_1 =\mathbf{{J}}\ddot{\bar{\mathbf{{x}}}}+\dot{\mathbf{{J}}}\dot{\bar{\mathbf{{x}}}}$ in above equation:

$$\begin{aligned} (r\mathbf{{M}}(\bar{\mathbf{{x}}})+r^{-1}\mathbf{{J}}^T \mathbf{{I}}_m \mathbf{{J}})\ddot{\bar{\mathbf{{x}}}}+(r\mathbf{{C}}(\bar{\mathbf{{x}}},\dot{\bar{\mathbf{{x}}}})\dot{\bar{\mathbf{{x}}}}+r^{-1}\mathbf{{J}}^{T} \mathbf{{I}}_m \dot{\mathbf{{J}}}\dot{\bar{\mathbf{{x}}}}) +r\mathbf{{G}}(\bar{\mathbf{{x}}})=\mathbf{{J}}^{T}\bar{\mathbf{{u}}}_r \end{aligned}$$

or

$$\begin{aligned} \mathbf{{M}}_{eq}(\bar{\mathbf{{x}}})\ddot{\bar{\mathbf{{x}}}}+\mathbf{{C}}_{eq}(\bar{\mathbf{{x}}},\dot{\bar{\mathbf{{x}}}})\dot{\bar{\mathbf{{x}}}}+\mathbf{{G}}_{eq}(\bar{\mathbf{{x}}})=\mathbf{{J}}^{T}\bar{\mathbf{{u}}}_r \end{aligned}$$

(25)

Equation (25) is called the quasi-steady state or slow subsystem. Note that (25) is the rigid model (1) in terms of $\bar{\mathbf{{x}}}$. Using Tikhonov’s theorem [19], for $t>0$ the elastic force $\mathbf{{z}}(t)$ and the end-effector position $\mathbf{{x}}(t)$ satisfy

$$\begin{aligned}&\mathbf{{z}}(t)=\bar{\mathbf{{z}}}(t)+\pmb \eta (\tau )+O(\varepsilon )\end{aligned}$$

(26)

$$\begin{aligned}&\mathbf{{x}}(t)=\bar{\mathbf{{x}}}(t)+O(\varepsilon ) \end{aligned}$$

(27)

where, $\tau =t/\varepsilon$ is the fast time scale and $\pmb \eta$ is the fast state variable and satisfies boundary layer equation

$$\begin{aligned} r^{-1}\mathbf{{I}}_m \frac{d^{2}\pmb \eta }{d\tau ^2}+\mathbf{{K}}_2 \frac{d\pmb \eta }{d\tau }+rK_1{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta =\mathbf 0 \end{aligned}$$

(28)

Considering these results, elastic system (22) and (23) can be approximated up to $O(\varepsilon )$ as

$$\begin{aligned}&\mathbf{{M}}(\mathbf{{x}})\ddot{\mathbf{{x}}}+\mathbf{{C}}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}+\mathbf{{G}}(\mathbf{{x}})=\mathbf{{J}}^{T} {\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)(\bar{\mathbf{{z}}}+\pmb \eta (\tau )) \\&\qquad r^{-1}\mathbf{{I}}_m \frac{d^{2}\pmb \eta }{d\tau ^2}+\mathbf{{K}}_2 \frac{d\pmb \eta }{d\tau }+rK_1{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta =\mathbf 0\end{aligned}$$

According to (24)

$$\begin{aligned}&\mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{x}}}+\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})\dot{\mathbf{{x}}}+\mathbf{{G}}_{eq}(\mathbf{{x}})= \mathbf{{J}}^{T}({\mathbf{{u}}}_r+r{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta (\tau )) \end{aligned}$$

(29)

$$\begin{aligned}&r^{-1}\mathbf{{I}}_m \frac{d^{2}\pmb \eta }{d\tau ^2}+\mathbf{{K}}_2 \frac{d\pmb \eta }{d\tau }+rK_1{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta =\mathbf 0 \end{aligned}$$

(30)

Since the gain $\mathbf{{K}}_2$ can be chosen suitably such that the boundary layer (28) becomes asymptotically stable, it follows that, with sufficiently small values of $\varepsilon$, the response of the elastic system (14) and (15) with the composite control (16), will be nearly the same as the response of rigid system (1) with the rigid control $\mathbf{{u}}_r$ alone, after some initially damped transient of fast variables $\pmb \eta (t/\varepsilon )$.

3.2 Stability Analysis

Control of rigid model and its stability analysis were discussed in previous section. It was demonstrated that the boundary layer or fast subsystem (28) is asymptotically stable, due to damping term. Separate stability of boundary layer and quasi-steady state subsystems does not generally guarantee that the total system is stable [19]. In this section the stability of the total system is analyzed, based on stability analysis of the subsystems.

Consider dynamic equations of elastic system (29) and (30), and control law (4) from previous section. Then

$$\begin{aligned}&\mathbf{{M}}_{eq}(\mathbf{{x}})\ddot{\mathbf{{e}}}+(\mathbf{{C}}_{eq}(\mathbf{{x}},\dot{\mathbf{{x}}})+\mathbf{{K}}_v)\dot{\mathbf{{e}}}+\mathbf{{K}}_p \mathbf{{e}}= -r\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta (t/\varepsilon ) \end{aligned}$$

(31)

$$\begin{aligned}&r^{-1}\mathbf{{I}}_m \frac{d^{2}\pmb \eta }{dt^2}+\mathbf{{K}}_d \frac{d\pmb \eta }{dt}+rEA{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)\pmb \eta =\mathbf 0 \end{aligned}$$

(32)

Let us denote $\mathbf{{y}}=\left[ \mathbf{{e}}^T\,,\,\dot{\mathbf{{e}}}^T\right] ^T$ and $\mathbf{{h}}=\left[ \pmb \eta ^T\,,\,\dot{\pmb \eta }^T\right] ^T$, in which $\mathbf{{e}}=\mathbf{{x}}_d-\mathbf{{x}}$, then one may write

$$\begin{aligned} \dot{\mathbf{{y}}}= & {} \mathbf{{A}}\mathbf{{y}}+\mathbf{{B}}\left[ \mathbf{{I}}\,\,\,\,\mathbf 0\right] \mathbf{{h}} \end{aligned}$$

(33)

$$\begin{aligned} \dot{\mathbf{{h}}}= & {} \tilde{\mathbf{{A}}}\mathbf{{h}} \end{aligned}$$

(34)

where

$$\begin{aligned}&\mathbf{{A}}=\left[ \begin{array}{cc} \mathbf 0&{} \mathbf{{I}}\\ -\mathbf{{M}}^{-1}_{eq}\mathbf{{K}}_p &{}-\mathbf{{M}}^{-1}_{eq}(\mathbf{{K}}_v +\mathbf{{C}}_{eq}) \end{array} \right] \\ \\&\mathbf{{B}}=\left[ \begin{array}{c} \mathbf 0\\ -r\mathbf{{M}}^{-1}_{eq}\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1) \end{array} \right] \\&\tilde{\mathbf{{A}}}=\left[ \begin{array}{cc} \mathbf 0&{} \mathbf{{I}}\\ -r^{2}EA\mathbf{{I}}_m^{-1}{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1) &{}-r\mathbf{{I}}_m^{-1}\mathbf{{K}}_d \end{array} \right] \end{aligned}$$

Lemma 1

There is a positive definite matrix $\mathbf{{K}}_d$ such that the closed-loop system described with (34) is asymptotically stable.

Proof

Consider the following Lyapunov function

$$\begin{aligned} V_F=\mathbf{{h}}^{T}\mathbf{{W}}\mathbf{{h}}\,\,\,\,,\,\,\,\,\, \mathbf{{W}}=\frac{1}{2}\left[ \begin{array}{cc} r^{2}\mathbf{{K}}_d &{} r\mathbf{{I}}_m\\ r\mathbf{{I}}_m &{} \mathbf{{I}}_m \end{array} \right] \end{aligned}$$

(35)

In order to have positive definite $\mathbf{{W}}$, according to the Shur complement, it is sufficient that $\mathbf{{K}}_d > \mathbf{{I}}_m$. Differentiate $V_F$ along trajectories of (34)

$$\begin{aligned} \dot{V}_F=-\mathbf{{h}}^T \mathbf{{S}}\mathbf{{h}}\end{aligned}$$

(36)

in which,

$$\begin{aligned} \mathbf{{S}}= \left[ \begin{array}{cc} r^{3}EA\,{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1) &{} 0.5r^{2}EA\,{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1) \\ 0.5r^{2}EA\,{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1) &{} r(\mathbf{{K}}_d-\mathbf{{I}}_m) \end{array} \right] \end{aligned}$$

According to Shur complement, $\mathbf{{S}}$ is positive definite, if and only if,

$$\begin{aligned}&\mathbf{{K}}_d > \mathbf{{I}}_m\\&\mathbf{{K}}_d-(\mathbf{{I}}_m+.25EA\,{\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_1)) >0 \end{aligned}$$

(37)

in which, $\mathbf{{K}}_d$ and $\mathbf{{I}}_m$ are diagonal positive definite matrices. Regarding to workspace constraints

$$\begin{aligned} 0<\gamma \le L_{1i}\le \beta (i=1,2,\cdots ,n) \end{aligned}$$

(38)

where $\gamma$ and $\beta$ are positive constants. Thus, if

$$\begin{aligned} K_{di} >I_{mi}+.25EA\gamma ^{-1}(i=1,2,\cdots ,n) \end{aligned}$$

(39)

then, $\dot{V}_F$ becomes negative definite and closed-loop system described by (34) is asymptotically stable.

Theorem 1

There exist positive definite controller gains $\mathbf{{K}}_v$, and $\mathbf{{K}}_d$, to stabilize the closed-loop system (33) and (34) asymptotically.

Proof

Consider the following composite Lyapunov function

$$\begin{aligned} V(\mathbf{{y}},\mathbf{{h}})=V_R+V_F \end{aligned}$$

(40)

where, $V_R$ is the Lyapunov function for the rigid subsystem, and $V_F$ is the Lyapunov function for the fast subsystem (28). Differentiate $V(\mathbf{{y}},\mathbf{{h}})$ along trajectories of (33) and (34):

$$\begin{aligned} \dot{V}(\mathbf{{y}},\mathbf{{h}})=\dot{V}_R+\dot{V}_F= -\dot{\mathbf{{e}}}^{T}\mathbf{{K}}_v\dot{\mathbf{{e}}}-r\dot{\mathbf{{e}}}^{T}\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1} (\mathbf{{L}}_1)\pmb \eta -\mathbf{{h}}^T \mathbf{{S}}\mathbf{{h}}\end{aligned}$$

(41)

According to Rayleigh-Ritz inequality,

$$\begin{aligned} -\mathbf{{h}}^T \mathbf{{S}}\mathbf{{h}}\le -\lambda _{min}(\mathbf{{S}})\Vert \mathbf{{h}}\Vert ^{2} \end{aligned}$$

(42)

Furthermore,

$$\begin{aligned}&-\dot{\mathbf{{e}}}^{T}\mathbf{{K}}_v\dot{\mathbf{{e}}}\le -\lambda _{min}(\mathbf{{K}}_v)\Vert \dot{\mathbf{{e}}}\Vert ^{2}\nonumber \\ -r\dot{\mathbf{{e}}}^{T}\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1} (\mathbf{{L}}_1)\pmb \eta&\le r\vert \dot{\mathbf{{e}}}^{T}\mathbf{{J}}^{T}{\mathop {\mathrm {{diag}}}}^{-1} (\mathbf{{L}}_1)\pmb \eta \vert \le r\gamma ^{-1}\sigma _{max}(\mathbf{{J}}^T)\Vert \dot{\mathbf{{e}}}\Vert \Vert \mathbf{{h}}\Vert \end{aligned}$$

(43)

in which, $\lambda _{min}$ and $\sigma _{max}$ denote the smallest eigenvalue and the largest singular value of the corresponding matrices, respectively. Using above inequalities, one may write

$$\begin{aligned} \dot{V}(\mathbf{{y}},\mathbf{{h}})\le -\lambda _{min}(\mathbf{{K}}_v)\Vert \dot{\mathbf{{e}}}\Vert ^{2}+r\gamma ^{-1}\sigma _{max}(\mathbf{{J}}^T)\Vert \dot{\mathbf{{e}}}\Vert \Vert \mathbf{{h}}\Vert - \lambda _{min}(\mathbf{{S}})\Vert \mathbf{{h}}\Vert ^{2} \end{aligned}$$

Or

$$\begin{aligned} \dot{V}(\mathbf{{y}},\mathbf{{h}})\le \left[ \begin{array}{cc} \Vert \dot{\mathbf{{e}}}\Vert&\Vert \mathbf{{h}}\Vert \end{array}\right] \cdot&\left[ \begin{array}{cc} -\lambda _{min}(\mathbf{{K}}_v)&{}0.5r\gamma ^{-1}\sigma _{max}(\mathbf{{J}}^T)\\ 0.5r\gamma ^{-1}\sigma _{max}(\mathbf{{J}}^T)&{}-\lambda _{min}(\mathbf{{S}}) \end{array}\right] \left[ \begin{array}{c} \Vert \dot{\mathbf{{e}}}\Vert \\ \Vert \mathbf{{h}}\Vert \end{array}\right] \end{aligned}$$

Fig. 2

a The schematics of planar cable mechanism. b Vector definitions for Jacobian derivation

in order to guarantee $\dot{V}(\mathbf{{y}},\mathbf{{h}})\le 0$, it is necessary to have

$$\begin{aligned} \lambda _{min}(\mathbf{{K}}_v)\lambda _{min}(\mathbf{{S}}) > 0.25r^2\gamma ^{-2}\sigma ^{2}_{max}(\mathbf{{J}}^T) \end{aligned}$$

(44)

Condition (44) may be simply satisfied by choosing appropriate values for $\mathbf{{K}}_v$ in (3) and $\mathbf{{K}}_d$ for the fast subsystem. Negative semi-definiteness of $\dot{V}(\mathbf{{y}},\mathbf{{h}})$ implies that $\mathbf{{y}}$ and $\mathbf{{h}}$ are bounded. This indicates that $\ddot{V}(\mathbf{{y}},\mathbf{{h}})$ is bounded. Hence, $\dot{V}(\mathbf{{y}},\mathbf{{h}})$ is uniformly continuous. Using Barbalat’s lemma one may conclude that $\dot{\mathbf{{e}}}\rightarrow 0$ and $\mathbf{{h}}\rightarrow 0$ as $t\rightarrow \infty$. Now, according to uniform continuity of $\ddot{\mathbf{{e}}}$, it can be concluded that $\ddot{\mathbf{{e}}}\rightarrow 0$ as $t\rightarrow \infty$. As a result the total closed-loop system (33) and (34) becomes asymptotically stable.

Table 1 Inertial parameter of the planar cable robot

Fig. 3

The closed-loop system experiences instability, if only rigid controller $\mathbf{{u}}_r$ is applied

4 Case Study

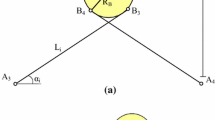
To show the effectiveness of the proposed control algorithm a simulation study has been performed. In the following simulation study, the results of the closed–loop performance of a planar cable driven manipulator are investigated. Our model of a planar cable robot consists of an end-effector that is connected by four cables to the base platform shown in Fig. (2a). As it is shown in Fig. (2), $A_i$ denote the fixed base points of the cables, $B_i$ denote points of connection of the cables on the end-effector, $L_i$ denote the cable lengths, and $\alpha _i$ denote the cable angles. The position of the center of mass of the end-effector $\mathbf{{P}}$, is denoted by $\mathbf{{P}}= [x_p,y_p]$, and the orientation of the manipulator end-effector is denoted by $\phi$ with respect to the fixed coordinate frame. Hence, the manipulator possesses three degrees of freedom $\mathbf{{x}}=[x_p,y_p,\phi ]$, with one degree of actuator redundancy. Furthermore, the Jacobian matrix of the manipulator, which relates the length variable velocities $\dot{\mathbf{{L}}}_1$ to the end-effector velocities $\dot{\mathbf{{x}}}$ , is given by

$$\begin{aligned} \dot{\mathbf{{L}}}_1=\mathbf{{J}}\dot{\mathbf{{x}}} \end{aligned}$$

(45)

Note that the Jacobian matrix $\mathbf{{J}}$ is a non-square $4\times 3$ matrix, since the manipulator is redundantly actuated.

Fig. 4

Suitable tracking performance of the closed-loop system to smooth reference trajectories; Proposed control algorithm

Fig. 5

Simulation results showing the cables tension for smooth reference trajectories

The equations of motion for the end-effector can be written in the following form

$$\begin{aligned} {{\mathbf{{M}}}}\ddot{{\mathbf{{x}}}}+{{\mathbf{{G}}}} ={{\mathbf{{F}}}} \end{aligned}$$

in which, $\mathbf{{x}}=[x_p,y_p,\phi ]$, and by considering flexibility in the cables, according to (14) and (15)

$$\begin{aligned}&\mathbf{{F}}=\mathbf{{J}}^T EA\cdot {\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)(\mathbf{{L}}_2-\mathbf{{L}}_1 )\,\,,\,\, \mathbf{{L}}_2=r\mathbf{{q}}+\mathbf{{L}}_0 \\&\mathbf{{I}}_{m}\ddot{\mathbf{{q}}}+rEA\cdot {\mathop {\mathrm {{diag}}}}^{-1}(\mathbf{{L}}_2)(\mathbf{{L}}_{2}-\mathbf{{L}}_{1})- \frac{r}{2}EA\cdot {\mathop {\mathrm {{diag}}}}^{-2}(\mathbf{{L}}_2){\mathop {\mathrm {{diag}}}}(\mathbf{{L}}_{2}-\mathbf{{L}}_{1})(\mathbf{{L}}_{2}-\mathbf{{L}}_{1})=\mathbf{{u}}\end{aligned}$$

and,

$$\begin{aligned} \mathbf{{M}}=\left[ \begin{array}{ccc}m&{}0&{}0\\ 0&{}m&{}0\\ 0&{}0&{}I_z \end{array}\right] \;\;\;\;\; {{\text {and}}}\;\;\;\;\; \mathbf{{G}}=\left[ \begin{array}{c} 0\\ mg \\ 0 \end{array}\right] \end{aligned}$$

All mechanical parameters of the cable robot are given in Table (1). In order to demonstrate a high flexible system EA is intentionally chosen very low (EA $=$ 1,000). To show the effectiveness of the proposed composite control algorithm suppose that the system is at the origin and has to track the following smooth reference trajectories in x, y, and $\phi$ coordinates,

$$\begin{aligned} x_d= & {} 0.4+2e^{-t}-2.4e^{-t/1.2}\\ y_d= & {} 0.4+2e^{-t}-2.4e^{-t/1.2}\\ \phi _d= & {} 0.1\pi \sin (0.1\pi t) \end{aligned}$$

in which, the task space variables $x_p,y_p$ and $\phi$ reach a final value of 0.4, 0.4 and $0.1\pi$ from the zero states, respectively. The controller is based on (16) and consists of rigid control $\mathbf{{u}}_r$ given by (3) and the corrective term. Controller gain matrices are chosen as $\mathbf{{K}}_p=200\;\mathbf{{I}}_{3\times 3}$, $\mathbf{{K}}_v=25\;\mathbf{{I}}_{3\times 3}$, and $\mathbf{{K}}_d=250\;\mathbf{{I}}_{4\times 4}$ to satisfy the stability conditions. In the first step, rigid control $\mathbf{{u}}_r$ alone is applied to the manipulator. As is illustrated in Fig. (3), the manipulator experiences instability if only the rigid control $\mathbf{{u}}_r$ is applied to the system. The main reason for instability is the divergence of its fast variables. Figure (4) illustrates dynamic behavior of the closed-loop system with the proposed control algorithm. Internal force $\mathbf{{Q}}$ is used whenever at least one cable becomes slack (or $L_{1i}<L_{2i}\,\,,\,i=1,\ldots ,4$) to ensure that the cables remain in tension. Although, the system is very flexible the proposed control algorithm can suitably stabilize the system. As it is seen in this figure, position and orientation outputs track the desired values very well and the steady state errors are very small, while as it is shown in Fig. (5), all cables are in tension for the whole maneuver. The simulation results clearly show the effectiveness of the proposed control algorithm to stabilize the system, while achieving positive tension in the cables.

5 Conclusions

In this paper modeling and control of parallel cable robots with elastic cables are examined in detail. In the modeling process of this class of manipulators cables are modeled by linear axial springs, and the model of fully constrained cable driven robot is derived using Euler-Lagrange approach. Since in this type of robots cables must remain in tension in the whole workspace, the notion of internal force is introduced and it is used in the proposed control algorithm. The proposed composite control algorithm consists of three components. Rigid control according to the rigid model of the system, the internal force to ensures that all cables are in tension, and a damping term in cable length space to stabilize fast subsystem. Then, the model of the system is formulated in the standard form of singular perturbation theory and fast and slow variables are separated and incorporated in the stability analysis. The stability of the closed-loop system is analyzed through Lyapunov second method, and it is shown that the proposed composite controller is capable to stabilize the system in presence of flexible cables. Finally, the performance of the proposed composite controller is examined by simulation results performed on a planar cable robot.