An Approach to the Characterization of Flexure Hinges for the Purpose of Optimizing the Design of a Micromanipulator

Abstract

A crucial factor for estimating the performance of a flexure hinge based micromanipulator requires knowledge of stiffness or compliance matrices. These can be determined by using an analytical method, the finite element method (FEM) or an experimental method. Hence, a generalization and a FEM enhancement of the analytical method for calculating the compliance or stiffness matrix of flexure hinges are suggested. For an experimental validation of the approach a test stand is necessary. This test stand permits testing of bending and torsional characteristics of flexure hinge specimen.

1 Introduction

Conventional joints allow translational and/or rotational degrees of freedom by form or force closure theoretically without stiffness in the direction of movement and with infinite stiffness in the other, so-called parasitic directions. In contrast to these, flexure hinges gain there movability due to their own compliance and therefore have certain stiffness in all directions [1].

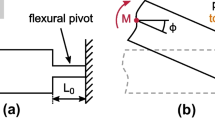
Among various types of flexure hinges, notch-joints are the most common [2]. There are different notch profiles to increase compliance in one or more directions [3]. Even though notch-joints are designable with two or three rotational degrees of freedom (DoF), those with only one DoF are preferably to be used, both in planar and spatial applications (cf. Fig. 1).

Fig. 1

Degrees of freedom and design of notch-joints 1DoF (a) 2DoF (b) and 3DoF (c)

Notch-joints have many advantages like free from backlash, frictionless and high potential for miniaturization. The disadvantages on the other hand are parasitic effects, motion deviation, and limited range of motion [4]. The stiffness- or compliance values need to be known to assess the operating characteristics. These values are necessary, because the stiffness or compliance matrix includes information about the desired and unwanted degrees of freedom, the motion accuracy and the range of motion [5].

The compliance matrix C defines a linear elastic context $\updelta = {\text{C}} \cdot\Lambda$ between the deformation vector δ and the load vector Λ in Eq. (1). Figure 2 shows a notch-joint that is cantilevered and subjected to forces (F_i) and torques (T_i) on the other side. The resulting translational and rotational deformations (u_i, θ_i) can be determined by either analytical methods, the finite element methods (FEM) or experimental methods These methods can be used to calculate the compliance matrix C and thus indirectly the stiffness matrix K = C⁻¹ of the notch-joint.

$$ \left( {\begin{array}{*{20}c} {{\text{u}}_{\text{x}} } \\ {{\text{u}}_{\text{y}} } \\ {{\text{u}}_{\text{z}} } \\ {\uptheta_{\text{x}} } \\ {\uptheta_{\text{y}} } \\ {\uptheta_{\text{z}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\text{C}}_{{{\text{u}}_{{_{\text{x}} }} ; {\text{F}}_{{_{\text{x}} }} }} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {{\text{C}}_{{{\text{u}}_{{_{\text{y}} }} ; {\text{F}}_{{_{\text{y}} }} }} } & 0 & 0 & 0 & {{\text{C}}_{{{\text{u}}_{{_{\text{y}} }} ; {\text{T}}_{{_{\text{z}} }} }} } \\ 0 & 0 & {{\text{C}}_{{{\text{u}}_{{_{\text{z}} }} ; {\text{F}}_{{_{\text{z}} }} }} } & 0 & {{\text{C}}_{{{\text{u}}_{{_{\text{z}} }} ; {\text{T}}_{{_{\text{y}} }} }} } & 0 \\ 0 & 0 & 0 & {{\text{C}}_{{\uptheta_{{_{\text{x}} }} ; {\text{T}}_{{_{\text{x}} }} }} } & 0 & 0 \\ 0 & 0 & {{\text{C}}_{{\uptheta_{\text{y}} ; {\text{F}}_{\text{z}} }} } & 0 & {{\text{C}}_{{\uptheta_{{_{\text{y}} }} ; {\text{T}}_{{_{\text{y}} }} }} } & 0 \\ 0 & {{\text{C}}_{{\uptheta_{\text{z}} ; {\text{F}}_{\text{y}} }} } & 0 & 0 & 0 & {{\text{C}}_{{\uptheta_{{_{\text{z}} }} ; {\text{T}}_{{_{\text{z}} }} }} } \\ \end{array} } \right)\,\left( {\begin{array}{*{20}c} {{\text{F}}_{\text{x}} } \\ {{\text{F}}_{\text{y}} } \\ {{\text{F}}_{\text{z}} } \\ {{\text{T}}_{\text{x}} } \\ {{\text{T}}_{\text{y}} } \\ {{\text{T}}_{\text{z}} } \\ \end{array} } \right)\,\, $$

(1)

Fig. 2

Notch-joint with right-elliptical cut-out

2 Generalization of the Analytical Method

The theory of the strength of materials provides a simple and rapid analytical method for calculating the compliance matrix of notch-joints. Because of this, there are already many approaches to describe the real operating behavior of notch-joints (first approach in [6]). In numerous previous publications set of formulas for a selected notch-joint was derived or optimized, whereas in this paper a general approach to the problem will be pursued.

Based on Castigliano’s second theorem (The first partial derivative of the strain energy U in a linear elastic structure with respect to the generalized force Q_i equals the generalized displacement q_i in the direction of Q_i [7]) the common elements of the compliance matrix C of notch-joints are determined [8] (cf. Eqs. (2–13).

Traction and Pressure along x-Axis:

$$ {\text{U}} = \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {\text{F}}\nolimits_{\text{x}}^{2} ({\text{x}})}}{{{\text{E}}\, \cdot {\text{A(x)}}}}} {\text{dx}}\,\, {\text{implies}}\,\,\left. {\frac{{\partial {\text{U}}}}{{\partial {\text{F}}_{\text{x}} }}} \right|_{{{\text{F}}_{\text{x}} { = 1}\,{\rm N}}} = {\text{C}}_{{{\text{u}}_{{_{\text{x}} }} ; {\text{F}}_{{_{\text{x}} }} }} = \frac{1}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{l} {\frac{\text{dx}}{\text{h(x)}}} $$

(2)

Deflection about z-Axis:

$$ {\text{U}} = \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {\text{T}}\nolimits_{\text{z}}^{ 2} ( {\text{x)}}}}{{{\text{E}}\, \cdot {\text{I}}_{\text{z}} ( {\text{x)}}}}} {\text{dx}} + \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {{\text{K}}\, \cdot {\text{F}}}\nolimits_{\text{y}}^{2} ({\text{x}})}}{{{\text{G}}\, \cdot {\text{A(x)}}}}} {\text{dx}} $$

(3)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{T}}_{\text{z}} }}} \right|_{{{\text{T}}_{\text{z}} { = 1}\,{\rm N}{\text{m,}}\,{\text{F}}_{\text{y}} { = 0}}} = {\text{C}}_{{\uptheta_{\text{z}} ; {\text{T}}_{\text{z}} }} = \frac{12}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} $$

(4)

$$ \begin{aligned} \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{F}}_{\text{y}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{z}} { = 0,} \\ \,{\text{F}}_{\text{y}} {\text{ = 1N}} \end{subarray} } & = {\text{C}}_{{{\text{u}}_{\text{z}} ; {\text{F}}_{\text{y}} }} \\ & = \frac{{12\, \cdot {\text{I}}^{2} }}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} - \frac{{24\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} {\text{dx}} + \frac{12}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{{{\text{x}}^{ 2} }}{{{\text{h}}^{ 3} ( {\text{x)}}}}} {\text{dx}} + \frac{\text{k}}{{{\text{G}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{\text{h(x)}}} \\ \end{aligned} $$

(5)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{T}}_{\text{z}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{z}} { = 0,}\, \\ {\text{F}}_{\text{y}} {\text{ = 1N}} \end{subarray} } = {\text{C}}_{{\uptheta_{\text{z}} ; {\text{F}}_{\text{y}} }} = \frac{{12\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} - \frac{12}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} {\text{dx}} $$

(6)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{F}}_{\text{y}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{z}} {\text{ = 1Nm,}} \\ \,{\text{F}}_{\text{y}} { = 0} \end{subarray} } = {\text{C}}_{{{\text{u}}_{\text{y}} ; {\text{T}}_{\text{z}} }} = \frac{{12\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} - \frac{12}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} {\text{dx}} $$

(7)

Deflection about y-Axis:

$$ {\text{U}} = \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {\text{T}}\nolimits_{\text{y}}^{ 2} ( {\text{x)}}}}{{{\text{E}}\, \cdot {\text{I}}_{\text{y}} ( {\text{x)}}}}} {\text{dx}} + \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {{\text{K}}\, \cdot {\text{F}}}\nolimits_{\text{z}}^{2} ({\text{x}})}}{{{\text{G}}\, \cdot {\text{A(x)}}}}} {\text{dx}} $$

(8)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{T}}_{\text{z}} }}} \right|_{{{\text{T}}_{\text{y}} { = 1}{\rm N}{\text{m,}}\,{\text{F}}_{\text{z}} { = 0}}} = {\text{C}}_{{\uptheta_{\text{z}} ; {\text{T}}_{\text{y}} }} = \frac{12}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} $$

(9)

$$ \begin{aligned} \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{F}}_{\text{z}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{z}} { = 0,} \\ \,{\text{F}}_{\text{y}} {\text{ = 1N}} \end{subarray} } & = {\text{C}}_{{{\text{u}}_{\text{z}} ; {\text{F}}_{\text{z}} }} \\ & = \frac{{12\, \cdot {\text{I}}^{2} }}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{{\text{h}}^{ 3} ( {\text{x)}}}}} - \frac{{24\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{\text{h(x)}}} {\text{dx}} + \frac{12}{{{\text{E}}\, \cdot {\text{w}}^{3} }}\int\limits_{0}^{\text{l}} {\frac{{{\text{x}}^{ 2} }}{\text{h(x)}}} {\text{dx}} + \frac{\text{k}}{{{\text{G}}\, \cdot {\text{w}}}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{\text{h(x)}}} \\ \end{aligned} $$

(10)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{T}}_{\text{y}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{y}} { = 0,}\, \\ {\text{F}}_{\text{z}} {\text{ = 1N}} \end{subarray} } = {\text{C}}_{{\theta_{\text{y}} - {\text{F}}_{\text{z}} }} = \frac{12}{{{\text{E}}\, \cdot {\text{w}}^{3} }}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{\text{h(x)}}} {\text{dx}} - \frac{{12\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}^{3} }}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{\text{h(x)}}} $$

(11)

$$ \left. {\frac{{\partial {\text{U}}}}{{\partial {\text{F}}_{\text{z}} }}} \right|_{\begin{subarray}{l} {\text{T}}_{\text{y}} { = 1}\,{\text{Nm,}}\, \\ {\text{F}}_{\text{z}} { = 0} \end{subarray} } = {\text{C}}_{{{\text{u}}_{\text{z}} - {\text{T}}_{\text{y}} }} = \frac{12}{{{\text{E}}\, \cdot {\text{w}}^{3} }}\int\limits_{0}^{\text{l}} {\frac{\text{x}}{\text{h(x)}}} {\text{dx}} - \frac{{12\, \cdot {\text{I}}}}{{{\text{E}}\, \cdot {\text{w}}^{3} }}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{\text{h(x)}}} $$

(12)

In the above equations ${\text{A(x)}} = {\text{w}}\, \cdot {\text{h(x)}}$ describes the cross-sectional area. If the shear effect is not negligible, the shear shape factor k is 1.2 (for rectangles) [7]. ${\text{I}}_{\text{z}} ({\text{x}}) = {\text{w}} \cdot {\text{h}}^{ 3} ( {\text{x)}}/12$ and ${\text{I}}_{\text{y}} ( {\text{x)}} = {\text{w}}^{3} \cdot {\text{h(x)}}/12$ are the moments of inertia about the z- and y-axis. E is the Young’s Modulus and G is the Modulus of Rigidity. In the above equations the notch-joint is fully described with a constant length l and width w and a variable height h(x). The variable height h(x) can be mathematically formulated for selected notch-joints for example a right-circular profile as ${\text{h(x)}} = 2{\text{r}} + {\text{t}} - 2\sqrt {{\text{r}}^{2} - ({\text{x}} - {\text{r}})^{2} }$ (cf. Fig. 2).

Such an approach is realized with mathematical software like MATLAB, because the problem of integrating several functions h(x) can be solved numerically instead of an analytical approach. Accordingly, a program for the efficient calculation of the compliance and stiffness matrix of user-modified notch-joint profiles has been developed with a graphical user interface where the compliance and stiffness matrixes are shown for chosen notch profiles and given parameters of geometry and material. It serves as a foundation for higher modules, in which the operating characteristics of a micromanipulator can be investigated by compliance and stiffness calculation of serial and parallel kinematic structures [9].

3 Extension of the Analytical Method with FEM

Based on the second theorem of Castigliano the general torsion of the compliance matrix of notch-joints can also be determined using Eq. (13).

$$ {\text{U}} = \frac{1}{2}\int\limits_{0}^{\text{l}} {\frac{{\mathop {\text{T}}\nolimits_{\text{x}}^{ 2} ( {\text{x)}}}}{{{\text{G}} \cdot {\text{I}}_{\text{x}} ( {\text{x)}}}}} {\text{dx}}\,\, {\text{implies}}\,\,\left. {\frac{{\partial {\text{U}}}}{{\partial {\text{T}}_{\text{x}} }}} \right|_{{{\text{T}}_{\text{x}} { = }1{\rm N}{\text{m}}}} = {\text{C}}_{{\uptheta_{\text{x}} - {\text{T}}_{\text{x}} }} = \frac{1}{\text{G}}\int\limits_{0}^{\text{l}} {\frac{\text{dx}}{{\mathop {\text{\rm I}}\nolimits_{\text{x}} ( {\text{x)}}}}} $$

(13)

I_x(x) is the moment of Inertia in case of a torsion about the x-Axis and results from various approximation formulas such as [10]

$$ {\text{I}}_{\text{x}} ( {\text{x)}} = {\text{w}} \cdot {\text{h}}^{3} ({\text{x}}) \cdot \left[ {0.333 - 0.21 \cdot \frac{\text{h(x)}}{\text{w}} \cdot \left( {1 - \frac{{{\text{h}}^{4} ({\text{x}})}}{{12 \cdot {\text{w}}^{4} }}} \right)} \right] $$

(14)

which is used in [8]. These approximation formulas lead to a very high torsional compliance, which is not detectable due to the lack of warping torsion in notch-joints (cf. Table 1).

Table 1 Torsional compliance of right circular notch-joint (w = 16 mm, r = 2 mm)

Reliable results for all elements of the compliance matrix (including torsion) can be achieved with the help of FEM (such as in [11]). Modelling a large variety of similar notch-joints within the FEM-software is a very complex process. To work around the problem of “modelling by hand” a script oriented solution has been used. An approach like this allows a comprehensive characterization of notch-joints based on the results of previous studies [12]. The focus here is on circular and elliptical notch-joint profiles, as special cases of a general elliptical notch profile [13] (Fig. 3b). An analysis is conducted, in which the geometry parameters are varied and their effects on the operating behavior are taken into account. The results show that corresponding circular and elliptical notch-joints have similar properties. Furthermore, the properties of the circular notch-joints are nearly linear in contrast to those of the elliptical notch-joints. Thus these properties can be formulated mathematically by using low degree polynomials [14] (cf. Fig. 3a).

Fig. 3

Comparisons of circular and elliptical notch-joints with reference to bending compliance (top) or motion range (bottom) (a) and different notch-profiles (b)

4 Experiment

For experimental validation of the method described above, a test stand has been constructed on which the bending and torsional compliance of the tested notch-joints could be examined. The bending compliance (about the z-axis) causes the desired rotary degree of freedom and the torsional compliance (about the x-axis) causes the “most” unwanted parasitic motion [14]. The test stand consists of the frame and the plate. In each of them one end of the tested notch-joint-specimen is clamped. The plate contains the force sensors and also serves as a lever arm through which the notch-joint is subjected to load and deformed. Micrometer screws are attached onto the frame and generate the stroke which corresponds to a bending- or torsional-deformation of the notch-joint. The subsequent bending- or torsional-stress is indicated by a voltage, which is measured by the force sensor (cf. Fig. 4).

Fig. 4

Test stand (a) and schematic representation of setup for estimating the bending compliance (b) and torsional compliance (d) of the test specimen (circular notch joints) (c)

The profile of the tested notch-joints is circular. The geometry parameters are as follows: w = 16 mm, l = 4 mm, t = 0.4 mm, r = 3 mm. Despite the tight manufacturing tolerances achieved by eroding, the influence of the deviation in the hinge thickness on the bending- and torsional compliance cannot be neglected (Fig. 5).

Fig. 5

The effect of deviation in the hinge thickness of circular notch-joints (based on FEM: w = 15.95 mm, l = 4 mm, r = 3 mm). a Bending compliance. b Torsional compliance

After the quality inspection using scanning electron microscopy two tested notch-joints with the same width (w = 15.952 mm) and maximum difference in minimum hinge thickness (t1 = 401.7 µm, t2 = 408.5 µm) are selected for the comparative analysis. In addition to the experimental results, the corresponding analytical and FEM results are presented in Tables 2, 3.

Table 2 Bending compliance of tested notch-joints (w = 15.95 mm, l = 4 mm, r = 3 mm)

Table 3 Torsional compliance of tested notch-joints (w = 15.95 mm, l = 4 mm, r = 3 mm)

5 Conclusions

The experimental results show that an increasing minimum hinge thickness in the tested notch-joints logically leads to a reduction of the bending and torsion compliances; bending: 7.5 %, torsion: 2.5 %. These results are in a good conformity with the FEM results; bending: 4.1 %, torsion 2.3 %. While comparing the compliance, the results of FEM using Young’s Modulus E ≈ 95 … 100 GPa also show good conformity. The material of the tested notch-joints-specimen is Ti-6Al-4 V. The Young’s Modulus of this material is E ≈ 110 GPa [15]. The real value of E for the semi-finished part before and after finishing is unknown. Therefore, an experimental verification of the Young’s Modulus of the notch-joints is necessary to evaluate the methods for calculating compliance matrices of notch-joints. Only with a reliable and accurate value of the elastic modulus is required to discuss measurement errors, and to examine correlations between the analytical method, the finite element method and the experimental method.