Detecting and Tracking Sports Players with Random Forests and Context-Conditioned Motion Models

Abstract

Player movements in team sports are often complex and highly correlated with both nearby and distant players. A single motion model would require many degrees of freedom to represent the full motion diversity of each player and could be difficult to use in practice. Instead, we introduce a set of Game Context Features extracted from noisy detection data to describe the current state of the match, such as how the players are spatially distributed. Our assumption is that players react to the current game situation in only a finite number of ways. As a result, we are able to select an appropriate simplified motion model for each player and at each time instant using a random decision forest which examines characteristics of individual trajectories and broad game context features derived from all current trajectories. Our context-conditioned motion models implicitly incorporate complex interobject correlations while remaining tractable. We demonstrate significant performance improvements over existing multitarget tracking algorithms on basketball and field hockey sequences of several minutes in duration containing 10 and 20 players, respectively.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Multitarget tracking has been a difficult problem of broad interest for years in computer vision. Surveillance is perhaps the most common scenario for multitarget tracking, but team sports is another popular domain that has a wide range of applications in strategy analysis, automated broadcasting, and content-based retrieval. Recent work in pedestrian tracking has demonstrated promising results by formulating multitarget tracking in terms of data association [1, 5, 8, 20, 25, 28, 30, 32]. A set of potential target locations are estimated in each frame using an object detector, and target trajectories are inferred by linking similar detections (or tracklets) across frames. However, if complex intertracklet affinity models are used, the association problem becomes NP-hard.

Fig. 6.1

Motion Models. A player’s future motion is contingent on the current game situation. The global distribution of players often indicates which team is attacking, and local distributions denote when opposing players are closely following each other. We use contextual information such as this to create a more accurate motion affinity model for tracking players. The overhead views of basketball and field hockey show the input detections and corresponding ground truth annotations. Player trajectories are strongly correlated with both nearby and distant players

Tracking players in team sports has three significant differences compared to pedestrians in surveillance. First, the appearance features of detections are less discriminative because players on the same team will be visually similar. As a result, the distinguishing characteristics of detections in team sports are primarily position and velocity. Second, sports players move in more erratic fashions, whereas pedestrians tend to move along straight lines at a constant speed. Third, although pedestrians deviate to avoid colliding with each other, the motions between pedestrians are rarely correlated in complex ways (some scenarios, like sidewalks, may contain a finite number of common global motions). The movements of sports players, on the other hand, are strongly correlated both locally and globally. For example, opposing players may exhibit strong local correlations when ‘marking’ each other (such as one-on-one defensive assignments). Similarly, players who are far away from each other move in globally correlated ways because they are reacting to the same ball (Fig. 6.1).

Simple, independent motion models have been popular for pedestrian tracking because they limit the complexity of the underlying inference problem [8]. However, the models may not always characterize the motion affinity between a pair of tracklets accurately. Brendel et al. [5] modeled intertarget correlations between pedestrians using context, which consisted of additional terms in the data association affinity measure based on the spatiotemporal properties of tracklet pairs. Following this convention, we will describe correlations between player movements in terms of game context. Much like the differences between the individual target motions in surveillance and team sports, game context is more complex and dynamic compared to context in surveillance. For example, teams will frequently gain and lose possession of the ball, and the motions of all players will change drastically at each turnover.

Because a player’s movement is influenced by multiple factors, the traditional multitarget tracking formulation using a set of independent autoregressive motion models is a poor representation of how sports players actually move. However, motion affinity models conditioned on multiple targets (and that do not decompose into a product of pairwise terms) make the data association problem NP-hard [8]. In this work, we show how data association is an effective solution for sports player tracking by devising an accurate model of player movements that remains tractable by conditioning on features describing the current state of the game, such as which team has possession of the ball. One of our key contributions is a new set of broad game context features (GCF) for team sports, and a methodology to estimate them from noisy detections. Using game context features, we can better assess the affinity between trajectory segments by implicitly modeling complex interactions through a random decision forest involving a combination of kinematic and game context features. We demonstrate the ability to track 20 players in over 30 min of international field hockey matches, and 10 players in 5 min of college basketball.

2 Related Work

Recent success in pedestrian tracking has posed multitarget tracking as hierarchical data association: long object trajectories are found by linking together a series of detections or short tracklets. The problem of associating tracklets across time has been investigated using a variety of methods, such as the Hungarian algorithm [10, 21], linear programming [11], cost flow networks [30], maximum weight independent sets [5], continuous-discrete optimization [4], and higher order motion models [8]. Data association is often formulated as a linear assignment problem where the cost of linking one tracklet to another is some function of extracted features (typically motion and appearance). More recent work (discussed shortly) considers more complex association costs.

Crowds are an extreme case of pedestrian tracking where it is often not possible to see each individual in their entirety. Because of congestion, pedestrian motions are often quite similar and crowd tracking algorithms typically estimate a finite set of global motions. Often, the affinity for linking two tracklets together depends on how well the hypothesized motion agrees with one of the global motions. References [1, 32] solve tracking in crowded structured scenes with floor fields estimation and Motion Structure Tracker, respectively. Reference [23] uses a Correlated Topic Model for crowded, unstructured scenes.

Team sports is another relevant domain for multitarget tracking [24], with algorithms based on particle filters being extremely popular [6, 9, 14, 16, 18, 27]. However, results are quite often demonstrated only on short sequences (typically less than two minutes). In contrast, only a small amount of work has investigated long-term sports player tracking. Nillius et al. [19] generated a Bayes network of splitting and merging tracklets for a long 10-minute soccer sequence, and found the most probable assignment of player identities using max-margin message passing. Kumar and Vleeschouer proposed discriminative label propagation [2] and Shitrit et al. use multicommodity network flow for tracking multiple people [26].

In both pedestrian and player tracking, object motions are often assumed to be independent and modeled as zero displacement (for erratic motion) and/or constant velocity (for smooth motion governed by inertia). In reality, the locations and motions of sports players are strongly correlated. Pairwise repulsive forces have been used in multitarget tracking to enforce separability between objects [3–5, 12, 29]. Recently, multiobject motion models have been used in pedestrian tracking to anticipate how people will change their trajectories to avoid collisions [20], or for estimating whether a pair of trajectories have correlated motions [5]. In team sports, Kim et al. [13] estimated motion fields using the velocities of tracklets to anticipate how the play would evolve, but did not use the motion fields to track players over long sequences. Zhang et al. [31] augmented the standard independent autoregressive motion model with a database of a priori trajectories manually annotated from other games.

3 Hierarchical Data Association Tracking

Our tracking formulation (see Fig. 6.2) employs an object detector to generate a set $\fancyscript{O}$ of hypothesized sports player locations through the duration of the video. Each detection $\fancyscript{O}_i = [ t_i, \mathbf {x}_i, \mathbf {a}_i ]$ contains a time stamp, the player’s location on the ground plane, and the player’s appearance information, respectively. The goal is to find the most probable set $\fancyscript{T}^\star = \{ \fancyscript{T}_1, \fancyscript{T}_2, \ldots , \fancyscript{T}_N \}$ of player trajectories where each trajectory is a temporal sequence of detections $\fancyscript{T}_n = \{ \fancyscript{O}_a, \fancyscript{O}_b, \ldots \}$

$$\begin{aligned} \fancyscript{T}^\star = \arg \max _\fancyscript{T} {P(\fancyscript{O} | \fancyscript{T})P(\fancyscript{T})}. \end{aligned}$$

(6.1)

The likelihood $P(\fancyscript{O} | \fancyscript{T})$ indicates how well a set of trajectories $\fancyscript{T}$ matches the observations, and the prior $P(\fancyscript{T})$ describes, in the case of sports tracking, how realistic the set of estimated player trajectories $\fancyscript{T}$ is. In multitarget tracking, the prior is often simplified to consider each trajectory as an independent Markov chain

$$\begin{aligned} P(\fancyscript{T})&\sim \prod _n P(\fancyscript{T}_n)\end{aligned}$$

(6.2)

$$\begin{aligned}&\sim \prod _n{\prod _{t}{P(\fancyscript{T}_n^t|\fancyscript{T}_n^{t-1})}}, \end{aligned}$$

(6.3)

where $\fancyscript{T}_n^t$ indicates the trajectory of the $n$th player at time interval $t$.

Fig. 6.2

Algorithm. Our tracking algorithm has five distinct phases: detection, low-level tracklets, mid-level tracks, game context features, and high-level trajectories

In team sports, the prior is a highly complex function and is not well approximated by a series of independent trajectory assessments. We maintain the formulation of conditional independence between trajectories, but condition each individual trajectory prior on a set of game context features $\theta$ which describe the current state of the match

$$\begin{aligned} P(\fancyscript{T}) \mathop {=}\limits ^{\mathrm {def}}\prod _{n,t} P(\fancyscript{T}_n^{t-1} \rightarrow \fancyscript{T}_n^{t} | \theta ). \end{aligned}$$

(6.4)

Conditioning the individual motion models on game context implicitly encodes higher order intertrajectory relationships and long-term intratrajectory information without sacrificing tractability.

3.1 Detection

We use the method of Carr et al. [7] to generate possible $(x,y)$ positions of players in all video frames. The technique requires a calibrated camera, and uses background subtraction to generate foreground masks. Player locations are estimated by evaluating how well a set of hypothesized 0.5-m-wide cylinders 1.8 m tall can explain each observed foreground mask. The method is tuned to only detect high confidence situations, such as when a player is fully visible and well separated from other players. For each detected position, a rectified patch is extracted from the image and a coarse RGB histogram (4 bins per channel) is computed as an appearance feature. The first few seconds of video are accompanied by user supplied labels: each detection is assigned to one of four categories {home, away, referee, none}. A random forest is constructed from the training data, and at test time, outputs the four-class probability histogram for each detection.

3.2 Hierarchical Association

Because the solution space of data association grows exponentially with the number of frames, we adopt a hierarchical approach to handle sequences that are several minutes long (see Fig. 6.3).

Fig. 6.3

Hierarchical data association. a Low-level tracklets $\varUpsilon$ from noisy detections; b mid-level tracks $\varGamma$ obtained via the Hungarian algorithm [10]; c $N$ high-level player trajectories $\fancyscript{T}$ via a cost flow network [30]

3.2.1 Low-Level Tracklets

A set $\varUpsilon$ of low-level trackletsis extracted from the detections by fitting constant velocity models to clusters of detections in $0.5$ s long temporal windows using RANSAC. Each $\varUpsilon _i$ represents an estimate of a player’s instantaneous position and velocity (see Fig. 6.4).

3.2.2 Mid-Level Tracks

Similar to [10], the Hungarian algorithm is used to combine subsequent low-level trajectories into a set $\varGamma$ of mid-level tracks up to $60$ s in duration. The method automatically determines the appropriate number of mid-level tracks, but is tuned to prefer shorter, more reliable tracks. Generally, mid-level tracks terminate when abrupt motions occur or when a player is not detected for more than 2 s.

Fig. 6.4

Low-level Tracklet Extraction. Each detection is represented as a circle with a frame number. a Detection responses within a local spatial-temporal volume; b identified clusters; and c RANSAC-fitted constant velocity models (red)

Fig. 6.5

Cost flow network from mid-level tracks. Each small circle with a number inside indicates a detection and its time stamp. Colored edges on the left indicate mid-level track associations. The corresponding cost flow network is shown on the right. Each mid-level track $\varGamma _i$, as well as the global source $s$ and sink $t$ forms a vertex, and each directed edge in black from vertex $a$ to $b$ has a cost indicating the negative affinity of associating $\varGamma _a$ to $\varGamma _b$

3.2.3 High-Level Trajectories

MAP association is equivalent to the minimum cost flow in a network [30] where a vertex $i$ is defined for each mid-level track $\varGamma _i$ and edge weights reflect the likelihood and prior in (6.4). Unlike the Hungarian algorithm, it is possible to constrain solutions to have exactly $N$ trajectories by pushing $N$ units of flow between special source $s$ and sink $t$ vertices (see Fig. 6.5). The complete trajectory $\fancyscript{T}_n$ of each player corresponds to the minimum cost path for one unit of flow from $s$ to $t$. The cost $c_{ij}$ per unit flow from $i$ to $j$ indicates the negative affinity, or negative log likelihood that $\varGamma _j$ is the immediate successor of $\varGamma _i$, which we decompose into probabilities in continuity of appearance, time, and motion

$$\begin{aligned} c_{ij}&= -\log {P(\fancyscript{O}|\varGamma _i \rightarrow \varGamma _j )P(\varGamma _i \rightarrow \varGamma _j|\theta )}\end{aligned}$$

(6.5)

$$\begin{aligned}&= -\log {( P_a \cdot P_\tau \cdot P_m )}. \end{aligned}$$

(6.6)

The probability that $\varGamma _i$ and $\varGamma _j$ belong to the same team is

$$\begin{aligned} P_a(\varGamma _i \rightarrow \varGamma _j)=a_i\cdot a_j +(1-a_i)\cdot (1-a_j) \end{aligned}$$

(6.7)

where $a_i$ and $1-a_i$ are the confidence scores of the mid-level track belonging to team $A$ and $B$, respectively.

Let $t_{i0}$ and $t_{i1}$ denote the start and end times of $\varGamma _i$, respectively. If $\varGamma _j$ is the immediate successor of $\varGamma _i$, any nonzero time gap implies that missed detections must have occurred. Therefore, the probability based on temporal continuity is defined as

$$\begin{aligned} P_{\tau }(\varGamma _i \rightarrow \varGamma _j) = \exp (-\lambda (t_{j0}-t_{i1})). \end{aligned}$$

(6.8)

Each mid-level trajectory $\varGamma _i$ has “miss-from-the-start” and “miss-until-the-end” costs on edges $(s, i)$ and $(i,t)$, respectively. The weights are computed using (6.8) for temporal gaps $(T_0,t_{i0})$ and $(t_{j1},T_1)$, where $T_0$ and $T_1$ are the global start and end times of the sequence.

Before describing the form of $P_m(\varGamma _i \rightarrow \varGamma _j | \theta )$ in more detail, we first discuss how to extract a set of game context features $\theta$ from noisy detections $\fancyscript{O}$.

4 Game Context Features

In team sports, players assess the current situation and react accordingly. As a result, a significant amount of contextual information is implicitly encoded in player locations. In practice, the set of detected player positions in each frame contains errors, including both missed detections and false detections. We introduce four game context features (two based on absolute position and two based on relative position) for describing the current game situation with respect to a pair of mid-level tracks that can be extracted from a varying number of noisy detected player locations $\fancyscript{O}$.

4.1 Absolute Occupancy Map

We describe the distribution of players during a time interval using an occupancy map, which is a spatial quantization of the number of detected players, so that we get a description vector of constant length regardless of missed and false detections. We also apply a temporal averaging filter of $1$s on the occupancy map to reduce the noise from detections. The underline assumption is that players may exhibit different motion patterns under different spatial distributions. For example, a concentrated distribution may indicate a higher likelihood of abrupt motion changes, and smooth motions are more likely to happen during player transitions with a spread-out distribution.

Fig. 6.6

Absolute occupancy map. Four clusters are automatically obtained via K-means: a center-concentrated, b center-diffuse, c goal, and d corner. The rows show: noisy detections (top), estimated occupancy map (middle), and the corresponding cluster center (bottom), which is symmetric horizontally and vertically

We compute a time-averaged player count for each quantized area. We assume the same distribution could arise regardless of which team is attacking, implying a $180^\circ$ symmetry in the data. Similarly, we assume a left/right symmetry for each team, resulting in a fourfold compression of the feature space.

Similar to visual words, we use K-means clustering to identify four common distributions (see Fig. 6.6) roughly characterized as: center-concentrated, center-diffuse, goal, and corner.

When evaluating the affinity for $\varGamma _i \rightarrow \varGamma _j$, we average the occupancy vector over the time window $(t_{i1},t_{j0})$ and the nearest cluster ID is taken as the context feature of absolute occupancy $\theta _{ij}^{(A)}=k\in \{1,\ldots K\}$.

The spatial quantization scheme may be tuned for a specific sport, and does not necessarily have to be a grid.

4.2 Relative Occupancy Map

The relative distribution of players is often indicative of identity [19] or role [17]. For example, a forward on the right side typically remains in front and to the right of teammates regardless of whether the team is defending in the back-court or attacking in the front-court. Additionally, the motion of a player is often influenced by nearby players.

Therefore, we define a relative occupancy map specific to each low-level tracklet $\varUpsilon _i$ which quantizes space similarly to the shape context representation: distance is divided into two levels, with a threshold of 4 m, and direction into four bins (see Fig. 6.7). The per-team occupancy count is then normalized to sum to one for both the inner circle and outer ring. Like absolute occupancy maps, we cluster the $16$ bin relative occupancy counts (first 8 bins describing same-team distribution, last 8 bins describing opponent distribution) into a finite set of roles using K-means.

For each pair of possible successive $\varGamma _i \rightarrow \varGamma _j$ mid-level tracks, we extract the occupancy vector $\mathbf {v}_i$ and $\mathbf {v}_j$, with cluster ID $k_i$, $k_j$, from the end tracklet of $\varGamma _i$ and the beginning tracklet of $\varGamma _j$. We also compute the Euclidian distance of $d_{ij}=|\mathbf {v}_i-\mathbf {v}_j|_2$. Intuitively, a smaller $d_{ij}$ indicates higher likelihood that $\varGamma _j$ is the continuation of $\varGamma _i$. The context feature of relative occupancy is the concatenation of $\theta _{ij}^{(R)}=(d_{ij}, k_i, k_j)$.

4.3 Focus Area

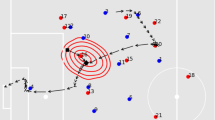
In team sports such as soccer or basketball, there is often a local region with relatively high player density that moves smoothly in time and may indicate the current or future location of the ball [13, 22]. The movement of the focus area in absolute coordinates also strongly correlates to high-level events such as turnovers. We assume the movement of individual players should correlate with the focus area over long time periods, thus this feature is useful for associations $\varGamma _i \rightarrow \varGamma _j$ with large temporal gaps (when the motion prediction is also less reliable). For example, mid-level trajectory $\varGamma _i$ in Fig. 6.8 is more likely to be matched to $\varGamma _{j1}$ with a constant velocity motion model. However, if the trajectory of the focus area is provided as in Fig. 6.8, it is reasonable to assume $\varGamma _i \rightarrow \varGamma _{j2}$ has a higher affinity than $\varGamma _i \rightarrow \varGamma _{j1}$.

Fig. 6.7

Relative occupancy map. The quantization scheme is centered on a particular low-level tracklet $\varUpsilon _i$ at time $t$. The same-team distribution and opponent distribution are counted separately

Fig. 6.8

Focus area. Kinematic constraints are less reliable across larger time windows. Because player motions are globally correlated, the affinity of two mid-level tracks over large windows should agree with the overall movement trend of the focus area

We estimate the location and movement of the focus area by applying meanshift mode-seeking to track the local center of mass of the noisy player detections. Given a pair of mid-level tracks with hypothesized continuity $\varGamma _i \rightarrow \varGamma _j$, we interpolate the trajectory within the temporal window $(t_{i1}, t_{j0})$ and calculate the variance of its relative distance to the trajectory of the focus area $\sigma _{ij}$. We also extract the average speed of the focus area $v_f$ during the time window, which describes the momentum of the global motion. The focus area context feature is thus set as $\theta _{ij}^{(F)}=(\sigma _{ij}, v_f)$.

4.4 Chasing Detection

Individual players are often instructed to follow or mark a particular opposition player. Basketball, for example, commonly uses a one-on-one defense system where a defending player is assigned to follow a corresponding attacking player. We introduce chasing (close-interaction) links to detect when one player is marking another. If the trajectories $\varGamma _i$ and $\varGamma _j$ both appear to be following a nearby reference trajectory $\varGamma _k$, there is a strong possibility that $\varGamma _j$ is the continuation of $\varGamma _i$ (assuming the mid-level track of the reference player is continuous during the gap between $\varGamma _i$ and $\varGamma _j$, see Fig. 6.9).

Fig. 6.9

Chasing. If $\varGamma _i$ and $\varGamma _j$ both correlate to a nearby track $\varGamma _k$, there is a higher likelihood that $\varGamma _j$ is the continuation of $\varGamma _i$

Fig. 6.10

Visualization of all game context features, where detections of different teams are plotted as blue and red dots. a The computed occupancy map based on noisy player detection; b the corresponding cluster center of the global occupancy map; c indicator of the role categories of each player based on its local relative occupancy map; d the focus area; and e chasing between players from different teams

We identify chasing links by searching for pairs of low-level tracklets $(\varUpsilon _i,\varUpsilon _k)$ that are less than 2 m apart and moving along similar directions (We use the angular threshold of $45^{\circ }$ during the experiment). Let $\tau _{ij|k}$ be the temporal gap between $\varGamma _i$’s last link with $\varGamma _k$ and $\varGamma _j$’s first link with $\varGamma _k$, and $\tau _{ij|k}=\infty$ when there are no links between either $\varGamma _i$ or $\varGamma _j$ and $\varGamma _k$. The chasing continuity feature $\theta _{ij}^{(C)}$ that measures whether trajectories $\varGamma _i$ and $\varGamma _j$ are marking the same player is given by

$$\begin{aligned} \theta _{ij}^{(C)}=\min _{k=1,\ldots /i,j}\{\tau _{ij|k}\}. \end{aligned}$$

(6.9)

Intuitively, the likelihood that ($\varGamma _i$, $\varGamma _j$) correspond to the same player increases as $\theta _{ij}^{(C)}$ decreases.

A visualization of all game context features is shown in Fig. 6.10. Features based on position appear on the left. The computed instantaneous occupancy map (a) and its corresponding cluster center (b) are shown underneath. Each mid-level track is assigned to one of the four role categories based on its local relative occupancy map as indicated in (c). Features based on motion appear on the right. The focus area (d) is shown as a dashed ellipse, and (e) detected correlated movements between opposition players is illustrated using green lines.

5 Context-Conditioned Motion Models

Although we have introduced a set of context features $\theta =\{\theta ^{(A)},\theta ^{(R)},\theta ^{(F)},\theta ^{(C)}\}$, it is nontrivial to design a single fusion method for generating the final motion likelihood score. For instance, each game context feature may have varying importance between different sports. For example, the chasing-based feature is less important in sports where one-on-one defense is less common. To make our framework general across different sports, we use a purely data-driven approach to learn a motion model which uses both the traditional kinematic features as well as our game context features.

The kinematic features $\mathbf {K}=\{t_g, e_0, e_1, e_2, \varDelta \mathbf {v}\}$ describe the motion smoothness between two successive mid-level tracks $\varGamma _i \rightarrow \varGamma _j$, and is based on the distance error with extrapolate constant position, constant velocity, and constant acceleration models, respectively. Additionally, the velocity change in velocity is also included (see Table 6.1).

Table 6.1 Our context-conditioned motion models employ traditional kinematic features [10], such as the position extrapolation error when joining two tracks across a temporal gap

We generate training data by extracting kinematic features $f_{ij}^{(K)}$ and game context features $\theta _{ij}$ for all pairs of mid-level tracks $(\varGamma _i,\varGamma _j)$ that have a temporal gap $t_{g|i\rightarrow j}\in [0, 60)$ seconds. Using ground truth tracking data, we assign binary labels $y_{ij}\in \{1,0\}$ indicating whether the association is correct or not (two trajectories belonging to the same ground truth player identity). However, the total number of incorrect associations are usually much more than the correct ones. To avoid severely unbalanced training data, we only select a subset of hard negative examples that has high motion smoothness.

A random forest containing $500$ decision trees is then trained to learn the mapping $C(f_{ij}^{(k)},\theta _{ij})\rightarrow y_{ij}$. A random forest is robust against the overfitting that might occur when using limited training data via bootstrapping, especially when the data is not easily separable due to association ambiguity in the real world. More importantly, by recursively splitting the data with random subsets of features, the random forest model automatically optimizes local adaptivity, i.e., decisions for linking pairs of tracks having small or large temporal gaps may be split at different levels and handled with different feature sets. As confirmed in our experiments (see Sect. 6.6), the occupancy feature is more effective at handling short-term association (when feature $t_g$ is small) and the chasing feature is more important in connecting trajectories with long temporal gaps ($t_g$ is big).

During the testing stage, the average classification score across all trees provides a continuous affinity score to approximate $P(\varGamma _i\rightarrow \varGamma _j|\theta )=C(f_{ij}^{(K)},\theta _{ij})$ in Eq. (6.5).

6 Experiments

We validate our framework on two sports: field hockey with 20 players and basketball with 10 players. Player detection is transformed from multiple calibrated views using the method in [7] with frame rates of $30$ (hockey) and $25$ (basketball), respectively. We use simple RGB-based color histogram classifiers to estimate the confidence score $a_i\in [0,1]$ of track $i$ belonging to home team or the away team. We also discard tracks likely to correspond to the referees and goalies.

6.1 Baseline Models and Evaluation Metrics

To verify the contribution of the various GCFs, we construct five models for a quantitative comparison. All models apply hierarchical association and start with the same set of mid-level tracks $\{ \varGamma \}$. The only difference between the models is the motion affinity used during the final association stage. Model 1 ($K$) only uses kinematic features ($f^{(K)}$) for training, which is equivalent to the combined algorithm of [10, 15, 30]. Models 2–4 use focus area features ($F$), chasing related features ($C$), and occupancy feature ($A+R$), respectively, in addition to motion-smoothness features. Model 5 uses all features $(f^{(K)},\theta )$.

We have also examined other features for describing aspects of game context, such as variance of track velocity or team separability. However we found these features to be less effective than the ones described in Sect. 6.4.

Three errors are commonly evaluated in the multitarget tracking literature: (1) the number of incorrect associations $N_{\mathrm{{err}}}$, (2) the number of missed detections $N_{\mathrm{{miss}}}$, and (3) the number of false detections $N_{\mathrm{{fa}}}$. The Multiple Object Tracking Accuracy measure $MOTA=1-(N_{\mathrm{{err}}}+N_{\mathrm{{miss}}}+N_{\mathrm{{fa}}})/N$ combines all three errors with equal weighting. However the equal weighting de-emphasizes $N_{\mathrm{{err}}}$ in a hierarchical association framework with a high frame rate. Therefore, we report the individual error sources and normalize for the situation of a known fixed number of objects: $N_{\mathrm{{err}}}^*$ is an average count of incorrect ID associations per minute per player; $P_{\mathrm{{miss}}}$ and $P_{\mathrm{{fa}}}$ are the proportion of missed and false mid-level trajectory segments of $\fancyscript{T}_n$ as compared to the ground truth, ranging from $0$ to $1$.

Fig. 6.11

Demonstration of evaluation metrics for high-level association (red)

In addition to overall tracking performance, we also evaluate in isolation the high-level association stage $\{ \varGamma \} \rightarrow \fancyscript{T}$, which is the key part of our framework. We report association precision and recall rate, where $\mathrm{precision }=N_{\mathrm{{TP}}}/(N_{\mathrm{{TP}}}+N_{\mathrm{{FA}}})$, and $N_{\mathrm{{TP}}}$, $N_{\mathrm{{FA}}}$ are correct/incorrect number of associations of $\varGamma _i \rightarrow \varGamma _j$. We define $\mathrm{recall }=1-T_{\mathrm{{miss}}}/T_{\mathrm{{gap}}}$, where $T_{\mathrm{{gap}}}$ is the accumulation of temporal gaps $t_{\mathrm{{gap}}}$ between high-level associations, and $T_{\mathrm{{miss}}}$ is the total length of mid-level tracks $\varGamma _i$ being missed. The motivation is to exclude miss-associations in previous stages. An illustration of these metrics is given in Fig. 6.11. Finally, we also report the statistics of average length temporal gap $\overline{t}_{\mathrm{{gap}}}$ being correctly associated during the high-level association, which reflects the algorithm’s ability to associate trajectories with long-term misses.

6.2 Field Hockey Dataset

We generated and labeled six field hockey sequences for a total length of 29 min, from three games played by different teams. The average player detection miss and false-alarm rates are $14.0$ and $10.3\,\%$, respectively, or the multitarget detection accuracy $\mathrm{MODA }=1-(N_{\mathrm{{miss}}}+N_{\mathrm{{fa}}})/N=0.75$. Our first experiment uses as much training data as possible: testing one sequence and using the remaining five for training.

The introduction of each individual GCF achieves better performance, and using all GCFs generally produces the best performance (see Table 6.2).

According to Table 6.2, all methods are good in terms of low false-alarm rate. Thus the major difference in their performances is reflected in the terms for incorrect association $N_{\mathrm{{err}}}^*$ and miss association $P_{\mathrm{{err}}}$.

We can also introduce a weighting $w_m$ on motion likelihood relative to the appearance likelihood into the objective function of Eq. (6.1), where $w_m$ plays an essential role in the trade-off between miss-associations and false associations:

$$\begin{aligned} \log P(\fancyscript{T}|\fancyscript{O},\theta ) = \log P(O|\fancyscript{T}) +w_m\cdot \log P(\fancyscript{T}|\theta ) +c. \end{aligned}$$

(6.10)

Instead of the default setting of $w_m=1$, a lower weight for the motion likelihood ($w_m<1$) gives higher priority to optimizing the observation likelihood $P(O|\varGamma )$, which prefers to have fewer missing players. On the other hand, a higher weighting $w_m>1$ encourages smoother motions and results in fewer false alarms but more missed detections. As we vary $w_m$ from $0.2$ to $3$, the tradeoff curves are plotted in Fig. 6.12a.

Table 6.2 Quantitative evaluations on field hockey dataset

Table 6.3 Quantitative evaluations on basketball dataset

We also conduct an experiment studying the cross-game-generalization of the GCFs. Instead of testing 1 sequence trained on the other 5, we perform all pairwise combinations (30 in total) of 1 sequence training with 1 other sequence testing. We then evaluate the resulting statistics for same-game learning and different-game learning, respectively, as summarized in Table 6.3.

Fig. 6.12

Trade-off curve between $P_{\mathrm{{miss}}}$ and $N_{\mathrm{{err}}}^*$ for a field hockey sequences and b basketball sequences. $N_{\mathrm{{err}}}^*$ is an averaged association error per minute per person. The triangle marks indicate the default operating point ($w_m=1$ in Eq. (6.10)). Our proposed method using all GCFs achieves more than $10\,\%$ of improvements on both cases

Table 6.4 Comparison of same/cross-game learning (hockey)

It can be seen that the introduction of GCFs again improves the result both in the case of same-game and different-game learning, yet this time the amount of training data used is much smaller (4 min on average). On the other hand, same-game learning outperforms cross-game learning in terms of generalization, which matches our intuition that the game context features are more similar within the same game with the same players, e.g., the team distribution/tactics and the velocity/acceleration of players are more consistent.

6.3 Basketball Dataset

We also conduct the same evaluation on a basketball dataset of four sequences for a total length of more than 5 min. The dataset is more challenging due to a higher player density and less training data. Each sequence is tested while using the other three sequences for training. The average testing performance is reported in the trade-off curve of Fig. 6.12b and Table 6.4. As can be seen, the chasing feature is much more important for basketball sequences, indicating that one-on-one defensive situations occur more frequently in basketball than field hockey.

6.4 Classifier

In addition to random forests, we also examined the performance of linear SVMs for representing context-conditioned motion models. We utilize all the training data for a fivefold cross-validation scheme and evaluate the RoC curves (see Fig. 6.13). The experiments suggest the underlying motion models are not linear functions of the features because random forests outperform SVMs in all parameter configurations.

Fig. 6.13

RoC Curve comparison between random forest (red) and SVM (blue) classifier

6.5 Feature Importance

When training a random forest, we can also calculate the average decrease in Gini-index after removing each feature, which indicates the significance of the feature as shown in Fig. 6.14. In general, kinematic features¹ have greater significance than context features, which makes sense because kinematic features have direct correlation with the track association affinity. The constant velocity model (feature $3$) is the most important among kinematic features. However, in hockey, the consistency of the local player distribution (feature $8$) is more important than any kinematic feature. Features 9–14 have low significance because they are binary features with each bit containing very limited information. Furthermore, game context features are individually more important in the hockey sequence than in the basketball sequence.

Fig. 6.14

Normalized feature significance in hockey (red) and basketball (blue) sequences

7 Summary

In this work, we use hierarchical association to track multiple players in team sports over long periods of time. Although the motions of players are complex and highly correlated with teammates and opponents, the short-term movement of each player is often reactive to the current situation. Using this insight, we define a set of game context features and decompose the motion likelihood of all players into independent per-player models contingent on game state. Higher order interplayer dependencies are implicitly encoded into a random decision forest based on track and game context features. Because the conditioned model decomposes into pairwise terms, our formulation remains efficiently solvable using cost flow networks. We validate our approach on 30 min of international field hockey and 10 min of college basketball. In both sports, motion models conditioned on game context features consistently improve tracking results by more than 10 %.