Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the recent years highly versatile exo-prostheses have emerged enabling an amputee patient to master various difficult gait situations, e.g. walking at different gait speeds, ascending and descending slopes, and walking on uneven terrain. With micro-processor assisted prosthetic devices that make use of sensory information and passive-adaptive mechanical elements highly dynamic locomotion became possible for the patient and mobility is enhanced. Nevertheless, stable walking is still challenging for above-knee amputee patients due to the absence of active control possibilities over the knee and ankle joint of the prosthetic devices. Understanding the strategy of healthy humans in maintaining balance while performing dynamic locomotion is the key-task to develop more versatile and safe prosthetic components. Analytical stability criteria need to be established to exploit the entire potential given by controlled prosthetic devices.

Dynamic stability of prosthetic walking was analyzed in [1] where commercially available microprocessor-controlled knee joints were compared in a biomechanical analysis. Here, the risk of falling with transfemoral prostheses was investigated in everyday situations such as abruptly stopping and side-stepping, stepping on an obstacle and stumbling. However, a measure to quantify stability has not been formulated. Stability in terms of variability and symmetry of prosthetic gait was studied in [4, 9] where unstable walking was defined to be related to deviation from symmetric motion patterns. In our work, however, we assume that stable walking can also be achieved with asymmetric gait.

We try to understand stability in human walking by exploiting the concept of Capturability and perform dynamic simulation using optimal control. Our motivation is to find a measure to quantify stability and predict unstable gait situations. We regard the typical trajectory of walking motion as a sequence of initiated falling motions into the walking direction followed by well-timed catch motions performed by the leg that has just swung forward [13].

In Sect. 2 we will describe the motion capture experiments performed in the gait lab. The multi-body model that is used as a mathematical representation of the human body and the formulation of the equations of motion are introduced in Sect. 3 followed by a short review about the most commonly used stability criteria in biped walking analysis in Sect. 4. Section 5 contains the formulation of the optimal control problem to generate the human walking motion. The results of our investigation are summarized in Sect. 6 and discussed in Sect. 7.

2 Motion Capture Experiments for Human Walking

We performed experiments in the gait laboratory involving healthy subjects walking on level ground. Data from one subject (male, 30 years, 1.87 m, 86 kg) walking on level ground (walking speed: v = 1. 5 m/s, step length l s  = 0. 83 m) were further processed.

The walking motion of the subject was recorded using an image-based motion capture system which consists of 12 Vicon [14] infrared-based cameras recording the 3-dimensional trajectories of 48 retro-reflective markers attached to the subject’s body. The images were recorded with a sample frequency of 120 Hz. The marker positions on the skin were chosen such that they can be easily identified, the relative movement between skin and bones was minimal, and the positions of the joint centers could easily by reconstructed from the markers.

The orientation and position of the major body segments in Euclidean space are reconstructed from the marker trajectories using the Plug-in Gait model [14], a marker-based representation of the joint centers of the human body. The body pose reconstruction provides us with the joint-angles for all degrees of freedom (DoF) of our model that we will introduce more detailed in Sect. 3.

3 Modeling the Human Body

Our investigation of balancing strategies in human walking concentrates on phenomena resulting from larger movements while smaller effects, such as deformations, can be omitted. This allows us to perform dynamic simulation using the methods of multi-body dynamics.

3.1 Multi-body Representation of the Human Body

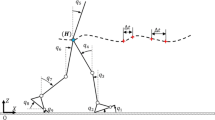
The parts of the body that are relevant for walking motions are represented by rigid bodies that are connected to each other by ball joints allowing three rotational degrees of freedom in each joint. For the upper body we consider the head, arms and trunk combined in a single rigid body which, accordingly, is named the HAT-segment (Head, Arms, Trunk). The multi-body model of the human body is comprised of eight rigid bodies representing the segments HAT, pelvis, right and left thigh, right and left shank, and right and left foot. These segments are connected by seven joints representing the lumbo-sacral joint, the right and left hip, right and left knee, right and left ankle. Figure 1 shows the configuration of the 27 DoF multi-body model.

Fig. 1
figure 1

The 27 DoF multi-body model of the human body is comprised of eight segments connected by seven ball joints

Full size image

The 27 DoF of the model are composed of 3 translational and 3 rotational DoF for the pelvis segment which are relative to the global frame and 7 × 3 rotational DoF that specify the rotation of a more distal segment relative to the next proximal one with the pelvis being the most proximal segment.

The anthropometric data of the subject which will be set as model parameters in our multi-body model are obtained using regression equations by de Leva [3] that receive the subject’s total mass (86 kg) and total height (1.87 m) as input. Table 1 lists all relevant parameters of the multi-body model where the CoM is assumed to be located on the longitudinal axis of each segment and assigned relative to the next proximal joint position.

Table 1 Anthropometric data of the subject (male, 30 years, 1.87 m, 86 kg) according to regression equations by de Leva
Full size table

3.2 Equations of Motion

To describe the dynamics of the multi-body model equations of motion are formulated using the modeling tool RigidBodyDynamicsLibrary [6]. Since our model is formulated with generalized coordinates q, the equations of motion can be expressed as

$$\displaystyle{ M(q)\,\ddot{q} + N(q,\dot{q}) =\tau }$$
(1)

where M(q) is the symmetric positive definite 27 × 27-mass-matrix, \(N(q,\dot{q})\) the 27 × 1-vector of generalized non-linear effects that contains the Coriolis, centrifugal and gravitational forces, and τ the 27 × 1-vector of generalized torques. We compute M(q) in a highly efficient way using the Composite Rigid Body Algorithm (CRBA) and \(N(q,\dot{q})\) using the Recursive Newton Euler Algorithm (RNEA) [5].

3.3 Ground Contact Model

The contact of the model with the ground is modeled as a rigid three point contact at each foot where the three contact points are located at the Calcaneus (heel), the medial Metatarsal Phalangeal Joint (mMTPJ) and the lateral Metatarsal Phalangeal Joint (lMTPJ), see Fig. 2. As soon as contact occurs, the vertical position of the contact points that are in touch with the ground are restricted to the ground by algebraic equality constraints. Furthermore, the horizontal accelerations of the contact points are set to zero.

Fig. 2
figure 2

The ground contact is modeled at the three contact points Calcaneus (heel), medial Metatarsal Phalangeal Joint (mMTPJ) and lateral Metatarsal Phalangeal Joint (lMTPJ)

Full size image

Using the ground contact model we receive the Index 1-DAE

$$\displaystyle\begin{array}{rcl} M(q)\ddot{q}& =& \tau -N(q,\dot{q}) + G(q)^{T}\lambda {}\end{array}$$
(2)
$$\displaystyle\begin{array}{rcl} G(q)\ddot{q}& =& -\gamma (q,\dot{q}),{}\end{array}$$
(3)

or in matrix notation

$$\displaystyle{ \left (\begin{array}{cc} M &G^{T} \\ G & 0 \end{array} \right )\left (\begin{array}{c} \ddot{q} \\ -\lambda \end{array} \right ) = \left (\begin{array}{c} \tau - N\\ -\gamma \end{array} \right ). }$$
(4)

where G are the point Jacobians of the contact points, λ the contact forces and γ the generalized acceleration independent part of the contact point accelerations [11].

In human walking, the occurrence of contact is subject to an impact and leads to discontinuities in the generalized velocities \(\dot{q}\). We compensate these by introducing events of infinitesimal length where we apply the system of equations

$$\displaystyle{ \left (\begin{array}{cc} M &G^{T} \\ G & 0 \end{array} \right )\left (\begin{array}{c} \dot{q}_{+} \\ -\varLambda \end{array} \right ) = \left (\begin{array}{c} M\dot{q}_{-} \\ 0 \end{array} \right ), }$$
(5)

where Λ refers to an inelastic impulse, \(\dot{q}_{+}\) denotes the generalized velocities right after the impact and \(\dot{q}_{-}\) the generalized velocities right before the impact, respectively.

With every change in G(q) that arises due to changing ground contact properties we formulate a separate model stage and create a new set of equations of motion (4). Figure 3 shows the human walking cycle and the resulting sequence of stages. Simulating the typical sequence of human gait with our three-point foot model leads to six different stages regarding the ground collision and lift-off of the contact points. This number of stages also includes transition stages that are needed to compensate impacts due to a touch-down of a contact point using (5).

Fig. 3
figure 3

The model stages according the typical human walking cycle

Full size image

4 Stability, Balance and Capturability

The investigation of balance and stability in human walking can lead to advances in the field of humanoid robotics motivated by the intention to find methods to efficiently control biped walking while avoiding the robot from falling down [18].

Considering strictly periodic motions, self-stable open-loop gait has been simulated exploiting Lyapunov’s first method as a mathematical definition of stability [11]. Here, asymptotic stability is given for a T-periodic solution of a T-periodic non-autonomous system \(\dot{x}(t) = f(t\,,\,x(t))\;\text{ with }\;f(t\,,\,\cdot ) = f(t\, +\, T,\,\cdot )\) if all eigenvalues λ i of the monodromy matrix \(X(t\, +\, T) = \frac{\text{d}x(t\,+\,T)} {\text{d}x(t)}\) are inside the unit circle \(\vert \lambda _{i}(X(t\, +\, T))\vert < 1\).

A very popular criterion to ensure balance of biped robots is used with the Zero Moment Point (ZMP) which is defined as a ground-reference point where the net moment generated from the ground reaction forces vanishes for the two axes that span the ground plane [17]. In humanoid robotics the dynamic feasibility of desired trajectories is usually ensured as long as the ZMP lies well within the borders of the base of support (BoS). Dynamic feasibility of the desired trajectory cannot be guaranteed if the ZMP lies on the edge of the BoS [15].

Another meaningful method which can also be used to quantify balance of a biped walking system keeps track of \(\dot{H}_{G}\), the rate of change of angular momentum at the center of mass (CoM) of the system [7]. This method refers to the preservation of rotational stability and considers a biped walking system to be rotational stable if the external forces and moments sum up to a zero centroidal moment. According to fundamental principles of mechanics this leads to a minimization of \(\dot{H}_{G}\). The ground-reference point Zero Rate of Change of Angular Momentum (ZRAM) indicates the position on the ground where \(\;\min \;\dot{H}_{G} = \mathit{GP} \times R\;\) with G denoting the position of the center of mass, P the position of the center of pressure and R referring to the resultant ground reaction force (GRF).

Push recovery, i.e. enabling a humanoid robot to recover itself from a sudden arbitrary push to avoid falling down, led to the concepts of N-Step Capturability with the main idea represented by the Capture Point [16]. The Capture Point (CP) is defined as the ground-reference point indicating the position where a biped walking system would have to step on to come to a complete stop. Assuming that the CP can be reached instantaneously and neglecting the time that is needed to swing the foot forward leads to the Instanteneous Capture Point (ICP).

In order to find the position of the ICP we regard the human body as an inverted pendulum with variable rod length. The position of the inverted pendulum’s point mass is equal to the CoM of our multi-body model while the pivot point of the inverted pendulum is located at the ground projection of the ankle joint \(r_{\mathit{ankle}} = (x_{\mathit{ankle}},y_{\mathit{ankle}},z_{\mathit{ankle}})^{T}\) of the current stance leg. Considering the orbital energy of the inverted pendulum

$$\displaystyle\begin{array}{rcl} E_{\mathit{IP},x}& =& \frac{1} {2}\left ( \frac{\dot{x}} {\omega _{0}z}\right )^{2} -\frac{1} {2}\left (\frac{x - x_{\mathit{ankle}}} {z} \right )^{2}\text{and}{}\end{array}$$
(6)
$$\displaystyle\begin{array}{rcl} E_{\mathit{IP},y}& =& \frac{1} {2}\left ( \frac{\dot{y}} {\omega _{0}z}\right )^{2} -\frac{1} {2}\left (\frac{y - y_{\mathit{ankle}}} {z} \right )^{2}{}\end{array}$$
(7)

with \(\;E_{\mathit{IP},x} = E_{\mathit{IP},y} \equiv 0\;\) we receive the location of the ICP:

$$\displaystyle\begin{array}{rcl} r_{\mathit{ICP}} = P\left [r + \frac{\dot{r}} {\omega _{0}} \right ]\text{ where }P = \left (\begin{array}{ccc} 1&0&0\\ 0 &1 &0 \\ 0&0&0 \end{array} \right )& & {}\\ \end{array}$$

projects r ICP on the ground, r refers to the position of the CoM and \(\omega _{0} = \sqrt{ \frac{g} {z_{0}}}\) is the reciprocal of the time constant of the inverted pendulum [8].

Since, as mentioned earlier, we regard human walking motion as a sequence of falling and catching, we hypothesize that walking can be described related to push recovery and exploiting the concept of N-Step Capturability. We try to find a correlation between the position of the ICP and the actual foot placement during human walking in order to quantify stability in human locomotion.

5 Optimal Control Problem

We intend to find joint angle trajectories x(t) and joint torques u(t) for our multi-body model that best fit the experimental data Φ MoCap using least-squares algorithms (LSQ) while considering given constraints. Considering also the contact properties as discussed in Sect. 3.3) this leads us to a multi-stage optimal control problem of the following form:

$$\displaystyle\begin{array}{rcl} \min _{x(\cdot ),\,u(\cdot )}& \:& \int _{0}^{t_{f} }\,\frac{1} {2}\vert \vert \varPhi _{\mathit{MoCap}}(t) -\varPhi _{\mathit{Opt}}(t,x(t))\vert \vert _{2}^{2}\;\mathrm{d}\,t{}\end{array}$$
(8)
$$\displaystyle\begin{array}{rcl} \text{subject to: }\dot{x}(t)& =& f_{i}(t,\,x(t),\,u(t))\;\;\text{ or DAE}{}\end{array}$$
(9)
$$\displaystyle\begin{array}{rcl} x(\hat{t}_{i}^{+})& =& h(x(\hat{t}_{ i}^{-})),{}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} g_{i}(t,x(t),u(t))& \geq & 0,{}\end{array}$$
(11)
$$\displaystyle\begin{array}{rcl} \text{for }\;\;t \in [\hat{t}_{i-1},\hat{t}_{i}],\;i& =& 1,\ldots,n_{\mathit{ph}},\;\hat{t}_{0} = 0,\;\hat{t}_{n_{\mathit{ph}}} = t_{f} \\ r^{\mathit{eq}}(x(0),\ldots,\,x(t_{ f}))& =& 0, {}\end{array}$$
(12)
$$\displaystyle\begin{array}{rcl} r^{\mathit{ineq}}(x(0),\ldots,\,x(t_{ f}))& \geq & 0,{}\end{array}$$
(13)

where we minimize the objective function (8) by modifying the states \(x(t) = (q(t),\dot{q}(t))\) and the controls u(t) = τ(t). In (9) we find the right hand side of the set of equations of motion that are formulated separately for each of the n ph model stages. With (10) stage transitions are modeled considering (5). The path constraints (11) define general limits to the states that are given by physiological constraints such as maximum joint angles. The equality constraints (12) and inequality constraints (13) ensure stage-wise general non-linear constraints such as contact point position at ground contact or positive contact forces.

This optimal control problem is solved using the direct multiple-shooting method that is implemented in the optimal control code MUSCOD-II [2, 10, 12]. This method uses a piecewise constant control discretization for the discretization of the optimal control problem. Furthermore, the original boundary value problem is transformed into a set of initial value problems with corresponding continuity and boundary conditions by the multiple shooting state parameterization.

With identical grids for the multiple-shooting state parameterization and the control discretization, this leads to a structured non-linear programming problem. This discretized problem can be efficiently solved with SQP algorithms adapted to the structure of the problem [10] as well as fast and reliable integration of the trajectories on the multiple-shooting intervals with regard to sensitivity information.

6 Results

We were able to simulate human gait fitting the model state variables to the experimental data in a least squares sense. Only the left step starting from left toe off until right toe off was simulated since we assume a healthy gait to be symmetric. The step is separated into the left swing phase (first 80 %) and the initial double stance (last 20 %). The trajectory of the simulated pelvis CoM in the global frame is compared to the measured trajectory in Fig. 4. The simulated and measured joint angle trajectories in the sagittal plane are shown in Fig. 5 for the left and the right leg, respectively.

Fig. 4
figure 4

Motion capture and simulation results for x,y,z-trajectories of the pelvis CoM

Full size image
Fig. 5
figure 5

Motion capture and simulation results for sagittal angles of right and left hip, knee and ankle

Full size image

The simulated and measured joint angle trajectories of both the right and the left leg as well as the simulated and measured displacement of the pelvis in the global frame show only small deviations. Larger deviations that occur in the double stance phase are due to the three-point foot model which does not precisely represent the complex kinematic behaviour of the human foot.

In the left and the middle plot of Fig. 6 the displacement in x and y-direction (in walking direction and to the left) of the ICP is depicted together with the displacement of the projection of the left and right ankle on the xy-plane for the whole step. The right plot shows the absolute distance from the ankle projections to the ICP. In x-direction the ICP trajectory is greater than the trajectory in both feet for the whole step with the position of the swing foot (left) converging to the ICP position during the swing phase. At the end of the swing phase when the left heel gains ground contact, the x-position of the left ankle is 0.089 m less than the ICP x-position. In y-direction the ICP position is less than the left ankle position but greater than the position of the right ankle for the whole step with the swing foot position converging to the ICP position as close as 0.091 m. The absolute distance of the swing foot to the ICP is strictly monotonic decreasing during the swing phase indicating that the ICP is directly approached by the swing foot. The fact that the swing foot does not reach as far as the ICP can be interpreted as a foot placement strategy in human walking where the ability to come to a stop after each step is intentionally risked in order to initiate the next step.

Fig. 6
figure 6

The first two plots show the displacement of ICP and left and right ankle projection on the ground (xy-plane) in x and y-direction during the left step. The third plot shows the absolute distance from right and left foot to the ICP

Full size image

7 Discussion

Our investigation was motivated by the need to understand the stability mechanisms of human walking in order to enhance stability in prosthetic devices. We hypothesize a correlation between the stability of human walking and the Instantaneous Capture Point. Although a human walker does not precisely step onto the ICP, we suggest that this point can be used to parameterize the location of the foot position. Using optimal control methods, joint angle trajectories of the multi-body model were generated that best fit the experimental data in a least-squares sense while considering the kinematic and physiological constraints of the human body. Our results on the actual foot placement at heel strike in relation to the current position of the Instantaneous Capture Point supported our assumption that human walking can be regarded as a sequence of falling and catching motions. The trajectory of the ICP was computed using the kinematic and kinetic data of the multi-body model that derived from the solution of our optimal control problem. The trajectory of the ground projection of the swing foot ankle was found to converge to the trajectory of the ICP. This suggests that the ICP trajectory can be used to compute the location of the foot position.