Shape-Preserving Response Prediction for Surrogate Modeling and Engineering Design Optimization

Abstract

Computer simulation models are fundamental tools of contemporary engineering design. The components, structures, and systems considered in most engineering disciplines are far too complex to be accurately described using simple theoretical models. Therefore, numerical simulation is often the only way to evaluate the performance of the design with sufficient reliability. However, accurate, high-fidelity simulations are computationally expensive. Consequently, their use for design automation, especially when exploiting conventional optimization algorithms is often prohibitive. Availability of faster computers and more efficient simulation software does not always translate into computational speedup due to growing demand for improved accuracy and the need to evaluate larger and larger systems. Surrogate-based optimization (SBO) techniques belong to the most promising approaches capable of alleviating these difficulties. SBO allows for reducing the number of expensive objective function evaluations in a simulation-driven design process. This is obtained by replacing the direct optimization of the expensive model by iterative updating and re-optimization of its cheap surrogate model. Among proven SBO techniques, the methods exploiting physics-based low-fidelity models are probably the most efficient. This is because the knowledge about the system of interest embedded in the low-fidelity model allows constructing the surrogate model that has good generalization capability at a cost of just a few evaluations of the original model. This chapter reviews one of the most recent SBO techniques, the so-called shape-preserving response prediction (SPRP). We discuss the formulation of SPRP, its limitations, and generalizations, and, most importantly, demonstrate its applications to solve design problems in various engineering areas, including microwave engineering, antenna design, and aerodynamic shape optimization. We also discuss the use of SPRP for creating fast surrogate models with illustrations from the microwave engineering area.

1 Introduction

Computer simulations are one of the most important tools in contemporary science and engineering. From miniature electronic components and circuits, through complete systems such as aircraft, to large-scale physical phenomena (e.g., climate models), simulations are used to describe the behavior, evaluate the performance, and validate designs. Nowadays, commercial simulation packages have matured and the computing resources are cheaper and in abundance. In spite of this, in many cases, accurate, high-fidelity simulations are computationally expensive, to the extent that their use in the design process, e.g., by employing simulations directly in an automated design optimization loop, may be impractical. The primary reason is that conventional optimization algorithms, both gradient-based [1] and derivative-free [2] typically require a large number of objective function evaluations. In some cases, the use of adjoint sensitivity [3] can alleviate this problem; however, this technique is not always available through commercial simulation packages. Conversely, design automation is key in situations where simple theoretical models are no longer capable to adequately account for complex interactions between the system components and, therefore, only yield an initial approximation of the optimum design which consequently has to be tuned further in order to meet the given performance requirements. In practice, design “tuning” is often based on parametric studies guided by engineering experience. This combination is often sufficient to obtain satisfactory designs in a reasonable time; however, it is far from being an automated process.

Surrogate-based optimization (SBO) [4, 5] is one of the most promising approaches to alleviate the difficulties discussed in the previous paragraph. In SBO, direct optimization of an expensive high-fidelity simulation model is replaced by iterative updating and re-optimization of its computationally cheap representation, a surrogate. The high-fidelity model is referenced occasionally to verify the prediction produced by the surrogate and to improve the latter. The overall design cost can be greatly reduced, because the optimization burden is shifted to the surrogate.

SBO methods differ mostly in the way the surrogate is created. A large group of function approximation modeling techniques exist. Here the surrogate is created by approximating sampled high-fidelity model data and the most popular methods include polynomial approximation [5], radial basis function interpolation [6], kriging [7], support vector regression [8], and neural networks [9]. Approximation models are very fast, however, a large number of training samples—and a high CPU cost of gathering the simulation data—are necessary to ensure reasonable accuracy. Furthermore, the number of required samples grows exponentially with the dimensionality of the design space (the curse of dimensionality). Depending on the model purpose, this initial computational overhead may or may not be justified. This depends for example whether the models are for a multiple-use library or a one-time optimization.

Correcting an auxiliary low-fidelity (or coarse) model is another approach to SBO. A low-fidelity model is a reduced-accuracy but faster representation of the system of interest. Low-fidelity models can be developed in various ways, such as by using simplified-physics, leaving out certain second-order effects, or by describing the system on a different physical level (e.g., equivalent circuit versus full-wave electromagnetic simulation in case of microwave components). Engineers have been using simplified models for decades: before the computer era simplified models and physical experiments were the only tools available to perform the design process. Because of the fact that a low-fidelity model contains certain knowledge about the system of interest, physics-based surrogates offer good generalization capabilities and can be set up using a limited number of training points. These are their biggest advantages over purely approximation models.

Several techniques have been proposed to exploit physics-based surrogate models in the SBO process, such as the approximation model management optimization (AMMO) framework [10], space mapping (SM) [11], manifold mapping [12], and simulation-based tuning [13]. Several of these methods are based on correcting the low-fidelity model output (response). The SBO process is provably convergent to the high-fidelity model optimum [13] when embedded in the trust-region framework[14] and the correction is realized by ensuring both zero- and first-order consistency [10] between the surrogate and the high-fidelity model. In some cases (with a notable example of SM), the correction can be done by introducing a mapping between the parameter spaces of the low- and high-fidelity models.

The shape-preserving response prediction (SPRP) technique [15] is a recently developed approach which exploits physics-based low-fidelity models. The method was originally developed in the microwave engineering area [15], but has also been applied to problems in antenna design [16] and aerodynamic design [17]. SPRP is a parameter-less method where the surrogate model response is constructed by tracking the changes of the low-fidelity model response when moving from a certain reference design to another one, and applying those changes (represented by translation vectors) to a reference response of the high-fidelity model. The SPRP surrogate exploits the knowledge embedded in the low-fidelity model to a greater extent than other physic-based surrogate modeling approaches, e.g., SM. Therefore, the generalization capability of SPRP is usually better than that of SM [15]. In this chapter, we review the SPRP technique, its basic and generalized formulations, and attempt to give an intuitive explanation of its efficiency. We also illustrate its operation and performance using several design examples from various engineering disciplines.

The chapter is organized as follows. In Sect. 2, we formulate the engineering optimization problem, briefly recall the basics of SBO, and introduce the concept of the SPRP methodology. Section 3 demonstrates the use of SPRP for optimization of microwave filters. Application of SPRP for antenna design is discussed in Sect. 4. Section 5 describes formulation and the use of SPRP for the design of transonic airfoils. Section 6 discusses the use of SPRP for surrogate modeling. Section 7 concludes the chapter.

2 Surrogate-Based Optimization and Shape-Preserving Response Prediction

In this section, we formulate the engineering design optimization problem, recall the concept of SBO, and discuss the SPRP methodology [15]. Examples illustrating application of SPRP in various engineering fields are provided in Sects. 3–6.

2.1 Engineering Design Optimization. Problem Formulation

The engineering design optimization problem can be defined as

$$ {\boldsymbol{x}}_f^{*}= \arg \underset{\boldsymbol{x}}{ \min }U\!\left(f\left(\boldsymbol{x}\right)\right) $$

(1)

where f: X _f  → R ^m, X _f  ⊆ R ⁿ, denotes the response vector of a high-fidelity (or fine) model of the device or system of interest; U: R ^m → R is a given objective function, e.g., minimax [18]. In microwave engineering, the response vector may contain, for example, the values of transmission coefficient |S ₂₁| evaluated over certain frequency band.

2.2 Surrogate-Based Optimization

Because of the high computational cost of evaluating f, its direct optimization is replaced by an iterative procedure [5]

$$ {\boldsymbol{x}}^{\left(i+1\right)}= \arg \underset{\boldsymbol{x}}{ \min }U\!\left({s}^{(i)}\left(\boldsymbol{x}\right)\right) $$

(2)

that generates a sequence of points (designs) x ⁽ⁱ⁾ ∈ X _f , i = 0, 1, …. Each x ⁽ⁱ⁺¹⁾ is the optimal design of the surrogate model s ⁽ⁱ⁾: X _s ⁽ⁱ⁾ → R ^m, X _s ⁽ⁱ⁾ ⊆ R ⁿ, i = 0, 1, …. s ⁽ⁱ⁾ is assumed to be a computationally cheap and sufficiently reliable representation of the fine model f, particularly in the neighborhood of the current design x ⁽ⁱ⁾. Under these assumptions, the algorithm (2) is likely to produce a sequence of designs that quickly approach x _f ^*. Because f is evaluated rarely (usually once per iteration), the surrogate model is supposedly fast, and the number of iterations for a well-performing algorithm is substantially smaller than for most direct optimization methods, and the process (2) may lead to substantial reduction of the computational cost of solving (1). If the surrogate model satisfies zero- and first-order consistency conditions with the fine model, i.e., s ⁽ⁱ⁾(x ⁽ⁱ⁾) = f(x ⁽ⁱ⁾) and (∂s ⁽ⁱ⁾/∂x)(x ⁽ⁱ⁾) = (∂f/∂x)(x ⁽ⁱ⁾) (verification of the latter requires f sensitivity data), and the algorithm (2) is enhanced by the trust-region method [19], then it is provably convergent to a local optimum of the fine model [10]. Convergence can also be guaranteed if the algorithm (2) is enhanced by properly selected local search methods [20].

2.3 Shape-Preserving Response Prediction: Concept [15]

SPRP [15] has been initially introduced in microwave engineering to reduce the cost of optimizing electromagnetic (EM)-simulated structures such as filters [15]. In SPRP, the surrogate model is constructed assuming that the change of the fine model response due to the adjustment of the design variables from can be predicted using the actual response changes of the auxiliary low-fidelity (or coarse) model c: X _c  → R ^m, X _c  ⊆ R ⁿ, that describes the same object as the high-fidelity model; c is less accurate but much faster to evaluate than f.

The choice of the coarse model very much depends on the engineering discipline. In microwave engineering, the coarse model might be an equivalent circuit of the considered microwave structure, that describes the structure using circuit theory methods rather than through solution of the Maxwell equations. It is critically important for SPRP that the coarse model is physically based, which ensures that the effect of the design parameter variations on the model response is similar for both the fine and coarse models. The change of the coarse model response is described by the translation vectors corresponding to certain (finite) number of characteristic points of the model’s response. These translation vectors are subsequently used to predict the change of the fine model response with the actual response of f at the current iteration point, f(x ⁽ⁱ⁾), treated as a reference.

Here, we explain the concept of SPRP using the specific case of a microwave filter. Figure 1aa shows the example of the coarse model response, |S ₂₁| in the frequency range 8–18 GHz, at the design x ⁽ⁱ⁾, as well as the coarse model response at some other design x. The responses come from the double folded stub bandstop filter [15]. Circles denote five characteristic points of c(x ⁽ⁱ⁾), here, selected to represent |S ₂₁| = −3 dB, |S ₂₁| = −20 dB, and the local |S ₂₁| maximum (at about 13 GHz). Squares denote corresponding characteristic points for c(x), while small line segments represent the translation vectors that determine the “shift” of the characteristic points of c when changing the design variables from x ⁽ⁱ⁾ to x. Because the coarse model is physics-based, the fine model response at the given design, here, x, can be predicted using the same translation vectors applied to the corresponding characteristic points of the fine model response at x ⁽ⁱ⁾, f(x ⁽ⁱ⁾). This is illustrated in Fig. 1bb. Figure 2 shows the predicted fine model response at x as well as the actual response, f(x), with a good agreement between both curves.

Fig. 1

The SPRP concept [15]: (a) Example coarse model response at the design x ⁽ⁱ⁾, c(x ⁽ⁱ⁾) (solid line), the coarse model response at x, c(x) (dotted line), characteristic points of c(x ⁽ⁱ⁾) (o) and c(x) (square), and the translation vectors (short lines); (b) Fine model response at x ⁽ⁱ⁾, f(x ⁽ⁱ⁾) (solid line) and the predicted fine model response at x (dotted line) obtained using SPRP based on characteristic points of this figure; characteristic points of f(x ⁽ⁱ⁾) (o) and the translation vectors (short lines) were used to find the characteristic points (square) of the predicted fine model response; coarse model responses c(x ⁽ⁱ⁾) and c(x) are plotted using thin solid and dotted line, respectively [9]

Fig. 2

(a) Fine model response at x, f(x) (solid line), and the fine model response at x obtained using the shape-preserving prediction (dotted line). Good agreement between both curves is observed, particularly in the areas corresponding to the characteristic points of the response; (b) Interpolating function F (solid line) corresponding to the fine/coarse model plots in Fig. 1; the identity function is denoted using the dotted line, the frequency components of the translation vectors are denoted as short solid lines; (c) Interpolating function R (solid line); the magnitude components of the translation vectors are denoted using short solid lines

2.4 Shape-Preserving Response Prediction: Formulation [15]

SPRP can be rigorously formulated as follows. Let f(x) = [f(x,ω ₁) … f(x,ω _m )]^T and c(x) = [c(x,ω ₁) … c(x,ω _m )]^T, where ω _j , j = 1, …, m, is the frequency sweep (it can be assumed without loss of generality that the model responses are parameterized by frequency). Let p _j ^f = [ω _j ^f r _j ^f]^T, p _j ^c0 = [ω _j ^c0 r _j ^c0]^T, and p _j ^c = [ω _j ^c r _j ^c]^T, j = 1, …, K, denote the sets of characteristic points of f(x ⁽ⁱ⁾), c(x ⁽ⁱ⁾), and c(x), respectively. Here, ω and r denote the frequency and magnitude components of the respective point. The translation vectors of the coarse model response are defined as t _j  = [ω _j ^t r _j ^t]^T, j = 1, …, K, where ω _j ^t = ω _j ^c − ω _j ^c0 and r _j ^t = r _j ^c − r _j ^c0. The SPRP surrogate model is defined as follows

$$ {s}^{(i)}\left(\boldsymbol{x}\right)={\left[{s}^{(i)}\left(\boldsymbol{x},{\omega}_1\right)\kern1em \dots \kern1em {s}^{(i)}\left(\boldsymbol{x},{\omega}_m\right)\right]}^T $$

(3)

where

$$ {s}^{(i)}\left(\boldsymbol{x},{\omega}_j\right)=\overline{f}\left({\boldsymbol{x}}^{(i)},F\left({\omega}_j,{\left\{-{\omega}_k^t\right\}}_{k=1}^K\right)\right)+R\left({\omega}_j,{\left\{{r}_k^t\right\}}_{k=1}^K\right) $$

(4)

for j = 1, …, m. $\overline{f}\left(\boldsymbol{x},\omega \right)$ is an interpolation of {f(x,ω ₁), …, f(x,ω _m )} onto the frequency interval [ω ₁,ω _m ]. The scaling function F interpolates the data pairs {ω ₁,ω ₁}, {ω ₁ ^f,ω ₁ ^f − ω ₁ ^t}, …, {ω _K ^f,ω _K ^f − ω _K ^t}, {ω _m ,ω _m }, onto the frequency interval [ω ₁,ω _m ]. The function R does a similar interpolation for data pairs {ω ₁,r ₁}, {ω ₁ ^f,r ₁ ^f − r ₁ ^t}, …, {ω _K ^f,r _K ^f − r _K ^t}, {ω _m ,ωr _m }; here r ₁ = R _c (x,ω ₁) − R _c (x ^r,ω ₁) and r _m  = c(x,ω _m ) − c(x ^r,ω _m ). In other words, the function F translates the frequency components of the characteristic points of f(x ⁽ⁱ⁾) to the frequencies at which they should be located according to the translation vectors t _j , while the function R adds the necessary magnitude component. The interpolation onto [ω ₁,ω _m ] is necessary because the original frequency sweep is a discrete set.

Formally, both the translation vectors t _j and their components should have an additional index (i) indicating that they are determined at iteration i of the optimization algorithm (2), however, this was omitted for the sake of simplicity.

Figure 2 shows the plots of the functions F and R corresponding to the fine/coarse model response plots of Fig. 1. The interpolation of {f(x,ω ₁), …, f(x,ω _m )}, F, and R is implemented using cubic splines.

As follows from its formulation, SPRP is developed assuming that the frequency components of the translation vectors are zero at the edges of the frequency spectrum (i.e., at ω ₁ and ω _m ). This limitation can be easily overcome either by extending the frequency range of the covarse model and applying extrapolation (cf. [15]). Also, it is assumed that the overall shape of both the fine and coarse model response is similar. This means, in particular, that the characteristic points of responses of both the coarse model c and the fine model f are in one-to-one correspondence. If this assumption is not satisfied, the surrogate model (3), (4) cannot be evaluated because the translation vectors t _i are not well defined. Generalizations of SPRP that allow alleviating this difficulty in some cases can be found in [15].

Fig. 3

Dual-band bandpass filter: (a) geometry [21], (b) coarse model (Agilent ADS)

Table 1 Optimization results for dual-band bandpass filter

3 SPRP for Microwave Design Optimization

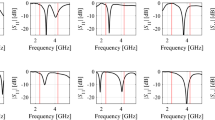
In this section, we demonstrate the use of SPRP for the design optimization of microwave components. Consider the dual-band bandpass filter [21] (Fig. 3aa). The design parameters are x = [L ₁ L ₂ S ₁ S ₂ S ₃ d g W]^T mm. The fine model is simulated in Sonnet em [22]. The design specifications are |S ₂₁| ≥ −3 dB for 0.85 GHz ≤ ω ≤ 0.95 GHz and 1.75 GHz ≤ ω ≤ 1.85 GHz, and |S ₂₁| ≤ −20 dB for 0.5 GHz ≤ ω ≤ 0.7 GHz, 1.1 GHz ≤ ω ≤ 1.6 GHz, and 2.0 GHz ≤ ω ≤ 2.2 GHz. The coarse model is implemented in Agilent ADS [23] (Fig. 3bb). The initial design is x ⁽⁰⁾ = [16.14 17.28 1.16 0.38 1.18 0.98 0.98 0.20]^T mm (the optimal solution of c). The following characteristic points are selected to set up functions F and R: four points for which |S ₂₁| = −20 dB, four points with |S ₂₁| = −5 dB, as well as six additional points located between −5 dB points. For the purpose of optimization, the coarse model was enhanced by tuning the dielectric constants and the substrate heights of the microstrip models corresponding to the design variables L ₁, L ₂, d, and g (original values of ε _r and H were 10.2 and 0.635 mm, respectively) [15]. The filter was optimized using two versions of SPRP, a regular one and SPRP enhanced by input SM (cf. Table 1). Figure 4 shows the initial fine model response as well as the fine model response at the design obtained using the SPRP method.

Fig. 4

Dual-band bandpass filter: fine model (dashed line) and coarse model (thin dashed line) response at x ⁽⁰⁾, and the optimized fine model response (solid line) at the design obtained using shape-preserving response prediction

As the second example, consider the third-order Chebyshev bandpass filter [29] shown in Fig. 5. The design parameters are x = [L ₁ L ₂ S ₁ S ₂]^T mm; W ₁ = W ₂ = 0.4 mm. The fine model is simulated in Sonnet em [22]. The design specifications are |S ₂₁| ≥ −3 dB for 1.8 GHz ≤ ω ≤ 2.2 GHz, and |S ₂₁| ≤ −20 dB for 1.0 GHz ≤ ω ≤ 1.6 GHz and 2.4 GHz ≤ ω ≤ 3.0 GHz. The coarse model is implemented in Agilent ADS [23] (Fig. 6). The initial design is x ⁽⁰⁾ = [14.6 15.3 0.56 0.53]^T mm (the optimal solution of the coarse model c). The following characteristic points are selected to set up functions F and R: two points for which |S ₂₁| = −30 dB, two points with |S ₂₁| = −20 dB, two points with |S ₂₁| = −6 dB, as well as ten additional points located between −6 dB points. Figure 7 shows the initial fine model response as well as the fine model response at the design obtained using SPRP. The numerical results including the design cost are presented in Table 2.

Fig. 5

Third-order Chebyshev bandpass filter: geometry [29]

Fig. 6

Third-order Chebyshev filter: coarse model (Agilent ADS)

Fig. 7

Wideband microstrip antenna [24]: top and side views. The dash-dot line in the top view shows the magnetic symmetry wall (XOY)

Table 2 Optimization results for third-order Chebyshev filter

4 SPRP for Antenna Design

In this section, we illustrate the use of SPRP for the design of antenna structures. As an example, consider an antenna shown in Fig. 7 [24], where x = [l ₁ l ₂ l ₃ l ₄ w ₂ w ₃ d ₁ s]^T are the design variables. Multilayer substrate is l _s  × l _s (l _s  = 30 mm). The antenna stack (bottom-to-top) comprises: metal ground, 0.813 mm thick RO4003, microstrip trace (w ₁ = 1.1 mm), 1.905 mm thick RO3006 and a trace-to-patch via (r ₀ = 0.25 mm), driven patch, 3.048 mm thick RO4003, and four patches at the top. The antenna stack is fixed with four M1.6 bolts at the corners (u = 3 mm). Metallization is with thick 50 μm copper. Feeding is through an edge mount 50Ω SMA connector with the 10 × 10 × 2 mm flange.

Fig. 8

Wideband microstrip antenna: (a) high-fidelity model response (dashed line) at the initial design x ^init, and high- (solid line) and low-fidelity (dotted line) model responses at the approximate low-fidelity model optimum x ⁽⁰⁾; (b) high-fidelity model |S ₁₁| at the final design; (c) realized gain at the final design for the zero zenith angle (solid line, XOZ co-pol.) and realized peak gain (dash line). Design constrain is shown with the horizontal line at the 5 dB level

The design objective is |S ₁₁| ≤ −10 dB for 3.1–4.8 GHz. Realized gain not less than 5 dB for the zero zenith angle is an optimization constrain over the frequency band. The initial design is x ^init = [−4 15 15 2 15 15 20 2]^T mm.

Both the high-fidelity model f (2,334,312 mesh cells at the initial design, 160 min of the evaluation time) and the low-fidelity model c (122,713 mesh cells, 3 min of the evaluation time) are simulated using the CST MWS transient solver [25]. Here, the first step is to find the rough optimum of c, x ⁽⁰⁾ = [−4.91 15.15 15.07 2.56 14.21 14.23 21.07 2.67]^T mm. The computational cost of this step is 82 evaluations of c (which corresponds to about 1.5 evaluations of the high-fidelity model). Figure 8aa shows the responses of f at x ^init and x ⁽⁰⁾, as well as the response of c at x ⁽⁰⁾. The final design x ⁽⁴⁾ = [−5.21 15.38 15.57 2.58 14.41 13.73 21.07 2.067]^T mm (|S ₁₁| ≤ −11 dB for 3.1–4.8 GHz, Fig. 8bb) is obtained after four iterations of the SPRP-based optimization. The gain of the final design is shown in Fig. 8cc which illustrates that the maximum of radiation points along the zero zenith angle closely over the bandwidth of interest. The total design cost corresponds to about ten evaluations of the high-fidelity model (Table 3).

As the second example, consider a planar antenna shown in Fig. 9. It consists of a planar dipole as the main radiator element and two additional strips. The design variables are x = [l ₀ w ₀ a ₀ l _p w _p s ₀]^T. Other dimensions are fixed to: a ₁ = 0.5 mm, w ₁ = 0.5 mm, l _s  = 50 mm, w _s  = 40 mm, and h = 1.58 mm. Substrate material is Rogers RT5880 [30].

The high-fidelity model f of the antenna structure (10,250,412 mesh cells at the initial design, evaluation time of 44 min) is simulated using the CST MWS transient solver. The design objective is to obtain |S ₁₁| ≤ −12 dB for 3.1–10.6 GHz. The initial design is x ^init = [20 10 1 10 8 2]^T mm. The low-fidelity model c is also evaluated in CST but with coarser discretization (108,732 cells at x ^init, evaluated in 43 s). For this example, the approximate optimum of c, x ⁽⁰⁾ = [18.66 12.98 0.526 13.717 8.00 1.094]^T mm, is found as the first design step. The computational cost is 127 evaluations of c, and it corresponds to about two evaluations of f. Figure 10aa shows the reflection responses of R _f at both x ^init and x ⁽⁰⁾, as well as the response of c at x ⁽⁰⁾. The final design x ⁽²⁾ = [19.06 12.98 0.426 13.52 6.80 1.094]^T mm (|S ₁₁| ≤ −13.5 dB for 3.1–10.6 GHz) is obtained after two iterations of the SPRP-based optimization with the total cost corresponding to about seven evaluations of the high-fidelity model (see Table 4). Figure 10bb shows the reflection response and Fig. 11 shows the gain response of the final design x ⁽²⁾.

Table 3 Wideband microstrip antenna: optimization cost

Fig. 9

UWB dipole antenna geometry: top and side views. The dash-dot lines show the electric (YOZ) and the magnetic (XOY) symmetry walls. The 50 Ω source impedance is not shown at the figure

Fig. 10

UWB dipole antenna reflection response: (a) high-fidelity model response (dashed line) at the initial design x ^init, and high- (solid line) and low-fidelity (dotted line) model responses at the approximate low-fidelity model optimum x ⁽⁰⁾; (b) high-fidelity model |S ₁₁| at the final design

5 SPRP for Aerodynamic Shape Optimization

The SPRP technique is illustrated here on aerodynamic design of airfoil sections at transonic flow conditions [17]. The airfoil shapes are parameterized with three parameters of the NACA four-digit method: m (the maximum ordinate of the mean camberline as a fraction of chord), p (the chordwise position of the maximum ordinate), and t/c (the thickness-to-chord ratio) [26]. The design variable vector is x = [m p t/c]^T.

The airfoil performance is obtained through computational fluid dynamic (CFD) models which are implemented using the ICEM CFD [27] grid generator and the FLUENT [28] flow solver. The high-fidelity CFD model f is a two-dimensional steady-state Euler analysis with roughly 400,000 mesh cells and an overall simulation time around 67 min. The low-fidelity CFD model c is the same as the high-fidelity one, but with a coarser mesh (roughly 30,000 cells) and relaxed convergence criteria (100 flow solver iterations). The low-fidelity model is roughly 80 times faster than the high-fidelity one.

In aerodynamic shape optimization, the SPRP technique is applied to the pressure distribution (C _p (x)) on the airfoil surface [17]. Figure 12aa shows the pressure distributions of two different designs obtained by the low-fidelity model. Shown are the characteristic points (red circles) and the translation vectors (blue lines) at important areas of the distributions. The application of the translation vectors to the high-fidelity model distributions is shown in Fig. 13bb.

Table 4 UWB dipole antenna: optimization cost

Fig. 11

UWB dipole antenna at the final design: IEEE gain pattern (x-pol.) in the XOY plane at 4 GHz (thick solid), 6 GHz (dash-dot line), 8 GHz (dash line), and 10 GHz (solid line)

Fig. 12

An illustration of the SPRP technique applied to the pressure distributions obtained by the low-fidelity CFD models of two designs, (a) initial characteristic points and translation vectors, (b) additional points

Fig. 13

Application of SPRP to the high-fidelity CFD model responses (thick lines) with (a) initial characteristic points and translation vectors (coarse model distributions are shown with thin lines), and (b) comparison of the actual and the predicted (dash) high-fidelity response

The design objective is to maximize the section lift coefficient (C _l (x)) subject to constraints on the section drag coefficient (C _dw (x)) and the non-dimensional cross-sectional area (A(x)). The problem is formulated as minimization of the high-fidelity model f(x) = −C _l (x) subject to g ₁(x) = C _dw (x) − C _dw.max  ≤ 0, and g ₂(x) = A _min  − A(x) ≤ 0, where C _dw.max  = 0.0041 is the maximum drag and A _min  = 0.065 the minimum cross-section. The free-stream Mach number is set M _∞ = 0.75 and the angle of attack α = 1°. The design variable bounds are 0 ≤ m ≤ 0.1, 0.2 ≤ p ≤ 0.8, and 0.05 ≤ t ≤ 0.20. The initial design is x ^init = [0.03 0.2 0.1]^T.

Due to unavoidable misalignment between the pressure distributions of the high-fidelity model and its SPRP surrogate, it is not convenient to handle the drag constraint directly, because the design that is feasible for the surrogate model may not be feasible for the high-fidelity model. This problem is alleviated by implementing the drag constraint through a penalty function. More specifically, the objective function is defined as

$$ H\left({C}_p\left(\boldsymbol{x}\right)\right)=-{C}_{l.s}\left({C}_p\left(\boldsymbol{x}\right)\right)+\beta {\left[\varDelta {C}_{dw.s}\left({C}_p\left(\boldsymbol{x}\right)\right)\right]}^2 $$

(5)

where ∆C _dw.s  = 0 if C _dw.s  ≤ C _dw.s.max and ∆C _dw.s  = C _dw.s  − C _dw.s.max otherwise. The cross-sectional area constraint is handled directly. We use β = 1,000 in the numerical study. Here, the pressure distribution for the surrogate model is C _p  = C _p.s , and for the high-fidelity model C _p  = C _p.f . Also, C _l.s and C _dw.s denote the lift and drag coefficients for the surrogate.

The optimization problem is solved by the direct optimization of the high-fidelity model using the pattern-search algorithm, as well as by the SPRP algorithm. The results are presented in Table 5. It can be seen that both approaches are able to meet the design goals and produce similar optimized airfoil shapes. The direct approach requires 120 high-fidelity model evaluations (N _f ). The SPRP algorithm requires 330 low-fidelity model evaluations (N _c ) and 11 high-fidelity ones, yielding a total cost of less than 18 equivalent high-fidelity model evaluations.

To meet the design goals, the optimizer does three fundamental shape changes: (1) the maximum ordinate of the mean camber line (m) is reduced, (2) the location of the maximum ordinate of the mean camber line (p) is moved aft, thus increasing the trailing-edge camber, and (3) the thickness-to-chord ratio (t/c) is reduced. Shape changes (1) and (3) reduce the shock strength and, thus, reduce the drag coefficient. The associated change in the pressure distribution reduces the lift coefficient. However, shape change (2) improves (or recovers a part of) the lift by opening up the pressure distribution behind the shock. These effects can be seen in the pressure distribution plot in Fig. 14, and the Mach contour plots in Figs. 15 and 16.

Table 5 Numerical results for the airfoil design optimization

Fig. 14

Airfoil optimization results: initial and optimized airfoils pressure distributions and shapes

Fig. 15

Airfoil optimization results: Mach contours at the initial design

Fig. 16

Airfoil optimization results: Mach contours at the optimized design

6 Fast Surrogate Modeling Using SPRP

In this section, we illustrate the use of SPRP for modeling of microwave components. We consider two versions of SPRP surrogates: the basic one and the modified implementation that exploits multiple training points. Further discussion on the recent developments of SPRP models can be found in [31].

6.1 SPRP Modeling: Basic Version [32]

Let X _R  ⊆ X be the region of interest where we want the surrogate model to be valid. Typically, X _R is an n-dimensional interval in R ⁿ with center at reference point x ⁰ = [x _0.1 … x _0.n ]^T ∈ R ⁿ and size δ = [δ ₁ … δ _n ]^T. Let X _B  = {x ¹, x ², …, x ^N} ⊂ X _R be the base set, such that the fine model response is known at all points x ^j, j = 1, 2, …, N. Here, the base points are allocated using so-called star-distribution [33], which is a design of experiments traditionally used by space mapping.

The SPRP surrogate model is defined as follows:

$$ s\left(\boldsymbol{x}\right)=S\left(\boldsymbol{x},{\boldsymbol{x}}^r\right) $$

(6)

where x ^r is the base point that is the closest to x, i.e.,

$$ {\boldsymbol{x}}^r= \arg \underset{\boldsymbol{y}\in {X}_B}{ \min}\left|\right|\boldsymbol{x}-\boldsymbol{y}\left|\right| $$

(7)

whereas S(x,x ^r) is the SPRP model created with x ^r used as a reference design (cf. Sect. 2.3).

Although, as demonstrated in [32], this simple modeling approach proves to be more accurate than SM, and it has some drawbacks. The model (6), (7) utilizes only one base point at a time. As shown in Fig. 17aa, the region of interest is divided into regions of “attractions” of particular base points. For all evaluation points x located in a given region of “attraction,” the surrogate model (6) is determined using the same single base point as a reference design. Due to this, the surrogate does not utilize all available f-model data at a time. Also, the surrogate model is discontinuous at the borders of the areas of “attraction” because the solution to (6) is not unique at these points. This may cause some problems while using the surrogate for design optimization.

Fig. 17

SPRP modeling (n = 2): (a) Original: Star-distributed base points are denoted using black circles. The region of interest is divided into areas of “attraction” of particular base points, determined by the Euclidean distance. An example evaluation design x is close to the base design x ³, and this point becomes a reference design for SPRP model; (b) Modified: Base points are denoted using black circles. A shaded area denotes a hypercube defined by a subset X _S of base points being the closest to an example evaluation design x. The surrogate at x is defined as a linear combination of SPRP models using all base points from X _S as reference designs. Coefficients of this linear combination are calculated by representing x through all points from X _S

6.2 Modified SPRP Modeling [34]

Here, a modified SPRP modeling technique is proposed that utilizes multiple reference designs and solves the discontinuity problem described in the previous section. Again, the base set is assumed to be allocated using star-distribution [33]; however, the model can also be formulated for more general setups.

The concept of the SPRP model exploiting multiple reference designs is explained in Fig. 17bb. For an evaluation point x, we find a subset X _S of the base set X _B that defines a rectangular area (hypercube) of the region of interest containing x. The surrogate model is set up using all points from X _S . The star-distribution base set contains N = 2n + 1 points as illustrated in Fig. 17aa for n = 2. Without loss of generality, we can assume that X _S  = {x ⁰, x ¹, …, x ⁿ}. We have

$$ \boldsymbol{x}={\boldsymbol{x}}^0+{\beta}_1{\boldsymbol{v}}_1+{\beta}_2{\boldsymbol{v}}_2+\dots +{\beta}_n{\boldsymbol{v}}_n $$

(8)

where β ₁, …, β _n determines a unique representation of x – x ⁰ using vectors v _i  = x ⁱ – x ⁰, i = 1, …, n. Coefficients β _i can be found as

$$ \left[\begin{array}{c}{\beta}_1\\ {}{\beta}_2\\ {}\\ {}{\beta}_n\end{array}\right]={\left[{\boldsymbol{v}}_1\kern0.5em {\boldsymbol{v}}_2\kern0.5em \dots \kern0.5em {\boldsymbol{v}}_n\right]}^{-1}\cdot \left(\boldsymbol{x}-{\boldsymbol{x}}^0\right) $$

(9)

The vector x can be the unique represented as

$$ \boldsymbol{x}={\alpha}_0{\boldsymbol{x}}^0+{\alpha}_1{\boldsymbol{x}}^1+{\alpha}_2{\boldsymbol{x}}^2+\dots +{\alpha}_n{\boldsymbol{x}}^n $$

(10)

where α ₀ = 1 − (α ₁ + … + α _n ), and α _i  = β _i , i = 1, …, n. The modified SPRP surrogate model is then defined as

$$ \widehat{s}\left(\boldsymbol{x}\right)={\alpha}_0S\left(\boldsymbol{x},{\boldsymbol{x}}^0\right)+{\alpha}_1S\left(\boldsymbol{x},{\boldsymbol{x}}^1\right)+\dots +{\alpha}_nS\left(\boldsymbol{x},{\boldsymbol{x}}^n\right) $$

(11)

with S(x, x ⁱ), i = 0, 1, …, n, being the SPRP models (1) determined using respective reference designs.

It can be verified that the model (11) is continuous with respect to x provided that both f and c are continuous functions of x. Also, it is expected to be more accurate than the model (6), (7) because it exploits the available fine model data in a more comprehensive way.

6.3 Verification: Fourth-Order Ring Resonator Bandpass Filter [35]

In this section we illustrate the use of SPRP for modeling of a microwave filter. We also compare both basic and modified SPRP with surrogate modeling using standard space mapping [33]. The standard SM model is quite involved because it is using input and output SM of the form A · c(B · x + c), enhanced by the implicit and frequency space mapping [33]. All surrogate models are set up using the same base set consisting of N = 2n + 1 points allocated according to the star-distribution [33]. The quality of the models is assessed using a relative error measure ||f(x) − s(x)||/||f(x)|| expressed in percent.

Consider the fourth-order ring resonator bandpass filter [35] (Fig. 18aa). The design parameters are x = [L ₁ L ₂ L ₃ S ₁ S ₂]^T mm. The fine model f is simulated in FEKO [36]. The coarse model, Fig. 18bb, is implemented in Agilent ADS [23]. The region of interest is defined by the reference point x ⁰ = [24.0 21.0 26.0 0.2 0.1]^T mm, and the region size δ = [2.0 2.0 2.0 0.1 0.05]^T mm.

Fig. 18

Fourth-order ring resonator bandpass filter: (a) geometry [35], (b) coarse model (AgilentADS)

The modeling accuracy has been verified using 50 random test points. The results shown in Table 6 and in Fig. 19 indicate that the modified SPRP model ensures better accuracy than both the standard SM model and the original version of SPRP [32].

Table 6 Fourth-order ring resonator filter: modeling results

Fig. 19

Fourth-order ring resonator bandpass filter: fine model (solid line) and surrogate model (circles) responses at three selected test points for: (a) standard SM model, (b) modified SPRP surrogate model

As an application example, the modified SPRP surrogate was utilized to optimize the filter with respect to the following design specifications: |S ₂₁| ≥ −1 dB for 1.75 GHz ≤ ω ≤ 2.25 GHz, and |S ₂₁| ≤ −20 dB for 1.0 GHz ≤ ω ≤ 1.5 GHz and 2.5 GHz ≤ ω ≤ 3.0 GHz. The initial design was x ⁰ = [24.0 21.0 26.0 0.2 0.1]^T mm.

Figure 20aa shows the fine model response of the filter at the initial design and at the design x ^* = [22.61 20.11 26.626 0.156 0.040]^T mm obtained by optimizing the surrogate. The specification error at the optimized design is −0.45 dB.

Fig. 20

Fourth-order ring resonator bandpass filter: (a) fine model responses at the reference point x ⁰ (dashed line) and at the optimal solution x ^* of the modified shape-preserving response prediction surrogate model (solid line); (b) statistical analysis at x ^* using the modified shape-preserving response prediction model. Estimated yield is 68 %. Thick black solid line denotes the fine model response at optimal design x ^*

The SPRP model was also used to estimate yield at the optimized design, assuming 0.2 mm deviation for length parameters (L ₁ to L ₂) and 0.02 mm for spacing parameters (S ₁ and S ₂). The yield estimation based on 200 random samples is 68 % (Fig. 9bb). This value is very close to the yield estimated directly using the fine model (70 %). The estimation performed with the SM model is less accurate (50 %). Note that the total computational cost of building the surrogate model, design closure, and statistical analysis is only 11 full-wave simulations of the filter structure!

7 Conclusion

A review of SPRP and its applications to solving simulation-driven design problems in various engineering disciplined has been presented. SPRP exploits the knowledge embedded in the low-fidelity model of the structure under consideration in order to predict the response of the expensive high-fidelity model. As a result, SPRP is capable of yielding a satisfactory design at a low computational cost as demonstrated using several examples involving design problems in electrical and mechanical engineering. As indicated in Sect. 5, SPRP can also be used to construct accurate global or quasi-global surrogate models. SPRP is a relatively novel technique that is still under development. Recent papers provide various enhancement of the technique in the context of both optimization (e.g., [37]) and modeling (e.g., [31]). It should also be mentioned that a potential limitation of SPRP is the fact that one-to-one correspondence of all the model (both low- and high-fidelity ones) responses involved in the process of creating the surrogate model is an important prerequisite for the technique to work. Various ways of ensuring such a correspondence can be found in the literature (e.g., [15]).