Evolutionary Dynamics of the Genotype-Phenotype Map

Abstract

Our aim is to study the evolutionary properties of a model of the genotype-phenotype. The relation between genotype and phenotype is very complicated. Such complexity is a consequence of the fact that the phenotype emerges from networks of interactions between genes and their products, which regulate gene expression and give rise to non-linear, high-dimensional dynamical systems. In addition, these gene regulatory networks (GRNs) are shaped by evolution by natural selection.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Our aim is to study the evolutionary properties of a model of the genotype-phenotype. The relation between genotype and phenotype is very complicated. Such complexity is a consequence of the fact that the phenotype emerges from networks of interactions between genes and their products, which regulate gene expression and give rise to non-linear, high-dimensional dynamical systems. In addition, these gene regulatory networks (GRNs) are shaped by evolution by natural selection. As a consequence, the genotype-phenotype map exhibits a number of features: the map is not a one-to-one map (many genotypes produce the same phenotype), robustness, evolvability and convergence, among others [2, 3].

We focus here in the characterisation of the genotype-phenotype map as a bipartite graph. We define the phenotype as the attractors of the dynamics of the gene regulatory network. Moreover, a bipartite network has been introduced to study genotype-phenotype relation (genotype-phenotype space) and their structural relationship. We also define some emergent biological properties such as robustness, evolvability, canalisation and convergence in terms of network or graph-theoretical properties such as the clustering coefficient and resilience of the giant connected component (percolation).

2 Network Representation of Properties of the Genotype-Phenotype Map

The four emergent properties of the genotype-phenotype map that we are going to focus on are: Robustness, evolvability, canalisation and convergence. For each one of these properties, we propose a metric in terms of properties of the (bipartite) genotype-phenotype network and analyse their evolutionary dynamics.

Robustness, which measures phenotypic resilience to gene mutations and evolvability, i.e., the ability of the system to innovate, can be considered to be opposites: whereas robustness is related to the ability of maintaining biological identity, evolvability measures the capability to change and adapt to varying conditions. The question arises as to whether these two concepts co-evolve. The quantitative analysis of these properties is associated with the a generalisation of the concept of neutral network which consists of a network where all genotypes (nodes) carrying the same phenotype connected by an edge if only if they differ by one gene mutation alone. We further add a second type of nodes, the phenotypes. Links are established between phenotypes and those genotypes that belong to the basin of attraction of the former.

We propose the clustering coefficient within the bipartite network to quantify phenotypic robustness, remember that the clustering coefficient for a (phenotype) node u is

$$\displaystyle{c_{u} = \frac{2T(u)} {\mathrm{deg}(u)(\mathrm{deg}(u) - 1)},}$$

where T(u) is the number of triangles through phenotype u and deg(u) is the degree of u, i.e., the number of genotypes belonging to the basin of attraction. c _u is a measure of robustness of u since it quantifies how many genotypes connected by single-mutation events exhibit the same phenotype.

Evolvability is measured in terms of metrics related to percolation, i.e., the existence of a giant connected component and its resilience against attacks (i.e., removal of nodes). Since evolvability is defined as the ability of an organism to adapt to changing conditions by modifying its phenotype, it is natural to define evolvability in terms of global connectivity and navigability of the genotype-phenotype space.

Canalisation is a term coined by Conrad Waddington and it can be defined as the tendency of phenotypes to increase robustness as time progresses or, as Waddington referred to it buffering of the genotype [5]. We will therefore quantify it in terms of the time evolution of the average clustering coefficient. Convergence, on the other hand, refers to the phenomenon whereby different species of disparate lineages evolve to acquire similar biological traits (phenotypes).

In order to analyse convergence in our model, we calculate the Hamming distance between genotypes linked to the same phenotype. The Hamming distance between genotypes (g ₁, g ₂) is measured as the number of mutations between two genotypes, d(g ₁, g ₂). Each phenotype has associated an average Hamming distance defined as the mean Hamming distance between every possible pair of genotypes connected to it.

3 The Model

In order to study the evolutionary dynamics of the genotype-phenotype map, we consider a multi-scale population dynamics model for a cell population where we consider two levels or scales:

Microscopic scale. It accounts for the intracellular dynamics of each cell, where we consider that each cell individual is characterised by a pair (G, g(0)), where G is a matrix accounting for the GRN (i.e., how a gene product affects the activation of all other genes), and g(0) corresponds to the initial condition which can be interpreted as the heritable developmental program. The GRN defines a dynamical system such that, with g(0) as an initial condition, and according to the rules (1), can either reach a fixed point or a periodic steady state,

$$\displaystyle{ I_{i} =\sum _{\langle j\rangle _{i}^{\mathrm{in}}}G_{\mathit{ji}}g_{j}, }$$

(1)

where $\langle j\rangle _{i}^{\mathrm{in}}$ is the set of in-neighbours of i, and

$$\displaystyle{\left \{\begin{array}{ll} g_{i}(t + 1) = 1, &\text{if }I_{i}(t) \geq 0 \\ g_{i}(t + 1) = -1,&\text{if }I_{i}(t) < 0.\\ \end{array} \right.}$$

The corresponding steady state g(∞) is our representation of the phenotype. Viability conditions are introduced that deem as lethal genotypes that induce oscillations with long cycles [4]. Thus, the intracellular dynamics of each cell determines whether the cell survives and, if it does, what its phenotype is.

Macroscopic scale. In order to obtain our evolving bipartite genotypes-phenotypes graph, we prescribe a population dynamics consists of a multi-type Wright–Fisher model with mutation [1]. In our case, each type corresponds to a genotype: when proliferation is attempted a mutation (consisting in changing the sign of a randomly chosen non-zero entry of the matrix G, leading to G ^′) occurs with probability p _mut. Then, we run the intracellular dynamics as per the microscopic scale. If the corresponding phenotype is viable, two descendants are added to the population with genotype (G ^′, g(0)) and the corresponding phenotype. If the mutation leads to a non-viable phenotype on a previously viable individual, this is eliminated from the population and we go through another Wright–Fisher step. From this process the bipartite graph is constructed as the population dynamics proceeds. Every time a new genotype is generated by mutation a genotype node is added to the network, as well as the corresponding edges, and the same occurs with the phenotypes. Finally, the pseudo-bipartite graph have two types of nodes: genotype nodes and phenotype nodes, and their corresponding two kinds of edges: edges between genotypes if the distance is 1, edges between genotype to the phenotype associated to it.

4 Results and Conclusions

After studying the properties described in the previous section, we have ran numerical simulations of our model and found the following results. When we analyse the phenotypic clustering coefficient, we observe that there is a strong inverse correlation between clustering coefficient and phenotype degrees, as shown in Fig. 1a. This implies the existence of, essentially, two kinds of phenotypes: (i) phenotypes with a big basin of attraction (high degree) but little robustness, and (ii) robust phenotypes (high clustering) but with low degree.

Fig. 1

(a) Strong inverse relation between phenotype clustering coefficients and phenotype degrees. (b) Time evolution of the average clustering

Also, we observe co-evolution of canalisation and evolvability: as time progresses, both the average clustering coefficient increases (see Fig. 1b), and a giant connected component emerges as shown in Fig. 2a.

Fig. 2

(a) Simulation results for the size distribution of connected components as a function of time. We observe that, as time progresses, a macroscopic proportion of nodes accumulate in a few components which eventually leads to the formation of a giant connected component. (b) How the microscopic parameters, i.e., those related to determining the structure of the GRN and its viability, affect the resilience of the giant connected component and can be thus used to control evolvability of the system

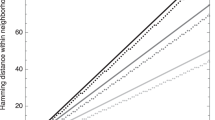
Another, interesting result concerns the correlation between the average Hamming distance between genotypes associated with a phenotype and the clustering coefficient (robustness) of the latter. We observe that convergence occurs in non-robust phenotypes (see Fig. 3): Average Hamming distance is systematically bigger for phenotypes with low clustering coefficient (low robustness).

Fig. 3

Relation between Hamming distance and clustering coefficient. Left: clustering vs Hamming distance. Right: log(clustering) vs log(Hamming distance)

Finally, another result concerns the influence of the GRN parameters in the structure of the bipartite graph. For example, Fig. 2b shows how microscopic parameters such as the rewiring probability and the viability conditions affects the resilience of the giant connected component, and therefore, the evolvability of the system.