Expectations, Firms’ Indebtedness and Business Fluctuations in a Structural Keynesian Monetary Growth Framework

Abstract

In this contribution we incorporate the main elements of the small-scale firms’ debt-finance model by Franke and Semmler (1989) into a medium-scale disequilibrium macroeconomic framework along the lines of Chiarella, Flaschel and Franke (2005). In a fully interdependent model incorporating investing firms, savings of rentier households, commercial banks and the government, the endogenously generated debt of firms (created through borrowing) feeds back dynamically to the investment behaviour of firms, their borrowing of funds, the asset market, the interest rate and the expected rate of return (representing the confidence of investors with regard to future development). The impact of debt-financing of firms on aggregate economic activity and its stability will be studied within this context. We also investigate the dynamics of the resulting model by means of numerical simulations.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent times, and especially since the recent global financial crisis, there has been a renewed interest in understanding the interplay between the financial markets and the macroeconomy, as well as the role played therein by the expectations of the different agents in the economy. As the role of both equity and debt financing has not only increased especially in the United-States since the late 1980s, and since both equity and debt issuance have become more volatile as well as correlated to each other, understanding the interaction between the firms’ indebtedness levels and the dynamics of the economy remains a central question in economic research. ¹

In the literature numerous and quite heterogeneous approaches to this topic have been developed over time, and many such approaches are directly linked to the assessment of the efficiency of financial markets. For instance, while according to the Modigliani and Miller (1958) theorem the value of a firm would be unaffected by its financing structure if capital markets are frictionless, in theoretical studies along the lines of Minsky (1975, 1982), high debt-asset ratios may reflect a dangerous liability structure of firms, increasing the risk of bankruptcy and developing fragile macroeconomic dynamics.

Already in the 1980s, early attempts were made to fully endogenise debt-financing in an interdependent economic system. For example, while in Foley (1986, 1987) borrowing, lending and capital outlays of firms are essentially determined by endogenously determined profit rate and liquidity, in Taylor (1985) and Taylor and O’Connell (1985), the savings generated by the rentier households, as already suggested by Kalecki, are channeled through the banking system to investing firms. However, despite the fact that this class of models develops rich macroeconomic dynamics—including financial instability as studied by Minsky in his financial crisis theory—the role of firms’ indebtedness and debt payment commitments is not fully worked out given the partial nature of those frameworks.

In this contribution we incorporate the main elements of the small-scale firms’ debt-finance model by Franke and Semmler (1989) into a medium-scale disequilibrium macroeconomic framework along the lines of Chiarella et al. (2005). In a fully interdependent model incorporating investing firms, savings of rentier households, commercial banks and the government, the endogenously generated debt of firms (created through borrowing) feeds back dynamically to the investment behaviour of firms, their borrowing of funds, the asset market, the interest rate and the expected rate of return (representing the confidence of investors with regard to future development). The impact of debt-financing of firms on aggregate economic activity will be studied within this context.

The remainder of this chapter is organised as follows: In Sect. 2, after describing briefly the main features of the Franke and Semmler (1989) framework, we discuss a medium-scale macroeconomic model which incorporates these features into a much richer Keynesian disequilibrium framework. We then investigate the dynamics of the resulting model by means of numerical simulations in Sect. 3. Finally, we draw some concluding remarks and mention the possible lines of future research in Sect. 4.

2 A Medium-Scale Keynes-Metzler Macroeconomic Framework of Firms’ Indebtedness and Business Fluctuations

The main objective of this contribution is to integrate the approach of Franke and Semmler (1989) towards financial markets, debt-financing of firms and expectations about the future state of the economy into a medium-scale macroeconomic framework of the Keynes–Metzler variety along the lines of Chiarella et al. (2005).

In a nutshell, the theoretical framework originally proposed by Franke and Semmler (1989) studies the complex macroeconomic dynamics resulting from a debt-financing strategy by the entrepreneurial sector in a closed economy and the state of confidence in the economy, and therefore, on the general expectations of the economic agents with respect to the current and future performance of the economy. The modelling strategy is as follows: In the first step, Franke and Semmler characterise the short-run equilibrium in goods and financial markets using a slight modification of a framework already employed several times in the literature (see e.g. Taylor and O’Connell (1985), Foley (1986, 1987)) and investigate the short-run stability properties of the resulting equilibrium. In this context, the ratio of indebtedness of firms and the economy’s “state of confidence” are considered to be exogenously given. Further, in a second step the debt-to-capital ratio and the state of confidence are then endogenised through the formulation of behavioural equations concerning their evolution over time based on the assumption of continuous market clearing in the goods and financial markets.

Concerning the latter dynamic variable, Franke and Semmler (1989) assume that it evolves over time according to

$$\begin{aligned} \dot{\psi }= v(\rho -r,\lambda ), \quad v_1 > 0,\; v_2 <0, \end{aligned}$$

(1)

where $\rho$ represents the actual real rate of profit and $\lambda$ the firms’ debt-to-capital ratio, i.e. $\lambda =\Lambda /(pK)$, where $\Lambda$ represents the firms’ aggregate debt level, $p$ the aggregate price level and $K$ the capital stock level. Accordingly, the state of confidence in the economy depends negatively on the firms’ debt-to-capital ratio, and positively on the differential between the actual profit rate and the real rate of interest, as originally proposed by Kalecki (1937) [84–95] in the following manner: “...the rate of investment decision is an increasing function of the gap between the prospective rate of profit and the rate of interest” and the difference between the “prospective rate of profit, and the rate of interest, is equal to the risk incurred”.

The growth rate of the firms’ indebtness is assumed to be a positive function of the difference between the expected profit rate and the current rate of interest, and a negative function of the debt-to-capital ratio,

$$\begin{aligned} \dot{\Lambda }/\Lambda = b(\rho ^e-r,\lambda ), \quad b_1 > 0,\; b_2 <0, \end{aligned}$$

(2)

where the expected rate of profit is defined through

$$\begin{aligned} \rho ^{e}&= \rho +\psi . \end{aligned}$$

(3)

In contrast, the growth rate of the capital stock $\dot{K}/K=I/K$ (where $I$ represents aggregate investment) is assumed to be driven solely by the relative expected profitability, i.e.

$$\begin{aligned} \dot{K}/K = g(\rho ^e-r), \quad g_1> 0, \; g_2<0. \end{aligned}$$

(4)

Since $\hat{\lambda } = \hat{\Lambda } - \hat{p} - \hat{K}$, the resulting 2D nonlinear system of differential equations of the Franke and Semmler (1989) framework is given by:

$$\begin{aligned} \dot{\lambda }&= (b(\rho +\psi -r,\lambda )-g(\rho +\psi -r))\cdot \lambda \end{aligned}$$

(5)

$$\begin{aligned} \dot{\psi }&= c(\rho -r,\lambda ) \end{aligned}$$

(6)

under the assumption that $\hat{p}=0$, and where we rewrite Eq. (1) again here for expositional clarity.

While different assumptions on the diverse reaction functions $b(\,\cdot \,)$, $g(\,\cdot \,)$ and $c(\,\cdot \,)$ make it possible to generate quite differentiated and complex dynamics, in Franke and Semmler (1989) essentially three types of scenarios are investigated. Two of them exhibit local (if not global) stability with respect to a unique long-run equilibrium of steady growth. The other one, the most interesting case, generates persistent fluctuations in the debt-to-capital ratio and the state of confidence in the economy tending to a closed orbit (so that a growth cycle results).

The Franke and Semmler (1989) framework is capable of delivering valuable insights on the interaction between the firms’ indebtedness levels, the economy’s state of confidence and macroeconomic activity. However, it contains still various assumptions, such as the continuous goods market equilibrium and the exogenously given labour share, which are not only unlikely on empirical grounds, but also at odds with a truly Keynesian framework from a theoretical point of view. Accordingly, in the following we incorporate their approach into a medium-scale macroeconomic framework along the lines of Chiarella et al. (2005).

The household sector is assumed to comprise two different types of agents: workers and asset holders. Workers are assumed to consume all their labour income, while asset holders are assumed to consume only a fraction of $1-s_c$. Under the assumption that all interest payments to banks are transferred to the household sector (and more specifically to the asset holders), the aggregate household consumption is determined by

$$\begin{aligned} C = \omega L^{d} + (1-s_{c})(\rho K + r\Lambda /p), \end{aligned}$$

(7)

where $\omega$ denotes the real wage $w/p$, $L^d$ the labour demand (which equals the actual level of employment given the underutilisation macroeconomic regime assumed here), $K$ the capital stock, $r$ the rate of interest, $\Lambda$ the total level of the households’ interest bearing deposits and $p$ the aggregate price level. Further, the rate of profit $\rho$ is defined as

$$\begin{aligned} \rho&= (Y^d - \delta K -\omega L^{d}- r\lambda K)/K, \end{aligned}$$

(8)

where $Y^d$ represents the aggregate demand level, as usual defined as

$$\begin{aligned} Y^{d}&= C +I +G+\delta K, \end{aligned}$$

(9)

where $I$ represents aggregate net investment, $G$ aggregate government expenditures and $\delta$ the depreciation rate of capital.

The households’ (meaning, asset holders’) real savings are allocated in new money holdings ${\dot{M}}$, new loans to the entrepreneurial sector ${\dot{\Lambda }}$ and new equity holding ${\dot{E}}$,

$$\begin{aligned} S_{p}&= s_{c}(\rho K + r\Lambda /p) = ({\dot{M}} + {\dot{\Lambda }} +p_{e}{\dot{E}})/p. \end{aligned}$$

(10)

Accordingly, the households’ financial wealth (consisting of course only of asset holders’ wealth) consists of money holdings, debt claims and equities (all expressed here in nominal terms), i.e.

$$\begin{aligned} W&= M + \Lambda +p_{e}E. \end{aligned}$$

(11)

Concerning the firms’ behaviour, labour demand $L^d$ is assumed to be fully determined by the aggregate output level $Y$ (see Eq. (17)), where $x=const.$ is the average labour productivity, i.e.

$$\begin{aligned} L^{d}&= Y^d/x. \end{aligned}$$

(12)

Further, aggregate net investment $I$ is assumed to depend not only on the difference between the expected profit rate and the rate of interest (as in Eq. (4)), but also on the deviation of the capacity utilisation $u$ from its normal level $\bar{u}$, and the trend growth of investment $\gamma =const.$ (which for simplicity is assumed to equal the growth rate of the population), namely

$$\begin{aligned} I&= i_{1}(\rho ^{e} - (r^{}-\pi ^e) )K+i_{2}(u-\overline{u})K +\gamma K, \end{aligned}$$

(13)

where $u=Y/Y^{p}$, with $Y^p= y^p K$ and $y^p=Y^p/K=const.$ representing the potential output-capital ratio. Further, Eq. (14) represents the budget restriction of firms, which states that net investment is either financed by new borrowing or by issuing new equities, i.e.

$$\begin{aligned} I&= (\dot{\Lambda }+p_{e}\dot{E})/p. \end{aligned}$$

(14)

with $\hat{K} = \dot{K}/K = I/K$ being the growth rate of capital by definition.

Total aggregate investment includes net investment, the replacement of depreciated capital and the actual change in the firms’ inventories $N$, i.e.

$$\begin{aligned} I^{a} = I + \delta K + \dot{N}, \end{aligned}$$

(15)

where $\dot{N}$ results from the discrepancies between actual output $Y$ and actual aggregate demand $Y^d$, i.e.

$$\begin{aligned} \dot{N}&= Y-Y^{d} = S_{f}. \end{aligned}$$

(16)

As extensively discussed in Chiarella and Flaschel (2000) and Chiarella et al. (2005), in an uncertain environment, firms have to decide on production before actual sales are known. Accordingly, actual aggregate output equals the expected output level $Y^e$ plus the additional change in actual inventories, i.e.

$$\begin{aligned} Y&= Y^{e} + \fancyscript{I}. \end{aligned}$$

(17)

with the change in the desired level of inventories $N^d$ being assumed to be determined through

$$\begin{aligned} \fancyscript{I} = \gamma N^{d} + \beta _{\gamma } (N^{d}-N), \end{aligned}$$

(18)

where

$$\begin{aligned} N^{d} = \beta _{\gamma ^{d}} Y^{e}, \end{aligned}$$

(19)

as in Chiarella et al. (2005). Further, the evolution of $Y^e$ is assumed to be given by:

$$\begin{aligned} \dot{Y}^{e} = \gamma Y^{e} + \beta _{y^{e}} (Y^{d}-Y^{e}). \end{aligned}$$

(20)

Accordingly, the expected output level is determined in an adaptive manner by aggregate demand $Y^d$, as well as by the trend population growth $\gamma$.

The firms’ pursued debt policy is described by Eq.(21), according to which the growth rate of debt financing of firms depends positively on the expected rate of profit (in nominal terms), negatively on interest payments (in capital stock terms) $r\lambda$.²

$$\begin{aligned} \dot{\Lambda } = d(\rho ^{e}+\pi ^{e},r\lambda )\cdot \Lambda , \quad \text{ with } d_{1}>0, d_{2}<0 \end{aligned}$$

(21)

For the sake of simplicity, the government’s behaviour is described in a very parsimonious manner. Real government expenditures are proportional to net investment and are totally money financed, so that government dissavings equal the current government expenditures as formulated in Eqs. (22)–(24), i.e.³

$$\begin{aligned} G&= \phi I, \;\; \phi = const. \end{aligned}$$

(22)

$$\begin{aligned} \dot{M}&= pG \end{aligned}$$

(23)

$$\begin{aligned} S_{g}&= -G, \end{aligned}$$

(24)

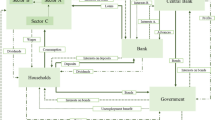
Turning next to the asset markets we first of all consider the balance sheets of the economy and their aggregation towards the determination of the nominal wealth of asset owning households, as shown in Table 1.

Table 1 The asset markets structure of the economy

The scheme illustrated in Table 1 is based on the assumption that there are no currency holdings of the public that holds (and use) liquidity in the form of interest-free demand deposits (with no fixed multiplier relationship connecting $M$ and $\Lambda ^{o}$, or $\Lambda ^o$ and $\Lambda ^r$).⁴ Interest bearing deposits of the public, by contrast, are not “liquid” and they exhibit a fixed price (as a deposit) and as the result of market interaction a variable rate of interest $r$. Further, it is assumed that this rate only holds ex ante (as a market clearing signal), while the ex post rate includes profits or losses of commercial banks $r\Lambda -r\Lambda ^{r}$ which are distributed as windfall profits to asset owning households ($r^{a}=r\Lambda /\Lambda ^{r}$). Commercial banks are thus pure intermediaries (which hold the high-powered money—issued by way of the government expenditure rule—as reserve for transaction processes) with no costs of production, no investment and no income, since the interest they receive from firms $r\Lambda$ is completely distributed to asset owning households.

The above scheme implies for the nominal wealth of households the identity:

$$ W=M + \Lambda + p_{e}E = \Lambda ^{o}+\Lambda ^{r}+p_{e}E = M + p_{k}K, $$

and for its intended and realised change (at current market prices):

$$ pS_{p} = {\dot{\Lambda }}^o + \dot{\Lambda }^r + p_e \dot{E} = \dot{M} + \dot{\Lambda } + p_{e}\dot{E}, $$

which explains the use of the wealth concept employed above and the allocation rule for the savings plans made by households.

On the basis of these identities we can now describe the reallocation of wealth that takes place in each moment of time (before the trading of any flows) by means of

$$\begin{aligned} p_{e}E&= e(\rho ^{e}+\pi ^{e}, r) W, \quad e_{1}>0, e_{2}<0, \end{aligned}$$

(25)

$$\begin{aligned} \Lambda ^{o}&= d^{o}(\rho ^{e}+\pi ^{e},r)W, \quad d^o_1<0, d^o_2>0,\end{aligned}$$

(26)

$$\begin{aligned} \Lambda ^{r}&= d^{r}(\rho ^{e}+\pi ^{e},r)W, \quad d_1<0, d_2>0, \end{aligned}$$

(27)

with $e(\,\cdot \,)+d^{o}(\,\cdot \,)+d^{r}(\,\cdot \,)= 1$, and $e(\,\cdot \,)$, $d^{o}(\,\cdot \,)$ and $d^{r}(\,\cdot \,) \ge 0$. The portions of nominal wealth that are desired to be held as equities, interest-free and interest-bearing deposits depend on two rates of return: the expected nominal rate of profit $\rho ^{e}+\pi ^{e}$ and the current market rate of interest $r$.⁵

As in Franke and Semmler, equity prices are determined by the canonical equation

$$\begin{aligned} p_{e}E = \frac{(\rho ^{e}+\pi ^{e})pK}{r}. \end{aligned}$$

(28)

Accordingly, as in Franke and Semmler (1989), we assume here the rate of interest and the equity prices are jointly determined by Eqs. (25) and (28), and thus that they adjust automatically to guarantee asset market equilibrium in every moment in time.⁶ In contrast, the composition of $\Lambda ^{o}+\Lambda ^{r}=M+\Lambda$ is chosen so as to be in line with the above allocation rules for these two asset demands.

Expressed in a different way the equilibrium situation on the markets for financial assets can also be derived and described as follows. The condition that the equity market clears is equivalent to assuming the following condition for interest-free and interest bearing deposits

$$ M+\Lambda = (d^{o}(\rho ^{e}+\pi ^{e},r)+d^{r}(\rho ^{e}+\pi ^{e},r))pW $$

and to assume that the interest rate on the latter deposits adjusts in order to get this equality between the high-powered money plus loans to firms and total deposit demand. The interest rate determination is thus described here through market forces, but is of course the same as the one we have determined through equity market equilibrium described by Eq. (25). Again the division of deposits in interest-free and interest-bearing deposits is made on the basis of the rates $r$ and $\rho ^{e}+\pi ^{e}$ and is of no consequence for the working of the economy. The public is therefore completely free to choose the degree of liquidity of its financial assets.

Concerning the determination of wage and price inflation, and thus of the real wage, following the work by Flaschel and Krolzig (2006), the wage and price inflation rates are assumed to be determined by the disequilibrium situations in the labour and goods markets, cross-over expectational terms and the medium-term inflationary climate, i.e.

$$\begin{aligned} \hat{w}&= \beta _{w} (e-\bar{e}) +\kappa _{w}\hat{p} +(1-\kappa _{w})\pi ^e \end{aligned}$$

(29)

$$\begin{aligned} \hat{p}&= \beta _{p} (u-\bar{u}) + \kappa _{p} \hat{w} + (1-\kappa _{p})\pi ^e \end{aligned}$$

(30)

$$\begin{aligned} \dot{\pi }^{e}&= \beta _{\pi _{1}}(\hat{p}-\pi ^{e})+\beta _{\pi _{2}}(\hat{M}-\gamma -\pi ^{e}) \end{aligned}$$

(31)

where $e=L^{d}/L=Y/(xL)$ represents the economy’s employment rate, and $\pi ^e$ the medium-run inflationary climate in the economy.

3 The Model in Intensive Form

Since the current model describes the dynamics of a growing economy, it is convenient to express the main dynamic equations of the model in intensive form. Accordingly, aggregate demand per unit of capital (see Eqs. (7), (13), (22) and (9)) is given by

$$\begin{aligned} y^d&= v y + (1-s_{c})[\rho + r\lambda ] +(1+\phi )(i_{1}(\rho + \psi - r+\pi ^{e}) )\nonumber \\&+\,i_{2}(u-\bar{u})+ \gamma + \delta , \end{aligned}$$

(32)

where $v=\omega /x$ is the wage share and $\rho = (1-v)y -\delta -r \lambda$ is the profit rate in intensive form terms. It should be pointed out that this expression would give rise to the same type of IS-equation as employed in Franke and Semmler (1989) [p. 45] if goods’ market equilibrium was assumed in place of the inventory adjustment process assumed here. The IS-equation that is implicitly contained in our model is therefore very close to the form used by Franke and Semmler (1989), who however use a different measure for relative profitability in the investment demand function, and who set $i_{2}$ and $\gamma$ equal to zero.

The condition for asset market equilibrium given by Eq. (25) can be rewritten in intensive form as:

$$\begin{aligned} \rho ^{e}+\pi ^{e}= e(\rho ^{e} +\pi ^{e},r) (\rho ^{e}+\pi ^{e} + r ), \end{aligned}$$

(33)

by making use of $p_e E/(pK) = (\rho ^{e}+\pi ^{e})/r$ as given by Eq. (28), see also Franke and Semmler (1989) [p. 43].

The complete model in intensive form is given by the following system of nonlinear dynamical equations:

$$\begin{aligned} \hat{\omega }&= \kappa [(1-\kappa _p)\beta _w (e-\bar{e}) + (\kappa _w-1)\beta _{p} (u-\bar{u})], \end{aligned}$$

(34)

$$\begin{aligned} \hat{l}&= -i_{1}(\rho + \psi -r^{}+\pi ^e) - i_{2}(u-\bar{u}), \end{aligned}$$

(35)

$$\begin{aligned} \hat{m}&= \phi g /m -\pi ^e -\gamma -\kappa [\beta _p (u-\bar{u}) + \kappa _p \beta _w (e-\bar{e})] + \hat{l}, \end{aligned}$$

(36)

$$\begin{aligned} \dot{\pi }^e&= \beta _{\pi _{1}} \kappa [\beta _p (u-\bar{u}) + \kappa _p \beta _w (e-\bar{e})] + \beta _{\pi _{2}} (\phi g /m-\gamma -\pi ^e ), \end{aligned}$$

(37)

$$\begin{aligned} \dot{y}^{e}&= \beta _{y^{e}} (y^{d} - y^{e})+\gamma y^{e}, \end{aligned}$$

(38)

$$\begin{aligned} \dot{\nu }&= y-y^{d} - (i_{1}(\rho + \psi -r+\pi ^e) + i_{2}(u-\bar{u})-\gamma ) \nu , \end{aligned}$$

(39)

$$\begin{aligned} \hat{\lambda }&= d(\rho +\psi ,(r-\hat{p})\lambda ) - \pi ^e -\kappa [\beta _p (u-\bar{u}) + \kappa _p \beta _w (e-\bar{e})] -\gamma +\hat{l},\qquad \end{aligned}$$

(40)

$$\begin{aligned} \dot{\psi }&= c(\rho + \psi -r+\pi ^{e}),\lambda ), \end{aligned}$$

(41)

where $u=Y/Y^{p}=y/y^{p}$, $l=L/K$, $m=M/(pK)$, $y^e = Y^e/K$, $\nu = N/K$, and $y = y^d + \nu$.

As Franke and Semmler (1989) provide a detailed analysis of the temporary equilibrium positions and their evolution in time, and the properties of macroeconomic models similar to the one discussed here have also been extensively studied in Chiarella and Flaschel (2000), Chiarella et al. (2005) and other related work, in this paper we will focus primarily on numerical simulation of particular submodules of this extended framework, namely the interaction between debt-to-capital ratio $\lambda$, the state of confidence $\psi$ (the two dynamical variables considered by Franke and Semmler (1989)) and the real wage $\omega$ in the following section, and leave the analysis of the complete macroeconomic framework for future research.

4 Numerical Analysis

As mentioned above, in this section we consider by means of numerical simulations only a subsystem of the complete macroeconomic framework consisting of the core dynamical variables $\lambda$, $\psi$ and $\omega$. The investigation of the full model must here be left for future research. Note however that the Metzlerian quantity dynamics as well as the price inflation dynamics have been studied extensively in the work of Chiarella, Flaschel, Franke and Semmler on various levels of their integration into larger models of disequilibrium macro-dynamics.

As previously mentioned, in Franke and Semmler (1989) goods market equilibrium is assumed, as well as a constant wage share. Further, they neglect the dynamics of factor proportions $l$ since there is no feedback of this magnitude into the rest of the dynamics due to the irrelevance of the rate of employment and the rate of capacity utilisation (wages and prices do not change).

By setting $\beta _{w}=\beta _{p}=0$, and $\pi ^{e}=0$, we can modify our more general framework to reflect these assumptions.

Under the assumption that firms can automatically adjust their production to the exact level of aggregate demand, so that $y=y^d$ in each moment in time goods market equilibrium (in intensive form) is then given as

$$\begin{aligned} y&= \frac{1}{(1-v)(s_c-(1+\phi )i_1)-i_2/y^p}\nonumber \\&\qquad \left( (1+\phi )i_{1}(-\delta - r \lambda + \psi - r) -i_{2}\bar{u} + \gamma + s_c \delta \right) \end{aligned}$$

(42)

Concerning the determination of the rate of interest through asset market equilibrium, for the sake of simplicity we assume that $e(\,\cdot ,\,)$ is such that

$$\begin{aligned} r&= \varepsilon _\psi (\psi -\psi _o) - \varepsilon _\lambda (\lambda -\lambda _o). \end{aligned}$$

(43)

On the basis of such temporary equilibrium position the evolution of the dynamically endogenous variables $\lambda$ and $\psi$ which gives rise to an autonomous differential equation system in these variables can then be considered under appropriate assumptions for the solution of the goods and asset markets.

The dynamical equations of the model are in the considered special situation:

$$\begin{aligned} \dot{\lambda }&= [d(\rho ^{}+\psi ,\lambda ) -(i_{1}(\rho +\psi -r)+i_{2}(y/y^{p}-\bar{u}) + \gamma ) -\hat{p}]\lambda , \end{aligned}$$

(44)

$$\begin{aligned} \dot{\psi }&= c(\rho -r,\lambda ), \end{aligned}$$

(45)

$$\begin{aligned} \hat{\omega }&= \kappa [(1-\kappa _p)\beta _w (e-\bar{e}) + (\kappa _w-1)\beta _{p} (u-\bar{u})]. \end{aligned}$$

(46)

This dynamical model is basically the model that is investigated in Franke and Semmler (1989) from the analytical as well as from the numerical point of view. Differences to our formulation concern our additional investment term $i_{2}(\cdot )$, and thus the somewhat different specifications that are used for the functions $d(\cdot ), c(\cdot )$ here, and the endogenisation of the rate of profit through aggregate demand-driven business dynamics and dividends, as well as of the real wage in a dynamic set-up. The general model thus exhibits in its analytical core a financial dynamic—based on an IS-LM theory of the rate of profit and the rate of interest—which is capable of generating persistent fluctuations around a well-defined steady state.

Table 2 summarises the parameter values used in the following simulations.

Table 2 Parameter values

Figure 1 illustrates the dynamic adjustments of the 3D dynamical system given by Eqs. (44)–(46) to an exogenous one-time positive shock to the steady-state debt-to-capital ratio. As it can be clearly observed, the fact that $\lambda _o > \lambda$ for one period leads to the emergence of long-lasting fluctuations in all model variables. In the immediate periods after the shock, aggregate output—and capacity utilisation—increases through the expansion of aggregate investment, which leads to a higher state of confidence in the economy and to a subsequent increase in the firms’ indebtedness. As real wages are procyclical (a result of the special choice of the parameter in the real wage equation), the increase in output leads to an increase in the real wage, which in turn would lead ceteris paribus to a decrease in the profit rate.

Fig. 1

Dynamic adjustments of the 3D model after an exogenous 10 % increase in the debt-to-capital ratio

This and more information can also be retrieved from the 2D cycles depicted in Fig. 1. On the one hand, as the capacity utilisation-real wage cycle shows, there is a clockwise movement (where capacity utilisation is depicted in the x-axis and the real wage in the y-axis) which clearly demonstrates the procyclical behaviour of the real wage, increasing when $u$ increases and vice versa. However, it is also interesting to note that given the error-correction terms present in both wage and price Phillips curves, the real wage tends to fall when $v \ge v_o$ and vice versa. This interaction generates the well-known cyclical behaviour in the real wage, and would, if labour productivity was endogenised as procyclical, generate anticyclical movements of the labour share, as discussed for example in Flaschel (2014).

The dynamics with the most pronounced procyclicality are the interaction between the capacity utilisation and the state of confidence in the economy. This is particularly interesting as this is an emergent feature of the model which results truly from the interaction of all model variables and not simply by a particular specification of one of the variables.

5 Concluding Remarks

In this contribution we have incorporated the main elements of the small-scale firms’ debt-finance model by Franke and Semmler (1989) into a medium-scale disequilibrium macroeconomic framework along the lines of Chiarella et al (2005). We illustrated by means of a simple numerical simulation of the resulting framework—which featured investing firms, savings of rentier households, commercial banks and the government—the dynamic feedback mechanisms of endogenously generated debt of firms (created through borrowing) into the investment behaviour of firms, their borrowing of funds, the asset market, the interest rate and the expected rate of return (representing the confidence of investors with regard to future development).

The theoretical framework we developed in this contribution is rich enough to allow for far more complex analytical and numerical investigations. For instance, one could investigate in detail how the model’s local stability is affected by increases in certain parameters such as the rentiers’ savings rate or the reactive of aggregate investment with respect to expected profitability. Also, a proper empirical analysis of the current framework which would also take into account the possibility time- and/or regime-dependent nature of various key parameters of the model seem like a promising next step of research.