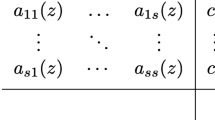Partially Implicit Runge-Kutta Methods for Wave-Like Equations

Abstract

Runge-Kutta methods are used to integrate in time systems of differential equations. Implicit methods are designed to overcome numerical instabilities appearing during the evolution of a system of equations. We will present partially implicit Runge-Kutta methods for a particular structure of equations, generalization of a wave equation; the partially implicit term refers to this structure, where the implicit term appears only in a subset of the system of equations. These methods do not require any inversion of operators and the computational costs are similar to those of explicit Runge-Kutta methods. Partially implicit Runge-Kutta methods are derived up to third-order of convergence. We analyze their stability properties and show the practical applicability in several numerical examples.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The evolution in time of many complex systems, governed by partial differential equations, implies, in a broad variety of cases, looking for the numerical solution of a system of ordinary differential equations. The most commonly used methods to integrate in time these systems are the well-known Runge-Kutta (RK) ones (see e.g. [4, 9] for a general review). Several classifications of the RK methods can be done, according to, e.g., their convergence order, the number of stages or their explicit/implicit structure.

Implicit methods are designed to overcome numerical instabilities appearing during the evolution of a system of equations. As an example, the so-called implicit-explicit RK (IMEX) methods have been used to evolve conservation laws with stiff terms or convection-diffusion-reaction equations (see, e.g., [1, 2, 12, 13]). In our case, although we will not focus on equations with stiff source terms, a partially implicit treatment of the source terms will avoid the development of numerical instabilities in the numerical evolution of wave-like equations.

An implicit treatment offers a solution to get a stable evolution and involves, in general, an inversion of some operators. Depending on the complexity of the equations, the inversion can be even prohibitive in practice from a numerical point of view. We will focus on a particular structure of equations which does not require any analytical or numerical inversion. Therefore, these methods have a computational cost similar to the explicit Runge-Kutta methods (ERK).

2 Structure of the Equations

Let us consider the following system of PDEs,

$$\displaystyle{ \left \{\begin{array}{l} u_{t} = \mathcal{L}_{1}(u,v) \\ v_{t} = \mathcal{L}_{2}(u) + \mathcal{L}_{3}(u,v)\end{array} \right., }$$

(1)

being $\mathcal{L}_{i},i = 1,2,3$, general non-linear differential operators. Let us denote by L _i their discrete operators. This particular structure is a generalization of a wave equation, written as a first-order system in time. $\mathcal{L}_{1}$ and $\mathcal{L}_{3}$ will be treated into an explicit way, whereas the $\mathcal{L}_{2}$ operator will be considered to contain the unstable terms and, therefore, treated implicitly. The partially implicit term refers to this structure, where the problematic term appears only in a subset of the system of equations.

Each stage of the derived partially implicit RK (PIRK) methods will proceed into two steps: (i) the variable u is evolved explicitly; (ii) the variable v is evolved taking into account the updated value of $u$ for the evaluation of the $\mathcal{L}_{2}$ operator. The computational costs of the PIRK methods are comparable to those of the explicit ones. The resulting numerical schemes do not need any inversion of operators.

Numerical methods based on a nonlinear stability requirement are very desirable. Such methods are referred to as strong stability preserving (SSP) ones [8]. Given an evolution equation ∂ _t U = L(U), Gottlieb and Shu [7] proved that the classical second-order method,

$$\displaystyle{ U^{(0)} = U^{n},\;\;U^{(1)} = U^{n} +\varDelta t\,L(U^{n}),\;\;U^{n+1} = \frac{1} {2}\,U^{n} + \frac{1} {2}\,U^{(1)} + \frac{\varDelta t} {2}\,L(U^{(1)}), }$$

(2)

is the optimal second-order two-stage SSP ERK method, and that the third-order one due to Shu and Osher [14],

$$\displaystyle\begin{array}{rcl} U^{(0)}& =& U^{n},\;\;U^{(1)} = U^{n} +\varDelta t\,L(U^{n}),\;\;U^{(2)} = \frac{3} {4}\,U^{n} + \frac{1} {4}\,U^{(1)} + \frac{\varDelta t} {4}\,L(U^{(1)}), \\ U^{n+1}& =& \frac{1} {3}\,U^{n} + \frac{2} {3}\,U^{(2)} + \frac{2\varDelta t} {3} \,L(U^{(2)}), {}\end{array}$$

(3)

is the optimal third-order three-stage SSP ERK method. The optimal adjective refers, for a given number of stages, to a maximization of the corresponding Courant-Friedrichs-Lewy (CFL) value (1 in both cases). In the derivation of the PIRK methods, the previously described optimal SSP ERK methods are recovered when the $\mathcal{L}_{2}$ operator is neglected, i.e., when implicitly treated parts are not taken into account. The remaining coefficients associated to the $\mathcal{L}_{2}$ operator are chosen according to stability criteria. The PIRK methods will minimize the number of stages, two (three) for the second-order (third-order) method.

3 Numerical Methods and Stability Analysis

Let us denote by $(\bar{\alpha }_{1}u,\bar{\alpha }_{2}v)$, $\bar{\lambda }u$ and $(\bar{\gamma }_{1}u,\bar{\gamma }_{2}v)$ the associated linearized parts of the $\mathcal{L}_{1}$, $\mathcal{L}_{2}$ and $\mathcal{L}_{3}$ operators, respectively. The linearized system (1) is rewritten as

$$\displaystyle{ \left \{\begin{array}{l} u_{t} =\bar{\alpha } _{1}u +\bar{\alpha } _{2}v, \\ v_{t} =\bar{\gamma } _{1}u +\bar{\gamma } _{2}v +\bar{\lambda } u.\end{array} \right. }$$

(4)

Let us denote $\alpha _{i}:=\bar{\alpha } _{i}\,\varDelta t$, $\lambda:=\bar{\lambda }\,\varDelta t$ and $\gamma _{i}:=\bar{\gamma } _{i}\,\varDelta t$. We assume that $\vert \omega _{i}\vert \leq 1$, where ω _i , i = 1, 2, denote the two eigenvalues of the following matrix

$$\displaystyle{ \left (\begin{array}{cc} 1 +\alpha _{1} & \alpha _{2} \\ \gamma _{1} & 1 +\gamma _{2} \end{array} \right ), }$$

(5)

which represents the explicit terms of the system. We are going to focus here in the linear stability of the system; the analysis of the linear stability is the most simple case regarding the study of the stability of the system of equations, but if a method does not verify even this criteria it is obviously not stable in general. In most cases, the linear part of the operators is the dominant one and the results obtained in the analysis of the linear stability are reproduced in the numerical simulations. Previous matrix determinant, dex, and trace, trex, are bounded by | dex | ≤ 1 and | trex | ≤ 2. Let us denote M _i the matrix which updates values for a ith-order method,

$$\displaystyle{ \left (\begin{array}{c} u^{n+1} \\ v^{n+1} \end{array} \right ) = M_{i}\left (\begin{array}{c} u^{n} \\ v^{n} \end{array} \right ). }$$

(6)

Stability thus requires that the absolute value of the two eigenvalues associated to the matrix M _i are bounded by 1. However, in order to simplify the derivation of the PIRK methods, we are going to relax this condition on the eigenvalues of the matrix M _i by a bound on its determinant, | det(M _i ) | ≤ 1. The restriction onto the eigenvalues will be shown in the numerical experiments as the boundaries of the stability region. $\mathrm{Re}(\lambda \alpha _{2}) \leq 0$ is also assumed; this condition is satisfied for general wave-like equations written as a first-order system in time (see numerical example).

3.1 First-Order Method

The one-stage first-order method for the system (1) can be written in terms of one coefficient, c ₁, as follows:

$$\displaystyle{ \left \{\begin{array}{l} u^{n+1} = u^{n} +\varDelta t\,L_{ 1}(u^{n},v^{n}), \\ v^{n+1} = v^{n} +\varDelta t\,[(1 - c_{1})\,L_{2}(u^{n}) + c_{1}\,L_{2}(u^{n+1}) + L_{3}(u^{n},v^{n})]. \end{array} \right. }$$

(7)

This method is a particular case for the system (1) of the IMEX-θ method (see, e.g., [10]). The matrix M ₁ satisfies $\det (M_{1}) =\mathrm{ dex} -\lambda \,\alpha _{2}\,(1 - c_{1})$. $c_{1} = 1$ guarantees $\vert \det (M_{1})\vert \leq 1,\forall (\lambda \,\alpha _{2})$.

3.2 Second-Order Method

The two-stages second-order method for the system (1), imposing SSP optimal two-stages second-order method for the pure explicit parts, can be written in terms of two coefficients, $c_{1}$ and c ₂, as follows:

$$\displaystyle{ \left \{\begin{array}{l} u^{(1)} = u^{n} +\varDelta t\,L_{ 1}(u^{n},v^{n}), \\ v^{(1)} = v^{n} +\varDelta t\,[(1 - c_{1})\,L_{2}(u^{n}) + c_{1}\,L_{2}(u^{(1)}) + L_{3}(u^{n},v^{n})]. \end{array} \right. }$$

(8)

$$\displaystyle{ \left \{\begin{array}{l} u^{n+1} = \frac{1} {2}[u^{n} + u^{(1)} +\varDelta t\,L_{ 1}(u^{(1)},v^{(1)})], \\ v^{n+1} = v^{n} + \frac{\varDelta t} {2}\,[L_{2}(u^{n}) + 2c_{ 2}\,L_{2}(u^{(1)}) + (1 - 2c_{ 2})\,L_{2}(u^{n+1}) \\ + L_{3}(u^{n},v^{n}) + L_{3}(u^{(1)},v^{(1)})].\end{array} \right. }$$

(9)

Matrix M ₂ satisfies $\det (M_{2}) = \frac{1} {4}[(1 -\mathrm{ dex})^{2} +\mathrm{ trex}^{2} +\lambda \,\alpha _{ 2}\,(1 -\mathrm{ dex})\,(1 - 2c_{1} + 2c_{2})]$. | det(M ₂) | ≤ 1 cannot be guarantee $\forall (\lambda \,\alpha _{2})$. We restrict to real numbers and consider the determinant of M ₂ as a polynomial in (λ α ₂); the extrema values of its coefficients can be analyzed. For | λ α ₂ | ≪ 1, the resulting optimal values for the coefficients are $c_{1} = 1/2$ and c ₂ = 0; we will denote this method by PIRK2a. For $\vert \lambda \,\alpha _{2}\vert \gg 1$, the optimal values for the coefficients are $c_{1} = 1 -\sqrt{2}/2$ and $c_{2} = (\sqrt{2} - 1)/2$; we will denote this method by PIRK2b. If | λ α ₂ | is not too big, the choice $(c_{1},c_{2}) = (1/2,0)$ is convenient since it avoids to compute the term $L_{2}(u^{(1)})$ to obtain v ⁿ⁺¹ in the final stage. Otherwise, the PIRK2b method is better.

3.3 Third-Order Method

The three-stages third-order method for the system (1), imposing SSP optimal three-stages third-order method for the pure explicit parts, can be written in terms of two coefficients, c ₁ and c ₂, as follows:

$$\displaystyle{ \left \{\begin{array}{l} u^{(1)} = u^{n} +\varDelta t\,L_{ 1}(u^{n},v^{n}), \\ v^{(1)} = v^{n} +\varDelta t\,[(1 - c_{1})\,L_{2}(u^{n}) + c_{1}\,L_{2}(u^{(1)}) + L_{3}(u^{n},v^{n})]. \end{array} \right. }$$

(10)

$$\displaystyle{ \left \{\begin{array}{l} u^{(2)} = \frac{1} {4}[3u^{n} + u^{(1)} +\varDelta t\,L_{ 1}(u^{(1)},v^{(1)})], \\ v^{(2)} = v^{n} + \frac{\varDelta t} {4}\,[\,2(c_{1} + 2c_{2})\,L_{2}(u^{n}) + 4c_{ 2}\,L_{2}(u^{(1)}) + 2(1 - c_{ 1} - 4c_{2})\,L_{2}(u^{(2)}) \\ + L_{3}(u^{n},v^{n}) + L_{3}(u^{(1)},v^{(1)})].\end{array} \right. }$$

(11)

$$\displaystyle{ \left \{\begin{array}{l} u^{n+1} = \frac{1} {3}[u^{n} + 2u^{(2)} + 2\varDelta t\,L_{ 1}(u^{(2)},v^{(2)})], \\ v^{n+1} = v^{n} + \frac{\varDelta t} {6}\,[L_{2}(u^{n}) + L_{ 2}(u^{(1)}) + 4L_{ 2}(u^{(2)}) \\ + L_{3}(u^{n},v^{n}) + L_{3}(u^{(1)},v^{(1)}) + 4L_{3}(u^{(2)},v^{(2)})].\end{array} \right. }$$

(12)

Matrix M ₃ satisfies

$$\displaystyle\begin{array}{rcl} \det (M_{3})& =& \frac{1} {36}[14 + 2(\mathrm{trex} - 1)^{3} + (\mathrm{dex} - 2)^{3} + 6\,\mathrm{trex}^{2} + 3\,\mathrm{dex}\,((\mathrm{trex} - 1)^{2} - 2)] \\ & & + \frac{1} {24}\lambda \,\alpha _{2}\,(-1 + c_{1} - 4c_{2})[(\mathrm{dex} - 2)^{2} + (\mathrm{trex} - 1)^{2} - 2] \\ & & + \frac{1} {12}\lambda ^{2}\,\alpha _{ 2}^{2}\,[c_{ 1} - 4c_{2} + (\mathrm{dex} - 1)(4c_{2} - c_{1}^{2} - 4c_{ 1}c_{2})] \\ & & -\frac{1} {72}\lambda ^{3}\,\alpha _{ 2}^{3}\,[-1 + 3(1 - 2c_{ 1})(c_{1} + 4c_{2})]. {}\end{array}$$

(13)

 | det(M ₃) | ≤ 1 cannot be guarantee $\forall (\lambda \,\alpha _{2})$. We proceed as in the second-order method. For $\vert \lambda \,\alpha _{2}\vert \ll 1$, the resulting optimal values for the coefficients are $(c_{1},c_{2}) = (1/4,1/16)$; we will denote this method by PIRK3a. For $\vert \lambda \,\alpha _{2}\vert \gg 1$, the resulting optimal values for the coefficients are $(c_{1},c_{2}) = ((3 -\sqrt{3})/6,(-1 + \sqrt{3})/8)$; we will denote this method by PIRK3b.

4 Numerical Experiments

In this section we show two examples of the application of PIRK methods to ODEs and PDEs, demostrating that the stability properties of the method hold in practice.

4.1 System of ODEs

Let us consider a system of ODEs of the following form:

$$\displaystyle{ u_{t} = c\,u + d\,v,\;\;\;\;v_{t} = a\,u + b\,v, }$$

(14)

where a, b, c and d are real constants. This system is interesting because it coincides with the linear part of the system of Eqs. (4) considered for our stability analysis, with $\bar{\alpha }_{1} = c$, $\bar{\alpha }_{2} = d$, $\bar{\gamma _{1}} = 0$, $\bar{\gamma _{2}} = b$ and $\bar{\lambda }= a$.

In the case $(b - c)^{2} + 4\,a\,d < 0$ and b + c ≤ 0, this system of equations has damped oscillatory solutions of the form,

$$\displaystyle{ u = \frac{\sqrt{-\mathit{ad}}} {a} v_{0}\cos (\omega t+\phi )e^{\sigma t},\;\;\;\;v = v_{ 0}\cos (\omega t)e^{\sigma t}, }$$

(15)

being v ₀, $\omega \equiv \frac{1} {2}\sqrt{-4\,a\,d - (b - c)^{2}}$, $\sigma \equiv \frac{b+c} {2}$ and $\tan \phi \equiv \frac{\omega } {\sigma -b}$ a constant set by the initial conditions, the frequency, decay rate and relative phase between u and v of the solution, respectively. This system corresponds to (1), with $\mathcal{L}_{1}(u,v) = u + v$, $\mathcal{L}_{2}(u) = a\,u$ and $\mathcal{L}_{3}(u,v) = b\,v$, and fulfills the applicability requirements of the PIRK methods, i.e. $\bar{\alpha }_{2}\,\bar{\lambda } < 0$, $\vert \mathrm{dex}\vert \leq 1$ and | trex | ≤ 2.

For our numerical experiment we will consider the case ω = 1 and $a = -d$, without loss of generality, since it is equivalent to a rescaling of t and v. The remaining coefficients depend only on the values of σ and ϕ. We have performed numerical simulations for $\sigma = 0,-0.01,-0.1,-1$, and $\phi /\pi = 1/2,1/3,1/4,1/10$, which are representative of all possible solutions of this set of equations.

Figure 1 shows the results for a representative test, comparing the first-order ERK with the PIRK. To estimate the relative error of the method we compute the time-averaged L ₂-norm of the difference between the analytic and the numerical solution

$$\displaystyle{ L_{2}(u)(t) = \frac{1} {t}\sqrt{\sum _{t_{n } <t } [u_{\mathrm{num } } (t_{n } ) - u_{\mathrm{ana } } (t_{n } )]^{2 } \varDelta t ^{2 } e^{-2\sigma \,t_{n }}}\;\;. }$$

(16)

Fig. 1

Numerical integration of the previous ODEs with $\sigma =\phi = 0$, using a first-order ERK (left panels) and a first-order PIRK (right panels). Upper panels show the time evolution of u, 10⁻⁴ ≤ Δ t ≤ 1. Dotted lines are the amplitude of the oscillatory analytic solution. Lower panels show the time averaged L ₂-norm of the difference between the numerical and analytical solutions, $10^{-4} \leq \varDelta t \leq 2.1$

For this test the ERK is unconditionally unstable (see left panel) and decreasing the time step leads to an exponentially increasing amplitude, provided the integration time is sufficiently long. By comparison, the first-order PIRK is stable for Δ t < 2, since | u | ≲ 1. For longer time steps (e.g. Δ t = 0. 1) using the PIRK, the solution losses accuracy (in this case a phase shift) but it is still bounded (even at t = 1, 000), and hence the numerical method is stable. We use the value of the time-averaged L ₂-norm at time t = 100 as a measure of the stability of a numerical method, for a particular numerical test with a given time step. Values < 1 ( > 1) usually indicate stability (instability). In Fig. 2 we compare the stability properties of ERK and PIRK methods observed in our numerical experiments. In all cases, the PIRK methods are superior to the ERK methods, as they can achieve stable numerical evolutions with significantly longer time steps. For small time steps, all numerical methods follow the expected order of convergence. For first and second-order methods, ERK methods are unconditionally unstable; despite L ₂-norm < 1 for small values of Δ t, longer evolutions always lead to exponentially growing amplitudes in all studied cases. In contrast, first and second-order PIRKs are numerically stable in all simulations tested (up to t = 1, 000), and only become unstable for Δ t larger than a certain threshold. For the third-order methods, all the schemes are stable for small Δ t, but the ERK becomes unstable at lower values of Δ t than PIRK methods, which behave similar to the tested IMEX scheme.

A change of the value of σ, fixed ϕ = 0, introduces a damping in the oscillatory solution, in a timescale of 1∕σ. As the parameters approach | σ ω | ∼ 1, the system becomes stiff, and the maximum time step providing stable evolutions decreases as expected. In the case of third-order methods (see upper panel of Fig. 3), and similarly for first and second-order ones, as we approach $\sigma = -1$, both ERK and PIRK methods behave almost identically. Despite of being partially implicit, the terms in Eq. (14) responsible for the stiffness cannot be included in the $\mathcal{L}_{2}$ operator, and both ERK and PIRK methods suffer from this stiffness.

Fig. 2

Numerical error integrating a system of ODEs with σ = 0 and ϕ = 0, using first (left panels), second (middle panels) and third (right panels) order methods. Upper panels show the transition between stable (L ₂ ≪ 1) and unstable (L ₂ ≫ 1) numerical evolutions. Lower panels, in logarithmic scale, show the behavior for small time steps, compared to the expected scaling for each method (dashed-dotted lines). As a reference, vertical dashed line at Δ t = 2 corresponds to the maximum time step for the first-order PIRK to be stable

Fig. 3

Behavior of error for third-order schemes varying the value of σ (upper panels, $\phi =\pi /2$) and ϕ (lower panels, σ = 0). From left to right, third-order ERK, PIRK3a and PIRK3b

In the case of varying ϕ, fixed σ = 0, all ERK schemes behave in an identical way (see lower-right panel of Fig. 3 for third-order schemes; first and second-order ones behave similarly). However, PIRK methods suffer from a significant reduction of the maximum time-step as ϕ ≈ 0 (see lower-middle and right panels of Fig. 3 for third-order schemes; first and second-order ones behave similarly). This is the only case in which ERK methods are superior to PIRK methods. Therefore, the class of systems for which PIRK methods are a good alternative to classical ERK methods are wave-like equations, in which the condition ϕ ≈ π∕2 is fulfilled.

4.2 Wave Equation in Spherical Coordinates

In this section, the PIRK methods are applied to the case of the time evolution of a wave equation for a scalar, h, in spherical coordinates. The evolution equation for h can be written as $\partial _{tt}h = \bigtriangleup h$, where $\bigtriangleup$ denotes the Laplacian operator. This equation can be rewritten as a first-order system in time, with the addition of an extra auxiliary variable, $A$, as follows: $\partial _{t}h = A,\;\;\partial _{t}A = \bigtriangleup h$. In this case, according to system (1), the variables can be identified as (u, v) = (h, A), and the operators as $\mathcal{L}_{1}(h,A) = A$, $\mathcal{L}_{2}(h) = \bigtriangleup h$ and $\mathcal{L}_{3}(h,A) = 0$. Spherical coordinates are used. This equation has solutions of the form $h(r,\theta,\varphi,t) \sim j_{l}(kr)\,Y _{lm}(\theta,\varphi )\,\cos kt$, being j _l the spherical Bessel function of first kind of order $l$ and $Y _{lm}$ the spherical harmonics. The value of $k \in \mathbb{R}^{+}$ is determined by imposing boundary conditions. We search for solutions inside a sphere of radius unity imposing $h(r = 1,\theta,\varphi,t) = 0$. We have performed 1D, 2D and 3D simulations using as initial data solutions with n = 1 at t = 0. We use (l, m) = (0, 0), (2, 0), (2, 2) for the 1D, 2D and 3D cases, respectively. We use a finite difference scheme and an equally-spaced grid with n _r , n _θ and $n_{\varphi }$ grid points in the coordinate directions. At r = 1 the analytical solution is imposed as boundary condition. L ₂-norm is used as a measure of the global absolute error,

$$\displaystyle{ L_{2}(h)(t) = \frac{1} {n_{r}n_{\theta }n_{\varphi }}\sqrt{\sum _{r,\theta,\varphi } [h_{\mathrm{num } } (r,\theta,\varphi, t) - h_{\mathrm{ana } } (r,\theta,\varphi, t)]^{2 } (k\,r)^{2}}. }$$

(17)

We will analyze the numerical stability of the derived PIRK methods using (n, l, m) = (1, 2, 0) for the initial data in 2D simulations with equatorial symmetry, $(n_{r},n_{\theta }) = (100,32)$ grid points and a fourth-order spatial discretization scheme (see more details in [6]). Let us denote CFL factor = $\frac{\varDelta t} {\varDelta l_{\mathrm{min}}} = \frac{\varDelta t} {\varDelta t_{\mathrm{max}}}$.

We study stability properties of the numerical solution depending on the coefficients of the methods and the time step Δ t. The bound for the determinant is a necessary but not sufficient condition; the boundaries of the stability region correspond to the bounds for the eigenvalues. For the first-order PIRK method, the estimated optimal value of the coefficient, c ₁ = 1, lays inside the stability region and is indeed the value such that the maximum CFL factor is achievable, as it can be checked in Fig. 4. The ERK method corresponds to c ₁ = 0, and is always unstable.

We have studied the numerical stability of the second-order PIRK method. Figure 5 shows the stability region on the (c ₁, c ₂) plane, for c ₁, c ₂ ∈ [−0. 5, 1. 5] and several CFL factors (0.5, 0.7, 0.8 and 0.9). The boundaries agree with the bounds for the eigenvalues, and the condition for the determinant overestimates this region. The optimal values corresponding to the PIRK2b and PIRK2a methods lie in the stability region almost for all the cases and all the cases, respectively, as it can be checked in Fig. 5. The ERK method corresponds to $(c_{1},c_{2}) = (0,1/2)$ and is always unstable.

Fig. 4

Stability of the first-order PIRK method. Left panel: time evolution of the L ₂-norm for simulations with CFL factor 0.5 and c ₁ values of 0.9 (blue), 0.99 (magenta), 1 (red), 1.5 (orange), 2 (green) and 2.05 (black). Solid and dashed lines represent numerically stable and unstable simulations, respectively. Right panel: stability region depending on the values for c ₁ and the CFL factor. Solid lines are the boundaries of the stability region (orange area). The boundary of the region | det(M ₁) | ≤ 1 is also plotted (dashed lines)

Fig. 5

Dependence of the numerically determined stability region (orange area) on the (c ₁, c ₂) coefficients using a second-order PIRK method for several CFL factors. Boundaries (solid lines) agree with the condition for the eigenvalues. The boundaries for the condition for the determinant (dashed lines), the optimal values for the coefficients, $(c_{1},c_{2}) = (1/2,0)$ (black circle) and $(c_{1},c_{2}) = 1/2(2 -\sqrt{2},\sqrt{2} - 1)$ (star symbol), and the ones corresponding to the second-order ERK method (black triangle) are also plotted

The same numerical stability analysis have been carried out for the third-order PIRK method, shown in Fig. 6 for several CFL factors. The boundaries of the stability region can be obtained in the same way as in the second-order method, the condition for the determinant being less restrictive. The optimal values of the coefficients lay inside the stability region for all CFL factors analyzed. For the coefficients corresponding to the third-order ERK method, stability is achieved if the CFL factor < 0.751 (see Fig. 6).

Fig. 6

Dependence of the numerically determined stability region (orange area) on the $(c_{1},c_{2})$ coefficients using a third-order PIRK method for several CFL factors. Boundaries (solid lines) agree with the condition for the eigenvalues. The boundaries for the condition for the determinant (dashed lines), the optimal values for the coefficients, $(c_{1},c_{2}) = (1/4,1/16)$ (black circle) and $(c_{1},c_{2}) = ((3 -\sqrt{3})/6,(\sqrt{3} - 1)/8)$ (star symbol), and the ones corresponding to the third-order ERK method (black triangle) are also plotted

We have studied the convergence of the PIRK methods by performing series of 1D, 2D and 3D simulations, with resolutions n _r  = 50, $(n_{\theta },n_{\varphi }) = (50,16)$ and $(n_{r},n_{\theta },n_{\varphi }) = (50,8,32)$, respectively. We use CFL=0.8. The L ₂-norm is used as an estimation of the error. Independently of the dimensionality of the simulation, the error falls with decreasing time step as expected from the convergence order of the PIRK method used.

Conclusions

PIRK methods, from first to third-order of convergence, have been derived to evolve in time wave-like systems of non-linear partial differential equations. Optimal SSP ERK methods are recovered when implicitly treated parts are neglected. No inversion is required and the computational costs of the PIRK methods are comparable to those of the ERK ones. The PIRK methods are stable for wave-like equations and larger time steps can be achieved. In contrast, first and second-order ERK methods result to be unconditionally unstable; third-order ERK method is stable, but the largest time step achievable is lower. PIRK methods are appropriate to evolve generalized complex wave equations in spherical coordinates, as it has been shown in [3, 5, 11] for the evolution of Einstein equations.