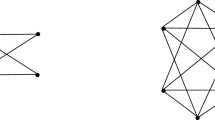On the Energy of Graphs

Abstract

The energy of a graph, E(G), is the sum of the absolute values of its eigenvalues. The energy concept has received a high interest over the last decade, at first due to its various applications in chemistry and then in its own right. This paper focuses on some of the most important results on the bounds for the energy of general graphs and the energy of bipartite graphs. Some known bounds for the change in the energy of a graph after deleting a vertex or an edge are also considered.

1 Introduction and Preliminaries

Let A(G) be the adjacency matrix of a simple, finite, undirected graph, G, with vertex set V (G) and edge set E(G). The set of the eigenvalues $\left \{\lambda _{1},\lambda _{2},\ldots,\lambda _{n}\right \}$ of A(G) is the spectrum of G. As the adjacency matrix is symmetric, its eigenvalues are real and have a sum equal to zero.

According to the interlacing theorem [22]: If G is a graph with spectrum $\lambda _{1} \geq \lambda _{2} \geq \cdots \geq \lambda _{n}$ and the spectrum of the graph obtained upon deleting a vertex u ₁, G − u ₁, is $\mu _{1} \geq \mu _{2} \geq \cdots \geq \mu _{n-1}$, then the spectrum of G − u ₁ is “interlaced” with the spectrum of G, and

$$\displaystyle{ \lambda _{1} \geq \mu _{1} \geq \lambda _{2} \geq \mu _{2} \geq \cdots \geq \mu _{n-1} \geq \lambda _{n}. }$$

(1)

Another important property of the eigenvalues of a graph G is: The number of closed walks of length k in G equals $\sum _{i}^{}\lambda _{i}^{k}$, the kth spectral moment of A(G). In particular, the trace of A ² is:

$$\displaystyle{ \sum _{i}^{}\lambda _{i}^{2} = 2m, }$$

(2)

and since $\sum _{i}^{}\lambda _{i} = 0$,

$$\displaystyle{ \sum _{i<j}^{}\lambda _{i}\lambda _{j} = -m. }$$

(3)

A graph, G, is singular if the adjacency matrix, A(G), is a singular matrix. The nullity, η(G), of a singular graph G is the algebraic multiplicity of the eigenvalue zero in the graph’s spectrum.

A strongly regular graph with parameters (v, k, λ, μ) is a graph with v vertices, such that each vertex has precisely k neighbors, every pair of its adjacent vertices has λ common neighbors, and every pair of non-adjacent vertices has μ common neighbors.

A 2 − (v,k,λ)-design is a family of k blocks of a set of v points, such that each 2-set of points lies in exactly λ blocks.

A semiregular bipartite graph is a bipartite graph whose vertices in the same class of bipartition have the same degree.

The concept of graph energy was first defined by Gutman in [9] and it emerged from the idea of Hückel energy in theoretical chemistry. Coulson [4] provided the following integral formula for the energy of a graph, E(G):

$$\displaystyle{ E(G) = \frac{1} {\pi } \int _{-\infty }^{\infty }\left (n -\frac{\mathrm{i}x\phi '(\mathrm{i}x)} {\phi (\mathrm{i}x)} \right )dx, }$$

(4)

where ϕ(x) is the characteristic polynomial of graph G, and ϕ′(x) its derivative.

The energy of a graph, G, is defined as the sum of the absolute values of its eigenvalues:

$$\displaystyle{ E(G) =\sum _{ i=1}^{n}\left \vert \lambda _{ i}\right \vert. }$$

(5)

In Sect. 2 of this paper, we focus on some of the most important bounds for the energy of a general graph and of a bipartite graph, in terms of a graph’s vertices, edges, degree sequence, and spectral moments. In Sect. 3, we cite several known bounds for the change in energy upon deleting a vertex or edge. We conclude this paper with some additional bounds for the energy of bipartite graphs.

We denote the complete graph of order n by K _n and the complete r-partite graph by K _{t, t, …, t} . The path and cycle with n vertices are denoted by P _n and C _n , respectively. By T _n we denote the tree and by S _n the star graph of order n.

2 Graph Energy Bounds

The calculation of the energy of certain graphs, such as the path, the cycle, or the complete graph, is straightforward as their spectrum is known. In this section, we focus on some of the most important bounds for the energy of general graphs and the energy of bipartite graphs.

McClelland considers the n vertices and m edges of a graph G for the following energy bounds:

Theorem 1 ([19]).

For an (n,m)-graph G,

$$\displaystyle{ \sqrt{2m + n(n - 1)\left \vert detA \right \vert ^{2/n}} \leq E(G) \leq \sqrt{2mn}. }$$

(6)

The upper bound is obtained by the use of the Cauchy–Schwartz inequality to (1, 1, …, 1) and $(\left \vert \lambda _{1}\right \vert,\left \vert \lambda _{2}\right \vert,\ldots,\left \vert \lambda _{n}\right \vert )$, so that

$$\displaystyle{ E(G) \leq \sqrt{n}\sqrt{\sum _{i }^{}\lambda _{i }^{2}}. }$$

(7)

Since $\sum _{i}^{}\lambda _{i}^{2} = 2m$, we get the desired result.

For the lower bound, Eq. (2) and the arithmetic-geometric means inequality is used in

$$\displaystyle{ E^{2}(G) = \left (\sum _{ i}^{}\left \vert \lambda _{i}\right \vert \right )^{2} =\sum _{ i}^{}\left \vert \lambda _{i}\right \vert ^{2} + 2\sum _{ i<j}^{}\left \vert \lambda _{i}\lambda _{j}\right \vert. }$$

(8)

The upper and lower bound of Ineq. (6) can be improved for singular graphs, by taking into account only the nonzero eigenvalues:

Proposition 1 ([9]).

Let G be a graph on n vertices, and nullity η(G). Then,

$$\displaystyle{ E(G) \leq \sqrt{2(n -\eta (G))m}. }$$

(9)

Proposition 2 ([2]).

Let G be a graph on n vertices, and nullity η(G). Then,

$$\displaystyle{ E(G) \geq n -\eta (G). }$$

(10)

In regard to the edges of a graph, a lower and upper bound for the energy of a graph was given:

Theorem 2 ([3]).

Let G be a graph with m edges. Then,

$$\displaystyle{ 2\sqrt{m} \leq E(G) \leq 2m. }$$

(11)

On the left side equality holds if and only if G is a complete bipartite graph and equality on the right side if and only if G consists of m copies of the complete graph K ₂.

The lower bound of the above inequality can be easily derived by using Eqs. (2) and (3) in $E^{2}(G) =\sum _{ i=1}^{n}\lambda _{i}^{2} + 2\left \vert \sum _{i<j}^{}\lambda _{i}\lambda _{j}\right \vert.$

The upper bound takes into consideration that the maximum number of vertices of a graph with m edges is 2m (this implies m copies of the complete graph K ₂).

If G is a graph with no isolated vertices, then a lower bound with reference to its vertices is given by the following theorem.

Theorem 3 ([10]).

Let G be a n-vertex graph, with no isolated vertices. Then,

$$\displaystyle{ E(G) \geq 2\sqrt{n - 1}. }$$

(12)

If G is connected, then m ≥ n − 1 and by using the left side of Ineq. (11), $E(G) \geq 2\sqrt{m} \geq 2\sqrt{n - 1}.$ The proof is analogous if G is disconnected.

From Ineq. (12), it is obvious that the star graph has minimum energy among all n-vertex graphs with no isolated vertices.

An upper bound for a graph with n vertices was given by Koolen and Moolton:

Theorem 4 ([12]).

Let G be a graph with n vertices. Then,

$$\displaystyle{ E(G) \leq \frac{1} {2}n\left (\sqrt{n} + 1\right ), }$$

(13)

with equality if and only if G is a strongly regular graph with parameters $\left (n, \frac{n+\sqrt{n}} {2}, \frac{n+2\sqrt{n}} {4}, \frac{n+2\sqrt{n}} {4} \right )$.

and later an upper bound for a bipartite graph with n vertices was provided by the same authors:

Theorem 5 ([13]).

Let G be a n-vertex bipartite graph. Then,

$$\displaystyle{ E(G) \leq \frac{1} {\sqrt{8}}n\left (\sqrt{n} + \sqrt{2}\right ). }$$

(14)

Equality holds if and only if n = 2v and G is the incidence graph of a $2 -\big (v, \frac{v+\sqrt{v}} {2}, \frac{v+2\sqrt{v}} {4} \big)$ -design.

In order to prove Ineq. (14), the following bound was taken into account:

Theorem 6 ([13]).

Let G be a bipartite graph with n > 2 vertices, and $m \geq \frac{n} {2}$ edges. Then,

$$\displaystyle{ E(G) \leq 2\left (\frac{2m} {n} \right ) + \sqrt{(n - 2)\left [2m - 2\left (\frac{2m} {n} \right )^{2}\right ]}. }$$

(15)

Moreover, equality holds in ( 15 ) if and only if at least one of the following statements is true:

• 1. n = 2m and G = mK ₂.

• 2. n = 2t, m = t ² and G = K _t,t.

• 3. n = 2u, $2\sqrt{m} < n < 2m$ , and G is the incidence graph of a symmetric 2 − (u,k,λ)-design with $k = \frac{2m} {n}$ and $\lambda = \frac{k(k-1)} {u-1}.$

In the above theorem, Eq. (2) and the symmetry of the spectrum of the bipartite graph G are considered, in order to get:

$$\displaystyle{ \sum _{i=2}^{n-1}\lambda _{ i}^{2} = 2m - 2\lambda _{ 1}^{2}. }$$

(16)

By the use of the Cauchy–Schwartz inequality to (1, 1, …, 1), $(\left \vert \lambda _{2}\right \vert,\ldots,\left \vert \lambda _{n-1}\right \vert )$, we get:

$$\displaystyle{ \sum _{i=2}^{n-1}\left \vert \lambda _{ i}\right \vert \leq \sqrt{(n - 2)(2m - 2\lambda _{1 }^{2}}). }$$

(17)

It follows that

$$\displaystyle{ E(G) \leq 2\lambda _{1} + \sqrt{(n - 2)(2m - 2\lambda _{1 }^{2}}). }$$

(18)

Since the function $F(x):= 2x + \sqrt{(n - 2)(2m - 2x^{2 } )}$ decreases on the interval $\sqrt{\frac{2m} {n}} < x \leq \sqrt{m}$ and 2m ≥ n, the result is obtained.

In order to get Ineq. (14), we only need to consider that Ineq. (15) is maximized when $m = \frac{n^{2}+n\sqrt{2n}} {8}.$ For a general graph Ineq. (15) is written:

Theorem 7 ([12]).

Let G be a graph with n vertices and m edges. If 2m ≥ n, then

$$\displaystyle{ E(G) \leq \left (\frac{2m} {n} \right ) + \sqrt{(n - 1)\left [2m - \left (\frac{2m} {n} \right )^{2}\right ]}. }$$

(19)

Moreover, equality holds in ( 19 ) if and only if $G\mathop{\cong}\frac{n} {2} K_{2}$ , or $G\mathop{\cong}K_{n}$ , or G is a noncomplete connected strongly regular graph with two nontrivial eigenvalues both having absolute values equal to $\sqrt{\frac{2m-\left (\frac{2m} {n} \right )^{2}} {n-1}}$.

An upper bound for the energy of a graph in terms of its vertex degree sequence is:

Theorem 8 ([28]).

If G is a graph with n vertices, m edges, and vertex degree sequence d ₁ ,d ₂ ,…,d _n then

$$\displaystyle{ E(G) \leq \sqrt{\frac{\sum _{i=1 }^{n }d_{i }^{2 }} {n}} + \sqrt{(n - 1)\left (2m - \frac{\sum _{i=1 }^{n }d_{i }^{2 }} {n} \right )}. }$$

(20)

Equality in ( 20 ) holds if and only if G is either $\frac{n} {2} K_{2}$ (if n = 2m), K _n $(if \, m = n(n - 1)/2)$ , or a noncomplete connected strongly regular graph with two nontrivial eigenvalues both with absolute value $\sqrt{\bigg(2m -\bigg (\frac{2m} {n} \bigg)^{2}\bigg)/\bigg(n - 1\bigg)}$ or nK ₁ (if m = 0).

For the proof of Ineq. (20), as in the proof of Ineq. (15), the Cauchy–Schwartz inequality is applied to (1, 1, …, 1), $(\left \vert \lambda _{2}\right \vert,\ldots,\left \vert \lambda _{n}\right \vert )$, to get

$$\displaystyle{ E(G) \leq \lambda _{1} + \sqrt{(n - 1)(2m -\lambda _{ 1 }^{2}}) }$$

(21)

and the inequation $\lambda _{1} \geq \sqrt{\frac{\sum _{i=1 }^{n }d_{i }^{2 }} {n}}$ [27] is taken into account. In a similar way, the following bound for bipartite graphs was proved by also considering the symmetry of the spectrum of bipartite graphs.

Theorem 9 ([28]).

If G is a bipartite graph with n > 2 vertices, m edges, and vertex degree sequence $d_{1},d_{2},\ldots,d_{n}$ , then

$$\displaystyle{ E(G) \leq 2\sqrt{\frac{\sum _{i=1 }^{n }d_{i }^{2 }} {n}} + \sqrt{(n - 2)\left (2m - \frac{2\sum _{i=1 }^{n }d_{i }^{2 }} {n} \right )}. }$$

(22)

Equality in (22) holds if and only if G is either $\frac{n} {2} K_{2}$ , a complete bipartite graph, or the incidence graph of a symmetric 2 − (v,k,λ)-design with $k = \frac{2m} {n}$ and $\lambda = \frac{k(k-1)} {v-1}$ , (n = 2v), or nK ₁.

The 2-degree sequence, t _i , of a vertex u _i  ∈ V (G) is the sum of degrees of the vertices adjacent to u _i .

An upper bound in terms of a graph’s degree sequence and 2-degree sequence is:

Theorem 10 ([26]).

Let G be a nonempty graph with n vertices, m edges, degree sequence $d_{1},d_{2},\ldots,d_{n}$ and 2-degree sequence $t_{1},t_{2},\ldots,t_{n}$ . Then,

$$\displaystyle{ E(G) \leq \sqrt{ \frac{\sum _{i=1 }^{n }t_{i }^{2 }} {\sum _{i=1}^{n}d_{i}^{2}}} + \sqrt{(n - 1)\left (2m - \frac{\sum _{i=1 }^{n }t_{i }^{2 }} {\sum _{i=1}^{n}d_{i}^{2}}\right )}. }$$

(23)

Equality holds if and only if one of the following statements holds:

• 1. $G\mathop{\cong}\frac{n} {2} K_{2}.$

• 2. $G\mathop{\cong}K_{n}.$

• 3. G is a nonbipartite connected p-pseudo-regular graph with three distinct eigenvalues $\bigg(p,\sqrt{\frac{2m-p^{2 } } {n-1}},-\sqrt{\frac{2m-p^{2 } } {n-1}} \bigg)$ where $p > \sqrt{\frac{2m} {n}}.$

For the proof of Ineq. (23), the Cauchy–Schwartz inequality is applied to get the function $F(x):= x + \sqrt{(n - 1)(2m - x^{2}})$ and since $\lambda _{1} \geq \sqrt{ \frac{\sum _{i=1 }^{n }t_{i }^{2 }} {\sum _{i=1}^{n}d_{i}^{2}}}$ the result is obtained.

For bipartite graphs Ineq. (23) is written:

Theorem 11 ([26]).

Let G = (X,Y) be a nonempty bipartite graph with n > 2 vertices, m edges, degree sequence $d_{1},d_{2},\ldots,d_{n}$ , and 2-degree sequence $t_{1},t_{2},\ldots,t_{n}$ . Then,

$$\displaystyle{ E(G) \leq 2\sqrt{ \frac{\sum _{i=1 }^{n }t_{i }^{2 }} {\sum _{i=1}^{n}d_{i}^{2}}} + \sqrt{(n - 2)\left (2m - 2 \frac{\sum _{i=1 }^{n }t_{i }^{2 }} {\sum _{i=1}^{n}d_{i}^{2}}\right )}. }$$

(24)

Equality holds if and only if one of the following statements holds:

• 1. $G\mathop{\cong}\frac{n} {2} K_{2}.$

• 2. $G\mathop{\cong}K_{r_{1},r_{2}} \cup (n - r_{1} - r_{2})K_{1}$ , where r ₁ r ₂ = m.

• 3. G is a connected (p _x ,p _y )-pseudo-semiregular bipartite graph with four distinct eigenvalues $\bigg(\sqrt{p_{x } p_{y}},\sqrt{\frac{2m-2p_{x } p_{y } } {n-2}},-\sqrt{\frac{2m-2p_{x } p_{y } } {n-2}},-\sqrt{p_{x } p_{y}}\bigg),$ where $\sqrt{p_{x } p_{y}} > \sqrt{\frac{2m} {n}}.$

Theorem 12 ([18]).

Let G be a nonempty simple graph with n vertices and m edges and let σ _i be the sum of the 2-degrees of vertices adjacent to vertex v _i . Then,

$$\displaystyle{ E(G) \leq \sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} + \sqrt{(n - 1)\left (2m - \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}\right )}. }$$

(25)

Equality holds if and only if one of the following statements holds:

• 1. $G\mathop{\cong}\frac{n} {2} K_{2}.$

• 2. $G\mathop{\cong}K_{n}.$

• 3. G is a non-bipartite connected graph satisfying $\frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ and has three distinct eigenvalues $\bigg(p,\sqrt{\frac{2m-p^{2 } } {n-1}},-\sqrt{\frac{2m-p^{2 } } {n-1}} \bigg)$ where $p = \frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{n}} {t_{n}} > \sqrt{\frac{2m} {n}}.$

For Ineq. (25), $\lambda _{1} \geq \sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}}$ is taken under consideration.

For bipartite graphs the above theorem can be written:

Theorem 13 ([18]).

Let G = (X,Y) be a nonempty bipartite graph with n > 2 vertices and m edges. Then,

$$\displaystyle{ E(G) \leq 2\sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} + \sqrt{(n - 2)\left (2m - 2 \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}\right )}. }$$

(26)

Equality holds if and only if one of the following statements holds:

• 1. $G\mathop{\cong}\frac{n} {2} K_{2}.$

• 2. $G\mathop{\cong}K_{r_{1},r_{2}} \cup (n - r_{1} - r_{2})K_{1}$ , where r ₁ r ₂ = m.

• 3. G is a connected bipartite graph with $V = \left \{v_{1},v_{2},\ldots,v_{s}\right \} \cup \left \{v_{s+1},v_{s+2},\ldots,v_{n}\right \}$ such that $\frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{s}} {t_{s}}$ and $\frac{\sigma _{s+1}} {t_{s+1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ , and has four distinct eigenvalues $\bigg(\sqrt{p_{x } p_{y}},\sqrt{\frac{2m-2p_{x } p_{y } } {n-2}},-\sqrt{\frac{2m-2p_{x } p_{y } } {n-2}},-\sqrt{p_{x } p_{y}}\bigg),$ where $p_{x} = \frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{s}} {t_{s}}$, $p_{y} = \frac{\sigma _{s+1}} {t_{s+1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ and $\sqrt{p_{x } p_{y}} > \sqrt{\frac{2m} {n}}.$

An upper bound that involves a graph’s spectral moments is:

Theorem 14 ([15]).

Let G be a nonempty graph on n vertices. If $\sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} \geq \left (\frac{M_{2k}} {n} \right )^{ \frac{1} {2k} }$ , where k is a positive integer, then the inequality

$$\displaystyle{ E(G) \leq \sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} + (n - 1)^{\frac{2k-1} {2k} }\left (M_{2k} -\left ( \frac{\sum _{i=1}^{n}\sigma _{i}^{2}} {\sum _{i=1}^{n}t_{i}^{2}}\right )^{k}\right )^{ \frac{1} {2k} } }$$

(27)

holds. Moreover, equality in 27 holds if and only if G is either $\frac{n} {2} K_{2}$ , K _n , or a non-bipartite connected graph satisfying $\frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ and has three distinct eigenvalues $\bigg(p,\bigg(\frac{M_{2k}-p^{2k}} {n-1} \bigg)^{ \frac{1} {2k} },-\bigg(\frac{M_{2k}-p^{2k}} {n-1} \bigg)^{ \frac{1} {2k} }\bigg)$ , where $p = \frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{n}} {t_{n}} >\bigg (\frac{M_{2k}} {n} \bigg)^{ \frac{1} {2k} }.$

If G is a bipartite graph, Ineq. (27) is written:

Theorem 15 ([15]).

Let G = (X,Y) be a nonempty bipartite graph with n > 2 vertices and m edges. If $\sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} \geq \bigg (\frac{M_{2k}} {n} \bigg)^{ \frac{1} {2k} }$ , where k is a positive integer, then the inequality

$$\displaystyle{ E(G) \leq 2\sqrt{ \frac{\sum _{i=1 }^{n }\sigma _{i }^{2 }} {\sum _{i=1}^{n}t_{i}^{2}}} + (n - 2)^{\frac{2k-1} {2k} }\left (M_{2k} - 2\left ( \frac{\sum _{i=1}^{n}\sigma _{i}^{2}} {\sum _{i=1}^{n}t_{i}^{2}}\right )^{k}\right )^{ \frac{1} {2k} } }$$

(28)

holds. Moreover, equality in ( 28 ) holds if and only if G is either $\frac{n} {2} K_{2}$, $K_{r_{1},r_{2}} \cup (n - r_{1} - r_{2})K_{1}$ , where r ₁ r ₂ = m, or a connected bipartite graph with $V = \left \{v_{1},v_{2},\ldots,v_{s}\right \} \cup \left \{v_{s+1},v_{s+2},\ldots,v_{n}\right \}$ such that $\frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{s}} {t_{s}}$ and $\frac{\sigma _{s+1}} {t_{s+1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ , and has four distinct eigenvalues $\bigg(\sqrt{p_{x } p_{y}},\bigg(\frac{M_{2k}-2(p_{x}p_{y})^{k}} {n-2} \bigg)^{ \frac{1} {2k} },-\bigg(\frac{M_{2k}-2(p_{x}p_{y})^{k}} {n-2} \bigg)^{ \frac{1} {2k} },-\sqrt{p_{x } p_{y}}\bigg),$ where $p_{x} = \frac{\sigma _{1}} {t_{1}} = \cdots = \frac{\sigma _{s}} {t_{s}}$, $p_{y} = \frac{\sigma _{s+1}} {t_{s+1}} = \cdots = \frac{\sigma _{n}} {t_{n}}$ and $\sqrt{p_{ x}p_{y}} > \left (\frac{M_{2k}} {n} \right )^{ \frac{1} {2k} }.$

In regard to the k-degree d _k (v) of a vertex v ∈ G, which is defined as the number of walks of length k of G starting at v, the next upper bound was given:

Theorem 16 ([11]).

Let G be a connected graph with n $(n \geq 2)$ vertices and m edges. Then,

$$\displaystyle{ E(G) \leq \sqrt{\frac{\sum _{v\in V (G) }^{}d_{k+1 }^{2 }(v)} {\sum _{v\in V (G)}^{}d_{k}^{2}(v)}} + \sqrt{(n - 1)\left (2m - \frac{\sum _{v\in V (G) }^{}d_{k+1 }^{2 }(v)} {\sum _{v\in V (G)}^{}d_{k}^{2}(v)} \right )}. }$$

(29)

Equality holds if and only if G is the complete graph K _n , or G is a strongly regular graph with two nontrivial eigenvalues both with absolute value $\sqrt{\frac{ 2m-\big(\frac{2m} {n} \big)^{2}} {n-1}}.$

If G is a bipartite graph, the above inequality is:

Theorem 17 ([11]).

Let G be a connected bipartite graph with n (n ≥ 2) vertices and m edges. Then,

$$\displaystyle{ E(G) \leq 2\sqrt{\frac{\sum _{v\in V (G) }^{}d_{k+1 }^{2 }(v)} {\sum _{v\in V (G)}^{}d_{k}^{2}(v)}} + \sqrt{(n - 2)\left (2m - 2\frac{\sum _{v\in V (G) }^{}d_{k+1 }^{2 }(v)} {\sum _{v\in V (G)}^{}d_{k}^{2}(v)} \right )}. }$$

(30)

Equality holds if and only if G is the complete bipartite graph or G is the incidence graph of a symmetric 2 − (v,k,λ)-design with $k = \frac{2m} {n}$ , n = 2v and $\lambda = \frac{k(k-1)} {v-1}$.

3 Graph Energy Change

In this section, we consider the change in the energy of a graph G when a vertex or an edge is deleted. Whereas when we remove a vertex u, the energy of the induced subgraph G − u always decreases, for the subgraph G − e, which is obtained upon deleting an edge e, it has been proved that the energy may increase, decrease, or stay the same [5].

By the interlacing theorem it can be easily shown that:

$$\displaystyle{ E(G - u) \leq E(G). }$$

(31)

For singular graphs, Ineq. (31) is improved if the null spread of a vertex u, η _u (G) = η(G) −η(G − u) [7], is taken into consideration:

Theorem 18 ([24]).

Let G = (V,E) be a graph and u ∈ V. If n _u (G) = −1, then

$$\displaystyle{ E(G - u) \leq E(G) - (\left \vert \lambda _{l}\right \vert + \left \vert \lambda _{m}\right \vert ), }$$

(32)

where λ _l and λ _m are the smallest nonnegative and the largest nonpositive eigenvalue, respectively.

In the case where G is a connected graph of nullity η(G) = n − 2, the equality holds if and only if G is a star graph and u is the center vertex of the graph.

Theorem 19 ([24]).

Let G = (V,E) be a graph and u ∈ V. If n _u (G) = 0, then

$$\displaystyle{ E(G - u) \leq E(G) -\left \vert \lambda _{i}\right \vert }$$

(33)

where λ _i is either the smallest nonnegative or the largest nonpositive eigenvalue of G.

In a similar way, Ineq. (31) can be improved to also include non-singular graphs. For example:

Let G = (V, E) be a graph and u ∈ V. Let m(G) be the multiplicity of a nonnegative eigenvalue λ for G, m(G − u) be the multiplicity of λ for G − u, and m _u (G) = m(G) − m(G − u) be the vertex spread of λ. Then by the interlacing inequalities,

Theorem 20.

Let G = (V,E) be a graph and u ∈ V. If m _u (G) = 0, then

$$\displaystyle{ E(G - u) \leq \max \left \{E(G) -\lambda _{l},E(G) -\left \vert \lambda _{m}\right \vert \right \} }$$

(34)

where λ _l (resp. λ _m ) is the smallest positive (resp. largest negative) eigenvalue of G.

Since the energy of a graph decreases with the removal of a vertex, it is clear that if H is an induced subgraph of graph G, then

$$\displaystyle{ E(H) \leq E(G). }$$

(35)

If we examine the subgraph G − e, obtained by deleting edge e from a graph G, we find that the change in energy does not always decrease. In fact, it may increase or stay the same. For example, let us consider the complete bipartite graph K _2, 2 with nonzero eigenvalues − 2, 2 in its spectrum. Then if we delete an edge e, the subgraph K _2, 2 − e is the path P ₃, with nonzero eigenvalues $-\sqrt{2}$ and $\sqrt{ 2}$ in its spectrum. Thus, the energy decreases upon deleting an edge. However, for the complete bipartite graph K _2, 3 with known nonzero eigenvalues $\sqrt{6}$, $-\sqrt{6}$, the energy increases if we remove an edge as we find the spectrum of the subgraph K _2, 3 − e to be $\left \{2.136,0.662,0,-0.662,-2.136\right \}.$

It has been shown that:

Proposition 3 ([24]).

Let K _p,q be a complete bipartite graph, with p + q > 4. Then, if we remove an edge e:

$$\displaystyle{ E(K_{p,q} - e) = 2\sqrt{pq - 1 + 2\sqrt{(p - 1)(q - 1)}}. }$$

(36)

By Ineq. (11),

$$\displaystyle{ E(K_{p,q} - e) - E(K_{p,q}) \geq 2\bigg(\sqrt{pq - 1 + 2\sqrt{(p - 1)(q - 1)}} -\sqrt{pq}\bigg), }$$

(37)

and the energy of the complete bipartite graph increases after removing an edge.

To obtain Ineq. (36) the symmetry of the graph’s spectrum is considered for its four nonzero eigenvalues μ ₁ ≥ μ ₂ ≥ μ ₃ ≥ μ ₄, so that the graph’s characteristic polynomial is written:

$$\displaystyle{ x^{p+q-4}(x^{4} - (\mu _{ 1}^{2} +\mu _{ 2}^{2})x^{2} +\mu _{ 1}^{2}\mu _{ 2}^{2}). }$$

(38)

By Eq. (2) and the trace of A ⁴, we obtain the desired conclusion.

For complete multipartite graphs:

Theorem 21 ([1]).

Let $G = K_{t_{1},t_{2},\ldots,t_{k}}$ be a complete k-partite graph, with k ≥ 2, t _i ≥ 2, for i = 1,…,k. Then for every edge e,

$$\displaystyle{ E(K_{t_{1},t_{2},\ldots,t_{k}} - e) \geq E(K_{t_{1},t_{2},\ldots,t_{k}}). }$$

(39)

Another example of a graph that increases its energy after an edge is removed is the singular hypercube Q _n (the hypercube with even vertices).

Theorem 22 ([24]).

Let Q _2k be a singular hypercube. If Q _2k − e is its subgraph after removing edge e, then:

$$\displaystyle{ E(Q_{2k} - e) \geq E(Q_{2k}). }$$

(40)

For Ineq. (40), the following lemma is considered for the adjacency matrix of the hypercube: $A(Q_{n}) = \left [\begin{array}{cc} A(Q_{n-1})& I_{2^{n-1}} \\ I_{2^{n-1}} & A(Q_{n-1}) \end{array} \right ]$, where $I_{2^{n-1}}$ denotes the identity matrix:

Lemma 1 ([23]).

For a partitioned matrix $C = \left [\begin{array}{cc} A&X\\ Y & B \end{array} \right ]$ , where both A and B are square matrices, we have:

$$\displaystyle{ \sum _{j}s_{j}(A) +\sum _{j}s_{j}(B) \leq \sum _{j}s_{j}(C), }$$

(41)

where s _j (⋅) denote the singular values of a matrix.

Let $G -\left \{m\right \}$ denote the graph obtained from G by deleting all m edges of a subgraph H but keeping all vertices of H. If G ₁ and G ₂ are two graphs without common vertices, let G ₁ ⊕ G ₂ denote the graph with vertex set $V (G_{1}) \cup V (G_{2})$ and edge set $E(G_{1}) \cup E(G_{2})$. Hence, $A(G_{1} \oplus G_{2}) = A(G_{1}) + A(G_{2}).$

Theorem 23 ([5]).

If F is a cut set of a simple graph G, then

$$\displaystyle{ E(G - F) \leq E(G). }$$

(42)

To obtain Ineq. (42), Lemma 1 is applied to $A(G) = \left [\begin{array}{cc} A(H)& X \\ X^{T} &A(K) \end{array} \right ]$, where H and K are two complementary induced subgraphs of G, such that G − F = H ⊕ K.

Theorem 24 ([8]).

Let A and B be two n × n complex matrices. Then

$$\displaystyle{ \sum _{i=1}^{n}s_{ i}(A + B)+ \leq \sum _{i=1}^{n}s_{ i}(A) +\sum _{ i=1}^{n}s_{ i}(B), }$$

(43)

where $s_{j}(\cdot )$ denote the singular values of a matrix.

Moreover equality holds if and only if there exists a unitary matrix P such that PA and PB are both positive semi-definite.

Theorem 25 ([6]).

Let H be an induced subgraph of a graph G. Then,

$$\displaystyle{ E(G) - E(H) \leq E(G -\left \{m\right \}) \leq E(G) + E(H). }$$

(44)

Moreover,

• 1. if H is nonsingular, then the left equality holds if and only if $G = H \oplus (G - H).$

• 2. the right equality holds if and only if m = 0.

For the left side of Ineq. (44) Theorem 24 is applied to

$$\displaystyle{ A(G) = \left [\begin{array}{cc} A(H)& X^{T} \\ X &A(G - H) \end{array} \right ] = \left [\begin{array}{cc} A(H)&0\\ 0 &0 \end{array} \right ]+\left [\begin{array}{cc} 0 & X^{T} \\ X &A(G - H) \end{array} \right ], }$$

(45)

where X represents edges connecting H and G − H.

For the right side of Ineq. (44) the same theorem is applied to

$$\displaystyle{ A(G-\left \{m\right \}) = A(G)+\left [\begin{array}{cc} - A(H)&0\\ 0 &0 \end{array} \right ]. }$$

(46)

It has been shown that:

Theorem 26 ([5]).

For any simple graph G with at least one edge,

$$\displaystyle{ E(G) \geq 2. }$$

(47)

Since the complete graph K ₂ is an induced subgraph of G, by Ineq. (35) the proof of the above bound is trivial.

Corollary 1 ([6]).

Let e be an edge of a graph G. Then the subgraph with the edge set $\left \{e\right \}$ is induced and nonsingular, hence

$$\displaystyle{ E(G) - 2 \leq E(G -\left \{e\right \}) \leq E(G) + 2. }$$

(48)

Moreover,

• 1. the left equality holds if and only if e is an isolated edge of G.

• 2. the right equality never holds.

From Ineq. (48), it is clear that:

• 1. if e is an edge of a connected graph G such that $E(G) = E(G -\left \{e\right \}) + 2$, then G = K ₂. 

• 2. there are no graphs G such that $E(G -\left \{e\right \}) = E(G) + 2.$

4 Energy of Bipartite Graphs

We conclude this paper with some additional bounds for the energy of bipartite graphs.

Theorem 27 ([2]).

If G is a connected bipartite graph of rank r, then

$$\displaystyle{ E(G) \geq \sqrt{(r + 1)^{2 } - 5}. }$$

(49)

Theorem 28 ([2]).

Let G be a bipartite graph with at least four vertices. If G is not full rank, then

$$\displaystyle{ E(G) \geq 1 + rank(G). }$$

(50)

Theorem 29 ([21]).

Let G be a bipartite graph with 2N vertices. Then,

$$\displaystyle{ E(G) \geq 2m\sqrt{\frac{m} {q}}, }$$

(51)

where $q =\sum _{ i=1}^{N}\lambda _{i}^{4}$ . The equality holds if and only if G = NK ₂ or G is the direct sum of isolated vertices and complete bipartite graphs $K_{r_{1},s_{1}},\ldots,K_{r_{j},s_{j}}$ such that $r_{1}s_{1} = \cdots = r_{j}s_{j}.$

It has been shown [21] that Ineq. (51) remains also true if G is a bipartite graph with 2N + 1 vertices.

Let B _n, m be the bipartite (n, m)-graph with two vertices on one side, one of which is connected to all vertices on the other side, as illustrated in Fig. 1.

Fig. 1

The graph B _n, m

Theorem 30 ([17]).

B _n,m (n ≤ m ≤ 2(n − 2)) is the unique graph with minimal energy in all bipartite connected (n,m)-graphs.

An n-vertex graph G is said to be hypoenergetic if E(G) < n. It has been shown [20] that almost all graphs are hyperenergetic (E(G) > 2(n − 1)), which implies that there are but a few hypoenergetic graphs.

Theorem 31 ([25]).

Let $G\mathop{\cong}K_{n_{1},n_{2}}$ , n ₁ ≠ n ₂ . Then G is hypoenergetic.

Since the spectrum of $K_{n_{1},n_{2}}$ is known, the proof of the above theorem is trivial.

Theorem 32 ([16]).

The complete bipartite graph K _2,3 is the only hypoenergetic connected cycle-containing (or cyclic) graph with maximum degree Δ ≤ 3.

Let G _rst be a graph of order n constructed as shown in Fig. 2, by identifying the center of a star K _1, t with a vertex of a complete bipartite graph K _r, s , where r + s + t = n.

Fig. 2

The graph G _rst

Theorem 33 ([25]).

Among the complete bipartite graphs with pendent vertices attached, some are hypoenergetic.

It is well known [14] that the graph $G\mathop{\cong}G_{rst}$ has a nullity of η(G) = n − 4. By Ineq. (9) and after some calculations, it can be easily shown that the graph G _rst is hypoenergetic for t ≥ r > s ≥ 5.