Keywords

Introduction

This chapter argues that the highest quality teaching maximises the learning of all students, not just a lucky few, and that teachers, schools and systems should address structural and other factors that might inhibit the goal of creating opportunities for all students. It begins with an overview of the aspirations of the Australian Curriculum Assessment and Reporting Agency (ACARA) for curriculum and schooling in Australia, then describes some of the challenges facing Australian schools, continues by arguing that the major issue is within-school differences, describes school and classroom grouping practices and concludes with an outline of an approach that seems to make heterogeneous grouping feasible. In the discussion, the focus is mainly on the mathematics curriculum and teaching, in part because it is the subject that seems to experience the greatest challenge due to differences in student readiness, and in part because closing off options for mathematics study restricts both study and employment options for students. While the focus of the discussion is on Australian contexts and Australian schools, the implications and conclusions are relevant internationally. In a sense, the focus on Australia can be taken as a case study.

Aspirations for Education in Australia and the Australian Curriculum

Fundamental to system, school and classroom decisions on maximising opportunity are the potential of education to create opportunity for citizens that they might not otherwise have. The commitment of government through its various agencies is unambiguous, as evident in the overarching Shape Paper (ACARA 2012) that established the principles for the Australian Curriculum (AC):

All Australian governments have committed to the goals of the Melbourne Declaration, which are that Australian schooling promotes equity and excellence; and that all young Australians become successful learners, confident and creative individuals, and active and informed citizens. (p. 5)

The Shape Paper went further to argue that schooling and the curriculum should ensure that young people

have a sense of self-worth, self-awareness and personal identity that enables them to manage their emotional, mental, spiritual and physical wellbeing. (p. 8)

This, in turn, is intended to prepare them for their

potential life roles as family, community and workforce members, [so they will be able to] embrace opportunities, make rational and informed decisions about their own lives and accept responsibility for their own actions. (p. 9)

This is even described as an entitlement

of each student to knowledge, skills and understandings that provide a foundation for successful and lifelong learning and participation in the Australian community. (p. 10)

The document also makes the explicit assumption

that each student can learn and the needs of every student are important. It enables high expectations to be set for each student as teachers account for the current levels of learning of individual students and the different rates at which students develop. (p. 10)

Similar sentiments are expressed in the principles for mathematics (ACARA 2009):

Building on the draft National Declaration on Educational Goals for Young Australians, a fundamental aim of the mathematics curriculum is to educate students to be active, thinking citizens, interpreting the world mathematically, and using mathematics to help form their predictions and decisions about personal and financial priorities. Mathematics also enables and enriches study and practice in many other disciplines. (p. 5)

It also argues

that schooling should create opportunities for every student. There are two aspects to this. One is the need to ensure that options for every student are preserved as long as possible, given the obvious critical importance of mathematics achievement in providing access to further study and employment and in developing numerate citizens. (p. 10)

In other words, the documents which can be taken to represent community aspirations, argue that all students have an entitlement to a curriculum that maximises their opportunities, that prepares them for a life in which creativity, imagination and an orientation to life-long learning are emphasised more than correct answers, compliant attitudes and acceptance of a designated place in a hierarchical social order. The assumption is that schools and classrooms should be structured to facilitate the achievement of the former curriculum goals for all students.

Challenges Facing Australian Schools in Maximising Opportunities for All

There are a number of factors that make the full implementation of a curriculum based on these principles difficult and urgent. One factor is the long ‘tail’ (McGaw 2007) that refers to the fact that while some Australian students are doing well in international comparisons, there are other students who are a long way behind them in readiness for further study.

The characteristics of this tail are elaborated by Thompson et al. (2010) who note that while the performance of Australian students in mathematics in PISA 2009 had remained strong in comparison to previous surveys, the ranking of the full cohort of Australian students in mathematics had declined, and this decline was reported as mainly due to a fall in the proportion of students achieving at the top levels. They also note that students in the lower groups were disproportionally those from

  • the lowest socioeconomic status (SES) quartile (of whom 23 % were not achieving level 2 in literacy compared with 5 % of the high SES background students, with the figures for numeracy being 22 and 5 %, respectively);

  • indigenous background (of whom 38 % were not achieving level 2 in literacy compared with 12 % of non-Indigenous students, with the figures for numeracy being 39 and 12 %, respectively); and

  • rural areas (of whom 24 % were not achieving level 2 in literacy compared with 12 % of metropolitan students, with the figures for numeracy being 28 and 12 %, respectively).

Importantly, in the case of numeracy, students not achieving level 2 are not yet able to use basic procedures or interpret results. These students would experience substantial difficulty with the mathematics curriculum relevant for their age and year level.

A key challenge for schools is to find ways to address the needs of these students. But a critical consideration is that within each of these subgroups there is widespread diversity. In elaborating this issue, Thompson et al. (2010) compare the reading levels of Australian-born, first generation, and foreign-born students. There was a slight advantage to the first generation students, but the real issue is that the diversity of achievement in each of the three groups of students was more or less identical, in that there were similar proportions of students from each group at each of the achievement levels as defined by PISA. Similarly, there is a diversity of achievement of low SES group students, Indigenous students and rural students, with students in each of these subgroups achieving at the top international levels. The challenge for schools is to ensure that students from these subgroups are not given a restricted curriculum but to find ways to address the diversity of readiness whatever the student population.

In other words, even though there is a long tail in achievement of Australian students, with particular subgroups over-represented in the tail, there are also students even within the subgroups achieving at the best international levels. These factors all make the task of structuring schools and classrooms to maximise opportunity challenging.

Between- and Within-School Differences

Even when acknowledging the disparity between the resourcing of schools in different sectors and the differences in status of government schools depending on their location, it seems that the major variances are within individual schools rather than between schools. In an Australian Council of Educational Research report on students’ tertiary entrance scores, Marks et al. (2001) argue that between-school differences account for approximately 22 % of the variation in student scores, and that about half of this variation is accounted for by differences in the academic and socioeconomic mix of students and school sector. In other words, 78 % of the variance in student scores is attributable to differences within each school. Similarly, in an analysis of systemic assessment results, Rothman and McMillan (2003) argue that less than 20 % of the variation in achievement scores on both reading and mathematics could be attributed to differences between schools. As with Marks et al., they note that around half of the between-school variance could be explained by student characteristics. In other words, the challenge facing Australian schools is not differences between school types and suburbs, but the wide range of achievement within each school, and that actions to maximise opportunity are the responsibility of individual schools and classroom teachers.

The inference is that differences within individual schools should be the focus of system and school policy development. These within-school differences related predominantly to differences between teachers and grouping practices that either minimise or exacerbate the differences.

Accommodating the Diversity of Readiness in School and Classroom Grouping Structures

It is no simple task to address this diversity of readiness and the challenges teachers face, particularly in years 5–10. Teachers at those levels are more likely than others to experience classrooms in which there are:

  • Fast learners who shout answers and criticise others who are still thinking through problems that the fast learners have already solved, and who complain to their parents about being under-extended.

  • Some other learners who have more or less given up believing that they cannot learn, and who prefer to interrupt others.

  • Extensive and exhaustive lists of content to cover that pressure teachers to move quickly from topic to topic.

  • Routines in schools that leave teachers with limited time for collaboration, sharing ideas, innovating, resource development and so on.

In other words, there are very real pressures on teachers that are directly relevant to their approaches to addressing differences in readiness for the curriculum at particular levels. The focus in this section is on the ways that schools respond to these pressures and in particular on the decisions about the ways students are grouped. Such decisions are often made based on the preferences of the teachers, which can be informed by their views on who can learn and also by their concerns for particular categories of students that they feel might be disadvantaged by certain school and class groupings. These issues are especially acute in the case of mathematics as the stratification of groups is most prevalent in mathematics.

There are different forms of this stratification. The most common is when students are assessed in mathematics and then grouped according to the results on that assessment. While elsewhere different terms are used, in Australia this is termed streaming. There are also many schools which select one or more high-achieving groups, but otherwise have the rest of the groups grouped heterogeneously (commonly described as tracking).

There is limited research on the extent of streaming practices in Victorian schools. In a detailed study, using an on-line survey of grouping practices in mathematics, Forgasz (2010) reports that 80 % of the 44 responding schools had some form of streaming in the years 7–10, with three quarters of the respondents indicating support for that streaming. Indeed, of the four schools which said that there was no streaming, three of the respondents were opposed to that policy. It can be inferred that the teachers who responded were overwhelmingly in favour of some streaming. A positive characteristic of the responses was that only 37 % of the schools reported streaming in year 7, 55 % in year 8 and 70 % in year 9. This indicates that the majority of these schools have heterogeneous groupings at year 7 and half of the schools at year 8. Clearly, it is possible to teach mathematics without streaming.

At the same time, it is easy to understand attempts to make grouping more homogeneous. Some of the difficulties that have been identified with heterogeneous grouping are:

  • Teachers set expectations and starting points based on low-achieving students and as a result the other students are under-extended and less satisfied with their learning environment.

  • Teachers over direct the learning of everyone (assuming low-achieving students cannot cope), which has the effect of encouraging a fixed mind set (Dweck 2000) and a passive approach to learning in the students.

  • There is negative peer pressure on hard-working students, which is very real. Sullivan et al. (2006), for example, found that the classroom culture exerts a more powerful (negative) influence on students than their individual aspirations.

  • Teachers can ignore the diversity of readiness and instead treat everyone as the same (possibly by giving routine tasks that everyone can and is willing to do) (see Doyle 1986).

  • Teachers teach different content to different groups, which not only increases the teachers’ workload, but destroys any sense of a classroom community.

  • Low-achieving students ‘performance avoid’ (Elliot 1999) by misbehaving, being a group-work passenger or pretending to work while not actually doing anything.

Clearly, if heterogeneous groups are to maximise the learning of all students substantial actions must be taken by teachers and schools to address these difficulties.

On the other hand, homogeneous groupings can have the effect of restricting student opportunities if:

  • Teachers teach different content to different groups, thereby not only narrowing the options of some students but also actually closing them off too early.

  • There is limited or no movement between groups, which appears to be the most common situation. If there is no chance of ‘promotion’, students are unlikely to try hard and, in any case, students develop affiliation with the group and so do not want to move.

  • Steps are not taken to avoid development of poor self-concept by some members of the upper streams. This was described by Marsh et al. (2005) as the Big fish little pond effect in which a substantial minority of students in such groups develops a low self-concept and subsequent little interest in the subject because they feel that their classmates are more able than they are.

There are, however, significant barriers to overcoming negative effects of homogeneous grouping. It is very difficult to ensure that students in all groups have the same opportunities if the curriculum is stratified and only a limited subset of the curriculum is offered to some groups. This can be exacerbated if teachers feel that skills precede other learning and so emphasise skills to the detriment of other aspects of mathematics, such as communication, meaning and relevance. Indeed, the very placement of students in low streams communicates to students that their teachers think they cannot learn. A further risk is that the ‘homogeneous’ grouping of students communicates to teachers that the students are indeed of like achievement.

In terms of seeking advice from research, Forgasz (2010) reviewed a range of studies on the effects of grouping classes of students by their achievement. She argues that the results are

inconclusive, particularly for those at the highest levels of achievement. There is general agreement, however, that those in middle and lower achieving mathematics classes may be disadvantaged with respect to achievement, and that their future mathematics and life options are likely to be curtailed. (p. 66)

More conclusively, in a major metanalysis, Hattie (2009) argues that stratification, streaming, tracking, setting has ‘minimal effect on learning outcomes and profound negative equity effects’ (p. 90). He argued that low-stream classes are ‘deadening, non educational environments’ (p. 90) that fail ‘to foster the outcomes schools value’ but are focused on ‘remediation through dull, repetitious seatwork’. Yet Hattie also argued that ‘it seems that the quality of teaching and the nature of students’ interactions are the key issues, rather than the compositional structure of the classes’ (p. 91).

In other words, streaming students for mathematics poses a threat to equity and opportunity but it is as much the ways classes are taught that is important as it is the method of grouping.

Self-Fulfilling Prophesy Effects

It is clear that both homogeneous and heterogeneous grouping practices create challenges for teachers and schools. To explore further the challenges that teachers experience, a particular effect that applies to both forms of grouping is outlined. It seems that if teachers believe that students are less likely to learn mathematics, then those students have restricted opportunities to learn.

This effect, referred to as self-fulfilling prophesy, has been reviewed over a broad range of contexts and the findings suggest that the effect applies when teachers attribute particular characteristics to students, such as whether they are high achieving or likely to experience difficulty in learning. The effect has also been noted in terms of teachers forming judgments about student potential based on race or ethnicity. For example, in making recommendations on ways to repay what he describes as an ‘educational debt’ to Maori students in New Zealand, Bishop (2010) refers to the ‘dominance of a deficit discourse among teachers’ (p. 130). He identifies this as the single pedagogical issue that needs to be addressed in teaching Maori students as it continues to be a major barrier to educational reform. Bishop calls for action to address the situation that ‘currently the majority of teachers are defining Maori potential in deficit terms’ (p. 134). This effect operates similarly in many classrooms and schools, and has a negative impact on the learning opportunities of students whom the teachers see as low achieving.

Almost three decades ago, Brophy (1983) posed a cyclic model that describes how this self-fulfilling prophecy might operate:

Step 1: Teachers form early differential expectations for students.

Step 2: As a result, the teachers behave differently to different students and this differential behaviour communicates the teachers’ expectations to the students. If such treatment of the students is consistent, and if the students do not resist, it will have an effect on their self-concept, achievement, motivation, aspirations and classroom conduct.

Step 3: The students’ responses will actually reinforce the teacher’s original expectations. Ultimately there will be differences in student achievement and outcomes directly due to this effect.

In other words, the effect in schools and classes is connected to the responses that teachers give to different types of students. Brophy (1983) argued that, for those students considered to have difficulty in learning mathematics, teachers:

  • wait less time for them to answer questions;

  • give them the answer or call on someone else rather than waiting;

  • use inappropriate reinforcements;

  • criticise them more for failure and praise them less frequently;

  • do not give them public feedback on their responses;

  • call on them less to respond;

  • demand less; and

  • have less friendly verbal and nonverbal contact.

One of the explanations for this effect relates to what Brophy called the teachers’ need for control. For example, when dealing with students whom the teachers think can learn well, teachers feel more able to predict student behaviour when interacting with them both privately and publicly, no matter who initiates the interaction. On the other hand, if teachers are worried about classroom control they are likely to avoid public interactions with low-expectation students, especially interactions the students have initiated. Teachers may call on students less if they believe that they will experience difficulty learning, and ignore or discount their attempts to initiate questions.

Another explanation for the way the effect works is related to attribution. In this, teachers who attribute to themselves a student’s failure to grasp an idea are likely to give further explanations and to seek other ways of explaining the difficult idea. If however teachers attribute the failure to a student’s lack of ability or some other characteristic, they may give up and move the student on to some other simpler task, thereby reducing the likelihood that the student will learn the intended content.

A third explanation is related to the notion of learning through challenge. Sullivan et al. (2011) argue that students are more likely to learn mathematics when they work on problems that they cannot yet do, as distinct from only practising routines that they already know. If teachers are not presenting low-achieving students with challenges, this also reduces their opportunities to learn.

Interestingly, Brophy (1983) argued that being aware of the potential impact self-fulfilling prophesy effects on particular groupings can minimise negative effects. For example, teachers in both heterogeneous and homogeneous groups can avoid the impact of their presumptions about the potential of individual students by consciously treating all students similarly. Further, even class groups designed to maximise homogeneity are diverse in their readiness. The explanation for this is that even though students are grouped by their achievement, the intent of streaming is to group students by their ability, which cannot be measured directly. Because there are high-ability students who may achieve low scores on a particular assessment for a variety of reasons, and some low-ability students who score well, perhaps due to their effort or even out of school tuition, even like achievement groups will have a range of abilities. In other words, if the students are grouping by their achievement, there will still be a diversity of readiness to learn mathematics and all teachers need to plan to address this diversity.

Further Data on the Diversity in Classrooms

The following explores this issue of within-class diversity further. Sullivan et al. (2013) present findings that illustrate the issue of diversity and the need to address it within each classroom. They administered a survey to students over 17 schools and 95 classes designed to capture some attitudes to mathematics. The first items in the survey asked the students to indicate on a scale of 1–7, ‘How good are you at maths?’ and ‘How happy are you in maths class?’ In the following discussion, responses to the first item are taken to be a measure of confidence, and responses to the second to be a measure of satisfaction.

The students’ responses were predominantly positive although they did vary from 1 to 7 indicating that there was a range of levels of confidence and satisfaction in every class. Interestingly, there was not much difference between the responses of the students at the respective year levels, given that junior secondary students appear to be less satisfied and less confident in their ability. Table 14.1, reproduced from Sullivan et al. (2013), presents a comparison of responses of students across these year levels.

Table 14.1 Comparison of students’ ‘confidence’ and ‘satisfaction’ across the year levels
Full size table

Overall, the students seemed to feel more confident than satisfied and there is a substantial spread of scores at each of the grade levels, meaning that while there were some students who gave positive responses, there were others who gave negative ones. While there were statistically significant differences between the grade levels for both confidence (F(3926) = 3.34, p < 0.02) and satisfaction (F(3926) = 4.11, p < 0.01), the differences within each year level were more substantial than those between year levels. In other words, the differences within year levels are more substantial than those between year levels and rather than teaching differently between years, the implication is that teachers need to address differences in confidence and satisfaction in the classes they are teaching whatever the level and whatever the grouping practice.

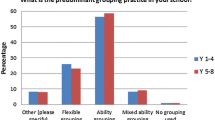
From another perspective on the challenge of addressing diversity, the following data are from a current project, with David Clarke and Doug Clarke, in which we surveyed a group of primary and secondary teachers working with us on the implementation of the AC. Table 14.2 presents the responses of teachers to a survey on classroom grouping practices. Nineteen teachers were asked to indicate the percentage of their lessons in which they used each of the nominated practices.

Table 14.2 Responses of teachers reporting frequency of use of particular grouping practices (n = 19)
Full size table

It seems that nearly all lessons involved students working on related or similar tasks, around one-third of lessons have students grouped by achievement, one-third of lessons have students completing a different quantity of tasks and around one-third of the lessons involved students working on differentiated tasks. These findings affirm that teachers are identifying ways to address the differences in readiness.

A Model of Teaching to Address Differences in the Preparedness of the Students

A particular model of teaching, designed to address the diversity in student readiness in mathematics (whatever the method of classroom grouping), was proposed by Sullivan et al. (2009a). It has five elements.

The first element relates to building a communal classroom experience. Sullivan et al. (2009b) argue that all students should have at least some core experiences that can form the basis of later discussions. The expectation is that teachers work with students to develop in them a sense of membership of the class as a whole. This notion is based on Wood’s (2002) research which emphasises how ‘social interactions with others substantially contribute to children’s opportunities for learning’ (p. 61) as well as the interplay between children’s developing cognition and the ‘unfolding structure that underlies mathematics’ (p. 61). Integral to this element is the assumption that mathematical communications in classrooms that are intended to include all students can best occur if there is some communal experience. If some students in a class are excluded from common experiences and are unable to participate in discussion, this voids the possibility of them feeling affiliated with the class as a whole. Further, such experiences not only create opportunities for social interaction but also promote thinking about mathematics.

The second element is the planning of a trajectory of mathematical tasks. Sullivan et al. (2009b) argue that there are two considerations for the trajectory of tasks. The first is that there are benefits to inclusivity if at least some of the tasks are open ended. A number of researchers have argued that open-ended tasks engage students in thinking about mathematics exploration, enhance motivation through increasing sense of control and encourage students to investigate, make decisions, generalise, seek patterns and connections, communicate, discuss and identify alternatives (Christiansen and Walther 1986; Middleton 1995; Sullivan 1999). The second consideration is that earlier tasks in the sequence provide experiences that scaffold students in the solution of later tasks, allowing them to engage in more sophisticated mathematics than would otherwise have been the case. This connects directly with the notion of a hypothetical trajectory.

There are different ways to create sequences of tasks. One type of sequence is where the problem formulation remains constant but the numbers used increase the complexity of the task, say moving from small numbers to larger numbers. Another type of sequence is where the problem is progressively made more complex by the addition of supplementary steps or variables, such as in a network task where additional nodes are added. A third type of sequence may be where the concept itself becomes more complex, such as in a sequence of finding areas or progressively more complex shapes from rectangles, to composite shapes, to irregular shapes. The creation of such sequences is a key component of the planning model.

The third element involves enabling prompts that are posed to engage students experiencing difficulty. Students are more likely to feel fully part of the class if teachers offer prompts to allow those experiencing difficulty to engage in active experiences related to the initial goal task, rather than, for example, requiring such students to listen to additional explanations or assuming that they will pursue goals substantially different from those of the rest of the class. There are some generic types of prompts. For example, it nearly always helps to draw a diagram or model, to remove one of the constraints, to offer more choice, or to change the form of representation.

A fourth element relates to anticipating that some students may complete the planned tasks quickly, and can be posed supplementary tasks that extend their thinking on that task. One of the characteristics of open-ended tasks is that they create opportunities for extension of mathematical thinking, since students can explore a range of options as well as considering forms of generalised response. In practice it is arguable that this is the most important and challenging of these planning elements. The premise is that the students in the class progress together through the lesson contributing to the sense of communal experience. Unless creative opportunities are provided for the students who have completed the tasks along the way then not only might they be bored, and so create difficulties for the teacher, but also they will not be using their time effectively. Note that this offers substantial advantages over the strategy of moving students who finish the work onto the next chapter of the text.

The fifth element of the framework is related to being explicit about the pedagogies of mathematics teaching. This is derived from the work of Bernstein (1996) who described pedagogies that are hidden from some students. Bernstein argued that, through different methods of teaching, students receive different messages about the overt and the hidden curriculum of schools. He suggested that some students are able to make sense of this ‘invisible’ pedagogy more effectively than others, due to their familiarity with the embedded sociocultural norms, and hence those students have more chance of success. As suggested by Delpit (1988), Zevenbergen (1998) and Dweck (2000), it may be possible to moderate the effect of the hidden curriculum by explicit attention to aspects of pedagogies associated with such teaching. Sullivan et al. (2002) list a range of strategies that teachers could use to make implicit pedagogies more explicit and so address aspects of possible disadvantage of particular groups. It seems that teachers are able to make explicit at least some of the key pedagogies associated with such teaching, and that students respond to this explicitness in the direction intended.

In other words, it is proposed that better learning outcomes are likely if lessons are based on sequenced tasks that have potential for students’ decision making, in which it is intended that all students participate, with prompts for those students who are experiencing difficulty and those who complete the work quickly, and for which the desired pedagogies are made explicit.

An Illustrative Example of Such Teaching

To exemplify what such teaching might look like, the following plan is presented to illustrate the elements of a lesson based on this model. The plan is written for an actual lesson hypothetically to be taught by other teachers. It is stressed that the project cited above gathered evidence of the applicability and effectiveness of this approach.

Introduction

Explain the mathematical focus of the lesson which is on ways of representing data sets using single scores, especially mean, median, mode and range.

Outline the expectation that students:

  • show how they got their answers on the worksheets,

  • give more than one possible solution strategy,

  • keep trying even if it is difficult (it is meant to be),

  • explain your thinking, and

  • listen to other explanations.

Task 1: Writing a Sentence

Pose the following problem:

  • Write a sentence with 5 words, with 4 as the mean of the number of letters in the words. Do not use any words of 4 letters.

Invite questions for clarity, but will not tell them how to do it. The students can get started without further explanation.

Possible enabling prompts are:

  • Write a sentence of 5 words.

  • Write a sentence of 20 letters.

As an extending prompt, ask students to make one of the words as long as possible.

Task 2: Fishing

Pose the following problem:

Seven people went fishing. The mean number of fish caught was 5, the median was 4 and the mode was 3. How many fish might each of the people have caught? (Give at least three answers.)

Possible enabling prompts are:

  • Seven people went fishing. The mode of the number of fish caught was 3. How many fish might each of the people have caught?

  • Seven people went fishing. The median number of fish caught was 4. How many fish might the each of the people have caught?

Possible extending prompts are:

  • Find all the possible answers if the range is 6.

  • What if it was 6 people that went fishing? What different does that make?

  • What is the maximum number of fish that an individual person might have caught?

In summary, the lesson exemplifies the planning model in which it is designed to maximise the chances that the whole class can feel part of the learning community, there is a trajectory of challenging tasks, tasks have both enabling and extending prompts, and there is some attempt to be explicit about the pedagogies.

Conclusion

The (Australian) curriculum is written assuming schools and classrooms will be structured to maximise learning opportunity. This chapter has described specific challenges facing Australian schools and, in particular, the large within-school differences in achievement. It has argued that even though there are challenges associated with teaching both heterogeneous and homogeneous groups, it seems that homogeneous groupings have the potential to restrict the opportunity to learn of some students. It was also argued that it is not so much the method of grouping but the approach that teachers take to addressing diversity that ensures that the needs of all students are addressed. A teaching model was presented which is designed to address the diversity of preparedness, whatever the classroom grouping.