The Fuzzy Time-Cost Tradeoff Problem

Abstract

The time-cost tradeoff problem is a specific type of the project scheduling problem, which studies how to modify project activities so as to achieve the tradeoff between the completion time and the project cost. In real projects, the tradeoff between the project cost and the completion time, and the uncertainty of the environment are both considerable aspects for managers. In this chapter, three new fuzzy time-cost tradeoff models are proposed, in which credibility theory is applied to describe the uncertainty of activity durations. A searching method by integrating fuzzy simulation and genetic algorithm is developed to search quasi-optimal schedules under some decision-making criteria. The purpose of this work is to reveal how to obtain the optimal balance of the completion time and the project cost in fuzzy environments.

1 Introduction

The time-cost tradeoff problem studies how to modify project activities so as to achieve the tradeoff between the completion time and the project cost, which is a specific type of the project scheduling problem. Kelley (1961) first studied this type of the project scheduling problem, which also initiated the research on project scheduling problems. In the following years, the research on the time-cost tradeoff problem mainly focused on the deterministic cases (Phillips and Dessouky 1977; Siemens 1971). For solving the deterministic time-cost tradeoff problem, the common analytical methods are linear programming and dynamic programming (Butcher 1967; Talbot 1982). Besides, some heuristic algorithms, such as genetic algorithm (Azaron et al. 2005; Chua et al. 1997; Feng et al. 1997), have also been introduced.

Though most research work on the time-cost tradeoff problem assumes that the problem is always in some deterministic environment, the real world is full of nondeterministic factors. For instance, the project completion time may vary due to many external influence factors, such as the change of weather, the increase of productivity level, the use of additional manpower, etc. Hence, many recent studies introduced uncertain factors. Furthermore, Goldratt (1997) questioned the validity of deterministic environments in the project scheduling problem. The readers may refer to Charnes and Cooper (1962), Freeman (1960), Golenko-Ginzburg and Gonik (1997), and Ke and Liu (2005) to see the progress in stochastic project scheduling. In recent years, the stochastic time-cost tradeoff problem has also attracted many researchers’ interest. Wollmer (1985) discussed a stochastic linear time-cost tradeoff problem, in which some discrete random variables were introduced. Gutjahr et al. (2000) designed a modified stochastic branch-and-bound approach and applied it into a specific stochastic discrete time-cost tradeoff problem. Laslo (2003) described a stochastic critical-path-method time-cost tradeoff model, including four fundamental formulations of the model and several new ideas for formulating the relationships between time-cost tradeoffs. Zheng and Ng (2005) presented a new approach for a time-cost optimization model by integrating fuzzy set theory and the nonreplaceable front concept with genetic algorithms, where fuzzy set theory was introduced to model the managers’ prediction on activity durations and costs as well as the associated risk levels. Zahraie and Tavakolan (2009) embedded two concepts of time-cost tradeoff and resource leveling and allocation in a stochastic multiobjective optimization model, where fuzzy set theory was applied to represent different options for each activity. Ke et al. (2009) presented three stochastic time-cost tradeoff models to meet different practical optimization requirements.

Probability theory can be regarded as a tool for the description of objective uncertainty, while credibility theory , a new theory dealing with fuzziness, is a powerful instrument for treating with subjective uncertainty. In fact, the activities of some projects may have been processed many times before, and with historical data, the uncertainty of the activity durations can be described by probability distributions. While the activities of some other projects may be short of statistical data, the durations can be better described by fuzzy variables. Zadeh (1965) originally introduced the concept of fuzzy set to describe fuzzy phenomena via membership function. Zadeh (1978) proposed the concept of possibility measure for measuring a fuzzy event. Liu and Liu (2002) presented a self-dual credibility measure for measuring a fuzzy event, as possibility measure has no self-duality property, which is a very important property for most applications. Liu (2004) provided axiomatic foundation for credibility theory.

With the development of the research on fuzziness, fuzzy set theory was also applied to project scheduling problems, originally by Prade (1979). Furthermore, many other authors, such as Chanas and Kamburowski (1981), Kaufmann and Gupta (1988), and Ke and Liu (2010), discussed the fuzzy project scheduling problem. In recent years, the study focuses on the resource-constrained project scheduling under fuzzy environments, which was initiated in Hapke et al. (1994) and Hapke and Slowinski (1993, 1996). Wang (1999, 2002) developed a fuzzy beam search approach for solving product development project scheduling. Hapke and Slowinski (2000) applied simulated annealing to the resource-constrained project scheduling problem for solving some multi-objective cases. Özdamar and Alanya (2001) established a nonlinear mixed-binary mathematical model for software development projects with fuzzy activity duration times, in which four priority-based heuristics were used on some case study. Long and Ohsato (2008) performed a fuzzy critical chain method for fuzzy resource-constrained project scheduling problem.

To the knowledge of the authors, the first work on the fuzzy time-cost tradeoff problem was done by Leu et al. (2001). In Leu et al. (2001), the activity durations were characterized by fuzzy numbers due to environmental variation, and the fuzzy relationship between the activity duration and the activity cost was taken into account by membership function. Furthermore, the philosophy of chance-constrained programming , which was initiated by Charnes and Cooper (1959), was introduced as a decision-making approach. Jin et al. (2005) gave a GA-based fully fuzzy optimal time-cost tradeoff model, in which all parameters and variables were characterized by fuzzy numbers and an example in ship building scheduling was demonstrated. Eshtehardian et al. (2008) established a multi-objective fuzzy time-cost model, in which fuzzy logic theory was introduced to represent accepted risk levels. Ghazanfari et al. (2008) and Ghazanfari et al. (2009) applied possibilistic goal programming to the time-cost tradeoff problem to determine the optimal duration for each activity in the form of triangular fuzzy numbers. However, as we mentioned above, possibility measure does not have self-duality property, which is an important property in many applications. Especially, self-duality property is necessary for well defining the concept of expected value of stochastic event or fuzzy event, which is the most widely used decision-making criterion in optimization problems.

In this chapter, with the credibility theory of Liu (2004), some decision-making criteria will be proposed, and some fuzzy time-cost tradeoff models will be established, which is the main contribution of this study. In addition, a hybrid intelligent algorithm integrating fuzzy simulation and genetic algorithm (GA) will be designed to deal with the proposed fuzzy time-cost tradeoff models.

This chapter is organized as follows: In Sect. 42.2, the fuzzy time-cost tradeoff problem is described, in which some assumptions and some parameters are given to deduce the project completion time and the project cost. In Sect. 42.3, some important concepts of credibility theory are introduced and based on these concepts, three fuzzy models are proposed. Section 42.4 introduces a hybrid intelligent algorithm integrating fuzzy simulation and GA. Then we give some numerical examples to illustrate the effectiveness of the proposed algorithm in Sect. 42.5. Section 42.6 draws some conclusions.

2 Problem Description

For the change of the environment influencing the project, the activity durations might vary, and meanwhile the corresponding activity costs also change. For example, hiring more workers might accelerate the project execution process and consequently decrease the project duration and simultaneously increase the total project cost. Actually, in most real projects, the managers always need to take account of the tradeoff between the total project cost and the project completion time. It is naturally desirable for managers to find the most effective way to complete a project within some predetermined completion time limit and with the “minimal” cost in some sense, which is just what the time-cost tradeoff problem is about.

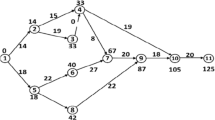
Generally, a project can be described by a directed acyclic graph as illustrated in Fig. 42.1. Let G = (V, E) be a directed acyclic graph with the activity-on-node (AoN) network structure representing a project, where $V =\{ 0,1,2,\ldots,n + 1\}$ is the set of nodes representing the activities of the project, and E is the set of arcs corresponding to the precedence relationships among the activities. Note that dummy activities 0 and n + 1 represent the beginning and completion of the project.

Fig. 42.1

Project network

First we introduce the parameter $\hat{p}_{i}$ as a fuzzy variable representing the normal duration of activity i, whose uncertainty is attributed to the variation of the external environment, and c _i as the normal cost per time unit of activity i, which is a constant. That is, $\hat{p}_{i}$ represents the duration of activity i without the influence of the decision made by the manager. The fuzzy normal activity durations are concisely written as $\hat{p} = (\hat{p}_{1},\hat{p}_{2},\ldots,\hat{p}_{n})$. The decision variable x _i , which is assumed to be an integer, represents the change of the duration of activity i, which may be due to some decisions of the manager, such as hiring more or less workers, applying better or worse instruments, etc. Owing to some practical conditions, the variable x _i is bounded by some interval $[x_{i}^{\mathit{min}},x_{i}^{\mathit{max}}]$, where $x_{i}^{\mathit{min}}$ and $x_{i}^{\mathit{max}}$ are assumed to be integers. Accordingly, for each activity i, there exists another associated cost d _i , which is the additional cost of per unit change of x _i and is also assumed to be a constant. Then our goal is to find the optimal vector $\boldsymbol{x} = (x_{1},x_{2},\ldots,x_{n})$ meeting some scheduling requirements.

We denote the starting time of activity i by $S_{i}(\boldsymbol{x},\hat{p})$ and the starting time of the project is assumed to be 0. For simplicity, we assume that each activity can be processed only if all the foregoing activities are finished, and it should be processed without interruption. With these assumptions, the starting time of activity j, j = 1, 2, …, n, can be determined by

$$\displaystyle{S_{j}(\boldsymbol{x},\hat{p}) =\max \limits _{(i,j)\in E}\left \{S_{i}(\boldsymbol{x},\hat{p}) +\hat{ p}_{i} + x_{i}\right \}}$$

and the completion time of the project can be calculated by

$$\displaystyle{ S_{n+1}(\boldsymbol{x},\hat{p}) =\max \limits _{(i,n+1)\in E}\left \{S_{i}(\boldsymbol{x},\hat{p}) +\hat{ p}_{i} + x_{i}\right \} }$$

(42.1)

Consequently, the total cost of the project is

$$\displaystyle{ C(\boldsymbol{x},\hat{p}) =\sum _{ i=1}^{n}(c_{ i}\hat{p}_{i} - d_{i}x_{i}) }$$

(42.2)

3 Fuzzy Models of Time-Cost Tradeoff Problem

3.1 Credibility Theory

Credibility theory, founded by Liu (2004), is a branch of mathematics for studying the behavior of fuzzy phenomena. In this subsection, we will introduce some basic concepts, which will be helpful for establishing some fuzzy models for the time-cost tradeoff problem . Let Θ be a nonempty set and $\mathcal{P}(\varTheta )$ be the power set of Θ.

Definition 42.1 (Liu and Liu 2002).

The set function Cr is called a credibility measure if it satisfies:

• (i) Cr{Θ} = 1.

• (ii) Cr{A} ≤ Cr{B} whenever A ⊂ B.

• (iii) $\mathrm{Cr}\{A\} +\mathrm{ Cr}\{A^{c}\} = 1$ for any $A \in \mathcal{P}(\varTheta )$, where A ^c represents the complement of set A.

• (iv) $\mathrm{Cr}\{ \cup _{i}A_{i}\} =\sup _{i}\mathrm{Cr}\{A_{i}\}$ for any A _i with $\sup _{i}\mathrm{Cr}\{A_{i}\} < 0.5$.

Next, we will introduce the concept of a credibility space, which will be used to define a fuzzy variable.

Definition 42.2 (Liu 2004).

Let Θ be a nonempty set, $\mathcal{P}(\varTheta )$ the power set of Θ, and Cr a credibility measure. Then the triplet $(\varTheta,\mathcal{P}(\varTheta ),\mathrm{Cr})$ is called a credibility space.

Definition 42.3 (Liu 2004).

A fuzzy variable is a function from a credibility space $(\varTheta,\mathcal{P}(\varTheta ),\mathrm{Cr})$ to the set of real numbers.

With the concept of fuzzy variable, we can define the membership function of a fuzzy variable.

Definition 42.4 (Liu 2004).

Let $\hat{z}$ be a fuzzy variable defined on the credibility space $(\varTheta,\mathcal{P}(\varTheta ),\mathrm{Cr})$. Then its membership function is derived from the credibility measure by

$$\displaystyle{\mu (z) = (2\mathrm{Cr}\{\hat{z} = z\}) \wedge 1\quad (z \in \mathbb{R})}$$

where ∧ is the minimum operator, i.e., for $a,b \in \mathbb{R}$, a ∧ b equals to the smaller one of a and b.

Actually, the credibility measure can also be derived from the membership function of a fuzzy variable, which is called the credibility inversion theorem.

Theorem 42.1 (Liu 2006a).

Let $\hat{z}$ be a fuzzy variable with membership function μ. Then for any set B of real numbers, we have

$$\displaystyle{\mathrm{Cr}\{\hat{z} \in B\} = \frac{1} {2}\left (\sup \limits _{z\in B}\mu (z) + 1 -\sup \limits _{z\in B^{c}}\mu (z)\right )}$$

For giving out some decision-making criteria for managers, we will introduce the following definitions:

Definition 42.5 (Liu and Liu 2002).

Let $\hat{z}$ be a fuzzy variable. The expected value of $\hat{z}$ is defined by

$$\displaystyle{E[\hat{z}] =\int _{ 0}^{+\infty }\mathrm{Cr}\{\hat{z} \geq r\}\mathrm{d}r -\int _{ -\infty }^{0}\mathrm{Cr}\{\hat{z} \leq r\}\mathrm{d}r}$$

provided that at least one of the above two integrals is finite.

Definition 42.6 (Liu 2002).

Let $\hat{z}$ be a fuzzy variable, and α ∈ (0, 1]. Then

$$\displaystyle{\hat{z}_{inf}(\alpha ) =\inf \left \{r\vert \mathrm{Cr}\{\hat{z} \leq r\} \geq \alpha \right \}}$$

is called the α-pessimistic value of $\hat{z}$.

3.2 α-Cost Minimization Model

The philosophy of chance-constrained programming (CCP) initiated by Charnes and Cooper (1959) is a useful decision-making approach, with which managers prefer satisfying some chance constraints with at least some given confidence levels. Liu and Iwamura (1998a,b) have studied several types of fuzzy CCP models. Based on the philosophy of fuzzy CCP, we can present a model as follows:

$$\displaystyle{\left \{\begin{array}{l} \text{Min.}\ \bar{C} \\ \text{s.t.}\ \ \ \ \mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq \alpha \\ \qquad \ \mathrm{Cr}\{S_{n+1}(\boldsymbol{x},\hat{p}) \leq d_{n+1}\} \geq \beta \\ \qquad \ x_{i} \in [x_{i}^{\mathit{min}},x_{i}^{\mathit{max}}]\quad (i = 1,2,\ldots,n) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,n)\end{array} \right.}$$

where α and β are predetermined confidence levels, d _n+1 is the due date of the project, $x_{i}^{\mathit{min}}$ and $x_{i}^{\mathit{max}}$ are integers given in advance, and $S_{n+1}(\boldsymbol{x},\hat{p})$ and $C(\boldsymbol{x},\hat{p})$ are defined by (42.1) and (42.2), respectively. The model is referred to as the α-cost minimization model, where the α-cost is defined by $\min \left \{\bar{C}\bigm |\mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq \alpha \right \}$.

3.3 Expected Cost Minimization Model

Comparing expected values is the most widely used decision-making criterion in practice. Managers, who are risk-averse, usually want to find the optimal decision with minimum expected project cost subject to some expected project completion time constraint. With this criterion, we can present the following expected cost minimization model:

$$\displaystyle{\left \{\begin{array}{l} \text{Min.}\ E[C(\boldsymbol{x},\hat{p})] \\ \text{s.t.}\ \ \ \ E[S_{n+1}(\boldsymbol{x},\hat{p})] \leq d_{n+1} \\ \qquad \ x_{i} \in [x_{i}^{\mathit{min}},x_{i}^{\mathit{max}}]\quad (i = 1,2,\ldots,n) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,n)\end{array} \right.}$$

where d _n+1 is the due date of the project, $x_{i}^{\mathit{min}}$ and $x_{i}^{\mathit{max}}$ are integers given in advance, and $S_{n+1}(\boldsymbol{x},\hat{p})$ and $C(\boldsymbol{x},\hat{p})$ are defined by (42.1) and (42.2), respectively.

3.4 Credibility Maximization Model

In practice, some project scheduling goals cannot be attained absolutely due to the uncertainty of the external environment. In that case, a realistic approach may be to maximize the chance of achieving the optimization goals, which corresponds to the philosophy of dependent-chance programming by Liu (1997, 1999). Following this approach, we can present the following credibility maximization model:

$$\displaystyle{\left \{\begin{array}{l} \text{Max.}\ \mathrm{Cr}\left \{C(\boldsymbol{x},\hat{p}) \leq b\right \} \\ \text{s.t.}\ \ \ \ \mathrm{Cr}\{S_{n+1}(\boldsymbol{x},\hat{p}) \leq d_{n+1}\} \geq \alpha \\ \qquad \ x_{i} \in [x_{i}^{\mathit{min}},x_{i}^{\mathit{max}}]\quad (i = 1,2,\ldots,n) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,n)\end{array} \right.}$$

where α is a predetermined confidence level, d _n+1 is the due date of the project, b is the budget, $x_{i}^{\mathit{min}}$ and $x_{i}^{\mathit{max}}$ are integers given in advance, and $S_{n+1}(\boldsymbol{x},\hat{p})$ and $C(\boldsymbol{x},\hat{p})$ are defined by (42.1) and (42.2), respectively.

4 Hybrid Intelligent Algorithm

In this section, we describe the design of a hybrid intelligent algorithm integrating fuzzy simulations and genetic algorithm for solving the above three models.

We have three types of fuzzy functions, i.e., $E[C(\boldsymbol{x},\hat{p})]$, $\mathrm{Cr}\left \{S_{n+1}(\boldsymbol{x},\hat{p}) \leq d_{n+1}\right \}$, and $\min \left \{\bar{C}\bigm |\mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq \alpha \right \}$, which are all to be estimated by fuzzy simulations. With the relationship between credibility measure and membership function shown in the credibility inversion theorem, the above three fuzzy functions can be formulated or estimated by the form of membership function. The detailed procedure of fuzzy simulations will be explained in this section. The theory and the application of fuzzy simulations can be found in Liu (2002) and Liu (2006b).

The first type of fuzzy functions is $E[C(\boldsymbol{x},\hat{p})]$. Let μ be the membership function of $\hat{p}$ and u _i the membership functions of $\hat{p}_{i}$, i = 1, 2, …, n, respectively. According to the concept of expected value of a fuzzy variable, the first type of fuzzy simulations can be performed as follows:

Algorithm 42.1: :

(Fuzzy Simulation for Expected Value)

Step 1.:

Set e = 0.

Step 2.:

Randomly generate $u_{1h},u_{2h},\ldots,u_{nh}$ from the $\varepsilon$-level sets of fuzzy variables $\hat{p}_{1},\hat{p}_{2},\ldots,\hat{p}_{n}$, and put $\boldsymbol{u}^{h}:= (u_{1h},u_{2h},\ldots,u_{nh})$, h = 1, 2, …, M, where $\varepsilon$ is a sufficiently small positive number and M is a sufficiently large number.

Step 3.:

Set $a = C(\boldsymbol{x},\boldsymbol{u}^{1}) \wedge C(\boldsymbol{x},\boldsymbol{u}^{2}) \wedge \cdots \wedge C(\boldsymbol{x},\boldsymbol{u}^{M})$, $b = C(\boldsymbol{x},\boldsymbol{u}^{1}) \vee C(\boldsymbol{x},\boldsymbol{u}^{2}) \vee \cdots \vee C(\boldsymbol{x},\boldsymbol{u}^{M})$.

Step 4.:

Randomly generate r from [a, b], and set $e:= e +\mathrm{ Cr}\{C(\boldsymbol{x},\hat{p}) \geq r\}$.

Step 5.:

Repeat the fourth step for N times, where N is a sufficiently large number.

Step 6.:

$E\left [C(\boldsymbol{x},\hat{p})\right ] = a + e \cdot (b - a)/N$.

The second type of fuzzy functions is credibility measure. According to the definition, the credibility can be obtained approximately by the following formula

$$\displaystyle\begin{array}{rcl} & & L = \frac{1} {2}\bigg(\max \limits _{1\leq k\leq N}\left \{\mu (\boldsymbol{u}^{k})\bigm |S_{ n+1}(\boldsymbol{x},\boldsymbol{u}^{k}) \leq d_{ n+1}\right \} {}\\ & & \qquad \qquad \left.+\min \limits _{1\leq k\leq N}\left \{1 -\mu (\boldsymbol{u}^{k})\bigm |S_{ n+1}(\boldsymbol{x},\boldsymbol{u}^{k}) > d_{ n+1}\right \}\right ) {}\\ \end{array}$$

Hence, the fuzzy simulation for credibility measure can be performed as follows:

Algorithm 42.2: :

(Fuzzy Simulation for Credibility Measure)

Step 1.:

Let k = 1.

Step 2.:

Randomly generate u _i from the $\varepsilon$-level sets of fuzzy variables $\hat{p}_{i}$, i = 1, 2, …, n, where $\varepsilon$ is a sufficiently small positive number.

Step 3.:

Set $\boldsymbol{u}^{k} = (u_{1},u_{2},\ldots,u_{n})$ and $\mu (\boldsymbol{u}^{k}) =\mu _{1}(u_{1}) \wedge \mu _{2}(u_{2}) \wedge \cdots \wedge \mu _{n}(u_{n})$.

Step 4.:

$k:= k + 1$. Turn back to Step 2 if k ≤ N, where N is a sufficiently large number, and else, go to Step 5.

Step 5.:

Return L.

The third type of fuzzy functions is $\min \left \{\bar{C}\bigm |\mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq \alpha \right \}$. In order to find the minimal $\bar{C}$ such that $\mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq \alpha$, we define

$$\displaystyle{L(r) = \frac{1} {2}\left (\max \limits _{1\leq k\leq N}\left \{\mu (\boldsymbol{u}^{k})\bigm |C(\boldsymbol{x},\boldsymbol{u}^{k}) \leq r\right \} +\min \limits _{ 1\leq k\leq N}\left \{1 -\mu (\boldsymbol{u}^{k})\bigm |C(\boldsymbol{x},\boldsymbol{u}^{k}) > r\right \}\right )}$$

Then the process of fuzzy simulation can be performed as follows:

Algorithm 42.3: :

(Fuzzy Simulation for α-Cost)

Step 1.:

Let k = 1.

Step 2.:

Randomly generate u _i from the $\varepsilon$-level sets of fuzzy variables $\hat{p}_{i}$, i = 1, 2, …, n, where $\varepsilon$ is a sufficiently small positive number.

Step 3.:

Set $\boldsymbol{u}^{k} = (u_{1},u_{2},\ldots,u_{n})$ and $\mu (\boldsymbol{u}^{k}) =\mu _{1}(u_{1}) \wedge \mu _{2}(u_{2}) \wedge \cdots \wedge \mu _{n}(u_{n})$.

Step 4.:

$k:= k + 1$. Turn back to Step 2 if k ≤ N, where N is a sufficiently large number, and else, go to Step 5.

Step 5.:

Find the minimal r satisfying L(r) ≥ α.

Step 6.:

Return r.

Subsequently, we embed the fuzzy simulations, which can simulate the above three types of uncertain functions, into GA to design a hybrid intelligent algorithm for searching quasi-optimal solutions for the fuzzy time-cost tradeoff models.

The procedure of the hybrid intelligent algorithm can be sketched as follows.

Algorithm 42.4: :

(Hybrid Intelligent Algorithm)

Step 1.:

Initialize σ _pop chromosomes, where the three types of fuzzy functions can be calculated and the feasibility can be checked by the proposed fuzzy simulations.

Step 2.:

Update the chromosomes by crossover and mutation operations, in which the feasibility of offsprings may also be checked by the proposed fuzzy simulations.

Step 3.:

Compute the objective values for all chromosomes and accordingly calculate the fitness of each chromosome.

Step 4.:

Select the chromosomes by spinning the roulette wheel.

Step 5.:

Run the second to fourth steps for a given number of cycles and report the best chromosome as the quasi-optimal solution.

Table 42.1 Fuzzy durations and costs of activities

5 Computational Results

Now let us consider a project as shown in Fig. 42.1. The durations, which are assumed as triangular fuzzy variables, the normal costs, and the additional costs of the activities in the project are listed in Table 42.1.

First, let us consider the following 0.90-cost minimization model:

$$\displaystyle{\left \{\begin{array}{l} \text{Min.}\ \bar{C} \\ \text{s.t.}\ \ \ \ \mathrm{Cr}\{C(\boldsymbol{x},\hat{p}) \leq \bar{ C}\} \geq 0.90 \\ \qquad \ \mathrm{Cr}\{S_{17}(\boldsymbol{x},\hat{p}) \leq 36\} \geq 0.90 \\ \qquad \ x_{i} \in [-3,3]\quad (i = 1,2,\ldots,16) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,16)\end{array} \right.}$$

The parameters of the algorithm, including the population size of one generation σ _pop , the probability of mutation ρ _mut , and the probability of crossover ρ _crs , will be set to different values to compare the different results. It can be seen from Table 42.2 that the “Δ _best ”s, calculated by the formula: (actual value−best value)/best value×100 %, do not exceed 0.88 %, which does not exceed the general project demand. Note that the “best value” here means the minimal value among the costs in Table 42.2.

Table 42.2 Computational results for the α-cost minimization model (α = 0. 90)

The second numerical experiment is about the expected cost minimization model. The manager may want to minimize the expected project cost with the expected project completion time limit as it is shown in the following expected cost minimization model:

$$\displaystyle{\left \{\begin{array}{l} \text{Min.}\ E[C(\boldsymbol{x},\hat{p})] \\ \text{s.t.}\ \ \ \ E[S_{17}(\boldsymbol{x},\hat{p})] \leq 34 \\ \qquad \ x_{i} \in [-3,3]\quad (i = 1,2,\ldots,16) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,16) \end{array} \right.}$$

The result comparison is shown in Table 42.3. As the maximal error is only 0.67 %, we can say that the proposed hybrid intelligent algorithm performs well on the expected cost minimization model.

Table 42.3 Computational results for the expected cost minimization model

The last model is the credibility maximization model. Suppose that the project budget is 17,800 and the project completion time limit is 36. With the philosophy of dependent-chance programming, the credibility maximization model can be established as follows:

$$\displaystyle{\left \{\begin{array}{l} \text{Max.}\ \mathrm{Cr}\left \{C(\boldsymbol{x},\hat{p}) \leq 17800\right \} \\ \text{s.t.}\ \ \ \ \mathrm{Cr}\{S_{17}(\boldsymbol{x},\hat{p}) \leq 36\} \geq 0.9 \\ \qquad \ x_{i} \in [-3,3]\quad (i = 1,2,\ldots,16) \\ \qquad \ x_{i} \in \mathbb{Z}\quad (i = 1,2,\ldots,16) \end{array} \right.}$$

The results of the credibility maximization model are shown in Table 42.4. The designed hybrid intelligent algorithm is stable for solving the model as all the errors do not exceed 1.18 %.

Table 42.4 Computational results for the credibility maximization model

6 Conclusions

The tradeoff between the project cost and the project completion time is an important issue for managers in real projects. In this chapter, we proposed three new fuzzy models: the α-cost minimization model, the expected cost minimization model, and the credibility maximization model of the time-cost tradeoff problem, in which the uncertainty of the activity durations was described by credibility theory. To solve the models, a hybrid intelligent algorithm integrating the fuzzy simulation and genetic algorithm was devised. The main contribution of this study is that we adopted credibility theory to establish a framework for the time-cost tradeoff problem with fuzzy factors, which can be studied more deeply in the future research.