Keywords

4.1 Introduction

4.1.1 Mathematical Modelling

Modelling a system is a Herculean task as the vast majority of systems which are studied, are extremely complex. A system may be open, i.e. the factors influencing it are numerous and are affected by the surroundings. Simpler to simulate are closed systems, in which, given justifiable assumptions, all components are precisely determinable. This type of system can be modelled with confidence and accuracy. This makes the identification of an exact problem more challenging. Hence, any attempt to model a system is founded on some inherent physical assumptions and some degree of simplification which makes the system theoretically “closed” and renders a robust formulation for the processes involved in the system practicable. We, therefore, make attempts to model a particular phenomenon of a system by initially ignoring the parameters with less influence on the phenomenon. The model is improved by gradually incorporating more and more parameters and applying advanced mathematical know-how, reinforced with experimentation and observation, where possible. Nevertheless, the parameters with meager effects remain neglected. The reliability of a model is dependent on the degree of exactness. Modelling is, therefore, a pragmatic attempt to simulate a reduced complexity and reality. In biological systems, such as transport processes in the human body [1] and external aerodynamics of natural fliers [2], mathematical modelling provides insights which may not be realizable with practical experimentation. In conjunction with computers, mathematical simulation in biology [3] now provides one of the most challenging, intriguing, and rewarding areas of scientific endeavour. In the same way that the twentieth century was the era of nuclear science and high-speed transport (aircraft, trains, automobiles and planetary exploration rovers) in which engineers mimicked and attempted to improve upon nature [4], the twenty-first century has emerged as a new frontier for biological modelling.

There has been a tremendous fusion of biologists, mathematicians, biomechanical engineers, biochemists and biophysicists, collectively focusing on resolving many types of problem at different scales [5]. In the same way that engineers mimicked biological mechanisms in the twentieth century (e.g. flight, naval propulsion, tensile structures), biology is now implementing “smart” technologies developed for astronautics, nanotechnology, microelectronics, lubrication technology (tribology), seismic bearings for bridge structures, etc. [6]. This transfer of engineering and scientific technology into medical and biological simulation has accelerated developments in many exciting and critical areas. Paramount among these has been the application of fluid mechanics to medical systems [7], i.e. biofluid mechanics. Blood is often termed the “fluid of life” and hemodynamics has received most attention from engineering scientists and mathematicians [8–11]. However, “biofluid mechanics” has infiltrated into a much wider spectrum of biomechanical problems. Excellent examples in this regard are hydroelastic flows mimicking marine swimmers [12], fish school group propulsion used to design optimal wind turbine farm layouts [13], mimicry of flapping wings for micro-unmanned air vehicles (mUAVs) [14], magnetic control of surgical extracorporeal blood flow circuits [15], hydroelastic vibration of inner ear membranes [16], peristaltic propulsion in the gastric system [17–19] and haemodialysis simulations [20–21]. Further, recent developments in the application of fluid mechanics to biomedical systems include viscous flow analysis of ophthalmic diseases [22], haematological purification devices [23], cerebrospinal flows [24], marine plankton dynamics [25], smart magnetic lubrication for prosthetics [26–27], larynx dynamics [28], biomagnetic response during astronaut re-entry [29–30], artificial heart-valve mechanics [31], and flows through capillaries and small blood vessels [32] and nasal ventilation aerodynamics [33]. Many of these applications have benefited from developments in chemical, aerospace, civil, mechanical, and computer engineering, and of course mathematics and physics. Numerical methods, applied mathematics, theoretical chemistry and physics, smart mechanics, laser Doppler anemometry (LDA), particle image velocimetry (PIV), lasers and computer science (imaging, scanning, simulation) are just some of the areas, which although originally developed to solve engineering problems have now found their way into the rapidly expanding domain of mathematical biosciences. The use of mathematical simulation in particular has resulted in garnering new insights into cerebral cortex formation, cancer spread, cartilage degeneration, epidemic disease prediction, pharmacology and even psychology. Many of these topics have utilized aspects of bio-fluid mechanics.

A particularly rich area which has emerged recently is that of nanotechnology, of which nano‐fluid [34] is an example. Nano‐fluids were developed by Choi [34] at the Argonne Energy Labs, Illinois in the 1990s. Applications have penetrated almost every area of engineering including rocket propellants, solar energy collectors, lubricant design, automotive and electronic cooling systems and medicine [35]. Coupled with this, many developments have taken place in micro-electromechanical systems and nano-systems including peristaltic pumps for medical applications [36]. In this discussion we, therefore, focus on recent progress in mathematical simulation of nano‐fluid propulsion by peristaltic mechanisms. This topic has immense applications in surgical exploration [37], drug delivery [38] hyperthermia cancer medication deployment [39], wound healing [40] and gastric pharmacological drug targeting [41, 42]. Recently the leading Swiss medical engineering corporation, Levitronix [43] has explored the fabrication of peristaltic nano‐fluid pumps for a range of pharmaceutical applications where the peristaltic transport mechanism has been shown to achieve maximum reliability, long life, and superior ability to pump precious fluids in the harshest of environments, compared with any other type of micropump. The drawbacks of nanoparticle agglomeration, dilution and dosing as well as filtration difficulties have now largely been eradicated in modern nano‐fluid peristaltic devices. This field is, therefore, very promising and will doubtlessly stimulate increased attention from the mathematical modelling community. We shall briefly review the mechanism of peristalsis, and then review the thermophysics and dynamics of nano‐fluids. Finally, a new model simulating double-diffusive pumping of nano‐fluids in peristaltic transport is presented with future recommendations for new simulations.

4.1.2 Peristaltic Transport

Peristalsis is a physiological mechanism (pumping process) in which physiological fluids are propelled (pumped) within living organs by contraction of circular smooth muscle behind the fluids and relaxation of circular smooth muscle ahead of it. Bayliss and Starling [44] historically first observed this phenomenon over a century ago. This type of pumping was first observed in physiology regarding:

  1. 1.

    Food movement in the digestive tract

  2. 2.

    Frine transportation from the kidney to the bladder through ureters

  3. 3.

    Semen movement in the vas deferens

  4. 4.

    Movement of lymphatic fluids in the lymphatic system

  5. 5.

    Bile flow from the gall bladder into the duodenum

  6. 6.

    Spermatozoa in the ductus efferent of the male reproductive tract

  7. 7.

    Ovum movement in the fallopian tube

  8. 8.

    Blood circulation in small blood vessels

Historically, however, the engineering analysis of peristalsis was initiated much later than physiological studies. A lucid summary of developments was presented by the modern “father of biomechanics” Fung in the early 1970s [45]. Latham [46] initiated modern fluid mechanics simulations of peristalsis using both theoretical and experimental techniques. Significant work was also reported by Shapiro and others [47] who delineated different zones for pumping. Fung and Yih [48] presented a model on peristaltic pumping using perturbation techniques. Burns and Parkes [49] studied the flow of Newtonian fluid through a channel and a tube by considering sinusoidal vibrations in the walls along the length. Barton and Raynor [50] studied the peristaltic motion in a circular tube by using long wavelength approximation for intestinal flow. Chaw [51] reported the solution for axisymmetric flow with initially nonstationary flow. Jaffrin [52] studied the effects of inertia and curvature on peristaltic pumping. Applications of peristalsis in industrial fluid mechanics usually involve peristaltic pumping of extremely hazardous liquids such as aggressive chemicals, high solids slurries, noxious fluid (nuclear industries), and other materials. Roller pumps, hose pumps, tube pumps, finger pumps, heart–lung machines, blood pump machines and dialysis machines are all engineered on the basis of peristalsis. In such applications and also medical flows, transport fluids are generally non-Newtonian. In recent years, therefore, researchers have developed new mathematical models utilizing a variety of viscoelastic rheological and microstructural models to simulate physiological fluids more accurately, demonstrating better correlation with clinical data than classical Newtonian viscous flow models, as examined in [45–52]. Relevant studies in this regard include Bohme and Fridrich [53] who employed a Walters-B model. Tsiklauri and Beresnew [54] used a Maxwell viscoelastic model. Tripathi [55] used Stokes’ couple‐stress models, and also employed fractional Maxwell models [56] and generalized Oldroyd-B viscoelastic models [57] to study peristaltic propulsion under various body forces. Hayat and others [58] have employed a Johnson–Segalman model to simulate elastic effects in peristaltic rheological flow. Tripathi and others [59] have also employed a Jeffery’s elasto-viscous model to investigate gastric flow and heat transfer in swallowing. Bég and others [60] have used the electrically conducting Williamson non-Newtonian model and also a differential transform algorithm to study peristaltic flow in a tube. Bhargava and others [61] have used a finite element method to study peristaltic waves in micropolar flow in a deformable conduit. Peristaltic nano‐fluid dynamics has also recently received some attention. We shall review works in this area in due course.

4.1.3 Nano‐Fluids

Nano‐fluids [34] are fluids containing nanoparticles (nanometer-sized particles of metals, oxides, carbides, nitrides or nanotubes). Nano-fluids exhibit enhanced thermal properties, notably higher thermal conductivity and convective heat transfer coefficients compared to the base fluid. Nano‐fluids are therefore a new class of fluids designed by dispersing nanometer-sized materials (nanoparticles, nanofibers, nanotubes, nanowires, nano-rods, nano-sheet, or droplets) in base fluids. They may also be regarded as nanoscale colloidal suspensions containing condensed nanomaterials. They are two-phase systems with one phase (solid phase) in another (liquid phase). Nano‐fluids have been found to also exhibit enhanced thermal diffusivity and viscosity compared to those of base fluids like oil or water. In many engineering simulations, including computational fluid dynamics (CFD), nano-fluids can be assumed to be single‐phase fluids. The classical theory of single‐phase fluids can be applied, where physical properties of nano-fluids are taken as a function of properties of both constituents and their concentrations. In recent years, a number of mathematical models have been proposed for nano-fluids. These have largely focused on the mechanism for thermal conductivity enhancement. A popular model is the Tiwari–Das [62] formulation, which has the advantage of not requiring a separate species diffusion equation for the nanoparticle volume fraction. This approach has been successfully utilized in a number of recent studies including Rashidi and others [63] for axisymmetric boundary layer flow from a cylinder with the homotopy analysis method and Bég and others [64] for transport in porous media. Rana and others [65] also very recently employed the Tiwari–Das model to simulate nano-fluid convection from an inclined cylindrical solar collector. Other models have also been developed aimed at further elucidating the properties of nano-fluids. Pre-eminent among these has been the Buongiorno model [66] in which multiple mechanisms are identified for the convective transport in nano-fluids using a two-phase nonhomogenous approach. In his two-component four-equation nonhomogeneous equilibrium model for mass, momentum, and heat transport in nano‐fluids, he emphasized the following mechanisms: inertia, Brownian diffusion, thermophoresis, diffusiophoresis, the Magnus effect, fluid drainage and gravity. Of all of these mechanisms, however, only Brownian diffusion and thermophoresis were found to be important in the absence of turbulence effects. It was also suggested that the boundary layer has different properties owing to the effect of temperature and thermophoresis. Taking Brownian motion and thermophoresis into account, Buongiorno [66] developed a correlation for the Nusselt number which was compared to the data from Xuan and Li [67] and Pak and Cho [68] and which correlated best with the latter [68] experimental data. The literature on the thermal conductivity and viscosity of nano-fluids has been reviewed by Eastman and others [69], Wang and Mujumdar [70] and Trisaksri and Wongwises [71]. In addition, a succinct review on applications and challenges of nano-fluids has also been provided by Wen and others [72] and Saidur and others [73]. Recently, the Buongiorno [66] model has been used by Kuznetsov and Nield [74] to study the natural convection flow of nano-fluid over a vertical plate and their similarity analysis identified four parameters governing the transport process. The Kuznetsov–Nield formulation has proved immensely popular in computational thermo-sciences. It has been deployed in many subsequent studies including double-diffusive free convection [75], Rayleigh–Benard nano‐fluid instability [76–79], tube nano‐fluid flows [80], boundary layers on translating sheets [81], vertical plate convection [82], nano-convection from a sphere in porous media [83], stagnation-point nano‐fluid flow in electronic components [84], unsteady radioactive hydromagnetic nano‐fluid materials processing [85], nano‐fluid flows in geothermal systems [86] and nano-fluid oxytactic bio-convection in hybrid microbial fuel cells [87]. These studies have all considered the nano‐fluid to be Newtonian. However, recently progress has also been made in non-Newtonian nano-fluid convection including simulations with an Ostwald–de Waele power law model [88]. The present discourse is restricted, however, to Newtonian nano-fluid dynamics, i.e. rheological features are discarded.

4.2 Mathematical Modelling

We now consider the peristaltic flow of a nano-fluid with double-diffusive convection in a deformable channel. A number of studies have appeared in the past few years on nano-fluid peristaltic fluid mechanics including endoscopic effects [89]. These works have generally employed the Kuznetsov–Nield model although the boundary conditions employed are debatable. Akbar and others [90] developed closed-form solutions for stream function and pressure gradient for the peristaltic flow of a nano-fluid in an asymmetric channel with wall slip effects, under long wavelength and small Reynolds number assumptions. Further studies include Akbar and others [91] who used the homotopy perturbation method to compute temperature and nanoparticle concentration for the effects of Brownian motion number, thermophoresis, local thermal Grashof number, and local nanoparticle Grashof number for five different peristaltic waves. They observed that pressure rise is reduced with increasing thermophoresis number whereas an increase in the Brownian motion parameter and the thermophoresis parameter enhances temperatures. Further studies include Mustafa and others [92] who considered viscous heating, Akbar and Nadeem [93] who used the Phan-Thien-Tanner rheological model for Jeffrey–Hamel nano-fluid peristaltic flow and Mustafa and others [94] who considered wall slip in nano-fluid peristaltic transport. In many drug-delivery applications [95] double-diffusive convection is significant. Thermal diffusion is the transport of the components of gaseous mixtures or solutions when subjected to a temperature gradient. If the temperature difference is held constant, thermal diffusion in a mixture will produce a concentration gradient. The production of such a gradient causes classical species diffusion. An excellent treatment of double-diffusion phenomena is provided by Gebhart and others [96]. These effects are also sometimes known as cross-diffusion effects or Soret–Dufour effects [97–99]. Very few investigations have been conducted on peristaltic pumping of nano-fluids with double‐diffusive (thermal and concentration) convection in nano-fluids. Therefore, this chapter aims to examine the peristaltic flow of nano-fluids with Soret–Dufour (double-diffusive) convection through a two-dimensional deformable channel. The analysis is performed under the well-established long wavelength and low Reynolds number approximations. A detailed mathematical formulation is presented and numerical computations reported. Mathematica software is employed to achieve visualization of the stream lines and trapping phenomenon. The influence of Brownian motion parameter, thermophoresis parameter, thermal Grashof number, concentration Grashof number, nanoparticle Grashof number, Soret parameter, Dufour parameter and peristaltic wave amplitude on nanoparticle fraction, temperature, pressure gradient, velocity and trapping are depicted.

4.2.1 Peristaltic Flow Geometry

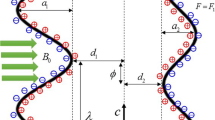
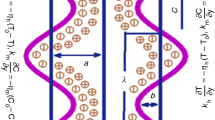
The constitutive equation for the peristaltic wall geometry due to propagation of a train of waves, considered in the present investigation, takes the form:

$$ \tilde{h}( \tilde{\xi },\tilde{t} )=a+b\sin \frac{2\pi }{\lambda }( \tilde{\xi }-c\tilde{t} ) $$
(4.1)

Here \(\tilde{h}{,}\tilde{\xi }{,}\tilde{t}{,}a{,}b{,}\lambda {,}\;\text{and}\;c\) represent transverse vibration of the wall, axial coordinate, time, half width of the channel, amplitude of the wave, wavelength, and wave velocity, respectively. The values of temperature (T), solute concentration (C) and nanoparticle fraction (F) at the centreline \(\eta =0\) and the wall of the channel \(\eta =h\) are taken as \({{T}_{0}}{,}{{C}_{0}}{,}{{F}_{0}}\;\text{and}\;{{T}_{1}}{,}{{C}_{1}}{,}{{F}_{1}}{,}\) respectively.

4.2.2 Governing Equations

Employing the Oberbeck–Boussinesq approximation, the governing equations for conservation of mass, momentum, thermal energy, solute concentration, and nanoparticle fraction [75] may be formulated thus:

$$ \frac{\partial \tilde{u}}{\partial \tilde{\xi }}+\frac{\partial \tilde{v}}{\partial \tilde{\eta }}=0, $$
(4.2)
$$ \begin{aligned}& {{\rho }_{\text{f}}}\left( \frac{\partial }{\partial \tilde{t}}+\tilde{u}\frac{\partial }{\partial \tilde{\xi }}+\tilde{v}\frac{\partial }{\partial \tilde{\eta }} \right)\,\tilde{u}=-\frac{\partial \tilde{p}}{\partial \tilde{\xi }}+\mu \left( \frac{{{\partial }^{2}}\tilde{u}}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}\tilde{u}}{\partial {{{\tilde{\eta }}}^{2}}} \right) \\& +[g( 1-{{F}_{0}} ){{\rho }_{\text{f0}}}\left\{ {{\beta }_{T}}( T-{{T}_{0}} )+{{\beta }_{C}}( C-{{C}_{0}} ) \right\}-( {{\rho }_{\text{p}}}-{{\rho }_{\text{f0}}} )( F-{{F}_{0}} )],\end{aligned} $$
(4.3)
$$ \begin{aligned}& {{\rho }_{\text{f}}}\left( \frac{\partial }{\partial \tilde{t}}+\tilde{u}\frac{\partial }{\partial \tilde{\xi }}+\tilde{v}\frac{\partial }{\partial \tilde{\eta }} \right)\,\tilde{v}=-\frac{\partial \tilde{p}}{\partial \tilde{\eta }}+\mu \left( \frac{{{\partial }^{2}}\tilde{v}}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}\tilde{v}}{\partial {{{\tilde{\eta }}}^{2}}} \right) \\& +g[ ( 1-{{F}_{0}} ){{\rho }_{\text{f0}}}\left\{ {{\beta }_{T}}( T-{{T}_{0}} )+{{\beta }_{C}}( C-{{C}_{0}} ) \right\}-( {{\rho }_{\text{p}}}-{{\rho }_{\text{f0}}} )( F-{{F}_{0}} ) ],\end{aligned} $$
(4.4)
$$ \begin{aligned}& {{(\rho c)}_{\text{f}}}\left( \frac{\partial }{\partial \tilde{t}}+\tilde{u}\frac{\partial }{\partial \tilde{\xi }}+\tilde{v}\frac{\partial }{\partial \tilde{\eta }} \right)\,T=k\left( \frac{{{\partial }^{2}}T}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{{\tilde{\eta }}}^{2}}} \right)+{{D}_{TC}}\left( \frac{{{\partial }^{2}}C}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}C}{\partial {{{\tilde{\eta }}}^{2}}} \right) \\& +{{(\rho c)}_{\text{p}}}\left\{ {{D}_{B}}\left( \frac{\partial F}{\partial \tilde{\xi }}\frac{\partial T}{\partial \tilde{\xi }}+\frac{\partial F}{\partial \tilde{\eta }}\frac{\partial T}{\partial \tilde{\eta }} \right)+\frac{{{D}_{T}}}{{{T}_{0}}}\left( {{\left( \frac{\partial T}{\partial \tilde{\xi }} \right)}^{2}}+{{\left( \frac{\partial T}{\partial \tilde{\eta }} \right)}^{2}} \right) \right\}\end{aligned} $$
(4.5)
$$ \left( \frac{\partial }{\partial \tilde{t}}+\tilde{u}\frac{\partial }{\partial \tilde{\xi }}+\tilde{v}\frac{\partial }{\partial \tilde{\eta }} \right)C={{D}_{S}}\left( \frac{{{\partial }^{2}}C}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}C}{\partial {{{\tilde{\eta }}}^{2}}} \right)+{{D}_{CT}}\left( \frac{{{\partial }^{2}}T}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{{\tilde{\eta }}}^{2}}} \right), $$
(4.6)
$$ \left( \frac{\partial }{\partial \tilde{t}}+\tilde{u}\frac{\partial }{\partial \tilde{\xi }}+\tilde{v}\frac{\partial }{\partial \tilde{\eta }} \right)F={{D}_{B}}\left( \frac{{{\partial }^{2}}F}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}F}{\partial {{{\tilde{\eta }}}^{2}}} \right)+\frac{{{D}_{T}}}{{{T}_{0}}}\left( \frac{{{\partial }^{2}}T}{\partial {{{\tilde{\xi }}}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{{\tilde{\eta }}}^{2}}} \right), $$
(4.7)

where \({{\rho }_{\textit f}},{{\rho }_{\textit p}},\tilde{u},\tilde{v},\tilde {\eta},\tilde{p},\mu ,g,{{\beta }_{T}},{{\beta }_{C}},{{(\rho c)}_{\textit f}},{{(\rho c)}_{\textit p}},k,T,F,C,{{D}_{B}},{{D}_{T}},{{D}_{S}},{{D}_{TC}}\,\text{and}\,{{D}_{CT}}\) denote the fluid density, nanoparticle mass density, axial velocity, transverse velocity, transverse coordinate, pressure, fluid viscosity, acceleration due to gravity, volumetric thermal expansion coefficient of the fluid, volumetric solute expansion coefficient of the fluid, heat capacity of fluid, effective heat capacity of nanoparticle, thermal conductivity, temperature, nanoparticle volume fraction, solute concentration, Brownian diffusion coefficient, thermophoretic diffusion coefficient, solute diffusivity of the porous medium, Dufour diffusivity and Soret diffusivity.

4.2.3 Non-Dimensionalization and Boundary Conditions

To facilitate analytical solutions, we introduce the following non-dimensional parameters:

$$\left. \begin{aligned} \xi = \frac{{\tilde \xi }}{\lambda},\,\,\,\eta = \frac{{\tilde \eta }}{a},\,\,\,t = \frac{{c\tilde t}}{\lambda },\,\,\,u = \frac{{\tilde u}}{c},\,\,v = \frac{{\tilde v}}{{c\delta }},\,\,\,p = \frac{{\tilde p{a^2}}}{{\mu c\lambda }},\,\,h = \frac{{\tilde h}}{a} = 1 + \phi \sin (2\pi \xi),\\\,\\\delta = \frac{a}{\lambda },\,\,\,\,\phi = \frac{b}{a},\, \,\nu = \frac{\mu }{{{\rho_{{\rm{f0}}}}}},\,\,\theta = \frac{{T - {T_0}}}{{{T_1} - {T_0}}},\,\,\gamma = \frac{{C - {C_0}}}{{{C_1} - {C_0}}}{,}\;\Phi = \frac{{F - {F_0}}}{{{F_1} - {F_0}}},\,\,\,{\mathop{\rm Re}\nolimits} = \frac{{{\rho _{\rm{f}}}ca}}{\mu },\\\,\,\\{P_r} = \frac{{\nu {{(\rho c)}_{\rm{f}}}}}{k}, G{r_{\rm{T}}} = \frac{{{\beta _T}\,g\,{a^3}(1 - {F_0})\,({T_1} - {T_0})}}{{{\nu ^2}}},G{r_{\rm{C}}} = \frac{{{\beta _C}\,g\,{a^3}(1 - {F_0})\,({C_1} - {C_0})}}{{{\nu ^2}}},\\G{r_{\rm{F}}} = \frac{{g\,{a^3}({\rho _{\rm{p}}} - {\rho _{{\rm{f0}}}})\,({F_1} - {F_0})}}{{{\rho _{{\rm{f0}}}}\,{\nu ^2}}},\, {N_b} = \frac{{{{(\rho c)}_{\rm{p}}}{D_B}({F_1} - {F_0})}}{k},\;\\{N_t} = \frac{{{{(\rho c)}_{\rm{p}}}{D_T}({T_1} - {T_0})}}{{k\,{T_0}}},{N_{TC}} = \frac{{{{(\rho c)}_{\rm{f}}}{D_{TC}}({C_1} - {C_0})}}{{k\,({T_1} - {T_0})}},{N_{CT}} = \frac{{{D_{CT}}({T_1} - {T_0})}}{{{D_S}\,({C_1} - {C_0})}}, \end{aligned} \right\}$$
(4.8)

where \(\delta ,\phi ,\nu ,\theta ,\,\gamma ,\,\Phi ,\operatorname{Re},\,G{{r}_{\text{T}}},\,G{{r}_{\text{C}}},\,G{{r}_{\text{F}}},\,{{P}_{r}},{{N}_{b}},\,{{N}_{t}},\,{{N}_{TC}},\;and\;{{N}_{CT}}\) are wave number, amplitude ratio, kinematic viscosity, dimensionless temperature, dimensionless solutal (species) concentration, rescaled nanoparticle volume fraction, Reynolds number, thermal Grashof number, solutal Grashof number, nanoparticle Grashof number, Prandtl number, Brownian motion parameter, thermophoresis parameter, Dufour parameter and Soret parameter, respectively. For low Reynolds number (Re→0) and long wavelength \(\lambda>>a\), Eqs. 4.2–4.7 reduce to:

$$ \frac{\partial u}{\partial \xi }+\frac{\partial v}{\partial \eta }=0, $$
(4.9)
$$ \frac{\partial p}{\partial \xi }=\frac{{{\partial }^{2}}u}{\partial {{\eta }^{2}}}+G{{r}_{\text{T}}}\theta +G{{r}_{\text{C}}}\gamma -G{{r}_{\text{F}}}\Phi ,\, $$
(4.10)
$$ \frac{\partial p}{\partial \eta }=0, $$
(4.11)
$$\frac{\partial p}{\partial \xi }=\frac{{{\partial }^{2}}u}{\partial {{\eta }^{2}}}+G{{r}_{T}}\theta +G{{r}_{C}}\gamma -G{{r}_{F}}\Phi ,\,$$
(4.12)
$$\frac{{{\partial }^{2}}\gamma }{\partial {{\eta }^{2}}}+{{N}_{CT}}\frac{{{\partial }^{2}}\theta }{\partial {{\eta }^{2}}}=0.$$
(4.13)
$$ \frac{{{\partial }^{2}}\Phi }{\partial {{\eta }^{2}}}+\frac{{{N}_{t}}}{{{N}_{b}}}\frac{{{\partial }^{2}}\theta }{\partial {{\eta }^{2}}}=0. $$
(4.14)

The following boundary conditions are prescribed:

$$ {{\left. \Phi\right|}_{\eta =0}}=0,\;{{\left. \Phi\right|}_{\eta =h}}=1,\,{{\left. \gamma\right|}_{\eta =0}}=0,\,{{\left. \gamma\right|}_{\eta =h}}=1,\,{{\left. \theta\right|}_{\eta =0}}=0,\,{{\left. \theta\right|}_{\eta =h}}=1,\,{{\left. \frac{\partial u}{\partial \eta } \right|}_{\eta =0}}=0,\,{{\left. u \right|}_{\eta =h}}=0. $$
(4.15)

4.2.4 Analytical Solutions

Integrating Eq. 4.13 twice, with respect to \(\eta \) and using the first and second boundary conditions of Eq. 4.15, the nanoparticle fraction field is obtained as follows:

$$ \Phi =\frac{{{N}_{t}}}{{{N}_{b}}}\left( \frac{{{e}^{-n\eta }}-1}{1-{{e}^{-nh}}} \right)+\left( \frac{{{N}_{b}}+{{N}_{t}}}{{{N}_{b}}} \right)\frac{\eta }{h}. $$
(4.16)

Double integrating Eq. 4.14 with respect to \(\eta \) and using the third and fourth boundary conditions of Eq. 4.15, the solute concentration field is obtained as:

$$ \gamma ={{N}_{CT}}\left( \frac{{{e}^{-n\eta }}-1}{1-{{e}^{-nh}}} \right)+( 1+{{N}_{CT}} )\frac{\eta }{h}. $$
(4.17)

Using Eqs. 4.16 and 4.17 in Eq. 4.12 and integrating it twice with respect to \(\eta \) and using the fifth and sixth boundary conditions of Eq. 4.15, the temperature field is obtained as follows:

$$ \theta =\left( \frac{{{e}^{-n\eta }}-1}{{{e}^{-nh}}-1} \right). $$
(4.18)

Using Eqs. 4.16–4.18 in Eq. 4.10 and integrating it with respect to \(\eta \) and using the seventh boundary condition of Eq. 4.15, the axial velocity gradient is obtained as follows:

$$ \frac{\partial u}{\partial \eta }=\frac{\partial p}{\partial \xi }\eta -A\left\{ \frac{{{e}^{-n\eta }}}{n}+\eta -\frac{1}{n} \right\}-\frac{B}{2}{{\eta }^{2}}, $$
(4.19)

where

$$A=\frac{1}{1-{{e}^{-nh}}}\left(G{{r}_{\text{T}}}-{{N}_{CT}}G{{r}_{C}}+\frac{{{N}_{t}}}{{{N}_{b}}}G{{r}_{\textit F}} \right),$$
(4.20)
$$B=\frac{1}{h}\left( (1+{{N}_{CT}})G{{r}_{C}}-\frac{{{N}_{b}}+{{N}_{t}}}{{{N}_{b}}}G{{r}_{\textit F}} \right),$$
(4.21)
$$ n=\frac{{{N}_{b}}+{{N}_{t}}}{( 1-{{N}_{TC}}{{N}_{CT}} )h}. $$
(4.22)

Integrating Eq. 4.19, and deploying the eighth boundary condition of Eq. 4.15, the axial velocity is then obtained as:

$$ u=\frac{1}{2}\frac{\partial p}{\partial \xi }( {{\eta }^{2}}-{{h}^{2}} )-A\left\{ \frac{1}{2}( {{\eta }^{2}}-{{h}^{2}} )-\frac{1}{{{n}^{2}}}( {{e}^{-n\eta }}-{{e}^{-nh}} )-\frac{1}{n}( \eta -h ) \right\}-\frac{B}{6}( {{\eta }^{3}}-{{h}^{3}} ), $$
(4.23)

4.2.5 Volumetric Flow Rate

The volumetric flow rate is given by integrating across the channel width:

$$ Q=\int\limits_{0}^{h}{ud\eta }. $$
(4.24)

Using Eq. 4.23 in Eq. 4.24 and solving the integral yields:

$$ Q=-\frac{{{h}^{3}}}{3}\frac{\partial p}{\partial \xi }-A\left\{ \frac{1}{{{n}^{3}}}( {{e}^{-nh}}(1+nh)-1 )+\frac{{{h}^{2}}}{2n}-\frac{{{h}^{3}}}{3} \right\}+\frac{B}{8}{{h}^{4}}. $$
(4.25)

Manipulating Eq. 4.25, the pressure gradient is obtained as:

$$ \frac{\partial p}{\partial \xi }=-\frac{3Q}{{{h}^{3}}}-A\left\{ \frac{3}{{{n}^{3}}{{h}^{3}}}( {{e}^{-nh}}(1+nh)-1 )+\frac{3}{2nh}-1 \right\}+\frac{3B}{8}h. $$
(4.26)

The transformations between a wave frame (\(\tilde{X},\tilde{Y}\)) moving with velocity \(c\) and the fixed frame \(( \tilde{\xi },\tilde{\eta } )\) are now introduced as follows:

$$ \tilde{X}=\tilde{\xi }-c\tilde{t},\;\tilde{Y}=\tilde{\eta },\;\tilde{U}=\tilde{u}-c,\;\tilde{V}=\tilde{v}, $$
(4.27)

where \((\tilde{U},\,\tilde{V})\) and \((\tilde{u},\tilde{v})\) are the velocity components in the wave and fixed frame, respectively.

The volumetric flow rate in the fixed frame is given by:

$$ Q=\int\limits_{0}^{h}{(U+1)dY}, $$
(4.28)

which, on integration, yields:

$$ Q=q+h. $$
(4.29)

Averaging volumetric flow rate along one time period, we have:

$$ \bar{Q}=\int\limits_{0}^{1}{Qdt}=\int\limits_{0}^{1}{(q+h)dt.} $$
(4.30)

Equation 4.30 yields:

$$ \bar{Q}=q+1=Q+1-h. $$
(4.31)

From Eq. 4.26 and Eq. 4.31, the pressure gradient is expressed in term of averaged flow rate as:

$$ \frac{\partial p}{\partial \xi }=-\frac{3(\bar{Q}-1+h)}{{{h}^{3}}}-A\left\{ \frac{3}{{{n}^{3}}{{h}^{3}}}( {{e}^{-nh}}(1+nh)-1 )+\frac{3}{2nh}-1 \right\}+\frac{3B}{8}h, $$
(4.32)

The pressure difference across one wavelength (Δp) is computed using:

$$ \Delta p=\int\limits_{0}^{1}{\frac{\partial p}{\partial \xi }d\xi ,} $$
(4.33)

Using Eq. 4.23 and the transformations of Eq. 4.27, the stream function in the wave frame (Cauchy–Riemann equations, that is, \(U=\frac{\partial \psi }{\partial \eta }\) and \(V=-\frac{\partial \psi }{\partial \xi }\)) is obtained as follows:

$$ \psi (\xi ,\eta )=\frac{1}{2}\frac{\partial p}{\partial \xi }\left( \frac{{{\eta }^{3}}}{3}-{{h}^{2}}\eta\right)-A\left\{ \frac{1}{{{n}^{2}}}\left( \frac{{{e}^{-n\eta }}}{n}+{{e}^{-nh}}\eta +\frac{1}{n} \right)+\frac{1}{2}\left( \frac{{{\eta }^{3}}}{3}-{{h}^{2}}\eta\right)-\frac{1}{n}\left( \frac{{{\eta }^{2}}}{2}-h\eta\right) \right\}-\frac{B}{6}\left( \frac{{{\eta }^{4}}}{4}-{{h}^{3}}\eta\right)-\eta . $$
(4.34)

4.3 Numerical Results and Discussion

Numerical and computational results of the mathematical model are discussed in this section. Mathematica is used to integrate the solutions due to the complicated definite integrals and plot (Figs. 4.1–4.7). The influences of the thermo-physical parameters characterizing double-diffusive convection in nano-fluids on the peristaltic flow patterns are also depicted.

Fig. 4.1
figure 1

Nanoparticle fraction profiles ϕ(η) at ϕ = 0.5, x = 1.0 for: a N t  = 1.0, N TC  = 0.1, N CT  = 0.1, N b  = 1.0, 2.0, 3.0, 4.0. b N b  =1.0, N TC  = 0.1 N CT  = 0.1,N t   = 1.0, 2.0, 3.0, 4.0. c N t  = 1.0, N b  = 1.0, N TC  = 0.1, N CT  = 0.1, 1.0, 2.0, 3.0. d N t  = 1.0, N b  = 1.0, N CT  = 0.1, N Tc  = 0.1, 1.0, 2.0, 3.0

Full size image

The effects of Brownian motion parameter (N b ), thermophoresis parameter (N t ), Soret parameter (N CT ) and Dufour parameter (N CT ) on nanoparticle fraction profile (\(\Phi (\eta )\)) are presented through the Figs. 4.1a–d. N b arises in both the dimensionless temperature and nanoparticle fraction conservation equations, i.e. Eqs. 4.12 and 4.14 in the mixed derivative term, \({{N}_{b}}(\partial \theta /\partial \eta )(\partial \Phi /\partial \eta )\) in the former, and the second order temperature derivative, \(( {{N}_{t}}/{{N}_{b}} )( {{\partial }^{2}}\theta /\partial {{\eta }^{2}} )\), in the latter. N b is a key parameter dictating the diffusion of nanoparticles. With an increase in Brownian motion parameter (N b), there is a strong reduction initially in nanoparticle fraction profile, \(\Phi (\eta )\). This effect is shown in Fig. 4.1a. The nano‐fluid is a two-phase fluid in nature and random movement of the suspended nanoparticles enhances energy exchange rates in the fluid but initially decreases nanoparticle concentrations in the flow regime. As dimensionless transverse coordinate, η, is increased there is change in the effect of the Brownian motion parameter-nanoparticle fraction (Φ) is distinctly increased with a divergence in profiles. Thermophoretic parameter (N t ) effects are depicted in Fig. 4.1b. A slight increase in \(\Phi (\eta )\) values is caused as N t from 1 to 4, for some distance from the channel centre line (η = 0); however, as η is further increased, there is a switch and thermophoresis is found to depress fraction ϕ values. As with the Brownian motion parameter, N t also features in both energy and nanoparticle fraction conservation Eqs. 4.12 and 4.14, respectively. Although it features in the same term in the latter as the N b parameter, in the former (Eq. 4.12) it appears in a separate term, consistent with the original formulation of Buongiornio [66] and Kuznetsov and Nield [74], viz \({{N}_{t}}{{(\partial \theta /\partial \eta )}^{2}}.\) Hence, nanoparticle fraction diffusion is found to be initially assisted by thermophoresis but subsequently opposed by it. This pattern is also consistent with macroscopic convection flows (non-nano‐fluids). The influence of Soret parameter (N CT ) and Dufour parameter (N TC ) on nanoparticle fraction (Φ) are provided in Figs. 4.1c and d.

When heat and mass transfer occur simultaneously in a moving fluid, an energy flux can be generated not only by temperature gradients but by composition gradients also. The energy flux caused by a composition gradient is termed the Dufour or diffusion-thermo effect. On the other hand, mass fluxes can also be created by temperature gradients and this embodies the Soret or thermal-diffusion effect. Such effects are significant when density differences exist in the flow regime. For example, when species are introduced at a surface in a fluid domain, with a different (lower) density than the surrounding fluid, both Soret (thermo-diffusion) and Dufour (diffuso-thermal) effects can become influential. Soret and Dufour effects are important for intermediate molecular weight fluids in coupled heat and mass transfer in fluid binary systems, often encountered in biophysical processes. N CT (Soret number) represents the effect of temperature gradients on mass (species) diffusion. N TC (Dufour number) simulates the effect of concentration gradients on thermal energy flux in the peristaltic flow domain. These parameters arise in the energy and species conservation equations, Eqs. 4.12 and 4.13, in the terms \({{N}_{TC}}( {{\partial }^{2}}\gamma /\partial {{\eta }^{2}} )\;and\,{{N}_{CT}}( {{\partial }^{2}}\theta /\partial {{\eta }^{2}} ),\) respectively.

However, they do not arise in the nanoparticle volume fraction (Eq. 4.14). As such both parameters will exert a minor role on Φ distributions. Inspection of Fig. 4.1c shows that a small decrease is induced in Φ by a strong increase in N CT from 0.1 to 3; subsequently there is, however, a marginal increase in Φ. An almost identical response is sustained by the nanoparticle volume fraction profiles with an increase in the Dufour number (N TC ).

Figures 4.2a–d show the concentration profile (\(\gamma (\eta )\)) for the effects of Brownian motion parameter (N b ), thermophoresis parameter (N t ), Soret parameter (N CT ) and Dufour parameter (N TC ). With increasing N b and N t , species concentration values are significantly reduced. A much more potent response is, however, observed with a change in Soret (N CT ) and Dufour (N TC ) parameters. Species concentration is found to be very strongly reduced with increasing Soret number (Fig. 4.2c) for some distance from the channel centre; with further distance from the channel centre, as we approach the periphery of the channel, this trend is noticeably reversed and thermo-diffusion is observed to accentuate concentration, i.e. enhance diffusion of the species. Figure 4.2d also confirms that Dufour number exerts a much weaker effect on species diffusion than the Soret effect, a slight reduction in concentration values is caused, and there is no significant alteration in the effect of Dufour number with transverse distance.

Fig. 4.2
figure 2

Concentration profiles γ(η) at ϕ = 0.5. x = 1.0 for: a N t  = 1.0, N TC  = 0.1, N CT  = 1.0, N b  = 1.0, 2.0, 3.0, 4.0. b N b  = 1.0, N TC  = 0.1, N CT  = 1.0 N t  = 1.0, 2.0, 3.0, 4.0. c N t  = 1.0, N b  = 1.0, N TC  = 0.1, N CT  = 0.1, 1.0, 2.0, 3.0. d N t  = 1.0, N b  = 1.0, N CT  = 0.1, N TC  = 0.1, 0.2, 0.3, 0.4

Full size image

Figures 4.3a–d illustrate the evolution of the temperature profile (\(\theta (\eta )\)) under the effects of Brownian motion parameter (N b ), thermophoresis parameter (N t ), Soret parameter (N CT ), and Dufour parameter (N TC ). A very different distribution of profiles is observed compared with the concentration profiles. Increasing Brownian motion parameter initially strongly elevates temperatures in the vicinity of the channel centreline; further away this effect is reversed. It is also apparent that with strong Brownian motion (N b  = 4.0) effects, temperature profile stabilizes and becomes approximately parallel, i.e. eventually becomes invariant with transverse distance; this effect is clearly visible in Fig. 4.3a. Parabolic trends are only retained at large η values for weak Brownian diffusion (N b  = 1.0). A similar evolution in temperature profiles is computed for the influence of thermophoresis parameter, N t , in Fig. 4.3b. With increasing Soret and Dufour numbers, the profiles for temperature are similar to those in Figs. 4.3a and b; however, they ascend more smoothly. The temperature is found to be enhanced both with Soret and Dufour numbers, initially; with further distance from the channel centre, both effects serve to reduce temperatures.

Fig. 4.3
figure 3

Temperature profiles θ(η) at ϕ = 0.5, x = 1.0 for: a N t  = 1.0, N TC  = 0.1, N CT  = 0.1, N b   = 1.0, 2.0, 3.0, 4.0. b N b   = 1.0, N TC   = 0.1, N CT  = 0.1, N t  = 1.0, 2.0, 3.0, 4.0. c N t  = 1.0, N b  = 1.0, N TC  = 0.1, N CT  = 0.1, 1.0, 2.0, 3.0. d N t  = 1.0, N b   = 1.0, N CT  = 0.1= N TC  = 0.1, 1.0, 2.0, 3.0

Full size image

Figures 4.4a–g illustrate the influence of Brownian motion parameter (N b ), thermophoresis parameter (N t ), Soret number (N CT ) Dufour number (N TC ) thermal Grashof number (Gr T ), concentration Grashof number (Gr C ), and nanoparticle Grashof number (Gr F ) on the axial velocity profile (u(η)) across the channel semi-width. Axial velocity, u, is generally negative for all Brownian motion parameters throughout the channel half-space defined by 0 ≤ η ≤ 1; flow reversal that is strong backflow is therefore taking place. Maximum velocities are always located at the channel centre, decaying smoothly to zero at the periphery (channel wall). Figure 4.4a indicates that an increase in Brownian motion parameter, N b , decreases magnitudes of the axial velocity, i.e. opposes backflow u values, therefore, become more positive. The flow is, therefore, actually decelerated with Brownian motion. A substantially different response is computed for the effect of thermophoresis parameter in Fig. 4.4b. At low N t value (= 1.0) negative axial velocity is observed; however, as N t is increased to 2 and then 3 and the maximum value of 4.0, velocity becomes positive, i.e. backflow is completely eliminated across the channel half-space. The profiles also descend for N t  > 1, from a maximum at the channel centre to a minimum at the channel wall. The rate of descent is also enhanced with greater thermophoresis parameter. There is an order of magnitude difference also in the values of axial velocity between Figs. 4.4a and b; velocities are much large in Fig. 4.4b. With increasing Soret number, velocities are caused to become more negative in Fig. 4.4c, i.e. flow deceleration is induced and backflow is accentuated. The contrary response is computed for increasing Dufour number in Fig. 4.4d, where velocities are found to become less negative, i.e. flow reversal is inhibited. The velocity magnitudes in Fig. 4.4c are evidently much greater than those in Fig. 4.4d. Figure 4.4e shows the effect of thermal Grashof number (Gr T ) on axial velocity distribution. This parameter arises in the momentum conservation equation (4.10), in the term, (Gr T θ). This parameter signifies the relative influence of thermal buoyancy force and viscous hydrodynamic force. For Gr T < 1, the peristaltic regime is dominated by viscous forces and vice versa for Gr T > 1. For the intermediate case of Gr T = 1 both thermal buoyancy and viscous forces are of the same order of magnitude, as described by Gebhart and others [96]. Velocity magnitudes are generally reduced with increasing thermal Grashof number. At low Gr T velocities are negative, i.e. back flow exists. However, for Gr T > 1, backflow is negated and a strong acceleration induced in the peristaltic axial flow. Figure 4.4f reveals that a similar response is induced by the concentration Grashof number, G rC however, there is still some minor backflow at Gr C  = 2; with larger concentration Grashof number as with thermal Grashof number, the backflow is completely eliminated and a strong acceleration achieved in the axial flow. Gr C represents the ratio of species buoyancy force to the viscous hydrodynamic force; it is the species diffusion analogy to thermal diffusion Grashof number. For the case where both forces are the same, i.e. Gr C  = 1, axial velocity magnitude is minimized. The same response is observed for thermal Grashof number. Figure 4.4g shows that increasing the nanoparticle Grashof number (Gr F ) exacerbates the axial velocity back flow, i.e. increases negative values.

Fig. 4.4
figure 4

Velocity profiles u(η) at ϕ = 0.5, ξ = 1.0, ∂p/∂ξ=1.0 for: a N t  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N b  =1, 2, 3, 4. b N b  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N t  =1, 2, 3, 4. c N b  = 1, N t  = 1, N TC  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N CT  = 1, 2, 3, 4. d N b  = 1, N t  = 1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N TC  = 1, 2, 3, 4. e N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr c  = 1, Gr F  = 1, Gr T  = 1, 2, 3, 4. f N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr T  = 1, Gr F  = 1, Gr c  = 1, 2, 3, 4. g N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr r  = 1, Gr c  = 1, Gr F  = 1, 2, 3, 4

Full size image

Figures 4.5a–g present the variation of pressure gradient \((\partial p/\partial \xi )\) with axial coordinate (\(\xi \)) under the influence of Brownian motion parameter (N b ), thermophoresis parameter (N t ), thermal Grashof number (Gr T ), concentration Grashof number (Gr C ), nanoparticle Grashof number (Gr F ). In all cases we have prescribed the wave amplitude and averaged volumetric flow rate as ϕ = 0.5, Ǭ = 0.5 respectively, which is characteristic of the actual physiological regimes as expounded in benchmark peristaltic studies by Shapiro and others [47]. In all profiles the strong periodic behaviour and fluctuations in pressure gradient caused by peristaltic motion are clearly visible. Effectively, Brownian motion is found to slightly enhance pressure gradient (Fig. 4.5a). A significantly greater accentuation in pressure gradient is generated with increasing thermophoresis parameter (Fig. 4.5b). Conversely, Soret number acts to strongly depress pressure gradient values, whereas there is a slight enhancement in them with increasing Dufour number. Thermal Grashof number is observed to depress pressure gradients, whereas the species (concentration) Grashof number and nanoparticle Grashof number distinctly enhance pressure gradients in the peristaltic flow regime in the channel. In all profiles the respective trends indicated above are consistent across all axial coordinate values.

Fig. 4.5
figure 5

Pressure gradient (∂p/∂ξ) vs. axial distance (ξ) at ϕ = 0.5, Ǭ = 0.5, a N t  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N b  =1, 2, 3, 4. b N b  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N t  =1, 2, 3, 4. c N b  = 1, N t  = 1, N TC  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N CT  = 1, 2, 3, 4. d N b  = 1, N t  = 1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N TC  = 1, 2, 3, 4. e N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr c  = 1, Gr F  = 1, Gr T  = 1, 2, 3, 4. f N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr T  = 1, Gr F  = 1, Gr c  = 1, 2, 3, 4. g N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr T  = 1, Gr c  = 1, Gr F  = 1, 2, 3, 4

Full size image

Figures 4.6a–g display the variation of pressure difference across one wavelength (Δp) with averaged flow rate (Ǭ) under the respective influences of Brownian motion parameter (N b ), thermophoresis parameter (N t ), thermal Grashof number (Gr T ), concentration Grashof number (Gr C ), nanoparticle Grashof number (Gr F ). Invariably linear distributions are observed. Three ranges of pumping are possible namely (a) Δp > 0, i.e. pumping region (b) Δp = 0 i.e. free pumping region, (c) Δp < 0, i.e. co-pumping region, and we have considered all three. Increasing Brownian motion parameter (N b ) reduces pressure difference, an effect which is clearly of significance in nano‐fluid drug-delivery systems. Conversely, increasing thermophoretic parameter (N t ) strongly increases the pressure difference. In both the cases this pattern is sustained for all values of averaged volume flow rate, Ǭ. In other words, in nano-peristaltic pumps, a pressure difference drop or rise can be maintained with increasing Brownian diffusion effect or increasing thermophoretic effect at all operating flow rates. Figures 4.6c and d show that increasing Soret number strongly decreases the pressure difference, whereas increasing Dufour number acts to slightly increase it. Figures 4.6e–g demonstrate that increasing thermal Grashof number, pressure gradient is curtailed, whereas it is strongly elevated with increasing species (concentration) Grashof number and nanoparticle Grashof number, for all flow rates. In all Figs. 4.6a–g, at higher volumetric flow rates pressure difference becomes negative.

Fig. 4.6
figure 6

Pressure difference across one wavelength (Δp) vs. averaged volume flow rate (Ǭ) at ϕ = 0.5 for: a N t  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N b  =0.1, 0.2, 0.3,0.4. b N b  = 1, N TC  = 0.1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N t  =1, 2, 3, 4. c N b  = 1, N t  = 1, N TC  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N CT  = 1, 2, 3, 4. d N b  = 1, N t  = 1, N CT  = 0.1, Gr T   = 1, Gr c  = 1, Gr F  = 1, N T  = 1, 2, 3, 4. e N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr c  = 1, Gr F  = 1, Gr T  = 1, 2, 3, 4. f Gr T  = 1, Gr F  = 1, N b  = 1, N t   = 1, N TC  = 0.1, N CT  = 0.1, Gr c  = 1, 2, 3, 4. g N b  = 1, N t  = 1, N TC  = 0.1, N CT   = 0.1, Gr T  = 1, Gr c  = 1, Gr F  = 1, 2, 3, 4

Full size image

Trapping is an inherent phenomenon of peristaltic motion in which an internally circulating bolus of fluid is formed by closed streamlines and this trapped bolus is pushed ahead along with the peristaltic wave. The effects of Brownian motion parameter (N b ), thermophoresis parameter (N t ), thermal Grashof number (Gr T ), concentration Grashof number (Gr C ), nanoparticle Grashof number (Gr F ) on streamlines and trapping phenomenon are therefore also depicted in Figs. 4.7(a–i). Nine streamline distributions are illustrated. A single parameter has been varied for each pair. In all cases, amplitude ratio (ϕ) is fixed at 0.5 and averaged volume flow rate, Ǭ constrained at 0.6. The streamlines on the centerline in the wave frame are found to compartmentalize under specific conditions in order to enclose a bolus of fluid particles circulating along closed streamlines. This phenomenon is known as trapping, which is a characteristic of peristaltic motion. Since this bolus appear to be trapped by the wave, the bolus moves with the same speed as that of the wave (celerity). Comparison of the appropriate figures shows that magnitude of trapped bolus clearly reduces with increasing the magnitude of different Grashof numbers. Brownian motion parameter decreasing acts to reduce the number of trapped boluses. With decreasing thermophoretic parameter, the magnitude of boluses is slightly enhanced. With decreasing thermal Grashof number, the bolus size is amplified. Increasing species Grashof number reduces the multiple bolus structure to a single bolus. Increasing species Grashof number, therefore, exerts a similar effect on streamlines and trapping to decreasing Brownian motion parameter (Figs. 7b and d). Nano‐fluid characteristics, therefore, undeniably exert a significant influence on peristaltic flow patterns. Where numbers of boluses are unchanged, the magnitudes are clearly affected by nano‐fluid dynamic characteristics. Conversely, there is very little influence detected for a change in Soret and Dufour parameters. Comparing Figs. 4.7b and 4.7h, where the Dufour parameter is increased from 1 to 3, or Figs. 4.7b and 4.7i, where the Soret parameter is increased, the streamline patterns are almost indistinguishable.

Fig. 4.7
figure 7figure 7

Streamlines in the wave frame at ϕ = 0.5, Ǭ = 0.6 and a N b  = 1, N t  = 0.1, N TC  = 0.1, N CT  = 1, Gr T   = 0, Gr c  = 0, Gr F  = 0. b N b  = 1, N t  = 0.1, N TC  = 0.1, N CT  = 1, Gr T   = 0.1, Gr c  = 1, Gr F  = 1. c N b  = 1, N t  = 0.1, N TC  = 0.1, N CT  = 1 Gr T   = 0.1, Gr c  = 1, Gr F  = 3. d N b  = 1, N t  = 0.1, N TC =0.1, N CT  = 1, Gr T   = 0.1, Gr c  = 3, Gr F  = 1. e N b  = 1, N t  = 0.1, N TC  = 0.1, N CT   = 1, Gr T  = 0.5, Gr c  = 1, Gr F  = 1. f N b  = 1, N t  =1, N TC  = 0.1, N CT  =1, Gr T  = 0.1, Gr c  = 1, Gr F  = 1. g N b  = 1, N t  = 0.1, N TC  = 0.1, N CT   = 1, Gr T  = 0.1, Gr c  = 1, Gr F  = 1. h N b  = 1, N t  = 0.1, N TC  = 0.1, N CT   = 3, Gr T  = 0.1, Gr c  = 1, Gr F  = 1. i N b  = 1, N t  = 0.1, N TC  = 0.5, N CT   = 1, Gr T  = 0.1, Gr c  = 1, Gr F  = 1

Full size image

4.4 Summary

In this chapter we have briefly reviewed the challenges and potential of mathematical modelling biofluid mechanics. The fundamentals of peristaltic transport and nano‐fluid dynamics have also been described qualitatively. A novel mathematical model has additionally been presented to simulate the influence of nano‐fluid and thermo-diffusive/diffuso-thermal characteristics on peristaltic heat and mass transfer in a two-dimensional axisymmetric channel, as a simulation of nano‐fluid peristaltic drug-delivery systems. The study has been motivated by applications in novel nano‐fluid pharmacological delivery. Numerical computations have shown that:

  1. a.

    Brownian and thermophoresis parameters exert a strong influence on nanoparticle fraction profile, ϕ(η) and temperature profile, θ(η).

  2. b.

    Axial velocity is strongly affected by Soret and Dufour parameters as is the species concentration distribution and temperature evolution through the channel.

  3. c.

    Pressure difference is increased weakly with Brownian motion, whereas it is very strongly enhanced with increasing thermophoresis parameter.

  4. d.

    Increasing Soret number considerably reduces the pressure gradient values, whereas increasing Dufour number slightly elevates pressure difference.

  5. e.

    Thermal Grashof number is observed to depress pressure gradients, whereas the species (concentration) Grashof number and nanoparticle Grashof number markedly elevate pressure gradients in the peristaltic flow regime.

  6. f.

    Streamline patterns illustrating the trapping of boluses are also found to be more strongly affected with Brownian and thermophoretic parameters and also all Grashof numbers (thermal, species, nanoparticle) than Soret and Dufour effects which exert almost a negligible influence on streamline profiles.